Analogue Gravitational Lensing in Bose-Einstein Condensates
Abstract
1. Introduction
2. Analogue Metric
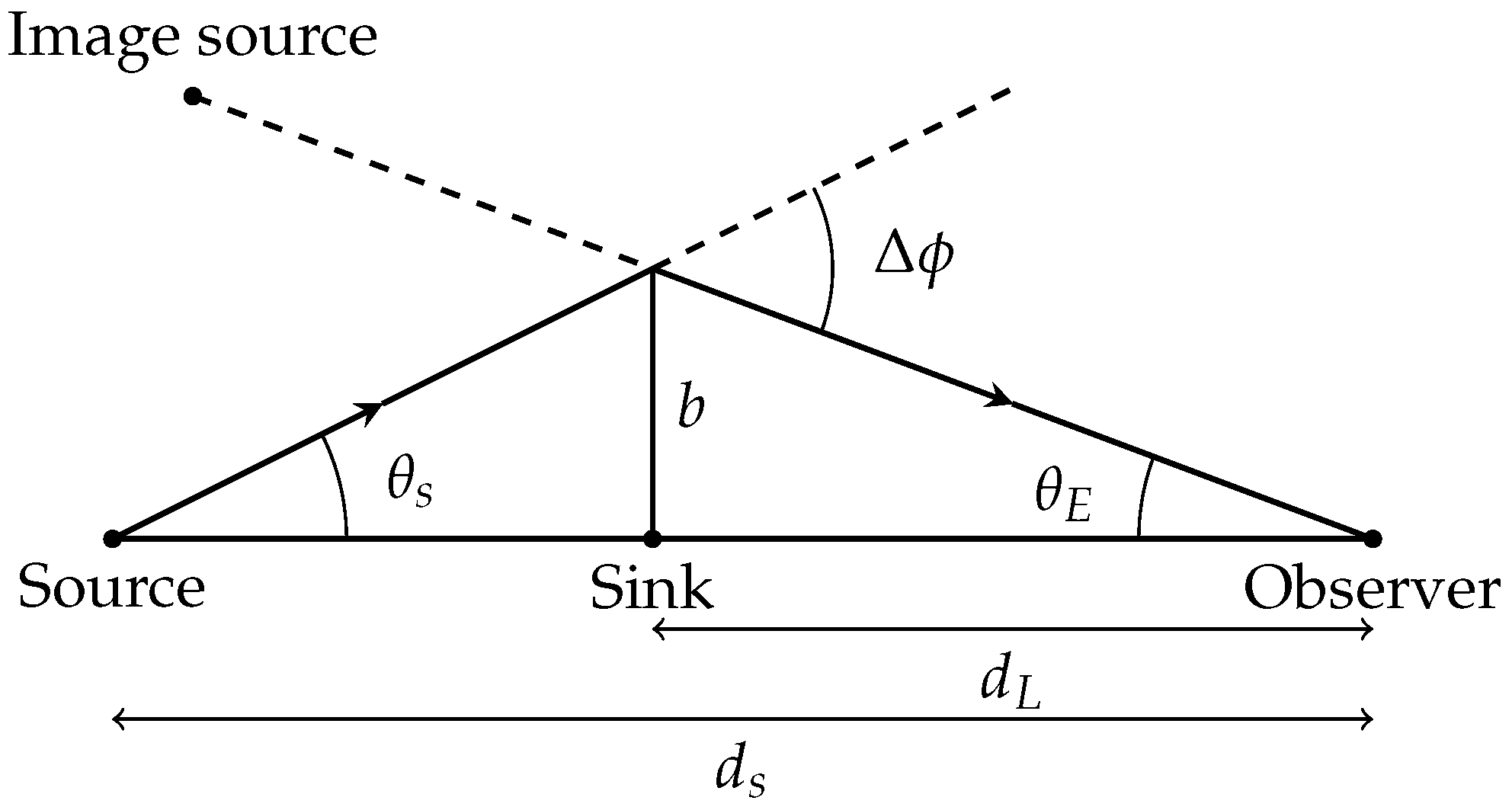
3. Analogue Gravitational Lensing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gordon, W. Zur Lichtfortpflanzung nach der Relativitätstheorie. Ann. Phys. 1923, 72, 421–456. [Google Scholar] [CrossRef]
- de Felice, F. On the gravitational field acting as an optical medium. Gen. Relativ. Gravit. 1971, 2, 347. [Google Scholar] [CrossRef]
- Unruh, W.G. Experimental black hole evaporation? Phys. Rev. Lett. 1981, 46, 1351. [Google Scholar] [CrossRef]
- Lahav, O.; Itah, A.; Blumkin, A.; Gordon, C.; Rinott, S.; Zayats, A.; Steinhauer, J. Realization of a sonic black hole analog in a Bose-Einstein condensate. Phys. Rev. Lett. 2010, 105, 240401. [Google Scholar] [CrossRef]
- Garay, L.J.; Anglin, J.R.; Cirac, J.I.; Zoller, P. Sonic analog of gravitational black holes in Bose-Einstein condensates. Phys. Rev. Lett. 2000, 85, 4643–4647. [Google Scholar] [CrossRef]
- Yatsuta, I.; Malomed, B. Yakimenko Acoustic analogue of Hawking radiation in quantized circular superflows of Bose-Einstein condensates. Phys. Rev. Res. 2020, 2, 043065. [Google Scholar] [CrossRef]
- Muñoz de Nova, J.R.; Golubkov, K.; Kolobov, V.I.; Steinhauer, J. Observation of thermal Hawking radiation and its temperature in an analogue black hole. Nature 2019, 569, 688. [Google Scholar] [CrossRef]
- Steinhauer, J. Observation of self-amplifying Hawking radiation in an analogue black-hole laser. Nat. Phys. 2014, 10, 864–869. [Google Scholar] [CrossRef]
- Steinhauer, J. Observation of quantum Hawking radiation and its entanglement in an analogue black hole. Nat. Phys. 2016, 12, 959–965. [Google Scholar] [CrossRef]
- Kolobov, V.I.; Golubkov, K.; Muñoz de Nova, J.R.; Steinhauer, J. Observation of stationary spontaneous Hawking radiation and the time evolution of an analogue black hole. Nat. Phys. 2021, 17, 362–367. [Google Scholar] [CrossRef]
- Steinhauer, J.; de Nova, J.R.M. Self-amplifying Hawking radiation and Its background: A numerical study. Phys. Rev. A 2017, 95, 033604. [Google Scholar] [CrossRef]
- Fedichev, P.O.; Fischer, U.R. Gibbons-Hawking effect in the sonic de Sitter space-time of an expanding Bose-Einstein-condensed gas. Phys. Rev. Lett. 2003, 91, 240407. [Google Scholar] [CrossRef]
- Fedichev, P.O.; Fischer, U.R. “Cosmological” quasiparticle production in harmonically trapped superfluid gases. Phys. Rev. A 2004, 69, 033602. [Google Scholar] [CrossRef]
- Eckel, S.; Kumar, A.; Jacobson, T.; Spielman, I.B.; Campbell, G.K. A rapidly expanding Bose-Einstein condensate: An expanding universe in the lab. Phys. Rev. X 2018, 8, 021021. [Google Scholar] [CrossRef]
- Vieira, H.S.; Destounis, K.; Kokkotas, K.D. Analog Schwarzschild black holes of Bose-Einstein condensates in a cavity: Quasinormal modes and quasibound states. Phys. Rev. D 2023, 107, 104038. [Google Scholar] [CrossRef]
- Balbinot, R.; Fabbri, A. Quantum correlations across the horizon in acoustic and gravitational black holes. Phys. Rev. D 2022, 105, 045010. [Google Scholar] [CrossRef]
- Rousseaux, G.; Mathis, C.; Maïssa, P.; Philbin, T.G.; Leonhardt, U. Observation of negative-frequency waves in a water tank: A classical analogue to the Hawking effect? New J. Phys. 2008, 10, 053015. [Google Scholar] [CrossRef]
- Weinfurtner, S.; Tedford, E.W.; Penrice, M.C.J.; Unruh, W.G.; Lawrence, G.A. Measurement of stimulated Hawking emission in an analogue system. Phys. Rev. Lett. 2011, 106, 021302. [Google Scholar] [CrossRef]
- Peloquin, C.; Euvé, L.-P.; Philbin, T.; Rousseaux, G. Analog wormholes and black hole laser effects in hydrodynamics. Phys. Rev. D 2016, 93, 084032. [Google Scholar] [CrossRef]
- Torres, T.; Patrick, S.; Coutant, A.; Richartz, M.; Tedford, E.W.; Weinfurtner, S. Rotational superradiant scattering in a vortex flow. Nat. Phys. 2017, 13, 833–836. [Google Scholar] [CrossRef]
- Chakraborty, C.; Majumdar, P. Spinning gyroscope in an acoustic black hole: Precession effects and observational aspects. Eur. Phys. J. C 2020, 80, 493. [Google Scholar] [CrossRef]
- Sheng, C.; Liu, H.; Wang, Y.; Zhu, S.N.; Genov, D.A. Trapping light by mimicking gravitational lensing. Nat. Photon. 2013, 7, 902–906. [Google Scholar] [CrossRef]
- Tinguely, R.A.; Turner, A.P. Optical analogues to the equatorial Kerr–Newman black hole. Commun. Phys. 2020, 3, 120. [Google Scholar] [CrossRef]
- Bekenstein, R.; Kabessa, Y.; Sharabi, Y.; Tal, O.; Engheta, N.; Eisenstein, G.; Agranat, A.J.; Segev, M. Control of light by curved space in nanophotonic structures. Nat. Photon. 2017, 11, 664–670. [Google Scholar] [CrossRef]
- Drori, J.; Rosenberg, Y.; Bermudez, D.; Silberberg, Y.; Leonhardt, U. Observation of stimulated Hawking radiation in an optical analogue. Phys. Rev. Lett. 2019, 122, 010404. [Google Scholar] [CrossRef]
- Sheng, C.; Liu, H.; Chen, H.; Zhu, S. Definite photon deflections of topological defects in metasurfaces and symmetry-breaking phase transitions with material loss. Nat. Commun. 2018, 9, 4271. [Google Scholar] [CrossRef]
- Zhong, F.; Li, J.; Liu, H.; Zhu, S. Controlling surface plasmons through covariant transformation of the spin-dependent geometric phase between curved metamaterials. Phys. Rev. Lett. 2018, 120, 243901. [Google Scholar] [CrossRef]
- Brevik, I. Spacelike Character of the Minkowski Four-Momentum in Analog Gravity. Phys. Rev. A 2019, 100, 032109. [Google Scholar] [CrossRef]
- Brevik, I. Classical and quantal aspects of Minkowski’s four-momentum in analog gravity. Phys. Rev. A 2020, 102, 052201. [Google Scholar] [CrossRef]
- Jannes, G.; Maïssa, P.; Philbin, T.G.; Rousseaux, G. Hawking radiation and the boomerang behaviour of massive modes near a horizon. Phys. Rev. D 2011, 83, 104028. [Google Scholar] [CrossRef]
- Roldán-Molina, A.; Nunez, A.S.; Duine, R.A. Magnonic black holes. Phys. Rev. Lett. 2017, 118, 061301. [Google Scholar] [CrossRef] [PubMed]
- Basak, S.; Majumdar, P. Superresonance from a rotating acoustic black hole. Class. Quantum Grav. 2003, 20, 3907–3913. [Google Scholar] [CrossRef]
- Balbinot, R.; Fagnocchi, S.; Fabbri, A.; Procopio, G.P. Backreaction in acoustic black holes. Phys. Rev. Lett. 2005, 94, 161302. [Google Scholar] [CrossRef] [PubMed]
- Patrick, S.; Goodhew, H.; Gooding, C.; Weinfurtner, S. Backreaction in an analogue black hole experiment. Phys. Rev. Lett. 2021, 126, 041105. [Google Scholar] [CrossRef]
- Finazzi, S.; Liberati, S.; Sindoni, L. Cosmological constant: A lesson from Bose-Einstein condensates. Phys. Rev. Lett. 2012, 108, 071101. [Google Scholar] [CrossRef]
- Volovik, G.E. The Universe in a Helium Droplet; Oxford University Press: Oxford, UK, 2003; ISBN 978-0-19-850782-6. [Google Scholar]
- Barcelo, C.; Visser, M.; Liberati, S. Einstein Gravity as an emergent phenomenon? Int. J. Mod. Phys. D 2001, 10, 799. [Google Scholar] [CrossRef]
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Dyson, F.W.; Eddington, A.S.; Davidson, C. A determination of the deflection of light by the sun’s gravitational field, from observations made at the total eclipse of 29 May 1919. Philos. Trans. R. Soc. Lond. A 1920, 220, 291. [Google Scholar]
- Bartelmann, M. Gravitational lensing. Class. Quantum Grav. 2010, 27, 233001. [Google Scholar] [CrossRef]
- Chakraborty, C. Gravitational analog of Faraday rotation in the magnetized Kerr and Reissner-Nordström spacetimes. Phys. Rev. D 2022, 105, 064072. [Google Scholar] [CrossRef]
- Fischer, U.R.; Visser, M. Riemannian geometry of irrotational vortex acoustics. Phys. Rev. Lett. 2002, 88, 110201. [Google Scholar] [CrossRef]
- Fischer, U.R.; Visser, M. On the space-time curvature experienced by quasiparticle excitations in the Painlevé–Gullstrand effective geometry. Ann. Phys. 2003, 304, 22–39. [Google Scholar] [CrossRef]
- Leggett, A.J. Bose-Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307–356. [Google Scholar] [CrossRef]
- Klaers, J.; Vewinger, F.; Weitz, M. Thermalization of a two-dimensional photonic gas in a ’white wall’ photon box. Nat. Phys. 2010, 6, 512. [Google Scholar] [CrossRef]
- Klaers, J.; Schmitt, J.; Vewinger, F.; Weitz, M. Bose–Einstein condensation of photons in an optical microcavity. Nature 2010, 468, 545–548. [Google Scholar] [CrossRef]
- Liao, L.; van der Wurff, E.C.I.; van Oosten, D.; Stoof, H.T.C. Proposal for an analog Schwarzschild black hole in condensates of light. Phys. Rev. A 2019, 99, 023850. [Google Scholar] [CrossRef]
- Nyman, R.A.; Szymańska, M.H. Interactions in dye-microcavity photon condensates and the prospects for their observation. Phys. Rev. A 2014, 89, 033844. [Google Scholar] [CrossRef]
- Kneer, B.; Wong, T.; Vogel, K.; Schleich, W.P.; Walls, D.F. Generic model of an atom laser. Phys. Rev. A 1998, 58, 4841–4853. [Google Scholar] [CrossRef]
- Solnyshkov, D.D.; Leblanc, C.; Koniakhin, S.V.; Bleu, O.; Malpuech, G. Quantum analogue of a Kerr black hole and the Penrose effect in a Bose-Einstein condensate. Phys. Rev. B 2019, 99, 214511. [Google Scholar] [CrossRef]
- Jacquet, M.J.; Boulier, T.; Claude, F.; Maître, A.; Cancellieri, E.; Adrados, C.; Amo, A.; Pigeon, S.; Glorieux, Q.; Bramati, A.; et al. Polariton fluids for analogue gravity physics. Phil. Trans. R. Soc. A 2020, 378, 20190225. [Google Scholar] [CrossRef]
- Brazhnyi, V.A.; Konotop, V.V.; Pérez-García, V.M.; Ott, H. Dissipation-induced coherent structures in Bose-Einstein condensates. Phys. Rev. Lett. 2009, 102, 144101. [Google Scholar] [CrossRef]
- Arecchi, F.T.; Bragard, J.; Castellano, L.M. Dissipative dynamics of an open Bose Einstein condensate. Opt. Commun. 2000, 179, 149–156. [Google Scholar] [CrossRef]
- Alperin, S.N.; Berloff, N.G. Multiply charged vortex states of polariton condensates. Optica 2021, 8, 301–307. [Google Scholar] [CrossRef]
- Carusotto, I.; Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299–366. [Google Scholar] [CrossRef]
- Klaers, J.; Schmitt, J.; Damm, T.; Vewinger, F.; Weitz, M. Bose–Einstein condensation of paraxial light. Appl. Phys. B 2011, 105, 17. [Google Scholar] [CrossRef][Green Version]
- Walker, B.T.; Flatten, L.C.; Hesten, H.J.; Mintert, F.; Hunger, D.; Trichet, A.A.P.; Smith, J.M.; Nyman, R.A. Driven-dissipative non-equilibrium Bose–Einstein condensation of less than ten photons. Nat. Phys. 2018, 14, 1173–1177. [Google Scholar] [CrossRef]
- Gross, E.P. Structure of a quantized vortex in boson systems. Nuovo C. 1961, 20, 454–477. [Google Scholar] [CrossRef]
- Pitaevskii, L.P. Vortex lines in an imperfect Bose gas. Sov. Phys. JETP 1961, 13, 451. [Google Scholar]
- Garay, L.J.; Anglin, J.R.; Cirac, J.I.; Zoller, P. Sonic black holes in dilute Bose-Einstein condensates. Phys. Rev. A 2001, 63, 023611. [Google Scholar] [CrossRef]
- Bilić, N. Analog Schwarzschild-like geometry in fluids with external pressure. Phys. Rev. D 2022, 105, 064052. [Google Scholar] [CrossRef]
- de Oliveira, C.C.; Mosna, R.A.; Pitelli, J.P.M.; Richartz, M. Analogue models for Schwarzschild and Reissner-Nordström spacetimes. Phys. Rev. D 2021, 104, 024036. [Google Scholar] [CrossRef]
- Visser, M. Acoustic black holes: Horizons, ergospheres and Hawking radiation. Class. Quantum Grav. 1998, 15, 1767–1791. [Google Scholar] [CrossRef]
- Barceló, C.; Liberati, S.; Visser, M. Analogue gravity. Living Rev. Relativ. 2011, 14, 3. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, T. Gravitation: Foundations and Frontiers; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-511-80778-7. [Google Scholar]
- Dolan, S.R.; Oliveira, E.S.; Crispino, L.C.B. Aharonov–Bohm effect in a draining bathtub vortex. Phys. Lett. B 2011, 701, 485–489. [Google Scholar] [CrossRef]
- Torres, T.; Patrick, S.; Richartz, M.; Weinfurtner, S. Analogue black hole spectroscopy; or, how to listen to dumb holes. Class. Quantum Grav. 2019, 36, 194002. [Google Scholar] [CrossRef]
- Dolan, S.R.; Oliveira, E.S. Scattering by a draining bathtub vortex. Phys. Rev. D 2013, 87, 124038. [Google Scholar] [CrossRef]
- Dempsey, D.; Dolan, S.R. Waves and null congruences in a draining bathtub. Int. J. Mod. Phys. D 2016, 25, 1641004. [Google Scholar] [CrossRef]
- Torres, T.; Coutant, A.; Dolan, S.; Weinfurtner, S. Waves on a vortex: Rays, rings and resonances. J. Fluid Mech. 2018, 857, 291–311. [Google Scholar] [CrossRef]
- Barontini, G.; Labouvie, R.; Stubenrauch, F.; Vogler, A.; Guarrera, V.; Ott, H. Controlling the dynamics of an open many-body quantum system with localized dissipation. Phys. Rev. Lett. 2013, 110, 035302. [Google Scholar] [CrossRef]
- Döring, D.; Dennis, G.R.; Robins, N.P.; Jeppesen, M.; Figl, C.; Hope, J.J.; Close, J.D. Pulsed pumping of a Bose-Einstein condensate. Phys. Rev. A 2009, 79, 063630. [Google Scholar] [CrossRef]
- Wertz, E.; Ferrier, L.; Solnyshkov, D.D.; Johne, R.; Sanvitto, D.; Lemaître, A.; Sagnes, I.; Grousson, R.; Kavokin, A.V.; Senellart, P.; et al. Spontaneous formation and optical manipulation of extended polariton condensates. Nat. Phys. 2010, 6, 860–864. [Google Scholar] [CrossRef]
- Sanvitto, D.; Pigeon, S.; Amo, A.; Ballarini, D.; De Giorgi, M.; Carusotto, I.; Hivet, R.; Pisanello, F.; Sala, V.G.; Guimaraes, P.S.S.; et al. All-optical control of the quantum flow of a polariton condensate. Nat. Photon. 2011, 5, 610. [Google Scholar] [CrossRef]
- Ozeri, R.; Katz, N.; Steinhauer, J.; Davidson, N. Colloquium: Bulk Bogoliubov excitations in a Bose-Einstein condensate. Rev. Mod. Phys. 2005, 77, 187–205. [Google Scholar] [CrossRef]
- Piekarski, C.; Liu, W.; Steinhauer, J.; Giacobino, E.; Bramati, A.; Glorieux, Q. Measurement of the static structure factor in a paraxial fluid of light using Bragg-like spectroscopy. Phys. Rev. Lett. 2021, 127, 023401. [Google Scholar] [CrossRef]
- Claude, F.; Jacquet, M.J.; Usciati, R.; Carusotto, I.; Giacobino, E.; Bramati, A.; Glorieux, Q. High-resolution coherent probe spectroscopy of a polariton quantum fluid. Phys. Rev. Lett. 2022, 129, 103601. [Google Scholar] [CrossRef]
- Claude, F.; Jacquet, M.J.; Carusotto, I.; Glorieux, Q.; Giacobino, E.; Bramati, A. Spectrum of collective excitations of a quantum fluid of polaritons. Phys. Rev. B 2023, 107, 174507. [Google Scholar] [CrossRef]
- de Leeuw, A.-W.; van der Wurff, E.C.I.; Duine, R.A.; van Oosten, D.; Stoof, H.T.C. Theory for Bose-Einstein condensation of light in nanofabricated semiconductor microcavities. Phys. Rev. A 2016, 94, 013615. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, D.; Jia, C.; Solano, E.; Céleri, L.C. Analogue Gravitational Lensing in Bose-Einstein Condensates. Universe 2023, 9, 443. https://doi.org/10.3390/universe9100443
Ma D, Jia C, Solano E, Céleri LC. Analogue Gravitational Lensing in Bose-Einstein Condensates. Universe. 2023; 9(10):443. https://doi.org/10.3390/universe9100443
Chicago/Turabian StyleMa, Decheng, Chenglong Jia, Enrique Solano, and Lucas Chibebe Céleri. 2023. "Analogue Gravitational Lensing in Bose-Einstein Condensates" Universe 9, no. 10: 443. https://doi.org/10.3390/universe9100443
APA StyleMa, D., Jia, C., Solano, E., & Céleri, L. C. (2023). Analogue Gravitational Lensing in Bose-Einstein Condensates. Universe, 9(10), 443. https://doi.org/10.3390/universe9100443





