Axionic Dark Matter in a Bi-Metric Universe
Abstract
:1. Introduction
2. A Review on Barotropic Matter and Dark Matter in the Two-Scale Factor Universe
3. Axionic Dark Matter
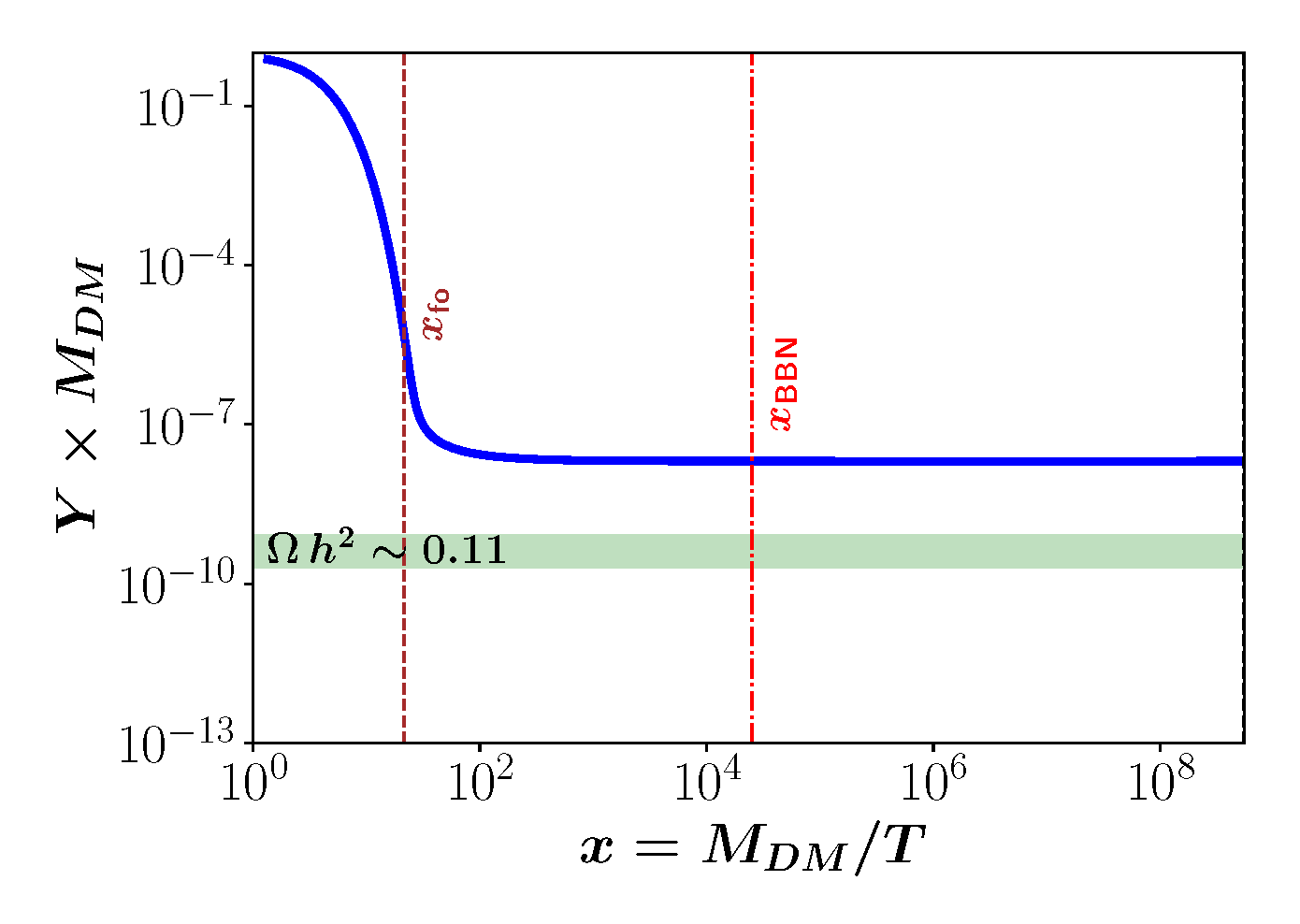
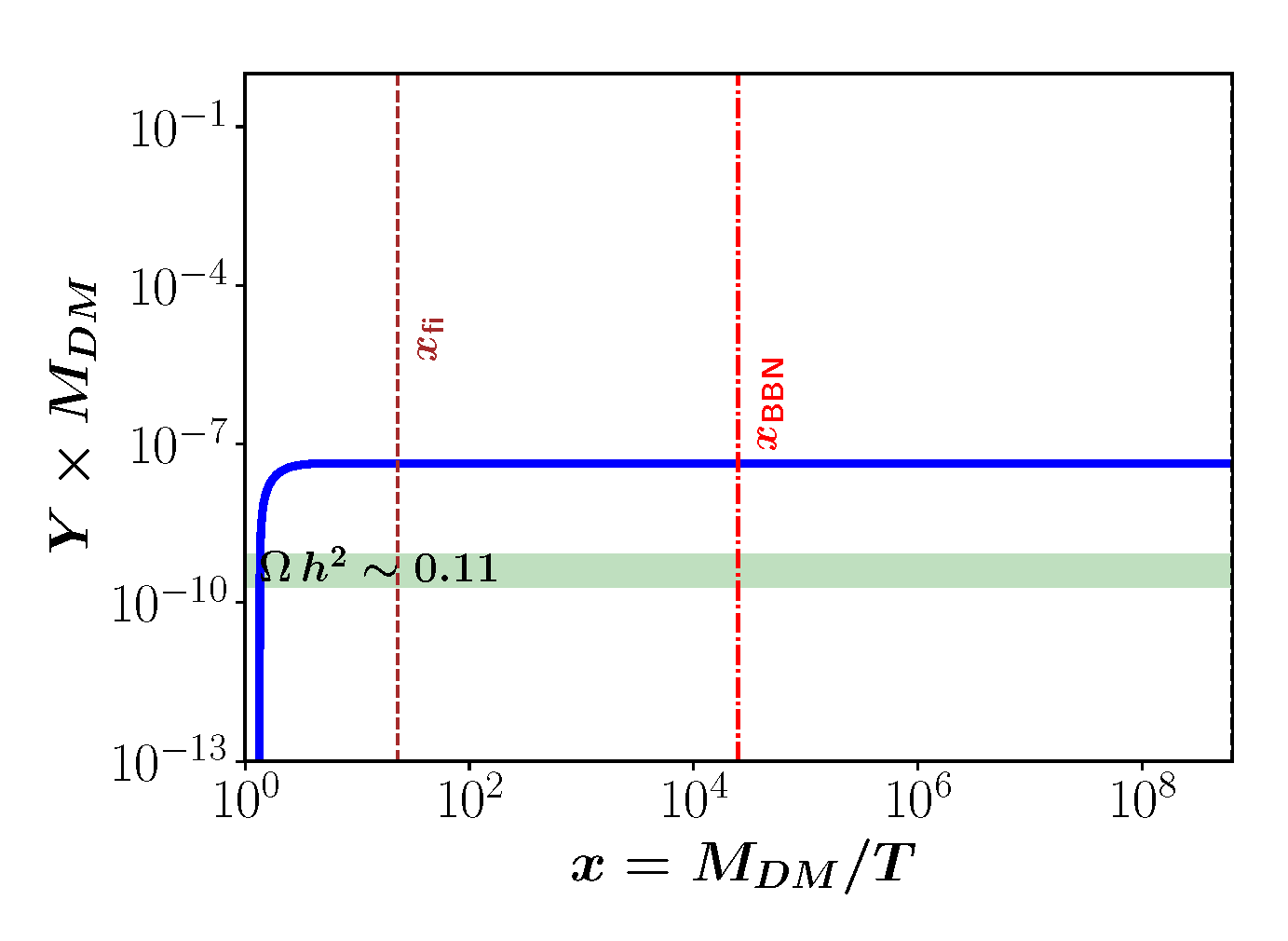
3.1. Axionic Dark Matter
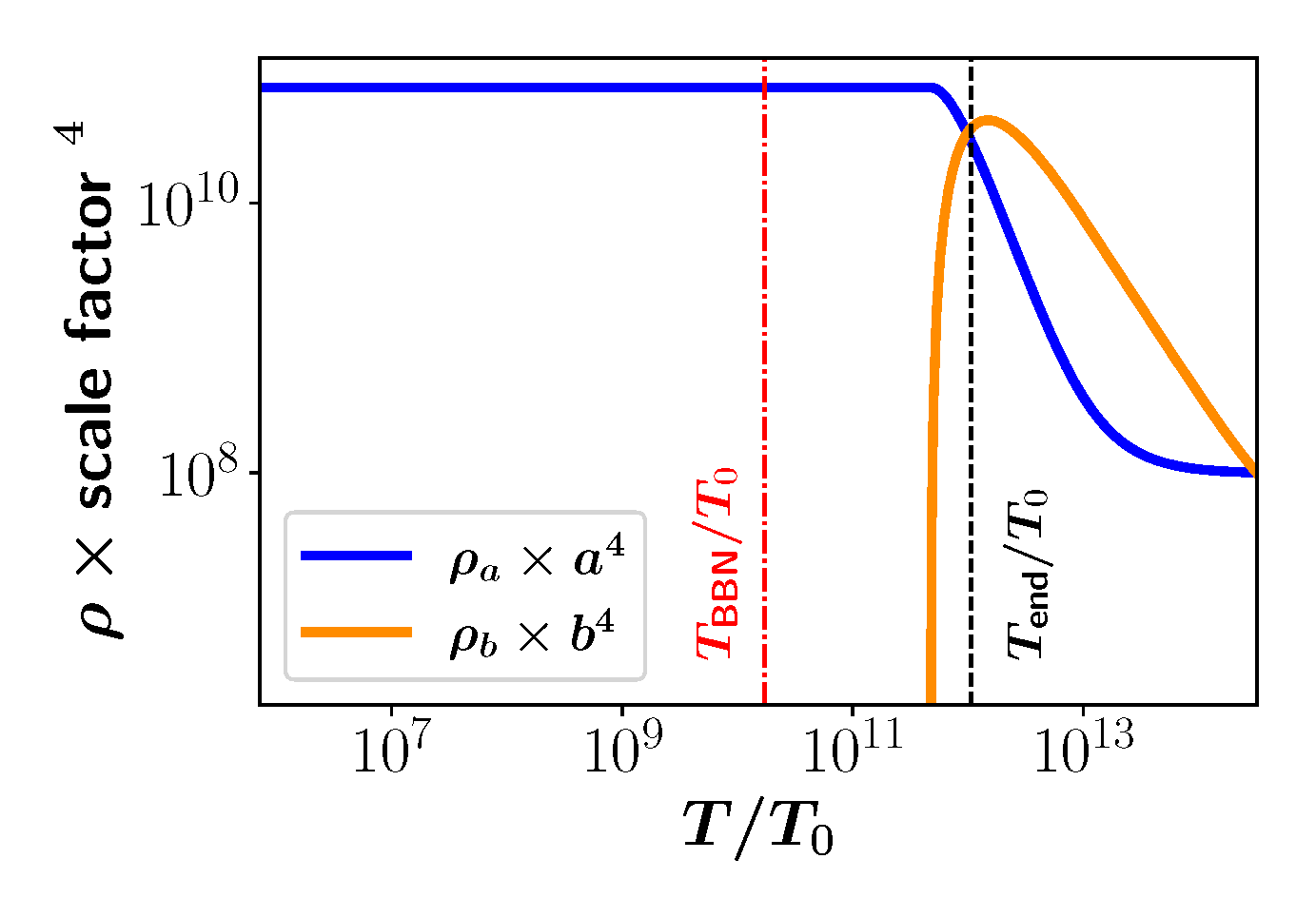
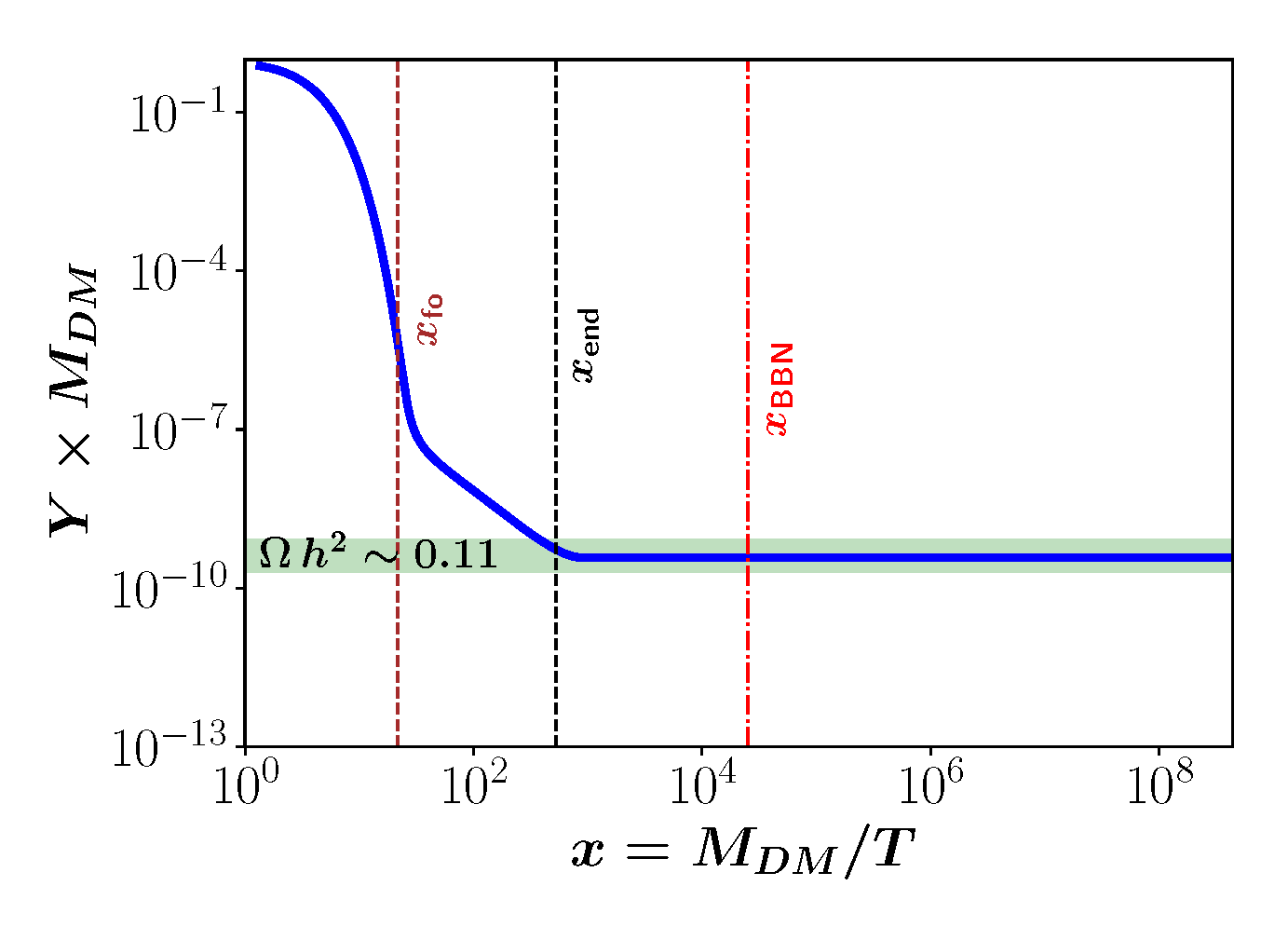
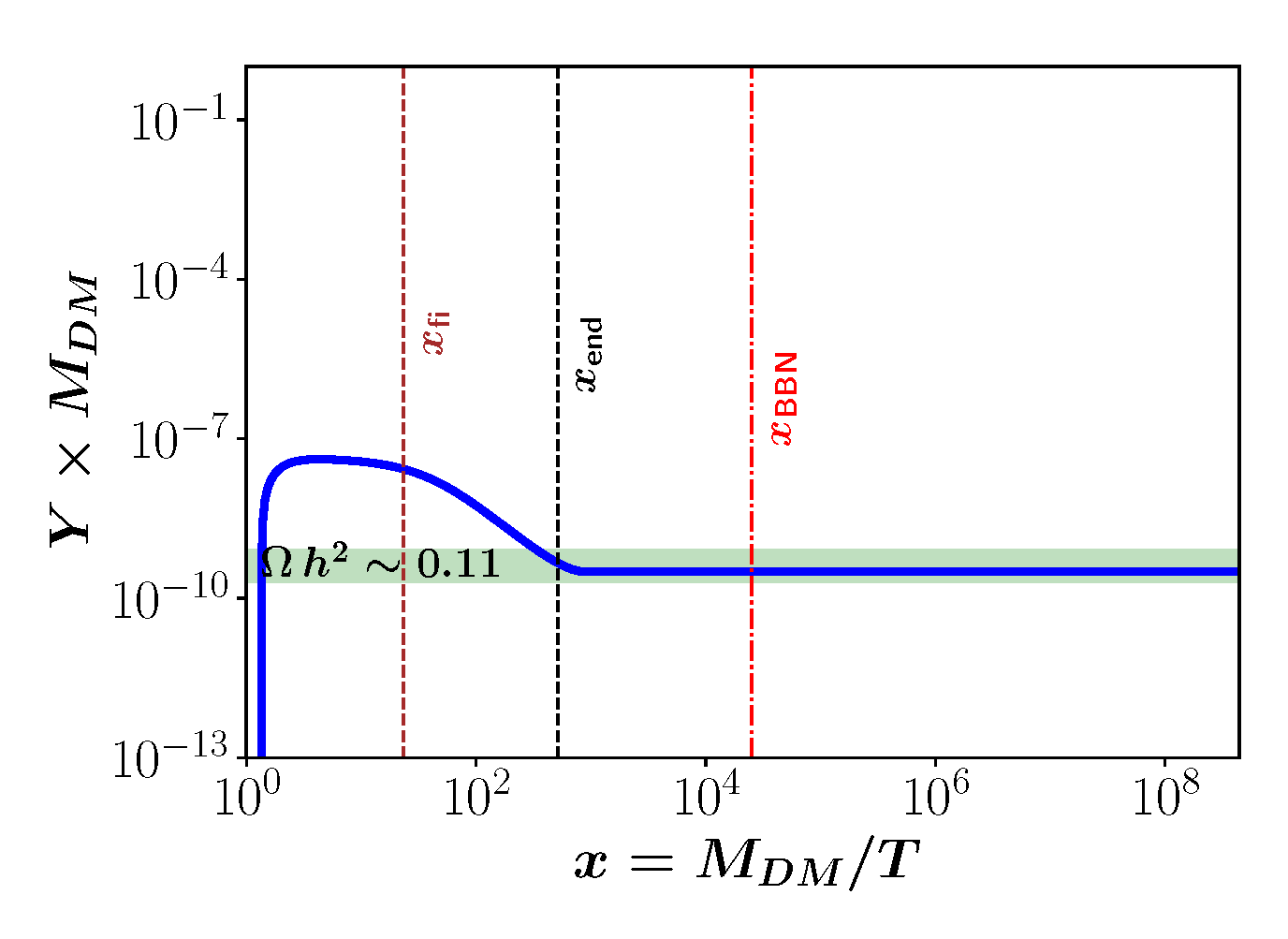
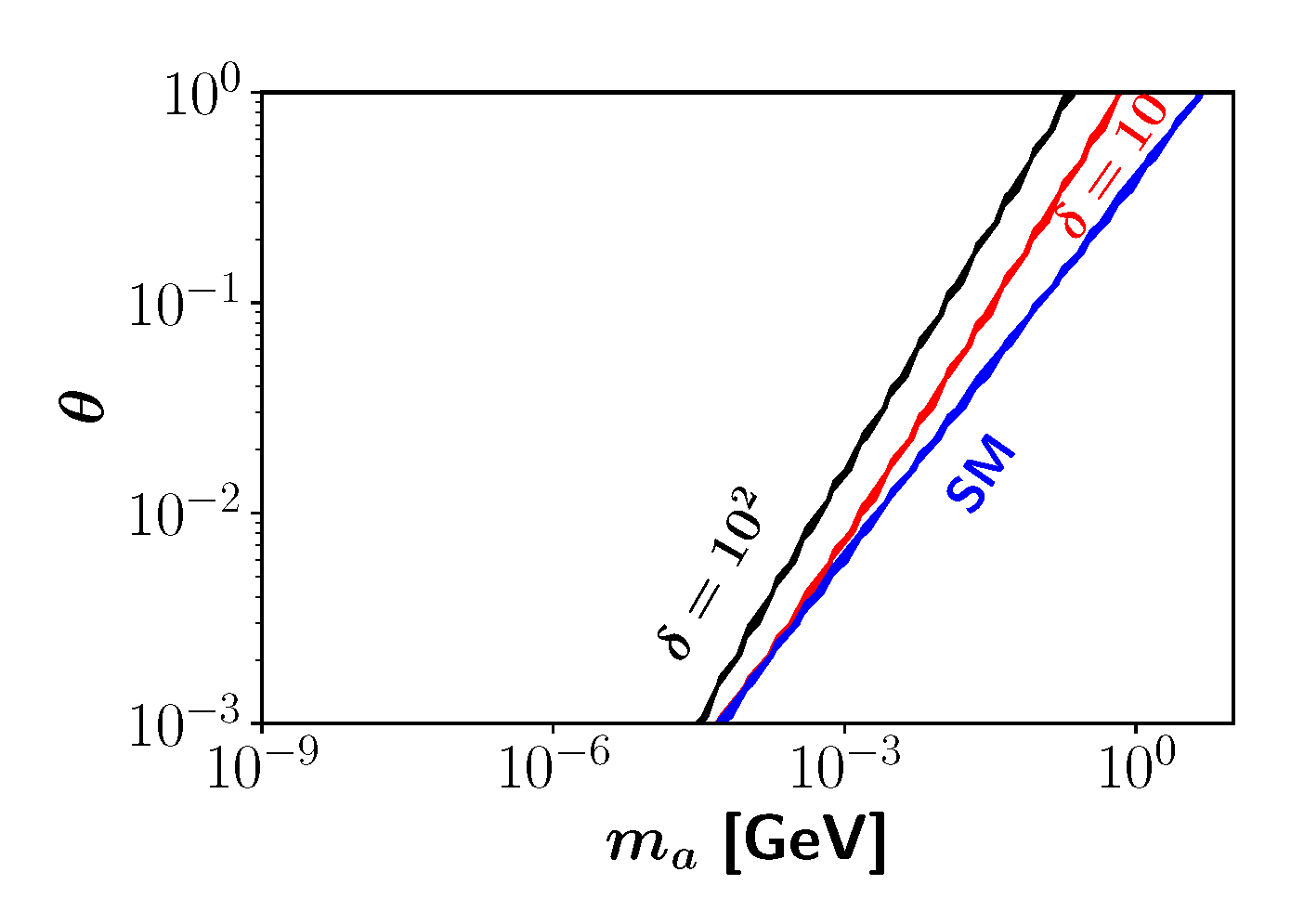
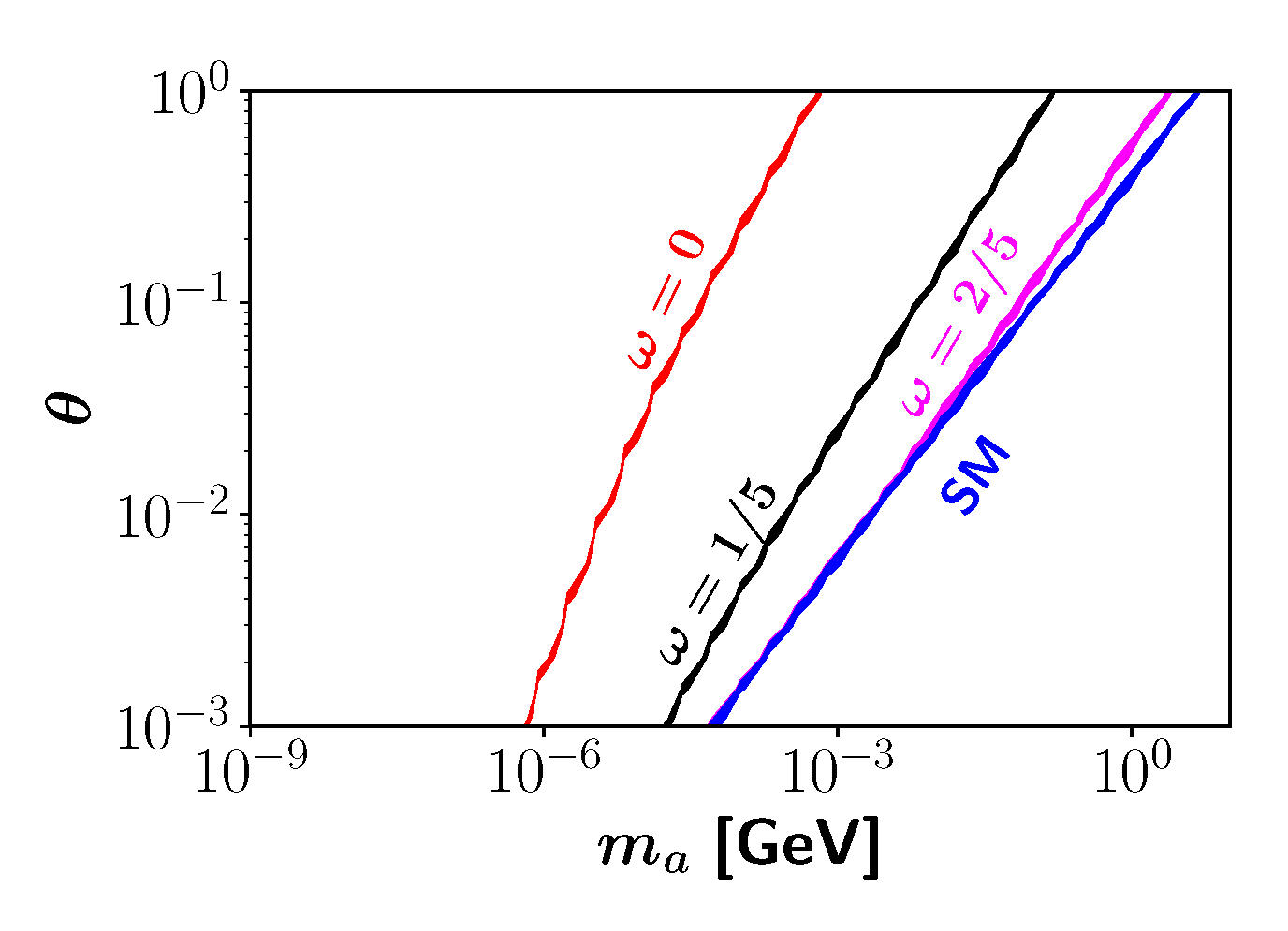
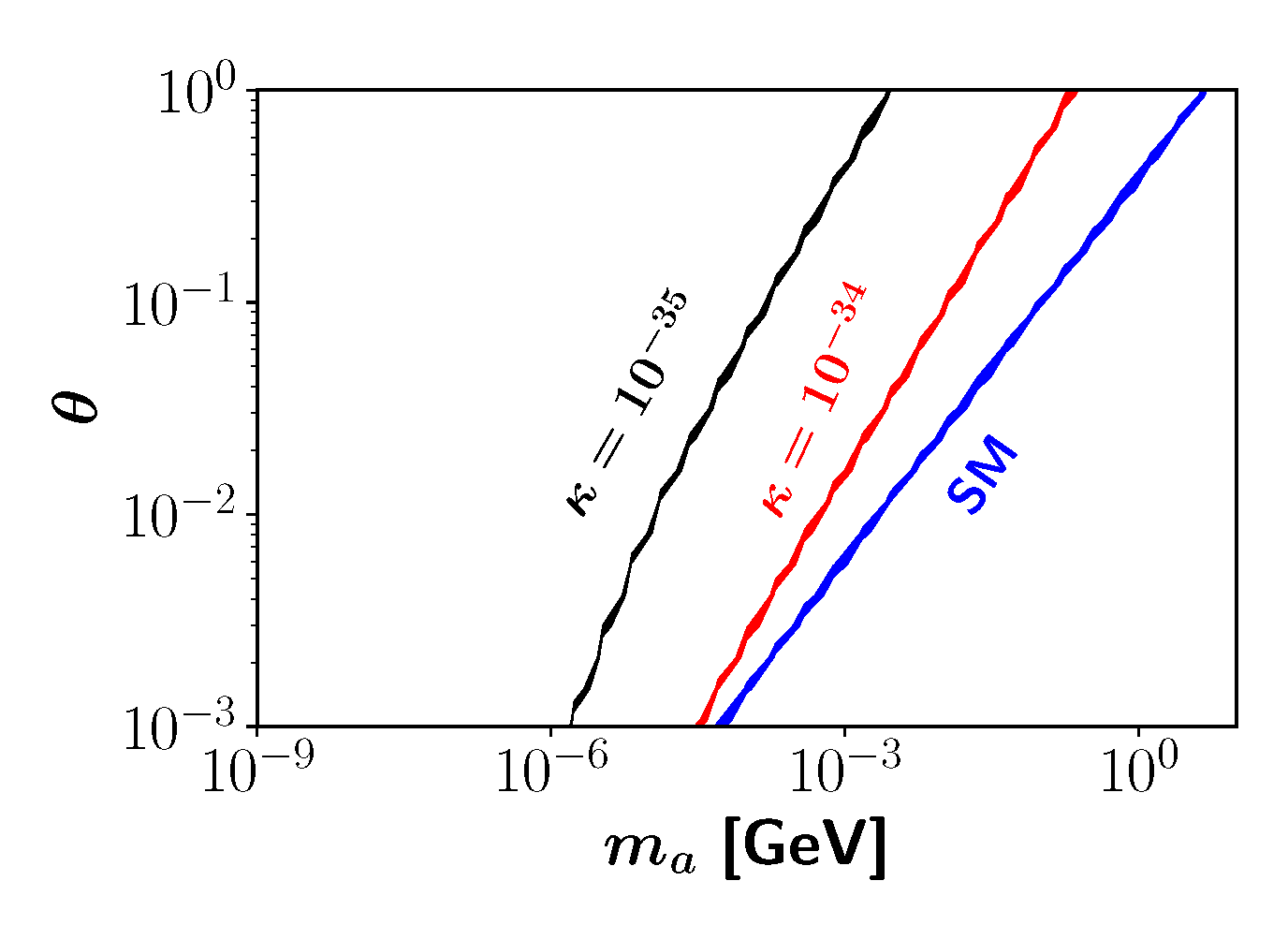
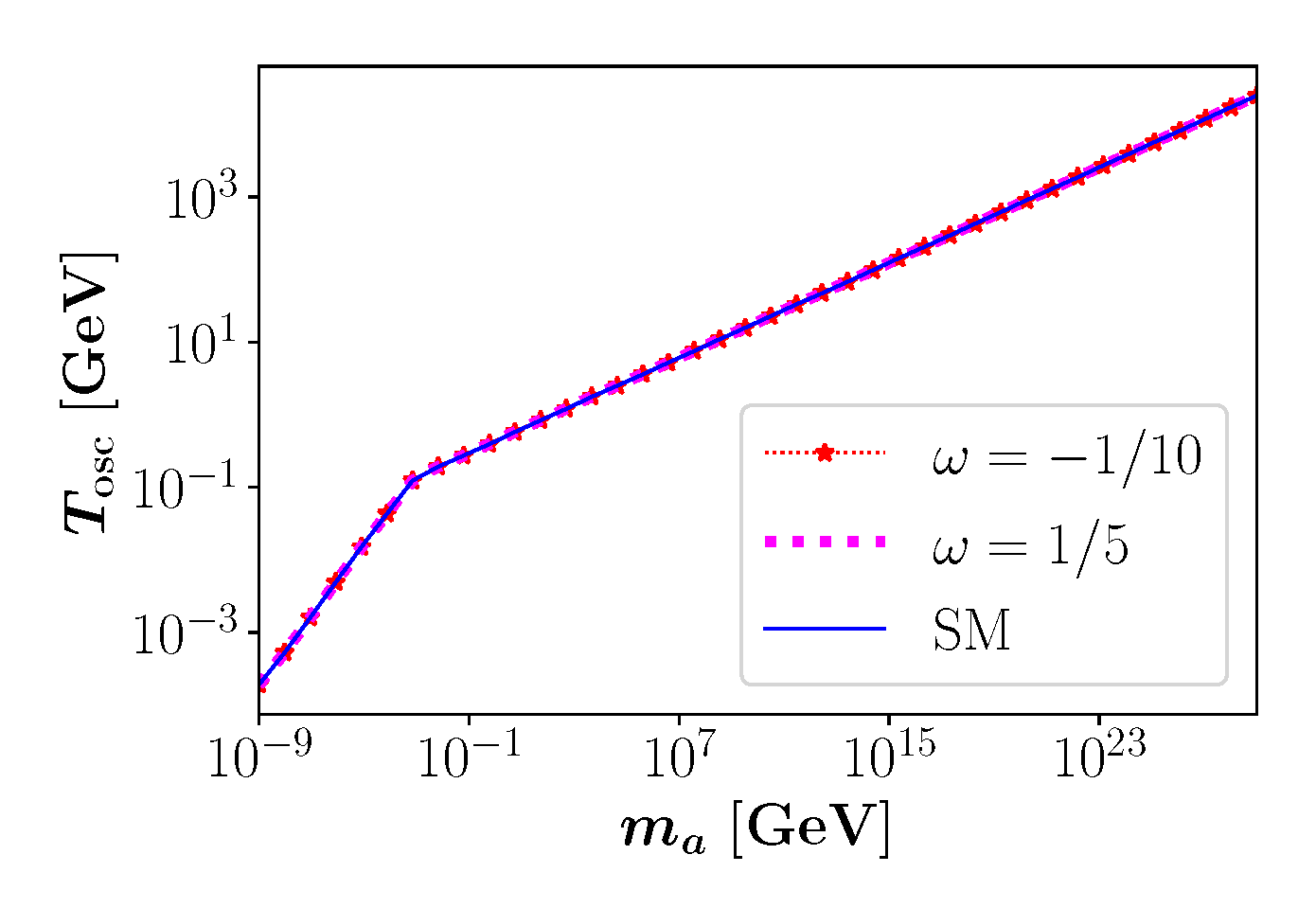
3.2. Axionic DM in the Bimetric Universe
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Rept. Prog. Phys. 2021, 84, 042001. [Google Scholar] [CrossRef]
- Carlip, S.; Chiou, D.W.; Ni, W.T.; Woodard, R. Quantum gravity: A brief history of ideas and some prospects. In One Hundred Years of General Relativity: From Genesis and Empirical Foundations to Gravitational Waves, Cosmology and Quantum Gravity; World Scientific: Singapore, 2017; Volume 2, pp. 325–347. [Google Scholar] [CrossRef]
- Oriti, D. Approaches to Quantum Gravity: Toward a New Understanding of Space, Time and Matter; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kiefer, C. Quantum Gravity, 2nd ed.; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Rovelli, C. Loop Quantum Gravity. Living Rev. Relativ. 1998, 1, 1. [Google Scholar] [CrossRef]
- Addazi, A.; Alvarez-Muniz, J.; Batista, R.A.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.L.; Bahamonde, S.; Bajardi, F.; et al. Quantum gravity phenomenology at the dawn of the multi-messenger era—A review. Prog. Part. Nucl. Phys. 2022, 125, 103948. [Google Scholar] [CrossRef]
- Rovelli, C. Considerations on Quantum Gravity Phenomenology. Universe 2021, 7, 439. [Google Scholar] [CrossRef]
- Torri, M.D.C. Quantum Gravity Phenomenology Induced in the Propagation of UHECR, a Kinematical Solution in Finsler and Generalized Finsler Spacetime. Galaxies 2021, 9, 103. [Google Scholar] [CrossRef]
- Hossenfelder, S. (Ed.) Experimental Search for Quantum Gravity. In Proceedings of the Giersch International Symposion 2016, Frankfurt, Germany, 19–23 September 2016. FIAS Interdisciplinary Science Series, 2018. [Google Scholar]
- Amelino-Camelia, G. Quantum-Spacetime Phenomenology. Living Rev. Relativ. 2013, 16, 5. [Google Scholar] [CrossRef]
- Brahma, S.; Ronco, M. Constraining the loop quantum gravity parameter space from phenomenology. Phys. Lett. B 2018, 778, 184–189. [Google Scholar] [CrossRef]
- Dowker, F.; Henson, J.; Sorkin, R. Discreteness and the transmission of light from distant sources. Phys. Rev. D 2010, 82, 104048. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Relativity in space-times with short distance structure governed by an observer independent (Planckian) length scale. Int. J. Mod. Phys. D 2002, 11, 35–60. [Google Scholar] [CrossRef]
- Bojowald, M.; Morales-Tecotl, H.A.; Sahlmann, H. On loop quantum gravity phenomenology and the issue of Lorentz invariance. Phys. Rev. D 2005, 71, 084012. [Google Scholar] [CrossRef]
- Carmona, J.M.; Cortes, J.L.; Gamboa, J.; Mendez, F. Noncommutativity in field space and Lorentz invariance violation. Phys. Lett. B 2003, 565, 222–228. [Google Scholar] [CrossRef]
- Carmona, J.M.; Cortes, J.L.; Gamboa, J.; Mendez, F. Quantum theory of noncommutative fields. JHEP 2003, 3, 058. [Google Scholar] [CrossRef]
- Carmona, J.M.; Cortes, J.L.; Das, A.K.; Gamboa, J.; Mendez, F. Matter-antimatter asymmetry without departure from thermal equilibrium. Mod. Phys. Lett. A 2006, 21, 883–892. [Google Scholar] [CrossRef]
- Gamboa, J.; Loewe, M.; Mendez, F.; Rojas, J.C. The Landau problem and noncommutative quantum mechanics. Mod. Phys. Lett. A 2001, 16, 2075–2078. [Google Scholar] [CrossRef]
- Horvathy, P.A. The Noncommutative Landau problem and the Peierls substitution. Ann. Phys. 2002, 299, 128–140. [Google Scholar] [CrossRef]
- Falomir, H.; Gamboa, J.; Méndez, F.; Gondolo, P. Inflation without Inflaton: A Model for Dark Energy. Phys. Rev. D 2017, 96, 083534. [Google Scholar] [CrossRef]
- Falomir, H.; Gamboa, J.; Gondolo, P.; Méndez, F. Magnetic Seed and Cosmology as Quantum Hall Effect. Phys. Lett. B 2018, 785, 399–402. [Google Scholar] [CrossRef]
- Falomir, H.; Gamboa, J.; Mendez, F. A Noncommutative Model of Cosmology with Two Metrics. Symmetry 2020, 12, 435. [Google Scholar] [CrossRef]
- Maldonado, C.; Mendez, F. Bimetric universe with matter. Phys. Rev. D 2021, 103, 123505. [Google Scholar] [CrossRef]
- Maldonado, C.; Mendez, F. Dark Matter in a bi-metric universe. Int. J. Mod. Phys. D 2023, 32, 2350059. [Google Scholar] [CrossRef]
- Cattaneo, A.S.; Indelicato, D. Formality and star products. Lond. Math. Soc. Lect. Note Ser. 2004, 323, 79–144. [Google Scholar] [CrossRef]
- Kontsevich, M. Deformation quantization of Poisson manifolds. 1. Lett. Math. Phys. 2003, 66, 157–216. [Google Scholar] [CrossRef]
- Fedosov, B.V. A simple geometrical construction of deformation quantization. J. Differ. Geom. 1994, 40, 213–238. [Google Scholar] [CrossRef]
- Bayen, F.; Flato, M.; Fronsdal, C.; Lichnerowicz, A.; Sternheimer, D. Deformation Theory and Quantization. 1. Deformations of Symplectic Structures. Ann. Phys. 1978, 111, 61. [Google Scholar] [CrossRef]
- Grasso, D.; Rubinstein, H.R. Magnetic fields in the early Universe. Phys. Rep. 2001, 348, 163–266. [Google Scholar] [CrossRef]
- Kandus, A.; Kunze, K.E.; Tsagas, C.G. Primordial magnetogenesis. Phys. Rep. 2011, 505, 1–58. [Google Scholar] [CrossRef]
- Nair, V.P.; Polychronakos, A.P. Quantum mechanics on the noncommutative plane and sphere. Phys. Lett. B 2001, 505, 267–274. [Google Scholar] [CrossRef]
- Acatrinei, C. Path integral formulation of noncommutative quantum mechanics. JHEP 2001, 9, 007. [Google Scholar] [CrossRef]
- Karabali, D.; Nair, V.P.; Polychronakos, A.P. Spectrum of Schrodinger field in a noncommutative magnetic monopole. Nucl. Phys. B 2002, 627, 565–579. [Google Scholar] [CrossRef]
- Freidel, L.; Kowalski-Glikman, J.; Leigh, R.G.; Minic, D. Theory of metaparticles. Phys. Rev. D 2019, 99, 066011. [Google Scholar] [CrossRef]
- Berglund, P.; Hübsch, T.; Minić, D. Dark Energy and String Theory. Phys. Lett. B 2019, 798, 134950. [Google Scholar] [CrossRef]
- Berglund, P.; Hubsch, T.; Minic, D. Dark energy and quantum gravity. Int. J. Mod. Phys. D 2019, 28, 1944018. [Google Scholar] [CrossRef]
- Berglund, P.; Hübsch, T.; Minic, D. String Theory, the Dark Sector and the Hierarchy Problem. LHEP 2021, 2021, 186. [Google Scholar] [CrossRef]
- Freidel, L.; Kowalski-Glikman, J.; Leigh, R.G.; Minic, D. Quantum gravity phenomenology in the infrared. Int. J. Mod. Phys. D 2021, 30, 2141002. [Google Scholar] [CrossRef]
- Particle Data Group; Zyla, P.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Giudice, G.F.; Kolb, E.W.; Riotto, A. Largest temperature of the radiation era and its cosmological implications. Phys. Rev. D 2001, 64, 023508. [Google Scholar] [CrossRef]
- Visinelli, L. (Non-)Thermal Production of WIMPs during Kination. Symmetry 2018, 10, 546. [Google Scholar] [CrossRef]
- Maldonado, C.; Unwin, J. Establishing the dark matter relic density in an era of particle decays. JCAP 2019, 6, 37. [Google Scholar] [CrossRef]
- Bernal, N.; Elahi, F.; Maldonado, C.; Unwin, J. Ultraviolet Freeze-in and Non-Standard Cosmologies. JCAP 2019, 11, 26. [Google Scholar] [CrossRef]
- Bernal, N.; Ghoshal, A.; Hajkarimc, F.; Lambiase, G. Primordial gravitational wave signals in modified cosmologies. JCAP 2020, 11, 051. [Google Scholar] [CrossRef]
- Arias, P.; Bernal, N.; Herrera, A.; Maldonado, C. Reconstructing non-standard cosmologies with dark matter. JCAP 2019, 10, 47. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Kolb, E.W.; Riotto, A. Production of massive particles during reheating. Phys. Rev. D 1999, 60, 063504. [Google Scholar] [CrossRef]
- Kolb, E.W.; Notari, A.; Riotto, A. Reheating stage after inflation. Phys. Rev. D 2003, 68, 123505. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rept. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Arcadi, G.; Dutra, M.; Ghosh, P.; Lindner, M.; Mambrini, Y.; Pierre, M.; Profumo, S.; Queiroz, F.S. The waning of the WIMP? A review of models, searches, and constraints. Eur. Phys. J. 2018, C78, 203. [Google Scholar] [CrossRef]
- Lin, T. Dark matter models and direct detection. PoS 2019, 333, 009. [Google Scholar] [CrossRef]
- Hooper, D. TASI Lectures on Indirect Searches For Dark Matter. PoS 2019, TASI2018, 010. [Google Scholar]
- Kolb, E.W.; Turner, M.S. The Early Universe; CRC Press: Boca Raton, FL, USA, 1990; Volume 69. [Google Scholar]
- Hall, L.J.; Jedamzik, K.; March-Russell, J.; West, S.M. Freeze-In Production of FIMP Dark Matter. JHEP 2010, 1003, 080. [Google Scholar] [CrossRef]
- Chu, X.; Hambye, T.; Tytgat, M.H.G. The Four Basic Ways of Creating Dark Matter Through a Portal. JCAP 2012, 1205, 034. [Google Scholar] [CrossRef]
- Bernal, N.; Heikinheimo, M.; Tenkanen, T.; Tuominen, K.; Vaskonen, V. The dawn of FIMP Dark Matter: A review of models and constraints. Int. J. Mod. Phys. A 2017, 32, 1730023. [Google Scholar] [CrossRef]
- McDonald, J. Thermally generated gauge singlet scalars as selfinteracting dark matter. Phys. Rev. Lett. 2002, 88, 091304. [Google Scholar] [CrossRef]
- Choi, K.Y.; Roszkowski, L. E-WIMPs. AIP Conf. Proc. 2006, 805, 30–36. [Google Scholar] [CrossRef]
- Kusenko, A. Sterile neutrinos, dark matter, and the pulsar velocities in models with a Higgs singlet. Phys. Rev. Lett. 2006, 97, 241301. [Google Scholar] [CrossRef] [PubMed]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440. [Google Scholar] [CrossRef]
- Nelson, A.E.; Scholtz, J. Dark Light, Dark Matter and the Misalignment Mechanism. Phys. Rev. D 2011, 84, 103501. [Google Scholar] [CrossRef]
- Gorghetto, M.; Villadoro, G. Topological Susceptibility and QCD Axion Mass: QED and NNLO corrections. JHEP 2019, 3, 033. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Guenther, J.; Kampert, K.H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 2016, 539, 69. [Google Scholar] [CrossRef]
- Hertzberg, M.; Tegmark, M.; Wilczek, F. Axion Cosmology and the Energy Scale of Inflation. Phys. Rev. D 2008, 78, 083507. [Google Scholar] [CrossRef]
- Harani, D.; Sikivie, P. On the evolution of global strings in the early universe. Phys. Lett. B 1987, 195, 361. [Google Scholar] [CrossRef]
- Ramberg, N.; Visinelli, L. Probing the early Universe with ax- ion physics and gravitational waves. Phys. Rev. D 2019, 99, 123513. [Google Scholar] [CrossRef]
- Arias, P.; Bernal, N.; Karamitros, D.; Maldonado, C.; Roszkowski, L.; Venegas, M. New opportunities for axion dark matter searches in nonstandard cosmological models. JCAP 2021, 11, 003. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado, C.; Méndez, F. Axionic Dark Matter in a Bi-Metric Universe. Universe 2023, 9, 429. https://doi.org/10.3390/universe9100429
Maldonado C, Méndez F. Axionic Dark Matter in a Bi-Metric Universe. Universe. 2023; 9(10):429. https://doi.org/10.3390/universe9100429
Chicago/Turabian StyleMaldonado, Carlos, and Fernando Méndez. 2023. "Axionic Dark Matter in a Bi-Metric Universe" Universe 9, no. 10: 429. https://doi.org/10.3390/universe9100429
APA StyleMaldonado, C., & Méndez, F. (2023). Axionic Dark Matter in a Bi-Metric Universe. Universe, 9(10), 429. https://doi.org/10.3390/universe9100429





