Abstract
Turbulence in space plasmas usually exhibits an energy cascade in which large-scale magnetic fluctuations are dominated by non-linear MHD wave–wave interactions following a Kolmogorov-like power-law spectrum. In addition, at scales at which kinetic effects take place, the magnetic spectrum follows a steeper power-law shape given by a spectral index . In a recent publication, a quasilinear model was used to study the evolution of ion temperatures in a collisionless plasma in which electromagnetic waves propagate along the background magnetic field, and it was found that the interaction between the plasma and a turbulent spectrum of ion-cyclotron waves may lead the plasma to states out of thermal equilibrium characterized by enhanced temperature anisotropies and with a reduction in the parallel proton beta, which is consistent with space observations. Here, we complement such studies by analyzing the quasilinear interaction between plasma and a solar-wind-like turbulent spectrum of fast magnetosonic waves, and study the role of firehose instability (FHI) in the regulation of temperature anisotropy. Our results show that the presence of turbulence significantly modifies the FHI marginal stability threshold, as predicted from linear theory. Moreover, depending on the value of the plasma , a turbulent magnetosonic spectrum may lead an initially thermally isotropic plasma to develop anisotropic states in which .
1. Introduction
Space plasmas are out-of-equilibrium driven systems, exhibiting several non-thermal features such as temperature anisotropy, supra-thermal tails, field-aligned beams, and differential streaming. One of the simplest ways to model non-thermal plasma populations is the use of bi-Maxwellian velocity distribution functions (VDFs), i.e., Maxwellian distribution functions with two temperatures: a temperature along the background magnetic field (), and another temperature in the perpendicular plane (). However, as these distributions do not represent a thermodynamic equilibrium state, linear Vlasov theory predicts that anisotropic VDFs () can become unstable to micro-instabilities and drive electromagnetic waves [1,2]. In such a case, the driven growing waves will produce pitch-angle scattering of the particles, and the plasma will relax towards a new quasi-stationary state. In general, this final state (the marginal stable state) does not correspond to thermodynamic equilibrium, but can be represented by VDFs that do not keep enough free energy to drive an instability in a limited timescale [3,4,5]. The relation between temperature anisotropy and the stability of the plasma has been widely addressed in different space environments, with solar wind being one of the most studied using theory, simulations and also observations [6,7,8].
Fast and slow solar wind has been found to approach anisotropic conditions with increasing distance from the Sun [9,10]. It is usually argued that the radially expanding solar wind develops temperature anisotropies as a result of the conservation of adiabatic moments [11]. If this were true, we should expect values of at 1 AU. However, the near-Earth solar-wind protons are consistently observed in a quasi-isotropic state with bounding temperature anisotropies given by the empirical law [6]
where S, a, and are free parameters; and , where n, and represent the plasma density, the Boltzmann constant and the strength of the background magnetic field, respectively. In general, it is expected that wave-particle interactions dominate at kinetic scales in collisionless solar wind [12]. Indeed, the empirical law Equation (1) has been found to be consistent with kinetic instabilities, in particular with the resonant left-hand polarized parallel Alfvén cyclotron and non-resonant oblique mirror instabilities when [13,14,15,16,17], and the right-handed parallel and oblique firehose instabilities, which destabilize magnetosonic waves when [6,18,19].
From fluid theory, a law similar to Equation (1) can be obtained, with , , and . However, empirical fits based on Vlasov theory and solar-wind observations have found precise values of , , and [5] for instabilities with a maximum growth rate of (where is the local proton gyrofrequency), or , , and when [6]. All these fits can be improved by including more effects in the calculations, such as the inclusion of He+2 ions, or differential streaming between species [5,20]. Among these effects, as the solar-wind plasma coexists with electromagnetic turbulence even in quasi-stables states below the marginal stability thresholds [7], turbulence and its properties may correspond to one important aspect to be considered in order to obtain empirical fits. However, linear or non-linear analyses usually neglect these effects, and only recently have more studies considered the coexistence and interplay between ambient turbulence and the evolution of kinetic instabilities. In this context, Markovskii and Vasquez [21] found that turbulence reduces the growth rates and saturation levels of the parallel and oblique firehose instabilities. Moreover, Opie et al. [22] found that turbulence may play an important role in setting the conditions for temperature-anisotropy-driven instabilities to effectively regulate the plasma, and that these conditions vary locally on scales much shorter than the correlation length of solar-wind turbulence. This is consistent with the results presented by Bandyopadhyay et al. [23], where it was found that, in general, microinstability linear growth rates are substantially less than the local nonlinear rates, but for extreme values of temperature anisotropy the instability growth rates are comparable or faster than the turbulence time scales.
Turbulence associated with magnetosonic waves is usually studied in conjunction with Alfvénic turbulence (see, e.g., Andrés et al. [24]). In this context, using particle-in-cell simulations, Svidzinski et al. [25] found conditions compatible with weak turbulence, in which electromagnetic fluctuations can be represented by turbulent spectra of Alfvénic and magnetosonic modes as observed in solar wind. Chandran [26] has shown that the presence of magnetosonic modes can affect the isotropy of the energy cascade and, thus, the scaling exponents, while Cho and Lazarian [27] showed that in both high- and low- plasmas, Alfvén and slow magnetosonic modes reveal a Kolmogorov spectrum and scale-dependent Goldreich–Sridhar anisotropy, with fast modes exhibiting a spectrum and isotropy. Moreover, Sharma and Kumar [28] numerically analyzed the nonlinear interaction between kinetic Alfvén waves and magnetosonic waves, showing that localized structures are formed with steep spectra with power law with .
In a recent article, Moya and Navarro [29] followed a quasilinear approach to analyze the effects of a background turbulent spectrum on the excitation and relaxation of the ion-cyclotron instability. Considering different models of turbulent cascades (different values of ) with a spectral break, they showed that a certain level of magnetic-field power can drive protons to an increase in and a reduction in the plasma beta. Therefore, the interaction of solar-wind protons and electromagnetic turbulence may drive protons far from thermodynamic equilibrium and near the ion-cyclotron instability thresholds, as observed in solar-wind [7,30] and numerical simulations [31]. Here, we aim to complement such analysis, but considering the parallel firehose instability and the role of the turbulent spectra of magnetosonic waves on the regulation of the plasma when . To do so, using a moment-based quasilinear theory, we will analyze the non-linear time evolution of an initially bi-Maxwellian plasma with and under both stable and unstable initial conditions. This article is organized as follows: in Section 2, we briefly introduce the main equations of our quasilinear method. In Section 3, we report our numerical results; and in Section 4 we summarize our findings, discuss their interpretations, and present the main conclusions of our work.
2. Method: Macroscopic Quasilinear Equations
We consider a magnetized plasma composed of bi-Maxwellian protons and cold electrons. The kinetic dispersion relation of right-handed circularly polarized waves, propagating along a background magnetic field , is given by [20,32,33]
where is the complex frequency that depends on the wavenumber ; is the Alfvén speed, with and the density and mass of protons, respectively; is the proton gyrofrequency with c the speed of light; where is the temperature anisotropy; and are the proton temperatures perpendicular and parallel with respect to , respectively; and are resonance factors [34]; is the parallel proton thermal speed; and the Boltzmann constant. is the plasma dispersion function [35], which is calculated numerically via the Faddeeva function provided by the Python SciPy library [36]. In Equation (2), we assumed charge neutrality (i.e., zero net charge such that the electron density is ), and .
Even though the linear theory of plasma instabilities usually considers no background fluctuations and an homogeneous plasma, this is not mandatory. Indeed, it is not necessary to prescribe the shape spectrum to deduce the dispersion relation. The only constraint is that the amplitude of the magnetic fluctuations must be small compared to the background plasma state at the early stages of the time evolution of the system. These fluctuations may exhibit ambient fluctuations [37], turbulence [21,29,38], and even inhomogeneities [39,40]. Thus, the dispersion relation Equation (2) is valid for the case under study.
We address the time evolution of the system through moment-based quasilinear theory. The moment-based quasilinear approximation assumes that the plasma evolves adiabatically, so that solves the dispersion relation Equation (2) instantaneously at all times. It is important to mention that the use of a moment-based quasilinear theory to study kinetic instabilities is well-established in the literature, and has been widely invoked at least during the last three decades considering Maxwellian and Kappa distributions, e.g., for the mirror instability [37,41], the ion-cyclotron instability [4,29,42], the electron whistler-cyclotron instability [43,44], and the firehose instability [19,45,46], among others. This is fundamentally different from the quasilinear diffusion model, where the equations are solved as a diffusion-like equation for the phase-space density (see, e.g., Isenberg and Vasquez [38] and references therein). However, several of the mentioned works have shown very good agreement between the quasilinear approach and hybrid or full-particle PIC simulations, particularly for the case of bi-Maxwellian distributions up to the saturation of the instabilities. For longer times, other non-linear effects may be relevant and the shape of the distribution may undergo non-trivial changes beyond the Maxwellian approach (see, e.g., Section 3.3 in Yoon [5]).
Within this context, the quasilinear evolution of the perpendicular and parallel thermal speeds are given by [32,47,48]
where L is the characteristic length of the plasma, and is the spectral wave energy satisfying
In solar wind, a non-negligible level of magnetic fluctuations is consistently observed [7,49,50,51], whose power spectra in terms of wavenumbers (using the Taylor hypothesis) is usually of the form:
corresponding to a Kolmogorov-like power-law spectrum with spectral break at the ion inertial length. Here, A is chosen depending on the initial total magnetic energy , with the integral calculated in the range . Notice that we are restricted to a reduced 1D background spectrum in . In general, for an assumed anisotropic turbulent spectrum and a reduced magnetic spectrum proportional to , the conservation of energy gives a parallel reduced spectrum proportional to with (see Moya and Navarro [29] and references therein). Therefore, for the particular case (Kolmogorov perpendicular turbulence) and anisotropic index , we obtain for the inertial range in Equation (6).
3. Results
Here, we report numerical solutions of the system of differential equations (3)–(5), using a fourth-order Runge–Kutta method with Equation (6) as he initial condition, together with the Muller method [52] to find the numerical roots of Equation (2). The dispersion relation Equation (2) supports an infinite number of solutions for as a function of , most of them being sound-like heavily damped modes with frequencies above and below the proton gyrofrequency [49,53]. Here, however, we focus on the quasilinear evolution of the plasma due to the firehose instability. As mentioned in Section 1, this instability grows out of the magnetosonic wave for and a sufficiently large .
Figure 1 shows results from two quasilinear simulation runs, one for an initially stable proton plasma with [Figure 1(left)], and the other for an initially unstable plasma to the proton-firehose instability with [Figure 1(right)]. In both cases, we initialize a turbulent magnetic spectrum as in Equation (6), with and a total magnetic energy .
Figure 1.
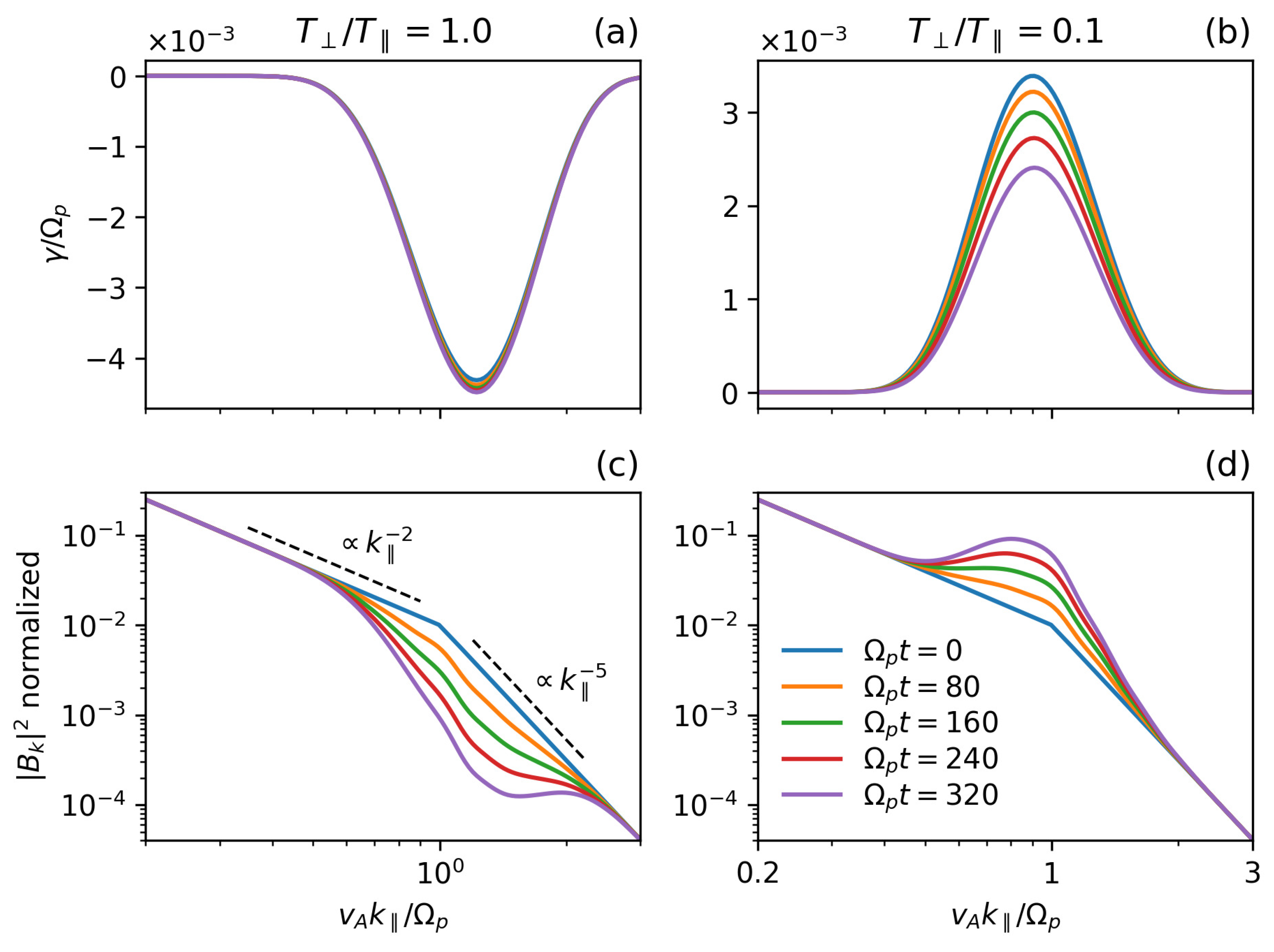
Time evolution of (a,b) the growth/damping rate of magnetosonic waves, and (c,d) the magnetic wave spectrum (normalized to ), both as a function of the normalized wavenumber . Initial conditions are , for a magnetic spectrum with , and (a,c) , and (b,d) . The axes showing wavenumber and magnetic power are in log-scale.
For the initially stable plasma, Figure 1a shows the imaginary part of the frequency, , as a function of corresponding to the magnetosonic wave mode resulting from Equation (2). Due to kinetic effects, the magnetosonic wave is damped () for wavelengths around the ion inertial length (). The figure also shows snapshots of the damping rate for different time steps. In general, we find that the wave-damping rate decreases very slowly towards over thousands of gyroperiods in the rrpresence of isotropic Maxwellian protons. In other words, the initial magnetic spectrum damps exponentially at an almost constant damping rate depending on its wavenumber, resulting in a slump around the ion inertial length which smooths the initial spectrum break, as shown in Figure 1c.
When the plasma is initially unstable to the firehose instability, the magnetosonic growth rate () also occurs around the ion inertial length. Due to the excess of free energy, represented by the initial , the instability growth rate decreases as time progresses, as shown in Figure 1b. Although not noticeable from the figures, the bandwidth of the instability shrinks and moves toward smaller wavenumbers as time evolves. This is consistent with previous results of quasilinear moment theory [48]. What is interesting here is that a band in the magnetic power spectrum grows over time, resulting in a bump which smooths the spectral break around , but keeps the spectrum in the inertial range , and the spectrum in the kinetic range . This is consistent with observations also showing a bump in the magnetic power spectrum, e.g., in the Earth’s magnetosheath [54,55,56].
This result is qualitatively different from our previous work (see [29]), where we report that the spectrum of both stable and unstable Alfvén–Cyclotron waves steepens (the value of grows in time) in the kinetic range for . However, observations and numerical simulations consistently show finite values of in the kinetic range [57,58,59,60,61,62,63,64,65,66]. Thus, we conclude that the observed power-law spectrum at kinetic scales is not only due to Alfvén–Cyclotron waves, but also to effects in coexistence with the magnetosonic waves that may dominate the plasma evolution, at least at quasilinear time scales.
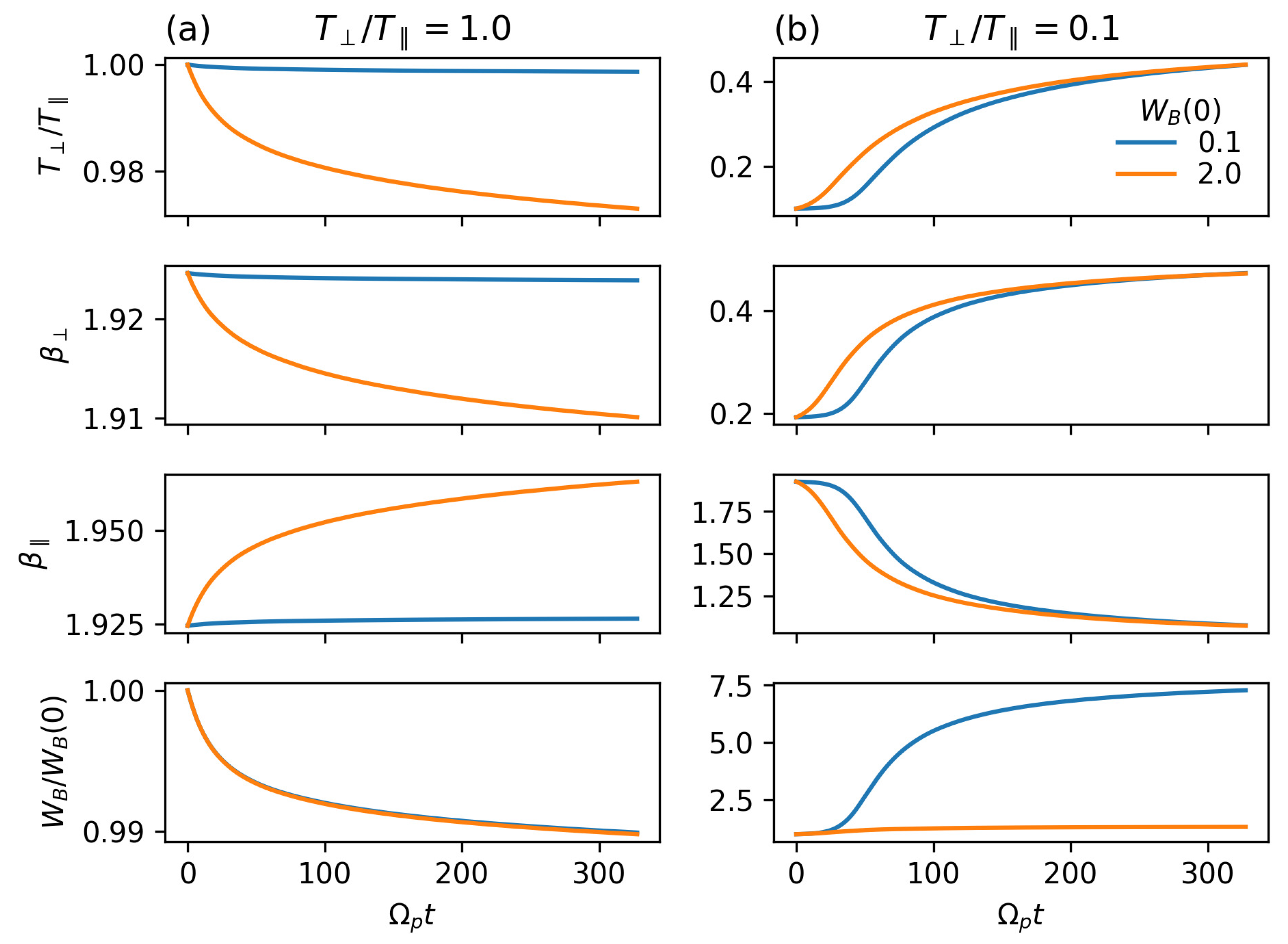
Figure 2 shows the quasilinear time evolution of the temperature anisotropy , the perpendicular and parallel , and the total magnetic energy normalized to its initial value , for similar initial parameters as in Figure 1. In this figure, we compare the effects of two values of and .
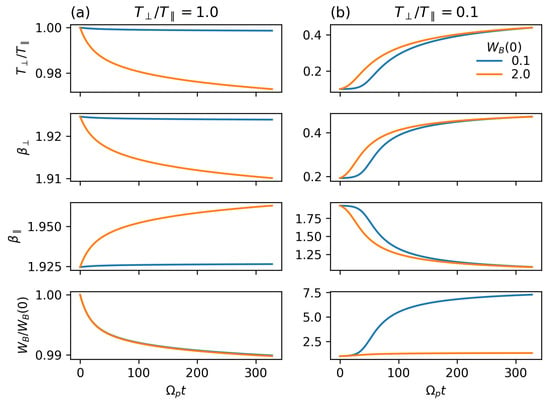
Figure 2.
Time evolution of the temperature anisotropy, , , and magnetic energy normalized to the initial . The initial conditions are , a magnetic spectrum with slope and with different values of , and (a) , and (b) .
According to linear theory, plasma is stable whenever , as shown in Figure 1a. Thus, it is expected that the macroscopic plasma parameters should remain constant in time if the initial conditions are close to isotropy. However, Figure 2a shows that, even in those cases, the temperature anisotropy slightly decreases in time to values . At the same time, grows and decreases from their initial values, showing that, due to the presence of magnetosonic turbulence with finite energy, the plasma is heating in the parallel direction with respect to the ambient magnetic field . In addition, the magnetic energy decreases slightly (only 1%) from its initial value, which is a result of the slump forming in the magnetic spectrum, as shown in Figure 1c. These effects are stronger for higher values of the initial , showing that high energy levels of a power spectrum may play a role in the generation of temperature anisotropy in solar wind.
Figure 2b shows results in the presence of firehose instabilities with . In this case, , , and grow in time, while the parallel decreases, i.e., protons are heating in the direction perpendicular to . It is worth mentioning that the temperature anisotropy reaches a quasi-stationary state at a value that is independent of the initial magnetic energy. In addition, as a result of the bump in the magnetic spectrum shown in Figure 1d, the magnetic energy grows times starting from a low value of , while the case grows only by a small fraction in the simulated time range. These results suggest that the free energy provided by may not be enough to compensate the effects of the firehose instability in the long run; thus, the latter will be dominant during the quasilinear plasma evolution, which is consistent with solar-wind measurements suggesting that low-frequency parallel-propagating fluctuations are dominated by kinetic instabilities [12].
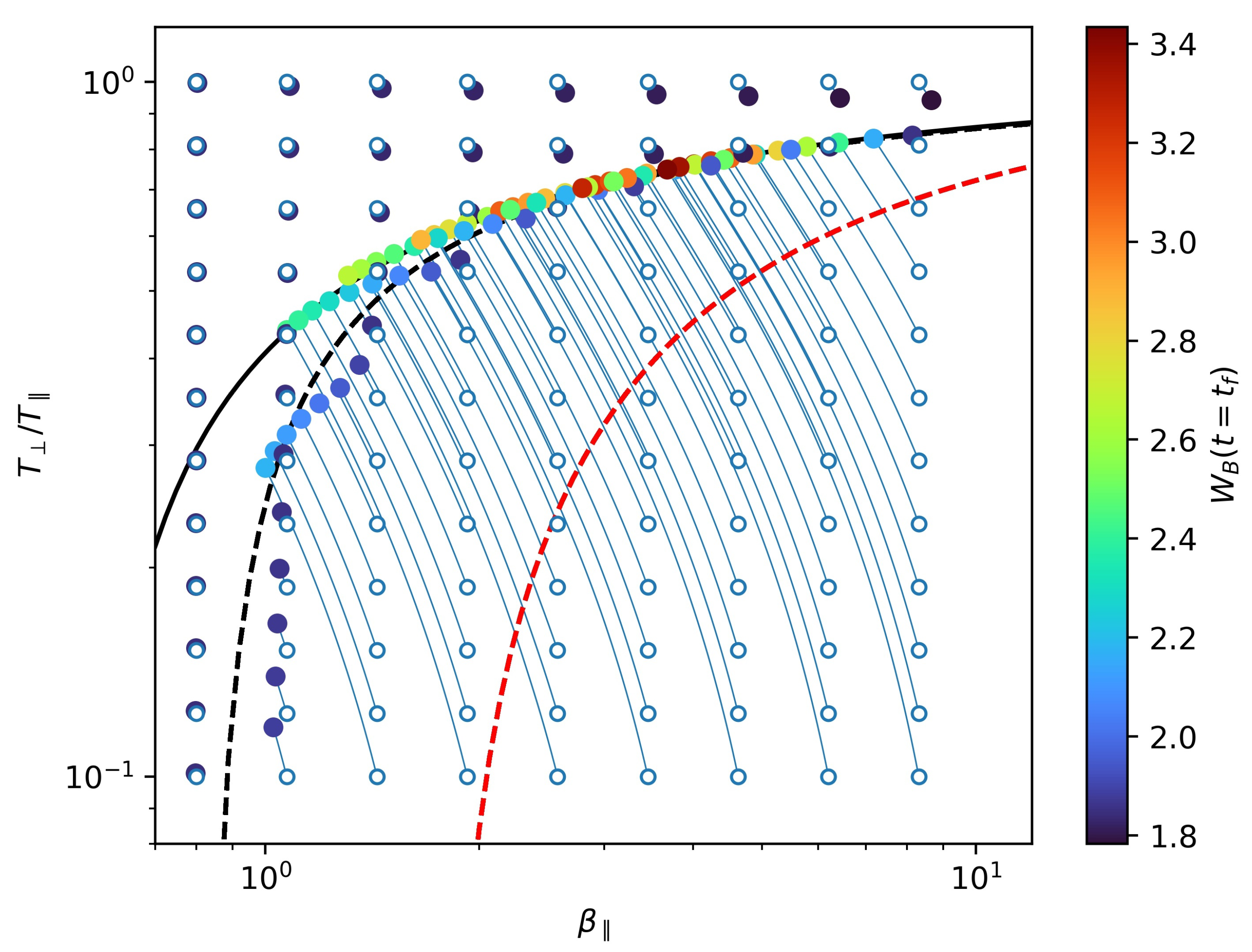
In Figure 3, we show results from a set of 108 quasilinear simulations with different initial conditions and , shown as white circles in the figure, with values chosen above and below the empirical threshold of the firehose instability [6]. This threshold, shown as a solid black line in Figure 3, is calculated numerically from Equation (2) by setting . As in Figure 1, the magnetic spectrum is initialized with slope and total energy for all simulations. The blue lines in Figure 3 are the trajectories, as and evolve in time. The colorized circles represent the final state of the simulations, with colors depending on the final value of the magnetic energy, at the time chosen so that all simulations saturate near a quasi-stationary state.
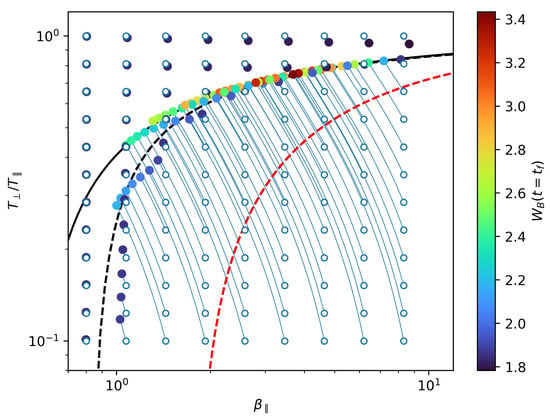
Figure 3.
Quasilinear evolution of the proton and anisotropy . Initial conditions (white circles) were chosen to be evenly spaced in log space in the range and . The initial magnetic spectrum is defined with with energy for all cases. The colorized circles correspond to the final (stationary) state of the plasma simulations with colors depending on the final value of the magnetic energy. (Dashed lines) Contours of the maximum growth-rate (black) and (red) of the firehose instability, as calculated from the dispersion relation Equation (2). (Solid black line) Fitted curve of the final states of the simulations starting with strongly-unstable conditions.
We focus first on simulations starting from a linearly stable condition, i.e., all points above the instability threshold (dashed-black line) in Figure 3. It can be seen that all these simulations evolve so that decreases and grows, both slowly in time, towards the instability threshold. The total magnetic energy also decreases from to a minimum value around . This description is consistent with the discussion of Figure 2a, where the free energy provided by was identified as being responsible of the parallel proton heating. In general, we observe that the temperature deviation from their initial values is greater for increasing values of .
Still, is not enough to drive the plasma towards temperature anisotropies below the instability threshold. Thus, energetic magnetosonic waves may not be able to excite a firehose instability from an initially stable plasma. This can be contrasted with our previous work [29], where it was shown that Alfvén-cyclotron waves can lead to the growth in the temperature anisotropy, sometimes exceeding the instability thresholds, thus triggering proton-cyclotron instabilities from an initially stable plasma even for low energy values . Therefore, if both wave modes coexist in a turbulent state, then the Alfvén-cyclotron waves will be predominant in the plasma evolution starting from a linearly stable condition.
Focusing now on simulations starting below the instability threshold, Figure 3 shows that these simulations also evolve towards the instability threshold. However, grows while decreases in time, which is consistent with the description of Figure 2b. In general, simulations starting far below the instability threshold (i.e., for strongly unstable plasmas) saturate rapidly to a state at or above the instability threshold, with energies in the range . This is consistent with previous results for quasilinear simulations assuming a constant background of magnetosonic fluctuations [48], and shows that the firehose instability is dominant through the quasilinear evolution. The final state seems to modify the threshold condition, which are found to relax to temperature anisotropies following Equation (1) with , , and . Except for , these parameters are similar to the values obtained by Hellinger et al. [6], indicating that the presence of turbulence mainly modifies the minimum allowing the firehose instability. On the other hand, simulations starting near the instability threshold (i.e., weakly unstable plasmas) slowly settle into a state at or below the threshold, and with lower energies compared to the previous discussion. Thus, these results suggest that there exists a balance or competition between the energy transfer from turbulent waves and the presence of firehose instabilities near the instability threshold.
4. Discussion and Conclusions
In this work, we used a quasilinear moment theory to study the effects of a background spectrum of magnetosonic waves, propagating along a background magnetic field in a bi-Maxwellian proton plasma, in the relaxation of the temperature anisotropy. As an initial condition for these simulations, a Kolmogorov-like power-law magnetic spectrum with a spectral break at the ion inertial length was assumed. The main results are summarized into three parts. First, for initially stable plasmas, i.e., for temperature anisotropies slightly below , magnetosonic waves can experience damping for wavelengths around the ion inertial length, . This results in smoothing of the initial spectral break in such a way as to form a slump in the magnetic spectrum. As a result, protons become thermally anisotropic, and decreases at a rate depending both on the initial values of and magnetic energy , which is consistent with fully numerical simulations [31]. However, we found that an initial energy is insufficient to push the plasma to anisotropies below the instability thresholds. Thus, we conclude that a turbulent spectrum of magnetosonic waves alone is unable to excite a firehose instability from initially stable plasmas.
Second, for simulations starting far below the empirical instability threshold with (i.e., [6]), the plasma is strongly unstable to the firehose instability. During the quasilinear evolution, grows rapidly in time until its saturation around a value slightly above the instability threshold, with a new fitted curve of the form . Compared to the fits obtained by Hellinger et al. [6], we found similar parameters, except for , indicating that magnetosonic turbulence shifts the marginal stability thresholds towards smaller values, especially when is small. This suggests that the firehose instability is dominant over the turbulent cascade, which is consistent with solar-wind observations [12]. In addition, the initial magnetic spectrum grows in a band around the ion inertial length , resulting in a bump that smooths the spectral break. The magnetic spectrum is unmodified outside this band, which is consistent with observations in the Earth’s magnetosheath [54,55,56], and by the first PSP perihelion encounter [67].
These results differ from Moya and Navarro [29], where it is shown that the spectrum of both stable and unstable Alfvén-cyclotron waves steepens (the value of grows in time) in the kinetic range for . However, observations and numerical simulations consistently show finite values of in the kinetic range [57,58,59,60,61,62,63,64,65,66]. In addition, since near-Earth plasmas are usually found in a state with [6,7,68], we conclude that the observed power-law turbulent spectrum observed at kinetic scales is probably due to the coexistence of Alfvén-cyclotron and magnetosonic waves at different wavelengths, which is also consistent with numerical simulations of plasma turbulence [25,28]. Lastly, for weakly unstable plasmas (i.e., starting near the instability threshold), the firehose instability (whose effect is to increase ) competes with the effects of (to decrease ), resulting in temperature anisotropies that relax near the instability threshold with in a shorter time compared to highly unstable plasmas.
In summary, considering this work and the quasilinear simulations reported in Moya and Navarro [29], our results show that the presence of turbulence significantly modifies the temperature anisotropy of the plasma, and subsequently may lead the system to states out of thermal equilibrium. Alfvénic turbulence may result in an enhancement of temperature anisotropies (and a reduction in the parallel proton beta), whereas a turbulent spectrum of magnetosonic modes leads an initially thermally isotropic plasma to develop anisotropic states in which . It is important to mention that we considered parallel propagating magnetosonic fluctuations (with ), since the compressibility of the fluctuations in the solar wind is reportedly small near the firehose-instability thresholds [7], and the lower bounds of in the solar wind are consistent with the parallel proton-firehose instability [5].
However, we recognize that this may be considered a crude approximation, since turbulence in solar wind follows an anisotropic cascade with critical balance (). Our quasilinear model does not address the nonlinear cascade effects that could spread the turbulent wave energy to different spectral ranges. That is, the spectral transfer of turbulence by non-linear mode coupling is also ignored. This is a challenging problem and, as far as we know, there is no suitable analytical theory to describe such a spectral transfer effects yet. Nevertheless, at the same time, we believe that our simplified approach provides valuable insights into the problem of the heating of solar wind, which is generally observed in a thermally anisotropic state. We expect to expand the scope of our approach and results with a subsequent study considering, e.g., oblique propagating waves and the presence of other ion species such as alphas and proton beams, hopefully corroborating or improving the results of our reduced model.
Author Contributions
Conceptualization, R.E.N. and P.S.M.; methodology, R.E.N. and P.S.M.; formal analysis, R.E.N. and P.S.M.; investigation, R.E.N. and P.S.M.; writing—original draft preparation, R.E.N. and P.S.M.; writing—review and editing, R.E.N. and P.S.M. Both authors contributed equally to this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by ANID, Chile, through FONDECyT grants No. 11180947 (R.E.N.), and No. 1191351 (P.S.M.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FHI | Firehose instability |
| VDF | Velocity distribution function |
References
- Krall, N.A.; Trivelpiece, A.W. Principle of Plasma Physics; San Francisco Press Inc.: San Francisco, CA, USA, 1986. [Google Scholar]
- Stix, T. Waves in Plasmas; American Institute of Physics: College Park, MD, USA, 1992. [Google Scholar]
- Gary, S.P. Theory of Space Plasma Microinstabilities; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Seough, J.; Yoon, P.H.; Kim, K.H.; Lee, D.H. Solar-Wind Proton Anisotropy Versus Beta Relation. Phys. Rev. Lett. 2013, 110, 071103. [Google Scholar] [CrossRef] [PubMed]
- Yoon, P.H. Kinetic instabilities in the solar wind driven by temperature anisotropies. Rev. Mod. Plasma Phys. 2017, 1, 4. [Google Scholar] [CrossRef]
- Hellinger, P.; Trávníček, P.; Kasper, J.C.; Lazarus, A.J. Solar wind proton temperature anisotropy: Linear theory and WIND/SWE observations. Geophys. Res. Lett. 2006, 33, 2–5. [Google Scholar] [CrossRef]
- Bale, S.D.; Kasper, J.C.; Howes, G.G.; Quataert, E.; Salem, C.; Sundkvist, D. Magnetic Fluctuation Power Near Proton Temperature Anisotropy Instability Thresholds in the Solar Wind. Phys. Rev. Lett. 2009, 103, 211101. [Google Scholar] [CrossRef]
- Adrian, M.L.; Viñas, A.F.; Moya, P.S.; Wendel, D.E. Solar Wind Magnetic Fluctuations and Electron Non-thermal Temperature Anisotropy: Survey of Wind-SWE-VEIS Observations. Astrophys. J. 2016, 833, 49. [Google Scholar] [CrossRef]
- Matteini, L.; Landi, S.; Hellinger, P.; Pantellini, F.; Maksimovic, M.; Velli, M.; Goldstein, B.E.; Marsch, E. Evolution of the solar wind proton temperature anisotropy from 0.3 to 2.5 AU. Geophys. Res. Lett. 2007, 34, L20105. [Google Scholar] [CrossRef]
- Huang, J.; Kasper, J.C.; Vech, D.; Klein, K.G.; Stevens, M.; Martinović, M.M.; Alterman, B.L.; Ďurovcová, T.; Paulson, K.; Maruca, B.A.; et al. Proton Temperature Anisotropy Variations in Inner Heliosphere Estimated with the First Parker Solar Probe Observations. Astrophys. J. 2020, 246, 70. [Google Scholar] [CrossRef]
- Chew, G.F.; Goldberger, M.L.; Low, F.E.; Chandrasekhar, S. The Boltzmann equation an d the one-fluid hydromagnetic equations in the absence of particle collisions. Proc. R. Soc. Lond. A Math. Phys. Sci. 1956, 236, 112–118. [Google Scholar] [CrossRef]
- Woodham, L.D.; Wicks, R.T.; Verscharen, D.; Owen, C.J.; Maruca, B.A.; Alterman, B.L. Parallel-propagating Fluctuations at Proton-kinetic Scales in the Solar Wind Are Dominated By Kinetic Instabilities. Astrophys. J. Lett. 2019, 884, L53. [Google Scholar] [CrossRef]
- Gomberoff, L.; Elgueta, R. Resonant acceleration of a-particles by ion-cyclotron waves in the solar wind. J. Geophys. Res. 1991, 96, 9801–9804. [Google Scholar] [CrossRef]
- Gary, S.P.; McKean, M.E.; Winske, D.; Anderson, B.J.; Denton, R.E.; Fuselier, S.A. The proton cyclotron instability and the anisotropy/β inverse correlation. J. Geophys. Res. 1994, 99, 5903–5914. [Google Scholar] [CrossRef]
- Gomberoff, L.; Valdivia, J.A. Ion cyclotron instability due to the thermal anisotropy of drifting ion species. J. Geophys. Res. 2003, 108, 1050. [Google Scholar] [CrossRef]
- Yoon, P.H.; Seough, J.J.; Khim, K.K.; Kim, H.; Kwon, H.J.; Park, J.; Parkh, S.; Park, K.S. Analytic model of electromagnetic ion-cyclotron anisotropy instability. Phys. Plasmas 2010, 17, 082111. [Google Scholar] [CrossRef]
- Navarro, R.E.; Muñoz, V.; Araneda, J.; Viñas, A.F.; Moya, P.S.; Valdivia, J.A. Magnetic Alfvén-cyclotron fluctuations of anisotropic nonthermal plasmas. J. Geophys. Res. 2015, 120, 2382–2396. [Google Scholar] [CrossRef]
- Gary, S.P.; Li, H.; O’Rourke, S.; Winske, D. Proton resonant firehose instability: Temperature anisotropy and fluctuating field constraints. J. Geophys. Res. 1998, 103, 14567–14574. [Google Scholar] [CrossRef]
- Seough, J.; Yoon, P.H.; Hwang, J. Simulation and quasilinear theory of proton firehose instability. Phys. Plasmas 2015, 22, 012303. [Google Scholar] [CrossRef]
- Navarro, R.E.; Muñoz, V.; Valdivia, J.A.; Moya, P.S. Feasibility of Ion-cyclotron Resonant Heating in the Solar Wind. Astrophys. J. 2020, 898, L9. [Google Scholar] [CrossRef]
- Markovskii, S.A.; Vasquez, B.J. The Effect of Solar Wind Turbulence on Parallel and Oblique Firehose Instabilities. Astrophys. J. 2022, 924, 111. [Google Scholar] [CrossRef]
- Opie, S.; Verscharen, D.; Owen, C.J.; Isenberg, P.A. Conditions for proton temperature anisotropy to drive instabilities in the solar wind. Astrophys. J. 2022, 941, 176. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Qudsi, R.A.; Gary, S.P.; Matthaeus, W.H.; Parashar, T.N.; Maruca, B.A.; Roytershteyn, V.; Chasapis, A.; Giles, B.L.; Gershman, D.J.; et al. Interplay of turbulence and proton-microinstability growth in space plasmas. Phys. Plasmas 2022, 29, 102107. [Google Scholar] [CrossRef]
- Andrés, N.; Clark di Leoni, P.; Mininni, P.D.; Dmitruk, P.; Sahraoui, F.; Matthaeus, W.H. Interplay between Alfvén and magnetosonic waves in compressible magnetohydrodynamics turbulence. Phys. Plasmas 2017, 24, 102314. [Google Scholar] [CrossRef]
- Svidzinski, V.A.; Li, H.; Rose, H.A.; Albright, B.J.; Bowers, K.J. Particle in cell simulations of fast magnetosonic wave turbulence in the ion cyclotron frequency range. Phys. Plasmas 2009, 16, 122310. [Google Scholar] [CrossRef]
- Chandran, B.D.G. Weak Compressible Magnetohydrodynamic Turbulence in the Solar Corona. Phys. Rev. Lett. 2005, 95, 265004. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Lazarian, A. Compressible magnetohydrodynamic turbulence: Mode coupling, scaling relations, anisotropy, viscosity-damped regime and astrophysical implications. Mon. Not. R. Astron. Soc. 2003, 345, 325–339. [Google Scholar] [CrossRef]
- Sharma, R.P.; Kumar, S. Nonlinear coupling of kinetic Alfvén waves and magnetosonic waves in plasma. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Moya, P.S.; Navarro, R.E. Effects of the Background Turbulence on the Relaxation of Ion Temperature Anisotropy in Space Plasmas. Front. Phys. 2021, 9, 1–12. [Google Scholar] [CrossRef]
- Hellinger, P.; Trávníček, P. Parallel and oblique proton fire hose instabilities in the presence of alpha/proton drift: Hybrid simulations. J. Geophys. Res. 2006, 111, A01107. [Google Scholar] [CrossRef]
- Servidio, S.; Osman, K.T.; Valentini, F.; Perrone, D.; Califano, F.; Chapman, S.; Matthaeus, W.H.; Veltri, P. Proton Kinetic Effects in Vlasov and Solar Wind Turbulence. Astrophys. J. Lett. 2014, 781, L27. [Google Scholar] [CrossRef]
- Moya, P.S.; Viñas, A.F.; Muñoz, V.; Valdivia, J.A. Computational and Theoretical study of the wave-particle interaction of protons and waves. Ann. Geophys. 2012, 30, 1361–1369. [Google Scholar] [CrossRef][Green Version]
- Gomberoff, L.; Muñoz, V.; Valdivia, J.A. Ion cyclotron instability triggered by drifting minor ion species: Cascade effect and exact results. Planet. Space Sci. 2004, 52, 679–684. [Google Scholar] [CrossRef]
- Gary, S.P.; Tokar, R.L. The second-order theory of electromagnetic hot ion beam instabilities. J. Geophys. Res. 1985, 90, 65–72. [Google Scholar] [CrossRef]
- Fried, B.D.; Conte, S.D. The Plasma Dispersion Function; Academic: San Diego, CA, USA, 1961. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Yoon, P.H. Quasilinear evolution of Alfvén-ion-cyclotron and mirror instabilities driven by ion temperature anisotropy. Phys. Fluids B 1992, 4, 3627–3637. [Google Scholar] [CrossRef]
- Isenberg, P.A.; Vasquez, B.J. Preferential perpendicular heating of coronal hole minor ions by the Fermi mechanism. Astrophys. J. 2007, 668, 546–556. [Google Scholar] [CrossRef]
- Azevedo, J.C.d.A.; Vianna, M.L. Theory of Waves in Inhomogeneous Warm Plasmas. Phys. Rev. 1969, 177, 300–305. [Google Scholar] [CrossRef]
- Sharma, R.P.; Goyal, R.; Gaur, N.; Scime, E.E. Linear kinetic Alfvén waves in inhomogeneous plasma: Effects of Landau damping. EPL 2016, 113, 25001. [Google Scholar] [CrossRef]
- Noreen, N.; Yoon, P.H.; Zaheer, S. Cyclotron instabilities driven by temperature anisotropy in the solar wind. Phys. Plasmas 2017, 24, 102902. [Google Scholar] [CrossRef]
- Moya, P.S.; Navarro, R.; Viñas, A.F.; Muñoz, V.; Valdivia, J.A. Weak Turbulence Cascading Effects in the Acceleration and Heating of Ions in the Solar Wind. Astrophys. J. 2014, 781, 76. [Google Scholar] [CrossRef]
- Lazar, M.; Yoon, P.H.; López, R.A.; Moya, P.S. Electromagnetic Electron Cyclotron Instability in the Solar Wind. J. Geophys. Res. Space Phys. 2018, 123, 6–19. [Google Scholar] [CrossRef]
- Shaaban, S.M.; Lazar, M.; Yoon, P.H.; Poedts, S. Quasilinear approach of the cumulative whistler instability in fast solar wind: Constraints of electron temperature anisotropy. Astron. Astrophys. 2019, 627. [Google Scholar] [CrossRef]
- Sarfraz, M.; Yoon, P.H.; Saeed, S.; Abbas, G.; Shah, H.A. Macroscopic quasilinear theory of parallel electron firehose instability associated with solar wind electrons. Phys. Plasmas 2017, 24, 012907. [Google Scholar] [CrossRef]
- Ali, Z.; Sarfraz, M.; Yoon, P.H. Combined electron firehose and electromagnetic ion cyclotron instabilities: Quasilinear approach. Mon. Not. R. Astron. Soc. 2020, 499, 659–667. [Google Scholar] [CrossRef]
- Moya, P.S.; Muñoz, V.; Rogan, J.; Valdivia, J.A. Study of the Cascading Effect During the Acceleration and Heating of Ions in the Solar Wind. J. Atmos. Solar-Terr. Phys. 2011, 73, 1390–1397. [Google Scholar] [CrossRef]
- Seough, J.; Yoon, P.H. Quasilinear theory of anisotropy-beta relations for proton cyclotron and parallel firehose instabilities. J. Geophys. Res. 2012, 117, A08101. [Google Scholar] [CrossRef]
- Navarro, R.E.; Moya, P.S.; Muñoz, V.; Araneda, J.A.; Viñas, A.F.; Valdivia, J.A. Solar wind thermally induced magnetic fluctuations. Phys. Rev. Lett. 2014, 112, 1–5. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Wang, L.; Tu, C.; Marsch, E.; Zong, Q. Evidence of Landa and Cyclotron Resonance Between Protons and Kinetic Waves in Solar Wind Turbulence. Astrophys. J. 2015, 800, L31. [Google Scholar] [CrossRef]
- Malaspina, D.M.; Halekas, J.; Berčič, L.; Larson, D.; Whittlesey, P.; Bale, S.D.; Bonnell, J.W.; de Wit, T.D.; Ergun, R.E.; Howes, G.; et al. Plasma Waves near the Electron Cyclotron Frequency in the Near-Sun Solar Wind. Astrophys. J. Suppl. Ser. 2020, 246, 21. [Google Scholar] [CrossRef]
- Muller, D.E. A Method for Solving Algebraic Equations Using an Automatic Computer. Math. Tables Other Aids Comput. 1956, 10, 208–215. [Google Scholar] [CrossRef]
- Astudillo, H.F. High-order modes of left-handed electromagnetic waves in a solar-wind-like plasma. J. Geophys. Res. 1996, 101, 24433. [Google Scholar] [CrossRef]
- Alexandrova, O.; Mangeney, A.; Maksimovic, M.; Cornilleau-Wehrlin, N.; Bosqued, J.M.; André, M. Alfvén vortex filaments observed in magnetosheath downstream of a quasi-perpendicular bow shock. J. Geophys. Res. Space Phys. 2006, 111, A12208. [Google Scholar] [CrossRef]
- Alexandrova, O.; Lacombe, C.; Mangeney, A. Spectra and anisotropy of magnetic fluctuations in the Earth’s magnetosheath: Cluster observations. Ann. Geophys. 2008, 26, 3585–3596. [Google Scholar] [CrossRef]
- Rakhmanova, L.; Riazantseva, M.; Zastenker, G. Plasma and Magnetic Field Turbulence in the Earth’s Magnetosheath at Ion Scales. Front. Astron. Space Sci. 2021, 7, 115. [Google Scholar] [CrossRef]
- Alexandrova, O.; Carbone, V.; Veltri, P.; Sorriso-Valvo, L. Small-Scale Energy Cascade of the Solar Wind Turbulence. Astrophys. J. 2008, 674, 1153–1157. [Google Scholar] [CrossRef]
- Boldyrev, S.; Perez, J.C. Spectrum of Kinetic-Alfvén Turbulence. Astrophys. J. 2012, 758, L44. [Google Scholar] [CrossRef]
- Chaston, C.C.; Bonnell, J.W.; Wygant, J.R.; Mozer, F.; Bale, S.D.; Kersten, K.; Breneman, A.W.; Kletzing, C.A.; Kurth, W.S.; Hospodarsky, G.B.; et al. Observations of kinetic scale field line resonances. Geophys. Res. Lett. 2014, 41, 209–215. [Google Scholar] [CrossRef]
- Moya, P.S.; Pinto, V.A.; Viñas, A.F.; Sibeck, D.G.; Kurth, W.S.; Hospodarsky, G.B.; Wygant, J.R. Weak kinetic Alfvén waves turbulence during the 14 November 2012 geomagnetic storm: Van Allen Probes observations. J. Geophys. Res. Space Phys. 2015, 120, 5504–5523. [Google Scholar] [CrossRef]
- Gamayunov, K.V.; Engebretson, M.J.; Zhang, M.; Rassoul, H.K. Source of seed fluctuations for electromagnetic ion cyclotron waves in Earth’s magnetosphere. Adv. Space Res. 2015, 55, 2573–2583. [Google Scholar] [CrossRef]
- Goldstein, M.L.; Wicks, R.T.; Perri, S.; Sahraoui, F. Kinetic scale turbulence and dissipation in the solar wind: Key observational results and future outlook. Phil. Trans. R. Soc. A 2015, 373, 20140147. [Google Scholar] [CrossRef]
- Franci, L.; Landi, S.; Matteini, L.; Verdini, A.; Hellinger, P. High-Resolution Hybrid Simulations of Kinetic Plasma Turbulence at Proton Scales. Astrophys. J. 2015, 812, 21. [Google Scholar] [CrossRef]
- Arzamasskiy, L.; Kunz, M.W.; Chandran, B.D.G.; Quataert, E. Hybrid-kinetic Simulations of Ion Heating in Alfvénic Turbulence. Astrophys. J. 2019, 879, 53. [Google Scholar] [CrossRef]
- Cerri, S.S.; Grošelj, D.; Franci, L. Kinetic Plasma Turbulence: Recent Insights and Open Questions From 3D3V Simulations. Front. Astron. Space Sci. 2019, 6, 64. [Google Scholar] [CrossRef]
- Franci, L.; Sarto, D.D.; Papini, E.; Giroul, A.; Stawarz, J.E.; Burgess, D.; Hellinger, P.; Landi, S.; Bale, S.D. Evidence of a “current-mediated” turbulent regime in space and astrophysical plasmas. arXiv 2020, arXiv:2010.05048. [Google Scholar]
- Bowen, T.A.; Bale, S.D.; Bonnell, J.W.; Dudok de Wit, T.; Goetz, K.; Goodrich, K.; Gruesbeck, J.; Harvey, P.R.; Jannet, G.; Koval, A.; et al. A Merged Search-Coil and Fluxgate Magnetometer Data Product for Parker Solar Probe FIELDS. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027813. [Google Scholar] [CrossRef]
- Wilson, L.B.; Stevens, M.L.; Kasper, J.C.; Klein, K.G.; Maruca, B.A.; Bale, S.D.; Bowen, T.A.; Pulupa, M.P.; Salem, C.S. The Statistical Properties of Solar Wind Temperature Parameters Near 1 AU. Astrophys. J. Suppl. Ser. 2018, 236, 41. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).