Dynamics of a Cosmological Model in f(R,T) Gravity: II. In Three-Dimensional Space
Abstract
1. Introduction
2. Field Equations of Gravity
3. Dynamic Analysis of the Model
3.1. Dynamic Equations
3.2. Dynamic Analysis in Three-Dimensional Space
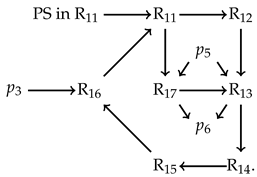
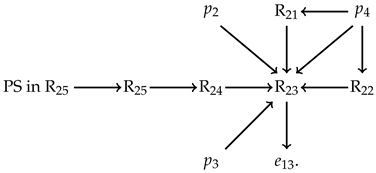
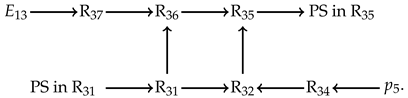
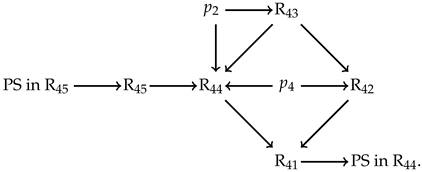
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- de Bernardis, P.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; Gasperis, G.D.; Farese, P.C.; et al. A flat Universe from high-resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955–959. [Google Scholar] [CrossRef]
- Bennett, B.C.L.; Hill, R.S.; Hinshaw, G.; Nolta, M.R.; Odegard, N.; Page, L.; Spergel, D.N.; Weiland, J.L.; Wright, E.L.; Halpern, M.; et al. First-year wilkinson microwave anisotropy probe (WMAP)* observations: Foreground emission. Astrophys. J. Suppl. Ser. 2003, 148, 97. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-year Wilkinson Microwave Anisotropy Probe (WMAP)* observations: Determination of cosmological parameters. Astrophys. J. Suppl. Ser. 2003, 148, 175. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Bennett, C.L.; Bay, M.; Halpern, M.; Hinshaw, G.; Jackson, C.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; Page, L.; et al. The microwave anisotropy probe* mission. Astrophys. J. 2003, 583, 1. [Google Scholar] [CrossRef]
- Peeebles, P.J.E. Probing general relativity on the scales of cosmology. Gen. Relativ. Gravit. 2005, 106–117. [Google Scholar]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.-Q. Quintom cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Errehymy, A.; Daoud, M. Studies an analytic model of a spherically symmetric compact object in Einsteinian gravity. Eur. Phys. J. C 2020, 80, 1–12. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living. Rev. Relativ. 2010, 13, 1–161. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Modified Gauss–Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D.; Gorbunova, O.G. Dark energy problem: From phantom theory to modified Gauss–Bonnet gravity. J. Phys. A Math. Gen. 2006, 39, 6627. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.I.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Otalora, G.; Saridakis, E.N. f(T,T) gravity and cosmology. J. Cosmol. Astropart. Phys. 2014, 2014, 021. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP. Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Tsujikawa, S. Observational signatures of f(R) dark energy models that satisfy cosmological and local gravity constraints. Phys. Rev. D 2007, 77, 023507. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D.; Sáez-Gómez, D. Cosmological reconstruction of realistic modified f(R) gravities. Phys. Lett. B 2009, 681, 74–80. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D.; Oikonomou, V.K. Unifying inflation with early and late-time dark energy in f(R) gravity. Phys. Dark Universe 2020, 29, 100602. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary cosmology in modified gravity theories. Symmetry 2015, 7, 220–240. [Google Scholar] [CrossRef]
- Sebastiani, L.; Myrzakulov, R. F(R)-gravity and inflation. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1530003. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Junction conditions in Palatini f(R) gravity. Class. Quantum Gravity 2020, 37, 215002. [Google Scholar] [CrossRef]
- Capozziello, S.; Mantica, C.A.; Molinari, L.G. Cosmological perfect-fluids in f(R) gravity. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950008. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Unifying of inflation with early and late dark energy epochs in axion f(R) gravity. Phys. Rev. D 2021, 103, 044036. [Google Scholar] [CrossRef]
- Arora, S.; Mandal, S.; Chakraborty, S.; Leon, G.; Sahoo, P.K. Can f(R) gravity isotropise a pre-bounce contracting universe? J. Cosmol. Astropart. Phys. 2022, 2022, 042. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Thermodynamics in f(R,T) theory of gravity. J. Cosmol. Astropart. Phys. 2012, 2012, 028. [Google Scholar] [CrossRef]
- Houndjo, M.J.S.; Alvarenga, F.G.; Rodrigues, M.E.; Jardim, D.F.; Myrzakulov, R. Thermodynamics in Little Rip cosmology in the framework of a type of f(R,T) gravity. Eur. Phys. J. Plus 2014, 129, 1–12. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Sahoo, P.K. Redshift drift in f(R,T) gravity. New Astron. 2020, 81, 101425. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. Nonexotic matter wormholes in a trace of the energy-momentum tensor squared gravity. Phys. Rev. D 2018, 57, 024007. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z.; Ilyas, M. Existence of wormhole solutions and energy conditions in f(R,T) gravity. J. Astrophys. 2018, 39, 1–11. [Google Scholar] [CrossRef]
- Alves, M.E.S.; Moraes, P.H.R.S.; De Araujo, J.C.N.; Malheiro, M. Gravitational waves in f(R,T) and f(R,Tϕ) theories of gravity. Phys. Rev. D 2016, 94, 024032. [Google Scholar] [CrossRef]
- Sharif, M.; Siddiqa, A. Propagation of polar gravitational waves in f(R,T) scenario. Gen. Relativ. Gravit. 2019, 51, 74. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Bhattacharjee, S. Gravitational baryogenesis in non-minimal coupled f(R,T) gravity. Int. J. Theor. Phys. 2020, 59, 1451–1459. [Google Scholar] [CrossRef]
- Shamir, M.F.; Jhangeer, A.; Bhatti, A.A. Exact solutions of Bianchi types I and V models in f(R,T) gravity. arXiv 2012, arXiv:1207.0708. [Google Scholar]
- Alvarenga, F.G.; De La Cruz-Dombriz, A.; Houndjo, M.J.S.; Rodrigues, M.E.; Sáez-Gómez, D. Dynamics of scalar perturbations in f(R,T) gravity. Phys. Rev. D 2013, 87, 103526. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Sahoo, P.K. Big bang nucleosynthesis and entropy evolution in f(R,T) gravity. Eur. Phys. J. Plus 2020, 135, 1–10. [Google Scholar] [CrossRef]
- Azmat, H.; Zubair, M. An anisotropic version of Tolman VII solution in f(R,T) gravity via gravitational decoupling MGD approach. Eur. Phys. J. Plus 2021, 136, 1–17. [Google Scholar] [CrossRef]
- Shaikh, A.Y. Panorama behaviors of general relativistic hydrodynamics and holographic dark energy in f(R,T) gravity. New Astron. 2022, 91, 101676. [Google Scholar] [CrossRef]
- Gashti, S.N.; Sadeghi, J.; Upadhyay, S.; Alipour, M.R. Swampland dS conjecture in mimetic f(R,T) gravity. Commun. Theor. Phys. 2022, 74, 085402. [Google Scholar] [CrossRef]
- Gonçalves, T.B.; Rosa, J.L.; Lobo, F.S. Cosmology in scalar-tensor f(R,T) gravity. Phys. Rev. D 2022, 105, 064019. [Google Scholar] [CrossRef]
- Santos, A.F. Gödel solution in f(R,T) gravity. Mod. Phys. Lett. A 2013, 28, 1350141. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z.; Yousaf, M. Stability of self-gravitating anisotropic fluids in f(R,T) gravity. Phys. Dark Universe 2020, 28, 100501. [Google Scholar] [CrossRef]
- Sharif, M.; Zubair, M. Cosmological reconstruction and stability in f(R,T) gravity. Gen. Relativ. Gravit. 2014, 46, 1723. [Google Scholar] [CrossRef]
- Singh, C.P.; Singh, V. Reconstruction of modified f(R,T) gravity with perfect fluid cosmological models. Gen. Relativ. Gravit. 2014, 46, 1696. [Google Scholar] [CrossRef]
- Azmat, H.; Zubair, M.; Ahmad, Z. Study of anisotropic and non-uniform gravastars by gravitational decoupling in f(R,T) gravity. Ann. Phys. 2022, 439, 168769. [Google Scholar] [CrossRef]
- Koussour, M.; Bennai, M. On a Bianchi type-I space-time with bulk viscosity in f(R,T) gravity. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250038. [Google Scholar] [CrossRef]
- Shabani, H.; Farhoudi, M. f(R,T) cosmological models in phase space. Phys. Rev. D 2013, 88, 044048. [Google Scholar] [CrossRef]
- Guo, J.Q.; Frolov, A.V. Cosmological dynamics in f(R) gravity. Phys. Rev. D 2013, 88, 124036. [Google Scholar] [CrossRef]
- Zonunmawia, H.; Khyllep, W.; Dutta, J.; Järv, L. Cosmological dynamics of brane gravity: A grobal dynamical system perspective. Phys. Rev. D 2018, 98, 083532. [Google Scholar] [CrossRef]
- Singh, A.; Singh, G.P.; Pradhan, A. Cosmic dynamics and qualitative study of Rastall model with spatial curvature. Int. J. Mod. Phys. A 2022, 37, 2250104. [Google Scholar] [CrossRef]
- Gao, F.B.; Llibre, J. Global dynamics of the Hořava-Lifshitz cosmological system. Gen. Relativ. Gravit. 2019, 51, 152. [Google Scholar] [CrossRef]
- Gao, F.B.; Llibre, J. Global dynamics of Hořava-Lifshitz cosmology with non-zero curvature and a wide range of potentials. Eur. Phys. J. C 2020, 80, 137. [Google Scholar] [CrossRef]
- Gao, F.B.; Llibre, J. Global dynamics of the Hořava-Lifshitz cosmological model in a non-flat universe with non-zero cosmological constant. Universe 2021, 7, 445. [Google Scholar] [CrossRef]
- Gao, F.B.; Llibre, J. Global dynamics of the Hořava-Lifshitz cosmology in the presence of non-zero cosmological constant in a flat space. Phys. Dark Universe 2022, 38, 101139. [Google Scholar] [CrossRef]
- Liu, J.W.; Wang, R.F.; Gao, F.B. Dynamics of a cosmological model in f(R,T) gravity: I. on invariant planes. Universe 2022, 8, 365. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 62, 043511. [Google Scholar] [CrossRef]
- Dumortier, F.; Llibre, J.; Ateés, J.C. Qualitative Theory of Planar Differential Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
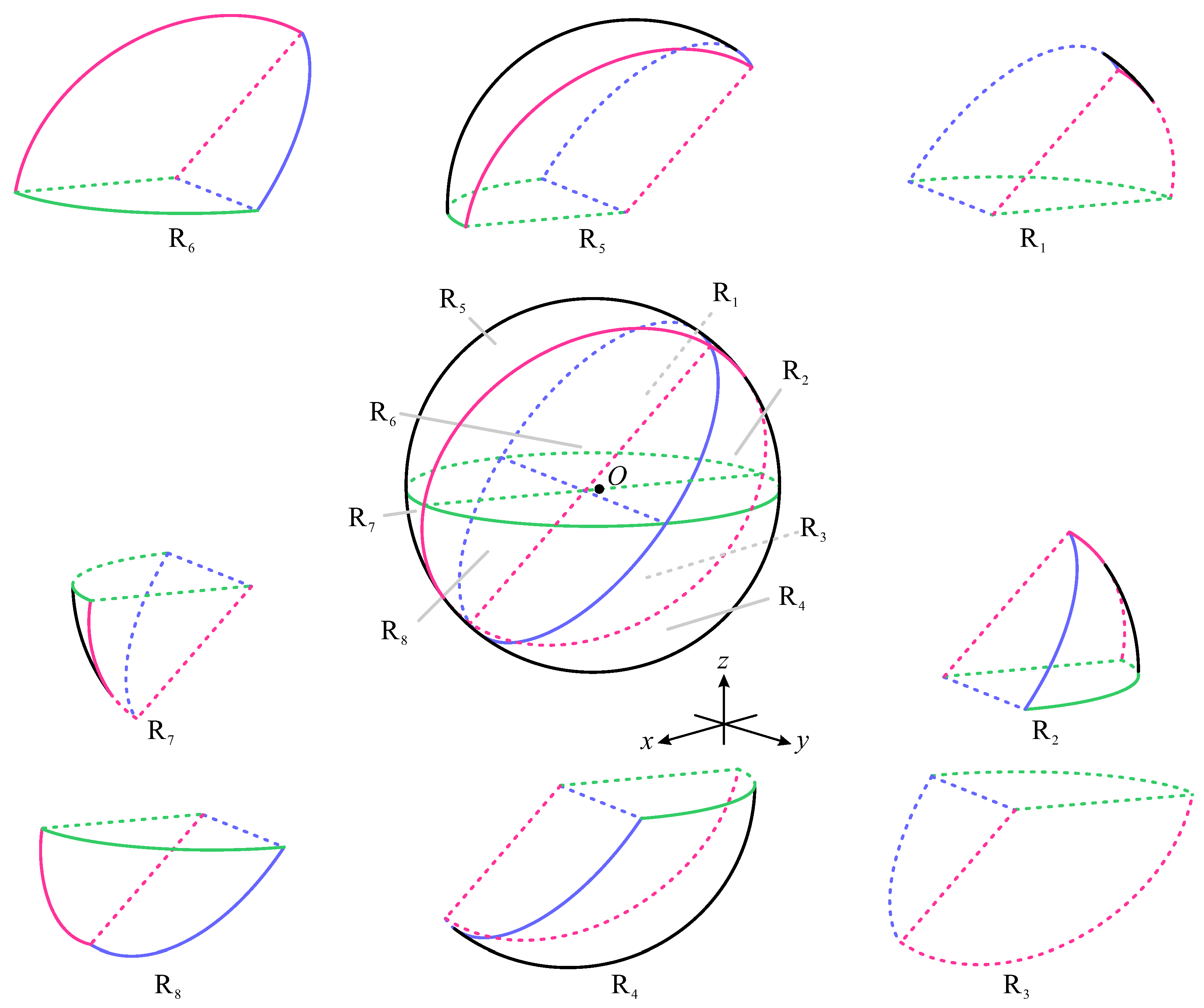
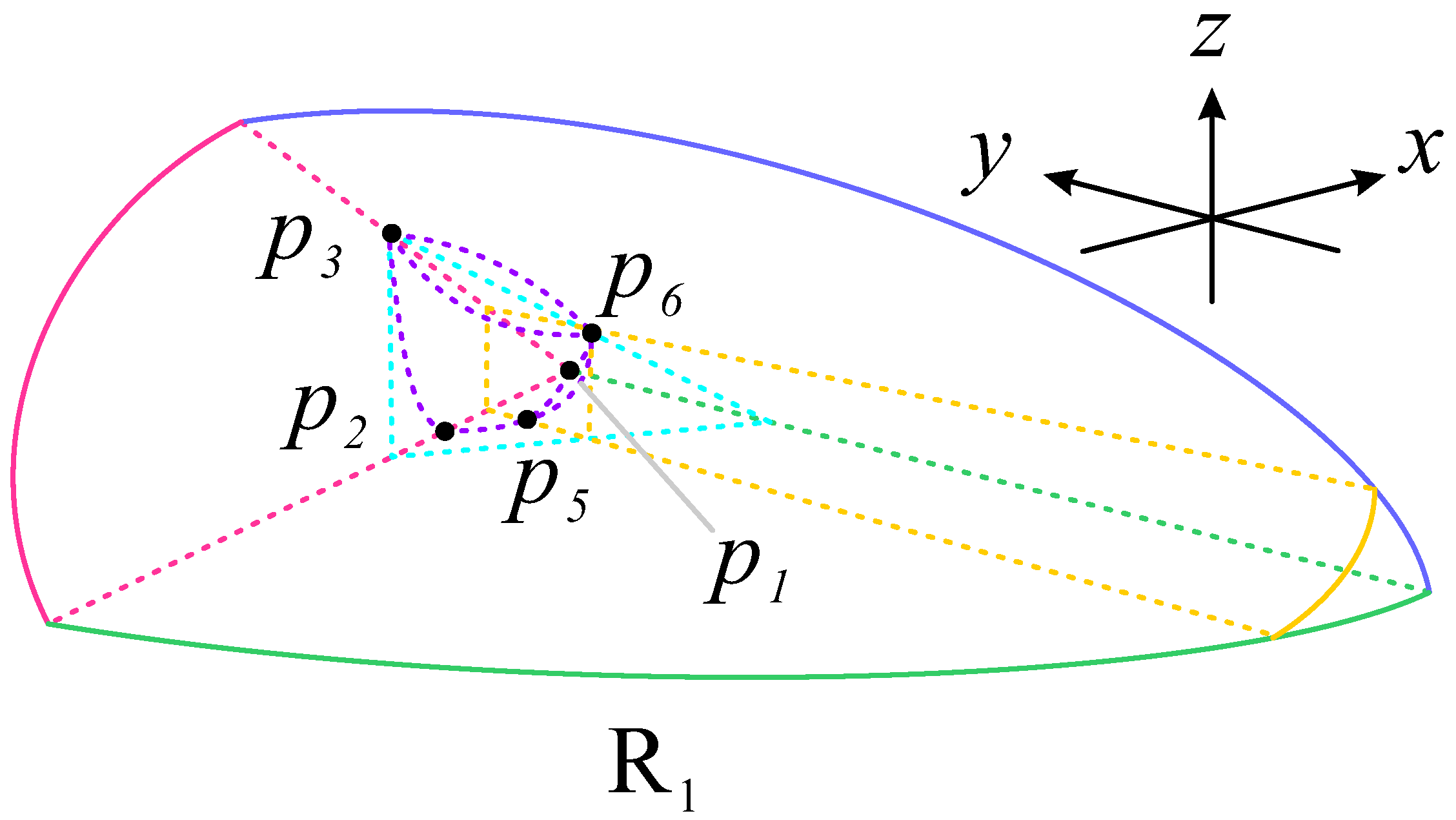
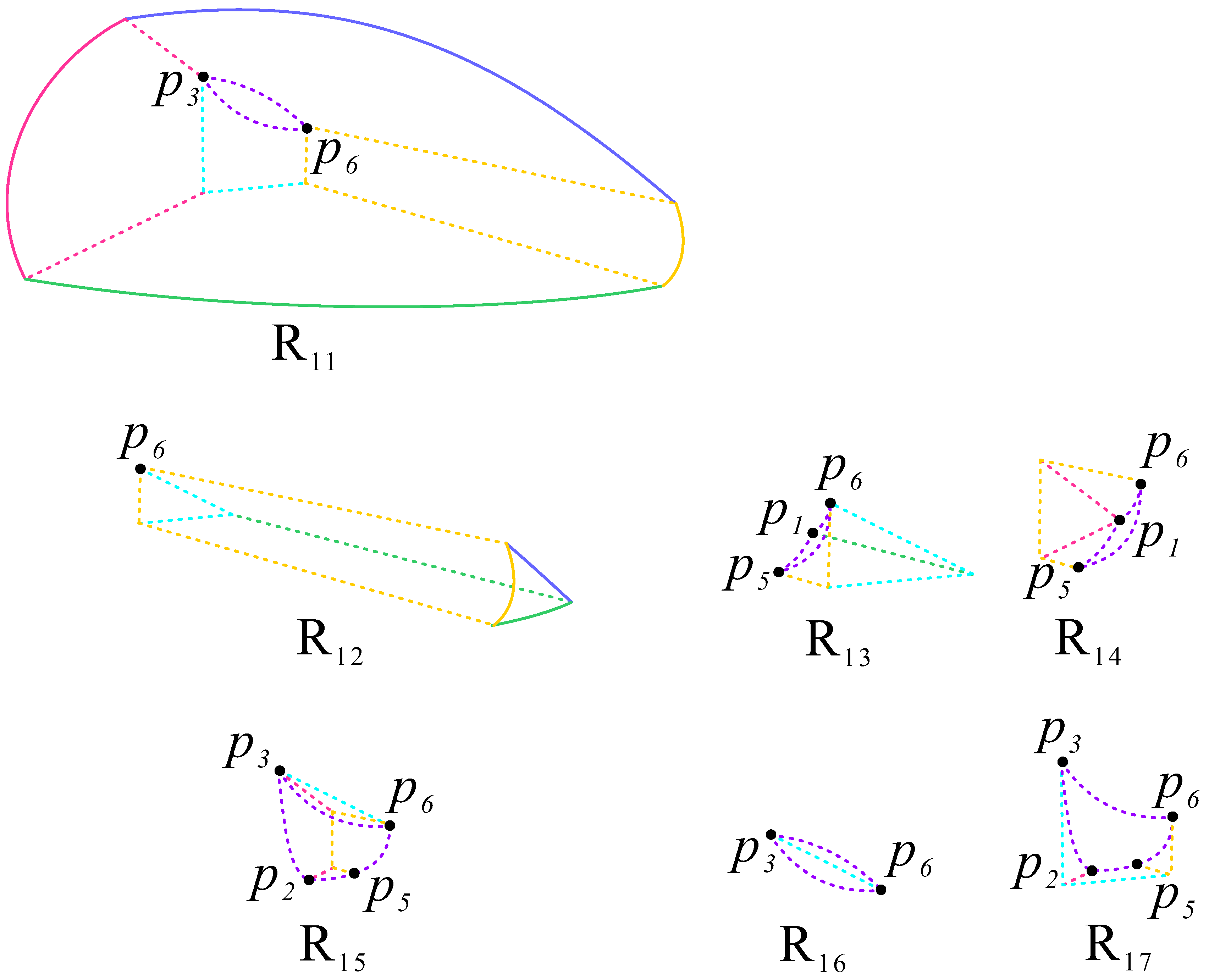

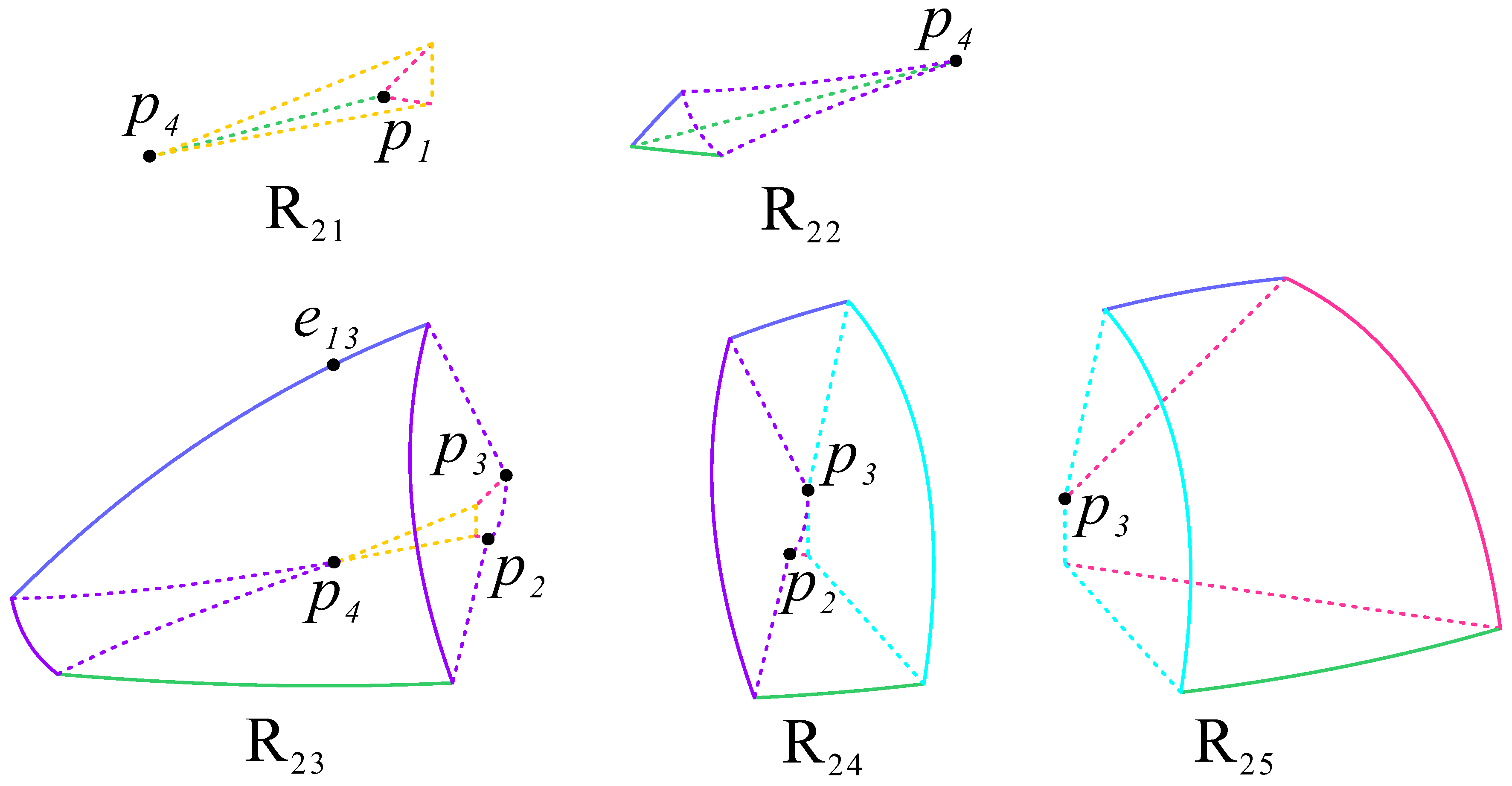
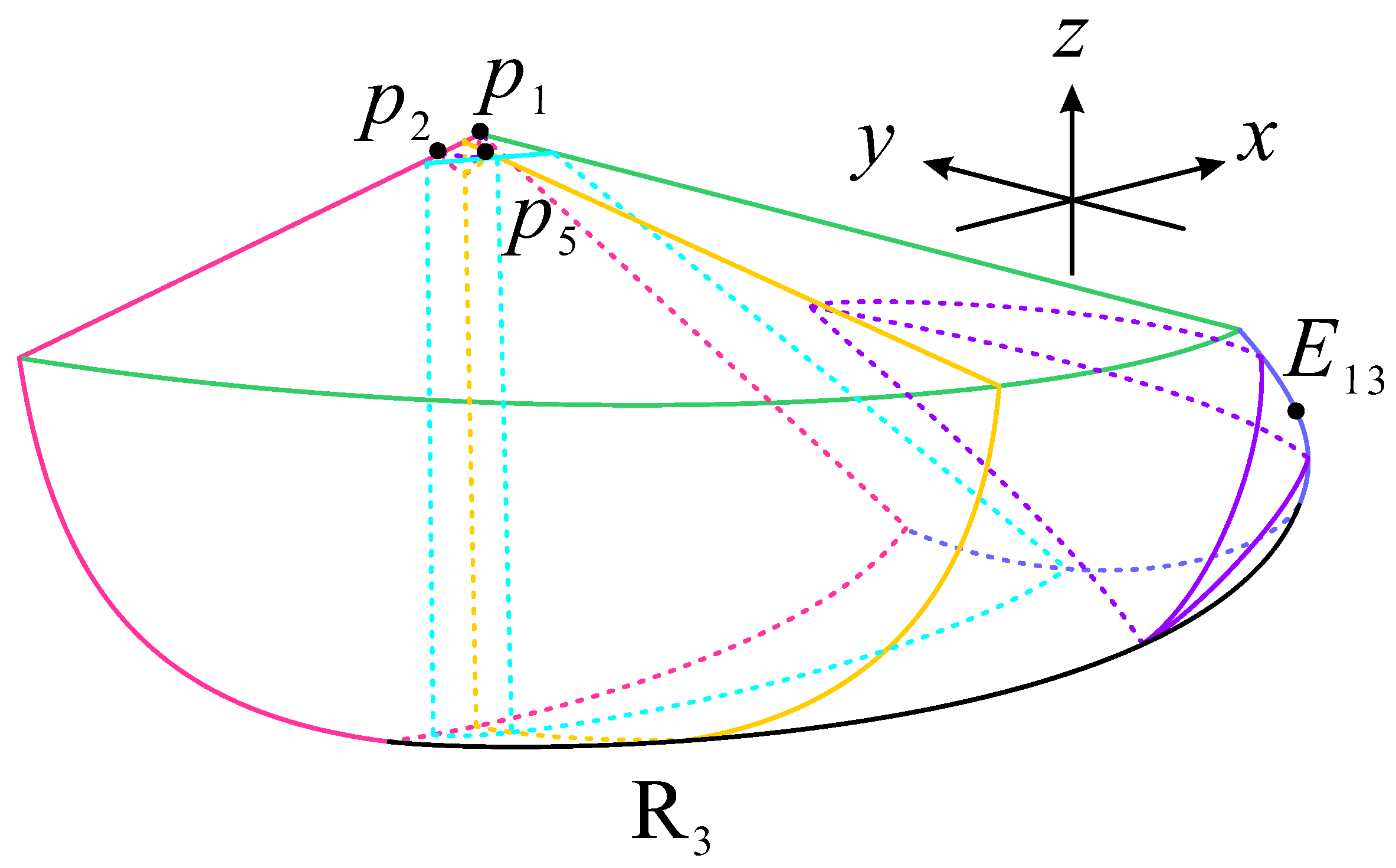

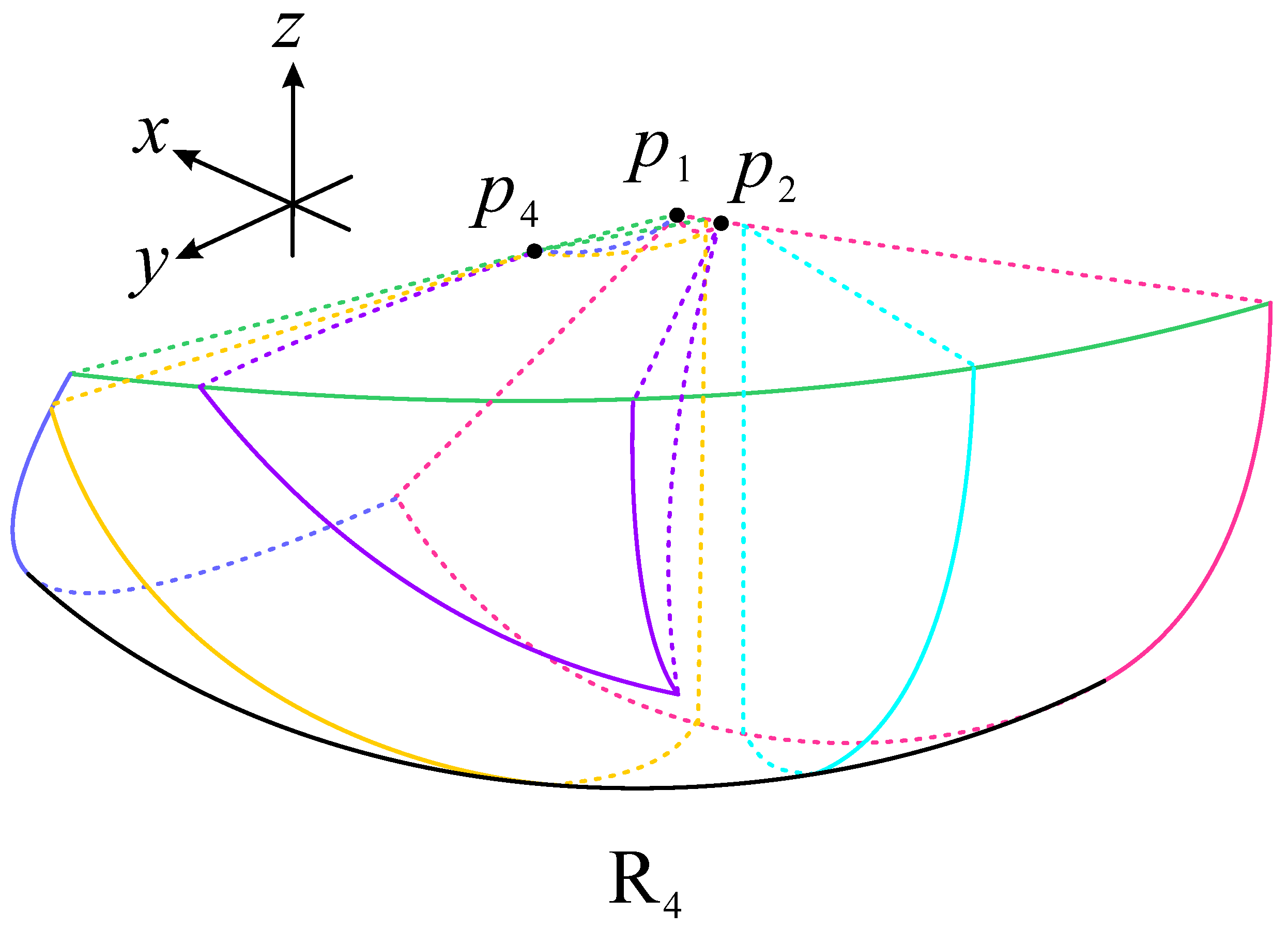
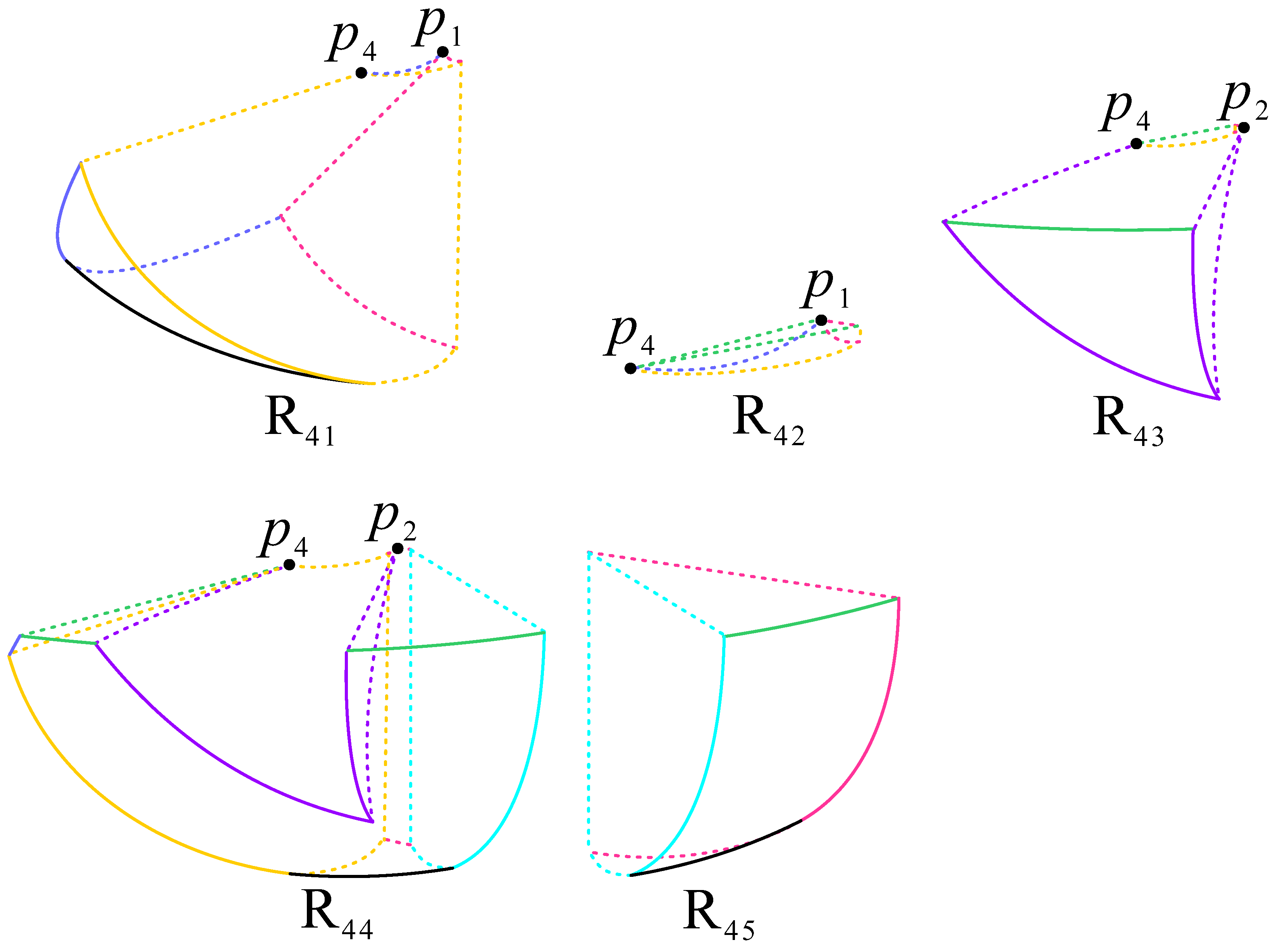
| Point | Coordinates | Scale Factor | Stability | ||
|---|---|---|---|---|---|
| () | 0 | saddle | |||
| () | 2 | saddle | |||
| () | 0 | saddle | |||
| () | 0 | 4 | unstable | ||
| () | unstable | ||||
| () | 0 | stable |
| Subregion | Corresponding Region | Dynamic Behavior |
|---|---|---|
| Subregion | Corresponding Region | Dynamic Behavior |
|---|---|---|
| Subregion | Corresponding Region | Dynamic Behavior |
|---|---|---|
| Subregion | Corresponding Region | Dynamic Behavior |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, R.; Gao, F. Dynamics of a Cosmological Model in f(R,T) Gravity: II. In Three-Dimensional Space. Universe 2023, 9, 49. https://doi.org/10.3390/universe9010049
Liu J, Wang R, Gao F. Dynamics of a Cosmological Model in f(R,T) Gravity: II. In Three-Dimensional Space. Universe. 2023; 9(1):49. https://doi.org/10.3390/universe9010049
Chicago/Turabian StyleLiu, Jianwen, Ruifang Wang, and Fabao Gao. 2023. "Dynamics of a Cosmological Model in f(R,T) Gravity: II. In Three-Dimensional Space" Universe 9, no. 1: 49. https://doi.org/10.3390/universe9010049
APA StyleLiu, J., Wang, R., & Gao, F. (2023). Dynamics of a Cosmological Model in f(R,T) Gravity: II. In Three-Dimensional Space. Universe, 9(1), 49. https://doi.org/10.3390/universe9010049






