An Attempt to Construct an Activity Cycle Catalog with Kepler Long-Cadence Light Curves
Abstract
1. Introduction
2. Data
2.1. Data Selection
2.2. Pre-Processing Kepler Light Curves
2.2.1. Correction for Instrument Modulation
2.2.2. Correction for Discontinuity in Kepler Light Curves
3. Method, Validation, and Results
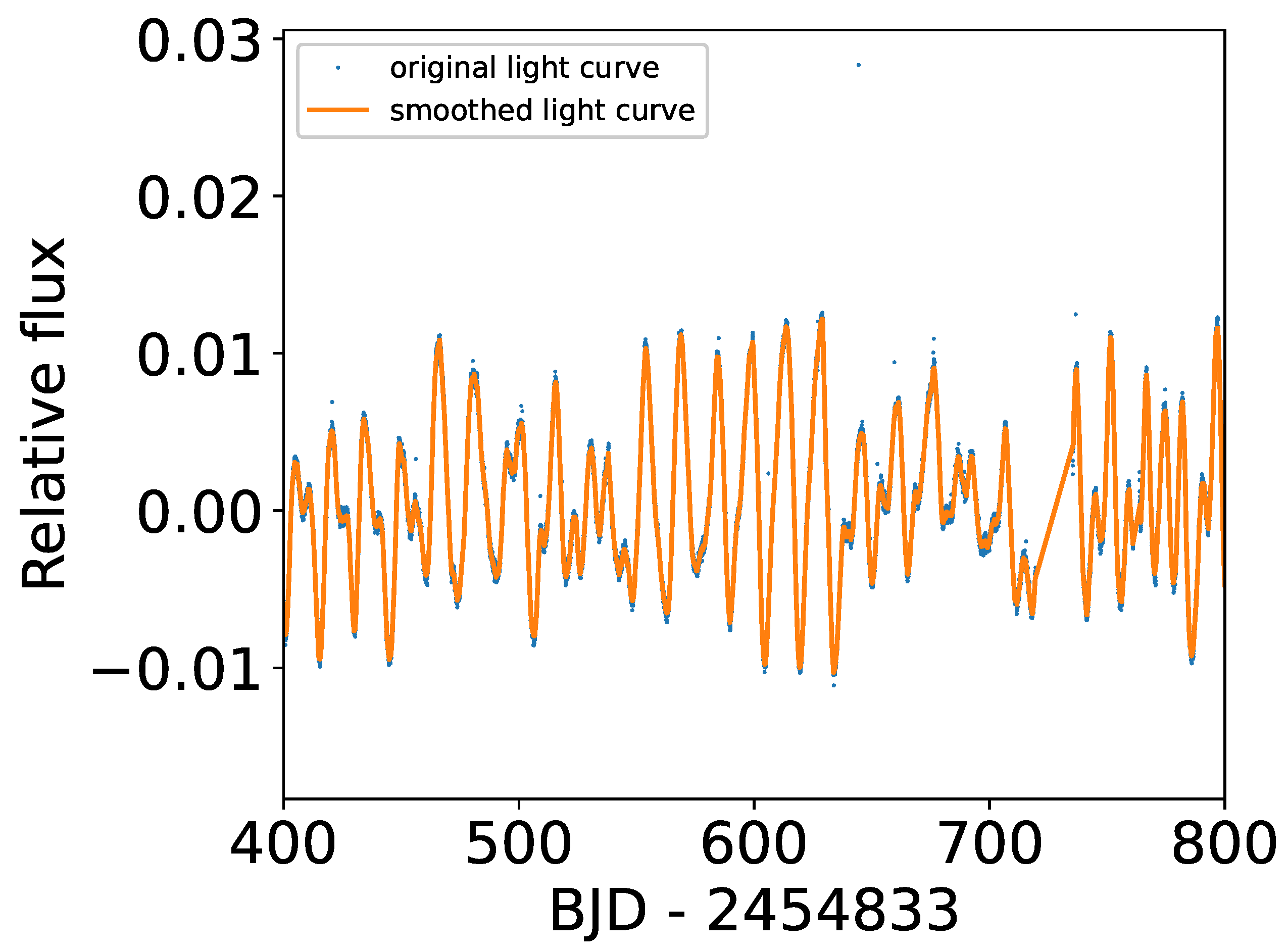
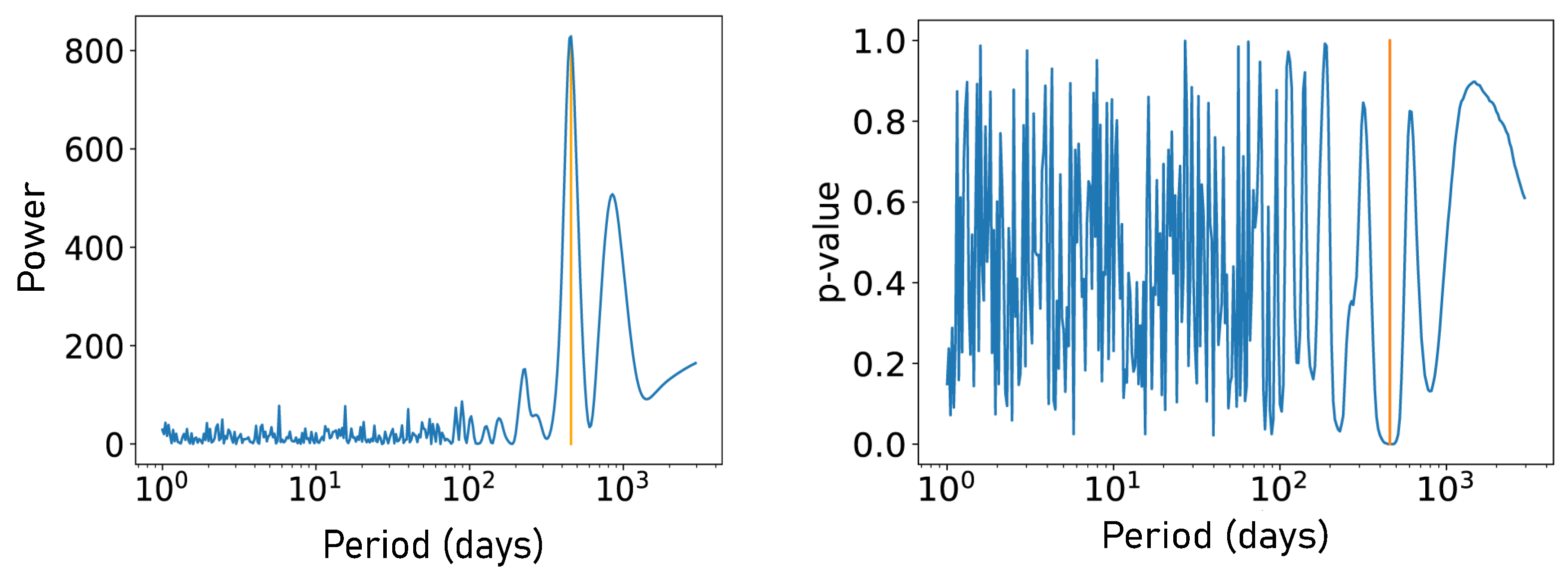
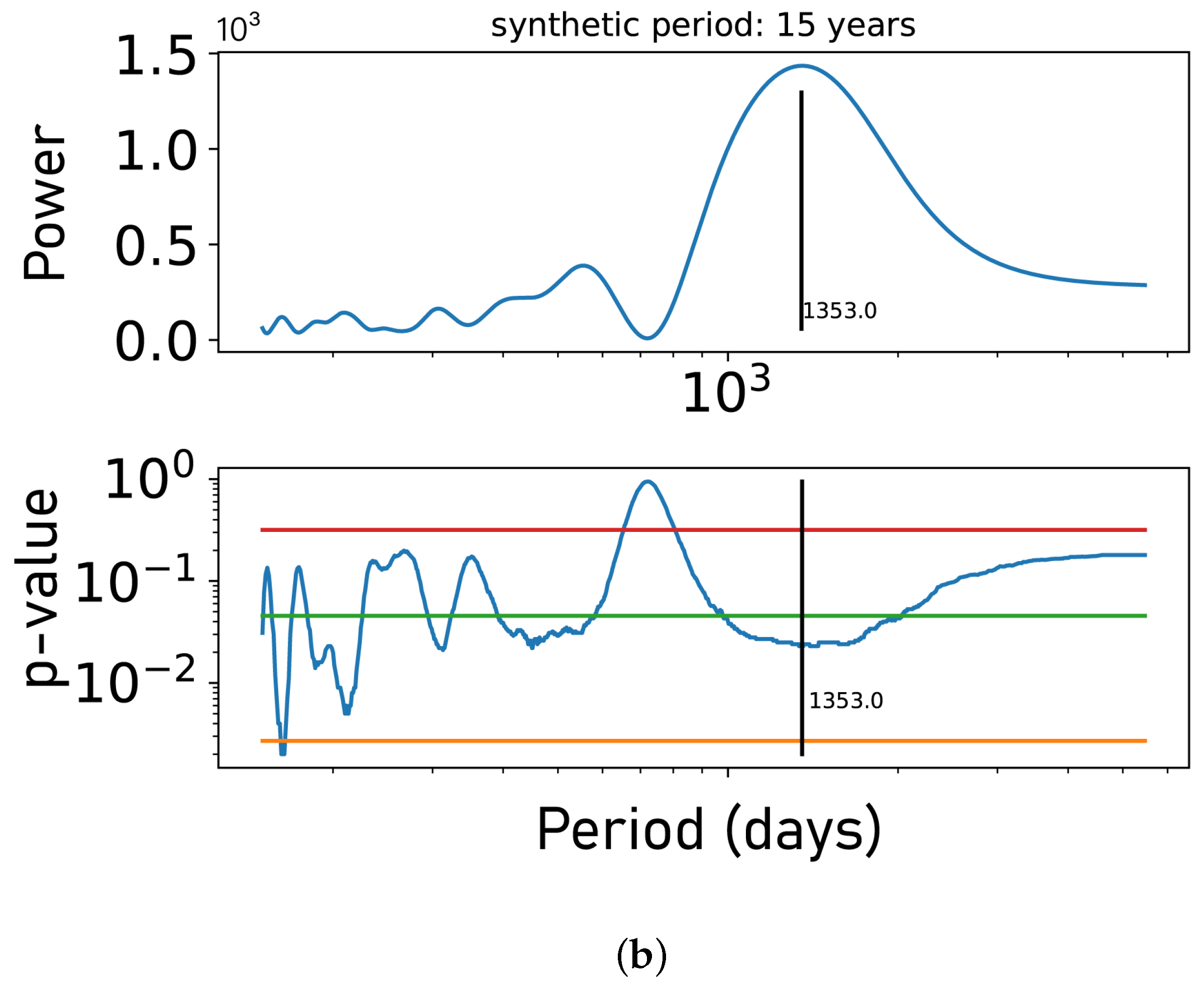
3.1. Method
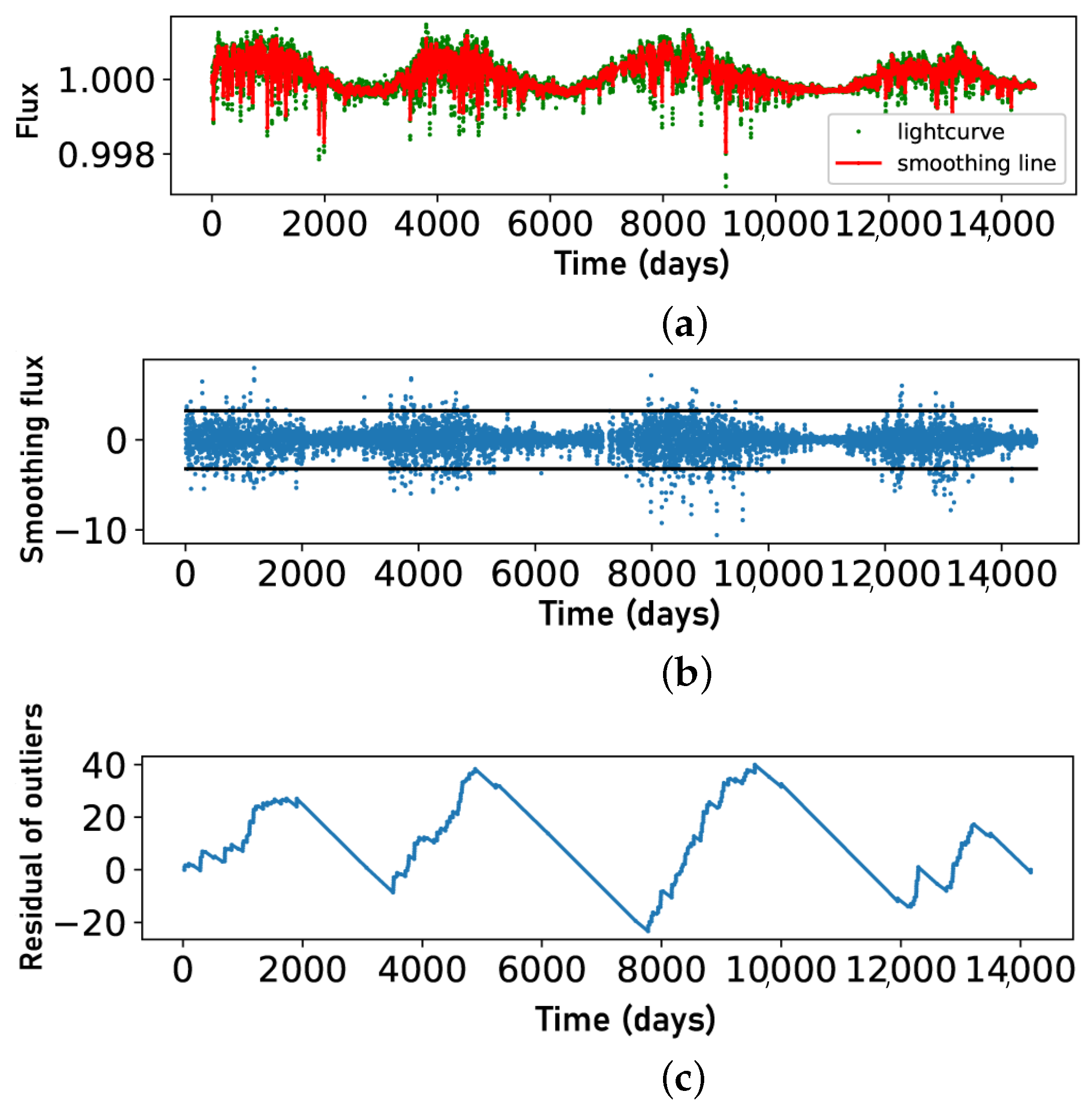
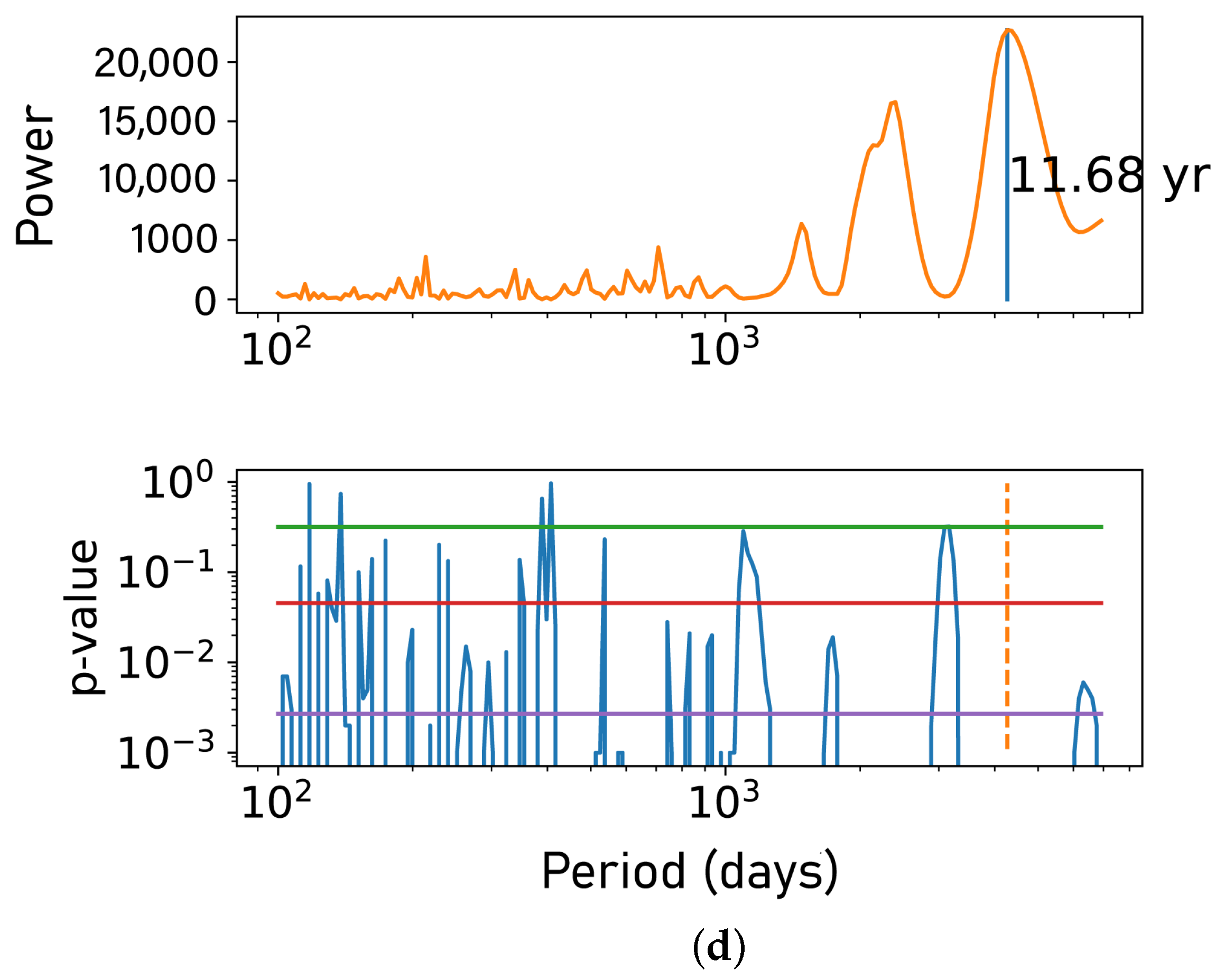
3.2. Validation with TSI Data
3.3. Result of the 92,084 Kepler Targets and the Disturbance Factors
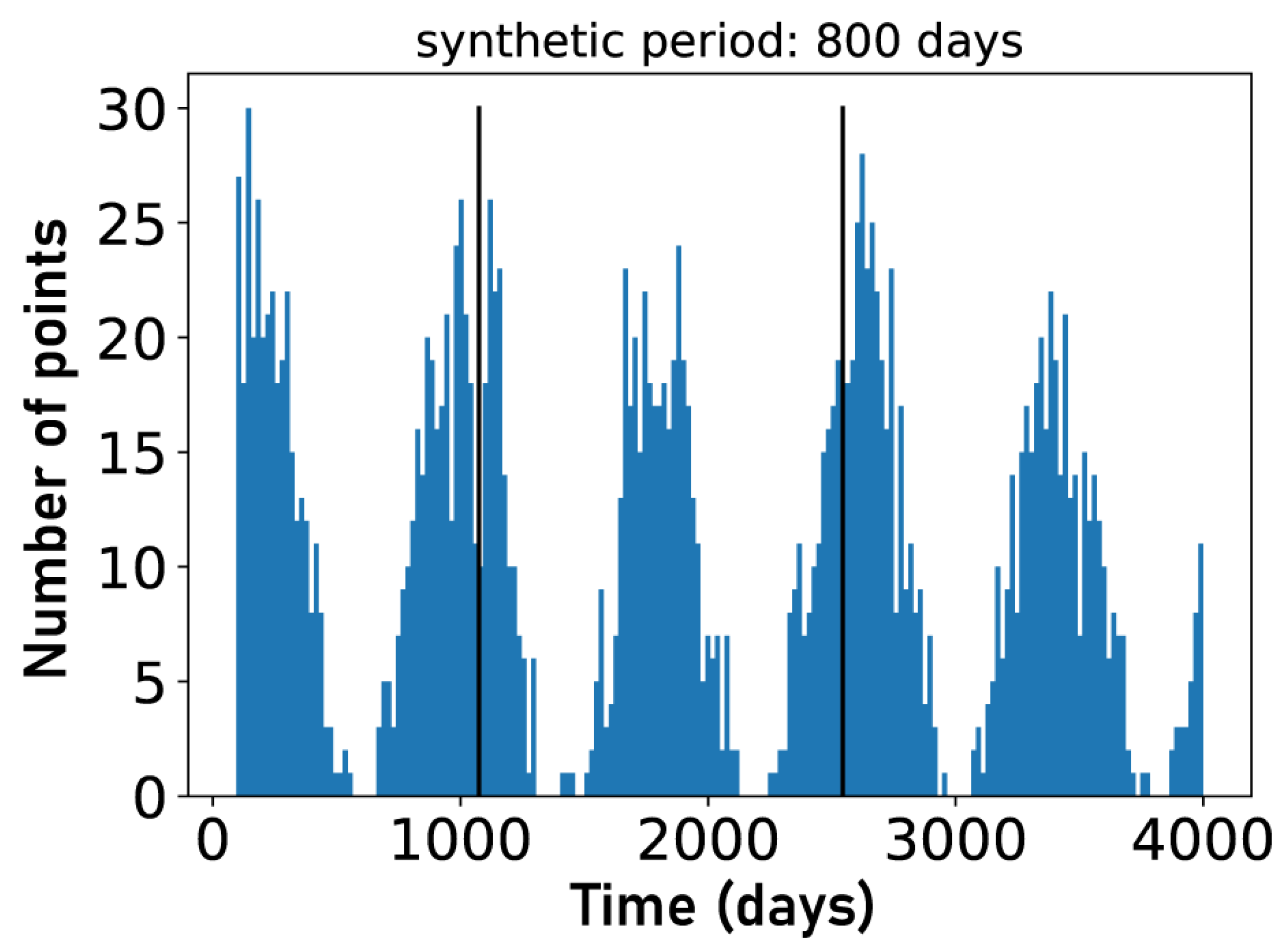
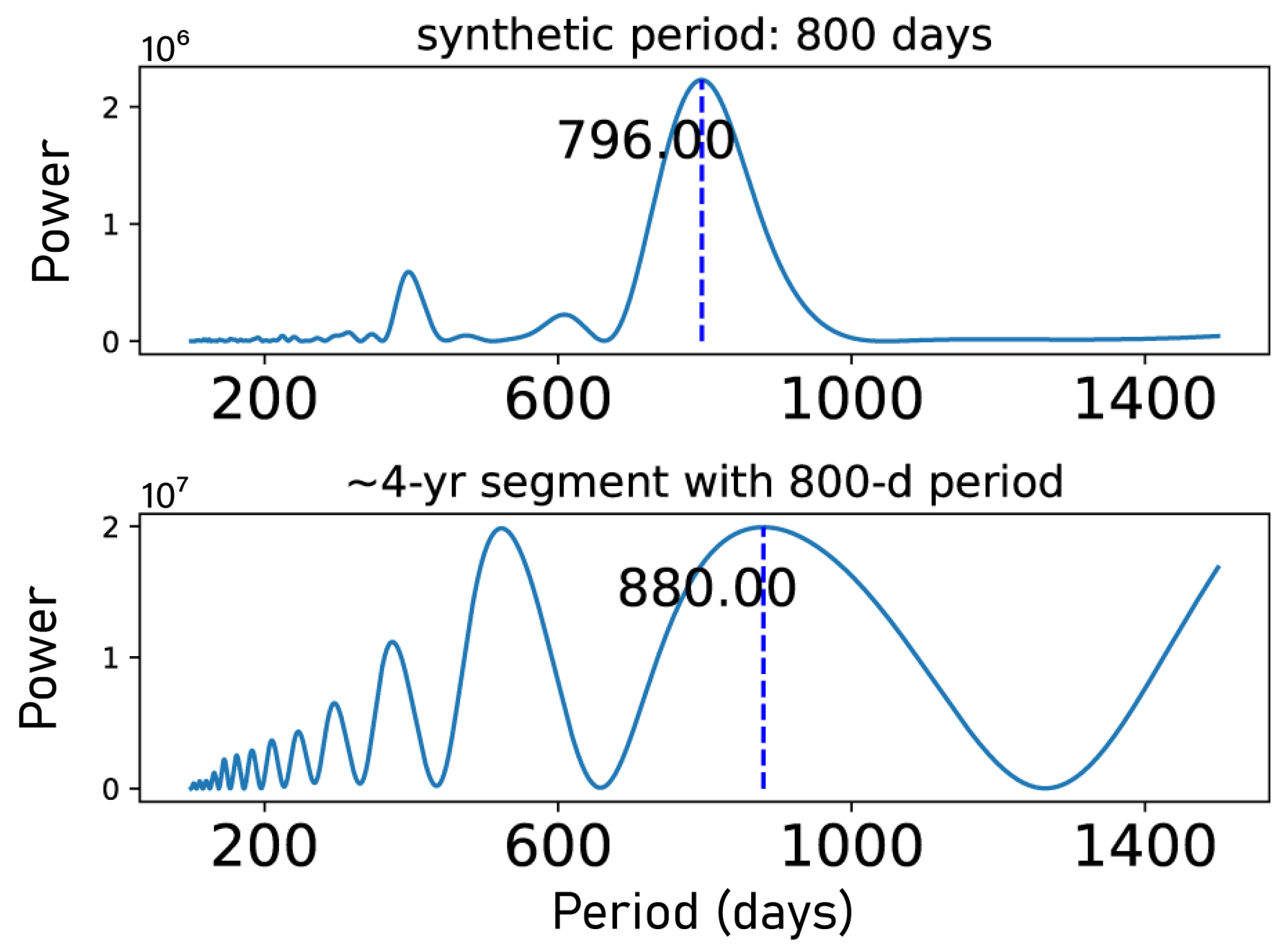
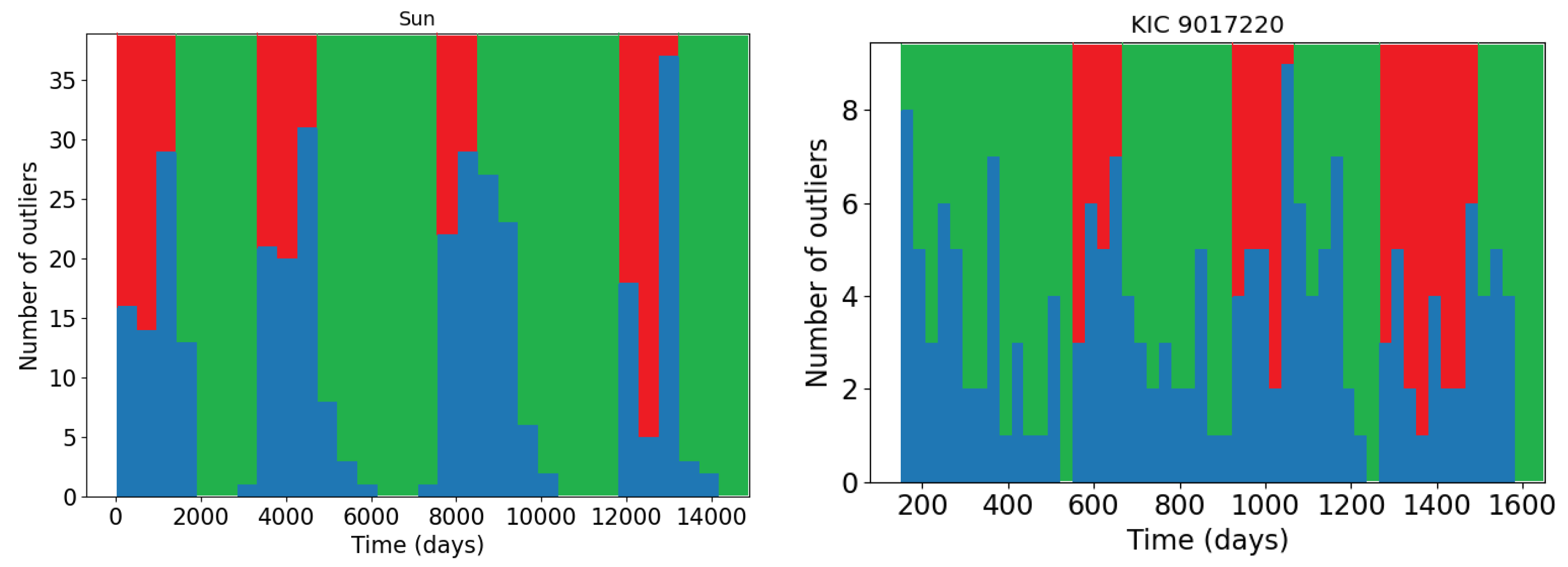
3.3.1. Effect of the Sampling Function
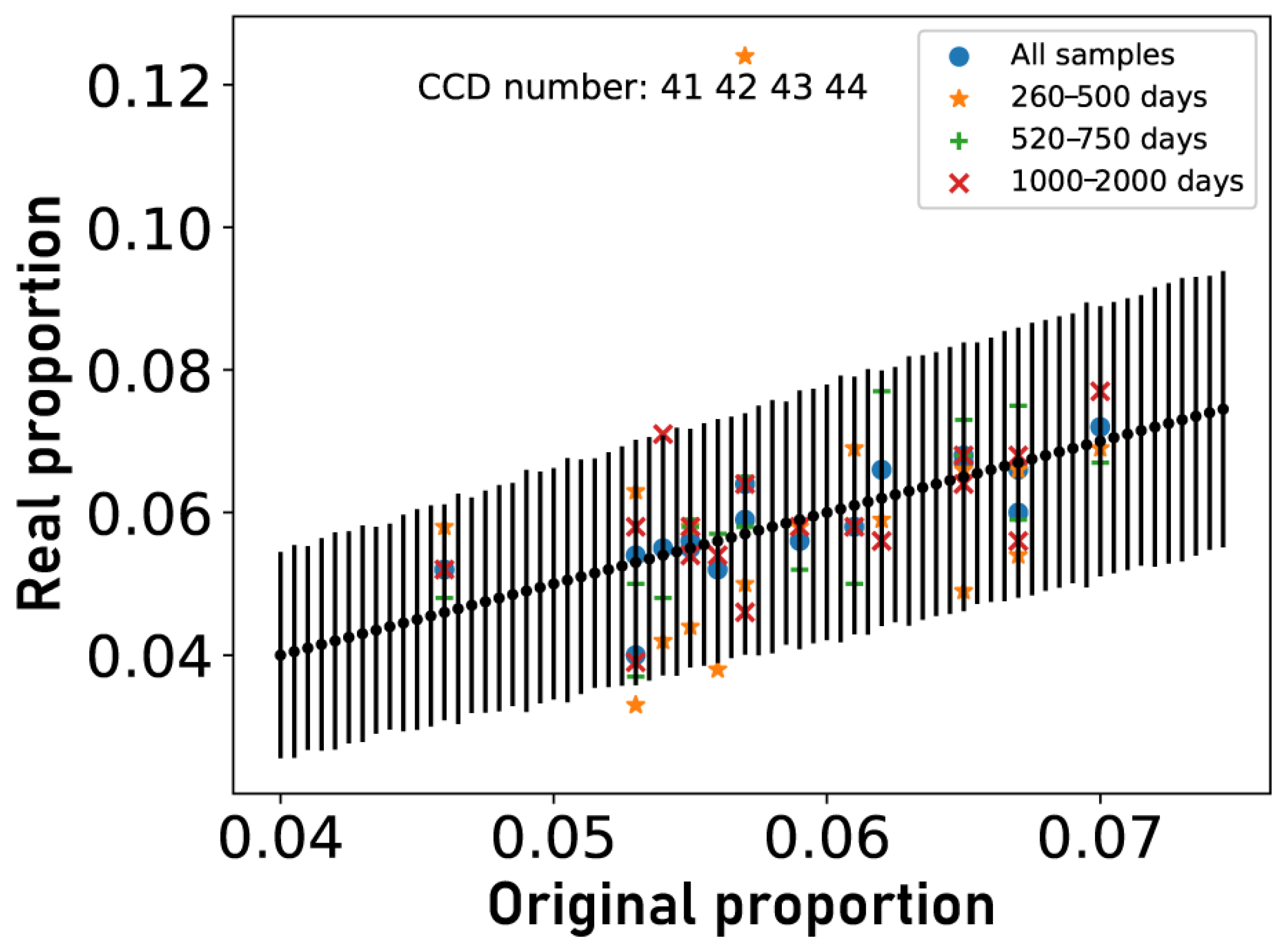
3.3.2. Difference between Kepler CCD Channels as a Cause of Spurious Periods
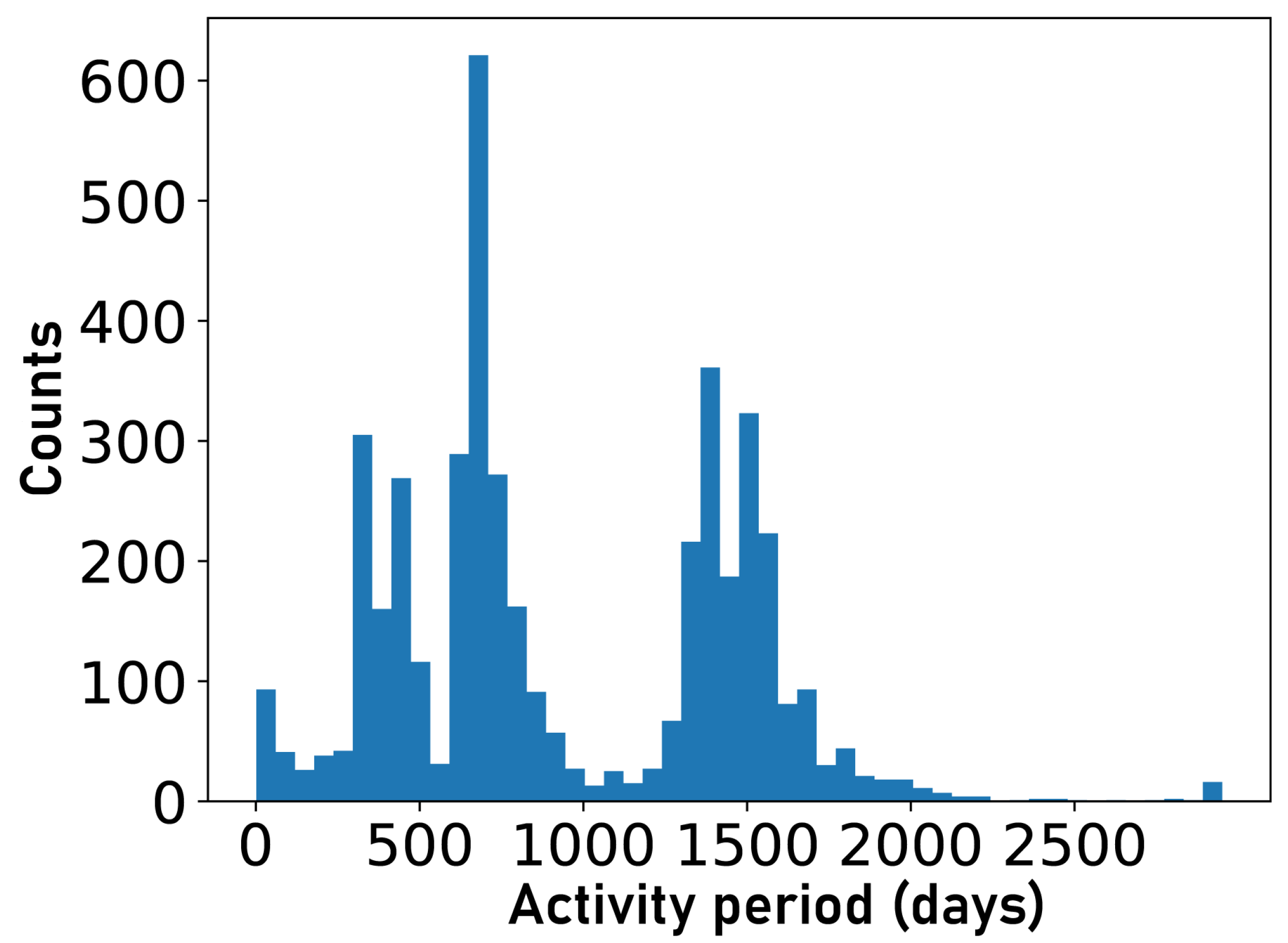
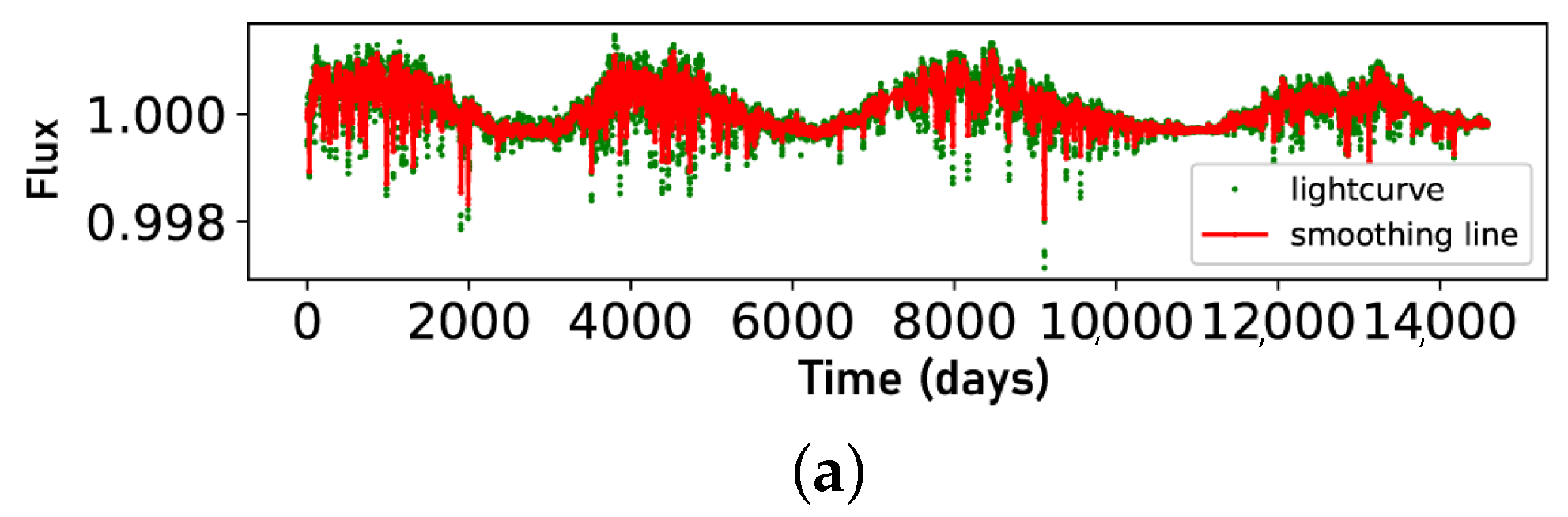
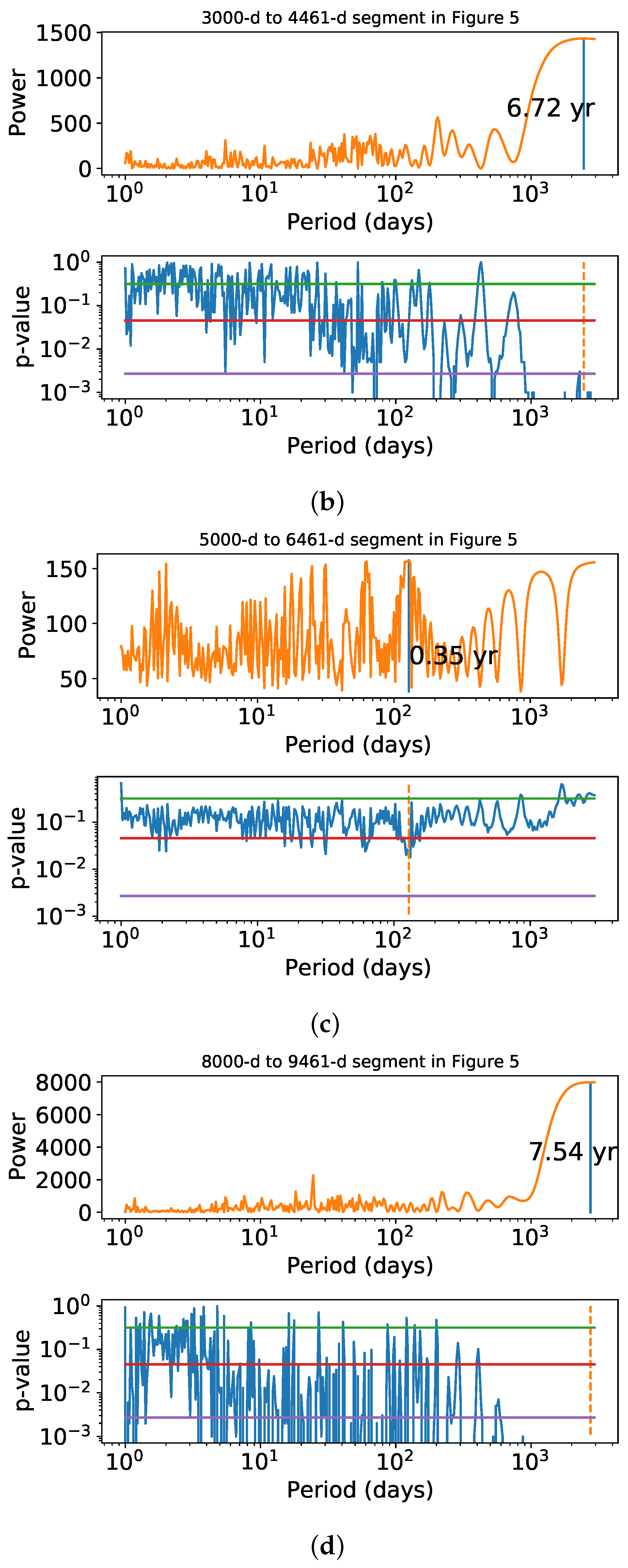
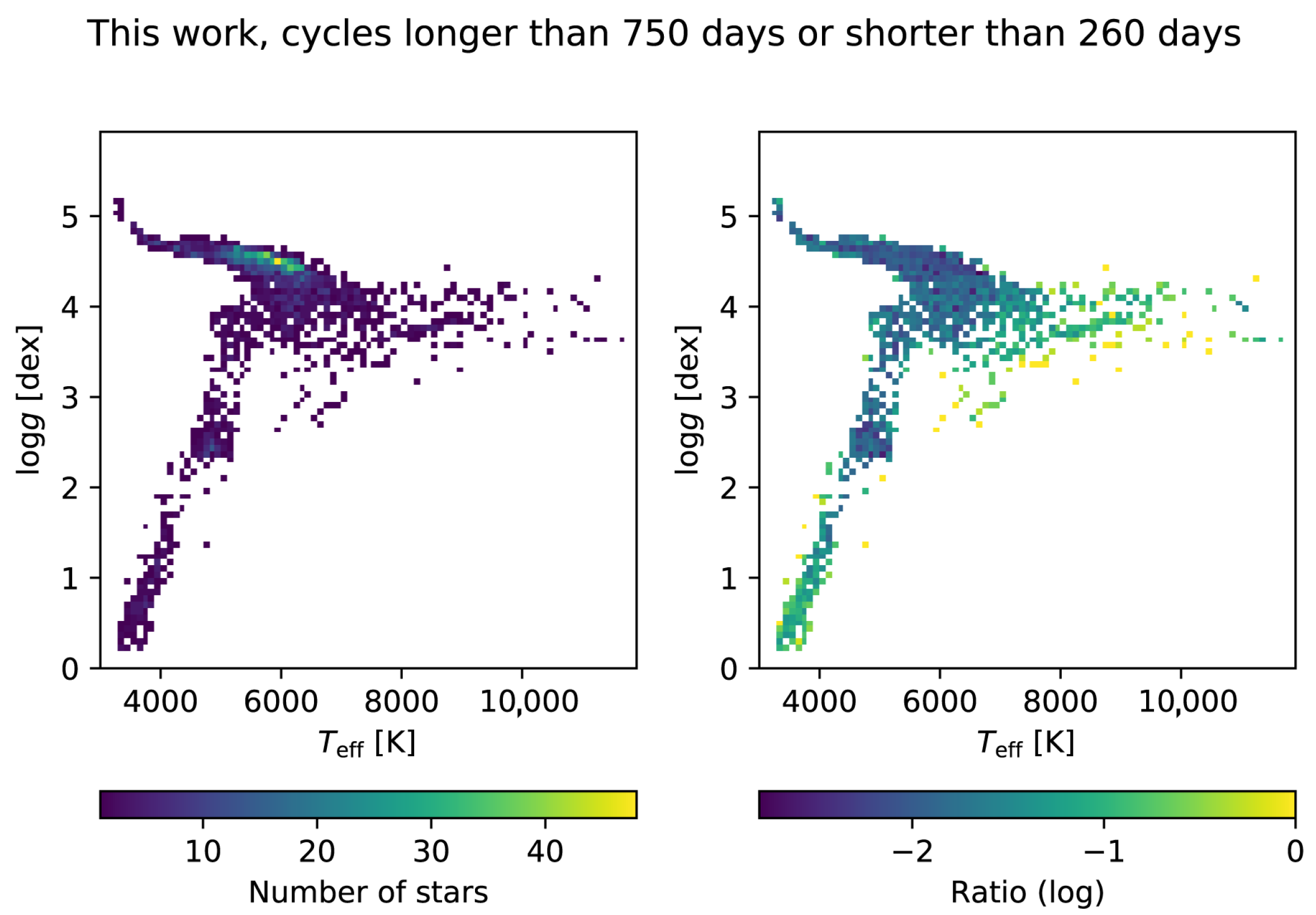
3.3.3. Results for Determination of Longer Cycles
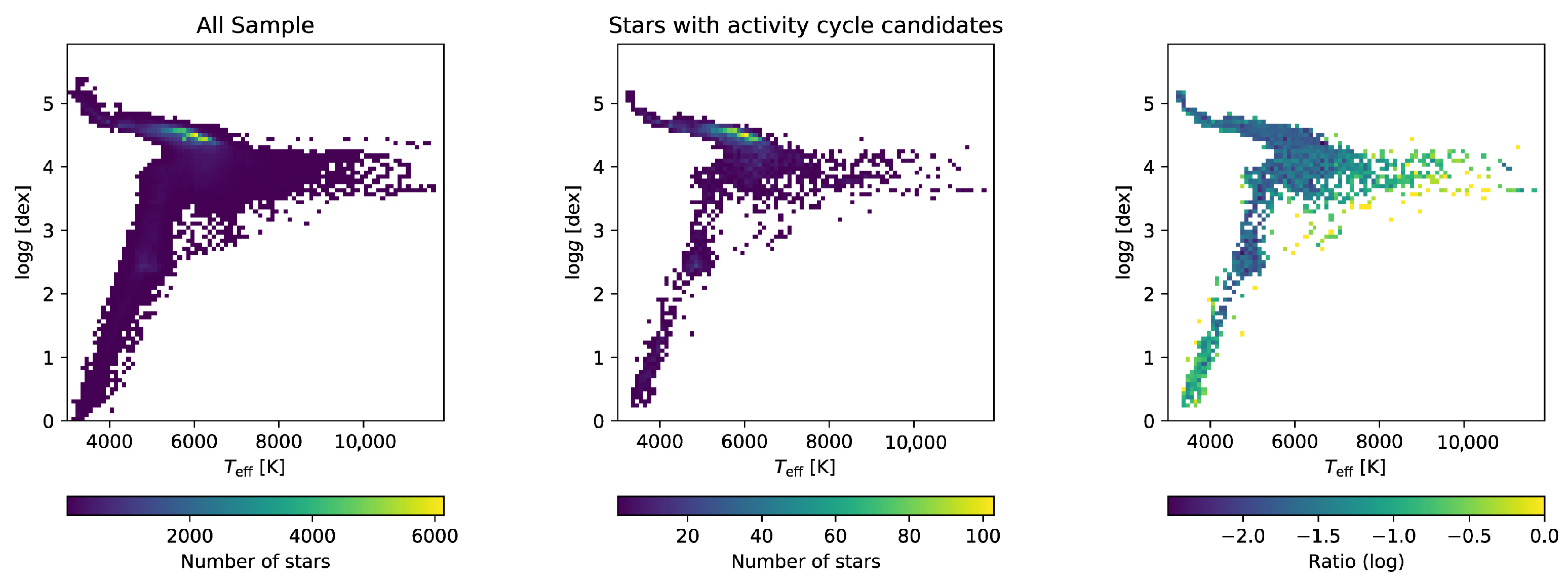
3.3.4. Evolutionary Stages of the Stars with Activity Cycles
4. Discussion
4.1. Cycle sequence
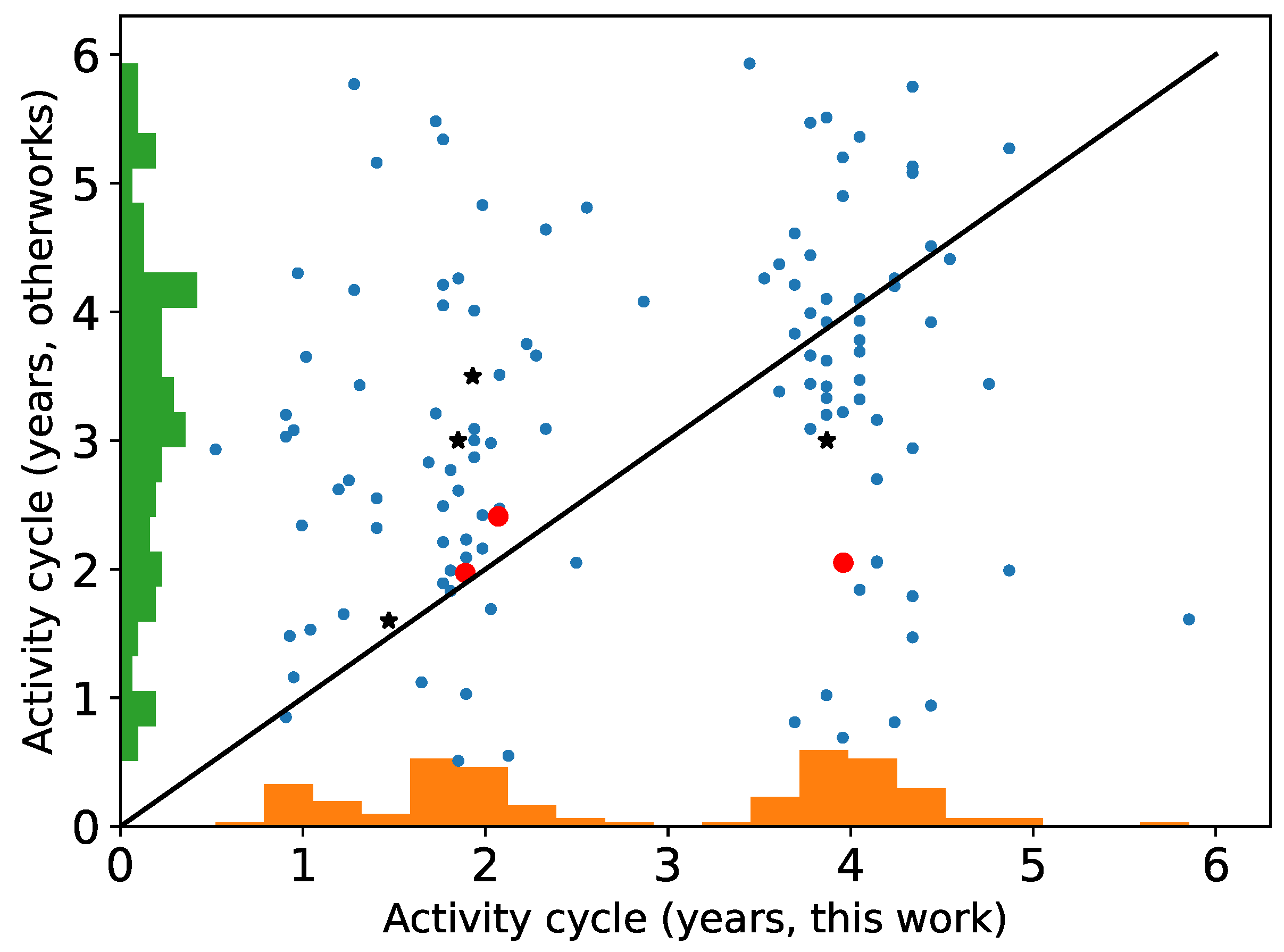
4.2. Comparison with Previous Work
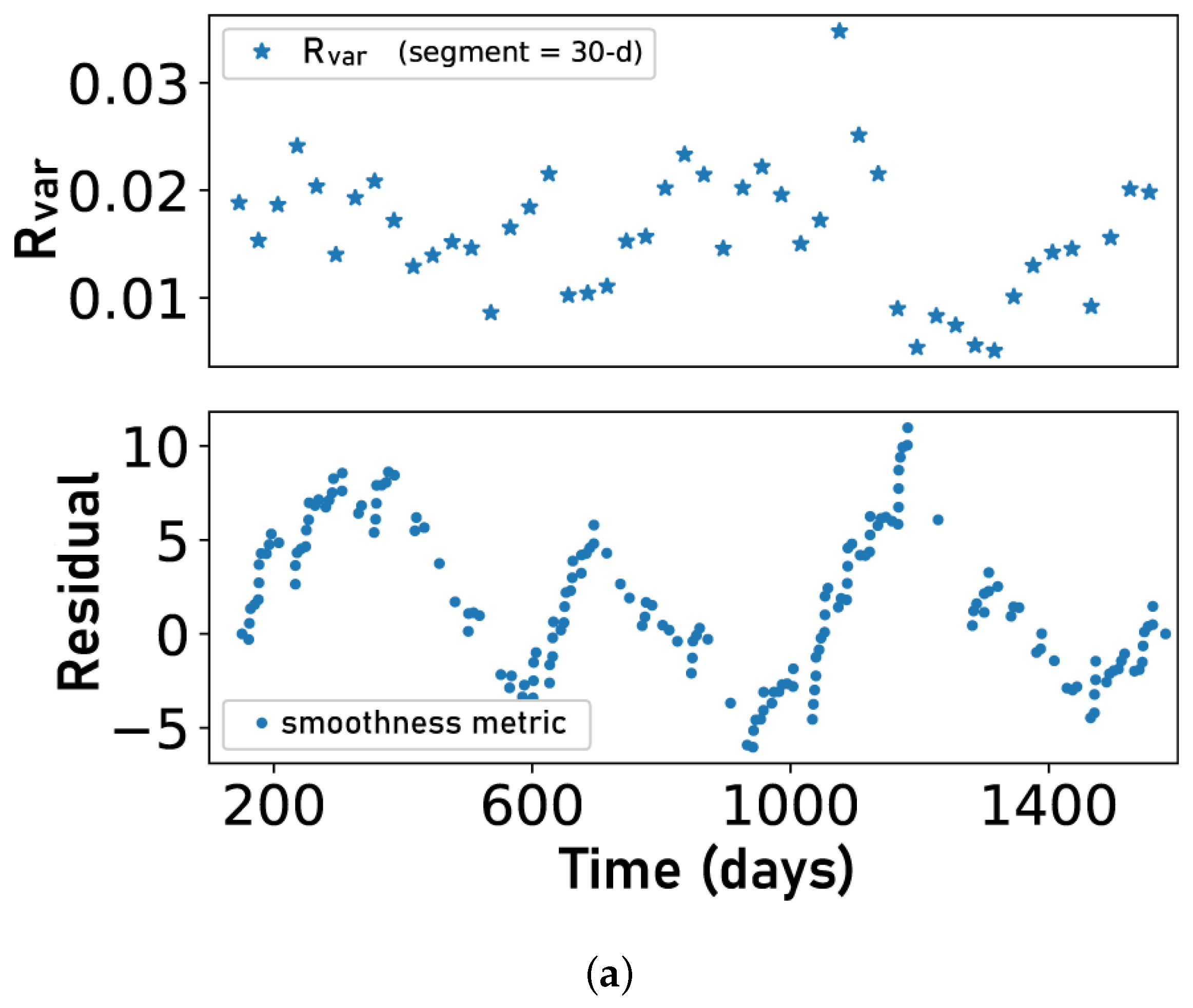
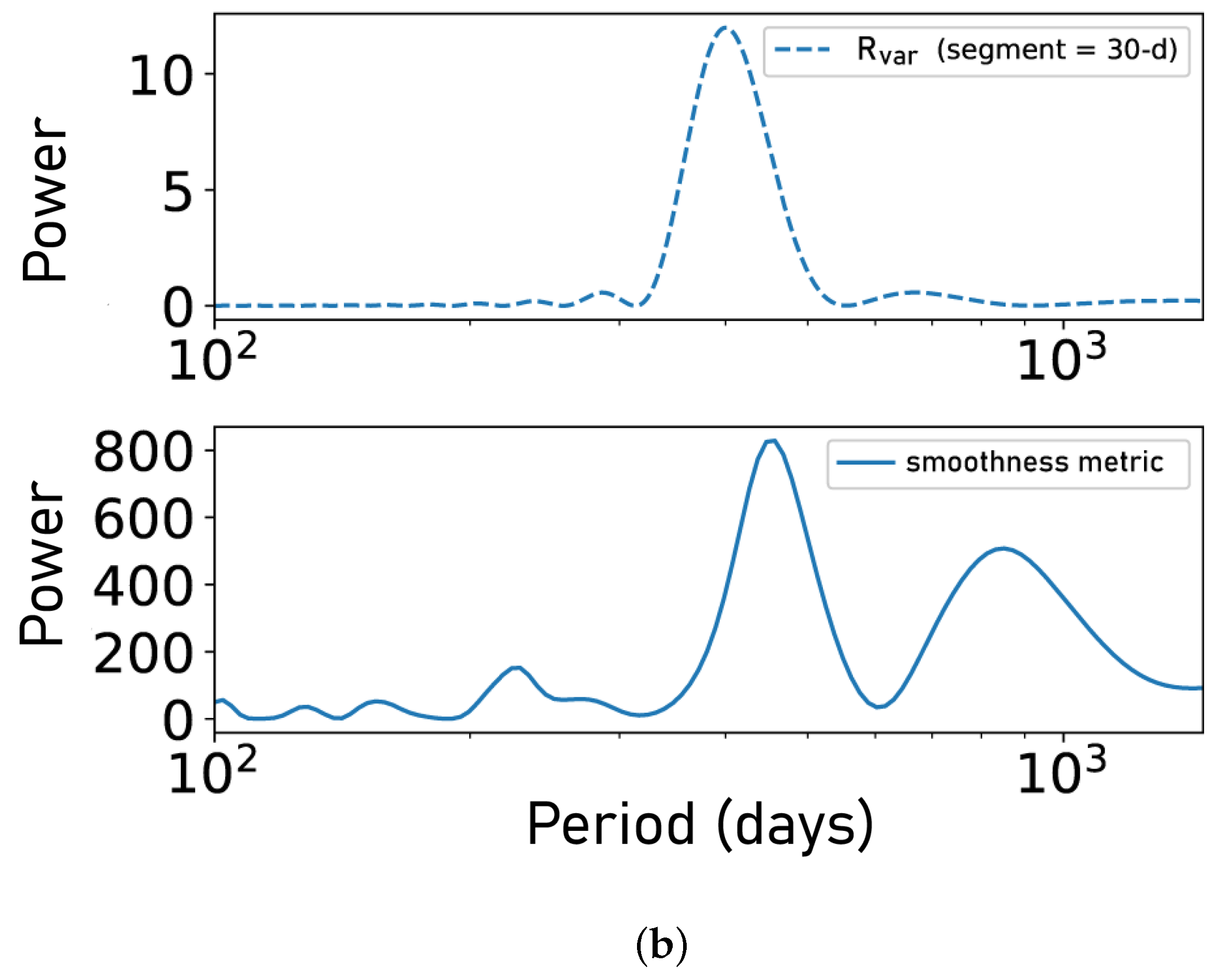
4.3. Comparison: , , and Our Metric
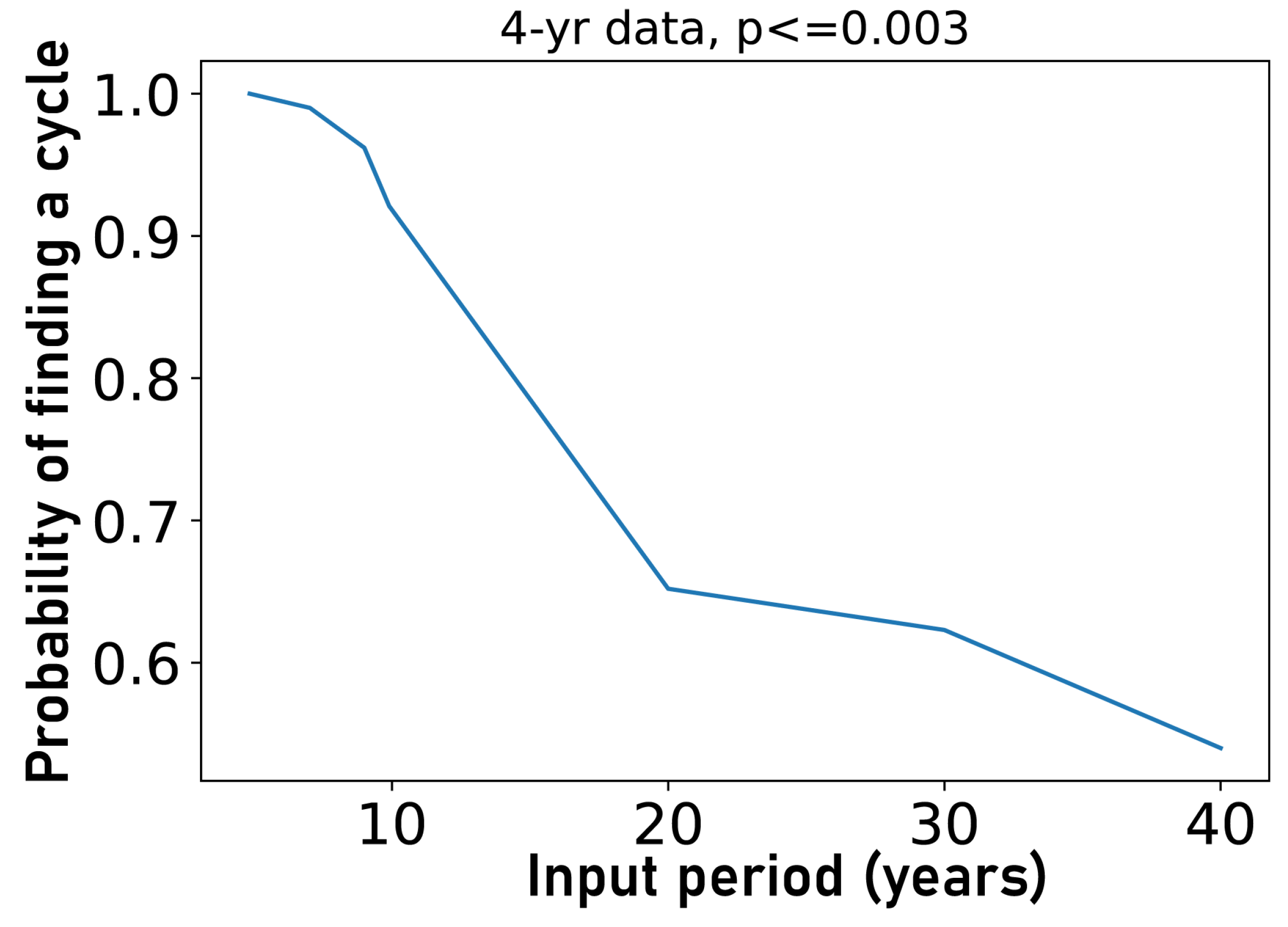
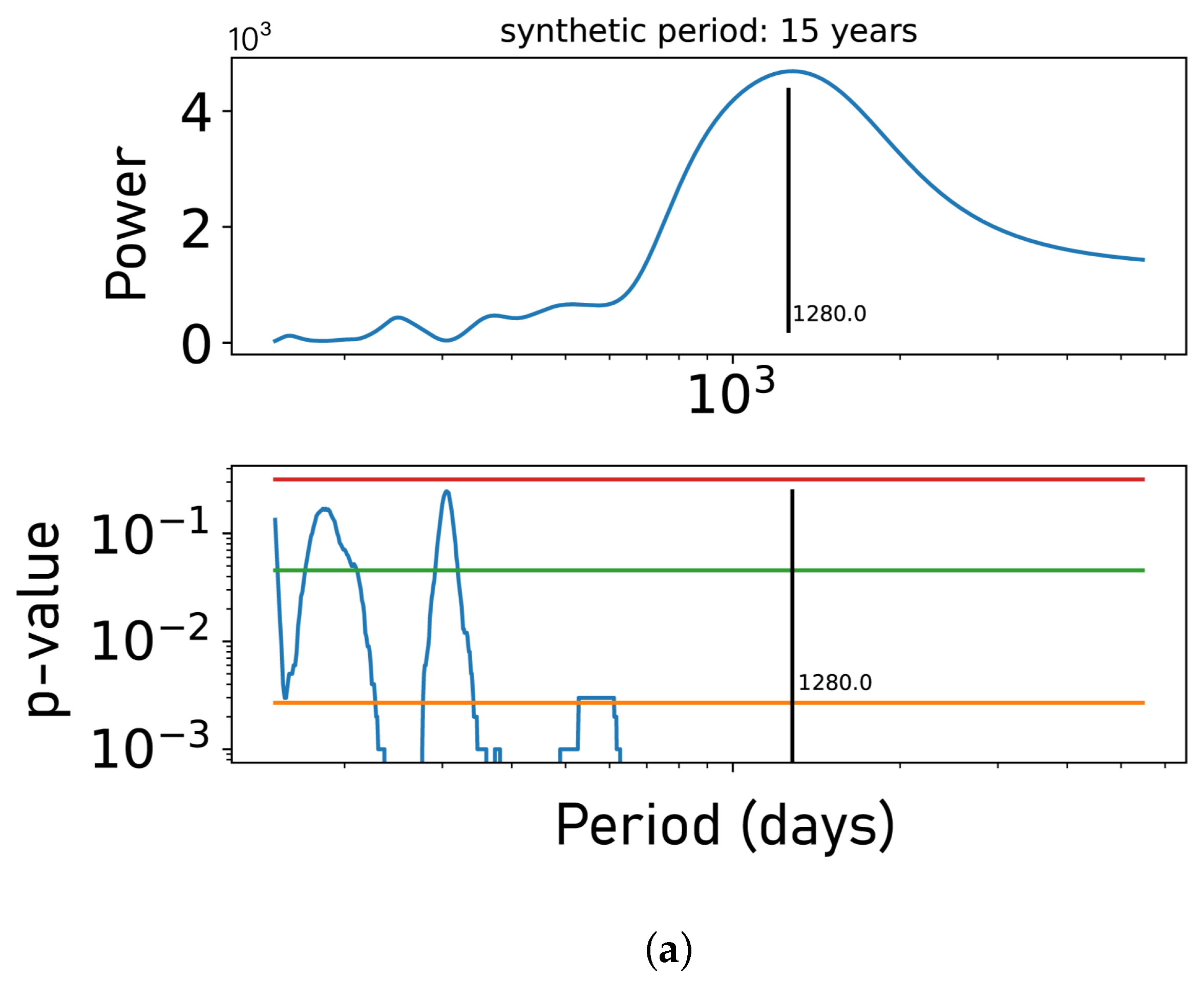
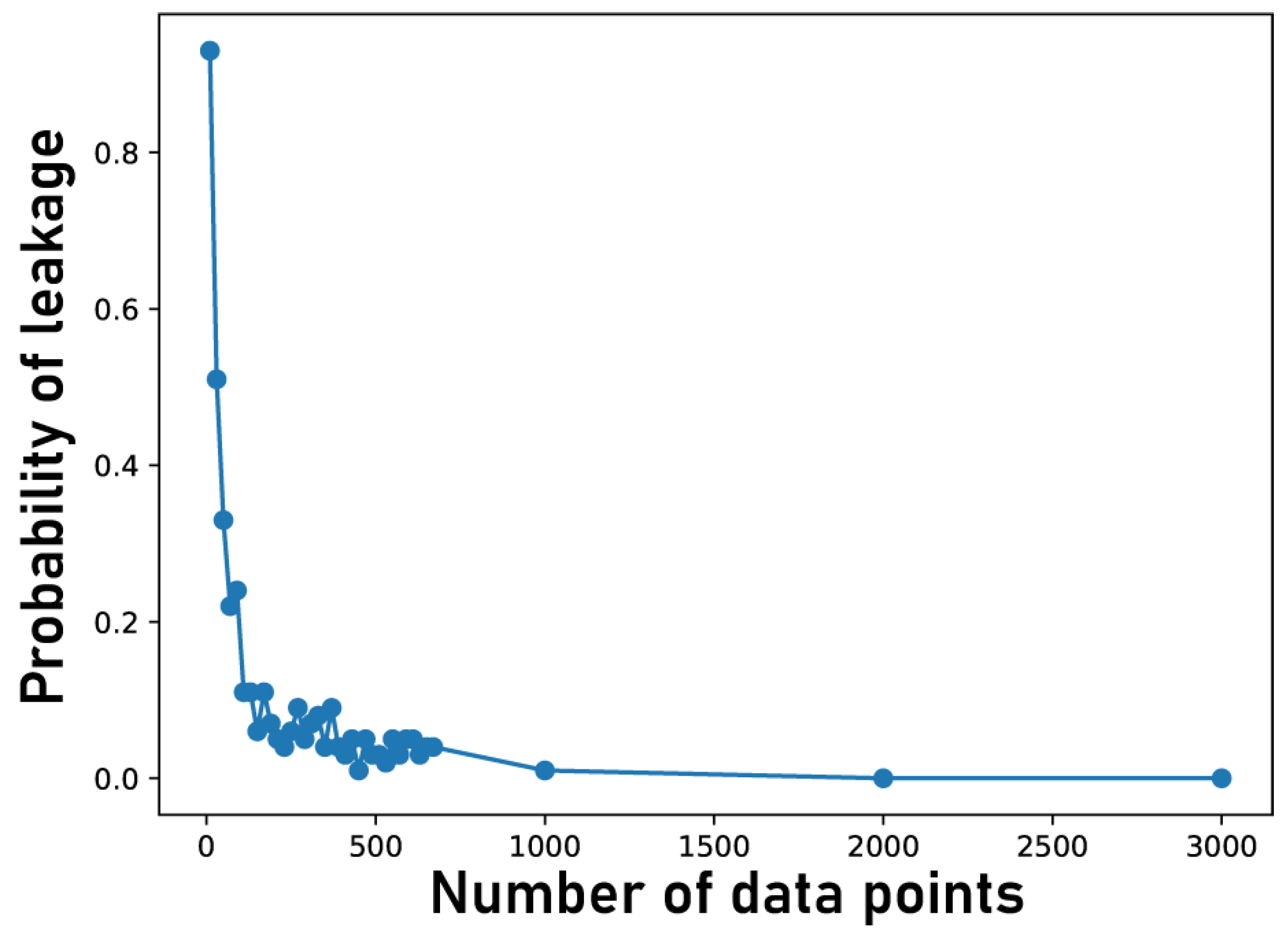
4.4. Invalidity of the p-Value Test Caused by a Lack of Data Points
4.5. Other Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Svensmark, H.; Friis-Christensen, E. Variation of cosmic ray flux and global cloud coverage-a missing link in solar-climate relationships. J. Atmos.-Sol.-Terr. Phys. 1997, 59, 1225–1232. [Google Scholar] [CrossRef]
- Charvàtovà, I. Solar-Terrestrial and Climatic Phenomena in Relation to Solar Inertial Motion. Surv. Geophys. 1997, 18, 131–146. [Google Scholar] [CrossRef]
- Kane, S.R.; Thirumalachari, B.; Henry, G.W.; Hinkel, N.R.; Jensen, E.L.N.; Boyajian, T.S.; Fischer, D.A.; Howard, A.W.; Isaacson, H.T.; Wright, J.T. Stellar Activity and Exclusion of the Outer Planet in the HD 99492 System. Astrophys. J. Lett. 2016, 820, L5. [Google Scholar] [CrossRef]
- Saar, S.H.; Brandenburg, A. Time Evolution of the Magnetic Activity Cycle Period. II. Results for an Expanded Stellar Sample. Astrophys. J. 1999, 524, 295–310. [Google Scholar] [CrossRef]
- Böhm-Vitense, E. Chromospheric Activity in G and K Main-Sequence Stars, and What It Tells Us about Stellar Dynamos. Astrophys. J. 2007, 657, 486–493. [Google Scholar] [CrossRef]
- Charbonneau, P. Dynamo Models of the Solar Cycle. In Solar and Stellar Dynamos, Saas-Fee Advanced Courses; Springer: Berlin/Heidelberg, Germany, 2013; Volume 39, p. 87. ISBN 978-3-642-32092-7. [Google Scholar] [CrossRef]
- Morris, B.M.; Hebb, L.; Davenport, J.R.A.; Rohn, G.; Hawley, S.L. The Starspots of HAT-P-11: Evidence for a Solar-like Dynamo. Astrophys. J. 2017, 846, 99. [Google Scholar] [CrossRef]
- Valio, A.; Estrela, R.; Netto, Y.; Bravo, J.P.; de Medeiros, J.R. Activity and Rotation of Kepler-17. Astrophys. J. 2017, 835, 294. [Google Scholar] [CrossRef]
- Mathur, S.; García, R.A.; Ballot, J.; Ceillier, T.; Salabert, D.; Metcalfe, T.S.; Régulo, C.; Jiménez, A.; Bloemen, S. Investigating magnetic activity of F stars with the Kepler mission. In IAU Symposium; Petit, P., Jardine, M., Spruit, H.C., Eds.; Magnetic Fields throughout Stellar Evolution; Cambridge University Press: Cambridge, UK, 2014; Volume 302, pp. 222–223. [Google Scholar] [CrossRef]
- Basri, G.; Walkowicz, L.M.; Batalha, N.; Gilliland, R.L.; Jenkins, J.; Borucki, W.J.; Koch, D.; Caldwell, D.; Dupree, A.K.; Latham, D.W.; et al. Photometric Variability in Kepler Target Stars. II. An Overview of Amplitude, Periodicity, and Rotation in First Quarter Data. Astrophys. J. 2011, 141, 20. [Google Scholar] [CrossRef]
- Sanz-Forcada, J.; Stelzer, B.; Metcalfe, T.S. ιHorologi, the first coronal activity cycle in a young solar-like star. Astron. Astrophys. 2013, 553, L6. [Google Scholar] [CrossRef]
- Woodard, M.F.; Noyes, R.W. Change of solar oscillation eigenfrequencies with the solar cycle. Nature 1985, 318, 449–450. [Google Scholar] [CrossRef]
- Libbrecht, K.G.; Woodard, M.F. Solar-cycle effects on solar oscillation frequencies. Nature 1990, 345, 779–782. [Google Scholar] [CrossRef]
- Jimenez-Reyes, S.J.; Regulo, C.; Palle, P.L.; Roca Cortes, T. Solar activity cycle frequency shifts of low-degree p-modes. Astron. Astrophys. 1998, 329, 1119–1124. [Google Scholar]
- García, R.A.; Mathur, S.; Salabert, D.; Ballot, J.; Régulo, C.; Metcalfe, T.S.; Baglin, A. CoRoT Reveals a Magnetic Activity Cycle in a Sun-Like Star. Science 2010, 329, 1032. [Google Scholar] [CrossRef] [PubMed]
- Salabert, D.; Régulo, C.; Pérez Hernández, F.; García, R.A. Frequency dependence of p-mode frequency shifts induced by magnetic activity in Kepler solar-like stars. Astron. Astrophys. 2018, 611, A84. [Google Scholar] [CrossRef]
- Kiefer, R.; Schad, A.; Davies, G.; Roth, M. Stellar magnetic activity and variability of oscillation parameters: An investigation of 24 solar-like stars observed by Kepler. Astron. Astrophys. 2017, 598, A77. [Google Scholar] [CrossRef]
- Metcalfe, T.S.; Monteiro, M.J.P.F.G.; Thompson, M.J.; Chaplin, W.J.; Basu, S.; Bonanno, A.; Di Mauro, M.P.; Doğan, G.; Eggenberger, P.; Karoff, C.; et al. Asteroseismology of solar-type stars with Kepler: II. Stellar modeling. Astron. Nachrichten 2010, 331, 977. [Google Scholar] [CrossRef]
- Mathur, S.; Bruntt, H.; Catala, C.; Benomar, O.; Davies, G.R.; García, R.A.; Salabert, D.; Ballot, J.; Mosser, B.; Régulo, C.; et al. Study of HD 169392A observed by CoRoT and HARPS. Astron. Astrophys. 2013, 549, A12. [Google Scholar] [CrossRef]
- Santos, A.R.G.; Campante, T.L.; Chaplin, W.J.; Cunha, M.S.; Lund, M.N.; Kiefer, R.; Salabert, D.; García, R.A.; Davies, G.R.; Elsworth, Y.; et al. Signatures of Magnetic Activity in the Seismic Data of Solar-type Stars Observed by Kepler. Astrophys. J. 2018, 237, 17. [Google Scholar] [CrossRef]
- Santos, A.R.G.; Campante, T.L.; Chaplin, W.J.; Cunha, M.S.; van Saders, J.L.; Karoff, C.; Metcalfe, T.S.; Mathur, S.; García, R.A.; Lund, M.N.; et al. Signatures of Magnetic Activity: On the Relation between Stellar Properties and p-mode Frequency Variations. Astrophys. J. 2019, 883, 65. [Google Scholar] [CrossRef]
- Baliunas, S.L.; Donahue, R.A.; Soon, W.H.; Horne, J.H.; Frazer, J.; Woodard-Eklund, L.; Bradford, M.; Rao, L.M.; Wilson, O.C.; Zhang, Q.; et al. Chromospheric variations in main-sequence stars. Astrophys. J. 1995, 438, 269–287. [Google Scholar] [CrossRef]
- Baliunas, S.L. Stellar Activity Cycles. Cool Stars, Stellar Systems and the Sun. In Lecture Notes in Physics; Zeilik, M., Gibson, D.M., Eds.; Springer: Berlin, Germany, 1986; Volume 254, p. 3. [Google Scholar]
- Hall, J.C.; Lockwood, G.W.; Skiff, B.A. The Activity and Variability of the Sun and Sun-like Stars. I. Synoptic Ca II H and K Observations. Astrophys. J. 2007, 133, 862–881. [Google Scholar] [CrossRef]
- Lockwood, G.W.; Hall, J.C.; Skiff, B.A.; Henry, G.W.; Radick, R.R.; Baliunas, S.L.; Soon, W.; Donahue, R.A. Gauging the Sun: Comparative photometric and magnetic activity measurements of sunlike stars, 1984-2001. American Astronomical Society Meeting Abstracts #200. Bull. Am. Astron. Soc. 2002, 34, 651. [Google Scholar]
- Oláh, K.; Kolláth, Z.; Granzer, T.; Strassmeier, K.G.; Lanza, A.F.; Järvinen, S.; Korhonen, H.; Baliunas, S.L.; Soon, W.; Messina, S.; et al. Multiple and changing cycles of active stars. II. Results. Astron. Astrophys. 2009, 501, 703–713. [Google Scholar] [CrossRef]
- Montet, B.T.; Tovar, G.; Foreman-Mackey, D. Long-term Photometric Variability in Kepler Full-frame Images: Magnetic Cycles of Sun-like Stars. Astrophys. J. 2017, 851, 116. [Google Scholar] [CrossRef]
- Morgenthaler, A.; Petit, P.; Morin, J.; Aurière, M.; Dintrans, B.; Konstantinova-Antova, R.; Marsden, S. Direct observation of magnetic cycles in Sun-like stars. Astron. Nachrichten 2011, 332, 866. [Google Scholar] [CrossRef]
- Reinhold, T.; Cameron, R.H.; Gizon, L. Evidence for photometric activity cycles in 3203 Kepler stars. Astron. Astrophys. 2017, 603, A52. [Google Scholar] [CrossRef]
- Basri, G.; Walkowicz, L.M.; Reiners, A. Comparison of Kepler Photometric Variability with the Sun on Different Timescales. Astrophys. J. 2013, 769, 37. [Google Scholar] [CrossRef]
- Mathur, S.; García, R.A.; Ballot, J.; Ceillier, T.; Salabert, D.; Metcalfe, T.S.; Régulo, C.; Jiménez, A.; Bloemen, S. Magnetic activity of F stars observed by Kepler. Astron. Astrophys. 2014, 562, A124. [Google Scholar] [CrossRef]
- Salabert, D.; García, R.A.; Beck, P.G.; Egeland, R.; Pallé, P.L.; Mathur, S.; Metcalfe, T.S.; do Nascimento, J.D.J.; Ceillier, T.; Andersen, M.F.; et al. Photospheric and chromospheric magnetic activity of seismic solar analogs. Observational inputs on the solar-stellar connection from Kepler and Hermes. Astron. Astrophys. 2016, 596, A31. [Google Scholar] [CrossRef]
- Salabert, D.; García, R.A.; Jiménez, A.; Bertello, L.; Corsaro, E.; Pallé, P.L. Photospheric activity of the Sun with VIRGO and GOLF. Comparison with standard activity proxies. Astron. Astrophys. 2017, 608, A87. [Google Scholar] [CrossRef]
- Reinhold, T.; Shapiro, A.I.; Solanki, S.K.; Montet, B.T.; Krivova, N.A.; Cameron, R.H.; Amazo-Gómez, E.M. The Sun is less active than other solar-like stars. Science 2020, 368, 518–521. [Google Scholar] [CrossRef] [PubMed]
- García, R.A.; Ceillier, T.; Salabert, D.; Mathur, S.; van Saders, J.L.; Pinsonneault, M.; Ballot, J.; Beck, P.G.; Bloemen, S.; Campante, T.L.; et al. Rotation and magnetism of Kepler pulsating solar-like stars. Towards asteroseismically calibrated age-rotation relations. Astron. Astrophys. 2014, 572, A34. [Google Scholar] [CrossRef]
- Estrela, R.; Valio, A. Stellar Magnetic Cycles in the Solar-like Stars Kepler-17 and Kepler-63. Astrophys. J. 2016, 831, 57. [Google Scholar] [CrossRef]
- Notsu, Y.; Maehara, H.; Shibayama, T.; Honda, S.; Notsu, S.; Namekata, K.; Nogami, D.; Shibata, K. Statistical Properties of Superflares on Solar-Type Stars with Kepler Data. In Proceedings of the 19th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (CS19), Uppsala, Sweden, 6–10 June 2016; p. 119. [Google Scholar] [CrossRef]
- Davenport, J.R.A. The Kepler Catalog of Stellar Flares. Astrophys. J. 2016, 829, 23. [Google Scholar] [CrossRef]
- Bastien, F.A.; Stassun, K.G.; Basri, G.; Pepper, J. An observational correlation between stellar brightness variations and surface gravity. Nature 2013, 500, 427–430. [Google Scholar] [CrossRef] [PubMed]
- Chaplin, W.J.; Bedding, T.R.; Bonanno, A.; Broomhall, A.M.; García, R.A.; Hekker, S.; Huber, D.; Verner, G.A.; Basu, S.; Elsworth, Y.; et al. Evidence for the Impact of Stellar Activity on the Detectability of Solar-like Oscillations Observed by Kepler. Astrophys. J. Lett. 2011, 732, L5. [Google Scholar] [CrossRef]
- He, H.; Wang, H.; Yun, D. Activity Analyses for Solar-type Stars Observed with Kepler. I. Proxies of Magnetic Activity. Astrophys. J. Suppl. Ser. 2015, 221, 18. [Google Scholar] [CrossRef][Green Version]
- Domingo, V.; Ermolli, I.; Fox, P.; Fröhlich, C.; Haberreiter, M.; Krivova, N.; Kopp, G.; Schmutz, W.; Solanki, S.K.; Spruit, H.C.; et al. Solar Surface Magnetism and Irradiance on Time Scales from Days to the 11-Year Cycle. Space Sci. Rev. 2009, 145, 337–380. [Google Scholar] [CrossRef]
- Batalha, N.M.; Borucki, W.J.; Koch, D.G.; Brown, T.M.; Caldwell, D.A.; Latham, D.W. Characteristics of the Kepler target stars. Highlights Astron. 2010, 15, 712–713. [Google Scholar] [CrossRef]
- Thompson, S.E.; Caldwell, D.A.; Jenkins, J.M.; Barclay, T.; Barentsen, G.; Bryson, S.T.; Burke, C.J.; Campbell, J.; Catanzarite, J.; Christiansen, J.L.; et al. Kepler Data Release 25 Notes. Available online: https://archive.stsci.edu/kepler/release_notes/release_notes25/KSCI-19065-002DRN25.pdf (accessed on 11 July 2022).
- Abdul-Masih, M.; Prša, A.; Conroy, K.; Bloemen, S.; Boyajian, T.; Doyle, L.R.; Johnston, C.; Kostov, V.; Latham, D.W.; Matijevič, G.; et al. Kepler Eclipsing Binary Stars. VIII. Identification of False Positive Eclipsing Binaries and Re-extraction of New Light Curves. Astrophys. J. 2016, 151, 101. [Google Scholar] [CrossRef]
- McQuillan, A.; Mazeh, T.; Aigrain, S. Rotation Periods of 34,030 Kepler Main-sequence Stars: The Full Autocorrelation Sample. Astrophys. J. Suppl. Ser. 2014, 211, 24. [Google Scholar] [CrossRef]
- Jose, P.D. Sun’s motion and sunspots. Astrophys. J. 1965, 70, 193. [Google Scholar] [CrossRef]
- Wolff, C.L.; Patrone, P.N. A New Way that Planets Can Affect the Sun. Sol. Phys. 2010, 266, 227–246. [Google Scholar] [CrossRef]
- Abreu, J.A.; Beer, J.; Ferriz-Mas, A.; McCracken, K.G.; Steinhilber, F. Is there a planetary influence on solar activity? Astron. Astrophys. 2012, 548, A88. [Google Scholar] [CrossRef]
- Stefani, F.; Giesecke, A.; Weber, N.; Weier, T. Synchronized Helicity Oscillations: A Link Between Planetary Tides and the Solar Cycle? Sol. Phys. 2016, 291, 2197–2212. [Google Scholar] [CrossRef]
- Ferreira Lopes, C.E.; Leão, I.C.; de Freitas, D.B.; Canto Martins, B.L.; Catelan, M.; De Medeiros, J.R. Stellar cycles from photometric data: CoRoT stars. Astron. Astrophys. 2015, 583, A134. [Google Scholar] [CrossRef][Green Version]
- Zhang, X.J.; Deng, L.H.; Fei, Y.; Li, C.; Tian, X.A.; Wan, Z.J. Hemispheric asymmetry of long-term sunspot activity: Sunspot relative numbers for 1939–2019. Mon. Not. R. Astron. Soc. 2022, 514, 1140–1147. [Google Scholar] [CrossRef]
- Aigrain, S.; Llama, J.; Ceillier, T.; Chagas, M.L.d.; Davenport, J.R.A.; García, R.A.; Hay, K.L.; Lanza, A.F.; McQuillan, A.; Mazeh, T.; et al. Testing the recovery of stellar rotation signals from Kepler light curves using a blind hare-and-hounds exercise. Mon. Not. R. Astron. Soc. 2015, 450, 3211–3226. [Google Scholar] [CrossRef]
- Karoff, C.; Metcalfe, T.S.; Santos, Â.R.G.; Montet, B.T.; Isaacson, H.; Witzke, V.; Shapiro, A.I.; Mathur, S.; Davies, G.R.; Lund, M.N.; et al. The Influence of Metallicity on Stellar Differential Rotation and Magnetic Activity. Astrophys. J. 2018, 852, 46. [Google Scholar] [CrossRef]
- Mathur, S.; Huber, D. Kepler Stellar Properties Catalog Update for Q1-Q17 DR25 Transit Search. Available online: https://exoplanetarchive.ipac.caltech.edu/docs/KSCI-19097-004.pdf (accessed on 11 July 2022).
- Noyes, R.W.; Weiss, N.O.; Vaughan, A.H. The relation between stellar rotation rate and activity cycle periods. Astrophys. J. 1984, 287, 769–773. [Google Scholar] [CrossRef]
- Baliunas, S.L.; Nesme-Ribes, E.; Sokoloff, D.; Soon, W.H. A Dynamo Interpretation of Stellar Activity Cycles. Astrophys. J. 1996, 460, 848. [Google Scholar] [CrossRef]
- Boro Saikia, S.; Marvin, C.J.; Jeffers, S.V.; Reiners, A.; Cameron, R.; Marsden, S.C.; Petit, P.; Warnecke, J.; Yadav, A.P. Chromospheric activity catalogue of 4454 cool stars. Questioning the active branch of stellar activity cycles. Astron. Astrophys. 2018, 616, A108. [Google Scholar] [CrossRef]
- Karak, B.B.; Tomar, A.; Vashishth, V. Stellar dynamos with solar and antisolar differential rotations: Implications to magnetic cycles of slowly rotating stars. Mon. Not. R. Astron. Soc. 2020, 491, 3155–3164. [Google Scholar] [CrossRef]
- Han, H.G.; Cui, K.M.; Liu, J.F.; Yang, H.Q.; Fang, X.; Zhao, R.N. Stellar activity cycles as revealed by long-term beat-like patterns from light curves of Kepler. Res. Astron. Astrophys. 2021, 21, 142. [Google Scholar] [CrossRef]
- Lehtinen, J.; Jetsu, L.; Hackman, T.; Kajatkari, P.; Henry, G.W. Activity trends in young solar-type stars. Astron. Astrophys. 2016, 588, A38. [Google Scholar] [CrossRef]
- Olspert, N.; Lehtinen, J.J.; Käpylä, M.J.; Pelt, J.; Grigorievskiy, A. Estimating activity cycles with probabilistic methods. II. The Mount Wilson Ca H&K data. Astron. Astrophys. 2018, 619, A6. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a World Beyond “p < 0.05”. Am. Stat. 2019, 73, 1–19. [Google Scholar]
- Twicken, J.D.; Chandrasekaran, H.; Jenkins, J.M.; Gunter, J.P.; Girouard, F.; Klaus, T.C. Presearch data conditioning in the Kepler Science Operations Center pipeline. In Software and Cyberinfrastructure for Astronomy, Proceedings of the SPIE Astronomical Telescopes + Instrumentation, San Diego, CA, USA, 27 June–2 July 2010; Radziwill, N.M., Bridger, A., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2010; Volume 7740, p. 77401U. [Google Scholar] [CrossRef]
- Garg, S.; Karak, B.B.; Egeland, R.; Soon, W.; Baliunas, S. Waldmeier Effect in Stellar Cycles. Astrophys. J. 2019, 886, 132. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, Y.Q.; Shi, J.R.; Liang, Y.C.; Hou, J.L.; Chen, L.; Zhang, H.W.; Li, A.G. Stellar Abundance and Galactic Chemical Evolution through LAMOST Spectroscopic Survey. Chin. J. Astron. Astrophys. 2006, 6, 265–280. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, Y.H.; Chu, Y.Q.; Jing, Y.P.; Deng, L.C. LAMOST spectral survey — An overview. Res. Astron. Astrophys. 2012, 12, 723–734. [Google Scholar] [CrossRef]
- Cui, X.Q.; Zhao, Y.H.; Chu, Y.Q.; Li, G.P.; Li, Q.; Zhang, L.P.; Su, H.J.; Yao, Z.Q.; Wang, Y.N.; Xing, X.Z.; et al. The Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST). Res. Astron. Astrophys. 2012, 12, 1197–1242. [Google Scholar] [CrossRef]
- Deng, L.C.; Newberg, H.J.; Liu, C.; Carlin, J.L.; Beers, T.C.; Chen, L.; Chen, Y.Q.; Christlieb, N.; Grillmair, C.J.; Guhathakurta, P.; et al. LAMOST Experiment for Galactic Understanding and Exploration (LEGUE) — The survey’s science plan. Res. Astron. Astrophys. 2012, 12, 735–754. [Google Scholar] [CrossRef]
- Fang, X.S.; Zhao, G.; Zhao, J.K.; Chen, Y.Q.; Bharat Kumar, Y. Stellar activity with LAMOST - I. Spot configuration in Pleiades. Mon. Not. R. Astron. Soc. 2016, 463, 2494–2512. [Google Scholar] [CrossRef]
- Fang, X.S.; Zhao, G.; Zhao, J.K.; Bharat Kumar, Y. Stellar activity with LAMOST - II. Chromospheric activity in open clusters. Mon. Not. R. Astron. Soc. 2018, 476, 908–926. [Google Scholar] [CrossRef]
- Liu, X.W.; Zhao, G.; Hou, J.L. Preface: The LAMOST Galactic surveys and early results. Res. Astron. Astrophys. 2015, 15, 1089. [Google Scholar] [CrossRef]
- Li, H.N.; Zhao, G.; Christlieb, N.; Wang, L.; Wang, W.; Zhang, Y.; Hou, Y.; Yuan, H. Spectroscopic Analysis of Metal-poor Stars from LAMOST: Early Results. Astrophys. J. 2015, 798, 110. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, Y. Low-α metal-rich stars with sausage kinematics in the LAMOST survey: Are they from the Gaia-Sausage-Enceladus galaxy? Sci. China Physics, Mech. Astron. 2021, 64, 239562. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.-F.; Zhao, G.; Bird, S.A. An Attempt to Construct an Activity Cycle Catalog with Kepler Long-Cadence Light Curves. Universe 2022, 8, 488. https://doi.org/10.3390/universe8090488
Shen Y-F, Zhao G, Bird SA. An Attempt to Construct an Activity Cycle Catalog with Kepler Long-Cadence Light Curves. Universe. 2022; 8(9):488. https://doi.org/10.3390/universe8090488
Chicago/Turabian StyleShen, Yu-Fu, Gang Zhao, and Sarah A. Bird. 2022. "An Attempt to Construct an Activity Cycle Catalog with Kepler Long-Cadence Light Curves" Universe 8, no. 9: 488. https://doi.org/10.3390/universe8090488
APA StyleShen, Y.-F., Zhao, G., & Bird, S. A. (2022). An Attempt to Construct an Activity Cycle Catalog with Kepler Long-Cadence Light Curves. Universe, 8(9), 488. https://doi.org/10.3390/universe8090488






