Astroparticle Constraints from Cosmic Reionization and Primordial Galaxy Formation
Abstract
1. Introduction
2. Methods and Analysis
2.1. An Empirical Model of Reionization
2.2. A Constraint from Primordial Galaxy Formation
2.3. Bayesian Analysis
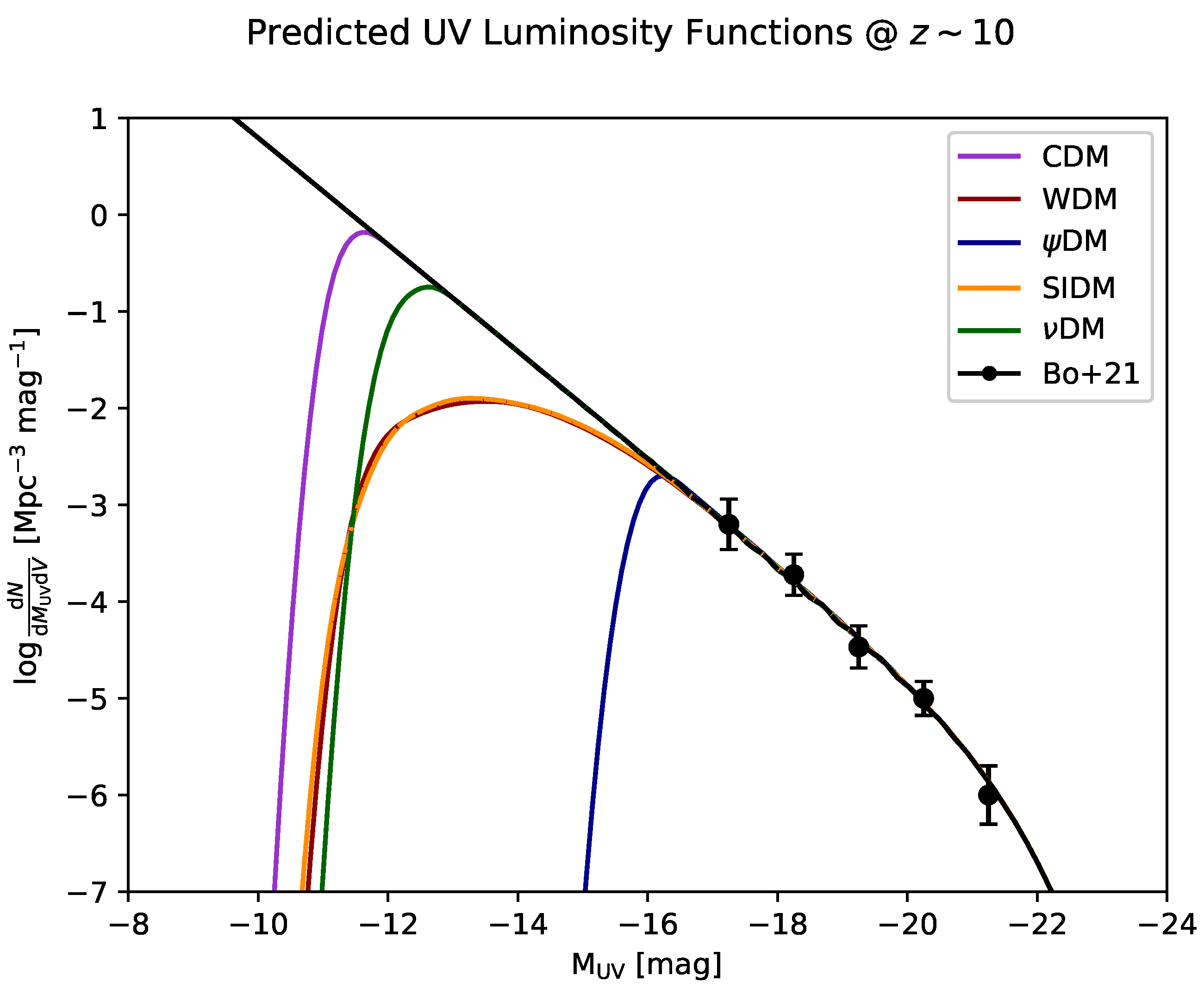
3. Results and Discussion
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Free-streaming is the process through which small-scale perturbations can be erased if particles with residual thermal velocities diffuse out of them before collapse. |
| 2 | Note that the clumping factor may actually depend on cosmology itself; in particular, as shown by [44], based on the model by [139], for a WDM scenario in the relevant redshift range , the clumping factor tends to be slightly lower than our fiducial case by [103]. We checked that adopting such a cosmology-dependent clumping factor has a minor impact on the posterior. |
References
- Meurer, G.R.; Heckman, T.M.; Calzetti, D. Shedding Light on Dark Matter at Colliders. Int. J. Mod. Phys. 2013, 28, 1330052. [Google Scholar]
- Kahlhoefer, F. Review of LHC dark matter searches. Int. J. Mod. Phys. 2017, 32, 1730006. [Google Scholar] [CrossRef]
- Argyropoulos, S.; Brandt, O.; Haisch, U. Collider Searches for Dark Matter through the Higgs Lens. Symmetry 2021, 13, 2406. [Google Scholar] [CrossRef]
- Aprile, E. et al. [XENON Collaboration] Dark Matter Search Results from a One Ton-Year Exposure of xenon1t. Phys. Rev. Lett. 2018, 121, 111302. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Caracciolo, V.; Cerulli, R.; Merlo, V.; Cappella, F.; D’Angelo, A.; Incicchitti, A.; di Marco, A.; Dai, C.J.; et al. DAMA/LIBRA-phase2 results and implications on several dark matter scenarios. Int. J. Mod. Phys. 2020, 35, 2044023. [Google Scholar] [CrossRef]
- Ackermann, M. et al. [The Fermi LAT Collaboration] Limits on dark matter annihilation signals from the Fermi LAT 4-year measurements of the isotropic gamma-ray background. J. Cosmol. Astropart. Phys. 2015, 2015, 008. [Google Scholar] [CrossRef]
- Ackermann, M. et al. [The Fermi LAT Collaboration] The Fermi Galactic Center GeV Excess and Implications for Dark Matter. Astrophys. J. 2017, 840, 43. [Google Scholar] [CrossRef]
- Albert, A. et al. [The Fermi-LAT and DES Collaborations] Searching for Dark Matter Annihilation in Recently Discovered Milky Way Satellites with Fermi-LAT. Astrophys. J. 2017, 834, 110. [Google Scholar] [CrossRef]
- Zornoza, J. Review on Indirect Dark Matter Searches with Neutrino Telescopes. Universe 2021, 7, 415. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Frenk, C.S.; White, S.D.M. Dark matter and cosmic structure. Ann. Phys. 2012, 524, 507–534. [Google Scholar] [CrossRef]
- Lapi, A.; Danese, L. A Stochastic Theory of the Hierarchical Clustering. I. Halo Mass Function. Astrophys. J. 2020, 903, 117. [Google Scholar] [CrossRef]
- Aghanim, M. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.-H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. The Milky Way’s bright satellites as an apparent failure of LambdaCDM. Mon. Not. R. Astron. Soc. 2012, 422, 1203–1218. [Google Scholar] [CrossRef]
- Bullock, J.S.; Boylan-Kolchin, M. Small-Scale Challenges to the ΛCDM Paradigm. Annu. Rev. Astron. Astrophys. 2017, 55, 343–387. [Google Scholar] [CrossRef]
- Gentile, G.; Famaey, B.; Zhao, H.; Salucci, P. Universality of galactic surface densities within one dark halo scale-length. Nature 2009, 461, 627–628. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Lelli, F.; Schombert, J.M. Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 201101. [Google Scholar] [CrossRef]
- El-Zant, A.; Shlosman, I.; Hoffman, Y. Dark Halos: The flattening of the density cusp by dynamical friction. Astrophys. J. 2001, 560, 636. [Google Scholar] [CrossRef]
- Tonini, C.; Lapi, A.; Salucci, P. Angular Momentum Transfer in Dark Matter Halos: Erasing the Cusp. Astrophys. J. 2006, 649, 591. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. Cold dark matter heats up. Nature 2014, 506, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Peirani, S.; Dubois, Y.; Volonteri, M.; Devriendt, J.; Bundy, K.; Silk, J.; Pichon, C.; Kaviraj, S.; Gavazzi, R.; Habouzit, M. Density profile of dark matter haloes and galaxies in the HORIZON-AGN simulation: The impact of AGN feedback. Mon. Not. R. Astron. Soc. 2017, 472, 2153–2169. [Google Scholar] [CrossRef]
- Freundlich, J.; Jiang, F.; Dekel, A.; Cornuault, N.; Ginzburg, O.; Koskas, R.; Lapiner, S.; Dutton, A.; Maccio, A.V. A model for core formation in dark matter haloes and ultra-diffuse galaxies by outflow episodes. Mon. Not. R. Astron. Soc. 2020, 491, 4523–4542. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rev. 2004, 405, 279–390. [Google Scholar] [CrossRef]
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Annu. Rev. Astron. Astrophys. 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L.; et al. Einstein, Planck and Vera Rubin: Relevant encounters between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 603190. [Google Scholar] [CrossRef]
- Bode, P.; Ostriker, J.P.; Turok, N. Halo Formation in Warm Dark Matter Models. Astrophys. J. 2001, 556, 93. [Google Scholar] [CrossRef]
- Viel, M.; Becker, G.; Bolton, J.S.; Haehnelt, M.G. Warm dark matter as a solution to the small scale crisis: New constraints from high redshift Lyman-alpha forest data. Phys. Rev. 2013, 88, 043502. [Google Scholar] [CrossRef]
- Lovell, M.R.; Frenk, C.S.; Eke, V.R.; Jenkins, A.; Gao, L.; Theuns, T. The properties of warm dark matter haloes. Mon. Not. R. Astron. Soc. 2014, 439, 300–317. [Google Scholar] [CrossRef]
- Hu, W.; Barkana, R.; Gruzinov, A. Fuzzy Cold Dark Matter: The Wave Properties of Ultralight Particles. Phys. Rev. Lett. 2000, 85, 1158. [Google Scholar] [CrossRef] [PubMed]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Cyr-Racine, F.-Y.; Pfrommer, C.; Bringmann, T.; Sigurdson, K. ETHOS—An effective theory of structure formation: Dark matter physics as a possible explanation of the small-scale CDM problems. Mon. Not. R. Astron. Soc. 2016, 460, 1399–1416. [Google Scholar] [CrossRef]
- Tulin, S.; Yu, H.-B. Dark Matter Self-interactions and Small Scale Structure. Phys. Rep. 2018, 730, 1–57. [Google Scholar] [CrossRef]
- Huo, R.; Kaplinghat, M.; Pan, Z.; Yu, H.-B. Signatures of self-interacting dark matter in the matter power spectrum and the CMB. Phys. Lett. B 2018, 783, 76–81. [Google Scholar] [CrossRef]
- Seljak, U.; Makarov, A.; McDonald, P.; Trac, H. Can Sterile Neutrinos Be the Dark Matter? Phys. Rev. Lett. 2006, 97, 191303. [Google Scholar] [CrossRef]
- Kusenko, A. Sterile neutrinos: The dark side of the light fermions. Phys. Rev. 2009, 481, 1–28. [Google Scholar] [CrossRef]
- Adhikari, R.; Agostini, M.; Ky, N.A.; Araki, T.; Archidiacono, M.; Bahr, M.; Baur, J.; Behrens, J.; Bezrukov, F.; Bhupal Dev, P.S.; et al. A White Paper on keV sterile neutrino Dark Matter. J. Cosmol. Astropart. Phys. 2017, 1, 025. [Google Scholar] [CrossRef]
- Schneider, A.; Smith, R.E.; Reed, D. Halo mass function and the free streaming scale. Mon. Not. R. Astron. Soc. 2013, 433, 1573–1587. [Google Scholar] [CrossRef]
- Dayal, P.; Mesinger, A.; Pacucci, F. Early Galaxy Formation in Warm Dark Matter Cosmologies. Astrophys. J. 2015, 806, 67. [Google Scholar] [CrossRef]
- Schive, H.-Y.; Chiueh, T.; Broadhurst, T.; Huang, K.-W. Contrasting Galaxy Formation from Quantum Wave Dark Matter, ψDM, with ΛCDM, using Planck and Hubble Data. Astrophys. J. 2016, 818, 89. [Google Scholar] [CrossRef]
- Menci, N.; Grazian, A.; Lamastra, A.; Calura, F.; Castellano, M.; Santini, P. Galaxy Formation in Sterile Neutrino Dark Matter Models. Astrophys. J. 2018, 854, 1. [Google Scholar] [CrossRef]
- Lovell, M.R. Toward a General Parameterization of the Warm Dark Matter Halo Mass Function. Astrophys. J. 2020, 847, 147. [Google Scholar] [CrossRef]
- Romanello, M.; Menci, N.; Castellano, M. The Epoch of Reionization in Warm Dark Matter Scenarios. Universe 2021, 7, 365. [Google Scholar] [CrossRef]
- Kulkarni, M.; Ostriker, J.P. What is the halo mass function in a fuzzy dark matter cosmology? Mon. Not. R. Astron. Soc. 2022, 510, 1425–1430. [Google Scholar] [CrossRef]
- Irsic, V. New constraints on the free-streaming of warm dark matter from intermediate and small scale Lyman-α forest data. Phys. Rev. 2017, 96, 023522. [Google Scholar]
- Irsic, V. First Constraints on Fuzzy Dark Matter from Lyman-α Forest Data and Hydrodynamical Simulations. Phys. Rev. Lett. 2017, 119, 031302. [Google Scholar] [CrossRef]
- Pacucci, F.; Mesinger, A.; Haiman, Z. Focusing on Warm Dark Matter with Lensed High-redshift Galaxies. Mon. Not. R. Astron. Soc. 2013, 435, L53. [Google Scholar] [CrossRef]
- Menci, N.; Grazian, A.; Castellano, M.; Sanchez, N.G. A Stringent Limit on the Warm Dark Matter Particle Masses from the Abundance of z=6 Galaxies in the Hubble Frontier Fields. Astrophys. J. 2016, 825, L1. [Google Scholar] [CrossRef]
- Shirasaki, M.; Ishiyama, T.; Ando, S. Virial Halo Mass Function in the Planck Cosmology. Astrophys. J. 2021, 922, 89. [Google Scholar] [CrossRef]
- Sabti, N.; Munoz, J.B.; Blas, D. New Roads to the Small-scale Universe: Measurements of the Clustering of Matter with the High-redshift UV Galaxy Luminosity Function. Astrophys. J. 2022, 928, L20. [Google Scholar] [CrossRef]
- De Souza, R.S.; Mesinger, A.; Ferrara, A.; Haiman, Z.; Perna, R.; Yoshida, N. Constraints on Warm Dark Matter models from high-redshift long gamma-ray bursts. Mon. Not. R. Astron. Soc. 2012, 432, 3218–3227. [Google Scholar] [CrossRef]
- Lapi, A.; Mancuso, C.; Celotti, A.; Danese, L. Galaxy Evolution at High Redshift: Obscured Star Formation, GRB Rates, Cosmic Reionization, and Missing Satellites. Astrophys. J. 2017, 835, 37. [Google Scholar] [CrossRef]
- Barkana, R.; Haiman, Z.; Ostriker, J.P. Constraints on Warm Dark Matter from Cosmological Reionization. Astrophys. J. 2001, 558, 482. [Google Scholar] [CrossRef]
- Lapi, A.; Danese, L. Cold or warm? Constraining dark matter with primeval galaxies and cosmic reionization after Planck. J. Cosmol. Astropart. Phys. 2015, 2015, 003. [Google Scholar] [CrossRef]
- Dayal, P.; Choudhury, T.R.; Bromm, V.; Pacucci, F. Reionization and Galaxy Formation in Warm Dark Matter Cosmologies. Astrophys. J. 2017, 836, 16. [Google Scholar] [CrossRef]
- Carucci, I.P.; Corasaniti, P. Cosmic Reionization History and Dark Matter Scenarios. Phys. Rev. D 2019, 99, 023518. [Google Scholar] [CrossRef]
- Carucci, I.P.; Villaescusa-Navarro, F.; Viel, M.; Lapi, A. Warm dark matter signatures on the 21cm power spectrum: Intensity mapping forecasts for SKA. J. Cosmol. Astropart. Phys. 2015, 2015, 047. [Google Scholar] [CrossRef][Green Version]
- Boyarsky, A.; Drewes, M.; Lasserre, T.; Mertens, S.; Ruchayskiy, O. Sterile neutrino Dark Matter. Prog. Part. Nucl. Phys. 2019, 104, 1–45. [Google Scholar] [CrossRef]
- Chatterjee, A.; Dayal, P.; Choudhury, T.R.; Hutter, A. Ruling out 3 keV warm dark matter using 21 cm EDGES data. Mon. Not. R. Astron. Soc. 2019, 487, 3560–3567. [Google Scholar] [CrossRef]
- Rudakovskyi, A.; Savchenko, D.; Tsizh, M. Can EDGES observation favour any dark matter model? Mon. Not. R. Astron. Soc. 2020, 497, 3393–3399. [Google Scholar]
- Bringmann, T.; Kahlhoefer, F.; Schmidt-Hoberg, K.; Walia, P. Strong Constraints on Self-Interacting Dark Matter with Light Mediators. Phys. Rev. Lett. 2017, 118, 141802. [Google Scholar] [CrossRef]
- Grand, R.J.J.; White, S.D.M. Dark matter annihilation and the Galactic Centre Excess. Mon. Not. R. Astron. Soc. 2022, 511, L55. [Google Scholar] [CrossRef]
- Weisz, D.R.; Johnson, B.D.; Conroy, C. The Very Faint End of the UV Luminosity Function over Cosmic Time: Constraints from the Local Group Fossil Record. Astrophys. J. 2014, 794, L3. [Google Scholar] [CrossRef]
- Weisz, D.R.; Boylan-Kolchin, M. Local Group ultra-faint dwarf galaxies in the reionization era. Mon. Not. R. Astron. Soc. 2017, 469, L83–L88. [Google Scholar] [CrossRef]
- Kennedy, R.; Frenk, C.; Cole, S.; Benson, A. Constraining the warm dark matter particle mass with Milky Way satellites. Mon. Not. R. Astron. Soc. 2014, 442, 2487–2495. [Google Scholar] [CrossRef]
- Nadler, E.O.; Birrer, S.; Gilman, D.; Wechsler, R.H.; Du, X.; Benson, A.; Nierenberg, A.M.; Treu, T. Dark Matter Constraints from a Unified Analysis of Strong Gravitational Lenses and Milky Way Satellite Galaxies. Astrophys. J. 2021, 917, 7. [Google Scholar] [CrossRef]
- Newton, O.; Leo, M.; Cautun, M.; Jenkins, A.; Frenk, C.S.; Lovell, M.R.; Helly, J.C.; Benson, A.J.; Cole, S. Constraints on the properties of warm dark matter using the satellite galaxies of the Milky Way. J. Cosmol. Astropart. Phys. 2021, 2021, 062. [Google Scholar] [CrossRef]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Publ. Astron. Soc. Pacific 2003, 115, 763. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Oesch, P.A.; Stefanon, M.; Illingworth, G.; Labbé, I.; Reddy, N.; Atek, H.; Montes, M.; Naidu, R.; Nanayakkara, T.; et al. New Determinations of the UV Luminosity Functions from z∼9 to 2 Show a Remarkable Consistency with Halo Growth and a Constant Star Formation Efficiency. Astron. J. 2021, 162, 47. [Google Scholar] [CrossRef]
- Oesch, P.A.; Bouwens, R.J.; Illingworth, G.D.; Labbé, I.; Stefanon, M. The Dearth of z∼10 Galaxies in All HST Legacy Fields—The Rapid Evolution of the Galaxy Population in the First 500 Myr. Astrophys. J. 2018, 855, 105. [Google Scholar] [CrossRef]
- Meurer, G.R.; Heckman, T.M.; Calzetti, D. Dust Absorption and the Ultraviolet Luminosity Density at z∼3 as Calibrated by Local Starburst Galaxies. Astrophys. J. 1999, 521, 64. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Illingworth, G.D.; Oesch, P.A. UV-continuum slopes of >4000 z∼4-8 galaxies from the HUDF/XDF, HUDF09, ERS, CANDELS-South, and CANDELS-North fields. Astrophys. J. 2014, 793, 115. [Google Scholar] [CrossRef]
- Kennicutt, R.C.; Evans, N.J. Star Formation in the Milky Way and Nearby Galaxies. Annu. Rev. Astron. Astrophys. 2012, 50, 531–608. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star-Formation History. Annu. Rev. Astron. Astrophys. 2014, 52, 415. [Google Scholar] [CrossRef]
- Cai, Z.; Lapi, A.; Bressan, A.; De Zotti, G.; Negrello, M.; Danese, L. A Physical Model for the Evolving Ultraviolet Luminosity Function of High Redshift Galaxies and their Contribution to the Cosmic Reionization. Astrophys. J. 2014, 785, 65. [Google Scholar] [CrossRef]
- Robertson, B.E.; Ellis, R.S.; Furlanetto, S.R.; Dunlop, J.S. Cosmic reionization and early star-forming galaxies: A joint analysis of new constraints from Planck and Hubble Space Telescope. Astrophys. J. 2015, 802, L19. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; D’Aloisio, A.; Paardekooper, J.-P.; Ryan, R., Jr.; Behroozi, P.; Finlator, K.; Livermore, R.; Upton Sanderbeck, P.R.; Dalla Vecchia, C.; Khochfar, S. Conditions for Reionizing the Universe with a Low Galaxy Ionizing Photon Escape Fraction. Astrophys. J. 2019, 879, 36. [Google Scholar] [CrossRef]
- Bose, S.; Deason, A.J.; Frenk, C.S. The Imprint of Cosmic Reionization on the Luminosity Function of Galaxies. Astrophys. J. 2018, 863, 123. [Google Scholar] [CrossRef]
- Munoz, J.B.; Qin, Y.; Mesinger, A.; Murray, S.G.; Greig, B.; Mason, C. The impact of the first galaxies on cosmic dawn and reionization. Mon. Not. R. Astron. Soc. 2022, 511, 3657–3681. [Google Scholar] [CrossRef]
- Mao, J.; Lapi, A.; Granato, G.L.; de Zotti, G.; Danese, L. The Role of the Dust in Primeval Galaxies: A Simple Physical Model for Lyman Break Galaxies and Ly-α Emitters. Astrophys. J. 2007, 667, 655. [Google Scholar] [CrossRef][Green Version]
- Rutkowski, M.J.; Scarlata, C.; Haardt, F.; Siana, B.; Henry, A.; Rafelski, M.; Hayes, M.; Salvato, M.; Pahl, A.J.; Mehta, V.; et al. Lyman Continuum Escape Fraction of Star-forming Dwarf Galaxies at z∼1. Astrophys. J. 2016, 819, 81. [Google Scholar] [CrossRef]
- Paardekooper, J.-P.; Khochfar, S.; Dalla Vecchia, C. The First Billion Years project: The escape fraction of ionizing photons in the epoch of reionization. Mon. Not. R. Astron. Soc. 2015, 451, 2544. [Google Scholar] [CrossRef]
- Vanzella, E.; Nonino, M.; Cupani, G.; Castellano, M.; Sani, E.; Mignoli, M.; Calura, F.; Meneghetti, M.; Gilli, R.; Comastri, A.; et al. Direct Lyman continuum and Lyα escape observed at redshift 4. Mon. Not. R. Astron. Soc. 2018, 476, L15–L19. [Google Scholar] [CrossRef]
- Alavi, A.; Colbert, J.; Teplitz, H.I.; Siana, B.; Scarlata, C.; Rutkowski, M.; Mehta, V.; Henry, A.; Dai, Y.S.; Haardt, F.; et al. Lyman Continuum Escape Fraction from Low-mass Starbursts at z=1.3. Astrophys. J. 2020, 904, 59. [Google Scholar] [CrossRef]
- Smith, B.M.; Windhorst, R.A.; Cohen, S.H.; Koekemoer, A.M.; Jansen, R.A.; White, C.; Borthakur, S.; Hathi, N.; Jiang, L.; Rutkowski, M.; et al. The Lyman Continuum Escape Fraction of Galaxies and AGN in the GOODS Fields. Astrophys. J. 2020, 897, 41. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Worseck, G.; Schaerer, D.; Guseva, N.G.; Chisholm, J.; Thuan, T.X.; Fricke, K.J.; Verhamme, A. Lyman continuum leakage from low-mass galaxies with M⋆<108M⊙. Mon. Not. R. Astron. Soc. 2021, 503, 1734–1752. [Google Scholar]
- Pahl, A.J.; Shapley, A.; Steidel, C.C.; Chen, Y.; Reddy, N.A. An uncontaminated measurement of the escaping Lyman continuum at z∼3. Mon. Not. R. Astron. Soc. 2021, 505, 2447–2467. [Google Scholar] [CrossRef]
- Atek, H.; Furtak, L.J.; Oesch, P.; van Dokkum, P.; Reddy, N.; Contini, T.; Illingworth, G.; Wilkins, S. The star formation burstiness and ionizing efficiency of low-mass galaxies. Mon. Not. R. Astron. Soc. 2022, 511, 4464–4479. [Google Scholar] [CrossRef]
- Naidu, R.P.; Matthee, J.; Oesch, P.A.; Conroy, C.; Sobral, D.; Pezzulli, G.; Hayes, M.; Erb, D.; Amorín, R.; Gronke, M.; et al. The synchrony of production and escape: Half the bright Lyα emitters at z≈2 have Lyman continuum escape fractions ≈50%. Mon. Not. R. Astron. Soc. 2022, 510, 4582–4607. [Google Scholar] [CrossRef]
- Puchwein, E.; Haardt, F.; Haehnelt, M.G.; Madau, P. Consistent modelling of the meta-galactic UV background and the thermal/ionization history of the intergalactic medium. Mon. Not. R. Astron. Soc. 2019, 485, 47–68. [Google Scholar] [CrossRef]
- Shen, X.; Hopkins, P.F.; Faucher-Giguère, C.-A.; Alexander, D.M.; Richards, G.T.; Ross, N.P.; Hickox, R.C. The bolometric quasar luminosity function at z=0–7. Mon. Not. R. Astron. Soc. 2020, 495, 3252–3275. [Google Scholar] [CrossRef]
- Shankar, F.; Mathur, S. On the Faint End of the High-Redshift Active Galactic Nucleus Luminosity Function. Astrophys. J. 2007, 660, 1051. [Google Scholar] [CrossRef]
- Giallongo, E.; Grazian, A.; Fiore, F.; Fontana, A.; Pentericci, L.; Vanzella, E.; Dickinson, M.; Kocevski, D.; Castellano, M.; Cristiani, S.; et al. Faint AGNs at z>4 in the CANDELS GOODS-S field: Looking for contributors to the reionization of the Universe. Astron. Astrophys. 2015, 578, A83. [Google Scholar] [CrossRef]
- Ricci, F.; Marchesi, S.; Shankar, F.; La Franca, F.; Civano, F. Constraining the UV emissivity of AGN throughout cosmic time via X-ray surveys. Mon. Not. R. Astron. Soc. 2017, 465, 1915–1925. [Google Scholar] [CrossRef]
- Giallongo, E.; Grazian, A.; Fiore, F.; Kodra, D.; Urrutia, T.; Castellano, M.; Cristiani, S.; Dickinson, M.; Fontana, A.; Menci, N.; et al. Space Densities and Emissivities of Active Galactic Nuclei at z>4. Astrophys. J. 2019, 884, 19. [Google Scholar] [CrossRef]
- Kulkarni, G.; Worseck, G.; Hennawi, J.F. Evolution of the AGN UV luminosity function from redshift 7.5. Mon. Not. R. Astron. Soc. 2019, 488, 1035–1065. [Google Scholar] [CrossRef]
- Ananna, T.T.; Urry, C.M.; Treister, E.; Hickox, R.C.; Shankar, F.; Ricci, C.; Cappelluti, N.; Marchesi, S.; Turner, T.J. Accretion History of AGNs. III. Radiative Efficiency and AGN Contribution to Reionization. Astrophys. J. 2020, 903, 85. [Google Scholar] [CrossRef]
- Grazian, A.; Giallongo, E.; Boutsia, K.; Cristiani, S.; Vanzella, E.; Scarlata, C.; Santini, P.; Pentericci, L.; Merlin, E.; Menci, N.; et al. The contribution of faint AGNs to the ionizing background at z>4. Astron. Astrophys. 2018, 613, A44. [Google Scholar] [CrossRef]
- Romano, M. Lyman continuum escape fraction and mean free path of hydrogen ionizing photons for bright z∼4 QSOs from SDSS DR14. Astron. Astrophys. 2019, 632, A45. [Google Scholar] [CrossRef]
- Madau, P.; Haardt, F.; Rees, M.J. Radiative transfer in a clumpy Universe. III. The nature of cosmological ionizing sources. Astrophys. J. 1999, 514, 648. [Google Scholar] [CrossRef]
- Loeb, A.; Barkana, R. The Reionization of the Universe by the First Stars and Quasars. Annu. Rev. Astron. Astrophys. 2001, 39, 19–66. [Google Scholar] [CrossRef]
- Pawlik, A.H.; Schaye, J.; van Scherpenzeel, E. Keeping the Universe ionized: Photoheating and the clumping factor of the high-redshift intergalactic medium. Mon. Not. R. Astron. Soc. 2009, 394, 1812–1824. [Google Scholar] [CrossRef]
- Haardt, F.; Madau, P. Radiative Transfer in a Clumpy Universe. IV. New Synthesis Models of the Cosmic UV/X-Ray Background. Astrophys. J. 2012, 746, 125. [Google Scholar] [CrossRef]
- Diemer, B. COLOSSUS: A Python Toolkit for Cosmology, Large-scale Structure, and Dark Matter Halos. Astrophys. J. Suppl. Ser. 2018, 239, 35. [Google Scholar] [CrossRef]
- Tinker, J.; Kravtsov, A.V.; Klypin, A.; Abazajian, K.; Warren, M.; Yepes, G.; Gottlober, S.; Holz, D.E. Toward a Halo Mass Function for Precision Cosmology: The Limits of Universality. Astrophys. J. 2008, 688, 709. [Google Scholar] [CrossRef]
- Schneider, A.; Smith, R.E.; Maccio, A.; Moore, B. Non-linear evolution of cosmological structures in warm dark matter models. Mon. Not. R. Astron. Soc. 2012, 424, 684–698. [Google Scholar] [CrossRef]
- Bulbul, E.; Markevitch, M.; Foster, A.; Smith, R.K.; Loewenstein, M.; Randall, S.W. Detection of an Unidentified Emission Line in the Stacked X-Ray Spectrum of Galaxy Clusters. Astrophys. J. 2014, 789, 13. [Google Scholar] [CrossRef]
- Aversa, R.; Lapi, A.; De Zotti, G.; Danese, L. Black Hole and Galaxy Coevolution from Continuity Equation and Abundance Matching. Astrophys. J. 2015, 810, 74. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. EMERGE—An empirical model for the formation of galaxies since z∼10. Mon. Not. R. Astron. Soc. 2018, 477, 1822. [Google Scholar] [CrossRef]
- Cristofari, P.; Ostriker, J.P. Abundance matching for low-mass galaxies in the CDM and FDM models. Mon. Not. R. Astron. Soc. 2019, 482, 4364–4371. [Google Scholar] [CrossRef]
- Behroozi, P.; Wechsler, R.H.; Hearin, A.P.; Conroy, C. UNIVERSEMACHINE: The correlation between galaxy growth and dark matter halo assembly from z=0–10. Mon. Not. R. Astron. Soc. 2020, 488, 3143–3194. [Google Scholar] [CrossRef]
- Efstathiou, G. Suppressing the formation of dwarf galaxies via photoionization. Mon. Not. R. Astron. Soc. 1992, 256, 43P–47P. [Google Scholar] [CrossRef]
- Sobacchi, E.; Mesinger, A. How does radiative feedback from an ultraviolet background impact reionization? Mon. Not. R. Astron. Soc. 2013, 432, 3340. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Becker, G.D.; Bolton, J.S. New measurements of the ionizing ultraviolet background over 2<z<5 and implications for hydrogen reionization. Mon. Not. R. Astron. Soc. 2013, 436, 1023–1039. [Google Scholar]
- Becker, G.D.; D’Aloisio, A.; Christenson, H.M.; Zhu, Y.; Worseck, G.; Bolton, J.S. The mean free path of ionizing photons at 5<z<6: Evidence for rapid evolution near reionization. Mon. Not. R. Astron. Soc. 2021, 508, 1853–1869. [Google Scholar]
- Konno, A.; Ouchi, M.; Ono, Y.; Shimasaku, K.; Shibuya, T.; Furusawa, H.; Nakajima, K.; Naito, Y.; Momose, R.; Yuma, S.; et al. Accelerated Evolution of the Lyα Luminosity Function at z≳7 Revealed by the Subaru Ultra-deep Survey for Lyα Emitters at z=7.3. Astrophys. J. 2014, 797, 16. [Google Scholar] [CrossRef]
- McGreer, I.D.; Mesinger, A.; D’Odorico, V. Model-independent evidence in favour of an end to reionization by z≈6. Mon. Not. R. Astron. Soc. 2015, 447, 499–505. [Google Scholar] [CrossRef]
- Davies, F.B.; Hennawi, J.F.; Banados, E.; Lukic, Z.; Decarli, R.; Fan, X.; Farina, E.P.; Mazzucchelli, C.; Rix, H.-W.; Venemans, B.P.; et al. Quantitative Constraints on the Reionization History from the IGM Damping Wing Signature in Two Quasars at z>7. Astrophys. J. 2018, 864, 142. [Google Scholar] [CrossRef]
- Mason, C.A.; Treu, T.; Dijkstra, M.; Mesinger, A.; Trenti, M.; Pentericci, L.; de Barros, S.; Vanzella, E. The Universe Is Reionizing at z∼7: Bayesian Inference of the IGM Neutral Fraction Using Lyα Emission from Galaxies. Astrophys. J. 2018, 856, 2. [Google Scholar] [CrossRef]
- Konno, A.; Ouchi, M.; Shibuya, T.; Ono, Y.; Shimasaku, K.; Taniguchi, Y.; Nagao, T.; Kobayashi, M.A.R.; Kajisawa, M.; Kashikawa, N.; et al. SILVERRUSH. IV. Lyα luminosity functions at z=5.7 and 6.6 studied with ∼1300 Lyα emitters on the 14–21 deg2 sky. Publ. Astron. Soc. Jpn. 2018, 70, S16. [Google Scholar]
- Hoag, A.; Bradac, M.; Huang, K.; Mason, C.; Treu, T.; Schmidt, K.B.; Trenti, M.; Strait, V.; Lemaux, B.C.; Finney, E.Q.; et al. Constraining the Neutral Fraction of Hydrogen in the IGM at Redshift 7.5. Astrophys. J. 2019, 878, 12. [Google Scholar] [CrossRef]
- Bolan, P.; Lemaux, B.C.; Mason, C.; Bradac, M.; Treu, T.; Strait, V.; Pelliccia, D.; Pentericci, L.; Malkan, M. Inferring the IGM Neutral Fraction at z∼6-8 with Low-Luminosity Lyman Break Galaxies. arXiv 2021, arXiv:2111.14912. [Google Scholar]
- Greig, B.; Mesinger, A.; Davies, F.B.; Wang, F.; Yang, J.; Hennawi, J.F. IGM damping wing constraints on reionisation from covariance reconstruction of two z≳7 QSOs. Mon. Not. R. Astron. Soc. 2022, 512, 5390. [Google Scholar] [CrossRef]
- Maccio, A.; Paduroiu, S.; Anderhalden, D.; Schneider, A.; Moore, B. Cores in warm dark matter haloes: A Catch 22 problem. Mon. Not. R. Astron. Soc. 2012, 424, 1105–1112. [Google Scholar] [CrossRef]
- Calabrese, E.; Spergel, D. Ultra-light dark matter in ultra-faint dwarf galaxies. Mon. Not. R. Astron. Soc. 2016, 460, 4397–4402. [Google Scholar] [CrossRef]
- Vegetti, S.; Despali, G.; Lovell, M.R.; Enzi, W. Constraining sterile neutrino cosmologies with strong gravitational lensing observations at redshift z∼0.2. Mon. Not. R. Astron. Soc. 2018, 481, 3661. [Google Scholar] [CrossRef]
- Horiuchi, S.; Humphrey, P.J.; Onorbe, J.; Abazajian, K.N.; Kaplinghat, M.; Garrison-Kimmel, S. Sterile neutrino dark matter bounds from galaxies of the Local Group. Phys. Rev. D 2014, 89, 025017. [Google Scholar] [CrossRef]
- Lovell, M.R.; Bose, S.; Boyarsky, A.; Cole, S.; Frenk, C.S.; Gonzalez-Perez, V.; Kennedy, R.; Ruchayskiy, O.; Smith, A. Satellite galaxies in semi-analytic models of galaxy formation with sterile neutrino dark matter. Mon. Not. R. Astron. Soc. 2016, 461, 60–72. [Google Scholar] [CrossRef]
- Burkert, A. Fuzzy Dark Matter and Dark Matter Halo Cores. Astrophys. J. 2020, 904, 161. [Google Scholar] [CrossRef]
- Kistler, M.D.; Yuksel, H.; Beacom, J.F.; Hopkins, A.M.; Wyithe, J.S.B. The Star Formation Rate in the Reionization Era as Indicated by Gamma-Ray Bursts. Astrophys. J. 2009, 705, L104. [Google Scholar] [CrossRef]
- Loiacono, F.; Decarli, R.; Gruppioni, C.; Talia, M.; Cimatti, A.; Zamorani, G.; Pozzi, F.; Yan, L.; Lemaux, B.C.; Riechers, D.A.; et al. The ALPINE-ALMA [C II] survey. Luminosity function of serendipitous [C II] line emitters at z∼5. Astron. Astrophys. 2021, 646, A76. [Google Scholar] [CrossRef]
- Khusanova, Y.; Bethermin, M.; Le Fevre, O.; Capak, P.; Faisst, A.L.; Schaerer, D.; Silverman, J.D.; Cassata, P.; Yan, L.; Ginolfi, M.; et al. The ALPINE-ALMA [CII] survey. Obscured star formation rate density and main sequence of star-forming galaxies at z>4. Astron. Astrophys. 2021, 649, A152. [Google Scholar] [CrossRef]
- Gruppioni, C.; Bethermin, M.; Loiacono, F.; Le Fevre, O.; Capak, P.; Cassata, P.; Faisst, A.L.; Schaerer, D.; Silverman, J.; Yan, L.; et al. The ALPINE-ALMA [CII] survey. The nature, luminosity function, and star formation history of dusty galaxies up to z≈6. Astron. Astrophys. 2020, 643, A8. [Google Scholar] [CrossRef]
- Harikane, Y.; Ouchi, M.; Oguri, M.; Ono, Y.; Nakajima, K.; Isobe, Y.; Umeda, H.; Mawatari, K.; Zhang, Y. A Comprehensive Study on Galaxies at z∼9–17 Found in the Early JWST Data: UV Luminosity Functions and Cosmic Star-Formation History at the Pre-Reionization Epocht. arXiv 2022, arXiv:2208.01612. [Google Scholar]
- Liddle, A.R. How many cosmological parameters? Mon. Not. R. Astron. Soc. 2004, 351, L49–L53. [Google Scholar] [CrossRef]
- Barkana, R.; Loeb, A. in the beginning: The first sources of light and the reionization of the universe. Phys. Rev. 2001, 349, 125–238. [Google Scholar] [CrossRef]
- Trombetti, T.; Burigana, C. Semi-analytical description of clumping factor and cosmic microwave background free-free distortions from reionization. Mon. Not. R. Astron. Soc. 2014, 437, 2507–2520. [Google Scholar] [CrossRef]
- Finlator, K.; Oh, S.P.; Ozel, F.; Dave, R. Gas clumping in self-consistent reionization models. Mon. Not. R. Astron. Soc. 2012, 427, 2464–2479. [Google Scholar] [CrossRef]
- Diemer, B. Universal at Last? The Splashback Mass Function of Dark Matter Halos. Astrophys. J. 2020, 903, 87. [Google Scholar] [CrossRef]
- Alavi, A.; Siana, B.; Richard, J.; Rafelski, M.; Jauzac, M.; Limousin, M.; Freeman, W.R.; Scarlata, C.; Robertson, B.; Stark, D.P.; et al. The Evolution of the Faint End of the UV Luminosity Function during the Peak Epoch of Star Formation (1<z<3). Astrophys. J. 2016, 832, 56. [Google Scholar]
- Gardner, J.P.; Mather, J.C.; Clampin, M.; Doyon, R.; Greenhouse, M.A.; Hammel, H.B.; Hutchings, J.B.; Jakobsen, P.; Lilly, S.J.; Long, K.S.; et al. The James Webb Space Telescope. Space Sci. Rev. 2006, 123, 485–606. [Google Scholar] [CrossRef]
- Atek, H.; Richard, J.; Kneib, J.-P.; Schaerer, D. The extreme faint end of the UV luminosity function at z∼6 through gravitational telescopes: A comprehensive assessment of strong lensing uncertainties. Mon. Not. R. Astron. Soc. 2018, 479, 5184–5195. [Google Scholar] [CrossRef]
- Park, J.; Gillet, N.; Mesinger, A.; Greig, B. Properties of reionization-era galaxies from JWST luminosity functions and 21-cm interferometry. Mon. Not. R. Astron. Soc. 2020, 491, 3891–3899. [Google Scholar] [CrossRef]
- Labbe, I.; Bezanson, R.; Atek, H.; Brammer, G.; Coe, D.; Dayal, P.; Feldmann, R.; Forster Schreiber, N.M.; Franx, M.; Geha, M.C.; et al. UNCOVER: Ultra-deep NIRCam and NIRSpec Observations Before the Epoch of Reionization. JWST Propos. Cycle 2021, 1, 2561. [Google Scholar]
- Robertson, B.E. Galaxy Formation and Reionization: Key Unknowns and Expected Breakthroughs by the James Webb Space Telescope. arXiv 2021, arXiv:2110.13160. [Google Scholar] [CrossRef]
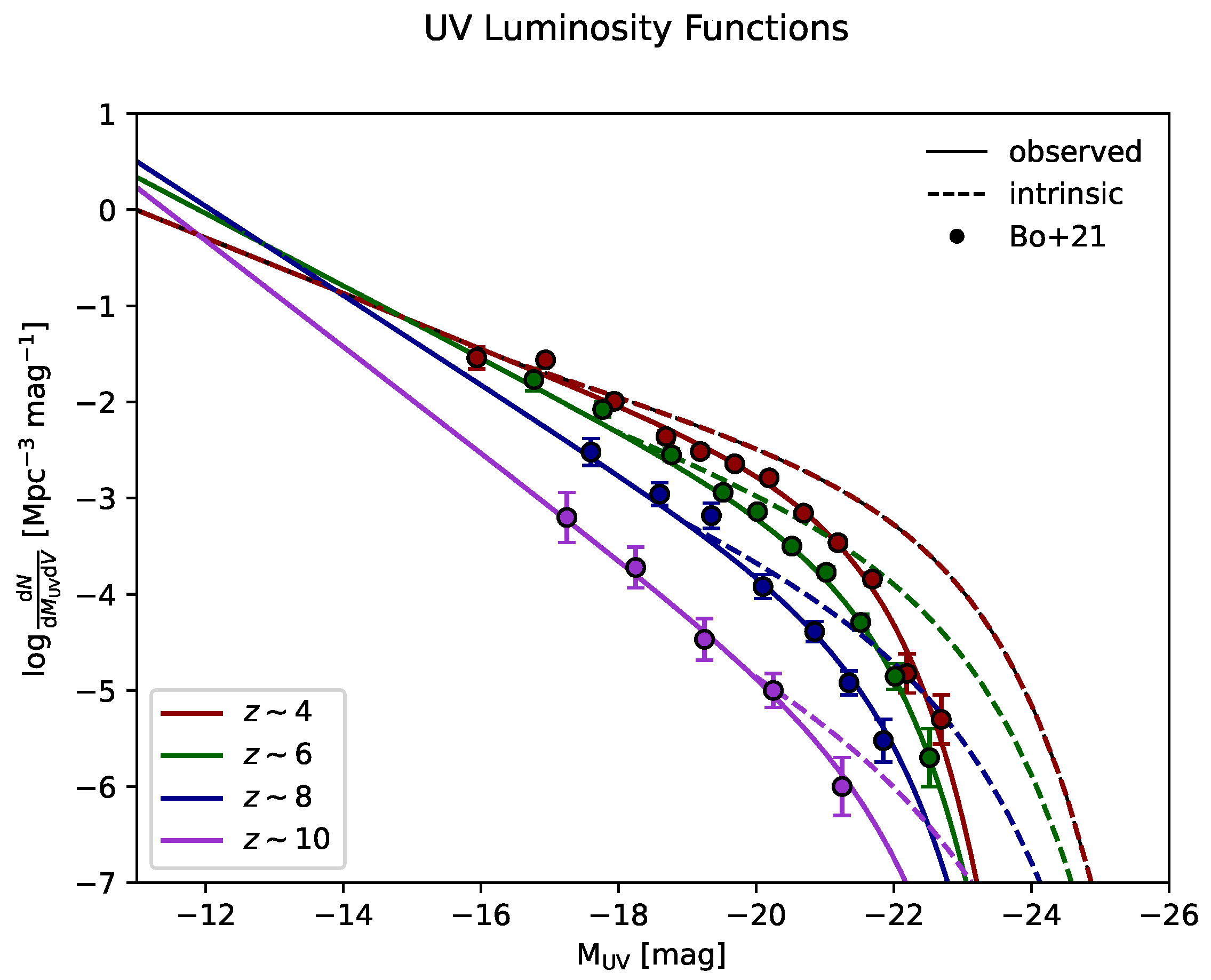
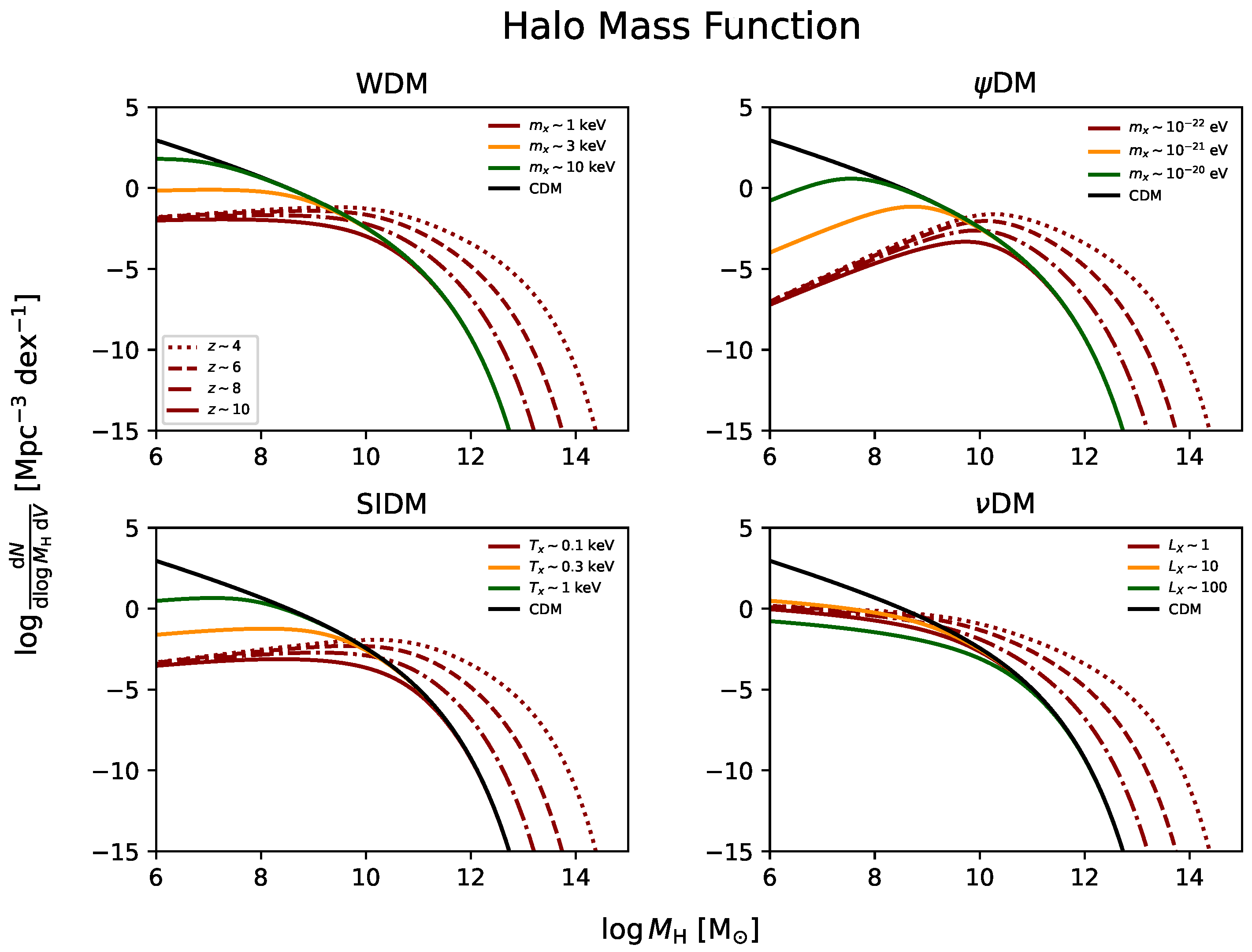


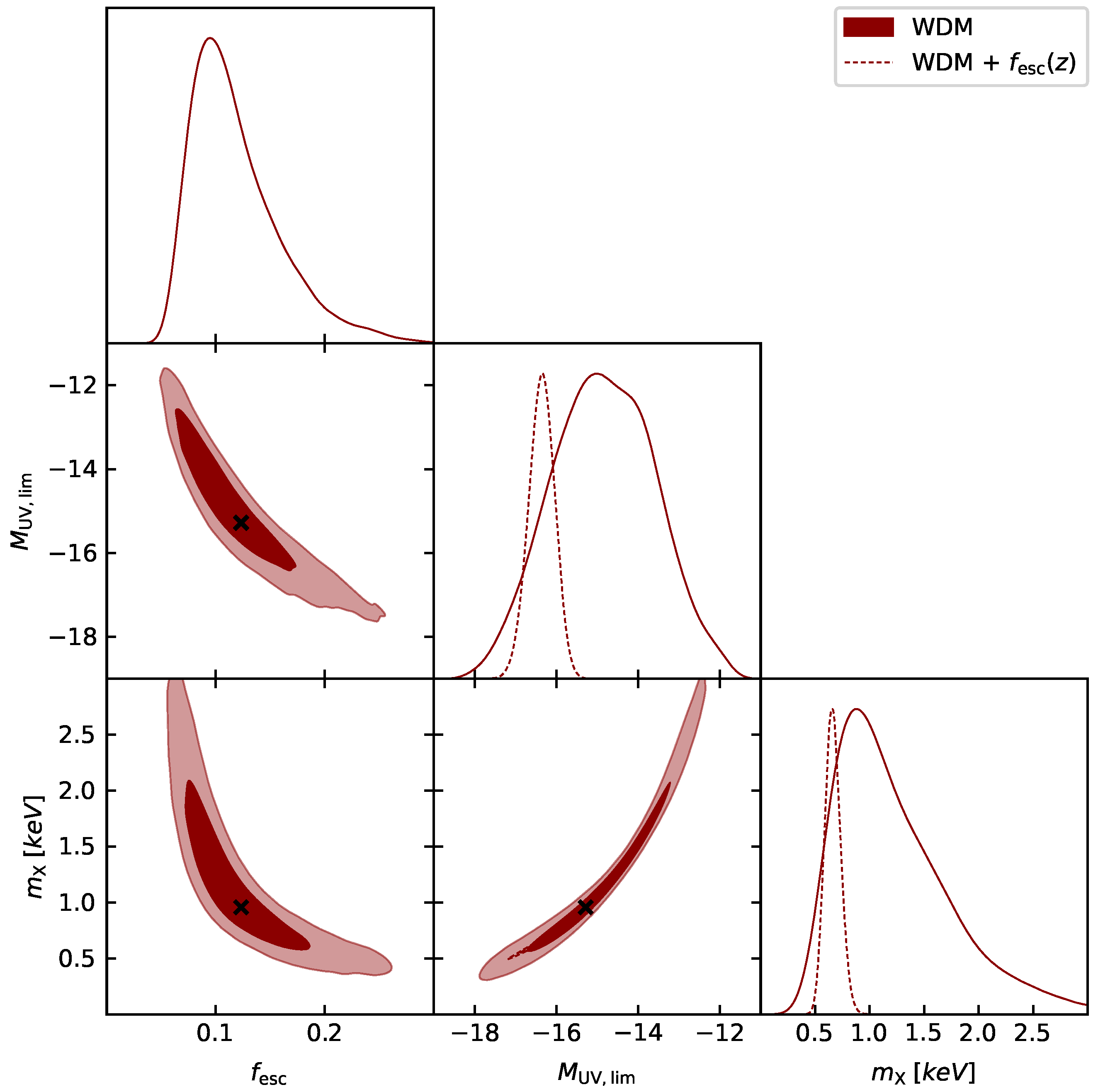

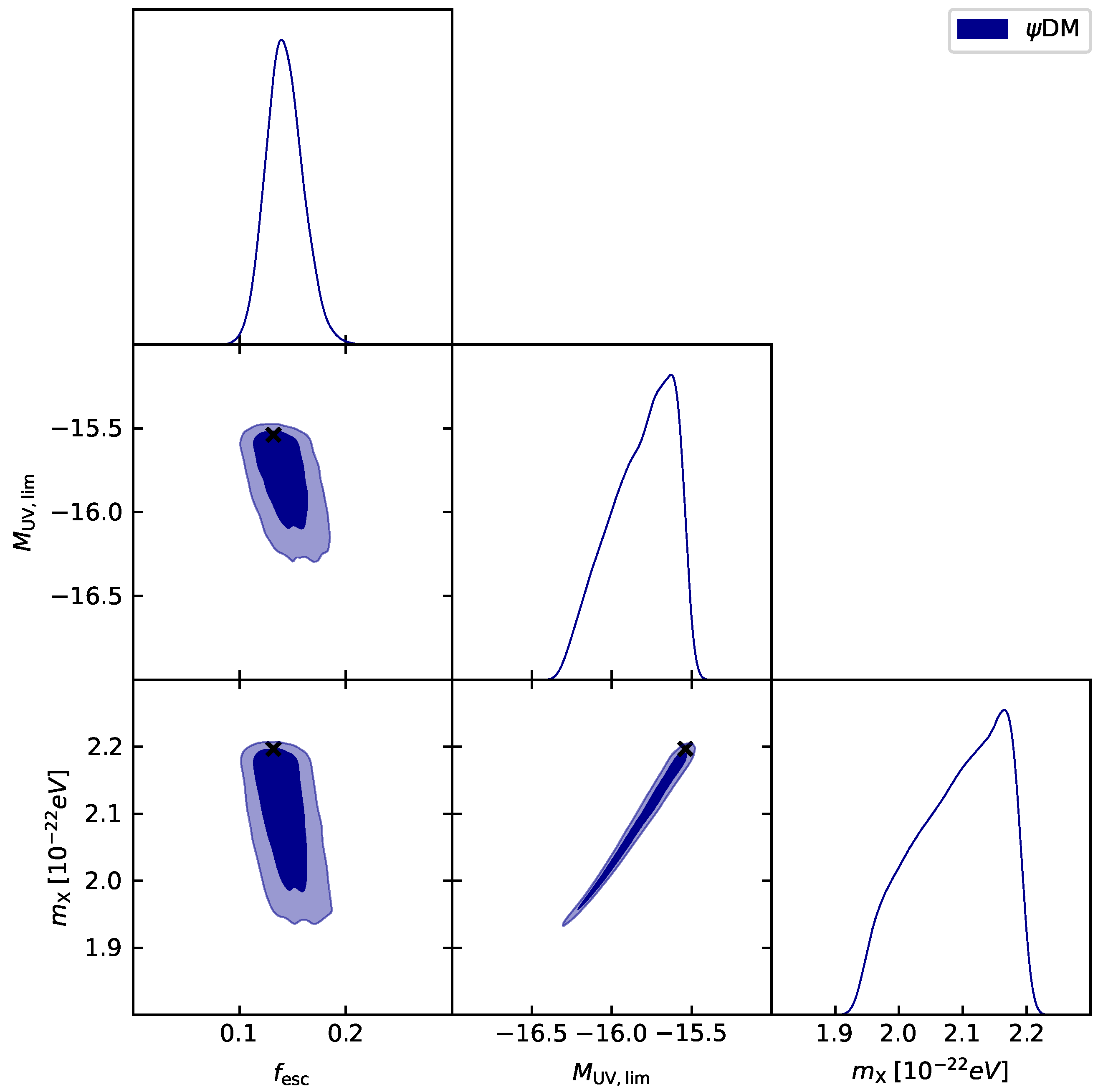


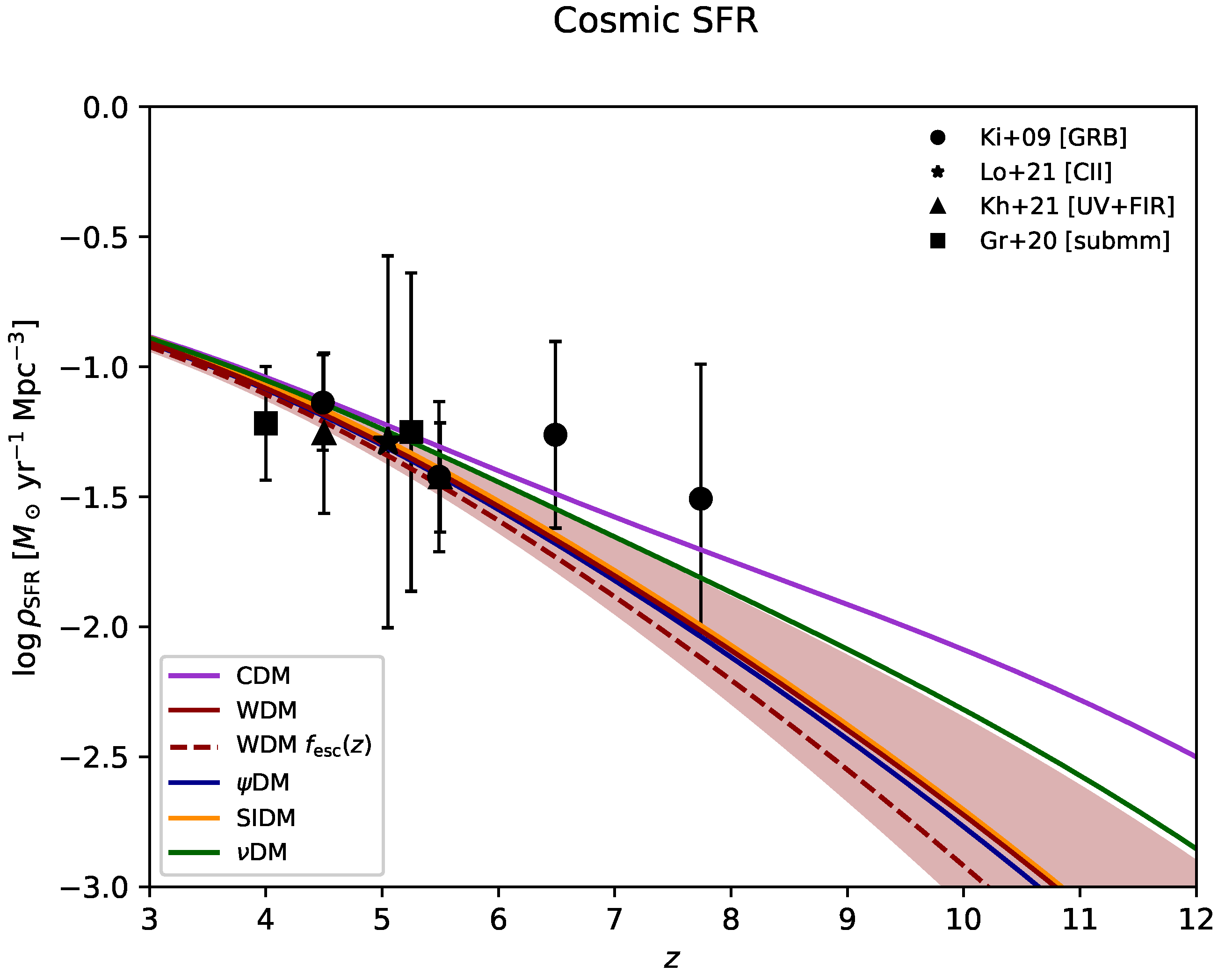

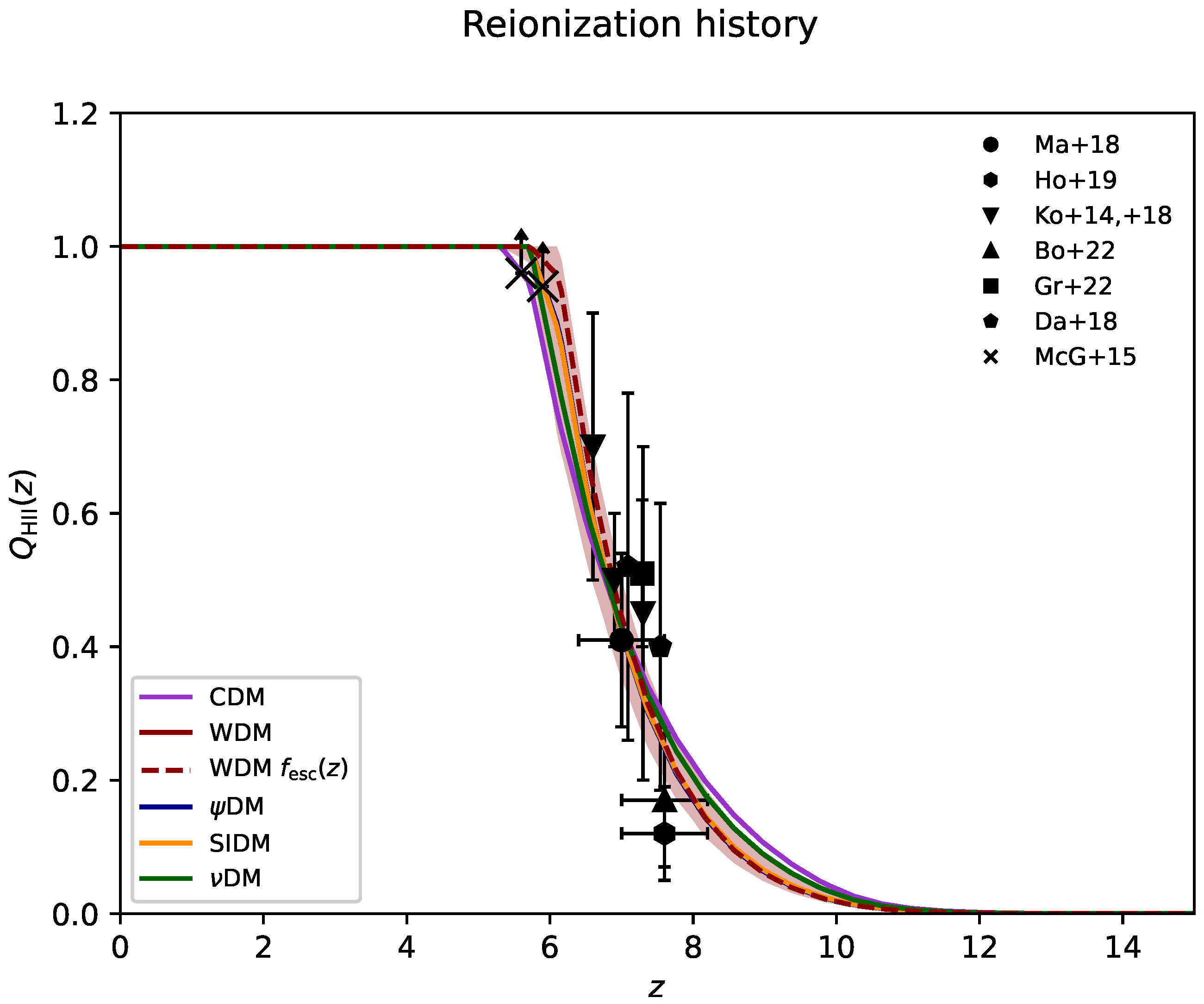
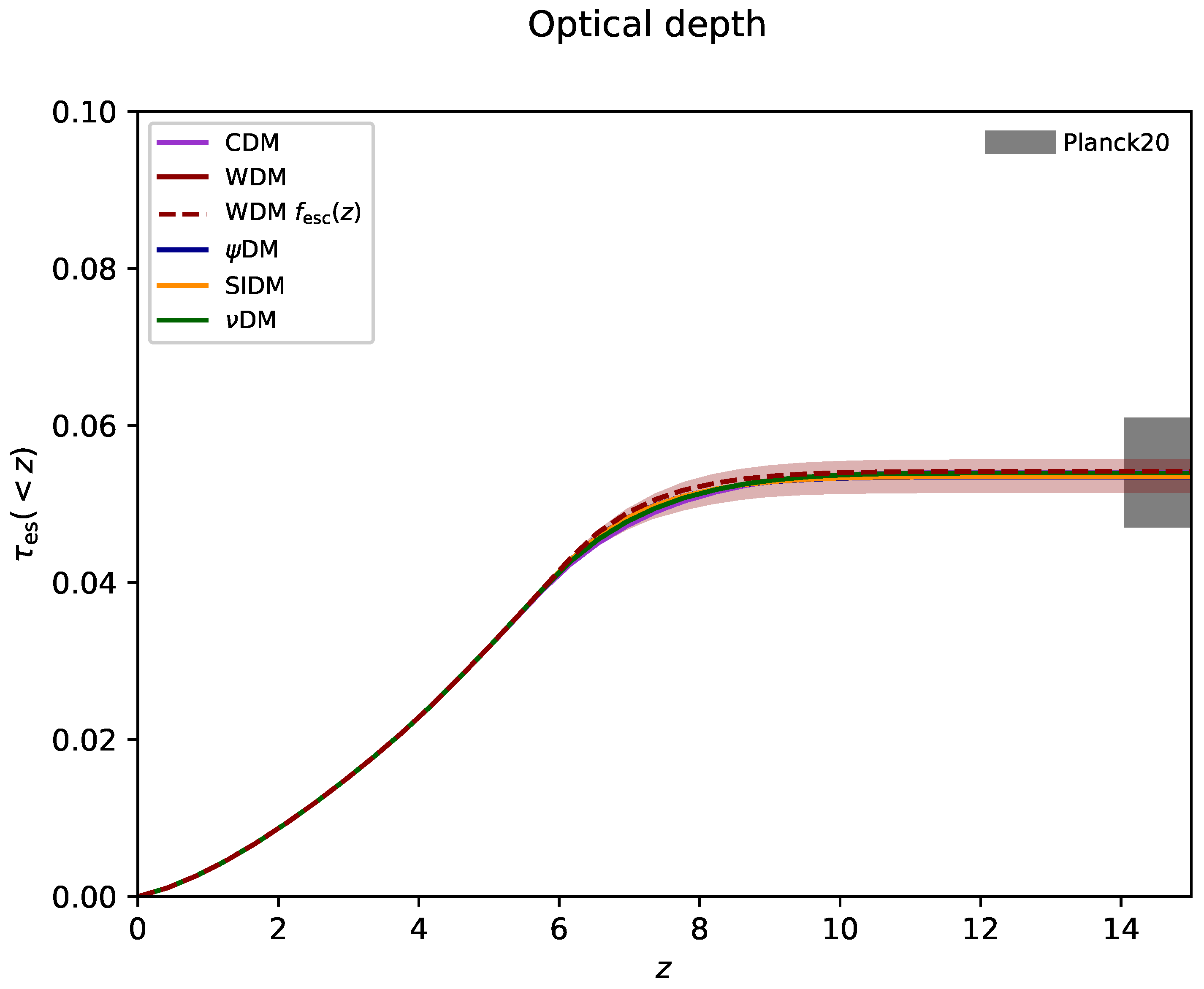
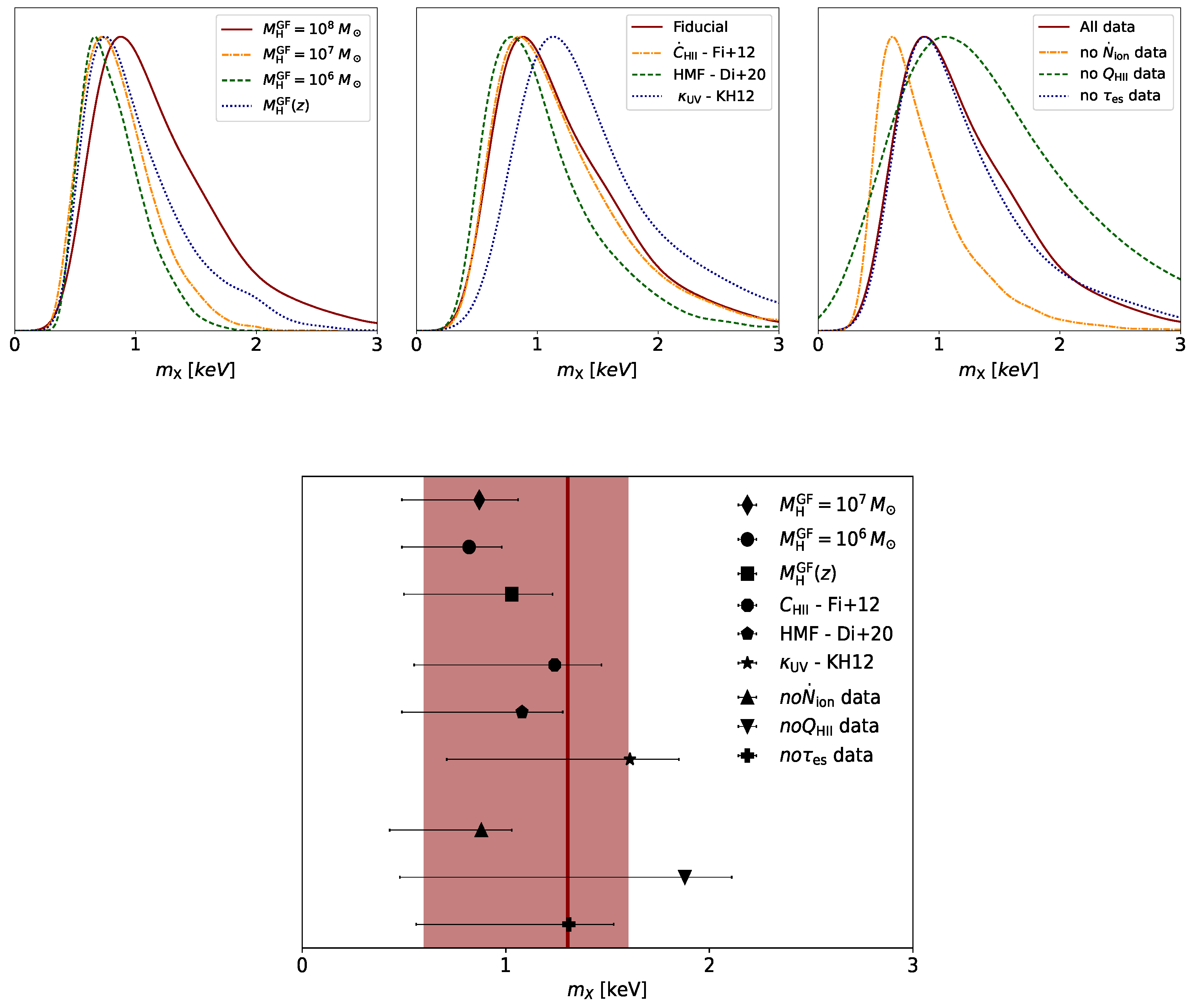
| Scenario | Ref. | |||
|---|---|---|---|---|
| WDM | [107] | |||
| DM | [41] | |||
| SIDM | [35] | |||
| DM | 1 | [43] |
| Observable [units] | Redshifts | Values | Errors | Ref. |
|---|---|---|---|---|
| [ s Mpc | ||||
| [116] | ||||
| [117] | ||||
| [121] | ||||
| [123] | ||||
| [118,122] | ||||
| [124] | ||||
| [125] | ||||
| [120] | ||||
| [119] | ||||
| [13] |
| Scenario | X | BIC | ||
|---|---|---|---|---|
| w/o GF | − | − | ||
| CDM | − | |||
| WDM | ||||
| WDM | − | |||
| DM | ||||
| SIDM | ||||
| DM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lapi, A.; Ronconi, T.; Boco, L.; Shankar, F.; Krachmalnicoff, N.; Baccigalupi, C.; Danese, L. Astroparticle Constraints from Cosmic Reionization and Primordial Galaxy Formation. Universe 2022, 8, 476. https://doi.org/10.3390/universe8090476
Lapi A, Ronconi T, Boco L, Shankar F, Krachmalnicoff N, Baccigalupi C, Danese L. Astroparticle Constraints from Cosmic Reionization and Primordial Galaxy Formation. Universe. 2022; 8(9):476. https://doi.org/10.3390/universe8090476
Chicago/Turabian StyleLapi, Andrea, Tommaso Ronconi, Lumen Boco, Francesco Shankar, Nicoletta Krachmalnicoff, Carlo Baccigalupi, and Luigi Danese. 2022. "Astroparticle Constraints from Cosmic Reionization and Primordial Galaxy Formation" Universe 8, no. 9: 476. https://doi.org/10.3390/universe8090476
APA StyleLapi, A., Ronconi, T., Boco, L., Shankar, F., Krachmalnicoff, N., Baccigalupi, C., & Danese, L. (2022). Astroparticle Constraints from Cosmic Reionization and Primordial Galaxy Formation. Universe, 8(9), 476. https://doi.org/10.3390/universe8090476








