Abstract
Relativistic plasma can be formed in strong electromagnetic or gravitational fields. Such conditions exist in compact astrophysical objects, such as white dwarfs and neutron stars, as well as in accretion discs around neutron stars and black holes. Relativistic plasma may also be produced in the laboratory during interactions of ultra-intense lasers with solid targets or laser beams between themselves. The process of thermalization in relativistic plasma can be affected by quantum degeneracy, as reaction rates are either suppressed by Pauli blocking or intensified by Bose enhancement. In addition, specific quantum phenomena, such as Bose–Einstein condensation, may occur in such a plasma. In this review, the process of plasma thermalization is discussed and illustrated with several examples. The conditions for quantum condensation of photons are formulated. Similarly, the conditions for thermalization delay due to the quantum degeneracy of fermions are analyzed. Finally, the process of formation of such relativistic plasma originating from an overcritical electric field is discussed. All these results are relevant for relativistic astrophysics as well as for laboratory experiments with ultra-intense lasers.
1. Introduction
Quantum electrodynamics is the most successful theory of elementary interactions, confirmed by a large variety of experiments and verified to an astonishingly good precision. Its effects can be broadly divided into two classes: perturbative and non-perturbative ones. The first class, given the smallness of the interaction constant (fine structure constant ), is vast and comprises all atomic physics and essentially interactions between the elementary quanta of electromagnetic and electron-positron fields. The second class is much less explored, as it requires extremely high electromagnetic fields with an electric field strength comparable to the critical value named after Schwinger [1]
where is the electron mass, e is its charge, c is the speed of light and ℏ is the reduced Planck constant. At such field strength, QED predicts vacuum breakdown with the occurrence of a number of phenomena, such as vacuum birefringence predicted [2] and observed [3], nonlinear Compton scattering, predicted [4,5] and observed already in undercritical electric fields [6,7], elastic photon–photon scattering [8] and non-perturbative electron–positron pair production [1,9,10].
Considerable effort has been made over the last two decades in increasing the intensity of high power lasers in order to explore these high field regimes. Yet, the Schwinger field is far from being reached; see [11,12] for recent reviews. There are indications that such technology is limited to undercritical fields due to the occurrence of avalanches [13,14] which deplete the external field faster than it can potentially be increased. With this in mind, there are claims [15] that “the critical QED field strength can be never attained for a pair creating electromagnetic field”.
While reaching such extreme conditions in laboratory appears very challenging, they might very well occur in astrophysical environments; see [16] for review. Dynamical mechanisms involving the increase in the initially small electric field toward its critical value appear problematic due to the occurrence of avalanches or other backreaction effects, which deplete the field energy and thus self-regulate the electric field; see [17]. In contrast, an overcritical electric field does exist in microphysical conditions, in particular around heavy nuclei, and is enhanced during heavy ion collisions [18,19], but these processes occur on too short of a time scale to be able to produce electron–positron pairs [20].
An overcritical electric field is hypothesized in quantum degenerate systems at high density, in which pair production is blocked due to the unavailability of the phase space of electrons, being completely occupied [21]. Such systems are discussed in the astrophysical context in compact stars, e.g., hypothetical quark stars [22] and neutron stars [23]. Pair production in such an overcritical field may occur either due to heating [24] or due to the gravitational collapse of a compact object [25,26]. Moreover, electron–positron pairs in this case are produced out of equilibrium, see [27], and their dynamics should be described using kinetic equations. It is well known that reaction rates are affected by the quantum degeneracy. Therefore, it is of primary interest to study the kinetics of high density quantum degenerate plasma, both in the presence and absence of external electromagnetic fields.
This review is organized as follows. In Section 2, we discuss the physical and astrophysical conditions under which degenerate plasmas can be produced. In Section 3, we derive relativistic kinetic equations accounting for plasma degeneracy and discuss binary and triple interactions. Then we review some recent results obtained in the analysis of relativistic kinetics of nonequilibrium electron–positron–photon plasma. We focus on the strong degeneracy effects both for the photon component in Section 4 and for the electron–positron component in Section 5. We also consider pair creation in a strong homogeneous electric field in Section 6. Conclusions follow.
2. Conditions for Formation of Relativistic Degenerate Plasma
In this section, we discuss conditions under which degenerate relativistic plasma can be formed and sustained. These conditions require the presence of either strong gravitational or strong electromagnetic fields. In many cases, such degenerate plasma is in thermodynamic equilibrium, for example, in white dwarfs or neutron stars. However, when plasma is generated rapidly or any other nonequilibrium processes are present, for instance, during the interaction of ultrastrong laser beams with solid targets, or in relativistic shock waves in gamma-ray bursts or supernova, the plasma may go out of thermodynamic equilibrium. In such conditions, the description of particle interactions and plasma dynamics requires a kinetic approach. In what follows, we introduce relativistic kinetic equations to describe basic interactions between electrons, positrons and photons.
2.1. Degenerate Plasmas in Compact Astrophysical Objects
Strong gravity provides confinement for matter, creating macroscopic objects with the highest possible density. A white dwarf is a textbook example of a star which counteracts its own gravity by the highly degenerate electron gas pressure. They form at the end of thermonuclear evolution of stars similar to our Sun, when fusion reactions in its interiors cease. They have no internal source of energy, and hence, isolated white dwarfs can only cool down emitting electromagnetic radiation. High thermal conductivity of degenerate electrons makes white dwarfs isothermal, and the energy loss occurs from the photosphere at a very low rate, due to the large opacity. Therefore, degenerate plasma in isolated white dwarfs is maintained in almost perfect thermal equilibrium.
Neutron stars represent even more extreme class of astrophysical objects, much denser than white dwarfs. Electrons cannot provide sufficient pressure at larger densities, so their stability is due to degenerate neutron gas pressure. Similar to white dwarfs, isolated neutron stars cool down by emitting electromagnetic radiation. The density at the surface of the bare neutron star decreases sharply, on the length scale determined by the nuclear forces. The density of electron gas decreases on a scale hundred times larger. Hence, on the surface of bare neutron stars, a strong electric field may develop, reaching overcritical values [23], provided that it is not buried under the thick crust. Such an electric field is not producing electron–positron pairs, as electrons are completely degenerate and their phase space is blocked due to the Pauli principle. A similar surface structure, called electrosphere, characterizes also hypothetical quark stars [22].
Relativistic plasma is formed in accretion discs around compact astrophysical sources. Nonequilibrium plasma may also form in relativistic shock waves [28] and outflows in supernovae and gamma-ray bursts [29].
2.2. Strong Electromagnetic Fields in Astrophysical Sources
In magnetospheres of white dwarfs and especially neutron stars, the strength of the electromagnetic field may be very large, leading to the formation of electron–positron pairs and their acceleration to ultrarelativistic energies. Much attention has been attracted by the systems with ultraintense magnetic fields [30], such as magnetars and central engines of supernovae and gamma-ray bursts. In such systems, the magnetic field strength may exceed the Schwinger limit, namely . For such magnetic field strength, the quantized cyclotron energy becomes comparable to the electron rest emergy . These field strengths correspond to very high energy density on the order of erg/cm, which in turn corresponds to electromagnetic radiation with a temperature on the order of MeV. Therefore, often, high density hot plasma is present in these sources, with typical kinetic energies of electrons , which means that positrons can be present in abundance, and the role of electron–positron pairs becomes important.
Within the magnetospheres, intense particle beams propagate along the magnetic field lines from one footpoint to another: once they hit the surface, energy dissipation occurs, resulting in the strong heating of the surface and as a result in intense and variable X-ray radiation, observed from magnetars [31]. Giant -ray flares in soft gamma repeaters [32] are thought to be produced by magnetic field reconnection events, which create plasma fireballs [33]. These are optically thick electron–positron plasma blobs, which expand until they become optically thin and emit previously trapped radiation. The same phenomena but on a larger energy scale occur in gamma-ray bursts that emit up to erg in -rays within seconds [34]. Some inner engine models propose that the overcritical magnetic field may generate electron–positron plasma either via Poynting flux and magnetic reconnection [35], or in strong electric field [36].
2.3. Pair Creation in Ultraintense Lasers
A strong electric field represents a testbed for experiments aiming at the study of nonperturbative effects in quantum electrodynamics. The possibility to obtain an electric field strong enough to produce electrons and positrons is offered by the mechanism of dynamical amplification of counter-propagating laser beams. It is now possible, thanks to the chirped pulse amplification (CPA) technique [37], whose development allowed the design of petawatt lasers generating pulses with intensity up to W/cm [38]; see also [39]. For this reason, large efforts are being devoted to generate it, in particular using the counter-propagating laser beams of ultrastrong intensity. Electric fields up to a few percentage points of the critical value will be reached using these advanced technologies in laboratory experiments [40,41,42]. The flagship projects in this direction are X-ray free electron laser facilities, such as XFEL1, optical high-intensity laser facilities such as extreme light infrastructure (ELI)2 and Exawatt Center for Extreme Light Studies (XCELS)3.While direct observation of the electron–positron pair creation in vacuum is not yet possible, many other nonlinear phenomena, including multiphoton Compton scattering and multiphoton pair creation have already been observed, in particular in the famous SLAC E144 experiment [6,7]. In fact, the interaction between high energy electron beam and intense laser creates the conditions for high Lorentz transformed electromagnetic fields, capable of multiple pair production [43]. Moreover, intense laser fields are powerful accelerators of particles [44].
The direct Schwinger process of pair production has not yet been observed in the laboratory; for recent reviews see [11,16]. It is likely that the technology described above is limited to undercritical fields. This is because of cascades and avalanches depleting the field energy [13,14,45] faster than the electric field is amplified.
In all of the mechanisms described above, the pair creation process introduces the back reaction onto the external field. Accounting for such back reaction is a very difficult task. Therefore, it is of crucial importance to have theoretical tools for description of the particle and field interactions in strong electromagnetic fields.
2.4. Fermion Critical Density
First let us discuss the physical conditions for quantum degeneracy of plasma. The degree of plasma degeneracy is characterized by the parameter [46,47]
where n is number density of particles in plasma, is the thermal wavelength, k is the Boltzmann constant, T is the temperature, and , h is the Planck constant. In thermal equilibrium, the total energy density of plasma is a function of temperature only . The number density—energy density diagram for relativistic electron–positron plasma is presented in Figure 1. Here, the black line corresponds to the degeneracy condition . Plasma is nondegenerate for and degenerate otherwise. The green curve represents thermal equilibrium states. The red curve shows the fully degenerate state for electron-positron pairs.
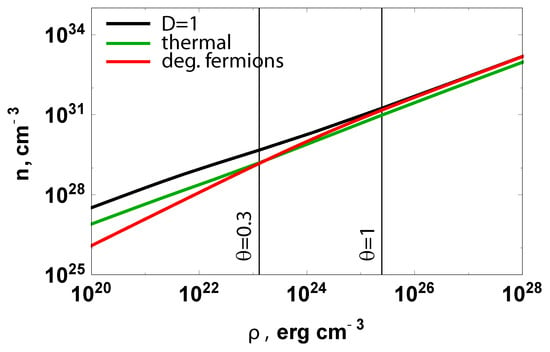
Figure 1.
Number density-energy density diagram of a photon–electron–positron plasma. Green curve corresponds to thermal equilibrium state. Black curve shows the transition from nondegenerate to degenerate plasma, where D is defined by Equation (2). Red curve corresponds to fully degenerate pair state defined by Equation (3). Vertical line on the left corresponds to the transition from nonrelativistic to relativistic pair plasma (). Vertical line on the right corresponds to relativistic pair plasma with .
Note that for fermions only (electrons and positrons without photons) both thermal and fully degenerate states have similar number density of particles at relativistic temperatures, see bottom Figure 1. The number density for the fully degenerate state is
and the thermal number density in the ultrarelativistic limit is
where is the Fermi energy, which plays a role of an upper particle energy boundary, and is the Riemann -function.
The occupation number of pairs is
where g is the number of helicity states and f is the distribution function. In Figure 2, we show the occupation number for selected temperatures (top), along with the corresponding spectral energy density (bottom). It is clear that for in thermal state, one has .
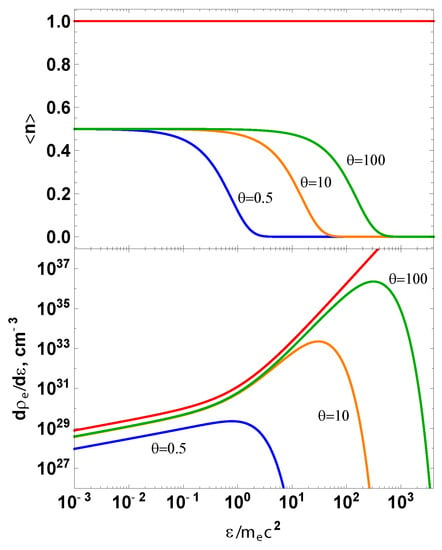
Figure 2.
Thermal average occupation numbers (top) and thermal spectral energy density (bottom) of pairs as function of their kinetic energy for selected temperatures: (blue), (orange), (green). The limiting spectral density for pairs according to Pauli principle is shown in red.
The amount of pairs in the relativistic regime becomes comparable to that of photons. Therefore, the thermal equilibrium state becomes degenerate at relativistic temperatures.
3. Relativistic Kinetic Equations
3.1. Derivation of Relativistic Kinetic Equations from Quantum Theory
The kinetic equation which takes into account quantum statistics of particles, the Uehling–Uhlenbeck equation [48], can be derived from the quantum Bogolyubov hierarchy [49]. Quantum mechanical Bogolyubov hierarchy is based on quantum Liouville equation (Liouville–von Neumann equation) for the average value of product of creation and annihilation operators. The quantum Liuville equation for any operator A is (in this section, we put ):
where angle brackets mean quantum averaging, H is the total Hamiltonian of a system, and square brackets denote the commutator of operators.
In the case of binary interactions, the Hamiltonian of a system has the form [50]:
where are matrix elements of binary potential U, and are particle energy eigenvalues.
We will consider the first equations of the hierarchy and we need to introduce the averaging of linear, squared and cubic product of creation and annihilation operators. They are as follows:
Additionally, it is convenient to reduce high-order products of creation and annihilation operators to sums of products of pairs of these operators and correlation terms. This procedure can be performed using Wick’s theorem [51]:
where and are binary and triple correlation terms. Here and below, the sign “±” denotes “+” for bosons and “−” for fermions.
For simplicity, we assume that the functions do not depend on space coordinates . This means that , where is the occupation number of state with energy . The first equation of the hierarchy is the following:
while the second equation is
To derive the Uehling–Uhlenbeck equation, one should keep only linear terms on coupling constant. Considering that both and have the first order on the coupling constant, we obtain from the second equation the following expression:
or denoting terms in square brackets as :
this linear differential equation has the following solution:
Finally, we should apply key principal assumptions. The first one is that the initial correlations of the system are vanishing, which allows to neglect the first term in Equation (15). The second one is that the system is Markovian (has no memory of the previous state), which allows to set the upper limit in the integral to infinity and remove the integration variable in . Thus, Equation (15) becomes
In the semiclassical (large occupation number) limit, the discrete spectrum becomes continuous, and one can replace discrete sums with integrals over the particle momentum. Then Equation (17) finally becomes
This is the Uehling–Uhlenbeck equation for occupation number . Using Equation (5), it can be rewritten for the distribution function and has the same form. One can derive this equation for any type of interaction characterized by the corresponding Hamiltonian of the system.
3.2. Collision Integrals in the Relativistic Kinetic Equation
In order to study kinetic evolution of optically thick electron–positron–photon plasma, taking into account the quantum degeneracy, one has to solve relativistic kinetic equations, derived in the previous section. In this paper, we assume the plasma is homogeneous in space, thus transport terms are dropped from the kinetic equations. We will adopt the radiative transport form of kinetic equations of electrons , positrons and photons ; see [47].
where are their distribution functions, index i denotes the sort of particles, is their energy, and and are the emission and the absorption coefficients of a particle of type “i” via the physical process labeled by q.
3.3. Binary Interactions
The emission and absorption coefficients for the particle I in a binary process have the following form:
where we defined the following transition rates: and , V is the normalization volume, is the differential reaction probability per unit time, and is +1, −1, 0 for Bose–Einstein, Fermi–Dirac, Maxwell–Boltzmann statistic, respectively. In what follows, we refer to these cases as quantum () and classical (), respectively, and h is Planck’s constant.
3.4. Triple Interactions
The emission and absorption coefficients for the particle I in a triple process have the following form:
where and . The expression for is given in QED as
where and are, respectively, the momenta and energies of outgoing particles, and are the momenta and energies of incoming particles, is the corresponding matrix element, and functions stand for energy–momentum conservation. The collision integrals on the right-hand side of Equation (19), are integrals over the phase space of interacting particles. These integrals contain the matrix elements of the corresponding QED processes. For binary interactions, the matrix elements are given in most textbooks; see [47,52]. For triple interactions, these matrix elements can be found in the literature: Ref. [53] for double Compton scattering, Ref. [54] for relativistic bremsstrahlung. Finally, matrix elements for all the other triple interactions can be found from the above two using the substitution rules [55]. All binary and triple interactions between electrons, positrons and photons, considered in this work, are listed in Table 1.

Table 1.
Binary and triple QED processes in the pair plasma.
Details of numerical integration scheme, which solves the coupled system of integro-differential Equation (19) on the grid in the phase space using a finite difference method is presented in [56,57,58,59,60,61], see also [47].
3.5. Kinetic versus Thermal Equilibrium
It was established [47] that the relaxation of non-equilibrium relativistic plasma with arbitrary initial conditions may proceed in two steps. If detailed balance is established first for all binary interactions, a metastable state is formed. This state is called kinetic equilibrium, and it is characterized by the following quantities: temperature and nonzero chemical potentials of particles. The distribution function of particles with energy E in the kinetic equilibrium is
where signs “+” and “−” correspond to Fermi–Dirac and Bose–Einstein statistics, respectively. The characteristic timescale of the kinetic equilibrium can be estimated as
where is the Thomson cross section, is the electron number density, and the coefficient [56]. The chemical potential of particles (including photons) do not vanish since binary interactions conserve the number of particles.
Triple interactions, which change the chemical potential of particles, can bring the system to thermal equilibrium. The characteristic timescale for establishing thermal equilibrium can be estimated as , where is the fine structure constant.
It was found [60] that kinetic equilibrium is formed only in nonrelativistic plasma. In relativistic plasma , the reaction rates of binary and triple interactions are comparable, and hence the thermal equilibrium is established directly.
After introducing the general formalism, we now consider specific effects occurring in degenerate plasmas. First, we turn to photons.
4. Bose–Einstein Condensation of Photons in Relativistic Plasma
One of the interesting phenomena in nonequilibrium relativistic optically thick plasmas is the occurrence of Bose–Einstein condensation (BEC) [62,63]. This phenomenon was first observed by cooling alkali atoms to nanokelvin degrees [64,65,66] and it is traditionally associated with low temperatures.
The possibility of condensation of photons in kinetic equilibrium state occurs if the initial number density of photons exceeds the one given by Equation (25) with zero chemical potential of photons , namely
where is the temperature in kinetic equilibrium. Since binary interactions do not change the number of photons, these particles may accumulate in low energy states and form an excess over the Planck distribution. This is possible as long as the kinetic equilibrium is maintained. Triple interactions reduce the photon number, leading eventually to the disappearance of this excess, as plasma relaxes to the thermal equilibrium.
In a pure photon gas, quantum condensation does not occur since photons are massless particles and cooling leads to their disappearance. What was shown in [63] is the possibility of this phenomenon to occur as a transient state during thermalization of the plasma. In particular it was shown that photon condensation may appear at any temperature, including relativistic one. Here we will report only the nonrelativistic case. We present the result of computations with total energy density . The final equilibrium temperature is then . The initial particle number density is five time larger than the thermal one, , where . We take the Wien distribution centered at the energy as the initial energy density spectrum for photons, and a function for pairs with kinetic energy . Clearly, the energy density and particle number density of pairs are much smaller than those of photons.
In Figure 3, we show the time evolution of energy density and particle number density in the system. In Figure 4, we show the spectral energy density and reaction rates at specific time moments.
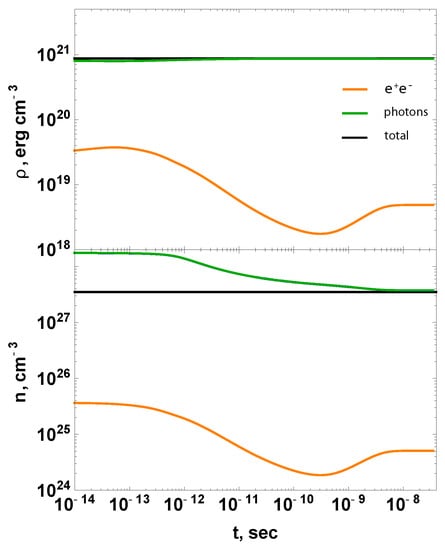
Figure 3.
Time evolution of energy density (top) and particle number density (bottom) of photons (blue), electrons/positrons (orange), all together (green) in nonrelativistic case. Black line represents the final equilibrium quantity. Final equilibrium temperature is .
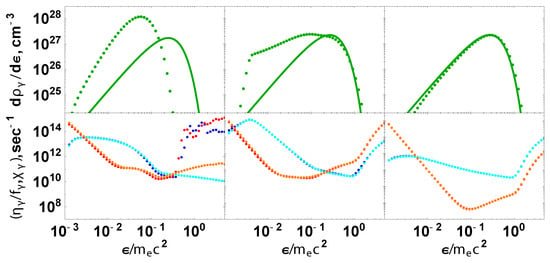
Figure 4.
Top: The spectral energy density (dots) with the associated Planck fit (solid) for selected time moments from left to right: s, in nonrelativistic case. Bottom: emission and absorption coefficients for photons (binary reactions: emission (blue) and absorption (cyan); triple reactions: emission (purple) and absorption (red). The left panel represents initial distribution of photons; the middle one shows photon condensation, while the right one corresponds to the final state.
The total energy density is constant. The total particle number density changes only due to the imbalance in the triple processes, which is relevant only for s. For shorter times, triple interactions are slow enough; for larger times, thermal equilibrium is established.
After the time moment s, the total particle number (mainly photon number) starts to decrease. As a result, at the time moment s, binary processes are balanced in a broad energy region, and we have . Photons are described by the distribution function (25). However, the number of photons supported by the equilibrium given by Equation (27) is , while we have cm. So photons in excess with the density form a condensate. This excess is visible in the middle panel of Figure 4. The steep decrease in the spectrum at low energies is due to faster triple interactions. This quantum condensation of photons persists until s, when the thermal equilibrium is finally established.
We also studied the development of photon condensation for different degrees of initial degeneracy by increasing the initial photon number density, which exceeded the equilibrium value by factors of 3, 5, 7 and 10. We found that the system loses memory of the initial distribution at the moment when the number density starts to change due to triple interactions, at s, correspondingly. At this moment, called pre-condensation, the photon distribution functions still have a non-equilibrium shape, but the power law excess over the Planck spectrum appears already. In all cases, the condensation occurs at about s, and it disappears at about s, independent of the degree of degeneracy.
We find that the low energy distribution can be fit as
with
where the Rayleigh–Jeans value is reached at s. The values of the spectral index a and its fit are shown in Figure 5.
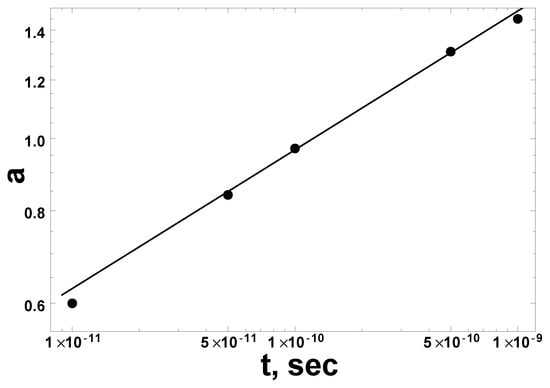
Figure 5.
The time evolution of the spectral index of the power law distribution of photons below the peak, starting at the moment when it is first established.
It is interesting to note that there are well-known solutions of kinetic equations with sources in the form of power law distributions, relevant for the theory of wave turbulence; see [67]. Within the theory of quantum systems out of equilibrium, which has a wide range of applications, ranging from high energy particle physics to ultracold quantum gases [68], and to cosmology [69,70], a universal behavior was found due to the existence of nonthermal fixed points [71,72,73]. The scaling law (29) can be a manifestation of this universality. However, the values of the power law index a are always larger than the values predicted for stationary solutions [67].
The details of computations and additional results can be found in [63]. Now we turn to the case of degenerate fermions.
5. Thermalization of Superdegenerate Plasma
The Pauli principle plays a crucial role in a dense matter state [74]; it affects conductivity in a dense Coulomb plasma [75], and for extreme plasma densities, it leads to the depression of ionization potential [76]. Thus, it is crucial in many nuclear physics problems [77,78,79,80]. As discussed in the introduction, the effects of fermionic quantum degeneracy are essential in preventing compact astrophysical objects from gravitational collapse.
In what follows, we discuss kinetic effects in degenerate fermion plasma [81]. Recall, that the probability of creation of electron–positron pairs from photons at a nonrelativistic temperature is exponentially suppressed. As a result, Pauli blocking may become important for the thermalization process.
Considering the thermalization process of relativistic plasma with an initially strongly degenerate distribution of fermions, we require that the initial conditions correspond to the condition . It is clear that the density of photons in such a state should be larger than the density of pairs, and the energy density of photons should be smaller than the energy of pairs. The latter condition arises because the contribution of photons to the total energy density should be minimized, while their density should be maximized. Such conditions are called the superdegenerate state [60].
In order to demonstrate the effect of the quantum degeneracy of electrons, we focus on the case of relativistic electron–photon plasma. The positive charge, needed to compensate for electron charge, is assumed to be present, in the form of protons or ions. It is assumed that positively charged particles are cold, and their presence does not affect the electron degeneracy.
We consider the initial state containing a large number of degenerate electrons (when ) and low energetic photons. The following initial conditions are chosen for the simulation: total energy density is corresponding to a final equilibrium temperature , total initial particle number density is , where . Thermalization dynamics is shown in Figure 6. As the energy of the initial photons is much less than , the pair creation process is suppressed, and the initial degenerate electron state can be preserved until photons acquire energy above .
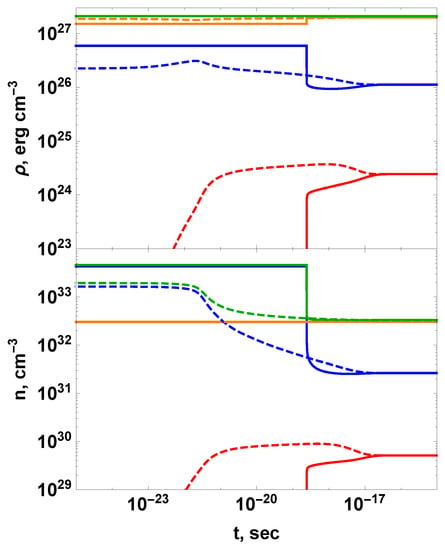
Figure 6.
Time evolution of energy density (top) and particle number density (bottom) for relativistic photon-electron plasma with degenerate initial pair state (solid) and nondegenerate initial electron state (dashed). Blue: photons, orange: electrons, red: positrons and green: total. Final equilibrium temperature is .
One can see a sharp decrease in thermodynamic quantities at the time moment s; the degenerate electron spectrum is preserved until the same time. The creation of positrons starts at the same moment. The thermalization process has an avalanche-like character. For the sake of comparison, we show also the simulation with nondegenerate initial electrons, which present a smooth monotonic thermalization process (dashed curves in Figure 6), which starts much earlier (solid curves on Figure 6).
We conclude that in superdegenarate electron–photon plasma, thermalization is delayed due to the Pauli blocking of interactions with electrons. Once reactions are unblocked, thermalization proceeds in an avalanche-like manner. This is because the initial state is preserved until photons can scatter degenerate electrons above their Fermi energy, where the states are not degenerate any more. Details of the calculations and additional results, also for nonrelativistic plasma, are presented in [60].
6. Phase Space Evolution of Pairs Created in Strong Electric Fields
In this section, we review the results obtained for pair production in a strong homogeneous electric field. Due to the complexity of the problem, particle degeneracy is not accounted for. Moreover, only 2-particle QED interactions are considered, and therefore, the system may relax only to a kinetic equilibrium.
The momentum space is axially symmetric, with the preferred direction determined by the direction of the electric field. The momentum vector has, therefore, the following components: parallel one () and orthogonal one () to the direction of the electric field. The azimuthal angle () describes the rotation of around . The momentum space is confined to the following intervals: , , . The integral over the momentum space is defined as , and the relativistic energy is
In this equation and hereafter we set .
The number density is given by its integral over the entire momentum space
Due to the assumed axial symmetry, f does not depend on . It is only a function of the two momentum components . The Boltzmann–Vlasov equations can be written in conservative form [27,57] for the quantity . The energy density is
The kinetic evolution of the system is described by the relativistic Boltzmann–Vlasov equation for pairs
where are the emission and absorption coefficients due to the interaction denoted by q, and the source term S, representing the pair production rate. In this equation, Pauli blocking and Bose enhancement factors are neglected. In particular, the electron–positron distribution functions in Equation (33) vary due to the acceleration by the electric field, the creation of pairs by the electric field, and the interactions with photons. Indeed, the Vlasov term describes the mean field produced by all particles, and the external field. Particle interactions, including Coulomb ones, are taken into account by collision terms. Particle motion between collisions is assumed to be subject to the external field only.
Pair creation introduces the specific distribution of particles in the momentum space [16]
Indeed, pairs are produced with nonzero orthogonal momentum, up to about . However, along the direction of the electric field, the momentum component is zero. Notice that for , the rate is exponentially suppressed.
Time evolution of the photon distribution function is described by the Boltzmann equation
Notice, that both the acceleration and pair creation terms in Equation (33) operate on a much shorter time scale than interactions with photons described by collision terms in Equations (33) and (35) [82,83]. For this reason, we perform two classes of simulations: in the first class, referred to as “collisionless”, particle interactions are neglected; interactions are accounted for in the second class, called “interacting”.
First we present the results for collisionless simulations. In the initial state, electric field and distribution function are specified as
In other words, we assume no particle is present at the beginning: electrons and positrons are produced from the electric field only. If particles are present from the beginning [84], the qualitative results are similar.
Initially, the energy is stored only in the electric field, with energy density
The final state of the equilibrated thermal electron–positron–photon plasma is characterized by only one parameter: temperature
where is the Stefan–Boltzmann constant. The energy conservation law implies that the total energy density of pairs and photons are related to the actual and initial electric fields, E and as
The maximum achievable pairs number density [84] is
which corresponds to the full conversion of the whole initial energy into electron–positron rest energy
where and are the electron and positron number densities, respectively. From the electron and positron distribution functions, we can extrapolate their bulk parallel momentum , and the symmetry of our problem implies that . We make use of this identity to define the kinetic energy density of pairs
Therefore, is the energy density as if all particles are put together in the momentum state with and , while their rest energy density is . The difference between the total energy density and all the others defined above is denoted as the internal energy density
The term ”internal” refers here to the dispersion of the distribution function around a given point with coordinates () in the momentum space.
In Figure 7, we show the time evolution of the pairs and photons energy densities for . From this plot, we can understand the hierarchy of time scales associated to the distinct physical phenomena. Electron–positron pairs are produced in a strong electric field, in the shortest time according to Equation (34). As soon as they are created, electrons and positrons are accelerated toward opposite directions as the back reaction effect on the external field. Hence, plasma oscillations are initiated [83,84]. The characteristic duration of the back reaction corresponds approximately to the first half of the oscillation period. The larger the electric field, the higher the rate of pairs production and consequently their number density. The process of pair production proceeds in this oscillating manner, until the electric field reduces to undercritical values.
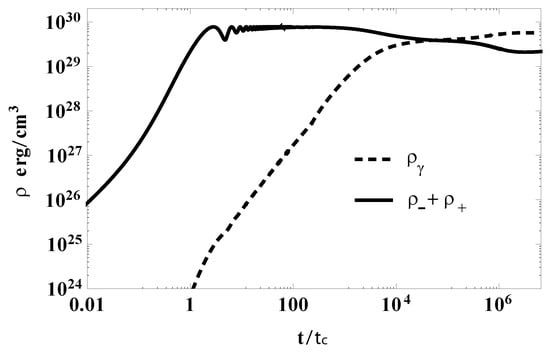
Now we turn to the dynamics of our system on much larger time scales, described by simulations with interactions taken into account. Since the interaction rate is proportional to particle number densities, they turn relevant sooner for a higher initial field.
After hundreds of oscillations, the energy density carried by the electric field is a small fraction of the pairs and photons energy densities. Due to this fact, the acceleration of electrons and positrons does not any more affect their distribution functions. Hence, we neglect the presence of the electric field.
Due to interactions, the photon energy density increases with time as a power law approaching the pairs energy density; see Figure 7. Then the slope of the photons curve in Figure 7 reduces, indicating that pairs annihilation has become less efficient than the inverse process. The main effect of collisions is the isotropization of particle distributions in the momentum space. After some time, the photons energy density becomes equal and then overcomes the pairs energy density. This growth continues until the equilibrium between pairs annihilation and creation processes is established . However, at this point, the distribution function is not yet isotropic in the momentum space, indicating that the kinetic equilibrium condition is not yet satisfied. In fact, kinetic equilibrium is achieved only at later times when other binary interactions come to the detailed balance as mentioned above.
In Figure 8, we present the momentum density plots of and on the left and right columns, respectively, for the simulation with . Their time evolution is from the top to the bottom, corresponding to three different times. On top, after , both distribution functions are highly anisotropic as indicated by the ratio . At this stage, the electric field is still overcritical, and a very small fraction of initial energy has been converted into pairs. They are accelerated up to relativistic velocities, indicated by the electron distribution function shifted on the right side of the phase space plane characterized by . Electrons are ultrarelativistic with a bulk Lorentz factor of about 170. In the middle, the time is , and the distribution functions are still anisotropic. However, the situation is different because the electric field is only slightly overcritical and many more pairs and photons have been generated. Here, interactions start to play a role. Both the electric field and collisions prevent particles to reach ultra-relativistic velocities, and for this reason, the electron distribution function is already symmetrical with respect to the plane . Finally, at the bottom, for , collisions dominate the evolution of the system, whereas the presence of the electric field can be neglected. The distributions are almost isotropic with .
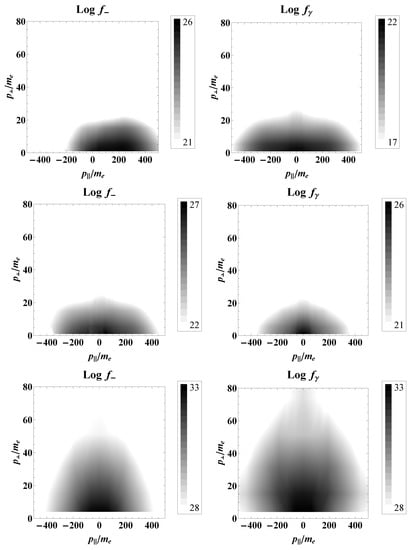
Figure 8.
Phase space distributions of electrons (left column) and photons (right column) for the initial condition . Top: , middle: , bottom: .
It remains to be seen how the effects of quantum degeneracy modify the dynamics described above.
7. Conclusions
The study of nonequilibrium relativistic plasma requires the use of kinetic equations. Previous work was mostly focusing on various aspects of plasma kinetics without accounting for quantum degeneracy. Recent progress in the inclusion of Pauli blocking and Bose enhancement factors in relativistic kinetic equations resulted in the discovery of a number of new phenomena.
Firstly, the quantum condensation of photons in relativistic plasma was predicted to occur as a transient phenomena during its thermalization, provided that the number of photons in its initial state is exceeding the number of photons in the thermal equilibrium and that binary interactions prevail over triple ones.
Secondly, avalanche thermalization was predicted to occur in superdegenerate relativistic plasma when electrons and positrons are entirely degenerate and a large number of low energy photons is present. Since such photons are not able to produce pairs, the process of thermalization is delayed until photons are upscattered to high enough energy to produce pairs so that the phase space of the electrons opens up, and quantum degeneracy is released.
These phenomena may be potentially observed in the laboratory in future experiments with ultraintense lasers interacting with solid targets or even in crossed laser beams. At the same time, the main arena for such phenomena is relativistic astrophysics, where strong gravitational fields provide confinement, and strong electromagnetic fields may generate such plasma via non-perturbative quantum electrodynamical processes.
As demonstrated above, the Bose condensation of photons can occur when a large number of photons is produced, and it interacts essentially via Compton scattering with cold electrons. This can happen in compact astrophysical sources, especially during their transient activity, for example in gamma-ray bursts. Avalanche thermalization may happen when the phase space of fermions suddenly opens up in such completely degenerate systems as white dwarfs or neutron stars, for example, during their gravitational collapse or merging.
Author Contributions
Conceptualization, G.V. and M.P.; methodology, G.V.; software, M.P.; validation, G.V. and M.P.; writing—original draft preparation, G.V. and M.P.; writing—review and editing, G.V. and M.P.; funding acquisition, G.V. and M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported within the joint BRFFR-ICRANet-2021 funding program under the grant No. F21ICR-003.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | http://www.xfel.eu (accessed on 8 September 2022). |
| 2 | https://eli-laser.eu/ (accessed on 8 September 2022). |
| 3 | https://xcels.ipfran.ru/img/site-XCELS.pdf (accessed on 8 September 2022). |
References
- Schwinger, J. On Gauge Invariance and Vacuum Polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Klein, J.J.; Nigam, B.P. Birefringence of the Vacuum. Phys. Rev. 1964, 135, 1279–1280. [Google Scholar] [CrossRef]
- Mignani, R.P.; Testa, V.; González Caniulef, D.; Taverna, R.; Turolla, R.; Zane, S.; Wu, K. Evidence for vacuum birefringence from the first optical-polarimetry measurement of the isolated neutron star RX J1856.5-3754. Mon. Not. R. Astron. Soc. 2017, 465, 492–500. [Google Scholar] [CrossRef]
- Nikishov, A.I.; Ritus, V.I. Quantum Processes in the Field of a Plane Electromagnetic Wave and in a Constant Field. Sov. Phys. J. Exp. Theor. Phys. 1964, 19, 1191. [Google Scholar]
- Brown, L.S.; Kibble, T.W. Interaction of Intense Laser Beams with Electrons. Phys. Rev. 1964, 133, 705–719. [Google Scholar] [CrossRef]
- Bula, C.; McDonald, K.T.; Prebys, E.J.; Bamber, C.; Boege, S.; Kotseroglou, T.; Melissinos, A.C.; Meyerhofer, D.D.; Ragg, W.; Burke, D.L.; et al. Observation of Nonlinear Effects in Compton Scattering. Phys. Rev. Lett. 1996, 76, 3116–3119. [Google Scholar] [CrossRef]
- Burke, D.L.; Field, R.C.; Horton-Smith, G.; Spencer, J.E.; Walz, D.; Berridge, S.C.; Bugg, W.M.; Shmakov, K.; Weidemann, A.W.; Bula, C.; et al. Positron Production in Multiphoton Light-by-Light Scattering. Phys. Rev. Lett. 1997, 79, 1626–1629. [Google Scholar] [CrossRef]
- Euler, H. Über die Streuung von Licht an Licht nach der Diracschen Theorie. Ann. Phys. 1936, 418, 398–448. [Google Scholar] [CrossRef]
- Sauter, F. Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs. Zeits. Phys. 1931, 69, 742–764. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Consequences of Dirac Theory of the Positron. Zeits. Phys. 1935, 98, 714–732. [Google Scholar] [CrossRef]
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177–1228. [Google Scholar] [CrossRef]
- Fedotov, A.; Ilderton, A.; Karbstein, F.; King, B.; Seipt, D.; Taya, H.; Torgrimsson, G. Advances in QED with intense background fields. arXiv 2022, arXiv:2203.00019. [Google Scholar]
- Bell, A.R.; Kirk, J.G. Possibility of Prolific Pair Production with High-Power Lasers. Phys. Rev. Lett. 2008, 101, 200403. [Google Scholar] [CrossRef]
- Bulanov, S.S.; Esirkepov, T.Z.; Thomas, A.G.R.; Koga, J.K.; Bulanov, S.V. Schwinger Limit Attainability with Extreme Power Lasers. Phys. Rev. Lett. 2010, 105, 220407. [Google Scholar] [CrossRef]
- Fedotov, A.M.; Narozhny, N.B.; Mourou, G.; Korn, G. Limitations on the Attainable Intensity of High Power Lasers. Phys. Rev. Lett. 2010, 105, 080402. [Google Scholar] [CrossRef]
- Ruffini, R.; Vereshchagin, G.; Xue, S.S. Electron-positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys. Rep. 2010, 487, 1–140. [Google Scholar] [CrossRef]
- Page, D.N. Evidence against Macroscopic Astrophysical Dyadospheres. ApJ 2006, 653, 1400–1409. [Google Scholar] [CrossRef]
- Gershteǐn, S.S.; Zel’Dovich, Y.B. Positron Production during the Mutual Approach of Heavy Nuclei and the Polarization of the Vacuum. Sov. J. Exp. Theor. Phys. 1969, 30, 358. [Google Scholar]
- Popov, V.S. Position Production in a Coulomb Field with Z > 137. Sov. J. Exp. Theor. Phys. 1971, 32, 526. [Google Scholar]
- Greiner, W.; Muller, B.; Rafelski, J. Quantum Electrodynamics of Strong Fields; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Usov, V.V. Bare Quark Matter Surfaces of Strange Stars and e+e− Emission. Phys. Rev. Lett. 1998, 80, 230–233. [Google Scholar] [CrossRef]
- Alcock, C.; Farhi, E.; Olinto, A. Strange stars. ApJ 1986, 310, 261–272. [Google Scholar] [CrossRef]
- Belvedere, R.; Pugliese, D.; Rueda, J.A.; Ruffini, R.; Xue, S.S. Neutron star equilibrium configurations within a fully relativistic theory with strong, weak, electromagnetic, and gravitational interactions. Nucl. Phys. A 2012, 883, 1–24. [Google Scholar] [CrossRef]
- Usov, V.V. Thermal Emission from Bare Quark Matter Surfaces of Hot Strange Stars. ApJ 2001, 550, L179–L182. [Google Scholar] [CrossRef]
- Ruffini, R.; Xue, S.S. Electron-positron pairs production in a macroscopic charged core. Phys. Lett. B 2011, 696, 416–421. [Google Scholar] [CrossRef][Green Version]
- Han, W.B.; Ruffini, R.; Xue, S.S. Electron and positron pair production of compact stars. Phys. Rev. D 2012, 86, 084004. [Google Scholar] [CrossRef]
- Aksenov, A.G.; Milgrom, M.; Usov, V.V. Structure of Pair Winds from Compact Objects with Application to Emission from Hot Bare Strange Stars. ApJ 2004, 609, 363–377. [Google Scholar] [CrossRef]
- Levinson, A.; Nakar, E. Physics of radiation mediated shocks and its applications to GRBs, supernovae, and neutron star mergers. Phys. Rep. 2020, 866, 1–46. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Relativistic fireballs—Energy conversion and time-scales. Mon. Not. R. Astron. Soc. 1992, 258, 41. [Google Scholar] [CrossRef]
- Uzdensky, D.A.; Rightley, S. Plasma physics of extreme astrophysical environments. Rep. Prog. Phys. 2014, 77, 036902. [Google Scholar] [CrossRef]
- Kaspi, V.M.; Beloborodov, A.M. Magnetars. Annu. Rev. Astron. Astrophys. 2017, 55, 261–301. [Google Scholar] [CrossRef]
- Mereghetti, S. The strongest cosmic magnets: Soft gamma-ray repeaters and anomalous X-ray pulsars. Astron. Astrophys. Rev. 2008, 15, 225–287. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The soft gamma repeaters as very strongly magnetized neutron stars—I. Radiative mechanism for outbursts. Mon. Not. R. Astron. Soc. 1995, 275, 255–300. [Google Scholar] [CrossRef]
- Piran, T. Gamma-ray bursts and the fireball model. Phys. Rep. 1999, 314, 575–667. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 413, 2031–2056. [Google Scholar] [CrossRef]
- Moradi, R.; Rueda, J.A.; Ruffini, R.; Li, L.; Bianco, C.L.; Campion, S.; Cherubini, C.; Filippi, S.; Wang, Y.; Xue, S.S. Nature of the ultrarelativistic prompt emission phase of GRB 190114C. Phys. Rev. D 2021, 104, 063043. [Google Scholar] [CrossRef]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Yanovsky, V.; Chvykov, V.; Kalinchenko, G.; Rousseau, P.; Planchon, T.; Matsuoka, T.; Maksimchuk, A.; Nees, J.; Cheriaux, G.; Mourou, G.; et al. Ultra-high intensity- 300-TW laser at 0.1 Hz repetition rate. Opt. Express 2008, 16, 2109–2114. [Google Scholar] [CrossRef]
- Mourou, G.A.; Tajima, T.; Bulanov, S.V. Optics in the relativistic regime. Rev. Mod. Phys. 2006, 78, 309–371. [Google Scholar] [CrossRef]
- Ringwald, A. Pair production from vacuum at the focus of an X-ray free electron laser. Phys. Lett. B 2001, 510, 107–116. [Google Scholar] [CrossRef]
- Tajima, T.; Mourou, G. Zettawatt-exawatt lasers and their applications in ultrastrong-field physics. Phys. Rev. Spec. Top. Accel. Beams 2002, 5, 031301. [Google Scholar] [CrossRef]
- Gordienko, S.; Pukhov, A.; Shorokhov, O.; Baeva, T. Coherent Focusing of High Harmonics: A New Way towards the Extreme Intensities. Phys. Rev. Lett. 2005, 94, 103903. [Google Scholar] [CrossRef]
- Sokolov, I.V.; Naumova, N.M.; Nees, J.A.; Mourou, G.A. Pair Creation in QED-Strong Pulsed Laser Fields Interacting with Electron Beams. Phys. Rev. Lett. 2010, 105, 195005. [Google Scholar] [CrossRef]
- Esarey, E.; Schroeder, C.B.; Leemans, W.P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229–1285. [Google Scholar] [CrossRef]
- Elkina, N.V.; Fedotov, A.M.; Kostyukov, I.Y.; Legkov, M.V.; Narozhny, N.B.; Nerush, E.N.; Ruhl, H. QED cascades induced by circularly polarized laser fields. Phys. Rev. Spec. Top. Accel. Beams 2011, 14, 054401. [Google Scholar] [CrossRef]
- de Groot, S.R.; van Leeuwen, W.A.; Weert, C.G. Relativistic Kinetic Theory: Principles and Applications; North Holland: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Vereshchagin, G.V.; Aksenov, A.G. Relativistic Kinetic Theory; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Uehling, E.A.; Uhlenbeck, G.E. Transport Phenomena in Einstein-Bose and Fermi-Dirac Gases. I. Phys. Rev. 1933, 43, 552–561. [Google Scholar] [CrossRef]
- Sadovskii, M. Statistical Physics; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Non-Relativistic Theory; Elsevier Science & Technology: Oxford, UK, 1980. [Google Scholar]
- Berestetskii, V.B.; Landau, L.D.; Lifshitz, E.M. Statistical Physics; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, V.B. Quantum Electrodynamics; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Mandl, F.; Skyrme, T.H.R. The Theory of the Double Compton Effect. Proc. R. Soc. Lond. Ser. A 1952, 215, 497–507. [Google Scholar] [CrossRef]
- Haug, E.; Nakel, W. The Elementary Process of Bremsstrahlung; World Scientific Publishing Co.: Singapore, 2004. [Google Scholar] [CrossRef]
- Jauch, J.M.; Rohrlich, F. The Theory of Photons and Electrons; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Aksenov, A.G.; Ruffini, R.; Vereshchagin, G.V. Thermalization of Nonequilibrium Electron-Positron-Photon Plasmas. Phys. Rev. Lett. 2007, 99, 125003. [Google Scholar] [CrossRef]
- Aksenov, A.G.; Ruffini, R.; Vereshchagin, G.V. Thermalization of the mildly relativistic plasma. Phys. Rev. D 2009, 79, 043008. [Google Scholar] [CrossRef]
- Aksenov, A.G.; Ruffini, R.; Vereshchagin, G.V. Pair plasma relaxation time scales. Phys. Rev. E 2010, 81, 046401. [Google Scholar] [CrossRef] [PubMed]
- Prakapenia, M.A.; Siutsou, I.A.; Vereshchagin, G.V. Numerical scheme for treatment of Uehling-Uhlenbeck equation for two-particle interactions in relativistic plasma. J. Comput. Phys. 2018, 373, 533–544. [Google Scholar] [CrossRef]
- Prakapenia, M.A.; Siutsou, I.A.; Vereshchagin, G.V. Thermalization of electron-positron plasma with quantum degeneracy. Phys. Lett. A 2019, 383, 306–310. [Google Scholar] [CrossRef]
- Prakapenia, M.A.; Siutsou, I.A.; Vereshchagin, G.V. Numerical scheme for evaluating the collision integrals for triple interactions in relativistic plasma. Phys. Plasmas 2020, 27, 113302. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Levich, E.V. Bose Condensation and Shock Waves in Photon Spectra. Sov. J. Exp. Theor. Phys. 1969, 28, 1287. [Google Scholar]
- Prakapenia, M.A.; Vereshchagin, G.V. Bose-Einstein condensation in relativistic plasma. Europhys. Lett. 2020, 128, 50002. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef]
- Bradley, C.C.; Sackett, C.A.; Tollett, J.J.; Hulet, R.G. Evidence of Bose-Einstein Condensation in an Atomic Gas with Attractive Interactions. Phys. Rev. Lett. 1995, 75, 1687–1690. [Google Scholar] [CrossRef]
- Davis, K.B.; Mewes, M.O.; Andrews, M.R.; van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Bose-Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef]
- Zakharov, V.E.; L’vov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence 1. Wave Turbulence; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Berges, J. Nonequilibrium Quantum Fields: From Cold Atoms to Cosmology. arXiv 2015, arXiv:1503.02907. [Google Scholar]
- Gasenzer, T.; Nowak, B.; Sexty, D. Charge separation in reheating after cosmological inflation. Phys. Lett. B 2012, 710, 500–503. [Google Scholar] [CrossRef]
- Berges, J.; Jaeckel, J. Far from equilibrium dynamics of Bose-Einstein condensation for axion dark matter. Phys. Rev. D 2015, 91, 025020. [Google Scholar] [CrossRef]
- Piñeiro Orioli, A.; Boguslavski, K.; Berges, J. Universal self-similar dynamics of relativistic and nonrelativistic field theories near nonthermal fixed points. Phys. Rev. D 2015, 92, 025041. [Google Scholar] [CrossRef]
- Schmied, C.M.; Mikheev, A.N.; Gasenzer, T. Non-thermal fixed points: Universal dynamics far from equilibrium. Int. J. Mod. Phys. A 2019, 34, 1941006. [Google Scholar] [CrossRef]
- Chantesana, I.; Orioli, A.P.; Gasenzer, T. Kinetic theory of nonthermal fixed points in a Bose gas. Phys. Rev. A 2019, 99, 043620. [Google Scholar] [CrossRef]
- Ebeling, W.; Fortov, V.E.; Filinov, V. Quantum Statistics of Dense Gases and Nonideal Plasmas; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Schmidt, M.; Janke, T.; Redmer, R. On the influence of the Pauli exclusion principle on the transport properties of dense Coulomb systems. Contrib. Plasma Phys. 1989, 29, 431–440. [Google Scholar] [CrossRef]
- Röpke, G.; Blaschke, D.; Döppner, T.; Lin, C.; Kraeft, W.D.; Redmer, R.; Reinholz, H. Ionization potential depression and Pauli blocking in degenerate plasmas at extreme densities. Phys. Rev. E 2019, 99, 033201. [Google Scholar] [CrossRef]
- Xing, Y.Z.; Zhang, H.F.; Liu, X.B.; Zheng, Y.M. Pauli-blocking effect in two-body collisions dominates the in-medium effects in heavy-ion reactions near Fermi energy. Nucl. Phys. A 2017, 957, 135–143. [Google Scholar] [CrossRef]
- Ray, L. Pauli blocking effects for nucleon-nucleus scattering. Phys. Rev. C 1993, 47, 2236–2241. [Google Scholar] [CrossRef]
- Bertulani, C.A.; de Conti, C. Pauli blocking and medium effects in nucleon knockout reactions. Phys. Rev. C 2010, 81, 064603. [Google Scholar] [CrossRef]
- Stefanini, A.M.; Montagnoli, G.; Del Fabbro, M.; Colucci, G.; Čolović, P.; Corradi, L.; Fioretto, E.; Galtarossa, F.; Goasduff, A.; Grebosz, J.; et al. Fusion hindrance and Pauli blocking in 58Ni + 64Ni. Phys. Rev. C 2019, 100, 044619. [Google Scholar] [CrossRef]
- Prakapenia, M.A.; Vereshchagin, G.V. Pauli blocking effects in thermalization of relativistic plasma. Phys. Lett. A 2020, 384, 126679. [Google Scholar] [CrossRef]
- Ruffini, R.; Vitagliano, L.; Xue, S.S. On plasma oscillations in strong electric fields. Phys. Lett. B 2003, 559, 12–19. [Google Scholar] [CrossRef]
- Ruffini, R.; Vereshchagin, G.V.; Xue, S.S. Vacuum polarization and plasma oscillations. Phys. Lett. A 2007, 371, 399–405. [Google Scholar] [CrossRef]
- Benedetti, A.; Han, W.B.; Ruffini, R.; Vereshchagin, G.V. On the frequency of oscillations in the pair plasma generated by a strong electric field. Phys. Lett. B 2011, 698, 75–79. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).