Kinetics of Degenerate Electron–Positron Plasmas
Abstract
1. Introduction
2. Conditions for Formation of Relativistic Degenerate Plasma
2.1. Degenerate Plasmas in Compact Astrophysical Objects
2.2. Strong Electromagnetic Fields in Astrophysical Sources
2.3. Pair Creation in Ultraintense Lasers
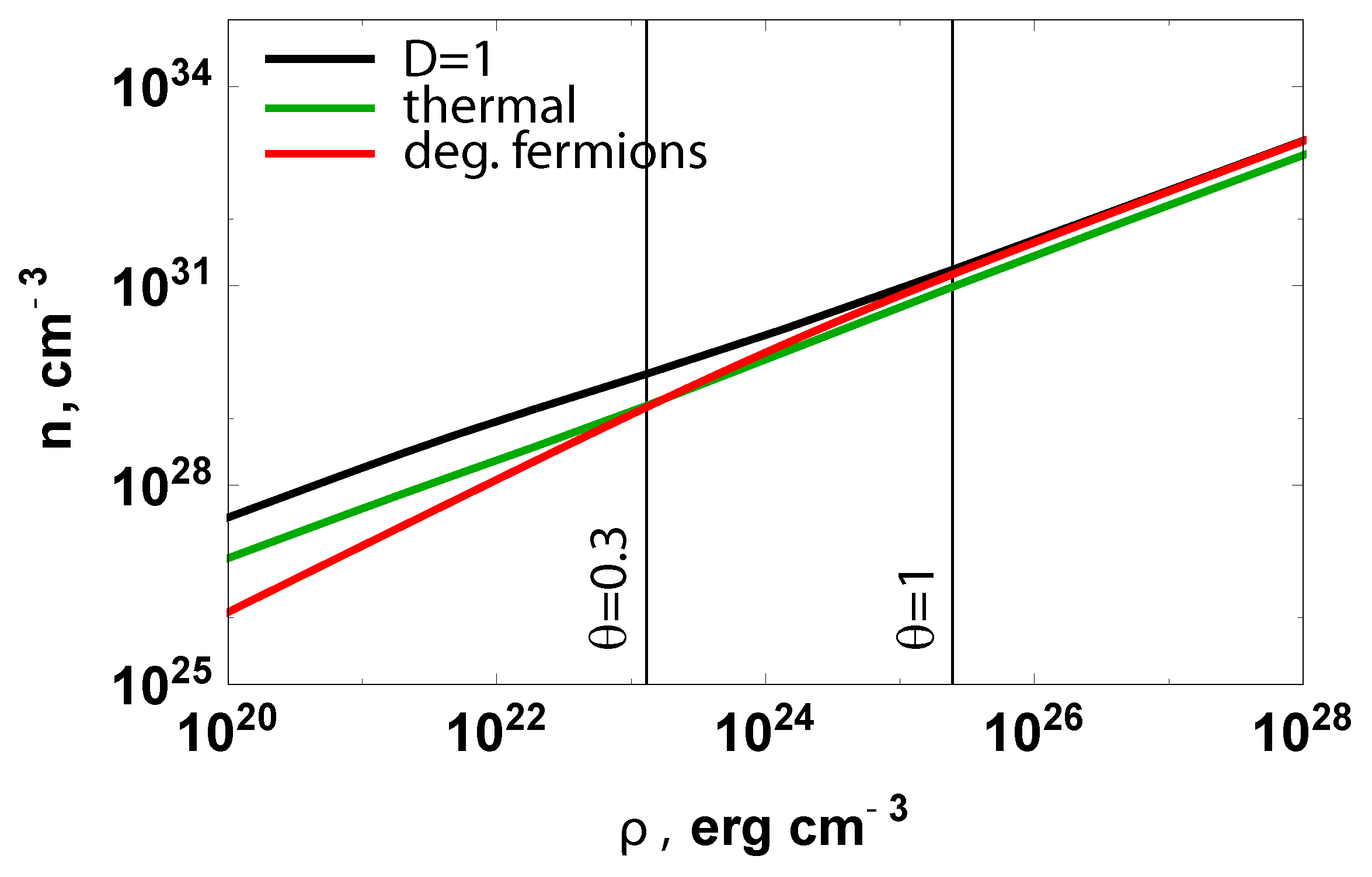
2.4. Fermion Critical Density
3. Relativistic Kinetic Equations
3.1. Derivation of Relativistic Kinetic Equations from Quantum Theory
3.2. Collision Integrals in the Relativistic Kinetic Equation
3.3. Binary Interactions
3.4. Triple Interactions
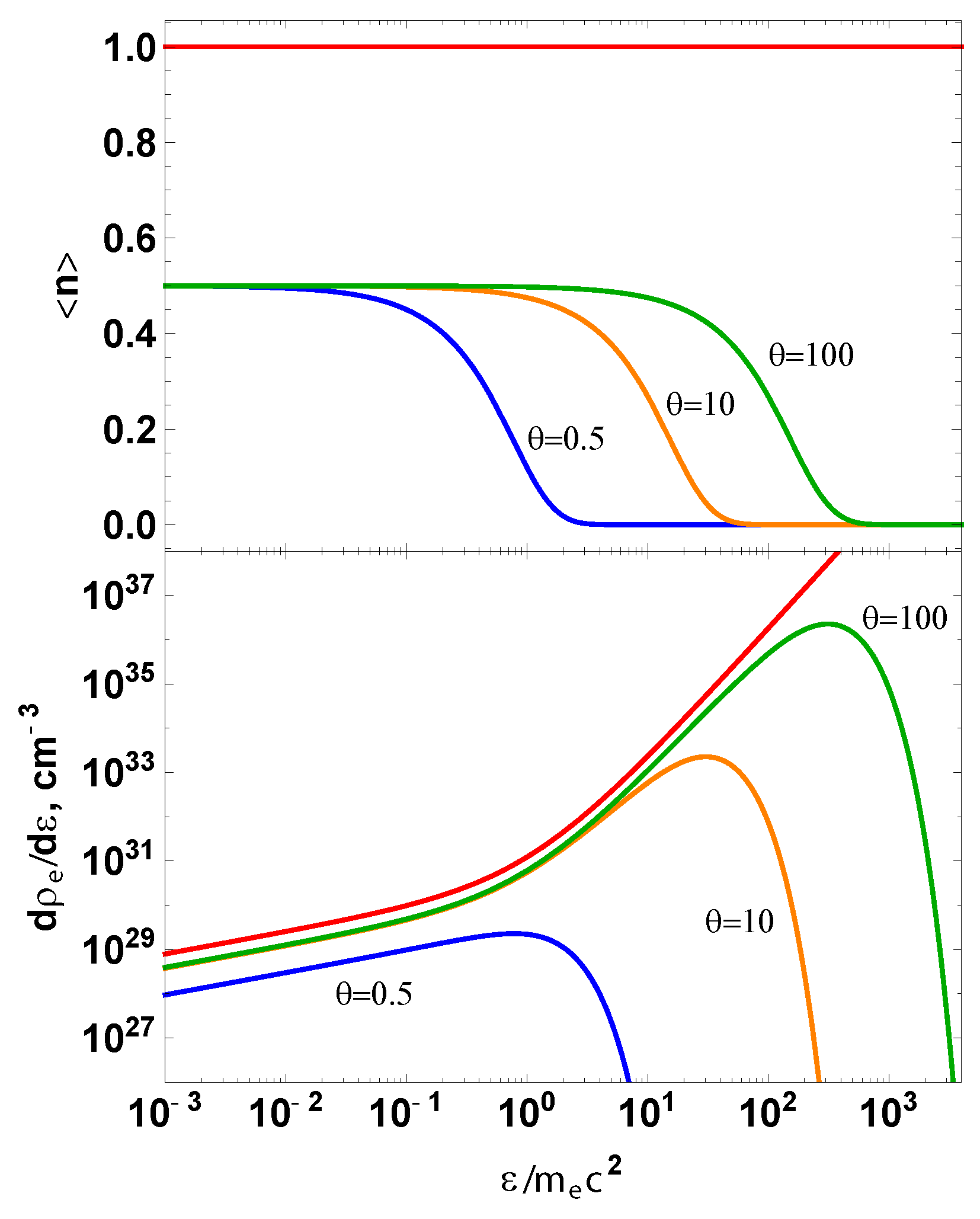
3.5. Kinetic versus Thermal Equilibrium
4. Bose–Einstein Condensation of Photons in Relativistic Plasma
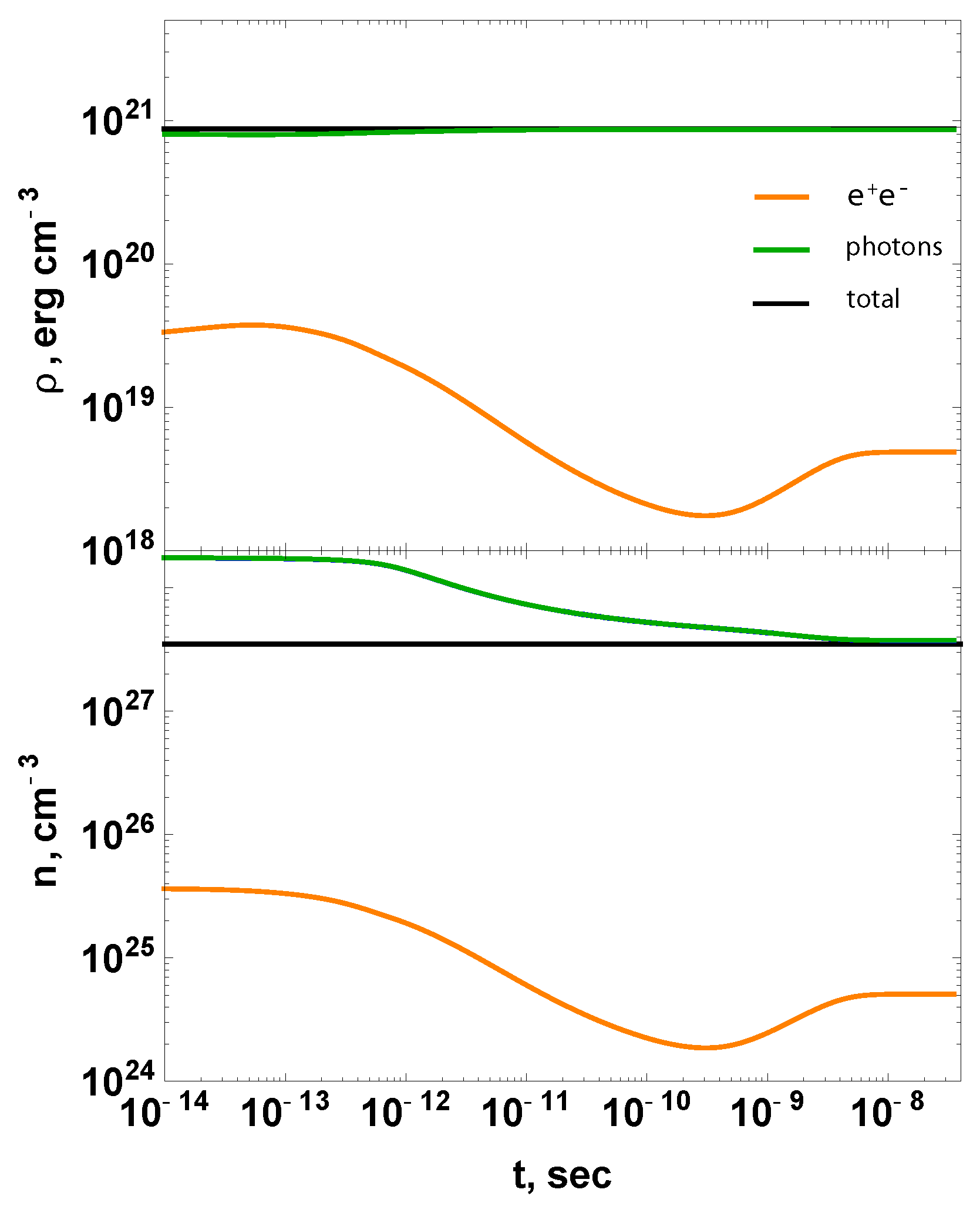
5. Thermalization of Superdegenerate Plasma
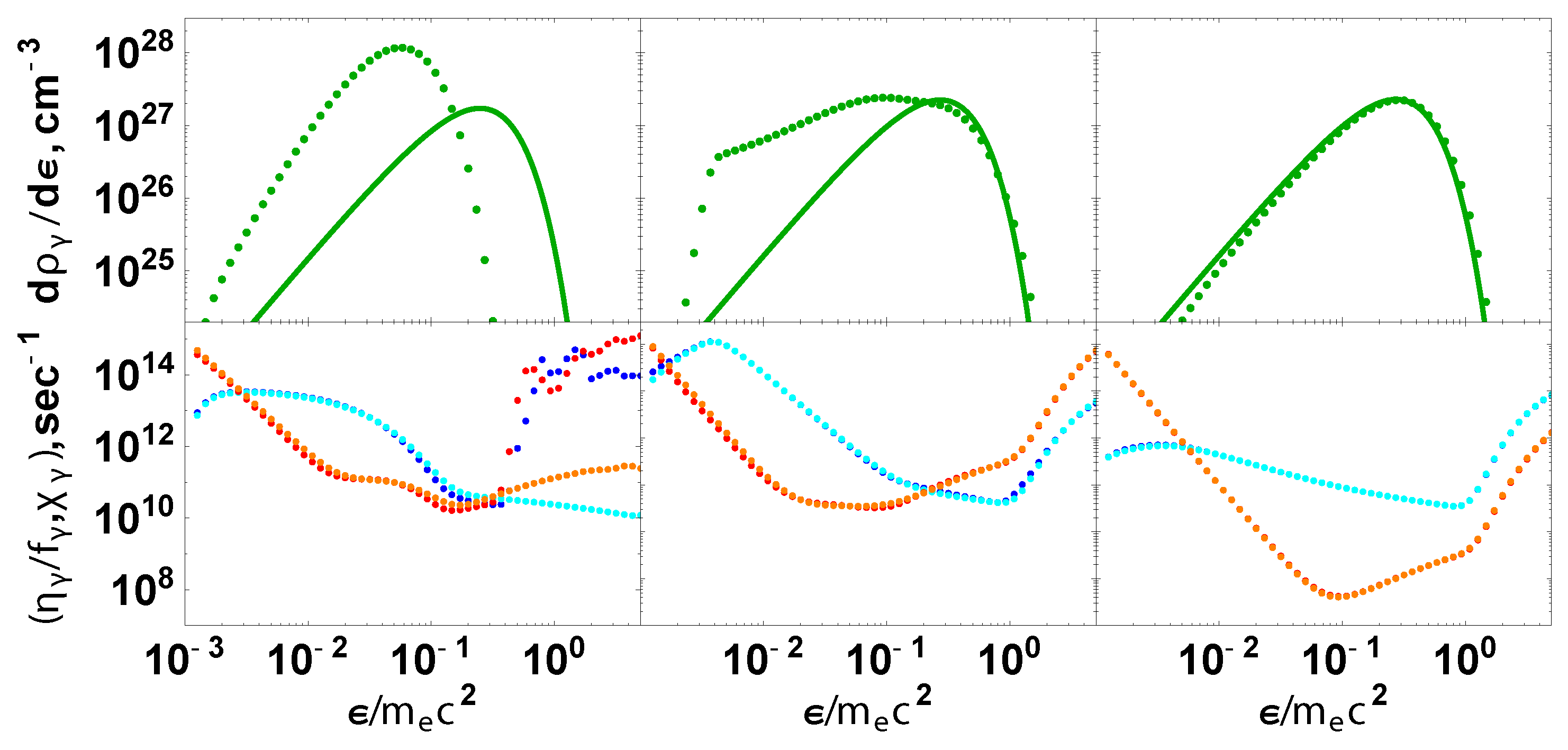
6. Phase Space Evolution of Pairs Created in Strong Electric Fields
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | http://www.xfel.eu (accessed on 8 September 2022). |
| 2 | https://eli-laser.eu/ (accessed on 8 September 2022). |
| 3 | https://xcels.ipfran.ru/img/site-XCELS.pdf (accessed on 8 September 2022). |
References
- Schwinger, J. On Gauge Invariance and Vacuum Polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Klein, J.J.; Nigam, B.P. Birefringence of the Vacuum. Phys. Rev. 1964, 135, 1279–1280. [Google Scholar] [CrossRef]
- Mignani, R.P.; Testa, V.; González Caniulef, D.; Taverna, R.; Turolla, R.; Zane, S.; Wu, K. Evidence for vacuum birefringence from the first optical-polarimetry measurement of the isolated neutron star RX J1856.5-3754. Mon. Not. R. Astron. Soc. 2017, 465, 492–500. [Google Scholar] [CrossRef]
- Nikishov, A.I.; Ritus, V.I. Quantum Processes in the Field of a Plane Electromagnetic Wave and in a Constant Field. Sov. Phys. J. Exp. Theor. Phys. 1964, 19, 1191. [Google Scholar]
- Brown, L.S.; Kibble, T.W. Interaction of Intense Laser Beams with Electrons. Phys. Rev. 1964, 133, 705–719. [Google Scholar] [CrossRef]
- Bula, C.; McDonald, K.T.; Prebys, E.J.; Bamber, C.; Boege, S.; Kotseroglou, T.; Melissinos, A.C.; Meyerhofer, D.D.; Ragg, W.; Burke, D.L.; et al. Observation of Nonlinear Effects in Compton Scattering. Phys. Rev. Lett. 1996, 76, 3116–3119. [Google Scholar] [CrossRef]
- Burke, D.L.; Field, R.C.; Horton-Smith, G.; Spencer, J.E.; Walz, D.; Berridge, S.C.; Bugg, W.M.; Shmakov, K.; Weidemann, A.W.; Bula, C.; et al. Positron Production in Multiphoton Light-by-Light Scattering. Phys. Rev. Lett. 1997, 79, 1626–1629. [Google Scholar] [CrossRef]
- Euler, H. Über die Streuung von Licht an Licht nach der Diracschen Theorie. Ann. Phys. 1936, 418, 398–448. [Google Scholar] [CrossRef]
- Sauter, F. Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs. Zeits. Phys. 1931, 69, 742–764. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Consequences of Dirac Theory of the Positron. Zeits. Phys. 1935, 98, 714–732. [Google Scholar] [CrossRef]
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177–1228. [Google Scholar] [CrossRef]
- Fedotov, A.; Ilderton, A.; Karbstein, F.; King, B.; Seipt, D.; Taya, H.; Torgrimsson, G. Advances in QED with intense background fields. arXiv 2022, arXiv:2203.00019. [Google Scholar]
- Bell, A.R.; Kirk, J.G. Possibility of Prolific Pair Production with High-Power Lasers. Phys. Rev. Lett. 2008, 101, 200403. [Google Scholar] [CrossRef]
- Bulanov, S.S.; Esirkepov, T.Z.; Thomas, A.G.R.; Koga, J.K.; Bulanov, S.V. Schwinger Limit Attainability with Extreme Power Lasers. Phys. Rev. Lett. 2010, 105, 220407. [Google Scholar] [CrossRef]
- Fedotov, A.M.; Narozhny, N.B.; Mourou, G.; Korn, G. Limitations on the Attainable Intensity of High Power Lasers. Phys. Rev. Lett. 2010, 105, 080402. [Google Scholar] [CrossRef]
- Ruffini, R.; Vereshchagin, G.; Xue, S.S. Electron-positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys. Rep. 2010, 487, 1–140. [Google Scholar] [CrossRef]
- Page, D.N. Evidence against Macroscopic Astrophysical Dyadospheres. ApJ 2006, 653, 1400–1409. [Google Scholar] [CrossRef]
- Gershteǐn, S.S.; Zel’Dovich, Y.B. Positron Production during the Mutual Approach of Heavy Nuclei and the Polarization of the Vacuum. Sov. J. Exp. Theor. Phys. 1969, 30, 358. [Google Scholar]
- Popov, V.S. Position Production in a Coulomb Field with Z > 137. Sov. J. Exp. Theor. Phys. 1971, 32, 526. [Google Scholar]
- Greiner, W.; Muller, B.; Rafelski, J. Quantum Electrodynamics of Strong Fields; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Usov, V.V. Bare Quark Matter Surfaces of Strange Stars and e+e− Emission. Phys. Rev. Lett. 1998, 80, 230–233. [Google Scholar] [CrossRef]
- Alcock, C.; Farhi, E.; Olinto, A. Strange stars. ApJ 1986, 310, 261–272. [Google Scholar] [CrossRef]
- Belvedere, R.; Pugliese, D.; Rueda, J.A.; Ruffini, R.; Xue, S.S. Neutron star equilibrium configurations within a fully relativistic theory with strong, weak, electromagnetic, and gravitational interactions. Nucl. Phys. A 2012, 883, 1–24. [Google Scholar] [CrossRef]
- Usov, V.V. Thermal Emission from Bare Quark Matter Surfaces of Hot Strange Stars. ApJ 2001, 550, L179–L182. [Google Scholar] [CrossRef]
- Ruffini, R.; Xue, S.S. Electron-positron pairs production in a macroscopic charged core. Phys. Lett. B 2011, 696, 416–421. [Google Scholar] [CrossRef][Green Version]
- Han, W.B.; Ruffini, R.; Xue, S.S. Electron and positron pair production of compact stars. Phys. Rev. D 2012, 86, 084004. [Google Scholar] [CrossRef]
- Aksenov, A.G.; Milgrom, M.; Usov, V.V. Structure of Pair Winds from Compact Objects with Application to Emission from Hot Bare Strange Stars. ApJ 2004, 609, 363–377. [Google Scholar] [CrossRef]
- Levinson, A.; Nakar, E. Physics of radiation mediated shocks and its applications to GRBs, supernovae, and neutron star mergers. Phys. Rep. 2020, 866, 1–46. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Relativistic fireballs—Energy conversion and time-scales. Mon. Not. R. Astron. Soc. 1992, 258, 41. [Google Scholar] [CrossRef]
- Uzdensky, D.A.; Rightley, S. Plasma physics of extreme astrophysical environments. Rep. Prog. Phys. 2014, 77, 036902. [Google Scholar] [CrossRef]
- Kaspi, V.M.; Beloborodov, A.M. Magnetars. Annu. Rev. Astron. Astrophys. 2017, 55, 261–301. [Google Scholar] [CrossRef]
- Mereghetti, S. The strongest cosmic magnets: Soft gamma-ray repeaters and anomalous X-ray pulsars. Astron. Astrophys. Rev. 2008, 15, 225–287. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The soft gamma repeaters as very strongly magnetized neutron stars—I. Radiative mechanism for outbursts. Mon. Not. R. Astron. Soc. 1995, 275, 255–300. [Google Scholar] [CrossRef]
- Piran, T. Gamma-ray bursts and the fireball model. Phys. Rep. 1999, 314, 575–667. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 413, 2031–2056. [Google Scholar] [CrossRef]
- Moradi, R.; Rueda, J.A.; Ruffini, R.; Li, L.; Bianco, C.L.; Campion, S.; Cherubini, C.; Filippi, S.; Wang, Y.; Xue, S.S. Nature of the ultrarelativistic prompt emission phase of GRB 190114C. Phys. Rev. D 2021, 104, 063043. [Google Scholar] [CrossRef]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Yanovsky, V.; Chvykov, V.; Kalinchenko, G.; Rousseau, P.; Planchon, T.; Matsuoka, T.; Maksimchuk, A.; Nees, J.; Cheriaux, G.; Mourou, G.; et al. Ultra-high intensity- 300-TW laser at 0.1 Hz repetition rate. Opt. Express 2008, 16, 2109–2114. [Google Scholar] [CrossRef]
- Mourou, G.A.; Tajima, T.; Bulanov, S.V. Optics in the relativistic regime. Rev. Mod. Phys. 2006, 78, 309–371. [Google Scholar] [CrossRef]
- Ringwald, A. Pair production from vacuum at the focus of an X-ray free electron laser. Phys. Lett. B 2001, 510, 107–116. [Google Scholar] [CrossRef]
- Tajima, T.; Mourou, G. Zettawatt-exawatt lasers and their applications in ultrastrong-field physics. Phys. Rev. Spec. Top. Accel. Beams 2002, 5, 031301. [Google Scholar] [CrossRef]
- Gordienko, S.; Pukhov, A.; Shorokhov, O.; Baeva, T. Coherent Focusing of High Harmonics: A New Way towards the Extreme Intensities. Phys. Rev. Lett. 2005, 94, 103903. [Google Scholar] [CrossRef]
- Sokolov, I.V.; Naumova, N.M.; Nees, J.A.; Mourou, G.A. Pair Creation in QED-Strong Pulsed Laser Fields Interacting with Electron Beams. Phys. Rev. Lett. 2010, 105, 195005. [Google Scholar] [CrossRef]
- Esarey, E.; Schroeder, C.B.; Leemans, W.P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229–1285. [Google Scholar] [CrossRef]
- Elkina, N.V.; Fedotov, A.M.; Kostyukov, I.Y.; Legkov, M.V.; Narozhny, N.B.; Nerush, E.N.; Ruhl, H. QED cascades induced by circularly polarized laser fields. Phys. Rev. Spec. Top. Accel. Beams 2011, 14, 054401. [Google Scholar] [CrossRef]
- de Groot, S.R.; van Leeuwen, W.A.; Weert, C.G. Relativistic Kinetic Theory: Principles and Applications; North Holland: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Vereshchagin, G.V.; Aksenov, A.G. Relativistic Kinetic Theory; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Uehling, E.A.; Uhlenbeck, G.E. Transport Phenomena in Einstein-Bose and Fermi-Dirac Gases. I. Phys. Rev. 1933, 43, 552–561. [Google Scholar] [CrossRef]
- Sadovskii, M. Statistical Physics; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Non-Relativistic Theory; Elsevier Science & Technology: Oxford, UK, 1980. [Google Scholar]
- Berestetskii, V.B.; Landau, L.D.; Lifshitz, E.M. Statistical Physics; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, V.B. Quantum Electrodynamics; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Mandl, F.; Skyrme, T.H.R. The Theory of the Double Compton Effect. Proc. R. Soc. Lond. Ser. A 1952, 215, 497–507. [Google Scholar] [CrossRef]
- Haug, E.; Nakel, W. The Elementary Process of Bremsstrahlung; World Scientific Publishing Co.: Singapore, 2004. [Google Scholar] [CrossRef]
- Jauch, J.M.; Rohrlich, F. The Theory of Photons and Electrons; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Aksenov, A.G.; Ruffini, R.; Vereshchagin, G.V. Thermalization of Nonequilibrium Electron-Positron-Photon Plasmas. Phys. Rev. Lett. 2007, 99, 125003. [Google Scholar] [CrossRef]
- Aksenov, A.G.; Ruffini, R.; Vereshchagin, G.V. Thermalization of the mildly relativistic plasma. Phys. Rev. D 2009, 79, 043008. [Google Scholar] [CrossRef]
- Aksenov, A.G.; Ruffini, R.; Vereshchagin, G.V. Pair plasma relaxation time scales. Phys. Rev. E 2010, 81, 046401. [Google Scholar] [CrossRef] [PubMed]
- Prakapenia, M.A.; Siutsou, I.A.; Vereshchagin, G.V. Numerical scheme for treatment of Uehling-Uhlenbeck equation for two-particle interactions in relativistic plasma. J. Comput. Phys. 2018, 373, 533–544. [Google Scholar] [CrossRef]
- Prakapenia, M.A.; Siutsou, I.A.; Vereshchagin, G.V. Thermalization of electron-positron plasma with quantum degeneracy. Phys. Lett. A 2019, 383, 306–310. [Google Scholar] [CrossRef]
- Prakapenia, M.A.; Siutsou, I.A.; Vereshchagin, G.V. Numerical scheme for evaluating the collision integrals for triple interactions in relativistic plasma. Phys. Plasmas 2020, 27, 113302. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Levich, E.V. Bose Condensation and Shock Waves in Photon Spectra. Sov. J. Exp. Theor. Phys. 1969, 28, 1287. [Google Scholar]
- Prakapenia, M.A.; Vereshchagin, G.V. Bose-Einstein condensation in relativistic plasma. Europhys. Lett. 2020, 128, 50002. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef]
- Bradley, C.C.; Sackett, C.A.; Tollett, J.J.; Hulet, R.G. Evidence of Bose-Einstein Condensation in an Atomic Gas with Attractive Interactions. Phys. Rev. Lett. 1995, 75, 1687–1690. [Google Scholar] [CrossRef]
- Davis, K.B.; Mewes, M.O.; Andrews, M.R.; van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Bose-Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef]
- Zakharov, V.E.; L’vov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence 1. Wave Turbulence; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Berges, J. Nonequilibrium Quantum Fields: From Cold Atoms to Cosmology. arXiv 2015, arXiv:1503.02907. [Google Scholar]
- Gasenzer, T.; Nowak, B.; Sexty, D. Charge separation in reheating after cosmological inflation. Phys. Lett. B 2012, 710, 500–503. [Google Scholar] [CrossRef]
- Berges, J.; Jaeckel, J. Far from equilibrium dynamics of Bose-Einstein condensation for axion dark matter. Phys. Rev. D 2015, 91, 025020. [Google Scholar] [CrossRef]
- Piñeiro Orioli, A.; Boguslavski, K.; Berges, J. Universal self-similar dynamics of relativistic and nonrelativistic field theories near nonthermal fixed points. Phys. Rev. D 2015, 92, 025041. [Google Scholar] [CrossRef]
- Schmied, C.M.; Mikheev, A.N.; Gasenzer, T. Non-thermal fixed points: Universal dynamics far from equilibrium. Int. J. Mod. Phys. A 2019, 34, 1941006. [Google Scholar] [CrossRef]
- Chantesana, I.; Orioli, A.P.; Gasenzer, T. Kinetic theory of nonthermal fixed points in a Bose gas. Phys. Rev. A 2019, 99, 043620. [Google Scholar] [CrossRef]
- Ebeling, W.; Fortov, V.E.; Filinov, V. Quantum Statistics of Dense Gases and Nonideal Plasmas; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Schmidt, M.; Janke, T.; Redmer, R. On the influence of the Pauli exclusion principle on the transport properties of dense Coulomb systems. Contrib. Plasma Phys. 1989, 29, 431–440. [Google Scholar] [CrossRef]
- Röpke, G.; Blaschke, D.; Döppner, T.; Lin, C.; Kraeft, W.D.; Redmer, R.; Reinholz, H. Ionization potential depression and Pauli blocking in degenerate plasmas at extreme densities. Phys. Rev. E 2019, 99, 033201. [Google Scholar] [CrossRef]
- Xing, Y.Z.; Zhang, H.F.; Liu, X.B.; Zheng, Y.M. Pauli-blocking effect in two-body collisions dominates the in-medium effects in heavy-ion reactions near Fermi energy. Nucl. Phys. A 2017, 957, 135–143. [Google Scholar] [CrossRef]
- Ray, L. Pauli blocking effects for nucleon-nucleus scattering. Phys. Rev. C 1993, 47, 2236–2241. [Google Scholar] [CrossRef]
- Bertulani, C.A.; de Conti, C. Pauli blocking and medium effects in nucleon knockout reactions. Phys. Rev. C 2010, 81, 064603. [Google Scholar] [CrossRef]
- Stefanini, A.M.; Montagnoli, G.; Del Fabbro, M.; Colucci, G.; Čolović, P.; Corradi, L.; Fioretto, E.; Galtarossa, F.; Goasduff, A.; Grebosz, J.; et al. Fusion hindrance and Pauli blocking in 58Ni + 64Ni. Phys. Rev. C 2019, 100, 044619. [Google Scholar] [CrossRef]
- Prakapenia, M.A.; Vereshchagin, G.V. Pauli blocking effects in thermalization of relativistic plasma. Phys. Lett. A 2020, 384, 126679. [Google Scholar] [CrossRef]
- Ruffini, R.; Vitagliano, L.; Xue, S.S. On plasma oscillations in strong electric fields. Phys. Lett. B 2003, 559, 12–19. [Google Scholar] [CrossRef]
- Ruffini, R.; Vereshchagin, G.V.; Xue, S.S. Vacuum polarization and plasma oscillations. Phys. Lett. A 2007, 371, 399–405. [Google Scholar] [CrossRef]
- Benedetti, A.; Han, W.B.; Ruffini, R.; Vereshchagin, G.V. On the frequency of oscillations in the pair plasma generated by a strong electric field. Phys. Lett. B 2011, 698, 75–79. [Google Scholar] [CrossRef][Green Version]
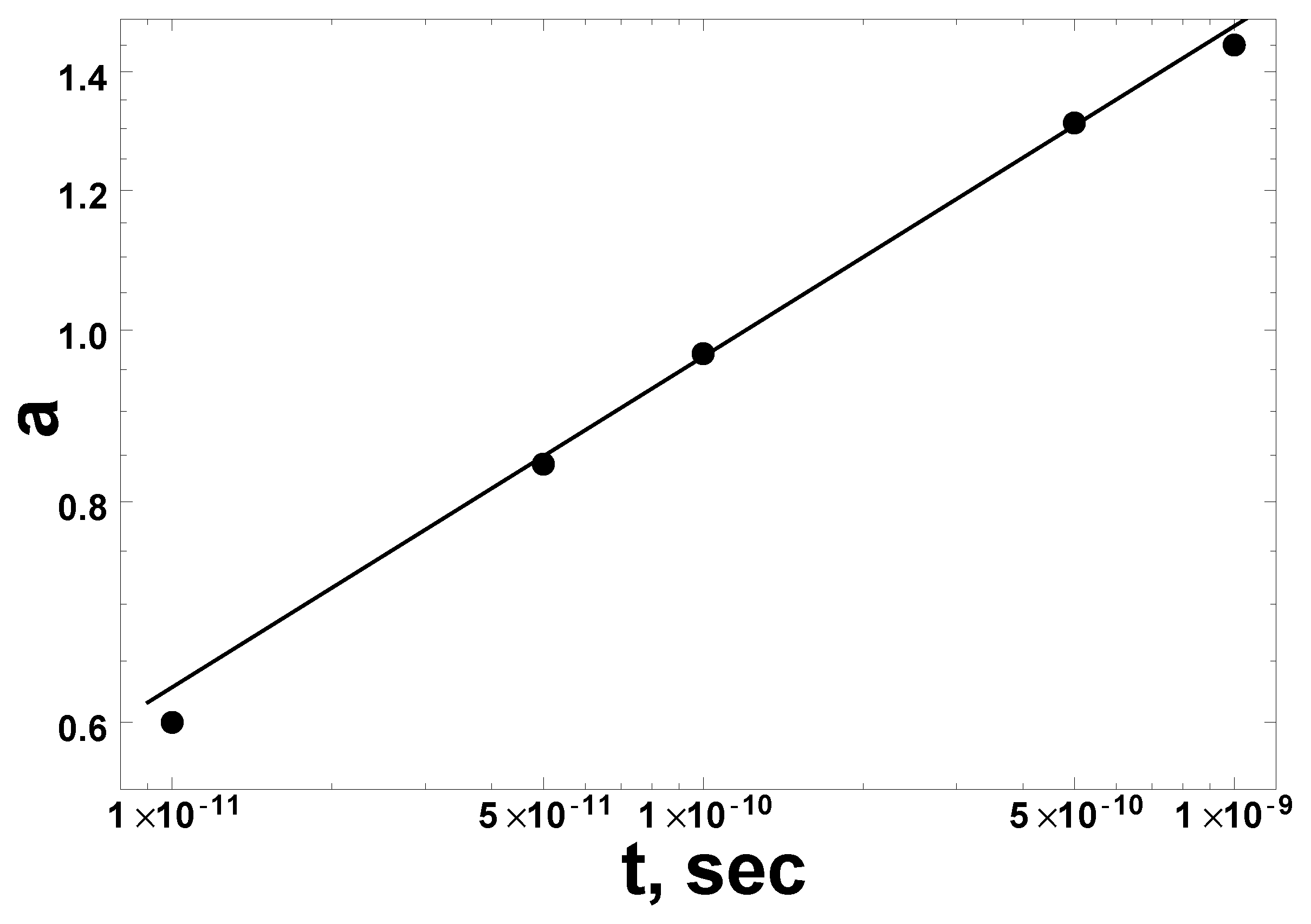
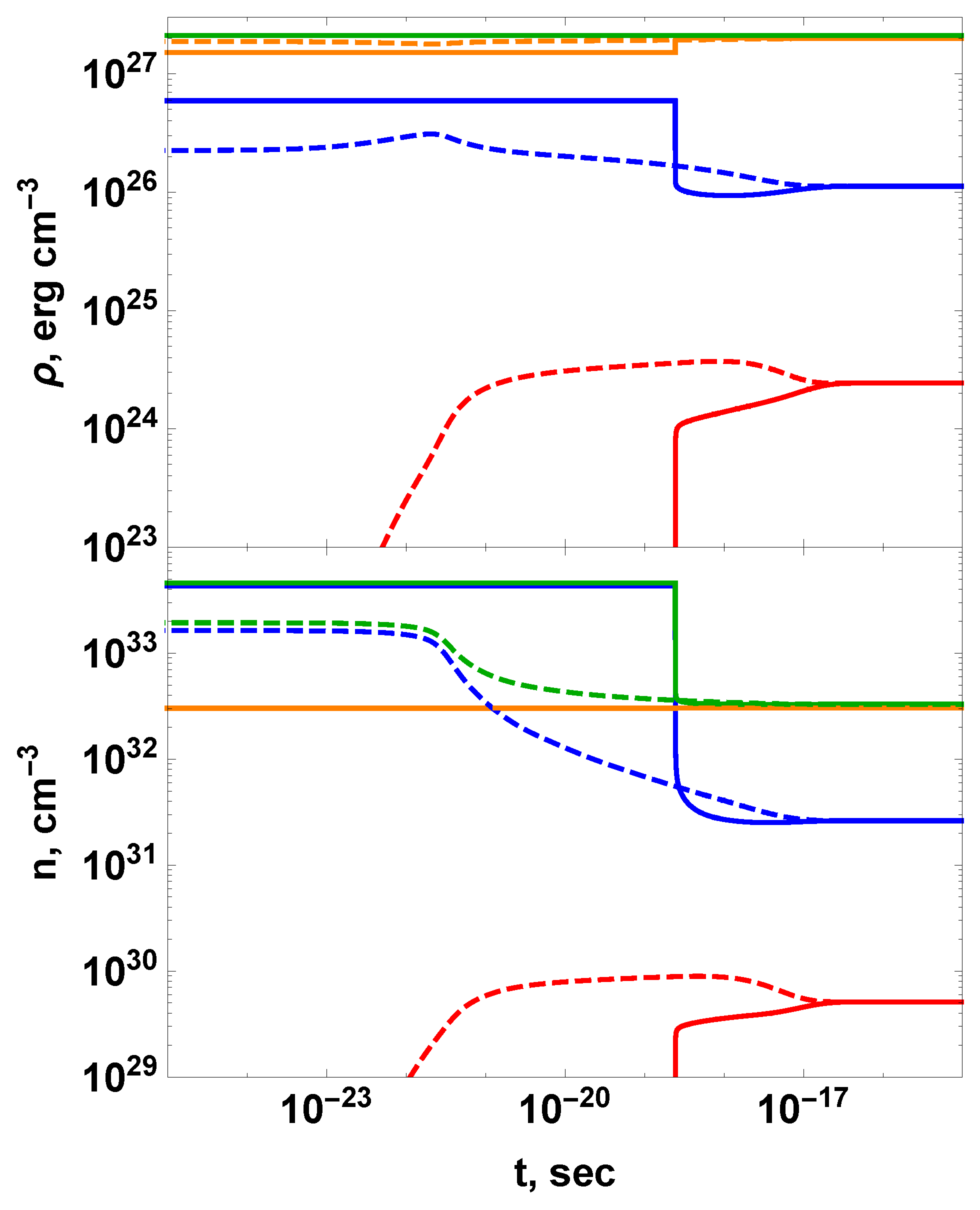
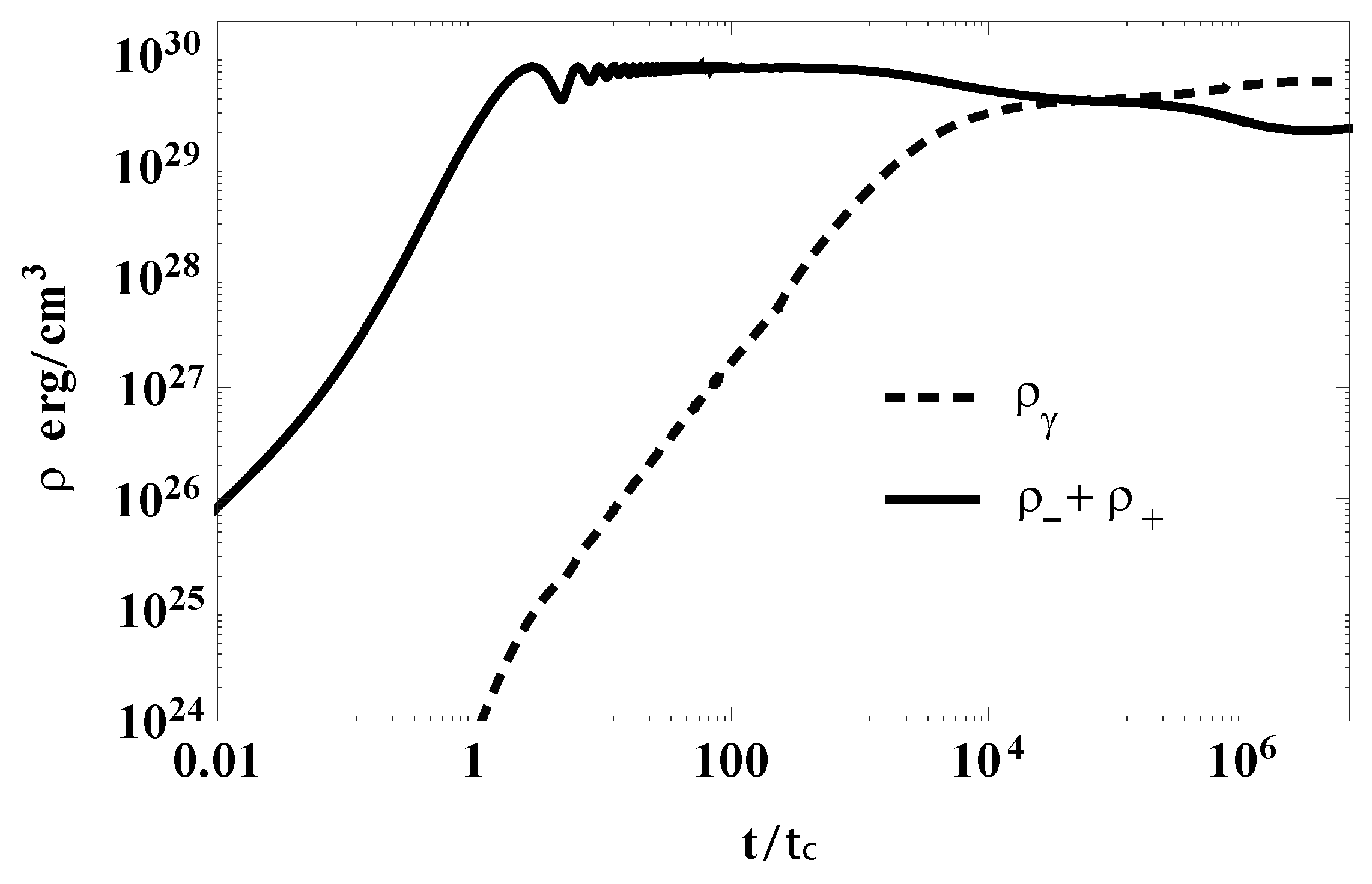

| Binary Processes | Triple Processes |
|---|---|
| Møller, Bhabha | Bremsstrahlung |
| Single Compton | Double Compton |
| Pair production and annihilation | Radiative pair production, triplet production and three photon annihilation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vereshchagin, G.; Prakapenia, M. Kinetics of Degenerate Electron–Positron Plasmas. Universe 2022, 8, 473. https://doi.org/10.3390/universe8090473
Vereshchagin G, Prakapenia M. Kinetics of Degenerate Electron–Positron Plasmas. Universe. 2022; 8(9):473. https://doi.org/10.3390/universe8090473
Chicago/Turabian StyleVereshchagin, Gregory, and Mikalai Prakapenia. 2022. "Kinetics of Degenerate Electron–Positron Plasmas" Universe 8, no. 9: 473. https://doi.org/10.3390/universe8090473
APA StyleVereshchagin, G., & Prakapenia, M. (2022). Kinetics of Degenerate Electron–Positron Plasmas. Universe, 8(9), 473. https://doi.org/10.3390/universe8090473






