The Variation of the X-ray Solar Flare’s Time Profile

Abstract

We have studied the variation of the time profile of X-ray emission of solar flares that occurred during the second half of solar cycle 23 (SC 23) and for about the full solar cycle 24 (SC 24) (2002–2018). We define a new index, called the “ratio index” (R_f), for all X-ray solar flares. This index is defined as the ratio of the flare’s rising time interval by its total duration period. According to the ratio index, the X-ray solar flares are classified into two types: (1) sudden flares [R_f < 0.5], and (2) gradual flares [R_f > 0.5]. The sudden flare type, with fast-rising and slow recovery, is more common and represents most of the flares that happen most of the time during the solar cycles but are less common during the minimum solar activity years. On the other hand, the gradual flare type (or R_f > 0.5) is less common but predominates during the minimum solar activity epochs. Sudden flares tend to be strong, large, and numerous in the polar regions, while gradual flares are weak, short, and countable in the latitude range between 50 and 70, both for northern and southern latitudes. However, both types appear to happen in the lower latitudes and the solar equatorial regions.

1. Introduction

The typical time profiles of solar flares at all frequencies have short rising times and long decaying times; the phases of a flare during which distinct physical processes occur [1] are used to classify the flares into two classes. The hard X-ray flare’s time profiles and spectra variations can reveal a lot of information about not only the particle acceleration processes but also particle propagation, as well as their possible strong impact on the terrestrial ionosphere [2] and earth’s environment. The physical processes responsible for the energization of the flare’s electrons were the bremsstrahlung, inverse Compton, and synchrotron mechanisms [3].

Electrons are accelerated rapidly to energies greater than 1 MeV at the impulsive phase, which is responsible for hard X-ray (HXR) and γ-ray emission, announcing the flare onset. In particular, the accelerated electrons control and govern the time profile of HXR [4]. While soft X-ray (SXR) emission enhances after the impulsive phase due to the thermal electrons [5]. Both HXR and SXR emissions are attributed to the Bremsstrahlung mechanism operated by very rapid electrons. Observations of solar flares in HXRs reveal bright, compact emission sources at flaring loop footpoints, where dense and cold chromospheric plasma is heated by beams of nonthermal electrons (NTEs). However, through the strong chromospheric hydrogen Hα line, the flare’s emission sources appear as kernels and ribbons [6]. Furthermore, the authors of ref. [7] introduced a very useful overview of the flare’s observations based on multiwavelength detection, which gives a good description of the flare’s development and its several stages: Rising, impulsive, and decaying phases [7].

Actually, in a large flare, the electromagnetic emission can be divided into three distinct parts, which are considered to express the phases of the flare. They are typically the precursors, the impulsive, or explosive, and the gradual phases. The X-ray emission is time-dependent. That is why it is crucial to study these profiles to understand the physical mechanisms behind these time profiles. As Syrovatskii [8] underlines, the initial phase is characterized by the appearance of local brightening in Hα and a gradual rise in the emission of SXR, while the explosive phase is the most impressive in the whole flare phenomena characterized by HXR emission. The decay phase is known as a gradual SXR phase [5]. Solar flare occurrence and background flux in SXR wavelength are delayed concerning the sunspot activity [9]. The relative phase shifts occur two to three years between the peak times of solar cycles SC 21 and SC 22. This is because SXR flare occurrence and background flux are considered to be dominated by the post-flare emission from the dominant active regions. Moreover, the author of [10] interpreted that the phase delay is possibly due to the increasing complexity of coronal magnetic structures in the decay phase of the solar cycle. Furthermore, the authors of [11] examined 79 impulsive near-relativistic beamlike electron events, the majority of which were associated with Hα flares, and they concluded that a median of 10 min. delay is observed between electromagnetic emissions (Hα, X-rays, microwave bursts, and, in particular, decametric solar type III radio bursts) and the injection of the energetic electrons into the solar wind, which produces the type II fast electrons.

Indeed, many studies regarding the flare’s time profile in several bands have been performed. For instance, the time profiles of hard X-rays of the very intense solar flares of 1972 August 4 and 7 were investigated by the authors of [4], showing that below—100 keV the X-ray energy spectrum is flatter when the flux is higher, and vice versa, but the trend is reversed at higher energies. In addition to X-ray wavelength, there were other studies on Hα, Microwave, EUV, and γ-ray bands [6,12,13,14,15,16,17]. Mathematical models have been used to investigate the flare’s characteristics [18]. Additionally, the authors of [14] applied a flare detection algorithm to the flare light curves detected by the Sphinx instrument to get a list of maxima, start, and end times.

Previous studies tried to index the solar flares depending on the heliographical distribution of solar flares [19,20,21,22]. Naturally, the periodicity of solar activity is evident in long-time period studies (1966–2001) [23].

Furthermore, the authors of [24] studied the morphology of average flare time profiles, particularly the decay phase. They concluded that chromospheric evaporation may contribute, but not alone, to the evolution of the flares’ decay phase.

Although these studies of the flares have been vital and useful to a large extent, none of them have deeply focused on the time profile’s morphology. In other words, namely, the rising and decay periods of the time profile have not been studied. The study of the rising and decaying times of flares has been carried out in the present work. We introduce a new flare index regarding the X-ray flare time profile to have a better understanding of the flare’s characteristics such as duration, amplitude, and variation with solar activity over a long time scale.

2. Methodology

Our study uses the flare data obtained by the Reuven Ramaty High-Energy Solar Spectroscopic Imager (RHESSI). RHESSI is a NASA Small Explorer Mission to study the acceleration and transport of high-energy particles in solar flares [25]. This is accomplished by high-resolution imaging spectroscopy of X-rays and gamma-rays from 3 keV through 17 MeV [26].

In this study, we examined the rising and decaying times of X-ray solar flares, obtained from GOES for all periods available. We have performed new determinations of solar flare timings; start, peak, and end times, as we have realized that they need some corrections to compensate for the mistakes in their determinations. This time’s definition changes every once in a while. In addition, the flare times are specified from the H-Alpha data of those flares that were obtained before 1996 [27,28]. However, some researchers used different algorithms to determine the start and end times of the solar flares. As a result, in our current study, we use the times of RHESSI solar flares instead of GOES ones.

According to the RHESSI catalog, there are three detected times of the X-ray solar flares: start, maximum, and end times.

Our approach depends on these progressive timings of solar flares. The synthesized algorithm relies basically on the ratio index value (R_f) between the time interval lasting from the flare’s start to maximum time divided by the total duration of the flare. This value is estimated according to the following formula:

R_f = T₁/(T₁ + T₂),

(1)

where R_f is the ratio index value, T₁ is the interval between the start and the maximum times of the X-ray solar flare, and T₂ is the interval between the maximum and the end times of the X-ray solar flare.

From Equation (1), the ratio’s value must lie between 0 and 1, and we define two cases. That is why our algorithm relies on dividing the flares into two types to represent these two cases.

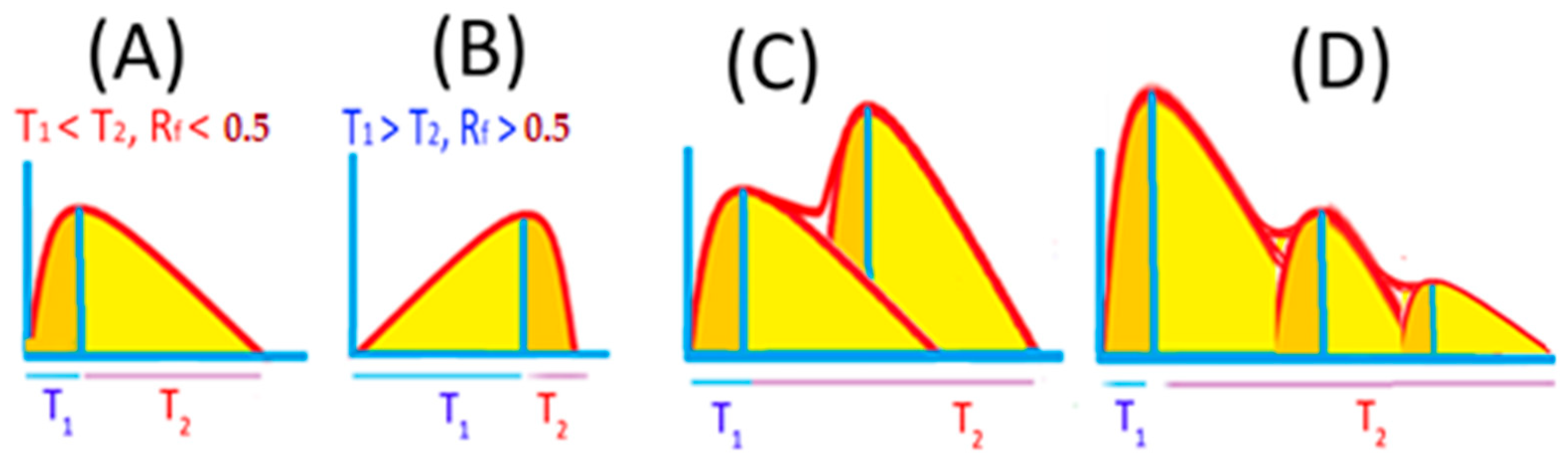
Case (1): T₁ < T₂ (rising rapidly and decaying gradually), then the ratio value is (R_f < 0.5). We call this case a “sudden flare”, in which the peak of the time profile curve is closer to the start time.

Case (2): T₁ > T₂ (rising gradually and decaying rapidly), then the ratio value is (R_f > 0.5). We call this case a “gradual flare”, in which the peak of the time profile curve is closer to the end time.

Figure 1A,B introduce a schematic diagram representing the two cases 1 and 2, respectively.

The solar flare’s time profile may have multiple peaks throughout its duration, as shown in Figure 1C,D. However, the time of the peak flux listed in the RHESSI catalog just corresponds to the highest peak of the detected multiple peaks. The current study took the first two cases only into account as an RHESSI catalog calculation of start, max, and end times.

Our method needs a comparison of the time profile of the solar flare with the solar activity. The number of solar cycles can be estimated from the knowledge of the solar flare’s time. The solar cycle number was estimated using the following equation, which was deduced from the linear fitting of the sunspot number (SSN) that was obtained from the Solar Influences Data Analysis Center (SIDC):

C = −157.43 + 0.090253 × D,

(2)

where C is the number of the solar cycle and D is the solar flare’s date as a floating number of the year including month, day, and time. For example, the value of D for the flare’s date: 26 April 1983, 16:07:00 is 1983.315063 and the corresponding value of C is 21.

3. Results and Discussions

3.1. The Types of the Flare’s Time Profile

During the period of study, 2002–2018, we considered about 120,524 solar flare events. From our analysis by applying Equation (1) and performing the algorithm, we have two types of flares according to their time profile morphology, which is shown previously in Figure 1. These types are:

(1)

Sudden flares, T₁ < T₂ [i.e., R_f < 0.5], seem to be rising rapidly more than decaying, which is the most common case and represents most of the flares that happened during most years of the solar cycles, except for the period of the minimum activity.

(2)

Gradual flares, T₁ > T₂ [i.e., R_f > 0.5], are countable and more common during the solar cycle’s minimum activity years, with their profiles rising gradually and taking longer to decay.

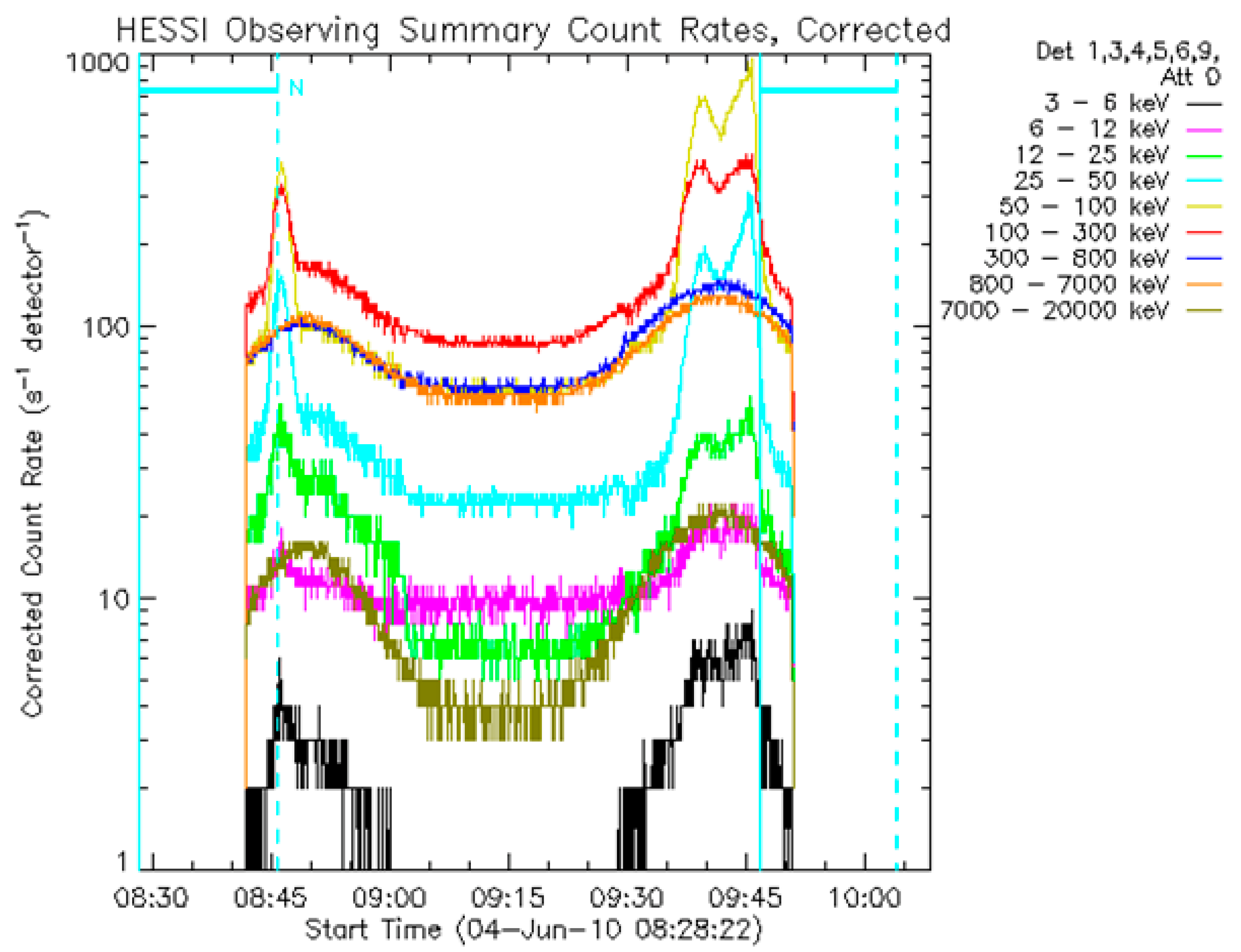
An example of the sudden flare (R_f < 0.5) and another one for the gradual flare (R_f > 0.5) are shown in Figure 2. Obviously, both types of solar flare happened on the same day, 4 June 2010. The first event was a sudden flare that started at about 08:45 GMT, while the second one was gradual and started at about 09:30 GMT. The different colors of the time profiles refer to the detected energy bands.

3.2. The Impact of Solar Activity

During our period of study, we have found that the total number of sudden flares is about 87,582 events, while that of the gradual ones is about 32,942 events, according to

Table 1. Several sudden and gradual flares were detected in SC 23 and SC 24.

Cycle	Sudden Flare (Rf < 0.5)	Gradual Flare (Rf > 0.5)
23	37,857	14,371
24	49,725	18,571

. Most of these gradual ones happened in the years 2008 and 2009 (the end of SC23 and the beginning of SC24). This indicates that the gradual flare type predominates during the minimum solar activity.

During the period of study (2002–2018), we considered about 120,524 solar flare events. From our analysis by applying Equation (1) and performing the algorithm, we have two types of flares according to their time profile morphology which is shown previously in Figure 1 (see Table 1). These types are:

Table 2. The time profile parameters of the RHESSI solar flares during the period 2002–2018.

Year	Duration (Min.)	T1 (Min.)	T2 (Min.)	Ratio, Rf
2002	8.65	3.17	5.48	0.38
2003	8.74	3.25	5.49	0.38
2004	8.22	3.01	5.22	0.38
2005	8.51	2.93	5.59	0.37
2006	7.59	2.63	4.96	0.38
2007	7.06	2.45	4.61	0.42
2008	4.82	2.08	2.74	0.58
2009	5.6	2.25	3.35	0.51
2010	7.04	2.29	4.74	0.35
2011	7.86	2.72	5.14	0.35
2012	8.01	2.82	5.19	0.36
2013	7.84	2.7	5.14	0.35
2014	8.46	3.01	5.46	0.36
2015	7.99	2.75	5.24	0.35
2016	7.68	2.46	5.22	0.34
2017	8.81	2.92	5.89	0.33
2018	7.04	2.57	4.47	0.41

presents the annual mean values of the duration, the rise and decay interval times of the solar flares, in addition to their ratio parameter, the R_f index. This table implies that the shorter-duration flares that seem to have greater values of the ratio index are most probable to occur during low solar activity (years 2007, 2008, 2009, and 2018). Meanwhile, the longer flares, having smaller ratio values, seem to be dominant through the high activity epochs.

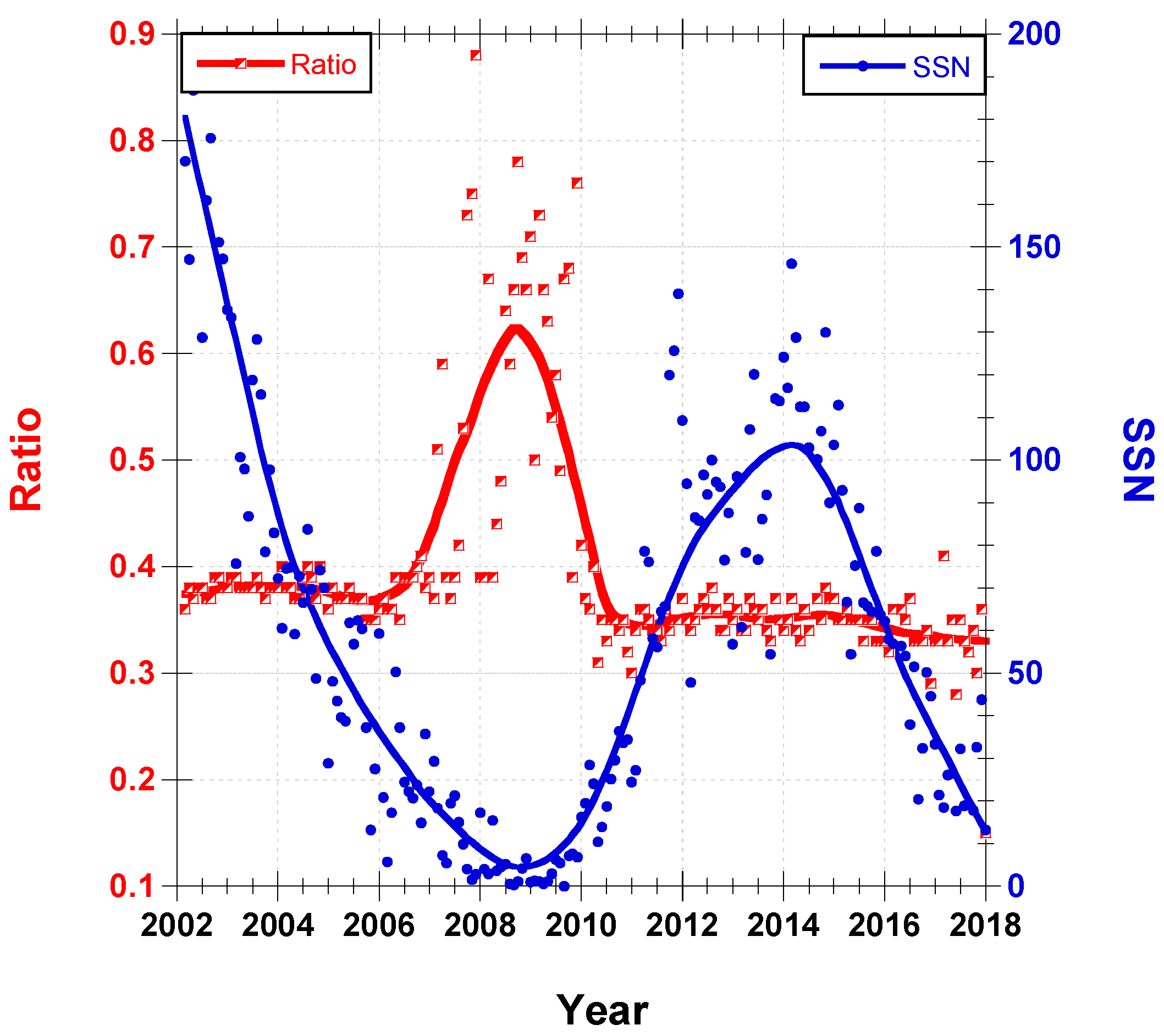
For a good investigation, it is preferable to show the time variation of ratios with the sunspot number (R_f—SSN). Figure 3 presents this comparison. There is no doubt that both solar flares and sunspots have similar quasi-periodic features because they have an intrinsic link with the solar magnetic field [29]. The ratio index is a function of the strength of the solar cycle, in which the ratio index decreases during strong epochs of solar activity. Whereas they have large values with weak activity times. In other words, this inverse correlation between the solar activity and the flare’s ratio index makes the sudden flare type, having a ratio index of less than 0.5, dominant during the maximum solar activity while the gradual flare type, having ratio values greater than 0.5, predominates during the weak solar activity years.

The monthly mean values of the ratios drawn in Figure 3 emphasize the strong link with the strength of the solar activity, which is most likely to be an inverse correlation.

Suppressed sudden flares are considered to be evolving in longer loops so that the decay time is longer than the rising time, and this is compatible with [30], who concluded that the events with longer decay times should have a larger separation of flare ribbons, i.e., evolve in longer loops. In other words, the longer decay time flares, sudden flares according to our criteria, are large. Whereas the gradual flares, having short decay times, are small ones. 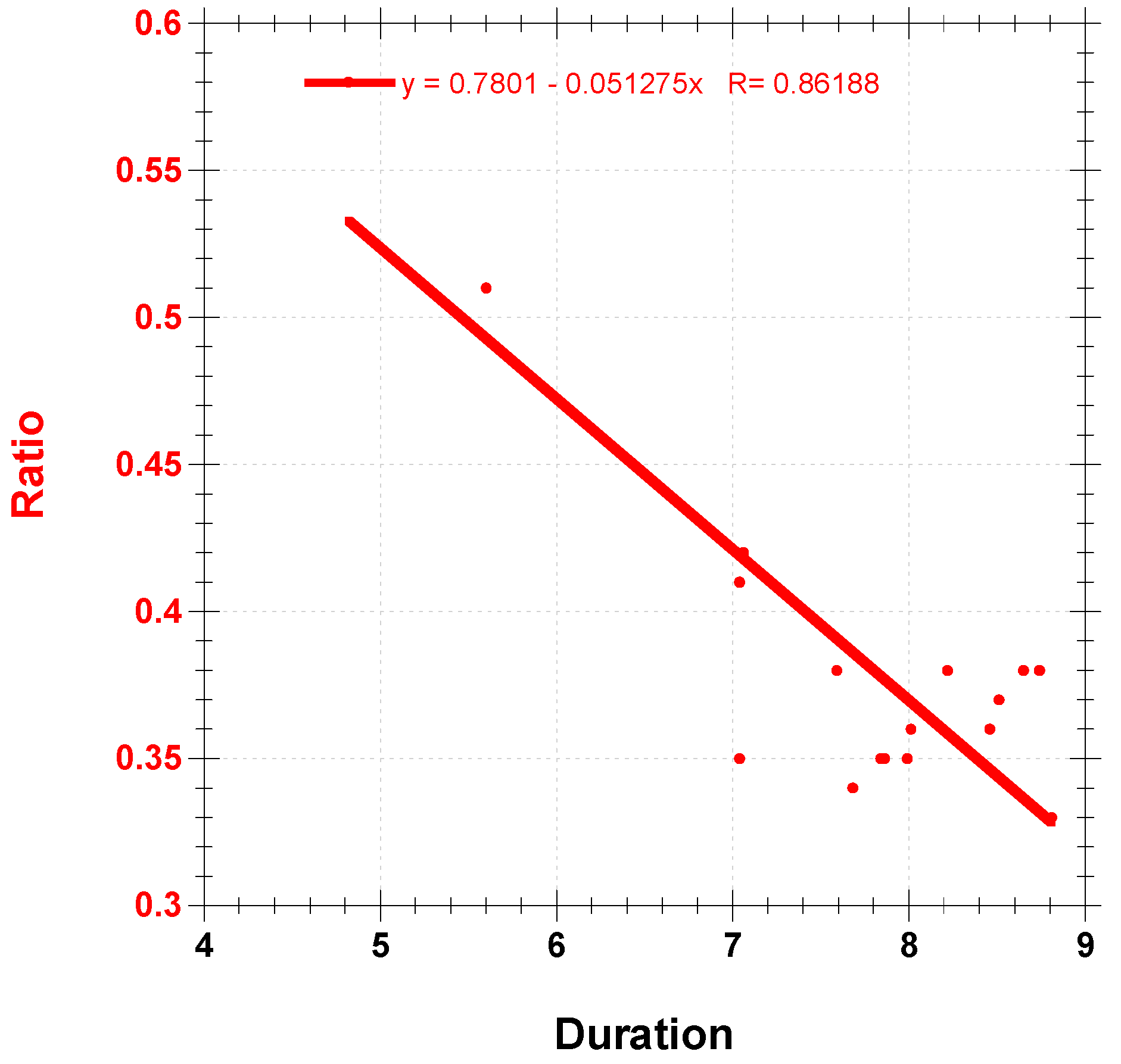Figure 4 confirms the prior interpretation since it shows the duration is inversely dependent on the flare’s ratio index. The gradual flares that increased during the years of low activity, 2008 and 2009, are typical of short duration.

3.3. Heliographical Distribution of the Flare Ratio

The heliographical distribution of the flare’s ratio index has been examined during the current period of study (2002–2018). To a large extent, the flare’s ratio index depends on its heliographical location as shown in Figure 5. The gradual flares tend to be highly concentrated within about ±(50°–70°) of latitude. While sudden flares are more prevalent in polar locations or at high latitudes ±(80°–90°). In addition, the equatorial region is characterized by the existence of both types. Further, there is no clear correlation with the longitudes.

4. Conclusions

The synthesis of the solar flare’s ratio index R_f for about 120524 detected RHESSI X-ray flares during the period 2002–2018, or almost the second half of SC 23 and SC 24, permits the classification of the flare’s time profiles morphologically. This index is obtained by getting the ratio of the rising time, which is the interval between the flare onset time and its peak time, by its total duration time. The study exhibits unexpected behavior during the weak and strong solar activity epochs. A study of this dramatic change in the ratio can reveal not-yet-known aspects of solar activity, the solar cycle, and solar flares.

The ratio of solar flares permits their classification into mainly two types according to the value of the ratio index as follows:

(1)

Sudden flares occur when R_f < 0.5 and appear to be rising rapidly more than decaying, which is the dominant case and accounts for the majority of flares that occur throughout the solar cycle and predominate away from low activity periods.

(2)

Gradual flares occur when R_f > 0.5 and are countable and more common during low solar activity years, with profiles such that they rise gradually taking more time than that for decaying.

We found that the number of sudden flares is about 37,857 and 49,725 events in SC 23 and SC 24, respectively. While the gradual flares are about 14,371 and 18,571 events in SC 23 and SC 24 respectively. The sudden flares are the common ones and tend to predominate during the maximum activity of the solar cycles. On the other hand, gradual flares are less common but tend to intensify during the years of minimum solar activity. However, both types may exist on the same day.

The relationship between the ratio index and solar activity was based on the inverse correlation between the monthly mean ratio index and that of SSN, which represents solar activity.

Further, according to the heliographic distribution of the flares within the period of study, we conclude that the number of gradual flares tends to be valuable within latitudes ±(50°–70°). Whereas the sudden fares tend to be more detectable within latitudes ±(80°–90°).

We believe that the flare’s ratio R_f is a significant index representing some aspects of the flare’s physical properties. It reflects the strength of the solar flare and its duration. It gives feedback about the X-ray emission from other sources rather than the solar flare itself.

In general, the gradual flares are expected to be small flares with a short duration, while the sudden flares are expected to be large ones with a long duration. The flare’s ratio index inversely correlates with the flare’s emissions. In other words, strong solar flares tend to be sudden, whereas weak ones are most likely to be gradual.

Additionally, according to the prior, we think that the recent work is important because of the following:

(1)

The comparison of the duration of rising time to the duration of recovering time shows how abrupt energy production is.

(2)

The observed lengthening of rising time during the last two solar cycles is a sign of a very drastic change in the energy production of flares that can help theory give better insight into the mechanisms of production.

In the end, we see that the study of flare ratio is important for understanding solar flares. For instance, it was found that this ratio index has an inverse correlation with solar activity, SSN. It was also found that the heliographical locations of solar flares are also related to this ratio. This new information may lead solar physicists to revise their views about the physical mechanisms behind each of the presented types of flares according to their sizes, strengths, and heliographical locations in a way that has not been studied before.