Analogue Non-Causal Null Curves and Chronology Protection in a dc-SQUID Array
Abstract
:1. Introduction
2. Simulator
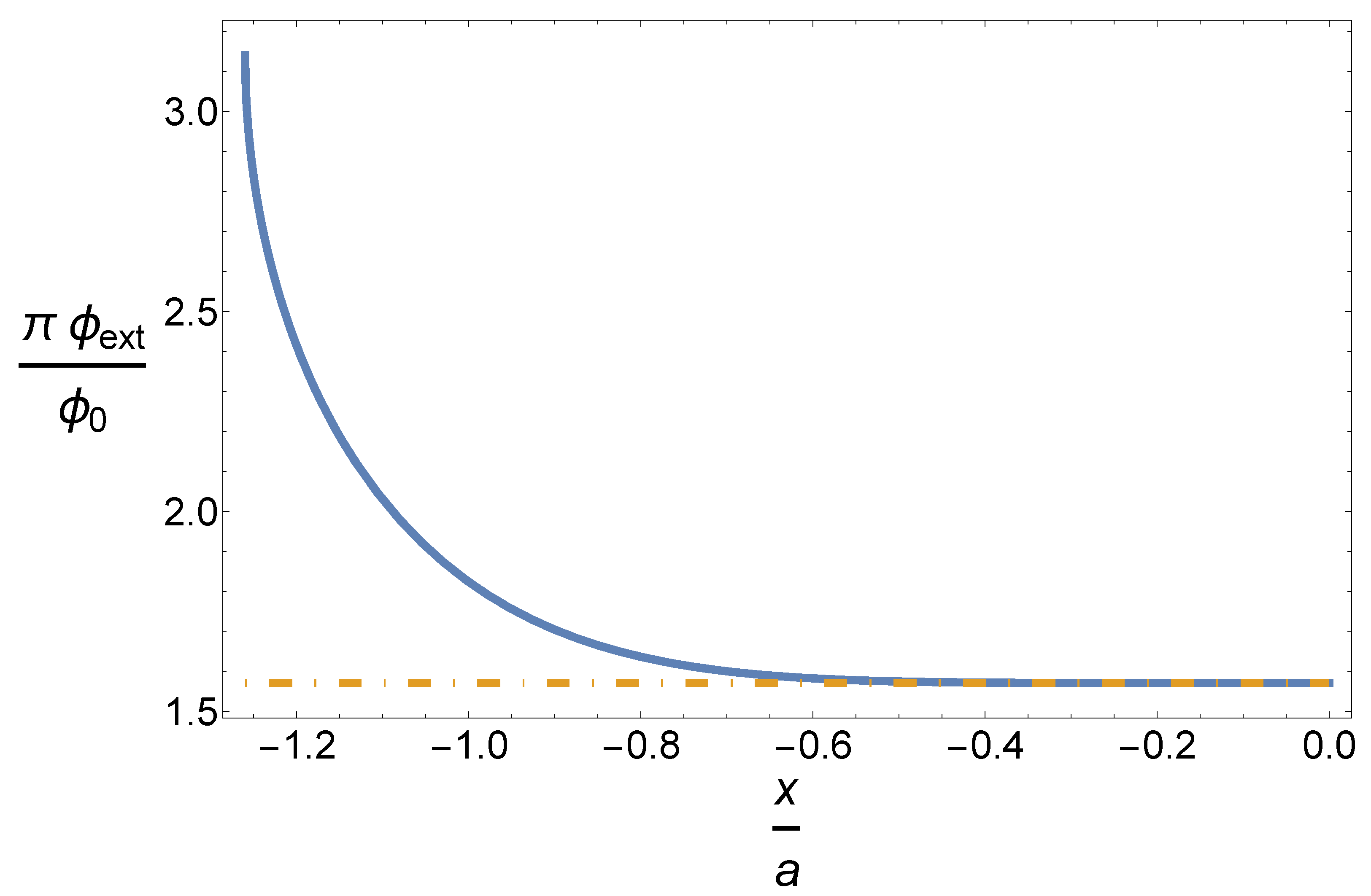
3. A Spacetime with Non-Causal Null Geodesics
4. Analogue Quantum Simulation of a Spacetime with Non-Causal Null Geodesics
5. Summary and Conclusions
Funding
Conflicts of Interest
References
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, Time Machines, and the Weak Energy Condition. Phys. Rev. Lett. 1988, 61, 1446–1449. [Google Scholar] [CrossRef] [PubMed]
- Thome, K.S. Closed timelike curves. In General Relativity and Gravitation; IOP Publishing: Bristol, UK, 1993; pp. 295–315. [Google Scholar]
- Hawking, S.W. Chronology protection conjecture. Phys. Rev. D 1992, 46, 603–611. [Google Scholar] [CrossRef] [PubMed]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar] [CrossRef]
- Barceló, C.; Liberati, S.; Visser, M. Analogue gravity. Living Rev. Relativ. 2011, 14, 3. [Google Scholar] [CrossRef] [PubMed]
- Greenleaf, A.; Kurylev, Y.; Lassas, M.; Uhlmann, G. Electromagnetic Wormholes and Virtual Magnetic Monopoles from Metamaterials. Phys. Rev. Lett. 2007, 99, 183901. [Google Scholar] [CrossRef]
- Peloquin, C.; Euvé, L.P.; Philbin, T.; Rousseaux, G. Analog wormholes and black hole laser effects in hydrodynamics. Phys. Rev. D 2016, 93, 084032. [Google Scholar] [CrossRef]
- Prat-Camps, J.; Navau, C.; Sanchez, A. A Magnetic Wormhole. Sci. Rep. 2015, 5, 12488. [Google Scholar] [CrossRef]
- Clerici, M.; Spalding, G.C.; Warburton, R.; Lyons, A.; Aniculaesei, C.; Richards, J.M.; Leach, J.; Henderson, R.; Faccio, D. Observation of image pair creation and annihilation from superluminal scattering sources. Sci. Adv. 2016, 2, e1501691. [Google Scholar] [CrossRef]
- Philbin, T.G.; Kuklewicz, C.; Robertson, S.; Hill, S.; König, F.K.; Leonhardt, U. Fiber-Optical Analog of the Event Horizon. Science 2008, 319, 1367. [Google Scholar] [CrossRef]
- Steinahuer, J. Observation of quantum Hawking radiation and its entanglement in an analogue black hole. Nat. Phys. 2016, 12, 959. [Google Scholar] [CrossRef] [Green Version]
- Nation, P.D.; Johansson, J.R.; Blencowe, M.P.; Nori, F. Colloquium: Stimulating uncertainty: Amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 2012, 84, 1–24. [Google Scholar] [CrossRef]
- Nation, P.D.; Blencowe, M.P.; Rimberg, A.J.; Buks, E. Analogue Hawking Radiation in a dc-SQUID Array Transmission Line. Phys. Rev. Lett. 2009, 103, 087004. [Google Scholar] [CrossRef] [PubMed]
- Acquaviva, G.; Iorio, A.; Pais, P.; Smaldone, L. Hunting Quantum Gravity with Analogs: The case of graphene. arXiv 2022, arXiv:2207.04097. [Google Scholar] [CrossRef]
- Mateos, J.; Sabín, C. Quantum simulation of traversable wormhole spacetimes in a Bose–Einstein condensate. Phys. Rev. D 2018, 97, 044045. [Google Scholar] [CrossRef]
- Sabín, C. Quantum simulation of traversable wormhole spacetimes in a dc-SQUID array. Phys. Rev. D 2016, 94, 081501. [Google Scholar] [CrossRef]
- Martín-Vázquez, G.; Sabín, C. Closed timelike curves and chronology protection in quantum and classical simulators. Class. Quantum Gravity 2020, 37, 045013. [Google Scholar] [CrossRef]
- Sabín, C. One-dimensional sections of exotic spacetimes with superconducting circuits. N. J. Phys. 2018, 20, 053028. [Google Scholar] [CrossRef]
- Barceló, C.; Eguia Sánchez, J.; García-Moreno, G.; Jannes, G. Chronology protection implementation in analogue gravity. Eur. Phys. J. C 2022, 82, 299. [Google Scholar] [CrossRef]
- Lähteenmäki, P.; Paraoanu, G.S.; Hassel, J.; Hakonen, P.J. Dynamical Casimir effect in a Josephson metamaterial. Proc. Natl. Acad. Sci. USA 2013, 110, 4234–4238. [Google Scholar] [CrossRef]
- Haviland, D.B.; Andersson, K.; Ågren, P. Superconducting and Insulating Behavior in One-Dimensional Josephson Junction Arrays. J. Low Temp. Phys. 2000, 118, 733–749. [Google Scholar] [CrossRef]
- Watanabe, M.; Haviland, D.B. Quantum effects in small-capacitance single Josephson junctions. Phys. Rev. B 2003, 67, 094505. [Google Scholar] [CrossRef]
- Ergül, A.; Schaeffer, D.; Lindblom, M.; Haviland, D.B.; Lidmar, J.; Johansson, J. Phase sticking in one-dimensional Josephson junction chains. Phys. Rev. B 2013, 88, 104501. [Google Scholar] [CrossRef]
- Simoen, M. Parametric Interactions with Signals and the Vacuum. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2015. [Google Scholar]
- You, J.Q.; Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 2011, 474, 589–597. [Google Scholar] [CrossRef] [PubMed]
- Collas, P. General relativity in two-and three-dimensional space–times. Am. J. Phys. 1977, 45, 833–837. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabín, C. Analogue Non-Causal Null Curves and Chronology Protection in a dc-SQUID Array. Universe 2022, 8, 452. https://doi.org/10.3390/universe8090452
Sabín C. Analogue Non-Causal Null Curves and Chronology Protection in a dc-SQUID Array. Universe. 2022; 8(9):452. https://doi.org/10.3390/universe8090452
Chicago/Turabian StyleSabín, Carlos. 2022. "Analogue Non-Causal Null Curves and Chronology Protection in a dc-SQUID Array" Universe 8, no. 9: 452. https://doi.org/10.3390/universe8090452
APA StyleSabín, C. (2022). Analogue Non-Causal Null Curves and Chronology Protection in a dc-SQUID Array. Universe, 8(9), 452. https://doi.org/10.3390/universe8090452







