Construction and Evolution of Equilibrium Configurations of the Schrödinger–Poisson System in the Madelung Frame
Abstract
:1. Introduction
2. Madelung Transform
2.1. Diagnostics
2.2. Ground State Equilibrium Configurations in the SP Frame
2.3. Ground State Equilibrium Configuration in the Madelung Frame
3. Evolution
3.1. Evolution in the SP Frame
3.2. Methods for the Madelung Frame
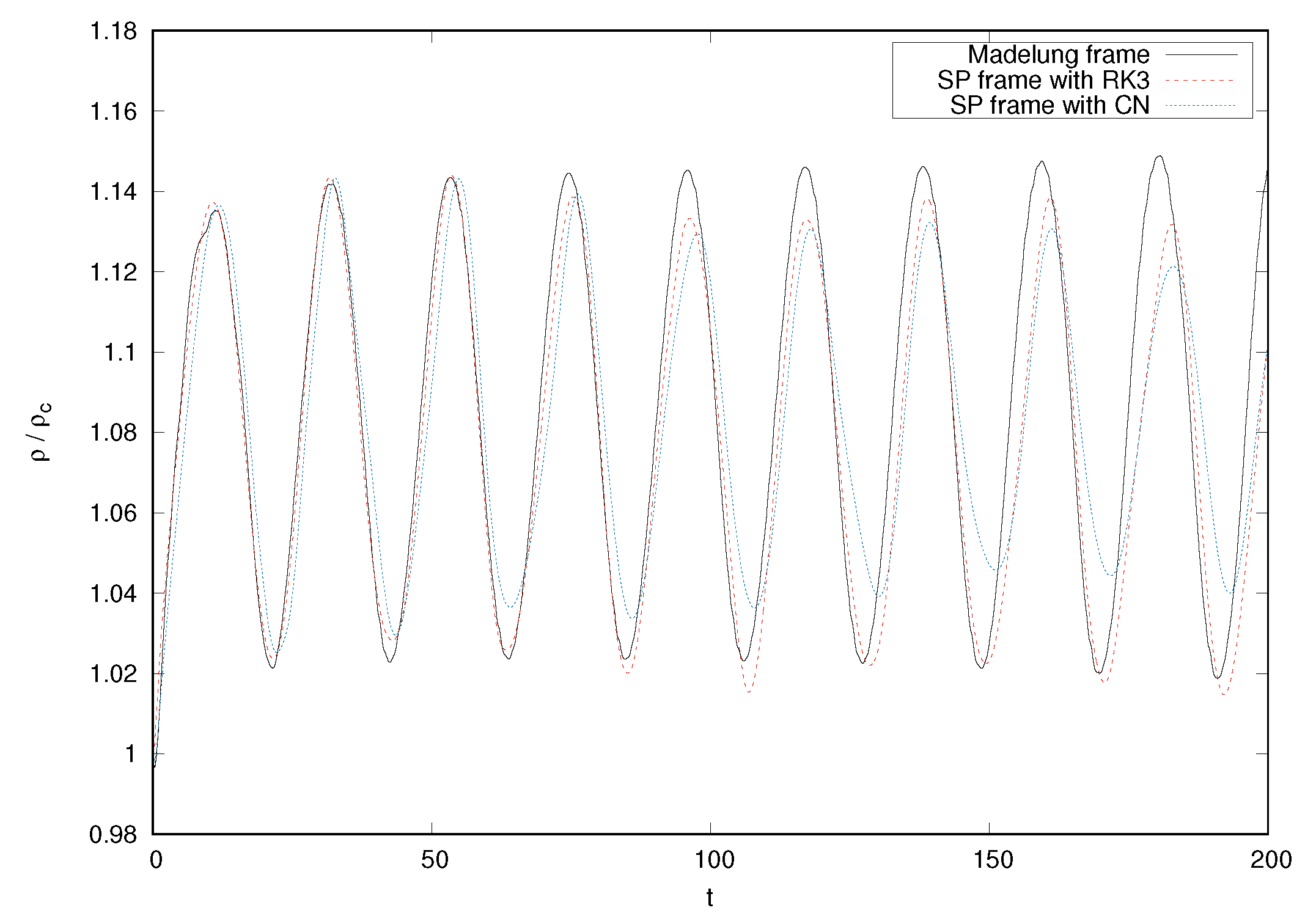
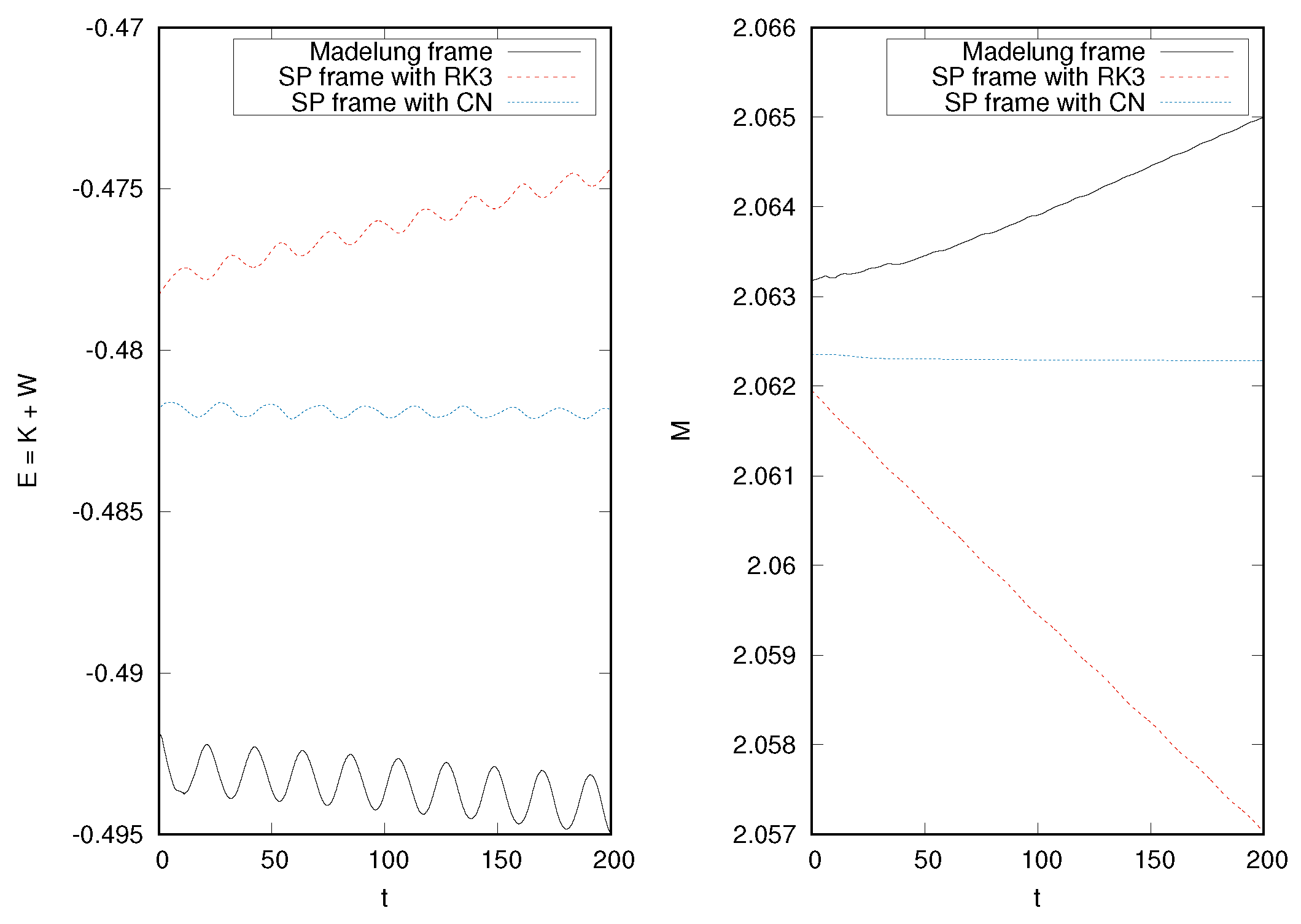
3.3. Evolution of an Equilibrium Configuration
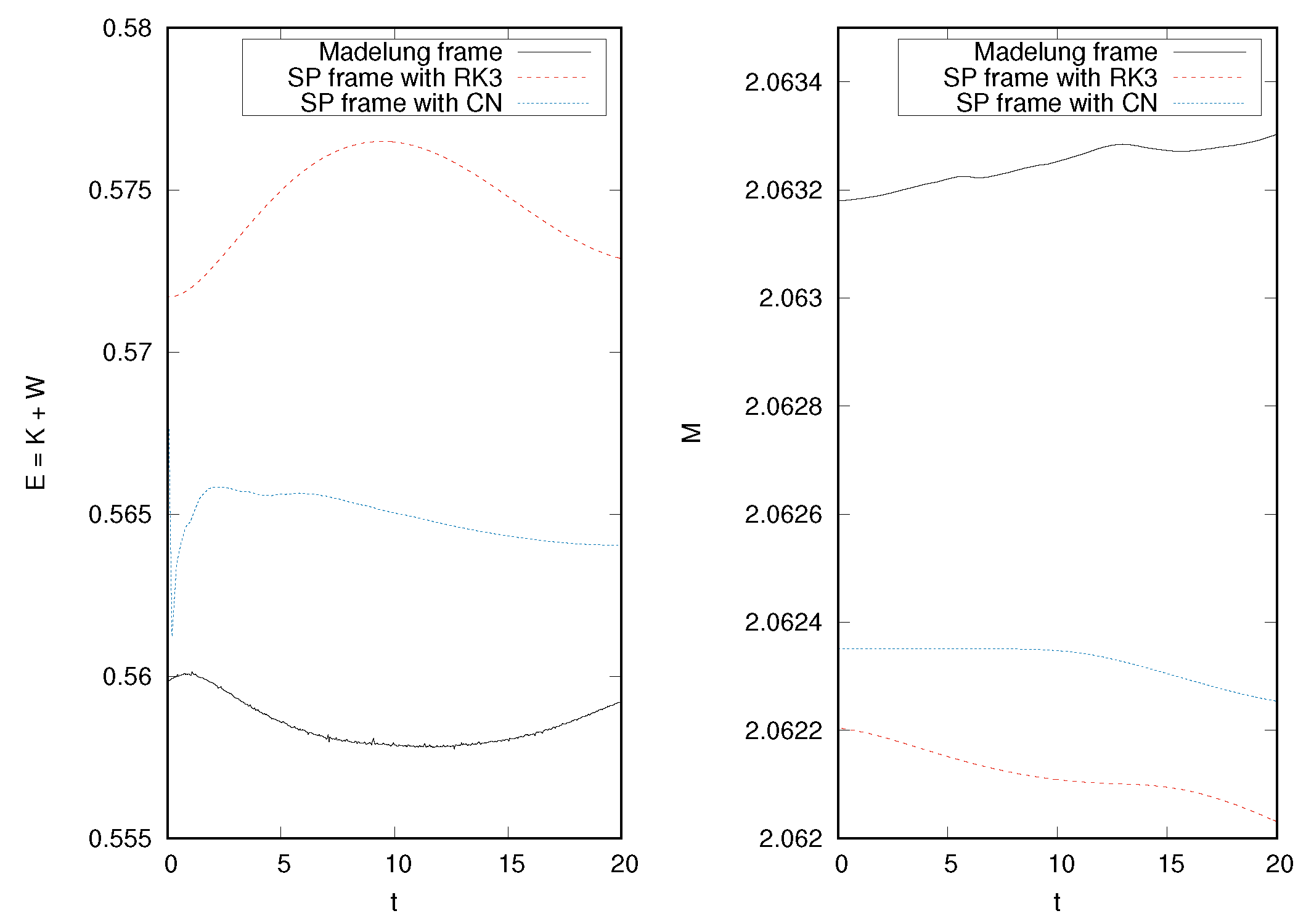
3.4. Boosted Equilibrium Configuration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matos, T.; Ureña-López, L.A. Quintessence and scalar dark matter in the Universe. Class. Quantum Grav. 2000, 17, L75–L81. [Google Scholar] [CrossRef] [Green Version]
- Sahni, V.; Wang, L. New cosmological model of quintessence and dark matter. Phys. Rev. D 2000, 62, 103517. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Barkana, R.; Gruzinov, A. Fuzzy Cold Dark Matter: The Wave Properties of Ultralight Particles. Phys. Rev. Lett. 2000, 85, 1158–1161. [Google Scholar] [CrossRef] [Green Version]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef] [Green Version]
- Schive, H.Y.; Chiueh, T.; Broadhurst, T. Cosmic Structure as the Quantum Interference of a Coherent Dark Wave. Nat. Phys. 2014, 10, 496–499. [Google Scholar] [CrossRef]
- Mocz, P.; Vogelsberger, M.; Robles, V.H.; Zavala, J.; Boylan-Kolchin, M.; Fialkov, A.; Hernquist, L. Galaxy formation with BECDM I. Turbulence and relaxation of idealized haloes. Mon. Not. R. Astron. Soc. 2017, 471, 4559–4570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruffini, R.; Bonazzola, S. Systems of Self-Gravitating Particles in General Relativity and the Concept of an Equation of State. Phys. Rev. 1969, 187, 1767–1783. [Google Scholar] [CrossRef] [Green Version]
- Guzmán, F.S.; Ureña López, L.A. Evolution of the Schrödinger-Newton system for a self-gravitating scalar field. Phys. Rev. D 2004, 69, 124033. [Google Scholar] [CrossRef] [Green Version]
- Guzmán, F.S.; Ureña López, L.A. Gravitational Cooling of Self?gravitating Bose Condensates. Astrophys. J. 2006, 645, 814. [Google Scholar] [CrossRef] [Green Version]
- Bernal, A.; Guzmán, F.S. Scalar field dark matter: Nonspherical collapse and late-time behavior. Phys. Rev. D 2006, 74, 063504. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Liu, H.; Chu, M.C. Cosmological Simulation for Fuzzy Dark Matter Model. Front. Astron. Space Sci. 2019, 5, 48. [Google Scholar] [CrossRef] [Green Version]
- Niemeyer, J.C. Small-scale structure of fuzzy and axion-like dark matter. Prog. Part. Nucl. Phys. 2020, 113, 103787. [Google Scholar] [CrossRef] [Green Version]
- Madelung, E. Quantentheorie in hydrodynamischer Form. Z. Fur Phys. 1927, 40, 322–326. [Google Scholar] [CrossRef]
- Chavanis, P.H. Mass-radius relation of Newtonian self-gravitating Bose-Einstein condensates with short-range interactions. I. Analytical results. Phys. Rev. D 2011, 84, 043531. [Google Scholar] [CrossRef] [Green Version]
- Woo, T.P.; Chiueh, T. High-Resolution Simulation on Structure Formation with Extremely Light Bosonic Dark Matter. Astrophys. J. 2009, 697, 850–861. [Google Scholar] [CrossRef] [Green Version]
- Guzmán, F.S. Oscillation modes of ultralight BEC dark matter cores. Phys. Rev. D 2019, 99, 083513. [Google Scholar] [CrossRef] [Green Version]
- Bernal, A.; Guzmán, F.S. Scalar field dark matter: Head-on interaction between two structures. Phys. Rev. D 2006, 74, 103002. [Google Scholar] [CrossRef] [Green Version]
- Mocz, P.; Fialkov, A.; Vogelsberger, M.; Becerra, F.; Amin, M.A.; Bose, S.; Boylan-Kolchin, M.; Chavanis, P.H.; Hernquist, L.; Lancaster, L.; et al. First Star-Forming Structures in Fuzzy Cosmic Filaments. Phys. Rev. Lett. 2019, 123, 141301. [Google Scholar] [CrossRef]
- Schwabe, B.; Niemeyer, J.C. Deep Zoom-In Simulation of a Fuzzy Dark Matter Galactic Halo. Phys. Rev. Lett. 2022, 128, 181301. [Google Scholar] [CrossRef]
- Schwabe, B.; Niemeyer, J.C.; Engels, J.F. Simulations of solitonic core mergers in ultralight axion dark matter cosmologies. Phys. Rev. D 2016, 94, 043513. [Google Scholar] [CrossRef] [Green Version]
- Du, X.; Schwabe, B.; Niemeyer, J.C.; Bürger, D. Tidal disruption of fuzzy dark matter subhalo cores. Phys. Rev. D 2018, 97, 063507. [Google Scholar] [CrossRef] [Green Version]
- Dawoodbhoy, T.; Shapiro, P.R.; Rindler-Daller, T. Core-envelope haloes in scalar field dark matter with repulsive self-interaction: Fluid dynamics beyond the de Broglie wavelength. Mon. Not. R. Astron. Soc. 2021, 506, 2418. [Google Scholar] [CrossRef]
- Schobesberger, S.O.; Rindler-Daller, T.; Shapiro, P.R. Angular momentum and the absence of vortices in the cores of fuzzy dark matter haloes. Mon. Not. R. Astron. Soc. 2021, 505, 802–829. [Google Scholar] [CrossRef]
- Li, X.; Hui, L.; Yavetz, T.D. Oscillations and random walk of the soliton core in a fuzzy dark matter halo. Phys. Rev. D 2021, 103, 023508. [Google Scholar] [CrossRef]
- Shapiro, P.R.; Dawoodbhoy, T.; Rindler-Daller, T. Cosmological structure formation in scalar field dark matter with repulsive self-interaction: The incredible shrinking Jeans mass. Mon. Not. R. Astron. Soc. 2021, 509, 145. [Google Scholar] [CrossRef]
- Maleki, A.; Baghram, S.; Rahvar, S. Investigation of two colliding solitonic cores in fuzzy dark matter models. Phys. Rev. D 2020, 101, 023508. [Google Scholar] [CrossRef] [Green Version]
- Mocz, P.; Succi, S. Numerical solution of the nonlinear Schrödinger equation using smoothed-particle hydrodynamics. Phys. Rev. E 2015, 91, 053304. [Google Scholar] [CrossRef] [Green Version]
- Mocz, P.; Lancaster, L.; Fialkov, A.; Becerra, F.; Chavanis, P.H. Schrödinger-Poisson-Vlasov-Poisson correspondence. Phys. Rev. D 2018, 97, 083519. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Hui, L.; Bryan, G.L. Numerical and perturbative computations of the fuzzy dark matter model. Phys. Rev. D 2019, 99, 063509. [Google Scholar] [CrossRef] [Green Version]
- Chavanis, P.H. Predictive model of BEC dark matter halos with a solitonic core and an isothermal atmosphere. Phys. Rev. D 2019, 100, 083022. [Google Scholar] [CrossRef] [Green Version]
- Guzmán, F.S.; Alvarez-Ríos, I.; González, J.A. Merger of galactic cores made of ultralight bosonic dark matter. Rev. Mex. Fis. 2021, 67, 75–83. [Google Scholar] [CrossRef]
- Guzmán, F.S.; Lora-Clavijo, F.D.; González-Avilés, J.J.; Rivera-Paleo, F.J. Rotation curves of rotating Galactic Bose-Einstein condensate dark matter halos. Phys. Rev. D 2014, 89, 063507. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.T.; Yeh, J.Y.; Chen, J.Y. High resolution finite volume scheme for the quantum hydrodynamic equations. J. Comput. Phys. 2009, 228, 1713–1732. [Google Scholar] [CrossRef]
- Thomas, J. Numerical Partial Differential Equations: Conservation Laws and Elliptic Equations; Texts in Applied Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Hopkins, P.F. A stable finite-volume method for scalar field dark matter. Mon. Not. R. Astron. Soc. 2019, 489, 2367–2376. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarez-Ríos, I.; Guzmán, F.S. Construction and Evolution of Equilibrium Configurations of the Schrödinger–Poisson System in the Madelung Frame. Universe 2022, 8, 432. https://doi.org/10.3390/universe8080432
Alvarez-Ríos I, Guzmán FS. Construction and Evolution of Equilibrium Configurations of the Schrödinger–Poisson System in the Madelung Frame. Universe. 2022; 8(8):432. https://doi.org/10.3390/universe8080432
Chicago/Turabian StyleAlvarez-Ríos, Iván, and Francisco S. Guzmán. 2022. "Construction and Evolution of Equilibrium Configurations of the Schrödinger–Poisson System in the Madelung Frame" Universe 8, no. 8: 432. https://doi.org/10.3390/universe8080432
APA StyleAlvarez-Ríos, I., & Guzmán, F. S. (2022). Construction and Evolution of Equilibrium Configurations of the Schrödinger–Poisson System in the Madelung Frame. Universe, 8(8), 432. https://doi.org/10.3390/universe8080432





