The Hubble Diagram: Jump from Supernovae to Gamma-ray Bursts
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Hubble Diagram as a Basic Cosmological Test
2.2. Gamma-ray Bursts as Standard Candles
- is the rest frame spectral peak energy, where is the observed spectrum peak energy;
- is the isotropic equivalent radiated energy in gamma-rays [36]. The distance and observed integral fluence are determined as quantities transferred per a unit energy frame area and that are corrected for the instrumental (observed) spectral energy range, and source redshift. The correction is performed by the equationwhere is the observed fluence, and is the instrumental spectral energy range, which is for the Swift’s BAT instrument;
- a and b are the Amati relation parameters mentioned above that can be calibrated empirically as in this study.
2.3. Catalogues of SNe Ia and LGRBs
2.4. Monte-Carlo Uncertainty Propagation
2.5. Best-Fitting Methods
- are observed table values;
- is error of i-th value;
- f is the model function and are the parameters.
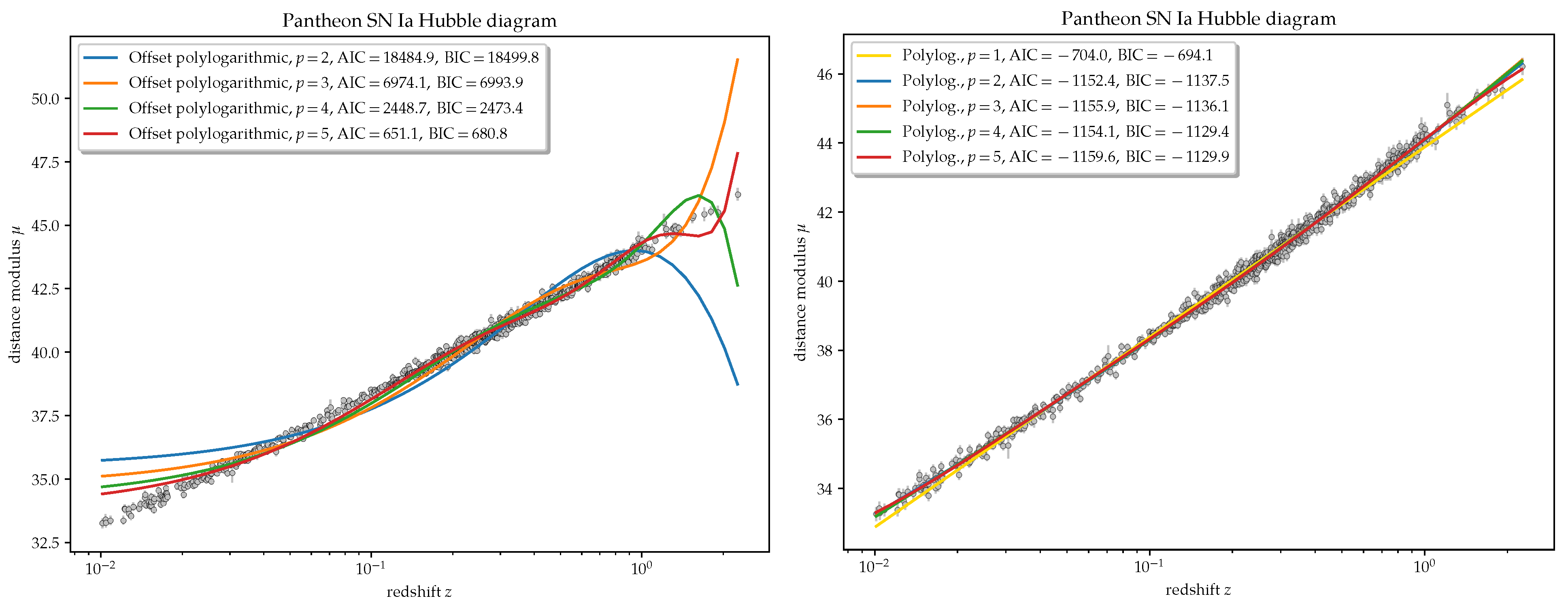
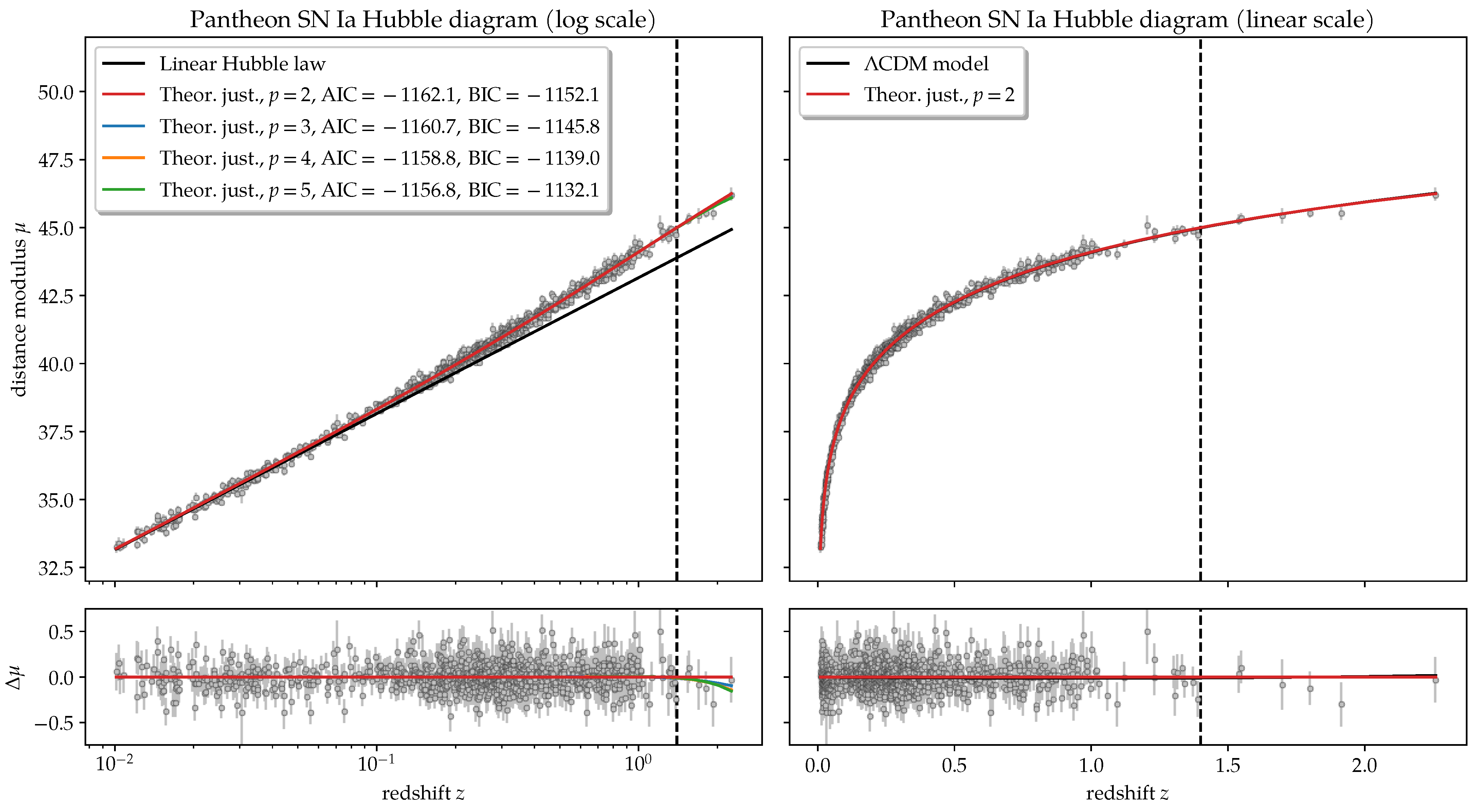
2.6. Interpolation Function of the SN HD
- Theoretically-inspired function
- Simple polylogarithmic function
- Shifted polylogarithmic function
3. Results
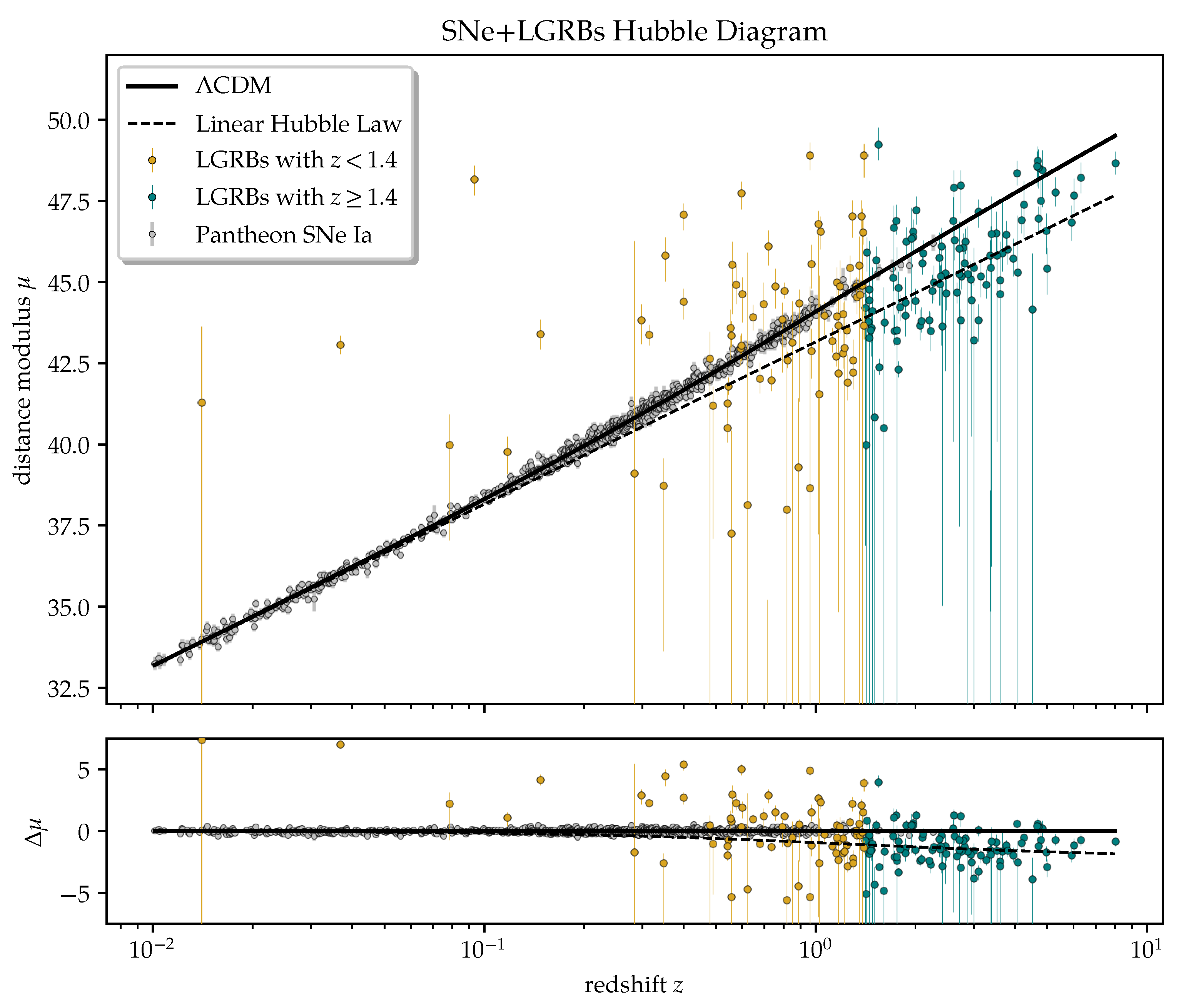
3.1. Approximation of the SN HD
3.2. Amati Relation Parameters Probing and Gamma-ray Bursts Hubble Diagram
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LGRB(s) | Long Gamma-ray Burst(s) |
| HD | Hubble Diagram |
| FLRW | Friedmann–Lemaitre–Robertson–Walker |
| SCM | Standard Cosmological Model |
| ΛCDM | Λ Cold Dark Matter |
| SN(e) | Supernova(e) |
| SC(s) | Standard Candle(s) |
References
- Sandage, A. Astronomical problems for the next three decades. In The Universe at Large: Key Issues in Astronomy and Cosmology; Galindo, G.M., Antonio, M., Francisco, S., Eds.; Cambridge University Press: Cambridge, UK, 1997; pp. 1–63. [Google Scholar]
- Baryshev, Y.; Teerikorpi, P. Fundamental Questions of Practical Cosmology: Exploring the Realm of Galaxies. In Astrophysics and Space Science Library; Springer: Berlin, Germany, 2012; Volume 383. [Google Scholar] [CrossRef] [Green Version]
- Shirokov, S.I.; Sokolov, I.V.; Lovyagin, N.Y.; Amati, L.; Baryshev, Y.V.; Sokolov, V.V.; Gorokhov, V.L. High Redshift Long Gamma-ray Bursts Hubble Diagram as a Test of Basic Cosmological Relations. Mon. Not. R. Astron. Soc. 2020, 496, 1530–1544. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.; Nugent, P.; Castro, P.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.; Barreiro, R.; Bartolo, N.; Basak, S.; et al. Planck 2018 results-VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Anderson, J.; MacKenty, J.W.; Bowers, J.B.; Clubb, K.I.; Filippenko, A.V.; Jones, D.O.; et al. New parallaxes of galactic cepheids from spatially scanning the hubble space telescope: Implications for the hubble constant. Astrophys. J. 2018, 855, 136. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G. The expansion of the universe is faster than expected. Nat. Rev. Phys. 2020, 2, 10–12. [Google Scholar] [CrossRef] [Green Version]
- Yershov, V.N.; Raikov, A.A.; Lovyagin, N.Y.; Kuin, N.P.M.; Popova, E.A. Distant foreground and the Planck-derived Hubble constant. Mon. Not. R. Astron. Soc. 2020, 492, 5052–5056. [Google Scholar] [CrossRef]
- Amati, L.; O’Brien, P.; Götz, D.; Bozzo, E.; Tenzer, C.; Frontera, F.; Ghirlanda, G.; Labanti, C.; Osborne, J.P.; Stratta, G.; et al. The THESEUS space mission concept: Science case, design and expected performances. Adv. Space Res. 2018, 62, 191–244. [Google Scholar] [CrossRef] [Green Version]
- Stratta, G.; Ciolfi, R.; Amati, L.; Bozzo, E.; Ghirlanda, G.; Maiorano, E.; Nicastro, L.; Rossi, A.; Vinciguerra, S.; Frontera, F.; et al. THESEUS: A key space mission concept for Multi-Messenger Astrophysics. Adv. Space Res. 2018, 62, 662–682. [Google Scholar] [CrossRef] [Green Version]
- Cano, Z.; Wang, S.Q.; Dai, Z.G.; Wu, X.F. The observer’s guide to the gamma-ray burst supernova connection. Adv. Astron. 2017, 2017, 8929054. [Google Scholar] [CrossRef]
- Willingale, R.; Mészáros, P. Gamma-ray Bursts and Fast Transients. Space Sci. Rev. 2017, 207, 63–86. [Google Scholar] [CrossRef]
- Fraija, N.; Veres, P.; Beniamini, P.; Galvan-Gamez, A.; Metzger, B.; Duran, R.B.; Becerra, R. On the origin of the multi-GeV photons from the closest burst with intermediate luminosity: GRB 190829A. Astrophys. J. 2021, 918, 12. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; Montanari, E.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81–89. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Lazzati, D. The collimation-corrected gamma-ray burst energies correlate with the peak energy of their νFν spectrum. Astrophys. J. 2004, 616, 331. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Nava, L.; Ghisellini, G.; Firmani, C. Confirming the γ-ray burst spectral-energy correlations in the era of multiple time breaks. Astron. Astrophys. 2007, 466, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Amati, L.; Guidorzi, C.; Frontera, F.; Della Valle, M.; Finelli, F.; Landi, R.; Montanari, E. Measuring the cosmological parameters with the E p, i–E iso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2008, 391, 577–584. [Google Scholar] [CrossRef] [Green Version]
- Amati, L.; D’Agostino, R.; Luongo, O.; Muccino, M.; Tantalo, M. Addressing the circularity problem in the E p- E iso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. Lett. 2019, 486, L46–L51. [Google Scholar] [CrossRef] [Green Version]
- Demianski, M.; Piedipalumbo, E.; Sawant, D.; Amati, L. Cosmology with gamma-ray bursts-I. The Hubble diagram through the calibrated Ep, i–Eiso correlation. Astron. Astrophys. 2017, 598, A112. [Google Scholar] [CrossRef] [Green Version]
- Demianski, M.; Piedipalumbo, E.; Sawant, D.; Amati, L. Cosmology with gamma-ray bursts-II. Cosmography challenges and cosmological scenarios for the accelerated Universe. Astron. Astrophys. 2017, 598, A113. [Google Scholar] [CrossRef]
- Lusso, E.; Piedipalumbo, E.; Risaliti, G.; Paolillo, M.; Bisogni, S.; Nardini, E.; Amati, L. Tension with the flat ΛCDM model from a high redshift Hubble Diagram of supernovae, quasars and gamma-ray bursts. Astron. Astrophys. 2019, 628, L4. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Nakamura, T.; Yamazaki, R.; Inoue, A.; Ioka, K. Gamma-ray burst formation rate inferred from the spectral peak energy-peak luminosity relation. Astrophys. J. 2004, 609, 935. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.Y.; Qi, S.; Dai, Z.G. The updated luminosity correlations of gamma-ray bursts and cosmological implications. Mon. Not. R. Astron. Soc. 2011, 415, 3423–3433. [Google Scholar] [CrossRef]
- Wei, J.J.; Wu, X.F. Gamma-ray burst cosmology: Hubble diagram and star formation history. Int. J. Mod. Phys. D 2017, 26, 1730002. [Google Scholar] [CrossRef] [Green Version]
- Shirokov, S.I.; Baryshev, Y.V. A crucial test of the phantom closed cosmological model. Mon. Not. R. Astron. Soc. 2020, 499, L101–L104. [Google Scholar] [CrossRef]
- Shirokov, S.I.; Sokolov, I.V.; Vlasyuk, V.V.; Amati, L.; Sokolov, V.V.; Baryshev, Y.V. THESEUS–BTA cosmological tests using Multimessenger Gamma-ray Bursts observations. Astrophys. Bull. 2020, 75, 207–218. [Google Scholar] [CrossRef]
- Kodama, Y.; Yonetoku, D.; Murakami, T.; Tanabe, S.; Tsutsui, R.; Nakamura, T. Gamma-ray bursts in 1.8 < z < 5.6 suggest that the time variation of the dark energy is small. Mon. Not. R. Astron. Soc. Lett. 2008, 391, L1–L4. [Google Scholar] [CrossRef] [Green Version]
- Scolnic, D.M.; Jones, D.; Rest, A.; Pan, Y.; Chornock, R.; Foley, R.; Huber, M.; Kessler, R.; Narayan, G.; Riess, A.; et al. The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined pantheon sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Hubble, E. A relation between distance and radial velocity among extra-galactic nebulae. Proc. Natl. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Byrd, R.H.; Schnabel, R.B.; Shultz, G.A. A Trust Region Algorithm for Nonlinearly Constrained Optimization. SIAM J. Numer. Anal. 1987, 24, 1152–1170. [Google Scholar] [CrossRef] [Green Version]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Anderson, G. Error propagation by the Monte Carlo method in geochemical calculations. Geochim. Cosmochim. Acta 1976, 40, 1533–1538. [Google Scholar] [CrossRef]
- Albert, D.R. Monte Carlo Uncertainty Propagation with the NIST Uncertainty Machine. J. Chem. Educ. 2020, 97, 1491–1494. [Google Scholar] [CrossRef] [Green Version]
- Ajello, M.; Arimoto, M.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bhat, P.; Bissaldi, E.; Blandford, R.; et al. A decade of gamma-ray bursts observed by Fermi-LAT: The second GRB catalog. Astrophys. J. 2019, 878, 52. [Google Scholar] [CrossRef] [Green Version]
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE observations of gamma-ray burst spectra. I-Spectral diversity. Astrophys. J. 1993, 413, 281–292. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Wiseman, P.; Schady, P.; Bolmer, J.; Krühler, T.; Yates, R.; Greiner, J.; Fynbo, J. Evolution of the dust-to-metals ratio in high-redshift galaxies probed by GRB-DLAs. Astron. Astrophys. 2017, 599, A24. [Google Scholar] [CrossRef] [Green Version]
- Butler, N.R.; Kocevski, D. X-ray hardness evolution in GRB afterglows and flares: Late-time GRB activity without NH variations. Astrophys. J. 2007, 663, 407. [Google Scholar] [CrossRef]
- Veres, P.; Bhat, N.; Fraija, N.; Lesage, S. Fermi-GBM Observations of GRB 210812A: Signatures of a Million Solar Mass Gravitational Lens. Astrophys. J. Lett. 2021, 921, L30. [Google Scholar] [CrossRef]
- Baryshev, Y.V.; Bukhmastova, Y.L. Gravitational mesolensing by king objects and quasar-galaxy associations. arXiv 2002, arXiv:astro-ph/0206348. [Google Scholar]
- Raikov, A.; Orlov, V. Ultraluminous quasars as a gravitational mesolensing effect. Astrophys. Bull. 2016, 71, 151–154. [Google Scholar] [CrossRef]
- Raikov, A.; Lovyagin, N.; Yershov, V. Superluminous quasars and mesolensing. arXiv 2021, arXiv:2110.11353. [Google Scholar]
- Fraija, N.; Laskar, T.; Dichiara, S.; Beniamini, P.; Duran, R.B.; Dainotti, M.; Becerra, R. GRB Fermi-LAT afterglows: Explaining flares, breaks, and energetic photons. Astrophys. J. 2020, 905, 112. [Google Scholar] [CrossRef]
- Schutz, B.F. Determining the Hubble constant from gravitational wave observations. Nature 1986, 323, 310–311. [Google Scholar] [CrossRef] [Green Version]
- Holz, D.E.; Hughes, S.A. Using gravitational-wave standard sirens. Astrophys. J. 2005, 629, 15. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.; et al. A gravitational-wave standard siren measurement of the Hubble constant. arXiv 2017, arXiv:1710.05835. [Google Scholar]
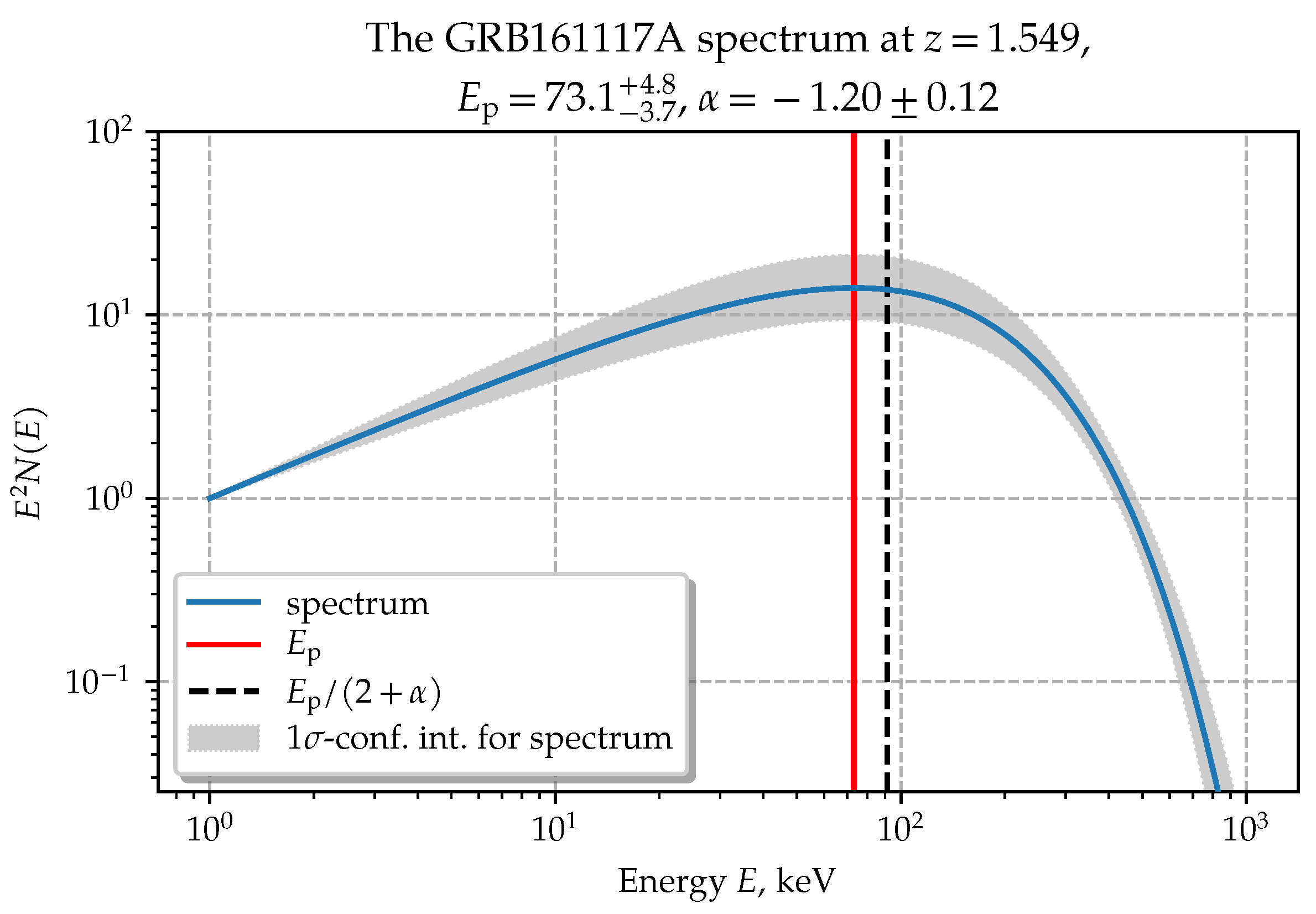
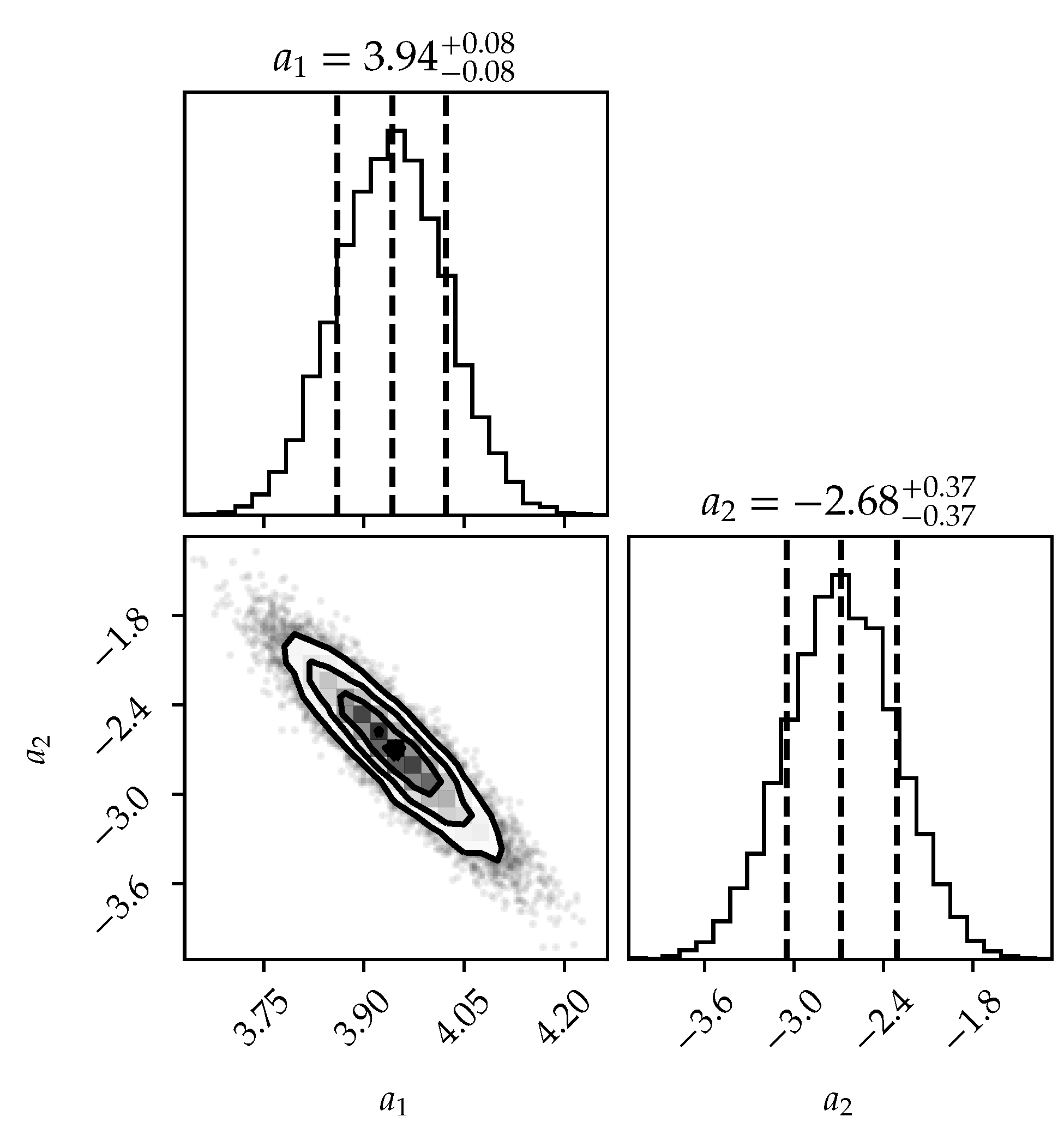
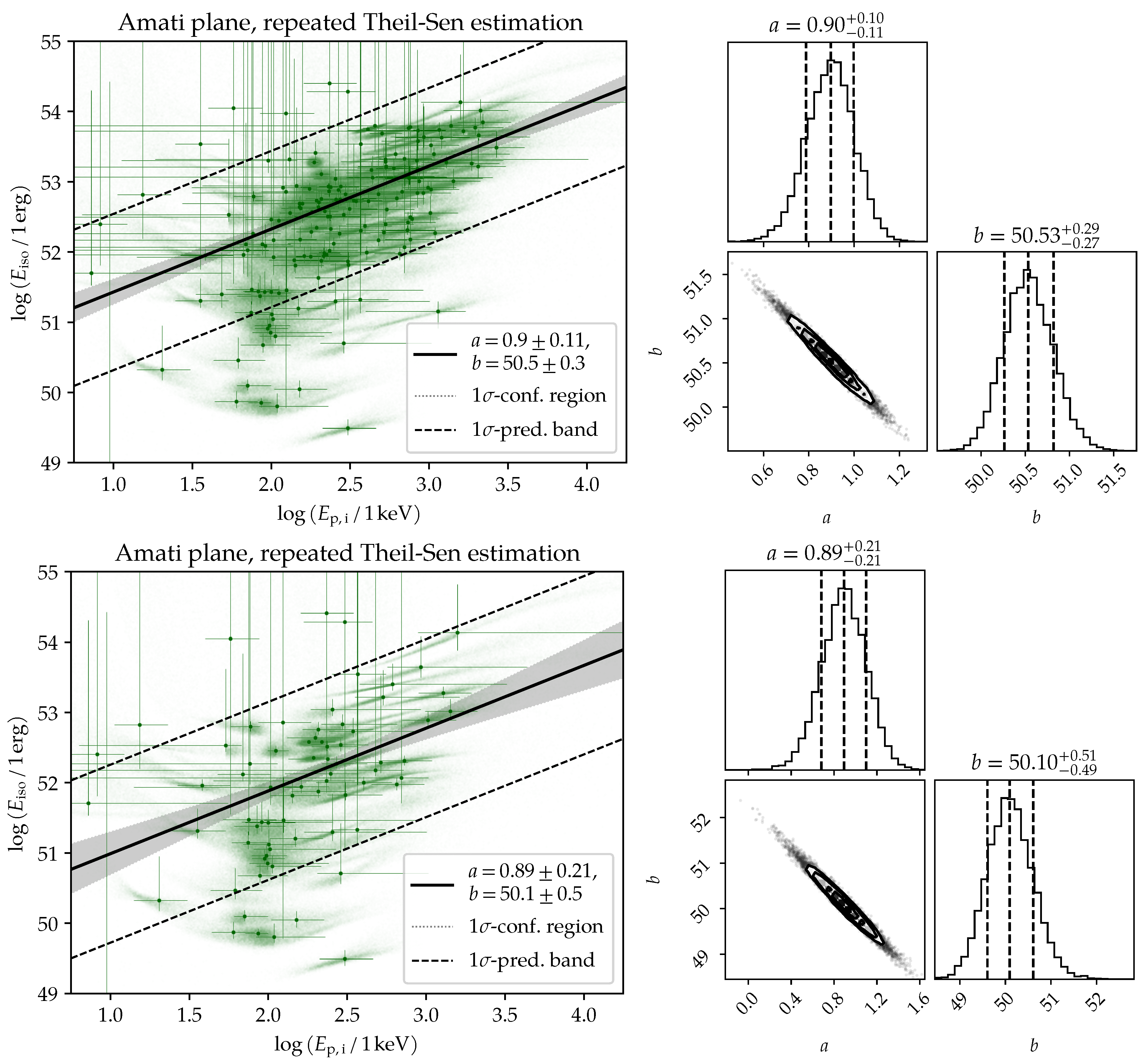
| Amati Parameter | a | b |
| Value from ΛCDM | ||
| Value from SN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovyagin, N.Y.; Gainutdinov, R.I.; Shirokov, S.I.; Gorokhov, V.L. The Hubble Diagram: Jump from Supernovae to Gamma-ray Bursts. Universe 2022, 8, 344. https://doi.org/10.3390/universe8070344
Lovyagin NY, Gainutdinov RI, Shirokov SI, Gorokhov VL. The Hubble Diagram: Jump from Supernovae to Gamma-ray Bursts. Universe. 2022; 8(7):344. https://doi.org/10.3390/universe8070344
Chicago/Turabian StyleLovyagin, Nikita Yu., Rustam I. Gainutdinov, Stanislav I. Shirokov, and Vladimir L. Gorokhov. 2022. "The Hubble Diagram: Jump from Supernovae to Gamma-ray Bursts" Universe 8, no. 7: 344. https://doi.org/10.3390/universe8070344
APA StyleLovyagin, N. Y., Gainutdinov, R. I., Shirokov, S. I., & Gorokhov, V. L. (2022). The Hubble Diagram: Jump from Supernovae to Gamma-ray Bursts. Universe, 8(7), 344. https://doi.org/10.3390/universe8070344






