Abstract
Recent measurements of the spectra and anisotropy of cosmic rays (CRs) show a fine structure that reflects the spectral hardenings of CRs nuclei at the rigidity ∼ 200 GV followed by softenings at ∼ 10 TV, and reveal complicated energy dependence of the amplitude and phase of anisotropy from 100 GeV to PeV. Numerous studies have shown that the existence of nearby CR sources and a local interstellar magnetic field (LIMF) near the solar system are crucial for such CR spectral and anisotropic patterns. In this work, we analyze the CR spectra of different CR components and the anisotropy considering the nearby Geminga supernova remnants (SNRs) source. In the calculation process, we also introduce the anisotropic diffusion of CRs induced by the LIMF based on the spatial-dependent propagation (SDP) model. As a result, our model can simultaneously account for the CR spectra and the anisotropy from 100 GeV to PeV. Future high-precision measurements of the CR anisotropy, for example, by the LHAASO experiment, would be of the essence in the assessment of our proposed model.
1. Introduction
It is widely believed that cosmic rays (CRs) below PeV energies originate from galactic sources, presumably supernova remnants (SNRs) [1]. CRs can be accelerated to form non-thermal power law spectra, , through the diffusive shock acceleration mechanism at SNRs, with being the rigidity and ν an injection power index [2,3,4,5]. After CRs are released by their sources, they enter the Milky Way Galaxy and interact with irregular magnetic fields and interstellar gas, which can be described by a diffusion process with the diffusion coefficient of and as inferred from the Boron-to-Carbon (B/C) ratio. After the diffusion transportation, the CR spectrum further softens into the form of [6].
Recent observations of the CR energy spectra indicate that the spectral structures are more complicated than ever expected. The spectral hardenings of CR nuclei at ~ 200 GV are shown by a large number of experiments, such as ATIC-2 [7], CREAM [8,9], PAMELA [10], AMS-02 [11] and the calorimeter experiment CALET [12]. Most recently, measurements of the proton and helium spectra by the DAMPE [13], CREAM [14] and NUCLEON experiments [15] reveal that the spectra become soft at 14 TeV.
Owing to the deflection of the galactic magnetic field (GMF), galactic cosmic rays (GCRs) lose their original direction and become almost isotropic. However, small CR anisotropy with relative amplitudes at the level of 10−4~10−3 is still observed at a wide energy range from 100 GeV to PeV. Complex energy dependence of the CR anisotropy is unveiled by numerous experiments, such as Tibet [16,17,18], Super-Kamiokande [19], Milagro [20,21], IceCube/IceTop [22,23,24,25,26], ARGO-YBJ [27,28], HAWC [29], EASTOP [30], and KASCADE [31]. Less than 100 TeV, the amplitude of anisotropy increases gradually up to 10 TeV at first with energy and then decreases, but increases again above 100 TeV. The phase reverses from to the galactic center (GC) at around 100 TeV.
In general, the CR anisotropy is attributed to the following reasons. One is the nearby sources, such as SNRs, which can influence the anisotropy by changing the spatial gradient of the CR particles in the solar system [32,33]. The second is the local interstellar magnetic field (LIMF) at the level of ~3 µG as inferred from the Interstellar Boundary Explorer (IBEX) [34] experiment along (l, b) = (210.5°, −57.1°). The Larmor radius of PeV CRs is much smaller than their scattering length in the LIMF, which indicates that the LIMF can deflect the PeV CR particles [35,36,37,38] so that the CR diffusion is anisotropic in the LIMF, i.e., stronger in the direction parallel to the LIMF and weaker in the perpendicular direction. Several literatures [36,39,40,41] also illustrate that the observation of the anisotropic phase of CRs is coincident with the LIMF.
Neither the spectral hardenings at ~200 GV nor the complex energy dependence of the anisotropy can be explained by the conventional propagation model. The common features of the CR energy spectra and anisotropy from 10 to 100 TeV indicate a common origin of the CRs. Based on the conventional propagation model, various improvements have been explored to explain the spectra and anisotropy, including those by introducing the nearby source [32,42,43,44], the spatially dependent diffusion process [45,46,47], the LIMF [36,48], and the ensemble fluctuations of CR sources.
The aim of this work is to explore a scenario that can simultaneously explain the CR anisotropy and energy spectra from 100 GeV to PeV. A large number of works have shown that the CR energy spectra and anisotropy are sensitive to the age, position, power, and cut-off rigidity of the nearby source [48,49,50]. Because the Geminga SNR is located close to the anti- GC direction and far from the galactic disk, it is regarded as a prime candidate [51]. Our method is based on the spatial-dependent propagation (SDP) model, with introducing the anisotropic diffusion induced by magnetic fields and considering the contribution from the nearby Geiminga SNR source. We calculated the energy spectra of different CR components and CR anisotropy. Ultimately, our model can simultaneously explain CR anisotropy and energy spectra. For example, the high-precision measurements of CR anisotropy by the LHAASO experiment could help test this scenario”.
2. The Model of Cosmic Rays Propagation
2.1. Spatially Dependent Diffusion
The recent HAWC observations [29] have shown that the diffusion coefficient of GCRs near the galactic disk is at least two orders of magnitude smaller than the conventional one [51]. Therefore, in this work, we adopt the SDP model [46,47,52], whose diffusion coefficients differ in the inner halo and the outer halo. The SDP model was first proposed to explain the hundred GeV spectral hardenings of CRs [10] and further applied to account for the secondary and heavier components [47,53,54,55,56], the diffuse gamma-ray distribution [57] and the large-scale anisotropy [49,50].
The diffusion volume of the SDP model is separated into two regions, i.e., the inner halo (|z| < ξzh) and the outer halo (|z| > ξzh). In the inner halo, particles diffuse slowly because the level of turbulence is expected to be high due to activities of supernova explosions; whereas in the outer halo, the diffusion coefficient is much larger.
The parameterized diffusion coefficient which we adopt is [55,57],
F(r, z) is parameterized as,
where g(r, z) = Nm/[1 + f(r, z)], and f(r, z) is the source density distribution. The spatial distribution of sources takes the form of the SNR distribution [58], and f(r, z) (r/r⊙)1.69exp[−3.33(r − r⊙)/r⊙] exp(−|z|/zs), where r⊙ = 8.5 kpc and zs = 0.2 kpc. In this work, we adopt the numerical package DRAGON to solve the transport equation [59].
The injection spectrum of background sources is assumed to be a power-law of rigidity with a high-energy exponential cutoff, exp(−/c).
2.2. Nearby Source
The Green’s function method is adopted to calculate the time-dependent propagation of CR particles from the nearby source, assuming a spherical geometry with infinite boundary conditions [42,43]. The GCR density of the nearby source as a function of the injection spectrum is described as,
where is the instantaneous injection spectrum of a point source, σ(, t) = the effective diffusion length within time t, and D() the diffusion coefficient which is adopted as the value near the solar system. The injection spectrum is also parameterized as a cutoff power-law form, . The normalization is obtained through fitting the GCR energy spectra.
In this work, we select the Geminga SNR as the contribution source to the spectral anomaly above 200 GeV and the complex evolution of anisotropy at lower than 100 TeV [49,50]. The Geminga SNR is located in the direction of l = 194.3°, b = −13° [60] and its distance to the solar system is d ~ 330 pc. Its explosion time was about τ = 3.4 × 105 years ago [51].
3. Anisotropic Diffusion and Large-Scale Anisotropy
3.1. Anisotropic Diffusion
According to the introduction, it seems clear that the LIMF (l, b = 210.5°, −57.1°) observed by IBEX should be a key factor in the explanation of the anisotropy of CRs. The diffusion of CRs in magnetic field is anisotropic, and the diffusion tensor Dij associated with the magnetic field is written as,
where bi is the i-th component of the unit vector of the ordered magnetic field B in the chosen coordinate system [61], and and are the diffusion coefficients aligned parallel and perpendicular to the ordered magnetic field, respectively.
In this work, two different rigidity dependents and are shown as follows [62],
where ε = is the ratio between the perpendicular and the parallel diffusion coefficients at the reference rigidity 0, which has been studied by numerous of literatures [38,42,63,64,65,66,67].
CR particles usually propagate in a magnetic field consisting of two parts, i.e., a regular part, B0, and a turbulent part, δB. The total magnetic field is their vector sum, B = δB + B0. The Larmor radius of a TeV CR particle in the LIMF is smaller than its mean free path. According to the quasi-linear theory [63,64], the ratio between and is given by,
where F(k) is the normalized power of the turbulent modes with wave number k [40,62,68], and δB(k)2 = . If δB/B0 ∼ 1, , then the diffusion of CRs with higher energies tends to be isotropic.
3.2. Large-Scale Anisotropy
It is known that the amplitude of the dipole anisotropy is proportional to the spatial gradient of the CR density and the diffusion coefficient. In an anisotropic diffusion model, its vector form can be written as [36,41],
The rigidity dependence of the dipole amplitude results from both the diffusion tensor Dij and ∇ψ/ψ.
4. Results and Discussion
4.1. The Energy Spectra of Different Primary CR Components
It is known that the observed spectra are inversely proportional to the diffusion coefficient, which is a reflection of the average interstellar environment. The range of the LIMF measured by the IBEX experiment is ~20 pc [34,62], however, the path length of the GCR propagation is much longer than this distance. Therefore, the LIMF is believed to have little influence on the energy spectra. Thus, the CR flux intensities from both the background and the nearby sources are approximately calculated under the isotropic diffusion model in this work.
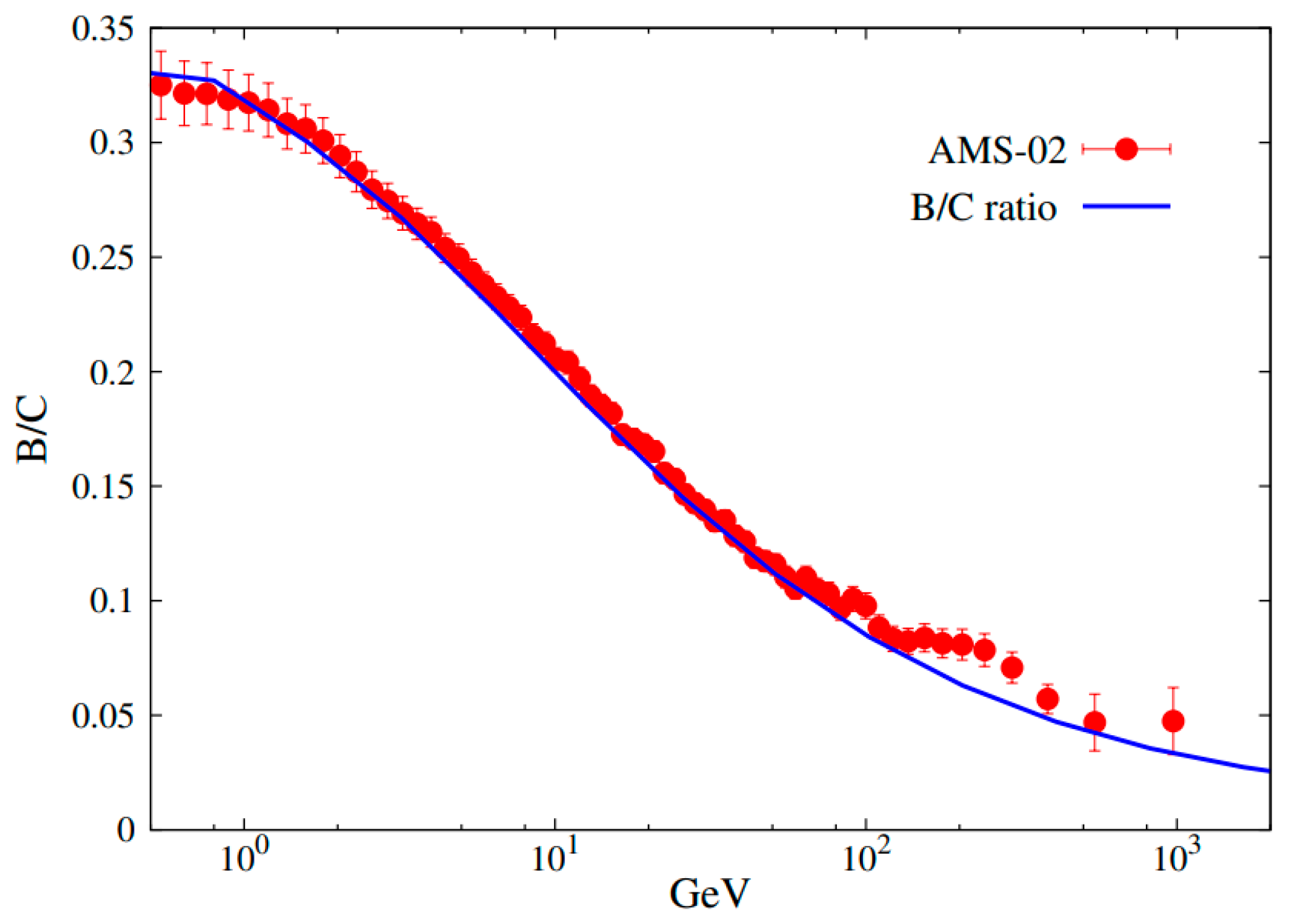
The propagation parameters are determined by fitting the B/C ratio. Figure 1 illustrates the fitting of the B/C ratio, which indicates that the relevant parameters are reasonable. The corresponding transport parameters are shown in Table 1.
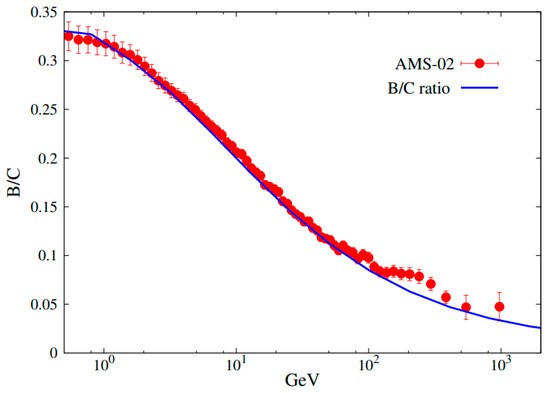
Figure 1.
Fitting to B/C ratio with the Model prediction. The B/C data points are taken from the AMS-02 experiment [69].

Table 1.
Transport parameters of SDP model.
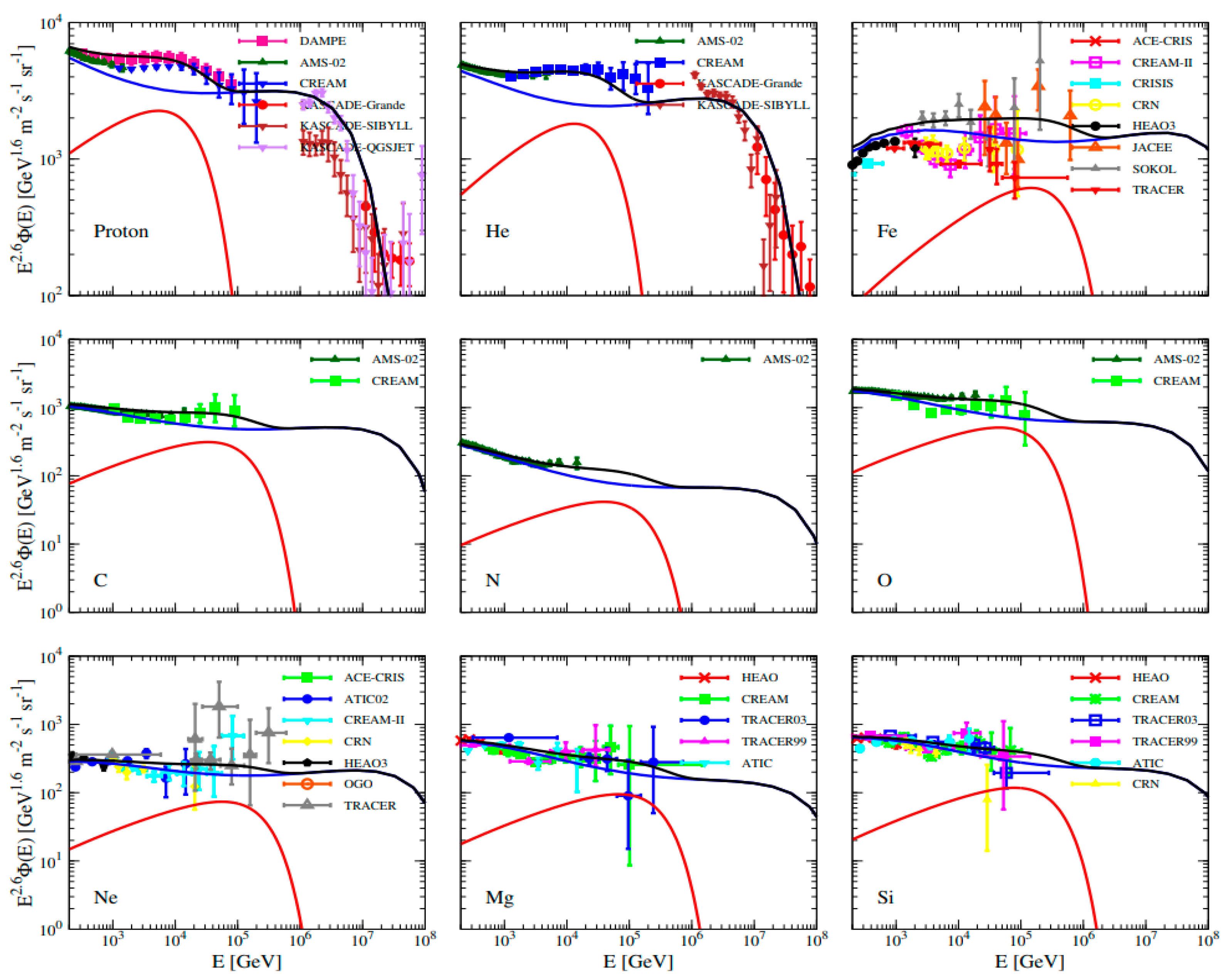
First, we calculate the energy spectra of primary CR components, including proton, He, C, N, O, Ne, Mg, Si and Fe nuclei. The injection spectra of background sources with a high-energy exponential cutoff are based on Z-dependent cutoff. The cutoff rigidity, c ~ 7 PV, is obtained by fitting the proton and helium spectra observed by KASCADE [70]. The injection power of each element roughly follows the rule that element abundance decreases from light to heavy nuclei. Similarly, the injection spectra of the nearby source are assumed to be Z-dependent cutoff with ~ 25 TV. The corresponding injection parameters are given by fitting the energy spectra, which are shown in Table 2. The spectral indices of the nearby source component are slightly harder than that of the background, which fits the experimental data better. The spectral index of the helium nuclei is slightly harder than that of the proton. Figure 2 shows the spectral results, where the red and blue lines represent the contributions from the nearby source and the background fluxes, respectively, and each of the black lines is the sum of them. It can be seen that the contribution by the nearby Geminga SNR source can simultaneously account for both the spectral hardening features at ∼ 200 GV and the softening features at ∼ 10 TV.

Table 2.
Injection parameters of the background and the nearby source (The normalization is set at total energy E = 100 GeV).
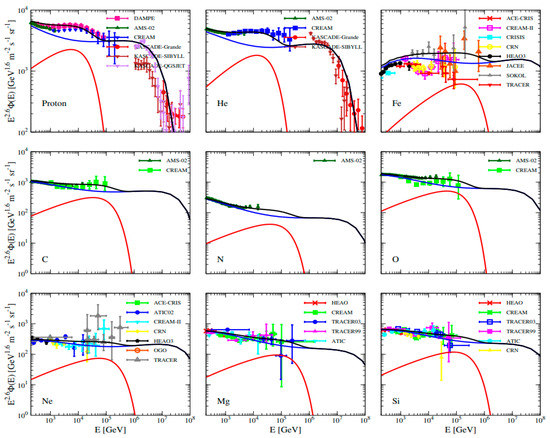
Figure 2.
The calculated energy spectra of proton, He, C, N, O, Ne, Mg, Si and Fe nuclei. The red and blue lines are the fluxes from the nearby and background sources, and the black line is their sum. For protons, He, C, N and O, the data points are taken from AMS-02 [71,72,73,74], CREAM [14,75], and KASCADE [70,76], respectively. For Ne, Mg, Si, and Fe, the data points are from HEAO [77], TRACER [78,79,80], ATIC [81], JACEE [82,83], SOKOL [84], CRISIS [85], ACE-CRIS [86] and CRN [87].
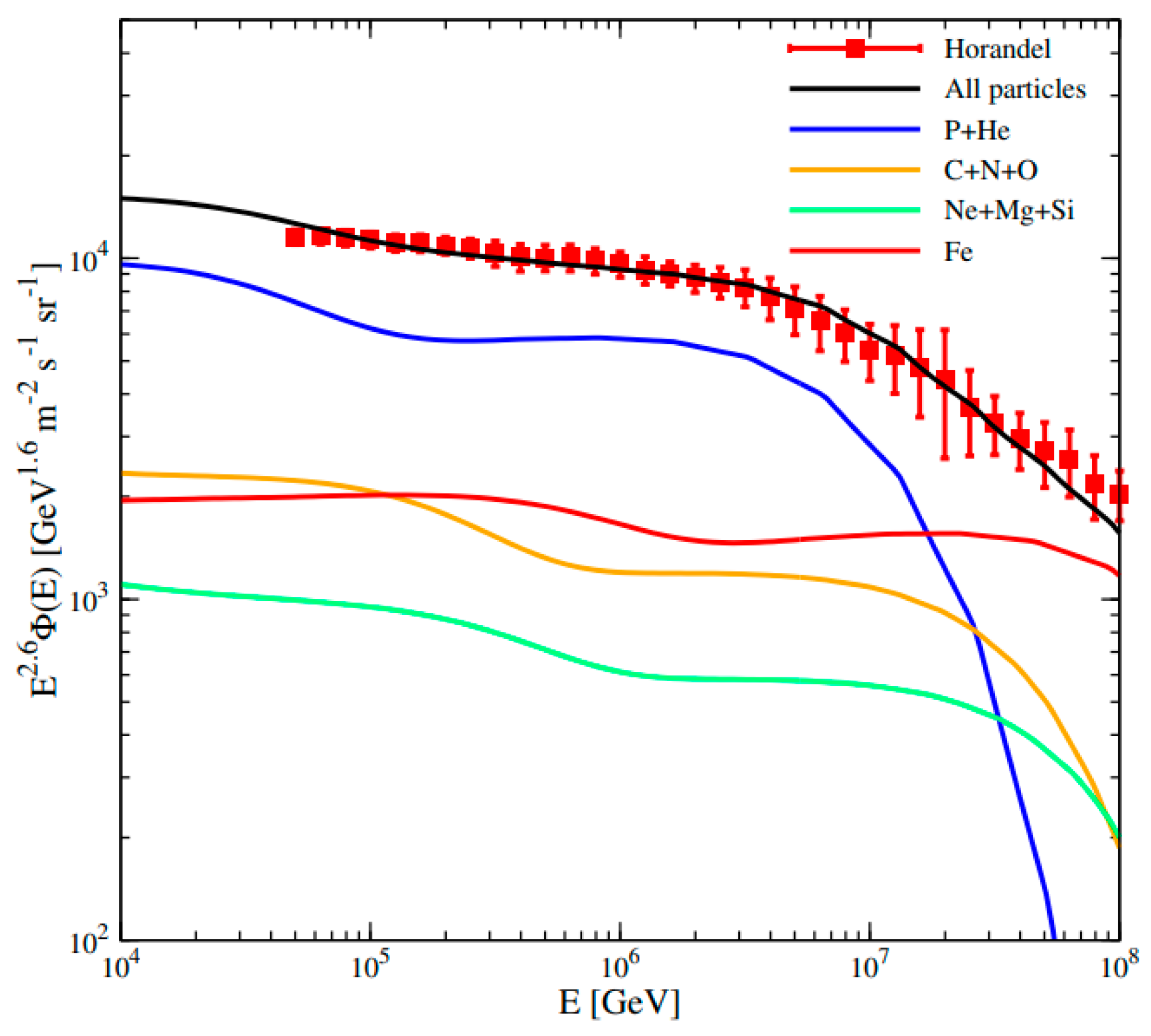
We further calculate the all-particle spectra of GCRs, as shown in Figure 3, which are consistent with the observational data.
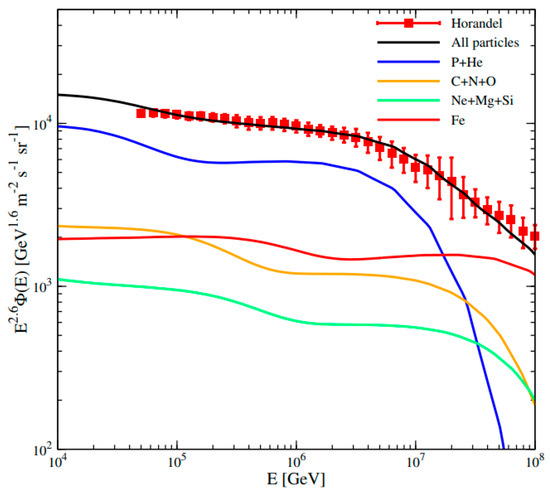
Figure 3.
The all-particle spectra multiplied by E2.6. The data points are taken from [88]. The solid lines with different colors are the model predictions for different mass groups, and the black solid line is the total contribution.
4.2. Anisotropy
Compared with the energy spectra, the LIMF can radically affect the anisotropy by altering the direction of CR flux entering into the solar system. Therefore, in the process of calculating the anisotropy, we introduce the anisotropic diffusion effect of CRs induced by the LIMF. Despite the uncertainties in the existing measurements, the LIMF is assumed to be in the direction as reported by the IBEX experiment [36,39].
The parameters of the parallel diffusion coefficient are set as those shown in Table 1. The CRs in the GeV–PeV energy region require , therefore, we set ε = 0.01 and the difference between and is 0.3.
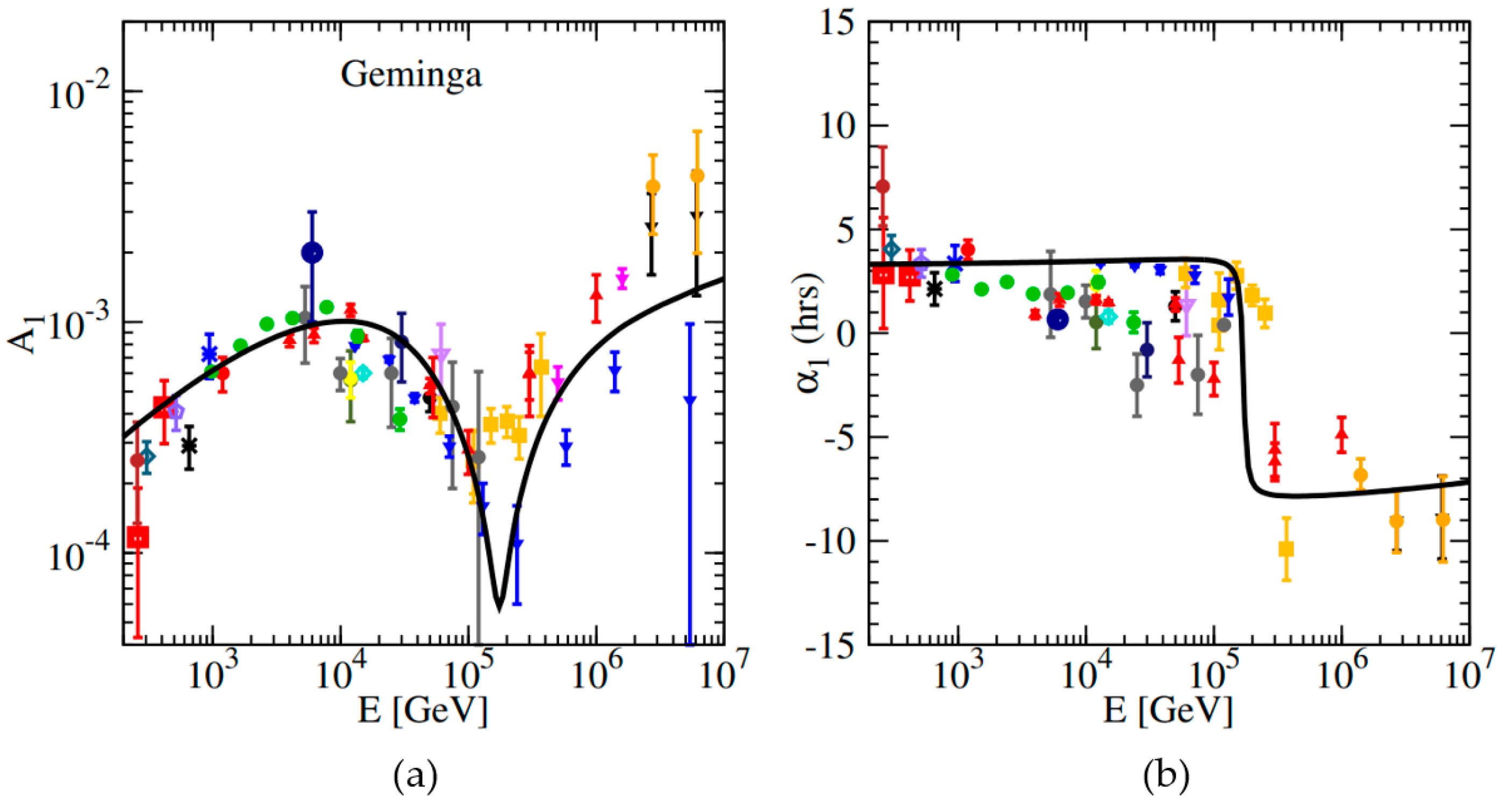
Taking into account the contribution of the Geminga SNR, the amplitude and phase of the CR anisotropy are shown in Figure 4. It is obvious that both the phase and the amplitude agree well with the observations. For E < 100 TeV, the nearby source dominates the anisotropic phase, although the nearby flux is sub-dominant. The phase of anisotropy clearly points in the direction of the LIMF (~R.A. = 3h). It is demonstrated that, compared with the model without considering the magnetic field, the anisotropic phase calculated with considering the LIMF fits better with the experimental observation [49]. The phase is flipped at 100 TeV from ~R.A. = 3h to the GC. For E ≥ 100 TeV, the contribution from the nearby source and LIMF decreases significantly, and the background becomes dominant instead. The phase of the anisotropy turns to the GC, since galactic CR sources are more abundant in the inner Galaxy.
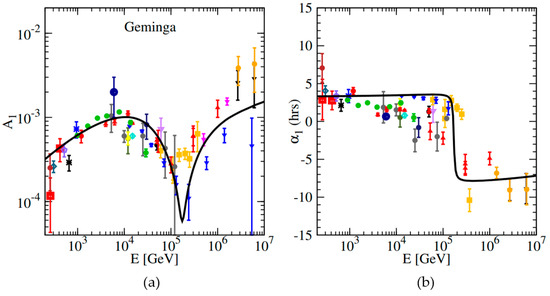
Figure 4.
The amplitude (a) and phase (b) of the dipole anisotropy with the contribution from the nearby Geminga SNR source. The data points are taken from underground muon detectors: Norikura [89], Ottawa [90], London [91], Bolivia [92], Budapest [92], Hobart [92], London [92], Misato [92], Socorro [92], Yakutsk [92], Banksan [93], Hong Kong [94], Sakashita [95], Utah [96], Liapootah [97], Matsushiro [98], Poatina [99], Kamiokande [100], Marco [101], SuperKamiokande [19]; and air shower array experiments: PeakMusala [102], Baksan [103], Norikura [104], EAS-TOP [30,105,106], Baksan [107], Milagro [21], IceCube [22,24], Ice-Top [25], ARGO-YBJ [28], Tibet [17,108,109].
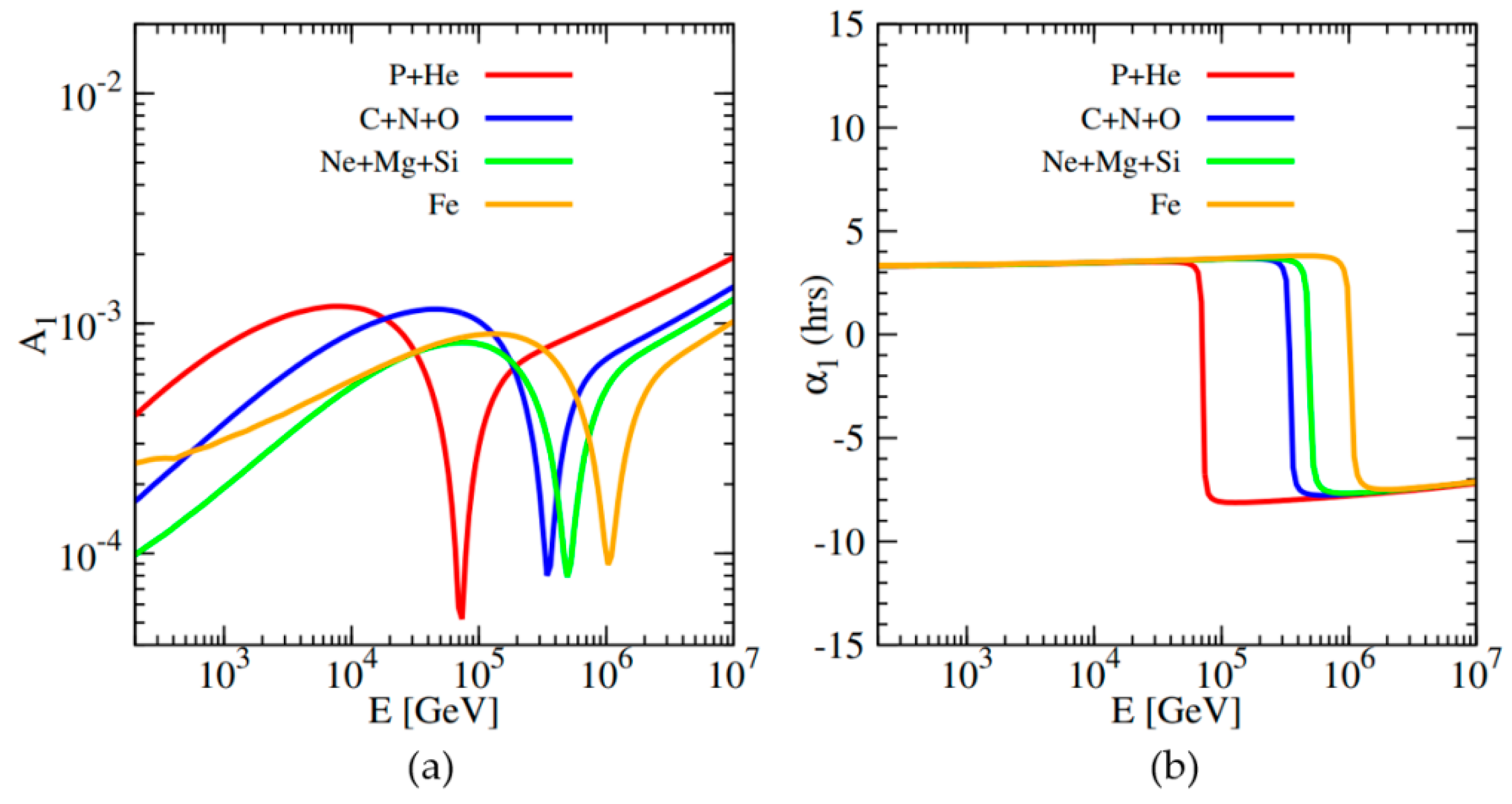
We further calculate the anisotropies of different compositions. The primary CR components are divided into four mass groups, i.e., P + He, C + N + O, Ne + Mg + Si, and Fe, and the calculated results are shown in Figure 5. The anisotropic amplitudes and phases of each mass group have a similar structure. However, as the nucleon number increases, the position of phase inversion moves towards a higher energy. We hope the coming high-precision measurements of the CR anisotropy will give a critical test on this point predicted by this model, such as the LHAASO experiment.
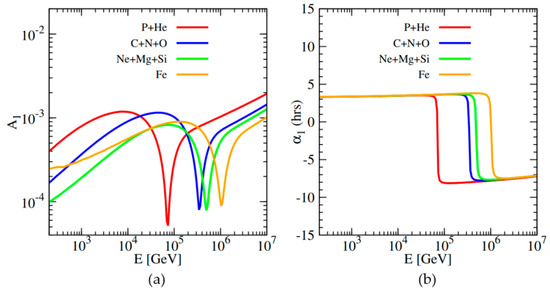
Figure 5.
The amplitude (a) and phase (b) of the dipole anisotropy for four different mass groups P + He, C + N + O, Ne + Mg + Si, and Fe, respectively.
5. Conclusions
In this work, in view of the CR spectra hardenings at ~ 200 GV and softenings at ~ 10 TV, as well as the variation of the CR anisotropy with energy from GeV to PeV, we developed a model to explain both the cosmic ray spectra and anisotropy based on the SDP model with consideration of the anisotropic diffusion of CRs induced by the LIMF near the solar system and the contribution by the nearby Geminga SNR source. We first analyzed the energy spectra of different components and the CR anisotropy. The results show that our model can simultaneously account for both the CR spectra hardenings at ~ 200 GV and softenings at ~ 10 TV, as well as the CR anisotropy. We further explored the anisotropies of different mass groups which have the similar trend of change in amplitude and phase but with different characteristic energies. We hope that future high-precision CR spectral and anisotropic measurements, such as the LHAASO experiment, will help to test our model.
Author Contributions
Conceptualization, A.L. and M.L.; methodology, A.L.; software, S.Y.; validation, A.L., H.W. and Y.L.; formal analysis, X.L.; investigation, A.L.; resources, A.L.; data curation, S.Y.; writing—original draft preparation, A.L.; writing—review and editing, H.W., X.L. and Y.L.; visualization, M.L.; supervision, A.L.; project administration, M.L.; funding acquisition, A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 11963004, U2031110 and 52062045; Shandong Province Natural Science Foundation, grant number ZR2020MA095; and Natural Science Foundation of Tibet Autonomous Region, grant number XZ202101ZR0121G.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baade, W.; Zwicky, F. Cosmic Rays from Super-Novae. Proc. Natl. Acad. Sci. USA 1934, 20, 259–263. [Google Scholar] [CrossRef]
- Cardillo, M.; Tavani, M.; Giuliani, A.E. The origin of Cosmic-Rays from SNRs: Confirmations and challenges after the first direct proof. Nucl. Phys. B Proc. Suppl. 2014, 256–257, 65–73. [Google Scholar] [CrossRef]
- Funk, S. Ground- and Space-Based Gamma-Ray Astronomy. Annu. Rev. Nucl. Part. Sci. 2015, 65, 245–277. [Google Scholar] [CrossRef]
- Dubner, G.; Giacani, E. Radio emission from supernova remnants. Astron. Astrophys. Rev. 2015, 23, 3. [Google Scholar] [CrossRef]
- Hewitt, J.W.; Lemoine-Goumard, M. Observations of supernova remnants and pulsar wind nebulae at gamma-ray energies. C. R. Phys. 2015, 16, 674–685. [Google Scholar] [CrossRef]
- Yuan, Q.; Lin, S.-J.; Fang, K.; Bi, X.-J. Propagation of cosmic rays in the AMS-02 era. Phys. Rev. D 2017, 95, 083007. [Google Scholar] [CrossRef]
- Panov, A.D.; Adams, J.H.; Ahn, H.S.; Batkov, K.E.; Bashindzhagyan, G.L.; Watts, J.W.; Wefel, J.P.; Wu, J.; Ganel, O.; Guzik, T.G.; et al. Elemental energy spectra of cosmic rays from the data of the ATIC-2 experiment. Bull. Russ. Acad. Sci. Phys. 2007, 71, 494–497. [Google Scholar] [CrossRef]
- Ahn, H.S.; Allison, P.; Bagliesi, M.G.; Beatty, J.; Bigongiari, G.; Childers, J.T.; Conklin, N.B.; Coutu, S.; Duvernois, M.A.; Ganel, O.; et al. Discrepant hardening observed in cosmic-ray elemental spectra. Astrophys. J. Lett. 2010, 714, L89–L93. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Ahn, H.S.; Allison, P.S.; Bagliesi, M.G.; Beatty, J.; Bigongiari, G.; Boyle, P.J.; Childers, J.T.; Conklin, N.B.; Coutu, S.; et al. Cosmic-ray proton and helium spectra from the first cream flight. Astrophys. J. 2011, 728, 122. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Borisov, S.; et al. PAMELA measurements of cosmic-ray proton and helium spectra. Science 2011, 332, 6025. [Google Scholar] [CrossRef]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Helium Flux in Primary Cosmic Rays of Rigidities 1.9 GV to 3 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 115, 211101. [Google Scholar] [CrossRef] [PubMed]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Bagliesi, M.G.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bonechi, S.; Bongi, M.; et al. Direct Measurement of the Cosmic-Ray Proton Spectrum from 50 GeV to 10 TeV with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2019, 122, 181102. [Google Scholar] [CrossRef] [PubMed]
- DAMPE Collaboration; An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; et al. Measurement of the cosmic ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Sci. Adv. 2019, 5, eaax3793. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.S.; Anderson, T.; Barrau, A.; Conklin, N.B.; Coutu, S.; Derome, L.; Han, J.H.; Jeon, J.A.; Kim, K.C.; Kim, M.H.; et al. Proton and Helium Spectra from the CREAM-III Flight. Astrophys. J. 2017, 839, 5. [Google Scholar] [CrossRef]
- Atkin, E.; Bulatov, V.; Dorokhov, V.; Gorbunov, N.; Filippov, S.; Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; et al. New Universal Cosmic-Ray Knee near a Magnetic Rigidity of 10 TV with the NUCLEON Space Observatory. J. Exp. Theor. Phys. Lett. 2018, 108, 5–12. [Google Scholar] [CrossRef]
- Amenomori, M.; Ayabe, S.; Bi, X.J.; Chen, D.; Cui, S.W.; Danzengluobu; Ding, L.K.; Ding, X.H.; Feng, C.F.; Feng, Z.; et al. Anisotropy and Corotation of Galactic Cosmic Rays. Science 2006, 314, 439–443. [Google Scholar] [CrossRef]
- Amenomori, M.; Bi, X.J.; Chen, D.; Cui, S.W.; Danzengluobu; Ding, L.K.; Ding, X.H.; Fan, C.; Feng, C.F.; Feng, Z.; et al. On Temporal Variations of The Multi-Tev Cosmic Ray Anisotropy using the Tibet Iii Air Shower Array. Astrophys. J. Lett. 2010, 711, 119–124. [Google Scholar] [CrossRef]
- Amenomori, M.; Bi, X.J.; Chen, D.; Chen, T.L.; Chen, W.Y.; Cui, S.W.; Danzengluobu; Ding, L.K.; Feng, C.F.; Feng, Z.; et al. Northern Sky Galactic Cosmic Ray Anisotropy between 10 and 1000 TeV with the Tibet Air Shower Array. Astrophys. J. 2017, 836, 153. [Google Scholar] [CrossRef]
- Guillian, G.; Hosaka, J.; Ishihara, K.; Kameda, J.; Koshio, Y.; Minamino, A.; Mitsuda, C.; Miura, M.; Moriyama, S.; Nakahata, M.; et al. Observation of the anisotropy of 10 TeV primary cosmic ray nuclei flux with the Super-Kamiokande-I detector. Phys. Rev. D 2007, 75, 062003. [Google Scholar] [CrossRef]
- Abdo, A.A.; Allen, B.; Aune, T.; Berley, D.; Blaufuss, E.; Casanova, S.; Chen, C.; Dingus, B.; Ellsworth, R.W.; Fleysher, L.; et al. Discovery of Localized Regions of Excess 10-TeV Cosmic Rays. Phys. Rev. Lett. 2008, 101, 221101. [Google Scholar] [CrossRef]
- Abdo, A.A.; Allen, B.T.; Aune, T.; Berley, D.; Casanova, S.; Chen, C.; Dingus, B.L.; Ellsworth, R.W.; Fleysher, L.; Gonzalez, M.M.; et al. The large-scale cosmic-ray anisotropy as observed with milagro. Astrophys. J. 2009, 698, 2121–2130. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Andeen, K.; Auffenberg, J.; Bai, X.; Baker, M.; et al. Measurement of the anisotropy of cosmic-ray arrival directions with icecube. Astrophys. J. Lett. 2010, 718, L194–L198. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Andeen, K.; Auffenberg, J.; Bai, X.; et al. Observation of Anisotropy in The Arrival Directions of Galactic Cosmic Rays at Multiple Angular Scales with IceCube. Astrophys. J. 2011, 740, 16. [Google Scholar] [CrossRef]
- Castro, P.J.; Gizis, J. Discovery of a late l dwarf: Wisep j060738.65+242953.4. Astrophys. J. 2012, 746, 3. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Abdou, Y.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Andeen, K.; Auffenberg, J.; et al. Observation of cosmic-ray anisotropy with the icetop air shower array. Astrophys. J. 2013, 765, 55. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Ansseau, I.; et al. Anisotropy in Cosmic-Ray Arrival Directions in The Southern Hemisphere Based on Six Years of Data from The Icecube Detector. Astrophys. J. 2016, 826, 220. [Google Scholar] [CrossRef]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Bolognino, I.; Branchini, P.; Budano, A.; Melcarne, A.K.C.; Camarri, P.; Cao, Z.; Cardarelli, R.; et al. Medium scale anisotropy in the TeV cosmic ray flux observed by ARGO-YBJ. Phys. Rev. D 2013, 88, 082001. [Google Scholar] [CrossRef]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Cao, Z.; Catalanotti, S.; Chen, S.Z.; Chen, T.L.; Cui, S.W.; Dai, B.Z.; D’Amone, A.; et al. Argo-Ybj Observation of the Large-Scale Cosmic Ray Anisotropy during The Solar Minimum Between Cycles 23 And 24. Astrophys. J. 2015, 809, 90. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Solares, H.A.A.; Barber, A.S.; Baughman, B.M.; Bautista-Elivar, N.; et al. Observation of Small-Scale Anisotropy in the Arrival Direction Distribution of Tev Cosmic Rays with Hawc. Astrophys. J. 2014, 796, 108. [Google Scholar] [CrossRef]
- Aglietta, M.; Alekseenko, V.V.; Alessandro, B.; Antonioli, P.; Arneodo, F.; Bergamasco, L.; Bertaina, M.E.; Bonino, R.; Castellina, A.; Chiavassa, A.; et al. Evolution of the Cosmic-Ray Anisotropy Above 1014 eV. Astrophys. J. 2009, 692, L130–L133. [Google Scholar] [CrossRef]
- Apel, W.D.; Arteaga-Velázquez, J.C.; Bekk, K.; Bertaina, M.; Blümer, J.; Bonino, R.; Bozdog, H.; Brancus, I.M.; Cantoni, E.; Chiavassa, A.; et al. Search for Large-scale Anisotropy in the Arrival Direction of Cosmic Rays with KASCADE-Grande. Astrophys. J. 2019, 870, 91. [Google Scholar] [CrossRef]
- Erlykin, A.; Wolfendale, A. The anisotropy of galactic cosmic rays as a product of stochastic supernova explosions. Astropart. Phys. 2006, 25, 183–194. [Google Scholar] [CrossRef]
- Blasi, P.; Amato, E. Diffusive propagation of cosmic rays from supernova remnants in the Galaxy. I: Spectrum and chemical composition. J. Cosmol. Astropart. Phys. 2012, 2012, 010. [Google Scholar] [CrossRef]
- Funsten, H.O.; DeMajistre, R.; Frisch, P.C.; Heerikhuisen, J.; Higdon, D.M.; Janzen, P.; Larsen, B.A.; Livadiotis, G.; McComas, D.J.; Möbius, E.; et al. Circularity of Theinterstellar Boundary Explorerribbon of Enhanced Energetic Neutral Atom (Ena) Flux. Astrophys. J. 2013, 776, 30. [Google Scholar] [CrossRef]
- Battaner, E.; Castellano, J.; Masip, M. Galactic Magnetic Fields and the Large-Scale Anisotropy at Milagro. Astrophys. J. 2009, 703, L90–L93. [Google Scholar] [CrossRef][Green Version]
- Ahlers, M. Deciphering the Dipole Anisotropy of Galactic Cosmic Rays. Phys. Rev. Lett. 2016, 117, 151103. [Google Scholar] [CrossRef] [PubMed]
- Ahlers, M.; Mertsch, P. Origin of small-scale anisotropies in Galactic cosmic rays. Prog. Part. Nucl. Phys. 2017, 94, 184–216. [Google Scholar] [CrossRef]
- Snodin, A.P.; Shukurov, A.; Sarson, G.R.; Bushby, P.J.; Rodrigues, L.F.S. Global diffusion of cosmic rays in random magnetic fields. Mon. Not. R. Astron. Soc. 2016, 457, 3975–3987. [Google Scholar] [CrossRef]
- Schwadron, N.A.; Adams, F.C.; Christian, E.R.; Desiati, P.; Frisch, P.; Funsten, H.O.; Jokipii, J.R.; McComas, D.J.; Moebius, E.; Zank, G.P. Global Anisotropies in TeV Cosmic Rays Related to the Sun’s Local Galactic Environment from IBEX. Science 2014, 343, 988–990. [Google Scholar] [CrossRef]
- Mertsch, P.; Funk, S. Solution to the Cosmic Ray Anisotropy Problem. Phys. Rev. Lett. 2015, 114, 021101. [Google Scholar] [CrossRef]
- Liu, W.; Lin, S.-J.; Hu, H.-B.; Guo, Y.-Q.; Li, A.-F. Two Numerical Methods for the 3D Anisotropic Propagation of Galactic Cosmic Rays. Astrophys. J. 2020, 892, 6. [Google Scholar] [CrossRef]
- Blasi, P.; Amato, E. Diffusive propagation of cosmic rays from supernova remnants in the Galaxy. II: Anisotropy. J. Cosmol. Astropart. Phys. 2012, 2012, 011. [Google Scholar] [CrossRef]
- Sveshnikova, L.; Strelnikova, O.; Ptuskin, V. Spectrum and anisotropy of cosmic rays at TeV–PeV-energies and contribution of nearby sources. Astropart. Phys. 2013, 50–52, 33–46. [Google Scholar] [CrossRef]
- Liu, W.; Bi, X.-J.; Lin, S.-J.; Wang, B.-B.; Yin, P.-F. Excesses of cosmic ray spectra from a single nearby source. Phys. Rev. D 2017, 96, 023006. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Grasso, D.; Maccione, L. Common Solution to the Cosmic Ray Anisotropy and Gradient Problems. Phys. Rev. Lett. 2012, 108, 211102. [Google Scholar] [CrossRef] [PubMed]
- Tomassetti, N. Origin of the Cosmic-Ray Spectral Hardening. Astrophys. J. 2012, 752, L13. [Google Scholar] [CrossRef]
- Guo, Y.; Tian, Z.; Jin, C. Spatial-dependent Propagation of Cosmic Rays Results in the Spectrum of Proton, Ratios of P/P, and B/C, and Anisotropy of Nuclei. Astrophys. J. 2016, 819, 54. [Google Scholar] [CrossRef]
- Li, A.; Yuan, Q.; Liu, W.; Guo, Y. A scenario for the anisotropy of galactic cosmic rays related to nearby source and local interstellar magnetic field. arXiv 2021, arXiv:2107.00313. [Google Scholar]
- Liu, W.; Guo, Y.-Q.; Yuan, Q. Indication of nearby source signatures of cosmic rays from energy spectra and anisotropies. J. Cosmol. Astropart. Phys. 2019, 2019, 010. [Google Scholar] [CrossRef]
- Qiao, B.-Q.; Liu, W.; Guo, Y.-Q.; Yuan, Q. Anisotropies of different mass compositions of cosmic rays. J. Cosmol. Astropart. Phys. 2019, 2019, 007. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Solares, H.A.A.; Barber, A.S.; et al. Extended gamma-ray sources around pulsars constrain the origin of the positron flux at Earth. Science 2017, 358, 911–914. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.; Guo, Y.; Hu, H.-B. Spatial dependent diffusion of cosmic rays and the excess of primary electrons derived from high precision measurements by AMS-02. Chin. Phys. C 2016, 40, 015101. [Google Scholar] [CrossRef][Green Version]
- Tomassetti, N. Cosmic-ray protons, nuclei, electrons, and antiparticles under a two-halo scenario of diffusive propagation. Phys. Rev. D 2015, 92, 081301. [Google Scholar] [CrossRef]
- Feng, J.; Tomassetti, N.; Oliva, A. Bayesian analysis of spatial-dependent cosmic-ray propagation: Astrophysical background of antiprotons and positrons. Phys. Rev. D 2016, 94, 123007. [Google Scholar] [CrossRef]
- Liu, W.; Yao, Y.-H.; Guo, Y.-Q. Revisiting the Spatially Dependent Propagation Model with the Latest Observations of Cosmic-Ray Nuclei. Astrophys. J. 2018, 869, 176. [Google Scholar] [CrossRef]
- Tian, Z.; Liu, W.; Yang, B.; Fu, X.-D.; Xu, H.-B.; Yao, Y.-H.; Guo, Y.-Q. Electron and positron spectra in three-dimensional spatial-dependent propagation model. Chin. Phys. C 2020, 44, 085102. [Google Scholar] [CrossRef]
- Guo, Y.-Q.; Yuan, Q. Understanding the spectral hardenings and radial distribution of Galactic cosmic rays and Fermi diffuse γ rays with spatially-dependent propagation. Phys. Rev. D 2018, 97, 063008. [Google Scholar] [CrossRef]
- Case, G.; Bhattacharya, D. Revisiting the galactic supernova remnant distribution. Astron. Astrophys. Suppl. Ser. 1996, 120, 437–440. [Google Scholar]
- Evoli, C.; Gaggero, D.; Grasso, D.; Maccione, L. Cosmic Ray propagation in the Galaxy and diffuse gamma-ray emission. AIP Conf. Proc. 2008, 1085, 380–383. [Google Scholar] [CrossRef]
- Faherty, J.; Walter, F.M.; Anderson, J. The trigonometric parallax of the neutron star Geminga. Astrophys. Space Sci. 2007, 308, 225–230. [Google Scholar] [CrossRef]
- Giacalone, J.; Jokipii, J.R. The Transport of Cosmic Rays across a Turbulent Magnetic Field. Astrophys. J. 1999, 520, 204–214. [Google Scholar] [CrossRef]
- Cerri, S.S.; Gaggero, D.; Vittino, A.; Evoli, C.; Grasso, D. A signature of anisotropic cosmic-ray transport in the gamma-ray sky. J. Cosmol. Astropart. Phys. 2017, 2017, 019. [Google Scholar] [CrossRef]
- Jokipii, J.R. Cosmic-Ray Propagation I. Charged Particles in a Random Magnetic Field. Astrophys. J. 1966, 146, 480. [Google Scholar] [CrossRef]
- Jokipii, J.R.; Parker, E.N. Random Walk of Magnetic Lines of Force in Astrophysics. Phys. Rev. Lett. 1968, 21, 44–47. [Google Scholar] [CrossRef]
- Casse, F.; Lemoine, M.; Pelletier, G. Transport of cosmic rays in chaotic magnetic fields. Phys. Rev. D. 2001, 65, 023002. [Google Scholar] [CrossRef]
- De Marco, D.; Blasi, P.; Stanev, T. Numerical propagation of high energy cosmic rays in the Galaxy: I. Technical issues. J. Cosmol. Astropart. Phys. 2007, 2007, 027. [Google Scholar] [CrossRef]
- Shalchi, A.; Büsching, I.; Lazarian, A.; Schlickeiser, R. Perpendicular diffusion of cosmic rays for a goldreich-sridhar spectrum. Astrophys. J. Lett. 2010, 725, 2117–2127. [Google Scholar] [CrossRef]
- Battaner, E.; Castellano, J.; Masip, M. Magnetic fields and cosmic-ray anisotropies at tev energies. Astrophys. J. 2015, 799, 157. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; et al. Precision Measurement of the Boron to Carbon Flux Ratio in Cosmic Rays from 1.9 GV to 2.6 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2016, 117, 231102. [Google Scholar] [CrossRef]
- Apel, W.; Arteaga-Velázquez, J.; Bekk, K.; Bertaina, M.; Blümer, J.; Bozdog, H.; Brancus, I.; Cantoni, E.; Chiavassa, A.; Cossavella, F.; et al. KASCADE-Grande measurements of energy spectra for elemental groups of cosmic rays. Astropart. Phys. 2013, 47, 54–66. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Alpat, B.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; et al. Observation of the Identical Rigidity Dependence of He, C, and O Cosmic Rays at High Rigidities by the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2017, 119, 251101. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; et al. Observation of New Properties of Secondary Cosmic Rays Lithium, Beryllium, and Boron by the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2018, 120, 021101. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Alpat, B.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; et al. Precision Measurement of Cosmic-Ray Nitrogen and its Primary and Secondary Components with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2018, 121, 051103. [Google Scholar] [CrossRef]
- Aguilar, M.; Asia, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Proton Flux in Primary Cosmic Rays from Rigidity 1 GV to 1.8 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 114, 171103. [Google Scholar] [CrossRef]
- Ahn, H.S.; Allison, P.; Bagliesi, M.G.; Barbier, L.; Beatty, J.; Bigongiari, G.; Brandt, T.J.; Childers, J.T.; Conklin, N.B.; Coutu, S.; et al. Energy spectra of cosmic-ray nuclei at high energies. Astrophys. J. Lett. 2009, 707, 593–603. [Google Scholar] [CrossRef]
- Antoni, T.; Apel, W.D.; Bekk, K.; Badea, A.F.; Bercuci, A.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Chilingarian, A.; Daumiller, K.; et al. KASCADE measurements of energy spectra for elemental groups of cosmic rays: Results and open problems. Astropart. Phys. 2005, 24, 1–25. [Google Scholar] [CrossRef]
- Engelmann, J.J.; Ferrando, P.; Soutoul, A.; Goret, P.; Juliusson, E.; Koch-Miramond, L.; Lund, N.; Masse, P.; Peters, B.; Petrou, N.; et al. Charge composition and energy spectra of cosmic-ray nucleifor elements from Be to Ni. Results from HEAO-3-C2. Astron. Astrophys. 1990, 233, 96–111. [Google Scholar]
- Ave, M.; Boyle, P.J.; Gahbauer, F.; Höppner, C.; Hörandel, J.; Ichimura, M.; Müller, D.; Romero-Wolf, A. Composition of Primary Cosmic-Ray Nuclei at High Energies. Astrophys. J. 2008, 678, 262. [Google Scholar] [CrossRef]
- Gahbauer, F.; Hermann, G.; Hörandel, J.R.; Müller, D.; Radu, A.A. A New Measurement of the Intensities of the Heavy Primary Cosmic-Ray Nuclei around 1 TeV amu−1. Astrophys. J. 2004, 607, 333. [Google Scholar] [CrossRef]
- Obermeier, A.; Ave, M.; Boyle, P.; Hoppner, C.; Horandel, J.; Muller, D. Energy spectra of primary and secondary cosmic-ray nuclei measured with TRACER. Astrophys. J. 2011, 742, 14. [Google Scholar] [CrossRef]
- Panov, A.D.; Adams, J.H.; Ahn, H.S.; Bashindzhagyan, G.L.; Watts, J.W.; Wefel, J.P.; Wu, J.; Ganel, O.; Guzik, T.G.; Zatsepin, V.I.; et al. Energy Spectra of Abundant Nuclei of Primary Cosmic Rays from the Data of ATIC-2 Experiment: Final Results. Bull. Russ. Acad. Sci. Phys. 2009, 73, 564–567. [Google Scholar] [CrossRef]
- Höorandel, J.R. A review of experimental results at the knee. J. Phys. Conf. Ser. 2006, 47, 41–50. [Google Scholar] [CrossRef]
- Asakimori, K.; Burnett, T.H.; Cherry, M.L.; Chevli, K.; Christ, M.J.; Dake, S.; Derrickson, J.H.; Fountain, W.F.; Fuki, M.; Gregory, J.C.; et al. Cosmic-Ray Proton and Helium Spectra: Results from the JACEE Experiment. Astrophys. J. Lett. 1998, 502, 278–283. [Google Scholar] [CrossRef]
- Ivanenko, I.P.; Shestoperov, V.Y.; Chikova, L.O.; Fateeva, I.M.; Khein, L.A.; Podoroznyi, D.M.; Rapoport, I.D.; Samsonov, G.A.; Sobinyakov, V.A.; Turundaevskyi, A.N.; et al. Energy Spectra of Cosmic Rays above 2 TeV as Measured by the ‘SOKOL’ Apparatus. In Proceedings of the 23rd International Cosmic Ray Conference, Alberta, AB, Canada, 19–30 July 1993. [Google Scholar]
- Young, J.S.; Freier, P.S.; Waddington, C.J.; Brewster, N.R.; Fickle, R.K. The elemental and isotopic composition of cosmic rays—Silicon to nickel. Astrophys. J. 1981, 246, 1014–1030. [Google Scholar] [CrossRef]
- Lave, K.A.; Wiedenbeck, M.E.; Binns, W.R.; Christian, E.R.; Cummings, A.C.; Davis, A.J.; De Nolfo, G.A.; Israel, M.H.; Leske, R.A.; Mewaldt, R.A.; et al. Galactic cosmic-ray energy spectra and composition during the 2009–2010 solar minimum period. Astrophys. J. 2013, 770, 117. [Google Scholar] [CrossRef]
- Mueller, D.; Swordy, S.P.; Meyer, P.; L’Heureux, J.; Grunsfeld, J.M. Energy spectra and composition of primary cosmic rays. Astrophys. J. Lett. 1991, 374, 356. [Google Scholar] [CrossRef]
- Hörandel, J. On the knee in the energy spectrum of cosmic rays. Astropart. Phys. 2003, 19, 193–220. [Google Scholar] [CrossRef]
- Sakakibara, S.; Ueno, H.; Fujimoto, K.; Kondo, I.; Nagashima, K. Sidereal Time Variation of Small Air Showers Observed at Mt. Norikura. 1973; Volume 2, p. 1058. Available online: https://ui.adsabs.harvard.edu/abs/1973ICRC....2.1058S (accessed on 9 April 2022).
- Bercovitch, M.; Agrawal, S.P. Cosmic ray anisotropies at median primary rigidities between 100 and 1000 GV. In Proceedings of the International Cosmic Ray Conference, Paris, France, 13–25 July 1981; Available online: https://ui.adsabs.harvard.edu/abs/1981ICRC...10..246B (accessed on 9 April 2022).
- Thambyahpillai, T. The Sidereal Diurnal Variation Measured Underground in London. In Proceedings of the International Cosmic Ray Conference, Bangalore, India, 22 August–3 September 1983; Available online: https://ui.adsabs.harvard.edu/abs/1983ICRC....3..383T (accessed on 9 April 2022).
- Swinson, D.B.; Nagashima, K. Corrected sidereal anisotropy for underground muons. Planet. Space Sci. 1985, 33, 1069–1072. [Google Scholar] [CrossRef]
- Andreyev, Y.M.; Chudakov, A.E.; Kozyarivsky, V.A.; Sidorenko, A.M.; Tulupova, T.I.; Voevodsky, A.V. Cosmic Ray Sidereal Anisotropy Observed by Baksan Underground Muon Telescope. 1987; Volume 2, p. 22. Available online: https://ui.adsabs.harvard.edu/abs/1987ICRC....2...22A (accessed on 9 April 2022).
- Lee, Y.W.; Ng, L.K. Observation of Cosmic-Ray Intensity Variation Using AN Underground Telescope. 1987; Volume 2, p. 18. Available online: https://ui.adsabs.harvard.edu/abs/1987ICRC....2...18L (accessed on 9 April 2022).
- Ueno, H.; Fujii, Z.; Yamada, T. 11 Years Variations of Sidereal Anisotropy Observed at Sakashita Underground Station. 1990; Volume 6, p. 361. Available online: https://ui.adsabs.harvard.edu/abs/1990ICRC....6..361U (accessed on 9 April 2022).
- Cutler, D.J.; Groom, D.E. Mayflower Mine 1500 GV Detector: Cosmic-Ray Anisotropy and Search for Cygnus X-3. Astrophys. J. 1991, 376, 322. [Google Scholar] [CrossRef]
- Munakata, K.; Yasue, S.; Mori, S.; Kato, C.; Koyama, M.; Akahane, S.; Fujii, Z.; Ueno, H.; Humble, J.E.; Fenton, A.G.; et al. Two Hemisphere Observations of the North-South Sidereal Asymmetry at ∼1 TeV. 1995; Volume 4, p. 639. Available online: https://ui.adsabs.harvard.edu/abs/1995ICRC....4..639M (accessed on 9 April 2022).
- Mori, S.; Yasue, S.; Munakata, K.; Kato, C.; Akahane, S.; Koyama, M.; Kitawada, T. Observation of Sidereal Anisotropy of Cosmic Rays at ∼1 TV. 1995; Volume 4, p. 648. Available online: https://ui.adsabs.harvard.edu/abs/1995ICRC....4..648M. (accessed on 9 April 2022).
- Fenton, K.B.; Fenton, A.G.; Humble, J.E. Sidereal Variations at High Energies—Observations at Poatina. 1995; Volume 4, p. 635. Available online: https://ui.adsabs.harvard.edu/abs/1995ICRC....4..635F. (accessed on 9 April 2022).
- Munakata, K.; Kiuchi, T.; Yasue, S.; Kato, C.; Mori, S.; Hirata, K.S.; Kihara, K.; Oyama, Y.; Mori, M.; Fujita, K. Large scale anisotropy of the cosmic ray muon flux in Kamiokande. Phys. Rev. D. 1997, 56, 23–26. [Google Scholar] [CrossRef]
- Ambrosio, M.; Antolini, R.; Baldini, A.; Barbarino, G.C.; Barish, B.C.; Battistoni, G.; Becherini, Y.; Bellotti, R.; Bemporad, C.; Bernardini, P. The Search for the sidereal and solar diurnal modulations in the total MACRO muon data set. Phys. Rev. D. 2003, 67, 042002. [Google Scholar] [CrossRef]
- Gombosi, T.; Kóta, J.; Somogyi, A.J.; Varga, A.; Betev, B.; Katsarski, L.; Kavlakov, S.; Khirov, I. Galactic Cosmic Ray Anisotropy at ≈6 × 1013 eV. 1975; Volume 2, pp. 586–591. Available online: https://ui.adsabs.harvard.edu/abs/1975ICRC....2..586G (accessed on 9 April 2022).
- Alexeyenko, V.V.; Chudakov, A.E.; Gulieva, E.N.; Sborschikov, V.G. Anisotropy of Small EAS (about 10(13) Ev). 1981; Volume 2, p. 146. Available online: https://ui.adsabs.harvard.edu/abs/1981ICRC....2..146A (accessed on 9 April 2022).
- Nagashima, K.; Fujimoto, K.; Sakakibara, S.; Fujii, Z.; Ueno, H.; Murakami, K.; Morishita, I. Galactic Cosmic Ray Anisotropy and Its modulation in the Heliomagnetosphere, Inferred from Air Shower Observation at Mt. Norikura. In Proceedings of the 21st International Cosmic Ray Conference, Adelaide, Australia, 6–19 January 1990; Available online: https://inspirehep.net/literature/309085 (accessed on 9 April 2022).
- Aglietta, M.; Alessandro, B.; Antonioli, P.; Arneodo, F.; Bergamasco, L.; Bertaina, M.; Bosio, A.; Castellin}, A.; Castagnoli, C.; Chaivasa, A.; et al. Study of the Cosmic Ray Anisotropy at Eo ∼ 100 TeV from EAS-TOP: 1992–1994. 1995, Volume 2, p. 800. Available online: https://ui.adsabs.harvard.edu/abs/1995ICRC....2..800A (accessed on 9 April 2022).
- Aglietta, M.; Alessandro, B.; Antonioli, P.; Arneodo, F.; Bergamasco, L.; Bertaina, M.; Bosio, A.; Castellina, A.; Castagnoli, C.; Chiavassa, A. A Measurement of the Solar and Sidereal Cosmic-Ray Anisotropy at E0 approximately 1014 eV. Astrophys. J. 1996, 470, 501–505. [Google Scholar] [CrossRef]
- Alekseenko, V.V.; Cherniaev, A.B.; Djappuev, D.D.; Klimenko, N.F.; Kudjaev, A.U.; Michailova, O.I.; Stenkin, Y.V.; Stepanov, V.I.; Volchenko, V.I. 10-100 TeV cosmic ray anisotropy measured at Baksan EAS ‘Carpet’ array. Nucl. Phys. B Proc. Suppl. 2009, 196, 179–182. [Google Scholar] [CrossRef]
- Amenomori, M.; Ayabe, S.; Cui, S.W.; Danzengluobu; Ding, L.K.; Ding, X.H.; Feng, C.F.; Feng, Z.Y.; Gao, X.Y.; Geng, Q.X. Large-scale sidereal anisotropy of Galactic cosmic-ray intensity observed by the Tibet air shower array. Astrophys. J. Lett. 2005, 626, L29–L32. [Google Scholar] [CrossRef]
- Amenomori, M.; Bi, X.J.; Chen, D.; Chen, T.L.; Chen, W.Y.; Cui, S.W.; Danzengluobu; Ding, L.K.; Feng, C.F.; Feng, Z.; et al. Northern Sky Galactic Cosmic Ray Anisotropy between 10-1000 TeV with the Tibet Air Shower Array. 2015; Volume 34, p. 355. Available online: https://ui.adsabs.harvard.edu/abs/2015ICRC...34..355A (accessed on 9 April 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).