The Higgs Mechanism and Cosmological Constant Today
Abstract
1. Introduction
2. From Symmetry Breaking to Symmetry Restoration
3. Summary and Conclusions
- (i)
- The Higgs field can be dynamically responsible for the universe evolution from the initial symmetry breaking to the final symmetry restoration.
- (ii)
- The presently observed value of corresponds to an absolute lower limit in its quantum spectrum.
- (iii)
- The value of today must be non-zero in principle.
- (iv)
- There exists the relevant energy scale, eV, characteristic for symmetry restoration related to the observed value of the cosmological constant.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Englert, F.; Brout, R. Broken Symmetries and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 1964, 13, 321. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 1964, 13, 508. [Google Scholar] [CrossRef]
- Quigg, C. Gauge Theories of the Strong, Weak and Electromagnetic Interactions; Addison-Wesley Publishing Company: Redwood City, CA, USA, 1983. [Google Scholar]
- Bezrukov, F.; Shaposhnikov, M. The Standard Model Higgs boson as the inflaton. Phys. Lett. B 2008, 659, 703–706. [Google Scholar] [CrossRef]
- Bezrukov, F.; Gorbunov, D.; Shaposhnikov, M. On initial conditions for the Hot Big Bang. J. Cosmol. Astropart. Phys. 2009, 2009, 29. [Google Scholar] [CrossRef]
- Bezrukov, F.; Magnin, A.; Shaposhnikov, M.; Sibiryakov, S. Higgs inflation: Consistency and generalisations. J. High Energy Phys. 2011, 16. [Google Scholar] [CrossRef]
- Bezrukov, F. The Higgs field as an inflaton. Class. Quant. Grav. 2013, 30, 214001. [Google Scholar] [CrossRef]
- Bezrukov, F.; Shaposhnikov, M. Higgs inflation at the critical point. Phys. Lett. B 2014, 734, 249–254. [Google Scholar] [CrossRef]
- Aguilar, J.E.M.; Zamarripa, J.; Monte, M.; Romero, C. Higgs inflation in complex geometrical scalar-tensor theory of gravity. Phys. Dark Universe 2020, 28, 100480. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I.; Nissimov, E.; Pacheva, S. Quintessential Inflation with Dynamical Higgs Generation as an Affine Gravity. Symmetry 2020, 12, 734. [Google Scholar] [CrossRef]
- Jain, M.; Hertzberg, M.P. Eternal Inflation and Reheating in the Presence of the Standard Model Higgs Field. Phys. Rev. D 2020, 101, 103506. [Google Scholar] [CrossRef]
- Gialamas, I.D.; Karam, A.; Lykkas, A.; Pappas, T.D. Palatini-Higgs inflation with non-minimal derivative coupling. Phys. Rev. D 2020, 102, 063522. [Google Scholar] [CrossRef]
- Bargach, A.; Bargach, F.; Mariam Bouhmadi-López, M.; Taoufik Ouali, T. Non-minimal Higgs inflation within holographic cosmology. Phys. Rev. D 2020, 102, 123540. [Google Scholar] [CrossRef]
- Barrie, N.D.; Sugamoto, A.; Takeuchi, T.; Yamashita, K. Higgs Inflation, Vacuum Stability, and Leptogenesis. J. High Energy Phys. 2020, 2020, 72. [Google Scholar] [CrossRef]
- Bojowald, M.; Brahma, S.; Crowe, S.; Ding, D.; McCracken, J. Quantum Higgs Inflation. Phys. Lett. B 2021, 816, 136193. [Google Scholar] [CrossRef]
- Cheong, D.Y.; Lee, S.M.; Park, C.S. Progress in Higgs inflation. J. Korean Phys. Soc. 2021, 78, 897–906. [Google Scholar] [CrossRef]
- Bostan, N. Palatini Higgs and Coleman-Weinberg inflation with non-minimal coupling. JCAP 2021, 2021, 42. [Google Scholar] [CrossRef]
- Karydas, S.; Papantonopoulos, E.; Saridakis, E.N. Successful Higgs inflation from combined nonminimal and derivative couplings. Phys. Rev. D 2021, 104, 023530. [Google Scholar] [CrossRef]
- Turner, M.S. Inflation after COBE.Fermilab-Conf.92/313-A. 1992. Available online: https://www.osti.gov/servlets/purl/10158604 (accessed on 24 May 2022).
- Horn, B. The Higgs Field and Early Universe Cosmology: A (Brief) Review. Physics 2020, 2, 503–552. [Google Scholar] [CrossRef]
- Hamada, Y.; Kawana, K.; Scherlis, A. On Preheating in Higgs Inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 62. [Google Scholar] [CrossRef]
- Dymnikova, I.; Krawczyk, M. First postinflationary particles equation of state. In Birth of the Universe; Occhionero, F., Ed.; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Kofman, L.; Linde, A.; Starobinsky, A. Reheating after inflation. Phys. Rev. Lett. 1994, 73, 3195. [Google Scholar] [CrossRef]
- Dymnikova, I.; Krawczyk, M. Equation of state and temperature of massive nonrelativistic bosons arising in the universe at the first stage of reheating. MPLA 1995, 10, 3069–3076. [Google Scholar] [CrossRef]
- Wu, Y.-P. Higgs as heavy-lifted physics during inflation. J. High Energy Phys. 2019, 2019, 125. [Google Scholar] [CrossRef]
- Mantziris, A.; Markkanen, T.; Rajantie, A. Vacuum decay constraints on the Higgs curvature coupling from inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 77. [Google Scholar] [CrossRef]
- Litsa, A.; Freese, K.; Sfakianakis, E.I.; Stengel, P.; Visinelli, L. Large Density Perturbations from Reheating to Standard Model particles due to the Dynamics of the Higgs Boson during Inflation. Phys. Rev. D 2021, 104, 123546. [Google Scholar] [CrossRef]
- Riess, A.G.; Kirschner, R.P.; Schmidt, B.P.; Iha, S.; Challis, P.; Garnavich, P.M.; Esin, A.A.; Carpenter, C.; Grashins, R.; Schild, R.E.; et al. BV RI light curves for 22 type Ia supernovae. Astron. J. 1999, 117, 707–724. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Bahcall, N.A.; Ostriker, J.P.; Perlmutter, S.; Steinhardt, P.J. The cosmic triangle: Revealing the state of the universe. Science 1999, 284, 1481–1488. [Google Scholar] [CrossRef]
- Corasaniti, P.S.; Copeland, E.J. Constraining the quintessence equation of state with SnIa data and CMB peaks. Phys. Rev. D 2002, 65, 043004. [Google Scholar] [CrossRef]
- Hannestad, S.; Mortsell, E. Probing the dark side: Constraints on the dark energy equation of state from CMB, large scale structure, and type Ia supernovae. Phys. Rev. D 2002, 66, 063508. [Google Scholar] [CrossRef]
- Bassett, B.A.; Kunz, M.; Silk, J.; Ungarelli, C. A late-time transition in the cosmic dark energy? Mon. Not. R. Astron. Soc. 2002, 336, 1217–1222. [Google Scholar] [CrossRef]
- Schmidt, B.P.; Barris, B.; Candia, P.; Challis, P.; Clocchiatti, A.; Cail, A.L.; Filippenko, A.V.; Garnavich, P.; Hogan, C.; Holland, S.T.; et al. Cosmological results from high-z supernovae. Astrophys. J. 2003, 594, 1–24. [Google Scholar]
- Rivera, A.B.; Farieta, J.G. Exploring the Dark Universe: Constraint on dynamical dark energy models from CMB, BAO and Growth Rate Measurements. Intern. J. Mod. Phys. D 2019, 28, 1950118. [Google Scholar] [CrossRef]
- Dymnikova, I.; Filchenkov, M. Gauge-noninvariance of quantum cosmology and vacuum dark energy. Phys. Lett. B 2006, 635, 181–185. [Google Scholar] [CrossRef]
- Halliwell, J.J. Derivation of the Wheeler-DeWitt equation from a path integral for minisuperspace models. Phys. Rev. D 1988, 38, 2468. [Google Scholar] [CrossRef]
- Dymnikova, I.; Khlopov, M. Decay of cosmological constant as Bose-condensate evaporation. Mod. Phys. Lett. A 2000, 15, 2305–2314. [Google Scholar] [CrossRef]
- Dymnikova, I. The Higgs Mechanism and Spacetime Symmetry. Universe 2020, 6, 179. [Google Scholar] [CrossRef]
- Dymnikova, I.G. Inflationary universe from the point of view of General Relativity. Zh. Eksper. Theor. Phys. 1986, 90, 1900–1907. [Google Scholar]
- Olive, K. Inflation. Phys. Rep. 1990, 190, 309–403. [Google Scholar] [CrossRef]
- Gibbons, G.W. Phantom Matter and the Cosmological Constant. arXiv 2003, arXiv:hep-th/0302199v1. [Google Scholar]
- Dymnikova, I. Dark energy and spacetime symmetry. Universe 2017, 3, 20. [Google Scholar] [CrossRef]
- Dymnikova, I. Fundamental roles of the de Sitter vacuum. Universe 2020, 6, 101. [Google Scholar] [CrossRef]
- Boyanovsky, D.; de Vega, H.J.; Schwarz, D.J. Phase Transitions in the Early and Present Universe. 2006 Ann. Rev. Nucl. Part. Sci 2006, 56, 441–500. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Overduin, J.M.; Cooperstock, F.I. Evolution of the scale factor with a variable cosmological term. Phys. Rev. D 1998, 58, 043506. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Solà, J.; Espana-Bonet, C.; Ruiz-Lapuente, P. Variable cosmological constant as a Planck scale effect. Phys. Lett. B 2003, 574, 149. [Google Scholar] [CrossRef]
- Espana-Bonet, C.; Ruiz-Lapuente, P.; Shapiro, I.L.; Solà, J. Testing the running of the cosmological constant with type Ia supernovae at high z. J. Cosmol. Astropart. Phys. 2004, 2004, 6. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A. The ΛCDM cosmology: From inflation to dark energy through running Λ. Int. J. Mod. Phys. D 2015, 24, 1541003. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; de Cruz Pérez, J.; Gómez-Valent, A. Possible signals of vacuum dynamics in the Universe. Mon. Not. R. Astron. Soc. 2018, 478, 4357. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Solà Peracaula, J. Running vacuum in quantum field theory in curved spacetime: Renormalizing ρ vac without ∼m4 terms. Eur. Phys. J. C 2020, 80, 692. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Solà Peracaula, J. Renormalizing the vacuum energy in cosmological spacetime: Implications for the cosmological constant problem. arXiv 2022, arXiv:2201.05827. [Google Scholar]
- Solà Peracaula, J. The Cosmological Constant Problem and Running Vacuum in the Expanding Universe. arXiv 2022, arXiv:2203.13757. [Google Scholar]
- Kennedy, A.; Lazarides, G.; Shafi, Q. Decay of the false vacuum in the very early universe. Phys. Lett. B 1981, 99, 38. [Google Scholar] [CrossRef][Green Version]
- Sahni, V.; Starobinsky, A. The Case for a Positive Cosmological Λ-term. Intern. J. Mod. Phys. D 2000, 9, 373–443. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Abdalla, E.; Graef, L.L.; Wang, B. A model for dark energy decay. Phys. Lett. B 2013, 726, 786–790. [Google Scholar] [CrossRef]
- Szydlowski, M.; Stachowski, A.; Urbanowski, K. Cosmology with a decaying vacuum energy parametrization derived from quantum mechanics. J. Phys. Conf. Ser. 2015, 626, 012033. [Google Scholar] [CrossRef]
- Dymnikova, I.; Dobosz, A.; Sołtysek, B. Lemaître Class Dark Energy Model for Relaxing Cosmological Constant. Universe 2017, 3, 39. [Google Scholar] [CrossRef]
- Márián, I.G.; Jentschura, U.D.; Defenu, N.; Trombettoni, A.; Nándori, I. Vacuum energy and renormalization of the field-independent term. J. Cosmol. Astropart. Phys. 2022, 3, 62. [Google Scholar]
- Urbanowski, K. Cosmological “constant” in a universe born in the metastable false vacuum state. Eur. Phys. J. C 2022, 82, 242. [Google Scholar] [CrossRef]
- Aich, A. Phenomenological dark energy model with hybrid dynamic cosmological constant. Class. Quant. Grav. 2022, 39, 035010. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113. [Google Scholar] [CrossRef]
- Wheeler, J.A. Superspace and the nature of quantum cosmology. In Battelle Rencontres; DeWitt, C.M., Wheeler, J.A., Eds.; W. A. Benjamin, Inc.: New York, NY, USA, 1968; pp. 242–308. [Google Scholar]
- Vilenkin, A. Approaches to quantum cosmology. Phys. Rev. D 1994, 50, 2581. [Google Scholar] [CrossRef] [PubMed]
- Vilenkin, A. Creation of universes from nothing. Phys. Lett. B 1982, 117, 25–28. [Google Scholar] [CrossRef]
- Dymnikova, I.; Fil’chenkov, M. Quantum birth of the hot universe. Phys. Lett. B 2002, 545, 214–219. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum creation of universes. Phys. Rev. D 1984, 30, 509. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics. Nonrelativistic Theory; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Bronnikov, K.; Dymnikova, I.; Galaktionov, E. Multihorizon spherically symmetric spacetime with several scales of vacuum energy. Class. Quant. Grav. 2012, 29, 095025. [Google Scholar] [CrossRef]
- Dymnikova, I. The algebraic structure of a cosmological term in spherically symmetric solutions. Phys. Lett. B 2000, 472, 33–38. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Vacuum dark fluid. Phys. Lett. B 2007, 645, 358–364. [Google Scholar] [CrossRef]
- Borghini, N.; Cottingham, W.N.; Mau, R.V. Possible cosmological implications of the quark-hadron phase transition. J. Phys. G 2000, 26, 771–785. [Google Scholar] [CrossRef]
- Boeckel, T.; Schaffner, J. A Little Inflation in the Early Universe at the QCD Phase Transition. Phys. Rev. Lett. 2010, 105, 041301. [Google Scholar] [CrossRef]
- Harko, T.; Mak, M.K. Bianchi type I universes with dilaton and magnetic fields. Int. J. Mod. Phys. D 2002, 11, 1171. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Chudayeva, E.N.; Shikin, G.N. Magneto-dilatonic Bianchi-I cosmology: Isotropization and singularity problems. Class. Quant. Grav. 2004, 21, 3389. [Google Scholar] [CrossRef]
- Szydlowski, M.; Stachowski, A.; Urbanowski, K. The evolution of the FRW universe with decaying metastable dark energy—A dynamical system analysis. J. Cosmol. Astropart. Phys. 2020, 4, 29. [Google Scholar] [CrossRef]
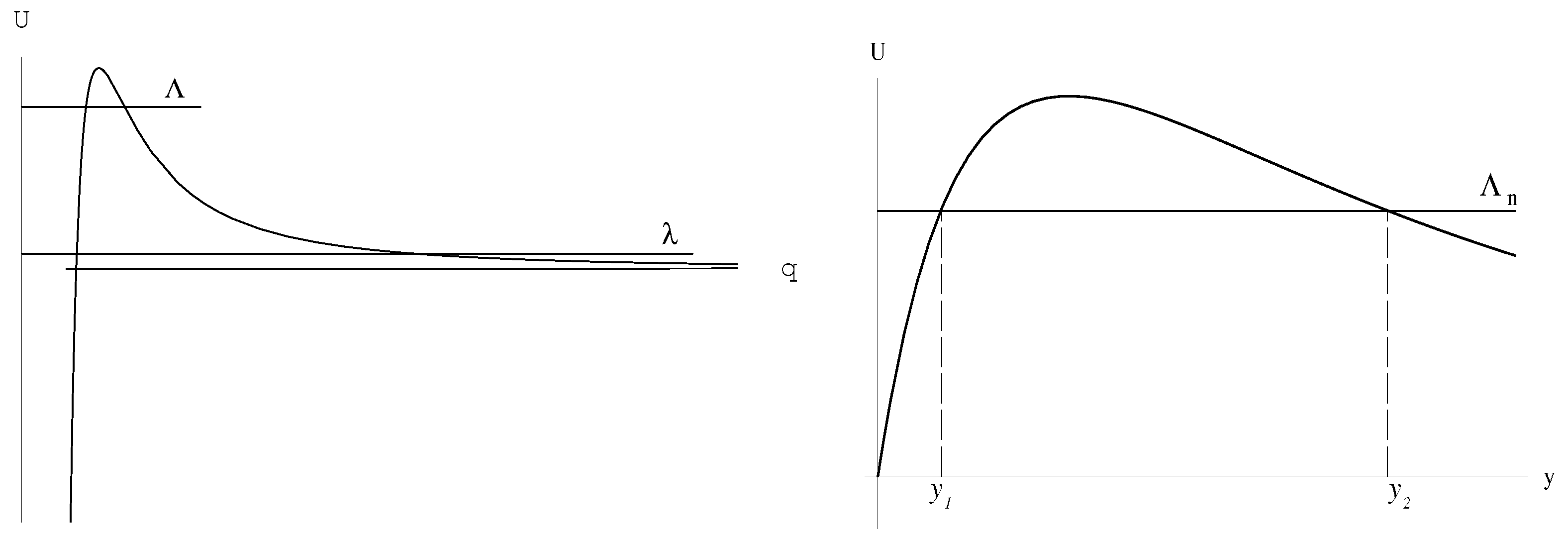
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dymnikova, I. The Higgs Mechanism and Cosmological Constant Today. Universe 2022, 8, 305. https://doi.org/10.3390/universe8060305
Dymnikova I. The Higgs Mechanism and Cosmological Constant Today. Universe. 2022; 8(6):305. https://doi.org/10.3390/universe8060305
Chicago/Turabian StyleDymnikova, Irina. 2022. "The Higgs Mechanism and Cosmological Constant Today" Universe 8, no. 6: 305. https://doi.org/10.3390/universe8060305
APA StyleDymnikova, I. (2022). The Higgs Mechanism and Cosmological Constant Today. Universe, 8(6), 305. https://doi.org/10.3390/universe8060305




