Cosmological Parameter Estimation Using Current and Future Observations of Strong Gravitational Lensing
Abstract
1. Introduction
2. Methodology and Data
2.1. Velocity Dispersion of Lens Galaxies
2.2. Time-Delay Measurements
3. Results and Discussions
3.1. The Constraints on Cosmological Parameters with Current Observations of SGL
3.2. Forecast for the Constraints on Cosmological Parameters with the Future Observations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; Page, L.; Spergel, D.N.; Tucker, G.S.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Preliminary maps and basic results. Astrophys. J. Suppl. 2003, 148, 1–27. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Zhang, X. Gravitational wave standard sirens and cosmological parameter measurement. Sci. China Phys. Mech. Astron. 2019, 62, 110431. [Google Scholar] [CrossRef]
- Qi, J.Z.; Zhang, X. A new cosmological probe using super-massive black hole shadows. Chin. Phys. C 2020, 44, 055101. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, L.; Zhang, J.F.; Zhang, X. Constraints on brane inflation after Planck 2015: Impacts of the latest local measurement of the Hubble constant. Sci. China Phys. Mech. Astron. 2019, 62, 30411. [Google Scholar] [CrossRef]
- Vattis, K.; Koushiappas, S.M.; Loeb, A. Dark matter decaying in the late Universe can relieve the H0 tension. Phys. Rev. D 2019, 99, 121302. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, J.F.; Zhang, X. Inflation model selection revisited after a 1.91% measurement of the Hubble constant. Sci. China Phys. Mech. Astron. 2020, 63, 290406. [Google Scholar] [CrossRef]
- Zhang, J.F.; Geng, J.J.; Zhang, X. Neutrinos and dark energy after Planck and BICEP2: Data consistency tests and cosmological parameter constraints. JCAP 2014, 10, 044. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, J.F.; Zhang, X. Can the H0 tension be resolved in extensions to ΛCDM cosmology? JCAP 2019, 02, 054. [Google Scholar] [CrossRef]
- Zhao, M.M.; He, D.Z.; Zhang, J.F.; Zhang, X. Search for sterile neutrinos in holographic dark energy cosmology: Reconciling Planck observation with the local measurement of the Hubble constant. Phys. Rev. D 2017, 96, 043520. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, X. Constraints on inflation revisited: An analysis including the latest local measurement of the Hubble constant. Eur. Phys. J. C 2017, 77, 882. [Google Scholar] [CrossRef]
- Feng, L.; He, D.Z.; Li, H.L.; Zhang, J.F.; Zhang, X. Constraints on active and sterile neutrinos in an interacting dark energy cosmology. Sci. China Phys. Mech. Astron. 2020, 63, 290404. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Z.; Luo, X.; Miao, H.; Singh, N.K.; Huang, L. Can Non-Standard Recombination Resolve the Hubble Tension? Sci. China Phys. Mech. Astron. 2020, 63, 290405. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Q.G. Measuring H0 from low-z datasets. Sci. China Phys. Mech. Astron. 2020, 63, 290402. [Google Scholar] [CrossRef]
- Ding, Q.; Nakama, T.; Wang, Y. A gigaparsec-scale local void and the Hubble tension. Sci. China Phys. Mech. Astron. 2020, 63, 290403. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Fantaye, Y.; Heavens, A. Bayesian evidence against the Harrison-Zel’dovich spectrum in tensions with cosmological data sets. Phys. Rev. D 2018, 98, 063508. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW–XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. R. Astron. Soc. 2020, 498, 1420–1439. [Google Scholar] [CrossRef]
- Millon, M.; Galan, A.; Courbin, F.; Treu, T.; Suyu, S.H.; Ding, X.; Birrer, S.; Chen, G.F.; Shajib, A.J.; Sluse, D.; et al. TDCOSMO. I. An exploration of systematic uncertainties in the inference of H0 from time-delay cosmography. Astron. Astrophys. 2020, 639, A101. [Google Scholar] [CrossRef]
- Rusu, C.E.; Wong, K.C.; Bonvin, V.; Sluse, D.; Suyu, S.H.; Fassnacht, C.D.; Chan, J.H.; Hilbert, S.; Auger, M.W.; Sonnenfeld, A.; et al. H0LiCOW XII. Lens mass model of WFI2033-4723 and blind measurement of its time-delay distance and H0. Mon. Not. R. Astron. Soc. 2020, 498, 1440–1468. [Google Scholar] [CrossRef]
- Chen, G.C.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; Chan, J.H.; Wong, K.C.; Auger, M.W.; Hilbert, S.; Bonvin, V.; Birrer, S.; et al. A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging. Mon. Not. R. Astron. Soc. 2019, 490, 1743–1773. [Google Scholar] [CrossRef]
- Shajib, A.J.; Birrer, S.; Treu, T.; Agnello, A.; Buckley-Geer, E.J.; Chan, J.H.H.; Christensen, L.; Lemon, C.; Lin, H.; Millon, M.; et al. STRIDES: A 3.9 per cent measurement of the Hubble constant from the strong lens system DES J0408-5354. Mon. Not. R. Astron. Soc. 2020, 494, 6072–6102. [Google Scholar] [CrossRef]
- Ivezić, Ž; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. Astrophys. J. 2019, 873, 111. [Google Scholar] [CrossRef]
- Huber, S.; Suyu, S.H.; Noebauer, U.M.; Bonvin, V.; Rothchild, D.; Chan, J.H.H.; Awan, H.; Courbin, F.; Kromer, M.; Marshall, P.; et al. Strongly lensed SNe Ia in the era of LSST: Observing cadence for lens discoveries and time-delay measurements. Astron. Astrophys. 2019, 631, A161. [Google Scholar] [CrossRef]
- Jee, I.; Komatsu, E.; Suyu, S.H.; Huterer, D. Time-delay Cosmography: Increased Leverage with Angular Diameter Distances. JCAP 2016, 04, 031. [Google Scholar] [CrossRef]
- Wen, X.; Liao, K. Calibrating the standard candles with strong lensing. Eur. Phys. J. C 2020, 80, 94. [Google Scholar] [CrossRef]
- Shajib, A.J.; Treu, T.; Agnello, A. Improving time-delay cosmography with spatially resolved kinematics. Mon. Not. R. Astron. Soc. 2018, 473, 210–226. [Google Scholar] [CrossRef]
- Dev, A.; Jain, D.; Mahajan, S. Dark energy and the statistical study of the observed image separations of the multiply imaged systems in the class statistical sample. Int. J. Mod. Phys. D 2004, 13, 1005–1018. [Google Scholar] [CrossRef]
- Cao, S.; Covone, G.; Zhu, Z.H. Testing the dark energy with gravitational lensing statistics. Astrophys. J. 2012, 755, 31. [Google Scholar] [CrossRef]
- Mitchell, J.L.; Keeton, C.R.; Frieman, J.A.; Sheth, R.K. Robust cosmological constraints from gravitational lens statistics. Astrophys. J. 2005, 622, 81–98. [Google Scholar] [CrossRef]
- Cao, S.; Zhu, Z.H. Constraints on cosmological models from lens redshift data. Astron. Astrophys. 2012, 538, A43. [Google Scholar] [CrossRef]
- Ma, Y.B.; Cao, S.; Zhang, J.; Geng, S.; Liu, Y.; Liu, T.; Pan, Y. Implications of the lens redshift distribution of strong lensing systems: Cosmological parameters and the global properties of early-type galaxies. Eur. Phys. J. C 2019, 79, 121. [Google Scholar] [CrossRef]
- Biesiada, M. Strong lensing systems as a probe of dark energy in the universe. Phys. Rev. D 2006, 73, 023006. [Google Scholar] [CrossRef]
- Grillo, C.; Lombardi, M.; Bertin, G. Cosmological parameters from strong gravitational lensing and stellar dynamics in elliptical galaxies. Astron. Astrophys. 2008, 477, 397. [Google Scholar] [CrossRef]
- Schwab, J.; Bolton, A.S.; Rappaport, S.A. Galaxy-Scale Strong Lensing Tests of Gravity and Geometric Cosmology: Constraints and Systematic Limitations. Astrophys. J. 2010, 708, 750–757. [Google Scholar] [CrossRef]
- Cao, S.; Biesiada, M.; Gavazzi, R.; Piórkowska, A.; Zhu, Z.H. Cosmology With Strong-lensing Systems. Astrophys. J. 2015, 806, 185. [Google Scholar] [CrossRef]
- Qi, J.Z.; Cao, S.; Zhang, S.; Biesiada, M.; Wu, Y.; Zhu, Z.H. The distance sum rule from strong lensing systems and quasars—Test of cosmic curvature and beyond. Mon. Not. R. Astron. Soc. 2019, 483, 1104–1113. [Google Scholar] [CrossRef]
- Li, Z.; Ding, X.; Wang, G.J.; Liao, K.; Zhu, Z.H. Curvature from strong gravitational lensing: A spatially closed Universe or systematics? Astrophys. J. 2018, 854, 146. [Google Scholar] [CrossRef]
- Cui, J.L.; Li, H.L.; Zhang, X. No evidence for the evolution of mass density power-law index γ from strong gravitational lensing observation. Sci. China Phys. Mech. Astron. 2017, 60, 080411. [Google Scholar] [CrossRef][Green Version]
- Cao, S.; Li, X.; Biesiada, M.; Xu, T.; Cai, Y.; Zhu, Z.H. Test of parametrized post-Newtonian gravity with galaxy-scale strong lensing systems. Astrophys. J. 2017, 835, 92. [Google Scholar] [CrossRef]
- Wang, B.; Qi, J.Z.; Zhang, J.F.; Zhang, X. Cosmological Model-independent Constraints on Spatial Curvature from Strong Gravitational Lensing and SN Ia Observations. Astrophys. J. 2020, 898, 100. [Google Scholar] [CrossRef]
- Wang, Y.J.; Qi, J.Z.; Wang, B.; Zhang, J.F.; Cui, J.L.; Zhang, X. Cosmological model-independent measurement on cosmic curvature using distance sum rule with the help of gravitational waves. arXiv 2022, arXiv:2201.12553. [Google Scholar]
- Wei, J.J.; Chen, Y.; Cao, S.; Wu, X.F. Direct Estimate of the Post-Newtonian Parameter and Cosmic Curvature from Galaxy-scale Strong Gravitational Lensing. Astrophys. J. Lett. 2022, 927, L1. [Google Scholar] [CrossRef]
- Geng, S.; Cao, S.; Liu, Y.; Liu, T.; Biesiada, M.; Lian, Y. The velocity dispersion function of early-type galaxies and its redshift evolution: The newest results from lens redshift test. Mon. Not. R. Astron. Soc. 2021, 503, 1319–1326. [Google Scholar] [CrossRef]
- Chen, Y.; Li, R.; Shu, Y.; Cao, X. Assessing the effect of lens mass model in cosmological application with updated galaxy-scale strong gravitational lensing sample. Mon. Not. R. Astron. Soc. 2019, 488, 3745–3758. [Google Scholar] [CrossRef]
- Liu, X.H.; Li, Z.H.; Qi, J.Z.; Zhang, X. Galaxy-Scale Test of General Relativity with Strong Gravitational Lensing. Astrophys. J. 2022, 927, 28. [Google Scholar] [CrossRef]
- Qi, J.Z.; Cui, Y.; Hu, W.H.; Zhang, J.F.; Cui, J.L.; Zhang, X. Strongly lensed type Ia supernovae as a precise late-universe probe of measuring the Hubble constant and cosmic curvature. arXiv 2022, arXiv:2202.01396. [Google Scholar]
- Oguri, M.; Marshall, P.J. Gravitationally lensed quasars and supernovae in future wide-field optical imaging surveys. Mon. Not. R. Astron. Soc. 2010, 405, 2579–2593. [Google Scholar] [CrossRef]
- Collett, T.E. The population of galaxy-galaxy strong lenses in forthcoming optical imaging surveys. Astrophys. J. 2015, 811, 20. [Google Scholar] [CrossRef]
- Goldstein, D.A.; Nugent, P.E.; Goobar, A. Rates and Properties of Supernovae Strongly Gravitationally Lensed by Elliptical Galaxies in Time-domain Imaging Surveys. Astrophys. J. Suppl. 2019, 243, 6. [Google Scholar] [CrossRef]
- Wojtak, R.; Hjorth, J.; Gall, C. Magnified or multiply imaged? – Search strategies for gravitationally lensed supernovae in wide-field surveys. Mon. Not. R. Astron. Soc. 2019, 487, 3342–3355. [Google Scholar] [CrossRef]
- Cao, S.; Pan, Y.; Biesiada, M.; Godlowski, W.; Zhu, Z.H. Constraints on cosmological models from strong gravitational lensing systems. JCAP 2012, 03, 016. [Google Scholar] [CrossRef]
- Cao, S.; Zhu, Z.H. Cosmic equation of state from combined angular diameter distances: Does the tension with luminosity distances exist? Phys. Rev. D 2014, 90, 083006. [Google Scholar] [CrossRef]
- Li, X.L.; Cao, S.; Zheng, X.G.; Li, S.; Biesiada, M. Comparison of cosmological models using standard rulers and candles. Res. Astron. Astrophys. 2016, 16, 084. [Google Scholar] [CrossRef][Green Version]
- Qi, J.Z.; Zhao, J.W.; Cao, S.; Biesiada, M.; Liu, Y. Measurements of the Hubble constant and cosmic curvature with quasars: Ultracompact radio structure and strong gravitational lensing. Mon. Not. R. Astron. Soc. 2021, 503, 2179–2186. [Google Scholar] [CrossRef]
- Cao, M.D.; Zheng, J.; Qi, J.Z.; Zhang, X.; Zhu, Z.H. A new way to explore cosmological tensions using gravitational waves and strong gravitational lensing. arXiv 2021, arXiv:2112.14564. [Google Scholar]
- Wu, P.J.; Shao, Y.; Jin, S.J.; Zhang, X. A path to precision cosmology: Synergy between four promising late-universe cosmological probes. arXiv 2022, arXiv:2202.09726. [Google Scholar]
- Suyu, S.H.; Treu, T.; Hilbert, S.; Sonnenfeld, A.; Auger, M.W.; Blandford, R.D.; Collett, T.; Courbin, F.; Fassnacht, C.D.; Koopmans, L.V.; et al. Cosmology from gravitational lens time delays and Planck data. Astrophys. J. Lett. 2014, 788, L35. [Google Scholar] [CrossRef]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the Early and the Late Universe. Nat. Astron. 2019, 3, 891. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Kormann, R.; Schneider, P.; Bartelmann, M. Isothermal elliptical gravitational lens models. Astron. Astrophys. 1994, 284, 285–299. [Google Scholar]
- Asada, H.; Hamana, T.; Kasai, M. Images for an isothermal ellipsoidal gravitational lens from a single real algebraic equation. Astron. Astrophys. 2003, 397, 825. [Google Scholar] [CrossRef]
- Koopmans, L.V.E. Gravitational lensing & stellar dynamics. EAS Publ. Ser. 2006, 20, 161. [Google Scholar] [CrossRef][Green Version]
- Jorgensen, I.; Franx, M.; Kjaergaard, P. Spectroscopy for E and S0 galaxies in nine clusters. Mon. Not. R. Astron. Soc. 1995, 276, 1341–1364. [Google Scholar]
- Jiang, G.; Kochanek, C.S. The Baryon Fractions and Mass-to-Light Ratios of Early-Type Galaxies. Astrophys. J. 2007, 671, 1568. [Google Scholar] [CrossRef]
- Schechter, P.L.; Bailyn, C.D.; Barr, R.; Barvainis, R.; Becker, C.M.; Bernstein, G.M.; Blakeslee, J.P.; Bus, S.J.; Dressler, A.; Falco, E.E.; et al. The Quadruple gravitational lens PG1115+080: Time delays and models. Astrophys. J. Lett. 1997, 475, L85–L88. [Google Scholar] [CrossRef]
- Fassnacht, C.D.; Pearson, T.J.; Readhead, A.C.S.; Browne, I.W.A.; Koopmans, L.V.E.; Myers, S.T.; Wilkinson, P.N. A determination of h_0 with the class gravitational lens b1608+656: I. time delay measurements with the vla. Astrophys. J. 1999, 527, 498. [Google Scholar] [CrossRef][Green Version]
- Fassnacht, C.D.; Xanthopoulos, E.; Koopmans, L.V.E.; Rusin, D. A determination of H(O) with the class gravitational lens B1608+656. 3. A Significant improvement in the precision of the time delay measurements. Astrophys. J. 2002, 581, 823–835. [Google Scholar] [CrossRef]
- Kochanek, C.S.; Morgan, N.D.; Falco, E.E.; McLeod, B.A.; Winn, J.N.; Dembicky, J.; Ketzeback, B. The Time delays of gravitational lens HE0435-1223: An Early-type galaxy with a rising rotation curve. Astrophys. J. 2006, 640, 47–61. [Google Scholar] [CrossRef][Green Version]
- Courbin, F.; Chantry, V.; Revaz, Y.; Sluse, D.; Faure, C.; Tewes, M.; Eulaers, E.; Koleva, M.; Asfandiyarov, I.; Dye, S.; et al. COSMOGRAIL: The COSmological MOnitoring of GRAvItational Lenses IX. Time delays, lens dynamics and baryonic fraction in HE 0435-1223. Astron. Astrophys. 2011, 536, A53. [Google Scholar] [CrossRef]
- Refsdal, S. On the possibility of determining Hubble’s parameter and the masses of galaxies from the gravitational lens effect. Mon. Not. R. Astron. Soc. 1964, 128, 307. [Google Scholar] [CrossRef]
- Suyu, S.H.; Marshall, P.J.; Auger, M.W.; Hilbert, S.; Blandford, R.D.; Koopmans, L.V.E.; Fassnacht, C.D.; Treu, T. Dissecting the Gravitational Lens B1608+656. II. Precision Measurements of the Hubble Constant, Spatial Curvature, and the Dark Energy Equation of State. Astrophys. J. 2010, 711, 201–221. [Google Scholar] [CrossRef]
- Bonvin, V.; Courbin, F.; Suyu, S.H.; Marshall, P.J.; Rusu, C.E.; Sluse, D.; Tewes, M.; Wong, K.C.; Collett, T.; Fassnacht, C.D.; et al. H0LiCOW–V. New COSMOGRAIL time delays of HE 0435-1223: H0 to 3.8 per cent precision from strong lensing in a flat ΛCDM model. Mon. Not. R. Astron. Soc. 2017, 465, 4914–4930. [Google Scholar] [CrossRef]
- Jee, I.; Suyu, S.; Komatsu, E.; Fassnacht, C.D.; Hilbert, S.; Koopmans, L.V.E. A measurement of the Hubble constant from angular diameter distances to two gravitational lenses. Science 2019, 365, 1134–1138. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.C.; Suyu, S.H.; Auger, M.W.; Bonvin, V.; Courbin, F.; Fassnacht, C.D.; Halkola, A.; Rusu, C.E.; Sluse, D.; Sonnenfeld, A.; et al. H0LiCOW–IV. Lens mass model of HE 0435-1223 and blind measurement of its time-delay distance for cosmology. Mon. Not. R. Astron. Soc. 2017, 465, 4895–4913. [Google Scholar] [CrossRef]
- Birrer, S.; Treu, T.; Rusu, C.E.; Bonvin, V.; Fassnacht, C.D.; Chan, J.H.H.; Agnello, A.; Shajib, A.J.; Chen, G.C.; Auger, M.; et al. H0LiCOW–IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant. Mon. Not. R. Astron. Soc. 2019, 484, 4726. [Google Scholar] [CrossRef]
- Agnello, A.; Lin, H.; Buckley-Geer, L.; Treu, T.; Bonvin, V.; Courbin, F.; Lemon, C.; Morishita, T.; Amara, A.; Auger, M.W.; et al. Models of the strongly lensed quasar DES J0408-5354. Mon. Not. R. Astron. Soc. 2017, 472, 4038–4050. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306–312. [Google Scholar] [CrossRef]
- Suyu, S.H.; Bonvin, V.; Courbin, F.; Fassnacht, C.D.; Rusu, C.E.; Sluse, D.; Treu, T.; Wong, K.C.; Auger, M.W.; Ding, X.; et al. H0LiCOW–I. H0 Lenses in COSMOGRAIL’s Wellspring: Program overview. Mon. Not. R. Astron. Soc. 2017, 468, 2590–2604. [Google Scholar] [CrossRef]
- Suyu, S.H.; Huber, S.; Cañameras, R.; Kromer, M.; Schuldt, S.; Taubenberger, S.; Yıldırım, A.; Bonvin, V.; Chan, J.H.H.; Courbin, F.; et al. HOLISMOKES–I. Highly Optimised Lensing Investigations of Supernovae, Microlensing Objects, and Kinematics of Ellipticals and Spirals. Astron. Astrophys. 2020, 644, A162. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhang, M.; Jin, S.J.; Qi, J.Z.; Zhang, X. Cosmological parameter estimation with future gravitational wave standard siren observation from the Einstein Telescope. JCAP 2019, 09, 068. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar] [CrossRef]
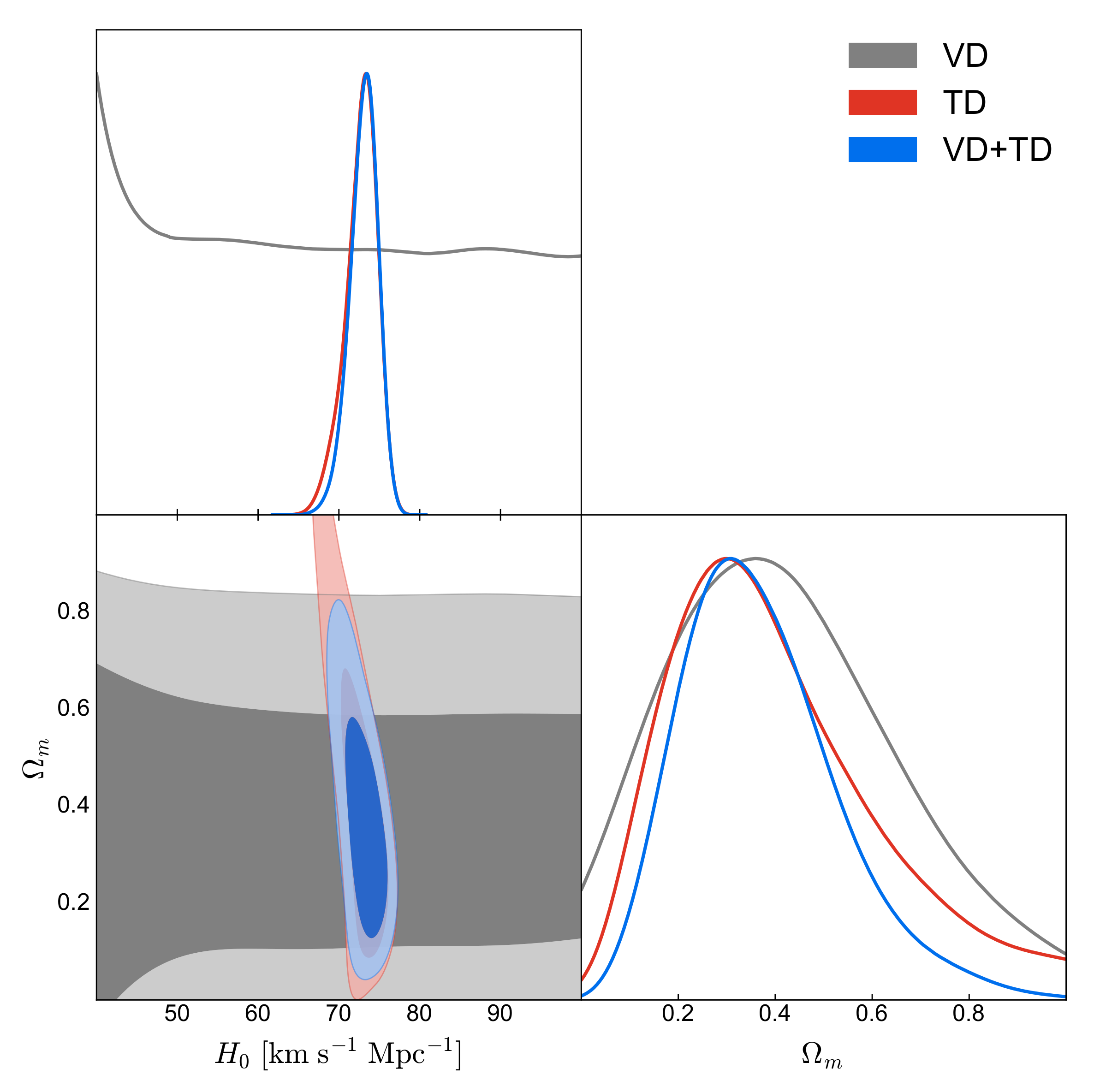
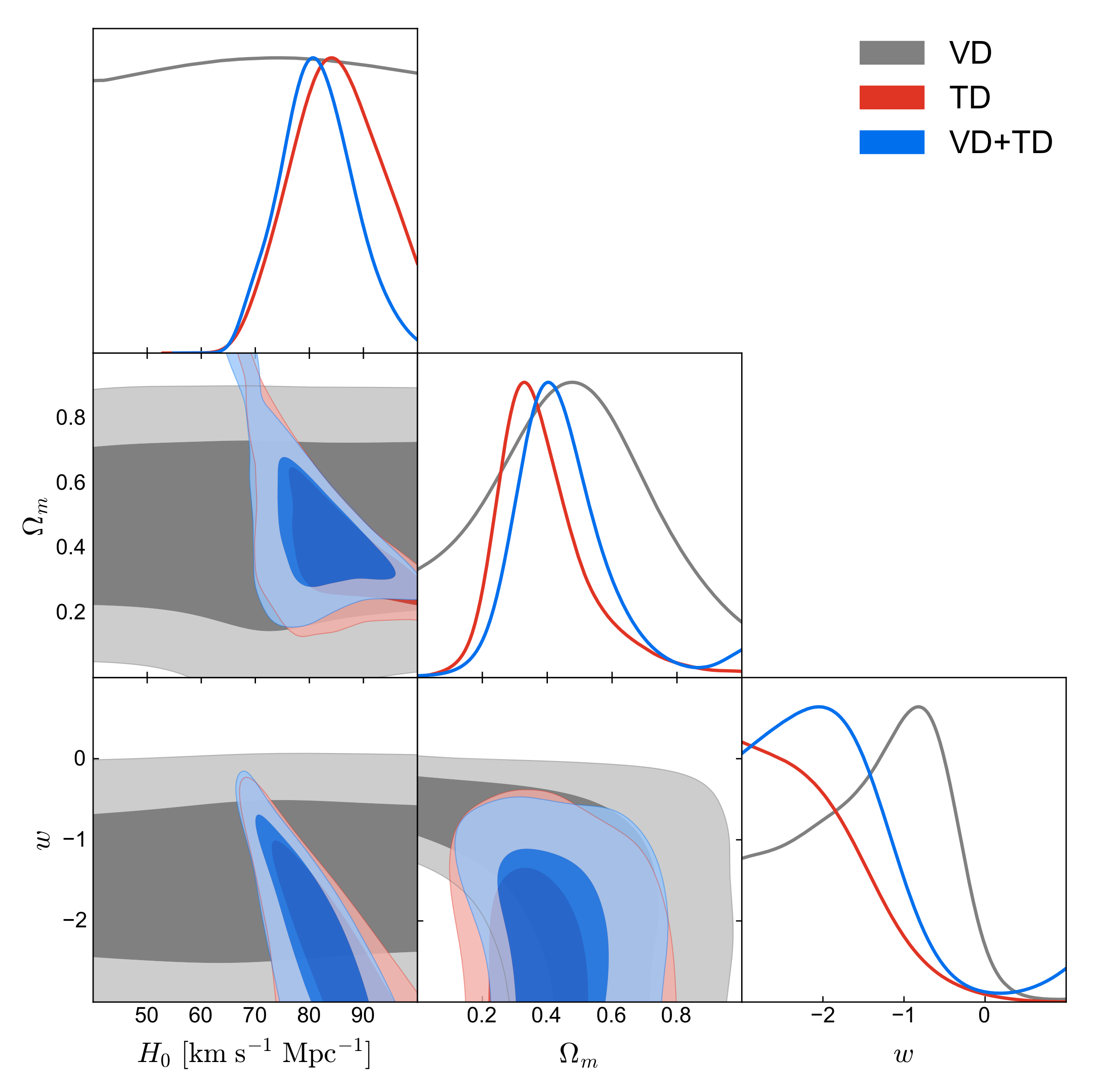


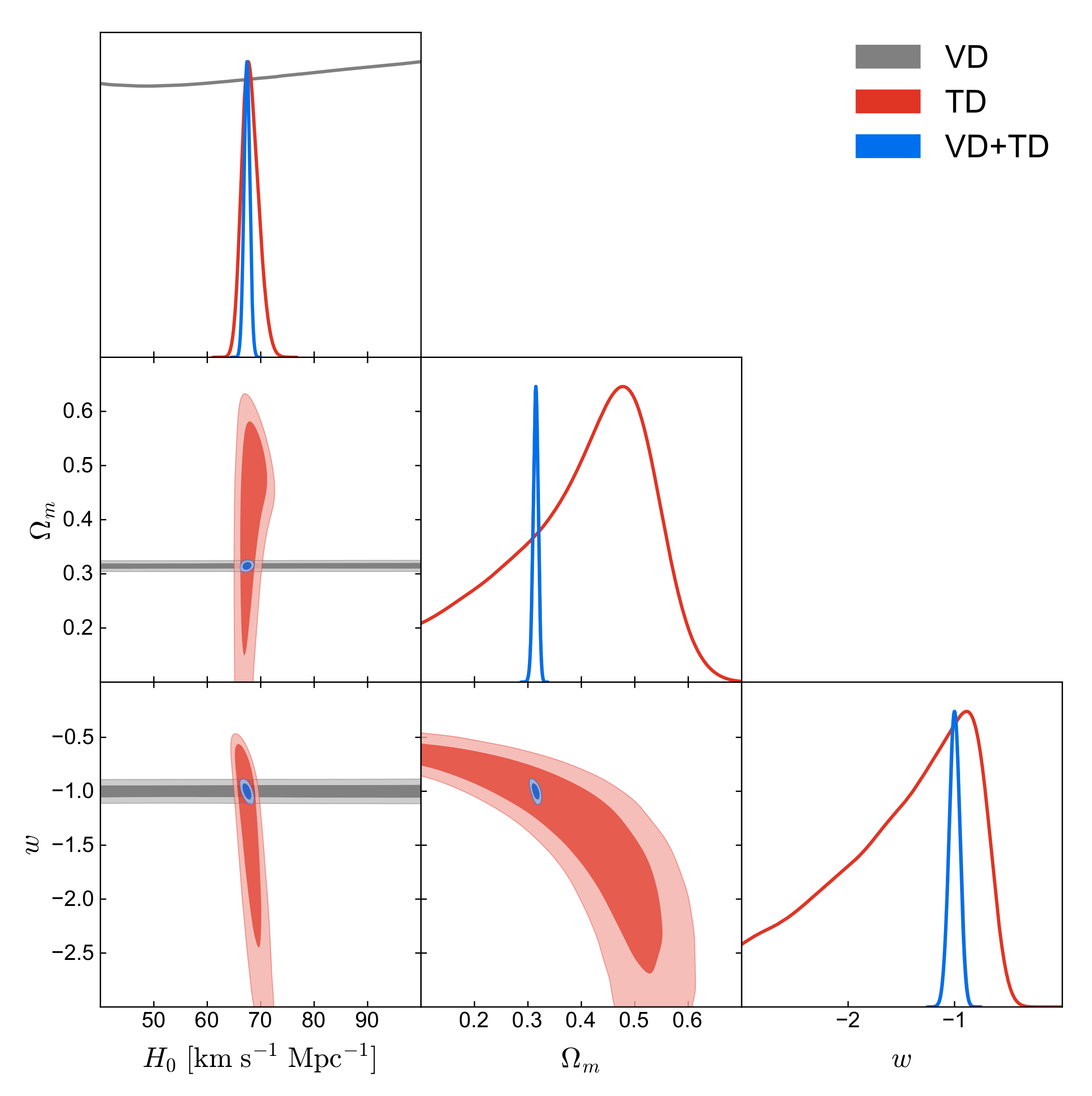

| Lens Name | (Mpc) | (Mpc) | References | ||
|---|---|---|---|---|---|
| B1608+656 | 0.6304 | 1.394 | [79,81] | ||
| RXJ1131−1231 | 0.295 | 0.654 | [28,65] | ||
| HE 0435−1223 | 0.4546 | 1.693 | - | [28,82] | |
| SDSS 1206+4332 | 0.745 | 1.789 | [83] | ||
| WFI2033−4723 | 0.6575 | 1.662 | - | [27] | |
| PG 1115+080 | 0.311 | 1.722 | [28] | ||
| DES J0408−5354 | 0.597 | 2.375 | [29,84] |
| Model | Parameter | VD | TD | VD+TD |
|---|---|---|---|---|
| CDM | - | |||
| wCDM | - | |||
| w | ||||
| CPL | - | |||
| Model | Parameter | VD | TD | VD+TD | CMB+BAO+SNe |
|---|---|---|---|---|---|
| CDM | - | ||||
| - | |||||
| wCDM | - | ||||
| - | |||||
| w | |||||
| CPL | - | ||||
| - | |||||
| - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.-Z.; Hu, W.-H.; Cui, Y.; Zhang, J.-F.; Zhang, X. Cosmological Parameter Estimation Using Current and Future Observations of Strong Gravitational Lensing. Universe 2022, 8, 254. https://doi.org/10.3390/universe8050254
Qi J-Z, Hu W-H, Cui Y, Zhang J-F, Zhang X. Cosmological Parameter Estimation Using Current and Future Observations of Strong Gravitational Lensing. Universe. 2022; 8(5):254. https://doi.org/10.3390/universe8050254
Chicago/Turabian StyleQi, Jing-Zhao, Wei-Hong Hu, Yu Cui, Jing-Fei Zhang, and Xin Zhang. 2022. "Cosmological Parameter Estimation Using Current and Future Observations of Strong Gravitational Lensing" Universe 8, no. 5: 254. https://doi.org/10.3390/universe8050254
APA StyleQi, J.-Z., Hu, W.-H., Cui, Y., Zhang, J.-F., & Zhang, X. (2022). Cosmological Parameter Estimation Using Current and Future Observations of Strong Gravitational Lensing. Universe, 8(5), 254. https://doi.org/10.3390/universe8050254







