Abstract
RR Lyrae stars are recognized as some of the oldest stars in the Universe. In addition, they are some of the few old celestial objects for which distances can be reliably inferred. As such, these stars are excellent tracers of the oldest structures that exist in the inner Galaxy. Although the inner Galaxy is where the oldest structures in the Milky Way are thought to be hidden, it is also a region notoriously difficult to study due to high extinction and crowding. Here, I will summarize how RR Lyrae stars have been used to obtain a more complete picture of the inner Galaxy. In particular, recently, a large sample of RR Lyrae star motions through space have been obtained and compared to younger, more metal-rich stars in the bulge/bar. It is seen that the inner Galaxy RR Lyrae star kinematics are complicated by a mix of a variety of Galactic components. After isolating only those RR Lyrae stars that are confined to the bulge, a subsample of these stars have slower rotation and are less barred than the dominant bar/bulge. Curiously, there is no discernible metallicity difference between these two subsamples. Old, metal-poor stars in the inner Galaxy need to be properly accounted for when discussing processes that gave rise to the formation of the inner Galaxy and the Galactic bar/bulge.
1. Introduction
Variable stars known as RR Lyrae stars (RRLs, hereafter) are a stellar tracer that has been trusted for decades to help piece together the size and structure of the Milky Way (MW) Galaxy [1,2,3,4,5]. RRLs are variables that fall under radially pulsating stars with periods ranging from ∼0.2 to 1.0 days. These stars begin their lives on the Hertzsprung-Russell (HR) diagram with masses and radii similar to that of our Sun [6]. They have since evolved off the main-sequence, and after helium flash, reside now on the horizontal branch, undergoing core helium burning. In particular, they fall within the instability strip that crosses the horizontal branch (see Figure 6 in Catelan 2007), [6]. Therefore, they have a relatively low mass (∼0.6–0.8M), temperatures between 6000 K–7250 K, and radii typically between 4–6 [7,8]. Due to this stellar evolution path, the existence of RRLs in a stellar population signifies a system older than about 10 Gyr [9]. RRLs therefore tell us about conditions in the Galaxy at the time they were formed [10].
The oscillatory phenomenon seen in RRLs is attributed to the propagation of sound waves throughout their stellar interior [11]. One of the first papers that systematically categorized variable stars was from Bailey (1902), who studied stars that change their brightness in the Globular cluster Centauri (NGC 5139) [12]. Bailey divided the RRLs into three subclasses, a, b, and c, which were distinguished by the shape of their light curve as well as their pulsation amplitudes and periods. It is now known that RRLs of “Bailey” types of a or b are RRLs that pulsate in the fundamental mode with periods typically longer than ∼0.45 days, and RRLs of “Bailey” type of c are RRLs that pulsate in the first overtone with periods typically shorter than ∼0.45 days [13]. Since then, RRLs that pulsate in a combination of the first and fundamental overtone—RRd—have been reported [14,15,16], as well as those that pulsate in the second overtone—RRe [17,18].
The physics of these stellar pulsations in RRLs is an active field. However, RRLs are also important standard candles for measuring the distances to very old stellar populations, such as globular clusters, as was realized already by Shapley (1918) [19]. In fact, RRLs were some of the first celestial objects that provided a distance to the center of the Galaxy [2,20]. In these studies, RRL distances were obtained using V-magnitudes of RR Lyrae stars. Indeed, until relatively recently, the absolute magnitude of an RRL was investigated mostly using the optical passbands, particularly the V-band.
RRLs have long been known to exist in the bulge [20]. Microlensing surveys such as the MACHO project [21] and Optical Gravitational Lensing Experiment (OGLE) [22] have uncovered thousands of RRLs in the central regions of the Galaxy. RRLs can be easily identified on the basis of their colors (bluer than typical bulge stars) and distinctive sawtooth-shaped light curves (with periods of about 1/2 day), thus enabling the selection of pure bulge samples. As they are well-understood standard candles (with a precision of <10%), their presence within the bulge can be securely established. RRLs are the most significant and identifiable population of metal-poor stars in the bulge.
The oldest stellar populations in the bulge can reveal the early history of formation and assembly for our Galaxy and can constrain models for the formation and assembly of spiral galaxies in a cosmological context. Here, we discuss how RRLs are contributing to the knowledge of the formation of the bulge and inner Galaxy. In Section 2, both spectroscopic and photometric metallicities of RRLs in the inner Galaxy are discussed. The RRL spatial distribution of the RRLs is reviewed in Section 3 particularly with respect to different RRL surveys. In Section 4 the motions of these stars are reviewed, as well as how velocities have helped constrain scenarios explaining the formation of the inner Galaxy.
2. Metallicities of Inner Galaxy RR Lyrae Stars
A fundamental characteristic of any stellar system is its metallicity distribution function (MDF). The distribution is related to the stellar system’s star formation and also provides constraints on models of chemical evolution. The majority of the bulge stars have metalllicites that are metal-rich (approximately solar), and their -elements are enhanced [23], suggesting rapid early star formation. The bulge seems to show a radial abundance gradient in the sense that more metal-rich stars dominate closer to the Galactic plane and more sub-solar metallicity stars increase further from the Galactic plane [24,25]. For RR Lyrae stars in particular, abundances are also desirable because the absolute magnitude of RRLs are dependent on metallicity, as described in Section 3.1 below.
2.1. Spectroscopic Metallicities of Inner Galaxy RR Lyrae Stars
Unfortunately, there are very few spectroscopic abundances of bulge RRLs. This is partly due to the complexity of measuring metallicities for RRLs at the distance of the bulge. The commonly used lines in the blue region of the spectrum (Ca H&K, the Mg complex) are difficult to use, firstly because spectrographs are relatively inefficient in the blue, and secondarily because these moderately hot stars are faint at these wavelengths (16). Furthermore, in order to obtain accurate metallicities, spectra can only be taken when the atmospheres are most stable, at minimum light, as the expansion and contraction during the pulsations create shocks and alter abundances and chemistry in difficult to predict ways.
For example, Pancino et al. analyzed a sample of 18 RRLs in high-resolution (R∼30,000), high signal-to-noise (SNR > 30) and measured the atmospheric parameter variations due to RR Lyrae pulsations [26]. They found that pulsations can reach Kelvin and dex. To overcome this, the optimal region for spectroscopic analysis is near minimum light, with a duration of approximately 10% of the pulsational period [26].
A proper survey of metal abundances for bulge RRL has not been carried out since the early work by Walker & Terndrup (1991) [27]. They analyzed RRLs in Baade’s window in the 3750–5300 Å range, comparing the hydrogen spectral type, using the equivalent widths of the H and H lines, to the Ca II K line spectral type, using the equivalent width of the Ca II K line. From 59 RRLs, they found that the bulge RRL has a sharply peaked distribution with a dispersion of only 0.16 dex, far smaller than other bulge stellar populations [27].
More recently, Savino et al. (2020) used the calcium II triplet (CaT) region, covering a wavelength range of about 8300–8800 Å, with a resolution of R∼10,000, to determine metallicities [28]. Because the SNR of the spectra was ∼20, their individual metallicities are not as reliable as looking at the mean of the MDF. Their bulge RRL MDF with ∼900 RRL measurements covers a wide range of metallicities, with a single prominent peak at = −1.39. This RRL metallicity distribution is shown in Figure 1, and compared to the distribution of ∼2 million bulge red clump stars from the Blanco DECam Bulge Survey (BDBS) [25]. Both BDBS and the Savino et al. (2020) RRL sample focus on stars located in the Southern bulge, and cover a similar range in Galactic latitude. However, BDBS covers a larger, more homogenous area of the sky, and extends to a significantly larger range in Galactic longitude. The uncertainty distribution of the RRL metallicity measurements almost entirely accounts for the width of the observed MDF peak, which suggests that the true underlying MDF has a very narrow, dominant, component, superimposed to wide metal-rich and metal-poor tails.
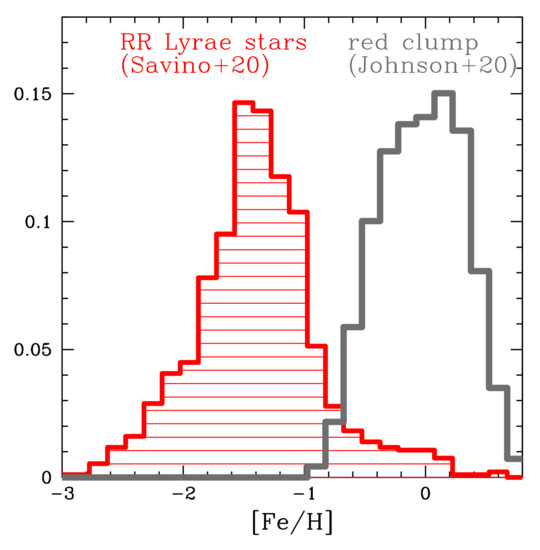
Figure 1.
The normalized metallicity distribution for ∼900 BRAVA-RR inner Galaxy RRLs (shaded histogram) in comparison with the distribution of ∼2 million inner Galaxy red giants (solid thick line) selected from the Bulge DECam Bulge Survey catalog of Johnson et al. (2020) [25]. The distribution of RRLs is considerably more metal-poor than the dominant bulge population.
The bulge RRLs therefore appear to have a metallicity distribution function centered around 1.0–1.4 [27,28]. This is at least 10× lower in metallicity than the dominant bulge population [29,30]. Their lower MDF indicates that they either trace a more ancient population as compared to the bulk of bulge stars or that their progenitors come preferentially from the more metal-poor stars (more metal-rich stars are less likely to evolve on to the instability strip). This is important because separating bulge stars into older/younger stars, or more metal-rich/metal-poor stars is challenging; the MDF of the bulge RRLs clearly indicates that targeting RRLs allows one to probe the older and metal-poor stellar population in the bulge.
2.2. Photometric Metallicities of Inner Galaxy RR Lyrae Stars
Besides deriving metallicities from spectra, there is also the possibility to estimate from the photometric light curves of RRLs. For photometric metallicity calibrations of RRLs, is estimated from the pulsation properties of the star (e.g., period and/or amplitude) and their Fourier coefficients. Five notable photometric metallicity calibrations of RRLs include those from Jurcsik and Kovacs (1996), Sandage (2004), Smolec (2005), Nemec et al. (2013), and Skowron et al. (2016), and these are respectively based off of measurements of 81, 54, 28, 34, and 55 spectroscopic abundance determinations [31,32,33,34]. Their typical offsets in derived photometric are ∼0.10 dex in the mean, and exceed 0.30 dex for the metal-poor ([Fe/H] 2.0) RRL. The typical dispersion between the derived photometric and spectroscopic values is 0.20 dex.
Each of these calibrations is widely used in the literature, and each is calibrated to be consistent with the scale of Jurcsik & Kovacs (1996) [31,35], which is itself compiled from a heterogeneous list of 31 different references, and includes only two stars with 2.0. It is worth noting that none of the above calibrations accounts for the effects of variable [/Fe] abundances. This may be a problem when using photometric calibrations to determine metallicities for RRLs in the bulge, since, for bulge RRLs, a shift of 0.4 dex in [/Fe] is equivalent to a 0.3 dex shift in [36]. Even in the solar neighborhood, Prudil et al. (2020) showed that a number of local RRLs originated from the Gaia–Enceladus system [37,38,39], and these have [/Fe] values that are ≈0.20 dex lower than the RRL in the halo stars [40]. For photometric metallicities accurate at the ∼0.1–0.2 dex level, accounting for [/Fe] is likely important.
Recently, Dekany et al. (2021) revisited the photometric metallicity prediction in the Cousins I passband, which is used in the OGLE survey [41]. They used a calibration sample of 80 RRab stars ranging from −2.6 to +0.2 dex, 60 of which had multiple independent metallicity determinations. They found that all previously used formulae overestimate the modes of the MDFs of the Galactic bulge, disk, and the Magellanic Clouds by ∼0.35–0.4 dex and cause distortions in their shapes. As such, at this time, it is not completely clear how well photometric metallicities predict the underlying MDF of the bulge RRLs—if the scatter in the metallicity distribution is dominated by intrinsic scatter or by difficulties associated in the calibration and methodology in estimating photometric metallicities.
The MACHO and OGLE surveys have used the extensive photometric RRL measurements in their surveys to investigate the bulge MDF using photometric metallicities. Results using 2435 MACHO RRLs [42], using 16,836 OGLE-III RRL [43], and using 27,258 OGLE-IV RRL [44] all suggest an inner Galaxy RRL bulge MDF with 1.25 (on the Zinn and West 1984 scale [45]), or 1.0 (on the Jurcsik 1995 scale [35]), with a broad metallicity range from 2.26 to −0.15 dex, and a dispersion of 0.25–0.30 dex. These studies also indicate that there is a slight gradient in metallicity as a function of distance from the Galactic center, with the central-most RRLs being more metal-rich than those as further Galactocentric distances. The most recent photometric metallicity analysis of bulge stars, by Dekany et al. (2021), finds that the mode of the bulge RRL MDF is approximately 1.4 dex, and they also see a shift in the bulge RRL MDF to slightly toward lower metallicity with increasing Galactocentric distance [41].
Pietrukowicz et al. (2020) suggest that the inner Galaxy MDF is better approximated by three peaks, and that each peak represents a different Galactic component that is superimposed within the inner Galaxy—the halo, bulge and disk [46]. There is no doubt that a complexity in determining the true MDF of bulge RRLs is the reality that all Galactic components overlap in the inner Galaxy, and, especially at the metal-poor end (1.0 dex), there will be a significant contamination from halo stars. It is now possible to clean the inner Galaxy RRLs from outliers, as has recently been done thanks to Gaia proper motions, and ongoing radial velocity surveys, as described in Section 4.4.
For photometric metallicities, both a homogeneously derived set of chemical abundances for a large sample of RR Lyrae stars with high-resolution, high signal-to-noise ratio spectra as well as inclusion of more RR Lyrae stars in the calibrating samples at both low (2.0) and high (0.3) metallicities would more robustly anchor photometric parameters and the trends with metallicity—in addition to being able to distinguish between the effects of and [/Fe] would be important when moving toward RRL in the bulge. For spectroscopic metallicities, it would be valuable to have more spectroscopic studies, and, especially, being able to measure elemental abundances of bulge RRLs spectroscopically would be exciting.
2.3. Age–Metallicity Relation
The dominant stellar populations of the bulge appear to be largely old (∼11 Gyr) [47,48], with little evidence of younger stars, although there have been also claims of a substantial intermediate-age population, especially from microlensing observations [49,50].
A landmark theoretical calculation by Lee (1992) [10] estimated that the RR Lyrae in the inner Milky Way were ∼1.5 Gyr older than typical Halo stars with 1.50. It is still widely accepted that the bulge RRLs are some of the oldest stars in the MW. RRLs can be used as age indicators because RRLs are horizontal branch (HB) stars, and the HB morphology changes dramatically as a function of metallicity. Therefore, the metallicity of RRLs yields constraints on this population’s age [10,28].
For example, using HB population models from the BaSTI alpha-enhanced isochrones, complemented with the BaSTI alpha-enhanced HB tracks [51], stars with an age of 10 Gyr and a metallicity of −1.62 dex will end up as red horizontal branch star—too red to populate the instability strip and become an RRL. However, stars with an age of 10 Gyr and a metallicity of −2.14 dex, will evolve to become a horizontal branch star blue enough to fall within the instability strip and will therefore pulsate as an RRL. At a given age, the more metal-poor a star, the bluer the star will be on the HB.
By increasing the age of the 1.62 dex stars to 13 Gyr, a stellar evolutionary path results that takes the star through the instability strip. Whereas different HB population models as well as the specific contribution of helium and heavy elements will factor into the exact position a star falls on the HB with age, metal-rich stars need to be older in age to become blue enough to fall within the instability strip (see, e.g., Figure 6 in Savino et al. 2020) [28].
In Savino et al. (2020), a set of synthetic stellar population models was built to match the modern metallicity distribution of the bulge RRLs [28]. They concluded that the bulge RRL population has an extremely ancient age of 13.41 ± 0.54 Gyr, which is the oldest among the Milky Way stellar populations to date.
The ages of the bulge RRLs are compared in Figure 2 to bulge field stars determined from Hasselquist et al. (2020) [52]. In Hasselquist et al. (2020), ages of ∼6000 bulge stars with 0.5 stars from the APOGEE survey were calculated using the Cannon label-transfer method [52]. They find that nearly all stars have ages consistent with being formed 8–10 Gyr ago, with a slight vertical age gradient in a sense that stars closer to the plane are younger than those further from the plane. Although ages of stars are notorious for having large uncertainties of ∼25–50%, these ages are similar to most studies of bulge stars that indicate that all, or nearly all, of the stars appear to be old—>9–10 Gyr [48,53,54,55]. However, there is also evidence for significant fractions of bulge stars with ages <8 Gyr [50,56,57,58]. The Hasselquist et al. (2020) analysis explains younger stars in the bulge as the vertical age gradient suggests that younger stars will preferentially be found at distances closer than 0.5 kpc from the plane and with 0.2.
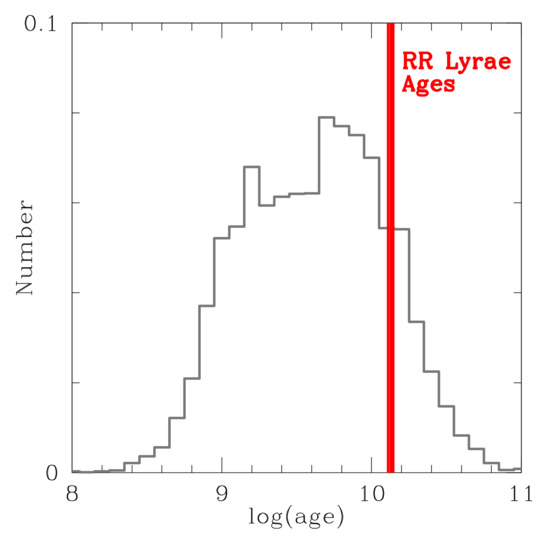
Figure 2.
Age distributions of the bulge field stars as compared to the ages of bulge RR Lyrae stars.
3. Spatial Distribution of RR Lyrae Stars in the Inner Galaxy
The appearance of the inner Galaxy is dominated by a bulge of stars, which is asymmetric and elongated, so that the bulge is a peanut-shaped bar pointing toward us [59,60]. In this section, we discuss how RRLs are used as distance indicators to probe the inner Galaxy and the bar/bulge.
3.1. Distances Derived from RR Lyrae Stars
It is typically believed that, in the V-band, the absolute magnitude of an RRL is a function of metallicity [61,62], and traditionally a linear relationship between and M(RR) is assumed, e.g., M(RR) = + . Because this relation of RRLs has been arguably the most widely discussed RRL luminosity relation in the literature, it is briefly reviewed here. Theoretical models do not predict that a simple linear relationship between M(RR) and exists [63,64,65,66]. For example, using computations of convective pulsation models, it was shown in Caputo et al. (2000) that the slope of the M(RR) and relation will increase as RRLs become more metal-rich. Using RRL in globular clusters, they show that observationally this effect can be seen as well. Despite these limitations in a M(RR) – relation, the slope () and zero-point () of this relationship are the subject of much discussion.
The Hipparcos satellite was only able to provide a parallax with an accuracy of <20% for one RRL (RR Lyrae itself), so different techniques, such as Statistical Parallax [67], Baade–Wesselink analysis [68], and theoretical HB models [64], have been used to calibrate the M(RR). Values for the slope range from 0.30–0.37 [69,70] to 0.13 [71]. This means that the M(RR) at = −1.6 ranges from 0.45 to 0.77 mag, depending on the technique used. One popular value for is ∼0.21–0.25 mag/dex, which is not only the best estimate of the M(RR) calibration from a number of different techniques [72] but is also in line with the value found from a photometric and spectroscopic study of about a hundred RRLs in the bar of the LMC from Clementini et al. (2003) and Gratton et al. (2004) [73,74].
It is exciting that today Gaia parallaxes of a statistical sample of RRLs can be used to investigate the absolute magnitudes of RRLs. Dambis et al. (2013) collected and homogenized literature values of period, pulsation mode and extinction in the visual passband (), metal abundance () and intensity-averaged magnitudes in the Johnson V, 2MASS and 1 passbands for 403 field RRLs [75]. The majority of these have Gaia DR2 parallaxes with uncertainties <20%. Using Gaia DR2 parallaxes and 381 RRLs from the Dambis et al. (2013) compilation, a surprisingly large value of = 0.34 ± 0.03 mag/dex is found [76]. When restricting the sample to 23 RRLs with metallicity estimated from high-resolution spectroscopy, and which are closer to us and span a narrower range of the distances, the slope of the M(RR) – decreases to = 0.25 ± 0.05 mag/dex, more in line with previous estimates. It should be noted that this analysis takes into account the correction for the zero point parallax offset of Gaia DR2 data. It is therefore still not settled what the best relation is between M(RR) and , but the situation will continually be revisited as Gaia parallaxes become more and more precise [77].
In recent years, there has been a growing body of literature exploring RRL luminosity relations in other passbands. In particular, there are advantages of using longer wavelengths of light when using RRLs as standard candles. Not only is longer-wavelength light less sensitive to reddening, but passbands such as the infrared K-band are shown to have less dependence on metallicity and also less dependence on evolutionary effects. Instead, an RRLs absolute magnitude M(RR) depends mainly on the RRLs period [78,79]. Such a period-luminosity (PL) relation is expected at nearly all wavelengths, with the exception of the V-band, as shown by theoretical models [64,80,81]
Therefore, currently RRL PL relations are well characterized from optical (R and I) to mid-IR wavelengths [82,83,84,85,86,87,88]. Combining period-luminosity relations with a metallicity term in general decreases the intrinsic scatter in finding M(RR); with Gaia DR2, the scatter in period-luminosity- relations is on the order of 0.2 mag, still dominated by uncertainties in the parallaxes [89,90]. In the PLZ relation with the form M(RR) = a + b + c , the slopes in the literature in log P range from b = −2.4 to −2.9 and the slopes in range from c = 0.03 to 0.18. Theoretical PLZ relations predict the slope in log P to range from b = −2.2 to −2.4 and the slope in to be c ∼ 0.18 [64,81]. As the PLZ relation becomes tighter constrained with forthcoming, improved Gaia parallaxes, it will be interesting to see if the slopes found observationally (b = −2.4 to −2.9) are consistently more negative than what the theoretical models predict (b = −2.2 to −2.4).
Regarding RRL in the inner Galaxy, the OGLE survey is the largest and most comprehensive publicly available RRL photometric catalog. Since OGLE is carried out in the V and I passbands, luminosity relations in and are needed for the many investigations that use the OGLE RRL as their foundation. Distances of RRL toward the Galactic center are typically found using the theoretical relations by Catelan et al. (2004b), given by
where P is the stars period, and Z is the RRL metal abundance [64].
Distances for the RRL from the VVV survey, which uses the passbands, use a variety of different and relations, mainly including those from Catelan et al. (2004b) but transformed to the VISTA band [64,91,92], and those from Muraveva et al. (2015) [93,94,95], and Muravera et al. (2018) [76,96]. The Muraveva et al. (2015) relation does not include a metallicity term, but still Alonso-García et al. (2021) use 22 RRL in inner Galaxy GC M22 to show that the Muraveva et al. (2015) relation provides RRL distances that agrees well with the Gaia determined parallax distance to M22 [97].
3.2. Inner Galaxy RR Lyrae Stars Spatial Distribution
Gaia parallaxes of RRLs alone are not sufficient for RRLs at the distance of the bulge. Distances to these stars are therefore determined adopting absolute magnitudes from the relations discussed above (Section 3.1). All-sky reddening maps, such as those from the VVV [98,99], can be used to enable corrections of the large and variable extinctions present in the inner Galaxy. Still, reddening variations down to a few arcseconds are clearly seen in maps of specific windows in the inner Galaxy [98,99,100], and interstellar extinction curve variations can exceed 20 percent [101]. It is therefore difficult for bulge RRL distances to be established with uncertainties of <10%, although, for some inner Galaxy GCs with well-studied extinctions and/or small differential reddening, RRL distances with a 5–8% precision have been reported [96].
From a sample of ∼4000 MACHO RRLs, it was reported that the inner Galaxy RRLs represent primarily the inner extension of the Galactic halo and not the bulge/bar [42,102]. This is because it was found that the spatial distribution of the inner Galaxy RRLs did not appear to trace out the bar in the bulge, whereas the more metal-rich and more populous red clump stars show a strong barred signature [42,102,103].
In contrast, the OGLE survey, using tens of thousands of inner Galaxy RRLs, reported that the bulge RRLs do trace the barred bulge, with a stronger signature for the stars closest to the Galactic plane [43,44]. These results favor that the inner Galaxy RRLs lie in the same gravitational potential as the bar. The OGLE photometry is more accurate for variable star studies than the MACHO photometry, which may be a factor in this discrepancy [104,105]. However, the VISTA Variables in the Vía Láctea (VVV) survey, using ∼8000 OGLE RRLs, have also reported a spheroidal, barely barred distribution [91,106]. The VVV survey has the advantage of being less sensitive to reddening than those in the optical passbands, such as OGLE and MACHO.
The completeness of the OGLE survey has been reported to be about 99% [107] based on the cross-identification with the MACHO RRLs. Therefore, this comparison is valid for RRL in the southern half of the bulge and those a few degrees from the Galactic plane (3). We note that OGLE and MACHO are both ground-based photometric surveys carried out in the optical passbands, so both will suffer from the same biases regarding crowding and reddening. The completeness of the OGLE sample falls with decreasing latitude, as at |b| <2, the apparent magnitudes of RRLs are heavily extincted and hence too faint for detection within OGLE and MACHO.
The VVV survey has by and large taken advantage of the RRLs identified in OGLE, and has supplemented these with their photometry [91]. For areas not able to be probed by OGLE, VVV has been successful in identifying thousands of RRLs, although the RRL along the slight-lines of dust clouds in the close proximity of the mid-plane still remain uncovered [106,108,109].
To date, there is no consensus on the exact 3D structure of the inner Galaxy RRLs. Recently, Kunder et al. (2020) argue that there are two populations of bulge RRLs, one population that follows the bar and is dominant at Galactocentric distances larger than ∼1 kpc, and another that is more centrally concentrated that does not follow the bar [110]. These results are based on ∼1000 RRLs with known radial velocities, proper motions, and extinction estimates.
That there are two populations of bulge RRLs—one population that is part of the bar, and one that does not have a bar-like signature—would suggest that the different RRL spatial distributions seen by OGLE and VVV are both correct, and that the differences arise due to both surveys focussing on RRLs in slightly different locations within the bulge. In particular, the results from the OGLE papers would be drawn from distances of RRL dominating further from the plane, and the VVV papers would be incorporating more distances of RRL closer to the plane. Because the longer passbands from the VVV photometry are less sensitive to dust, VVV has the advantage of being less hampered by reddening, especially for stars with a closer proximity to the plane. This could in turn give greater accuracy in the VVV distances, especially for RRL closer to the plane.
The BRAVA-RR survey is not thought to be affected by any significant biases. Their sample is selected from OGLE, which has a high completeness in the Southern fields that were selected by BRAVA-RR, and the full RRL period-amplitude plane is sampled. The BRAVA-RR fields have RRLs with apparent magnitudes that not only reach the bulge, but also to that of the Sagittarius dwarf Galaxy at ∼25 kpc.
Figure 3 shows the spatial distribution of ∼4000 inner bulge RRLs as a function of Galactocentric distance. The top panel highlights the spatial location of these RRLs, as this is an area where contiguous celestial coverage can not be provided by OGLE; instead, the first statistical sample of RRLs in this region was uncovered using the VVV by Dekany et al. (2020) [109]. These authors analyzed time series data from the the VVV survey to identify RRLs also in some of the more extinct regions of the Galaxy—an area that is too faint for optical surveys to probe. To find distances to these stars, the theoretical calibration of the RRL period-luminosity relation from the Catelan et al. (2004b) [64] on the VIRCAM/VISTA filter system is used:
where P is the period of the RRL, and Z is its metallicity [111].
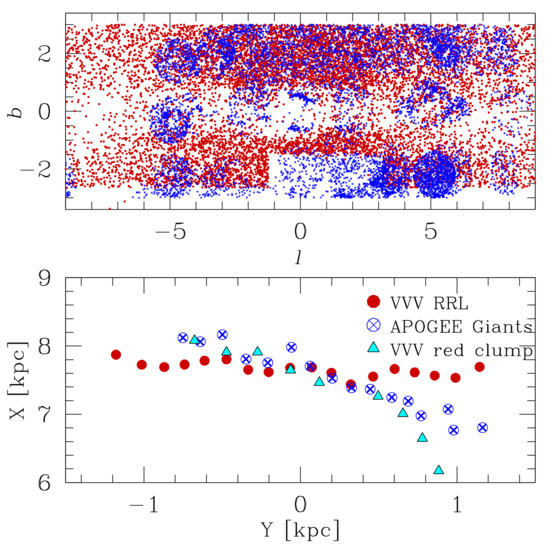
Figure 3.
A comparison of the spatial properties of the RRLs in the inner Galaxy (red) compared to the giants in the inner Galaxy (blue). The top panel shows the location in Galactic coordinates of the APOGEE giants (blue) and the VVV RRLs from Dekany and Grebel (2020) [109] (red). The bottom panel shows the mean spatial distribution of these two inner Galaxy stellar traces. The red-clump stars studied in Gonzalez et al. (2012) [98] to trace the bar/bulge are shown as triangles.
To correct for reddening, the Bulge Extinction And Metallicity (BEAM) extinction values [98] is used with the extinction law from Cardelli et al. (1989) [112], which in the VVV passbands is = 0.73 [92]. It is then straightforward to calculate the distance to the individual RRLs,
where D the individual distance in parsecs.
The spatial distribution of the VVV inner bulge RRL sample does not clearly appear to trace the bar/bulge. In Figure 3, the x and y distances of VVV inner Galaxy RRL are compared to the spatial distribution of APOGEE giants with distances from StarHorse [113] and VVV red clump stars studied by Gonzalez et al. (2012) [98] (which use the same BEAM reddening map). The bulk of the inner Galaxy RRL stars do not appear to trace the bar as clearly as the giants or red clump giants. Combined with the metal-poor nature of these RRLs (see Figure 1), it is apparent that the inner Galaxy RRLs warrant further investigations on how they fit into the bulge population, or if they are even a bulge population [114]. The spatial properties of the inner Galaxy RRLs in combination with their kinematics is useful for a more detailed look as to their origin.
4. The Inner Galaxy and Galactic Bulge/Bar Kinematics
4.1. The First Inner Galaxy Kinematic Surveys
One of the first indications of rotation of the bulge came from radial velocity measurements of planetary nebulae (PNe) [115]. The velocities of the PNe toward the Galactic center showed a large dispersion with a trend of increasing velocity with increasing longitude. Twenty-five years later, 26 bulge Miras were observed to show a rotation gradient, whereas disk Miras did not show such rotation [116]. Then, ∼1000 K-giants in two off-axis fields at (l, b) = (8, 7) and (l, b) = (12, 3) were used as metal-rich bulge tracers to show a similar result [117]. These observations therefore suggested rotation of the bulge/bar.
The first dynamical survey that covered a wide area of the bulge was carried out by Beaulieu et al. (2000) [118]. They combined PNe from a new survey with those already known from existing catalogs to obtain a sample of ∼400 PNe that cover both the Northern and Southern portions of the bulge (−20 and 3.3). The velocities of the PNe in this survey clearly indicated rotation of the bulge. It was further found that N-body models, in which the bar/bulge grows from the disk via bar-forming instabilities, give a good representation of these bulge PNe kinematics [118].
PNe are short-lived and are therefore rare, and their population memberships (and especially distances) are uncertain. A more extensive survey of the bulge using red giant stars, which are the most common type of luminous evolved stars in the bulge/bar, was undertaken by Rich (2007) [119]. In this Bulge Radial Velocity Assay (BRAVA), eventually 10,000 stars in 84 different fields across the southern bulge were observed [120]. There it was demonstrated that the bulge follows pure cylindrical rotation [121], similar to boxy/peanut bulges in external galaxies [122]. It was also shown in Shen et al. (2010) that the BRAVA kinematics (Figure 2 in Shen et al. 2010) [123] is consistent with most of the mass being in the stellar bar, with <8% (of the mass of the disk) allowed within a slow/non-rotating pressure-supported classical component.
The Abundances and Radial velocity Galactic Origins Survey (ARGOS) Survey used ∼28,000 red clump giant stars (RCGs) over 28 fields to probe the chemistry and dynamics of the bulge [124,125]. RCGs are representative for most of the bulge stars, tracing old stellar populations except for low metallicities [126]. In the ARGOS survey, ∼95% of the sample contains stars with with metallicities . The near-cylindrical rotation is seen for RGC stars of all metallicities up to 1.
ARGOS and BRAVA by and large avoided the plane of the Galaxy; the plane is plagued by high and variable reddening, as well as stellar blending and crowding issues. To fill in this gap, the Giraffe Inner Bulge Survey (GIBS) [29,127] targeted ∼5000 red clump giants in 24 bulge fields, to probe both elemental abundances and velocities of stars also close to the plane of the Galaxy (b = −1). GIBS confirmed cylindrical rotation also along the plane of the Galaxy and showed that differences may exist between super-solar and sub-solar bulge stars. In particular, they find that the metal poor population (0.3) is more centrally concentrated than the metal rich one ( +0.1), and with a more axisymmetric spatial distribution. The metal rich population, on the other hand, is arranged in a boxy distribution, consistent with an edge-on bar.
The APOGEE survey [128,129] also is collecting spectroscopic observations of stars along the plane of the Galaxy. From ∼10,000 giants at low-latitudes, the kinematic profile of the bulge is found with stars with 1.0 having cylindrical rotation.
From the Gaia-ESO Survey (GES) [130,131], ∼2500 red clump stars in 11 bulge fields were compared to ∼6300 disk stars to study the chemo-dynamics of the bulge. They found differences in dynamics of the metal-rich stars and the metal-poor subpopulation.
Figure 4 shows the extent of the bulge covered by these surveys and the metal-poor surveys described in the following section. Because the Northern bulge tends to be more crowded than the Southern bulge, this area of the sky is not as well studied. There is no indication that the Northern bulge has different global kinematic properties than the Southern bulge, and it is generally assumed that the bulge exhibits symmetry about the Galactic plane [132,133].
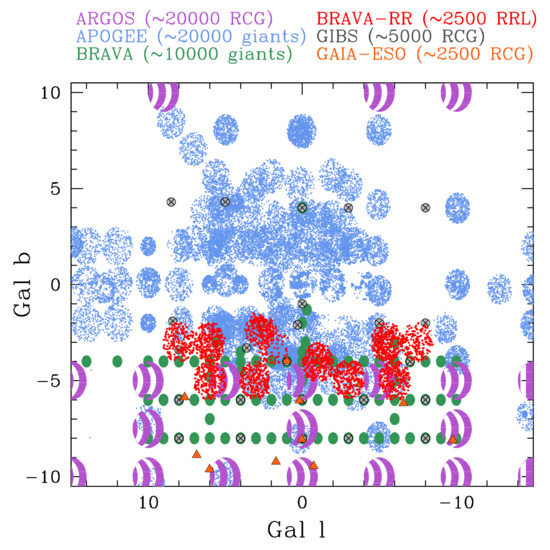
Figure 4.
The spatial extent of recent spectroscopic surveys of bulge stars are shown—ARGOS (magenta), APOGEE (light blue), BRAVA (green), BRAVA-RR (red), GIBS (grey), and Gaia-ESO (orange).
4.2. Kinematics of Stars with 1
Whereas there is disagreement as to exact metallicity distribution of the bulge stars from different bulge surveys (see, e.g., Figure 4 in Barbuy et al. 2018), there is a remarkable agreement regarding the distribution of radial velocities of bulge stars [55]. Figure 5 (left panel) shows the Galactocentric velocities as a function of longitude for the BRAVA, GIBS, APOGEE and ARGOS fields within |b| < 5. All surveys show that the bulge is rotating, as the radial velocity is positive (stars are, on average, going away from the Galactic center) at positive longitudes and negative (stars are on average going toward the Galactic center) at negative longitudes.
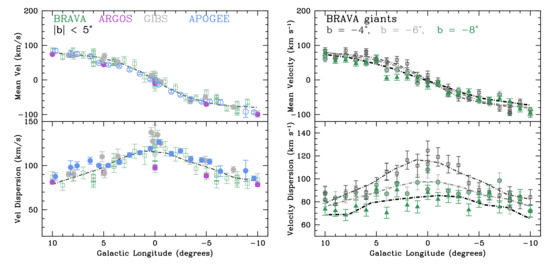
Figure 5.
(Top) The mean velocity profiles for the stars within 5 in the ARGOS (magenta), APOGEE (light blue), BRAVA (green) and GIBS (grey) surveys as a function of Galactic longitude. The lines represent the model by Shen et al. (2010) with a pure bar and no classical component. (Bottom) The velocity dispersion of the same surveys as a function of Galactic longitude. The surveys all agree well, and are consistent with the bulge being in pure cylindrical rotation. There are no obvious signs of cold substructure, indicating the lack of recent mergers.
Figure 5 (right panel) shows only BRAVA velocities for all Galactic latitudes. It is evident that the Galactocentric velocities do not change as a function of latitude or height above the disk plane—this same result is found for other bulge kinematic surveys as well. This is what is expected for the bulge rotating in a cylindrical manner [121]. If the bulge was rotating spherically (e.g., similar to the Sun or the Earth), the velocities would be faster near the Galactic plane (the mid-point) and slower closer to the poles. Cylindrical rotation of bulges is also seen in most other boxy bulges of other galaxies, and so this rotation is strong evidence that the MW bulge is an edge-on bar [134].
The velocity dispersion is not the same at all latitudes. Instead, the velocity dispersion drops with latitude, indicating that the stellar populations near the Galactic plane are kinematically hotter than the stellar populations further from the Galactic plane. This is expected from N-body models in which the Galaxy self-consistently develops a bar [123].
N-body models of bars also rotate cylindrically when viewed edge-on [135,136,137]. Therefore, all of these surveys agree that the dynamics are consistent with a boxy bulge being formed via dynamical instabilities in massive early disks [123,138]. Although a radial metallicity gradient observed in bulges was at first considered a signature of a classical bulge, it has now been shown that metallicity gradients may be reproduced in these models [139]. This suggests that our galaxy has not experienced a significant merger since at least the epoch of disk formation (3), since otherwise one expects a classical bulge to result [124].
Using observations from the GIBS survey, Zoccali et al. (2017) showed that, upon dividing bulge red giant stars by 0, those that have 0 (i.e., the subsolar population) are more centrally concentrated than those with 0 (i.e., the metal rich one), and with a more axisymmetric spatial distribution [29]. The more metal rich population has a more boxy distribution, consistent with an edge-on bar. Curiously, the kinematics of the two populations show no statistical difference, so it is unclear if these spatial differences arise from having different origins. Figure 6 shows the different metallicity components found in the GIBS survey, but that these do not have different rotation signatures.
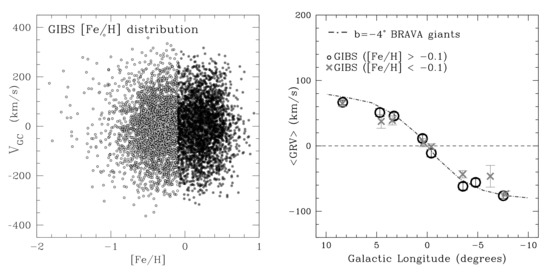
Figure 6.
(Left) Metallicity versus Galactocentric velocity for the GIBS sample. A division between sub-solar (0.1 dex) and solar (0.1 dex) samples can be seen. (Right) The Galactocentric velocity versus longitude distribution at fixed latitudes, split up into sub-solar (grey) and solar (black) samples. There is no statistical difference in kinematics between these two metallicity groups.
Rojas-Arriagada et al. (2019) argue that the apparent spatial dichotomy for subsolar and solar metallicity bulge stars does not translate into a dichotomy in -abundance space [30]. At least within the solar and subsolar bulge stellar population, there is a limited possibility for different origin scenarios, and hence no strong indication that accretion played a relevant role in the formation of the bulge.
Recent discovery of accretion events that undoubtedly extend to the inner Galaxy include the Inner Galaxy Structure [140] and the Kraken [141], accretion events that occurred around z = 2.2, and which may be the same event [140], Gaia–Enceladus [39,142], an accretion event that occurred around z = 1.4, and the Sagittarius dwarf galaxy [143], an accretion event that occurred around z = 0.8. These have all been shown to be significant building blocks of the Galactic halo, contributing to the properties and build-up of the halo. The Milky Way halo also extends to the inner Galaxy but is more difficult to study there due to the high extinction in the inner Galaxy as well as the complications of disentangling inner halo stars from the foreground stars and bulge stars. Because the halo does have a connection to the formation of the disk [142], it is not implausible that there may be some signatures of these accretion events within bulge stars. To date, however, there is no connection reported between bulge stars and those from the halo accretion events listed above.
4.3. Kinematics of Stars with 1
Most of the recent spectroscopic surveys do not specifically target metal-poor stars: BRAVA and APOGEE use K and M giants as tracers and these largely consist of the dominant metal-rich stellar population as metal-poor stars do not become M giants. It is therefore not surprising that APOGEE has found very few stars with 1. ARGOS and GIBS use red clump giants, i.e., metal-rich core Helium burning stars. ARGOS identified but 16 stars with 2.0 dex out of 14,000, while, in the APOGEE survey, 10 stars with 0.8 are highlighted [144], still a considerably larger population than previously observed [145,146]. The EMBLA survey, dedicated to searching for metal-poor stars in the bulge, has uncovered ∼40 metal-poor stars [147,148,149], including a handful with . This sample is too small for a large scale kinematic investigation, but they do show that at least some of these metal-poor stars are confined to the bulge and on tight orbits.
The Pristine Inner Galaxy Survey (PIGS) first data release [150], on the other hand, did target metal-poor stars and was successful in uncovering ∼600 stars in the inner Galaxy with 2.0 dex. With especially the PIGS sample, it seems that the bulge rotation curves are similar for different metallicity bins until 1.5 dex. As the becomes more metal-poor, the velocity dispersion increases. The rotation curve begins to slow with inclusion of stars more metal-poor than 1.5 dex, and the velocity dispersion continues to increase. Figure 7 shows this trend from the PIGS survey.
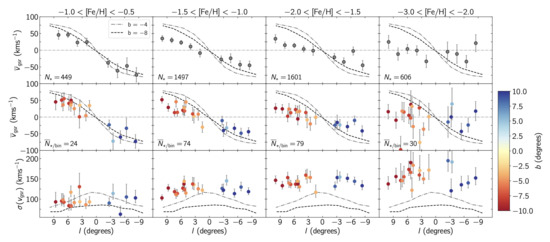
Figure 7.
(Top) Galactic longitude versus mean Galactocentric velocity for different metallicity ranges. (Middle row) the same, but separately for each observed field with colors indicating the latitude of the field. (Bottom row) Galactic longitude versus standard deviation of the velocities, figure from Arentsen et al. (2020) [150]. Reproduced with permission from Arentsen, A., Monthly Notices of the Royal Astronomical Society Letters; published by Oxford University Press, 2020.
The reason for the slower rotation and higher velocity in the more metal-poor inner Galaxy stars could be due to a number of different factors. First, as the stellar population becomes more metal-poor, greater contamination from, e.g., the halo will enter the sample. Halo stars would naturally cause the bulge/bar rotation curve to slow and the velocity dispersion to be higher. Second, we could be seeing a change from the bulge/bar being dominated by a rotation-supported population of a bar or disk at higher metallicities (1.0) to being fully dominated by the pressure-supported component, like a classical bulge at the lowest metallicities. Third, the metal-poor stars could be a few Gyr older than the more metal-rich stars, and therefore have been mapped into the boxy/peanut bulge in different ways because of their different initial velocity distributions at the time of the bar formation [151,152]. This is commonly referred to as kinematic fractionation.
Whether the PIGS metal-poor stars are actually confined to the inner bulge could be tested through an orbital analysis. In this way, halo outliers could be removed, and a “clean” sample of bulge stars could be obtained. Unfortunately, whereas most of the PIGS stars will have proper motions form Gaia, uncertain distances have prevented an orbital analysis from being carried out. At the moment, therefore, it is not clear if these metal-poor stars are actually confined to the bulge, or an inner halo or halo interlopers.
Whether the PIGS metal-poor stars are a rotation-supported classical bulge could be investigated by exploring the differences in elemental abundances between the most metal-poor stars and the “normal” bulge stars. Recently, Arentsen et al. (2021) have compared the fraction of their carbon-enhanced metal-poor (CEMP) stars in their sample to other Galactic components [153]. The PIGS inner Galaxy CEMP fraction for 3 is consistent with the halo fraction found in the literature. In contrast, at higher metallicities ( between −1.5 and −2.5), the PIGS fraction is substantially lower. This may indicate a fast chemical enrichment in the early building blocks of the inner Galaxy and/or a larger contribution of the low-metallicity bulge from former globular cluster stars. More high-resolution follow-up of the PIGS CEMP stars, as well as an orbital analysis of PIGS stars, can make progress on this front.
4.4. Kinematics of RR Lyrae Stars
The first study of the kinematics of RRLs toward the inner Galaxy came from Kunder et al. (2016) [154]. Using ∼1000 RRLs, it was found that the RRL kinematics do not follow the rotation pattern of any of the other bulge populations. They trace a slow or non-rotating component, possibly corresponding to the classical (pressure-supported) bulge.
Du et al. (2020) use Gaia DR2 proper motions of ∼15,000 OGLE RRL to probe the rotation of the Galactic bulge [155]. They confirm slower rotation of the inner Galaxy RRL, as first reported in the BRAVA-RR survey. Splitting their sample of RRLs into those that are more metal-poor than 1.0 and those more metal-rich than 0.5, they find that the more metal-rich RRLs (0.5) rotate similarly to the bar, and also with a similar velocity dispersion. The metal-poor RRLs are those that rotate slowest. The Du et al. (2020) sample of RRLs do not have radial velocities, and the Kunder et al. (2016) sample of RRLs did not have proper motions, so neither survey was able to clean for halo stars, which will be more present in a metal-poor population, and will of course inflate any velocity dispersion and decrease any rotation signature.
Missing, therefore, are the full space velocities of the RRLs. This is a problem because not all RRLs in the direction of the Galactic bulge are actually confined to the bulge, as shown explicitly for especially the high-velocity RRLs [156]. Other metal-poor stars located toward the Galactic bulge have also been shown to be interlopers from other Galactic components [148]. Obtaining a “pure” sample of bulge stars based on photometry/distance and spatial position alone, which is the usual approach when selecting bulge targets, is not statistically probable for more metal-poor stellar populations.
Prudil et al. (2019) were the first to derive orbits for a significant sample of bulge RRLs [37]. They reported that the RRLs in the central region of the Galactic bulge are consistent with random motions expected for a classical bulge component. They further searched for differences in the bulge RRLs based on their position in a period–amplitude diagram, or Oosterhoff group [37]. From ∼450 RRLs, they did not find significant kinematic differences between a RRL and its position in the period–amplitude diagram.
Using a sample of ∼1400 stars with radial velocities and Gaia DR2 proper motions, Kunder et al. (2020) carried out an orbital analysis to determine which RRLs actually belong to the bulge [110]. Now that Gaia eDR3 proper motions are available, this analysis can be repeated using more precise proper motions from eDR3. There is furthermore a ∼40% greater overlap between a BRAVA-RR star and one with an eDR3 Gaia proper motion. Therefore, the sample of BRAVA-RR stars for which orbits can be computed is almost doubled—2628 RRLs.
Orbits of the BRAVA-RR + Gaia eDR3 sample are calculated employing a non-axisymmetric model for the Galactic gravitational potential, as in Kunder et al. (2020). The model has an axisymmetric background made by an exponential disk built from the superposition of three Miyamoto–Nagai potentials [157], and a Navarro–Frenk–White density profile [158] to model the dark matter halo, which has a circular velocity = 241 km s at = 8.2 kpc. The RRLs are separated into two groups, based on their apocenter distances, , and the maximum distance from the Galactic plane that the stars reach during their orbit, .
Figure 8 shows the rotation curve of the BRAVA-RR stars in the inner bulge, where the inner bulge is defined as those stars having 3.5 kpc and 2.5 kpc. It is believed that the bulge/bar likely extends out to ∼5 kpc [159], but the focus is on the inner bulge to ensure the RRL sample is truly confined to the bulge.
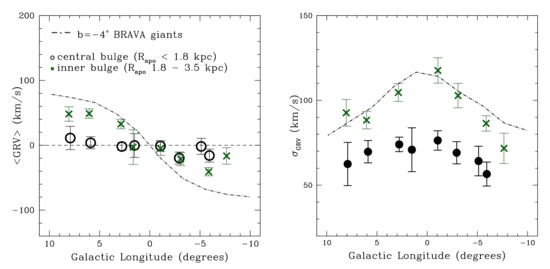
Figure 8.
(Left) The mean velocity for RR Lyrae stars in the BRAVA-RR survey as a function of Galactic longitude. (Right) The velocity dispersion profile for the same stars. The lines represent the model by Shen et al. (2010) with a pure bar and no classical component.
There is a striking difference in the rotation profile of the stars on the most centrally concentrated orbits (1.8 kpc) compared to those of the bar/bulge RRL that have apocenter distances between 1.8 kpc and 3.5 kpc. The central bulge RRLs show almost no rotation, even out to 7. In contrast, the inner bulge RRLs show rotation, although the amplitude of rotation is smaller. The velocity dispersion of the two populations is also different, with the central bulge RRLs having a smaller velocity dispersion than those in the inner bulge.
Kunder et al. (2020) illustrate that it is not only the kinematics that differ between the more centrally concentrated RRLs and those that are less tightly bound, but that these populations also have different spatial distributions. Figure 9 shows that, although neither of these populations of RRL show a strong bar/bar spatial distribution, the less tightly bound RRL follow the bar/bulge weakly. In contrast, the more central RRLs show almost no trace of a bar.
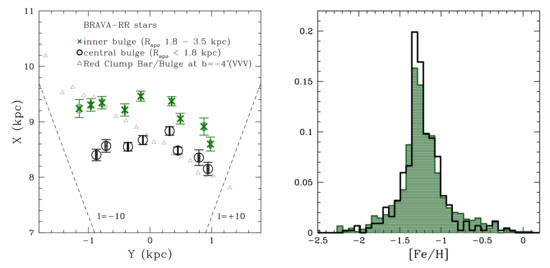
Figure 9.
(Left) The mean spatial distribution of the most centrally concentrated RRLs ( < 1.8 kpc) as compared to bulge RRLs with apocenter distances between 1.8 and 3.5 kpc. The spatial distribution of red clump stars from Gonzalez et al. (2012) that trace out the bar/bulge is also shown. (Right) The photometric metallicity distribution for the RRLs in the inner bulge (green, filled histogram) as well as the RRLs in the central bulge (black, solid line histogram). There is no obvious metallicity difference between these two RRL populations.
Both of these RRL groups have similar distributions. Therefore, within the metal-poor stars, two distinct spatial and kinematic groups can be seen based on how centrally confined they are within the bulge. As such, it may be more appropriate to separate bulge stars based on their orbits, rather than their metallicity. Theoretically, it is also predicted that stellar populations with the oldest ages and origins will have centrally confined orbits compared to other bulge populations [160].
4.5. Kinematics of RR Lyrae Stars in the Context of Milky Way Formation Scenarios
Martinez-Valpuesta and Gerhard (2011) show that, when the disk evolves to form a boxy bulge through a buckling instability, the stellar disk can also extend to a longer in-plane bar [161]. Therefore, secular evolution of a disk galaxy, a natural mechanism for galaxies like ours, can be responsible for a variety of different stellar features. Using a similar N-boday simulation, Shen et al. (2010) find that the velocities of the boxy bulge agree well with what is found from bulge radial velocity surveys [123], leaving little doubt that the boxy bulge was formed from secular evolution of the disk.
Regarding the chemical gradients observed in the bar/bulge, Martinez-Valpuesta and Gerhard (2013) further show that chemical gradients in the initial disk can transform into gradients in the boxy bulge. Therefore, depending on when the bulge formed and on the properties of the precursor disk at that time, boxy bulges can have stars with differences in metallicities depending on their spatial location within the bulge. It is therefore expected that a mix of stars can co-exist in the boxy bulge, all resulting from secular evolution of the MW disk. Whether this is the case also for the old, metal-poor RRLs is still under debate.
One promising explanation for a barred population of stars co-existing with a population of stars that is either less-barred or un-barred is that the bulge stars formed from disk buckling and ended up with different spatial distributions due to having slightly different ages and initial velocity distributions, i.e., kinematic fractionation [152]. In this scenario, the different stellar populations originate from the Galaxy’s disk. They would have slightly different ages (difference of ∼1.5–2 Gyr) and different initial velocity distributions. As the Galaxy evolves and the disk buckles, they would end up tracing the barred bulge in different ways—the hotter and older initial population would weakly trace the bar, whereas the cooler and younger population would follow a stronger barred spatial distribution.
The issue with kinematic fractionation being an explanation for the RRL populations is that the weakly-barred, central RRLs have a larger velocity dispersion compared to the barred RRLs (see Figure 8). Another issue is that since, in general, metallicity and age of an RRL are related (see Section 2.3), and there is no difference in the mean distributions of the two populations (see Figure 9), it is difficult to conclude these two populations have age differences on the order of 1.5–2 Gyr. However, until the abundances are sufficiently known, in particular, if the RRLs have a spread in [/Fe], relative ages will have uncertainties at the ∼1 Gyr level.
That the ages of the RRLs are >10 Gyr also renders the cosmological hydrodynamical simulation of Buck et al. (2018) unable to explain the bulge RRL properties. In Buck et al. (2018), stars with ages >10 Gyr form a roughly spheroidal and nonbarred distribution of stars in the central few kiloparsecs of the Galaxy, and only stars with ages ∼8 Gyr or younger contribute to the bar [162]. However, the inner Galaxy RRLs do show that there is a population of bulge RRLs that contribute to the bar, despite their old ages.
There has been indication from a number of studies that the metal-rich and metal-poor bulge stars show different spatial distribution [29], which could suggest that the metal-poor and metal-rich bulge stars trace different Galactic components. However, the photometric distribution of the two groups of RRLs do not show a difference in mean photometric metallicity—both groups have an average of −1.23 dex with a dispersion in of 0.30 dex. Therefore, formation scenarios indicating metal-rich and metal-poor stars trace different bulge populations are not complete and/or too limited. Within the old, metal-poor bulge RRL ( 3.5 kpc) different bulge populations are seen—one that traces out the bar with a similar spatial distribution and kinematic signature as seen in more metal-rich populations, and one that does not trace out the bar, with slower rotation. The bulge RRLs suggest that it is not the case that bulge metal-poor stars arose from one common origin.
Saha et al. (2016) predict that a massive classical bulge will gain some angular momentum from the bar, and so classical bulge rotation will be small in the center, but significant at larger radii [163]. Rotation at the larger longitudes that is absent in the center of the bulge could be interpreted as a population of stars belonging to a relatively massive classical bulge. Low-mass classical bulges would likely follow the cylindrical rotation even at the center [164]. The RRLs do show some suggestion of rotation at larger longitudes compared to the center, but the sample size of the RRLs is still small. The Milky Way harboring a massive classical bulge would be surprising, especially given the paucity of studies, suggesting that a classical bulge exists in the MW.
5. Conclusions
The oldest stars in the Bulge that likely witnessed the earliest episodes of star formation and assembly of our Galaxy are key to our understanding of its mechanisms. For example, within CDM-based simulations, the oldest stars in the Galaxy, those formed in the primordial dark matter halos at 10–15, are expected to be tightly bound in the center of the Milky Way as it forms from the inside out. These stars lie in the bulge, but do not share its abundance patterns or kinematics [160]. The greatest chance of uncovering a classical component, formed by the early (10) collapse of baryons within dark matter halos, would therefore be within the old, metal-poor stars in the inner few kpc of our Galaxy.
Unfortunately, it has been difficult for studies to specifically target old stars, although the stellar population of the bulge appears to be predominantly old and approximately solar in metal abundance. For example, the K and M giants and red clump giants, used as tracers in the past and current Bulge surveys (BRAVA, ARGOS, GIBS and APOGEE) are a mixed population of stars of different ages and metal abundances. Surveys such as EMBLA and PIGS are now beginning to uncover larger samples of metal-poor stars in the inner Galaxy. Still, today there are only a few low metallicity stars known to reside in the bulge, and, from these samples, it is not possible to have a complete picture into the structure and properties of the (likely) oldest stars in the bulge of our Galaxy.
This review discusses a number of advantages in using the bulge RRL population to trace the old, metal-poor bulge. These stars are at least ∼10x more metal-poor than the subsolar metallicity stars probed by many other bulge surveys, (Section 2) they are distance indicators (Section 3), and it is well-known from stellar evolution theory that RRLs are old (>10 Gyr) core Helium burning stars.
There is still no consensus as to if the bulge RRLs spatially trace out the bar, or if they are more consistent with a more spheroidal bulge population; different RRL photometric surveys in different wavelengths (i.e., OGLE in the optical and VVV in the infrared) present differing results. There is a broad consensus from the RRL proper motions and the RRL radial velocities that the kinematics of the bulge RRLs rotate slower than the bar/bulge, although there does appear to be a subset of bulge RRLs that rotate in a similar manner to the bar [110,155,165].
Possibly the most intriguing aspect of the RRLs is that there are two different metal-poor, bulge populations that coexist together in the bulge [110]. The population of RRLs on the tightest orbits ( 1.8 kpc) have both a spatial distribution and kinematic signature unlike the bar. Instead, this population has an average Galactocentric velocity consistent with no rotation, and a small velocity dispersion. The inner Galaxy RRLs ( between 1.8 kpc and 3.5 kpc) are more consistent with following the bar, with a signature of rotation and an elongated spatial distribution consistent with the bar.
These observations can be compared in the context of bulge formation scenarios. In Saha et al. (2016), a classical bulge coexists with a pseudobulge [163]; in Debattista et al. (2017), kinematic fractionation naturally gives rise to bulge populations with different spatial and kinematic signatures [152], and in Buck et al. (2018), the oldest (>10 Gyr) stars have different properties than younger (∼8 Gyr and younger) stars [162]. Although these scenarios naturally give rise to a bulge population that is barred and one that is not because the barred and un-barred RRL populations are so similar in and therefore age, and because the velocity dispersion of the unbarred RRL is smaller than that of the barred RRL, none of these scenarios adequately interpret the RRL observations. It is therefore still not clear as to the origin of the bulge RRLs. One promising avenue to make progress on this front is to combine the RRL kinematics with reliable spectroscopic metallicities of bulge RRLs, in particular elemental abundances. In this way, the bulge RRLs may be able to be conclusively linked to the bar, or to inner Galaxy merger events (e.g., the IGS [140]), or to the dissolution of a globular cluster or dwarf Galaxy stars [166,167].
Funding
This research was funded by the National Science Foundation from grant AST-2009836.
Conflicts of Interest
The author declares no conflict of interest.
References
- Kinman, T.D.; Pier, J.R.; Suntzeff, N.B.; Harmer, D.L.; Valdes, F.; Hanson, R.B.; Klemola, A.R.; Kraft, R.P. An RR LYR star survey with the Lick 20-inch. astrograph. IV. A survey of 3 fields near North galactic pole. Astron. J. 1966, 111, 1164. [Google Scholar] [CrossRef]
- Oort, J.H.; Plaut, L. The distance to the galactic center derived from RR-Lyrae variables, the distribution of these variables in the Galaxy’s inner region and halo, and a rediscussion of the galactic rotation constants. Astron. Astrophys. 1975, 41, 71–86. [Google Scholar]
- Saha, A. RR Lyrae stars and the distant galactic halo: Distribution, chemical composition, kinematics and dynamics. Astrophys. J. 1985, 289, 310. [Google Scholar] [CrossRef]
- Layden, A.C. The Metallicities and Kinematics of RR Lyrae Variables. II. Galactic Structure and Formation from Local Stars. Astron. J. 1995, 110, 2288. [Google Scholar] [CrossRef]
- Catelan, M. Horizontal branch stars: The interplay between observations and theory, and insights into the formation of the Galaxy. Astrophys. Space Sci. 2009, 320, 261. [Google Scholar] [CrossRef]
- Catelan, M. Structure and Evolution of Low-Mass Stars: An Overview and Some Open Problems. In Proceedings of the GRADUATE SCHOOL IN ASTRONOMY: XI Special Courses at the National Observatory of Rio de Janeiro (XI CCE), Rio de Janeiro, Brazil, 16–20 October 2006; Alcaniz, J., Reza, R.d., Roig, F., Lopes, D.F., Eds.; AIP Conference Proceedings: Rio de Janeiro, Brazil, 2006; Volume 930, pp. 39–90. [Google Scholar]
- Catelan, M. The Evolutionary Status of M3 RR Lyrae Variable Stars: Breakdown of the Canonical Framework? Astrophys. J. 2004, 1, 409–418. [Google Scholar] [CrossRef]
- Marconi, M.; Nordgren, T.; Bono, G.; Schnider, G.; Caputo, F. Predicted and Empirical Radii of RR Lyrae Stars. Astrophys. J. 2005, 623, 133. [Google Scholar] [CrossRef]
- Smith, H.A. RR Lyrae Stars; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Lee, Y.-W. Evidence for an Old Galactic Bulge From RR Lyrae Stars in Baade’s Window: Implications for the Formation of the Galaxy and the Age of the Universe. Astron. J. 1992, 104, 1780. [Google Scholar] [CrossRef]
- Catelan, M.; Smith, H.A. Pulsating Stars; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 2015; pp. 157–182. [Google Scholar]
- Bailey, S.I. A discussion of variable stars in the cluster ω Centauri. Ann. Harv. Coll. Obs. 1902, 38, 1. [Google Scholar]
- Schwarzschild, M. Overtone Pulsations for the Standard Model. Astrophys. J. 1941, 94, 245. [Google Scholar] [CrossRef]
- Jerzykiewicz, M.; Wenzel, W. Analysis of the light variation of the RR Lyrae star AQ Leonis. Acta Astron. 1977, 27, 35. [Google Scholar]
- Cox, A.N.; Hodson, S.W.; Clancy, S.P. Double-mode RR Lyrae variables in M15. Astrophys. J. 1983, 266, 94–104. [Google Scholar] [CrossRef]
- Nemec, J.M. Double-mode RR Lyrae stars in M 15: Reanalysis and experiments with simulated photometry. Astron. J. 1985, 90, 240. [Google Scholar] [CrossRef]
- Clement, C.C.; Dickens, R.J.; Bingham, E.E. The RR Lyrae variable stars in the globular cluster IC 4499. Astron. J. 1979, 84, 217–230. [Google Scholar] [CrossRef]
- Walker, A.R.; Nemec, J.M. CCD Photometry of Galactic Globular Clusters. III. IC 4499 Astron. J. 1994, 112, 2026. [Google Scholar]
- Shapley, H. Studies based on the colors and magnitudes in stellar clusters. VI. On the determination of the distances of globular clusters. Astrophys. J. 1918, 48, 89. [Google Scholar] [CrossRef]
- Blanco, V.M.; Blanco, B.M. RR Lyraes in Baade’s Window and the value of Ro. Mem. Della Soc. Astron. Ital. 1985, 56, 15–22. [Google Scholar]
- Alcock, C.; Allsman, R.A.; Axelroc, T.S.; Bennett, D.P.; Cook, K.H.; Freeman, K.C.; Griest, K.; Guern, J.A.; Lehner, M.J.; Marshall, S.L.; et al. The MACHO Project First-Year Large Magellanic Cloud Results: The Microlensing Rate and the Nature of the Galactic Dark Halo. Astrophys. J. 1996, 461, 84. [Google Scholar] [CrossRef]
- Udalski, A.; Szymański, M.; Kaluzny, J.; Kubiak, M.; Mateo, M. The Optical Gravitational Lensing Experiment. Acta Astron. 1992, 42, 253–284. [Google Scholar]
- McWilliam, A.; Rich, R.M. The First Detailed Abundance Analysis of Galactic Bulge K Giants in Baade’s Window. Astrophys. J. Suppl. 1994, 91, 749. [Google Scholar] [CrossRef]
- Gonzalez, A.; Zoccali, M.; Vasquez, S.; Hill, V.; Rejkuba, M.; Valenti, E.; Rojas-Arriagada, A.; Renzini, A.; Babusiaux, C.; Minniti, D.; et al. The GIRAFFE Inner Bulge Survey (GIBS). II. Metallicity distributions and alpha element abundances at fixed Galactic latitude. Astron. Astrophys. 2015, 584, 46. [Google Scholar] [CrossRef]
- Johnson, C.I.; Rich, R.M.; Young, M.D.; Simion, I.T.; Clarkson, W.I.; Pilachowski, C.A.; Michael, S.; Kunder, A.; Koch, A.; Vivas, A.K. Blanco DECam Bulge Survey (BDBS) II: Project performance, data analysis, and early science results. Mon. Not. R. Astron. Soc. 2020, 499, 2357–2379. [Google Scholar] [CrossRef]
- Pancino, E.; Britavskiy, N.; Romano, D.; Cacciari, C.; Mucciarelli, A.; Clementini, G. Chemical abundances of solar neighbourhood RR Lyrae stars. Mon. Not. R. Astron. Soc. 2015, 447, 2404–2419. [Google Scholar] [CrossRef]
- Walker, A.R.; Terndrup, D.M. The Metallicity of RR Lyrae Stars in Baade’s Window. Astrophys. J. 1991, 378, 119. [Google Scholar] [CrossRef]
- Savino, A.; Koch, A.; Prudil, Z.; Kunder, A.; Smolec, R. The age of the Milky Way inner stellar spheroid from RR Lyrae population synthesis. Astron. Astrophys. 2020, 641, 96. [Google Scholar] [CrossRef]
- Zoccali, M.; Vasquez, S.; Gonzalez, O.A.; Valenti, E.; Rojas-Arriagada, A.; Minniti, J.; Rejkuba, M.; Minniti, D.; McWilliam, A.; Babusiaux, C.; et al. The GIRAFFE Inner Bulge Survey (GIBS). III. Metallicity distributions and kinematics of 26 Galactic bulge fields. Astron. Astrophys. 2017, 599, 12. [Google Scholar] [CrossRef]
- Rojas-Arriagada, A.; Zoccali, M.; Schultheis, M.; Recio-Blanco, A.; Zasowski, G.; Minniti, D.; Jönsson, H.; Cohen, R.E. The bimodal [Mg/Fe] versus [Fe/H] bulge sequence as revealed by APOGEE DR14. Astron. Astrophys. 2019, 626, 16. [Google Scholar] [CrossRef]
- Jurcsik, J.; Kovacs, G. Determination of [Fe/H] from the light curves of RR Lyrae stars. Astron. Astrophys. 1996, 312, 111–120. [Google Scholar]
- Sandate, A. The Metallicity Dependence of the Fourier Components of RR Lyrae Light Curves Is the Oosterhoff-Arp-Preston Period Ratio Effect in Disguise. Astron. J. 2004, 128, 858. [Google Scholar] [CrossRef]
- Szymański, M.; Udalski, A.; Soszyxnxski, I.; Kubiak, M.; Pietrzyxnxski, G.; Poleski, R.; Wyrzykowski, L.; Ulaczyk, K. Metallicity Dependence of the Blazhko Effect. Acta Astron. 2005, 55, 59–84. [Google Scholar]
- Nemec, J.M.; Cohen, J.G.; Ripepi, V.; Derekas, A.; Moskalik, P.; Sesar, B.; Chadid, M.; Bruntt, H. Metal Abundances, Radial Velocities, and Other Physical Characteristics for the RR Lyrae Stars in The Kepler Field. Astrophys. J. 2013, 773, 181. [Google Scholar] [CrossRef]
- Jurcsik, J. Revision of the [Fe/H] Scales Used for Globular Clusters and RR Lyrae Variables. Acta Astron. 1995, 45, 653–660. [Google Scholar]
- Salaris, M.; Chieffi, A.; Straniero, O. The alpha -enhanced Isochrones and Their Impact on the FITS to the Galactic Globular Cluster System. Astrophys. J. 1993, 414, 580. [Google Scholar] [CrossRef]
- Prudil, Z.; Dékány, I.; Grebel, E.K.; Catelan, M.; Skarka, M.; Smolec, R. Evidence for Galactic disc RR Lyrae stars in the solar neighbourhood. Mon. Not. R. Astron. Soc. 2019, 487, 3270–3278. [Google Scholar] [CrossRef]
- Zinn, R.; Chen, X.; Layden, A.C.; Casetti-Dinescu, D.I. Local RR Lyrae stars: Native and alien. Mon. Not. R. Astron. Soc. 2020, 492, 2161–2176. [Google Scholar] [CrossRef]
- Helmi, A.; Babusiaux, C.; Koppelman, H.H.; Massari, D.; Veljanoski, J.; Brown, A.G.A. The merger that led to the formation of the Milky Way’s inner stellar halo and thick disk. Nature 2018, 563, 85. [Google Scholar] [CrossRef]
- Mackereth, J.T.; Schiavon, R.P.; Pfeffer, J.; Hayes, C.R.; Bovy, J.; Anguiano, B.; Allende Prieto, C.; Hasselquist, S.; Holtzman, J.; Johnson, J.A.; et al. The origin of accreted stellar halo populations in the Milky Way using APOGEE, Gaia, and the EAGLE simulations. Mon. Not. R. Astron. Soc. 2019, 482, 3426. [Google Scholar] [CrossRef]
- Dékány, I.; Grebel, E.K.; Pojmański, G. Metallicity Estimation of RR Lyrae Stars From Their I-Band Light Curves. Astrophys. J. 2021, 920, 33. [Google Scholar] [CrossRef]
- Kunder, A.; Chaboyer, B. Metallicity Analysis of MACHO Galactic Bulge RR0 Lyrae Stars from their Light Curves. Astron. J. 2008, 136, 2441–2452. [Google Scholar] [CrossRef]
- Pietrukowicz, P.; Udalski, A.; Soszy’nski, I.; Nataf, D.M.; Wyrzykowski, L.; Poleski, R.; Kozlowski, S.; Szymański, M.K.; Kubiak, M.; Pietrzyński, G.; et al. The Optical Gravitational Lensing Experiment: Analysis of the Bulge RR Lyrae Population from the OGLE-III Data. Astrophys. J. 2012, 750, 169. [Google Scholar] [CrossRef]
- Pietrukowicz, P.; Kozlowski, S.; Skowron, J.; Soszyński, I.; Udalski, A.; Poleski, R.; Wyrzykowski, L.; Szymański, M.K.; Pietrzyński, G.; Ulaczyk, K.; et al. Deciphering the 3D Structure of the Old Galactic Bulge from the OGLE RR Lyrae Stars. Astrophys. J. 2015, 811, 113. [Google Scholar] [CrossRef]
- Zinn, R.; West, M.J. The globular cluster system of the Galaxy. III. Measurements of radial velocity and metallicity for 60 clusters and a compilation of metallicities for 121 clusters. Astrophys. J. Suppl. Ser. 1984, 55, 45–66. [Google Scholar] [CrossRef]
- Pietrukowicz, P.; Udalski, A.; Soszyński, I.; Skowron, D.M.; Wrona, M.; Szymański, M.K.; Poleski, R.; Ulaczyk, K.; Kozlowski, S.; Skowron, J.; et al. Properties of the Milky Way’s Old Populations Based on Photometric Metallicities of the OGLE RR Lyrae Stars. Acta Astron. 2020, 70, 121–139. [Google Scholar]
- Clarkson, W.; Sahu, K.; Anderson, J.; Smith, T.E.; Brown, T.M.; Rich, R.M.; Casertano, S.; Bond, H.E.; Livio, M.; Minniti, D.; et al. Stellar Proper Motions in the Galactic Bulge from Deep Hubble Space Telescope ACS WFC Photometry. Astrophys. J. 2008, 684, 1110–1142. [Google Scholar] [CrossRef]
- Renzini, A.; Gennaro, M.; Zoccali, M.; Brown, T.M.; Anderson, J.; Minniti, D.; Sahu, K.C.; Valenti, E.; VandenBerg, D.A. The WFC3 Galactic Bulge Treasury Program: Relative Ages of Bulge Stars of High and Low Metallicity. Astrophys. J. 2018, 863, 16. [Google Scholar] [CrossRef]
- Haywood, M.; Di Matteo, P.; Snaith, O.; Calamida, A. Hiding its age: The case for a younger bulge. Astron. Astrophys. 2016, 593, 82. [Google Scholar] [CrossRef]
- Bensby, T.; Feltzing, S.; Gould, A.; Yee, J.C.; Johnson, J.A.; Asplund, M.; Meléndez, J.; Lucatello, S.; Howes, L.M.; McWilliam, A.; et al. Chemical evolution of the Galactic bulge as traced by microlensed dwarf and subgiant stars. VI. Age and abundance structure of the stellar populations in the central sub-kpc of the Milky Way. Astron. Astrophys. 2017, 605, 89. [Google Scholar] [CrossRef]
- Pietrinferni, A.; Cassisi, S.; Salaris, M.; Castelli, F. A Large Stellar Evolution Database for Population Synthesis Studies. II. Stellar Models and Isochrones for an α-enhanced Metal Distribution. Astron. J. 2006, 642, 797. [Google Scholar] [CrossRef]
- Hasselquist, S.; Zasowski, G.; Feuillet, D.K.; Schultheis, M.; Nataf, D.M.; Anguiano, B.; Beaton, R.L.; Beers, T.C.; Cohen, R.E.; Cunha, K. Exploring the Stellar Age Distribution of the Milky Way Bulge Using APOGEE. Astrophys. J. 2020, 901, 109. [Google Scholar] [CrossRef]
- Zoccali, M.; Renzini, A.; Ortolani, S.; Greggio, L.; Saviane, I.; Cassisi, S.; Rejkuba, M.; Barbuy, B.; Rich, R.M.; Bica, E. Age and metallicity distribution of the Galactic bulge from extensive optical and near-IR stellar photometry. Astron. Astrophys. 2003, 399, 931–956. [Google Scholar] [CrossRef]
- Clarkson, W.; Sahu, K.; Anderson, J.; Rich, R.M.; Smith, T.E.; Brown, T.M.; Bond, H.E.; Livio, M.; Minniti, D.; Renzini, A.; et al. The First Detection of Blue Straggler Stars in the Milky Way Bulge. Astrophys. J. 2011, 735, 37. [Google Scholar] [CrossRef]
- Barbuy, B.; Chiappini, C.; Gerhard, O. Chemodynamical History of the Galactic Bulge. Annu. Rev. Astron. Astrophys. 2018, 56, 223–276. [Google Scholar] [CrossRef]
- Van Loon, J.T.; Gilmore, G.F.; Omont, A.; Blommaert, J.A.D.L.; Glass, I.S.; Messineo, M.; Schuller, F.; Schultheis, M.; Yamamura, I.; Zhao, H.S. Infrared stellar populations in the central parts of the Milky Way galaxy. Mon. Not. R. Astron. Soc. 2003, 338, 857–879. [Google Scholar] [CrossRef][Green Version]
- Bensby, T.; Yee, J.C.; Feltzing, S.; Johnson, J.A.; Gould, A.; Cohen, J.G.; Asplund, M.; Meléndez, J.; Lucatello, S.; Han, C.; et al. Chemical evolution of the Galactic bulge as traced by microlensed dwarf and subgiant stars. V. Evidence for a wide age distribution and a complex MDF. Astron. Astrophys. 2013, 549, 147. [Google Scholar] [CrossRef]
- Catchpole, R.M.; Whitelock, P.A.; Feast, M.W.; Hughes, S.M.G.; Irwin, M.; Alard, C. The age and structure of the Galactic bulge from Mira variables. Mon. Not. R. Astron. Soc. 2016, 455, 2216–2227. [Google Scholar] [CrossRef]
- Blitz, L.; Spergel, D.N. Direct Evidence for a Bar at the Galactic Center. Astrophys. J. 1991, 379, 631–638. [Google Scholar] [CrossRef]
- Dwek, E.; Arendt, R.G.; Hauser, M.G.; Kelsall, T.; Lisse, C.M.; Moseley, S.H.; Silverberg, R.F.; Sodroski, T.J.; Weil, J.L. Morphology, Near-Infrared Luminosity, and Mass of the Galactic Bulge from COBE DIRBE Observations. Astrophys. J. 1995, 445, 716. [Google Scholar] [CrossRef]
- Sandage, A. The Oosterhoff period groups and the age of globular clusters. II. Properties of RR Lyrae stars in six clusters: The P-L-A relation. Astrophys. J. 1981, 248, 161. [Google Scholar] [CrossRef]
- Sandage, A. Evidence for a period-luminosity-amplitude relation for RR Lyrae stars. Astrophys. J. 1981, 244, 23. [Google Scholar] [CrossRef]
- Caputo, F. The period-magnitude diagram of RR Lyrae stars—I. The controversy about the distance scale. Mon. Not. R. Astron. Soc. 1997, 284, 994. [Google Scholar] [CrossRef]
- Catelan, M.; Pritzl, B.J.; Smith, H.A. The RR Lyrae Period-Luminosity Relation. I. Theoretical Calibration. Astrophys. J. Suppl. Ser. 2004, 154, 633. [Google Scholar] [CrossRef]
- Demarque, P.; Zinn, R.; Lee, Y.-W.; Yi, S. The Metallicity Dependence of RR Lyrae Absolute Magnitudes from Synthetic Horizontal-Branch Models. Astron. J. 2000, 119, 1398. [Google Scholar] [CrossRef][Green Version]
- Caputo, F.; Castellani, V.; Marconi, M.; Ripepi, V. Pulsational MV versus [Fe/H] relation(s) for globular cluster RR Lyrae variables. Mon. Not. R. Astron. Soc. 2000, 316, 819–826. [Google Scholar] [CrossRef][Green Version]
- Gould, A.; Popowski, P. Systematics of RR Lyrae Statistical Parallax. III. Apparent Magnitudes and Extinctions. Astrophys. J. 1998, 508, 844–853. [Google Scholar] [CrossRef][Green Version]
- Fernley, J.; Carney, B.W.; Skillen, I.; Cacciari, C.; Janes, K. Radial velocities and iron abundances of field RR Lyraes. I. Mon. Not. R. Astron. Soc. 1998, 293, 61. [Google Scholar] [CrossRef]
- Sandage, A. The Oosterhoff Period-Metallicity Relation for RR Lyrae Stars at the Blue Fundamental Edge of the Instability Strip. I. Astrophys. J. 1993, 106, 687. [Google Scholar] [CrossRef]
- Feast, M.W. RR Lyraes, Galactic and extragalactic distances, and the age of the oldest globular clusters. Mon. Not. R. Astron. Soc. 1997, 284, 761–766. [Google Scholar] [CrossRef][Green Version]
- Fusi Pecci, F. The M(v)-HB Verses [Fe/H] Calibration. I. HST Color-Magnitude Diagrams of Eight Globular Clusters in M31. Astron. J. 1996, 112, 1461. [Google Scholar] [CrossRef][Green Version]
- Chaboyer, B.C. Globular Cluster Distance Determinations. In Post-Hipparcos Cosmic Candles; Heck, A., Caputo, F., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; Volume 137, p. 111. [Google Scholar]
- Clementini, G.; Gratton, R.; Bragaglia, A.; Carretta, E.; Di Fabrizio, L.; Maio, M. Distance to the Large Magellanic Cloud: The RR Lyrae Stars. Astron. J. 2003, 125, 1309–1329. [Google Scholar] [CrossRef]
- Gratton, R.G.; Bragaglia, A.; Clementini, G.; Carretta, E.; Di Fabrizio, L.; Maio, M.; Taribello, E. Metal abundances of RR Lyrae stars in the bar of the Large Magellanic Cloud. Astron. Astrophys. 2004, 421, 937. [Google Scholar] [CrossRef]
- Dambis, A.K.; Berdnikov, L.N.; Kniazev, A.Y.; Kravtsov, V.V.; Rastorguev, A.S.; Sefako, R.; Vozyakova, O.V. RR Lyrae variables: Visual and infrared luminosities, intrinsic colours and kinematics. Mon. Not. R. Astron. Soc. 2013, 435, 3206–3220. [Google Scholar] [CrossRef]
- Muraveva, T.; Delgado, H.E.; Clementini, G.; Sarro, L.M.; Garofalo, A. RR Lyrae stars as standard candles in the Gaia Data Release 2 Era. Mon. Not. R. Astron. Soc. 2018, 481, 1195–1211. [Google Scholar] [CrossRef]
- Clementini, G.; Ripepi, V.; Molinaro, R.; Garofalo, A.; Muraveva, T.; Rimoldini, L.; Guy, L.P.; Jevardat de Fombelle, G.; Nienartowicz, K.; Marchal, O.; et al. Gaia Data Release 2. Specific characterisation and validation of all-sky Cepheids and RR Lyrae stars. Astron. Astrophys. 2019, 622, 60. [Google Scholar] [CrossRef]
- Longmore, A.J.; Fernley, J.A.; Jameson, R.F. RR Lyrae stars in globular clusters: Better distances from infrared measurements? Mon. Not. R. Astron. Soc. 1986, 220, 279–287. [Google Scholar] [CrossRef]
- Dall’Ora, M.; Storm, J.; Bono, G.; Ripepi, V.; Monelli, M.; Testa, V.; Andreuzzi, G.; Buonanno, R.; Caputo, F.; Castellani, V.; et al. The Distance to the Large Magellanic Cloud Cluster Reticulum from the K-Band Period-Luminosity-Metallicity Relation of RR Lyrae Stars. Astrophys. J. 2004, 610, 269–274. [Google Scholar] [CrossRef]
- Bono, G.; Caputo, F.; Castellani, V.; Marconi, M.; Storm, J.; Degl’Innocenti, S. A pulsational approach to near-infrared and visual magnitudes of RR Lyr stars. Mon. Not. R. Astron. Soc. 2003, 344, 1097–1106. [Google Scholar] [CrossRef]
- Marconi, M.; Coppola, G.; Bono, G.; Braga, V.; Pietrinferni, A.; Buonanno, R.; Castellani, M.; Musella, I.; Ripepi, V.; Stellingwerf, R.F. On a New Theoretical Framework for RR Lyrae Stars. I. The Metallicity Dependence. Astrophys. J. 2015, 808, 50. [Google Scholar] [CrossRef]
- Madore, B.F.; Hoffman, D.; Freedman, W.L.; Kollmeier, J.A.; Monson, A.; Persson, S.E.; Rich, J.A., Jr.; Scowcroft, V.; Seibert, M. Predicted and Empirical Radii of RR Lyrae Stars. Astrophys. J. 1994, 776, 135. [Google Scholar] [CrossRef]
- Dambis, A.K.; Rastorguev, A.S.; Rastorguev, A.S.; Zabolotskikh, M.V. Mid-infrared period-luminosity relations for globular cluster RR Lyrae. Mon. Not. R. Astron. Soc. 2014, 439, 3765. [Google Scholar] [CrossRef]
- Braga, V.F.; Dall’Ora, M.; Bono, G.; Stetson, P.B.; Ferraro, I.; Iannicola, G.; Marengo, M.; Neeley, J.; Persson, S.E.; Buonanno, R.; et al. On the Distance of the Globular Cluster M4 (NGC 6121) Using RR Lyrae Stars. I. Optical and Near-infrared Period-Luminosity and Period-Wesenheit Relations. Astrophys. J. 2015, 799, 165. [Google Scholar] [CrossRef]
- Neeley, J.R.; Marengo, M.; Bono, G.; Braga, V.F.; Dall’Ora, M.; Stetson, P.B.; Buonanno, R.; Ferraro, I.; Freedman, W.L.; Iannicola, G.; et al. On the Distance of the Globular Cluster M4 (NGC 6121) Using RR Lyrae Stars. II. Mid-infrared Period-luminosity Relations. Astrophys. J. 2015, 808, 11. [Google Scholar] [CrossRef]
- Delgado, H.E.; Sarro, L.M.; Clementini, G.; Muraveva, T.; Garofalo, A. Hierarchical Bayesian model to infer PL(Z) relations using Gaia parallaxes. Astron. Astrophys. 2019, 623, 156. [Google Scholar] [CrossRef]
- Layden, A.C.; Tiede, G.P.; Chaboyer, B.; Bunner, C.; Smitka, M.T. Infrared K-band Photometry of Field RR Lyrae Variable Stars. Astron. J. 2019, 158, 105. [Google Scholar] [CrossRef]
- Cusano, F.; Moretti, M.I.; Clementini, G.; Ripepi, V.; Marconi, M.; Cioni, M.-R.L.; Rubele, S.; Garofalo, A.; de Grijs, R.; Groenewegen, M.A.T.; et al. The VMC Survey—XLII. Near-infrared period-luminosity relations for RR Lyrae stars and the structure of the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 2021, 504, 1–15. [Google Scholar] [CrossRef]
- Neeley, J.R.; Massimo, M.; Freedman, W.L.; Madore, B.F.; Beaton, R.L.; Hatt, D.; Hoyt, T.; Monson, A.J.; Rich, J.A.; Sarajedini, A.; et al. Standard Galactic field RR Lyrae II: A Gaia DR2 calibration of the period-Wesenheit-metallicity relation. Mon. Not. R. Astron. Soc. 2019, 490, 4254–4270. [Google Scholar] [CrossRef]
- Muhie, T.D.; Dambis, A.K.; Berdnikov, L.N.; Kniazev, A.Y.; Grebel, E.K. Kinematics and Multi Band Period-Luminosity-Metallicity Relation of RR Lyrae Stars via Statistical Parallax. Mon. Not. R. Astron. Soc. 2021, 502, 4074–4092. [Google Scholar] [CrossRef]
- Dékány, I.; Minniti, D.; Catelan, M.; Zoccali, M.; Saito, R.K.; Hempel, M.; Gonzalez, O.A. VVV Survey Near-infrared Photometry of Known Bulge RR Lyrae Stars: The Distance to the Galactic Center and Absence of a Barred Distribution of the Metal-poor Population. Astrophys. J. Lett. 2013, 776, 19. [Google Scholar] [CrossRef]
- Gran, F.; Minniti, D.; Saito, R.K.; Navarrete, C.; Dékány, I.; McDonald, I.; Ramos, R.C.; Catelan, M. Bulge RR Lyrae stars in the VVV tile b201. Astron. Astrophys. 2015, 575, 114–123. [Google Scholar] [CrossRef]
- Muraveva, T.; Palmer, M.; Clementini, G.; Luri, X.; Cioni, M.-R.L.; Moretti, M.I.; Marconi, M.; Ripepi, V.; Rubele, S. New Near-infrared Period-Luminosity-Metallicity Relations for RR Lyrae Stars and the Outlook for Gaia. Astrophys. J. 2015, 807, 127. [Google Scholar] [CrossRef]
- Minniti, D.; Dékany, I.; Majaess, D.; Palma, T.; Pullen, J.; Rejkuba, M.; Alonso-García, J.; Catelan, M.; Contreras Ramos, R. Characterization of the VVV Survey RR Lyrae Population across the Southern Galactic Plane. Astron. J. 2017, 153, 179. [Google Scholar] [CrossRef]
- Minniti, D.; Palma, T.; Dékany, I.; Hempel, M.; Rejkuba, M.; Pullen, J.; Alonso-García, J.; Barbá, R.; Barbuy, B.; Bica, E.; et al. FSR 1716: A New Milky Way Globular Cluster Confirmed Using VVV RR Lyrae Stars. Astrophys. J. Lett. 2017, 838, 14. [Google Scholar] [CrossRef]
- Oliveira, R.A.P.; Ortolani, S.; Barbuy, B.; Kerber, L.O.; Maia, F.F.S.; Bica, E.; Cassisi, S.; Souza, S.O.; Pérez-Villegas, A. Precise distances from OGLE-IV member RR Lyrae stars in six bulge globular clusters. Astron. Astrophys. 2022, 657, 123. [Google Scholar] [CrossRef]
- Alonso-García, J.; Smith, L.C.; Catelan, M.; Minniti, D.; Navarrete, C.; Borissova, J.; Carballo-Bello, J.A.; Contreras Ramos, R.; Fernández-Trincado, J.G.; Ferreira Lopes, C.E.; et al. Variable stars in the VVV globular clusters. II. NGC 6441, NGC 6569, NGC 6626 (M 28), NGC 6656 (M 22), 2MASS-GC 02, and Terzan 10. Astron. Astrophys. 2021, 651, 18. [Google Scholar] [CrossRef]
- Gonzalez, O.A.; Rejkuba, M.; Zoccali, M.; Valenti, E.; Minniti, D.; Schultheis, M.; Tobar, R.; Chen, B. Reddening and metallicity maps of the Milky Way bulge from VVV and 2MASS. II. The complete high resolution extinction map and implications for Galactic bulge studies. Astron. Astrophys. 2012, 543, 13. [Google Scholar] [CrossRef]
- Surot, F.; Valenti, E.; Gonzalez, O.A.; Zoccali, M.; Sökmen, E.; Hidalgo, S.L.; Minniti, D. Mapping the stellar age of the Milky Way bulge with the VVV. III. High-resolution reddening map. Astron. Astrophys. 2020, 644, 140. [Google Scholar] [CrossRef]
- Gosling, A.J.; Bandyopadhyay, R.M.; Blundell, K.M. The complex, variable near-infrared extinction towards the Nuclear Bulge. Mon. Not. R. Astron. Soc. 2009, 394, 2247–2254. [Google Scholar] [CrossRef]
- Nataf, D.M.; Gonzalez, O.A.; Casagrande, L.; Zasowski, G.; Wegg, C.; Wolf, C.; Kunder, A.; Alonso-Garcia, J.; Minniti, D.; Rejkuba, M.; et al. Interstellar extinction curve variations towards the inner Milky Way: A challenge to observational cosmology. Mon. Not. R. Astron. Soc. 2016, 456, 2692–2706. [Google Scholar] [CrossRef]
- Alcock, C.; Allsman, R.A.; Alves, D.R.; Axelrod, T.S.; Becker, A.C.; Basu, A.; Baskett, L.; Bennett, D.P.; Cook, K.H.; Freeman, K.C.; et al. The RR Lyrae Population of the Galactic Bulge from the MACHO Database: Mean Colors and Magnitudes. Astrophys. J. 1998, 492, 190–199. [Google Scholar] [CrossRef]
- Stanek, K.Z.; Mateo, M.; Udalski, A.; Szymanski, M.; Kaluzny, J.; Kubiak, M. Color-Magnitude Diagram Distribution of the Bulge Red Clump Stars: Evidence for the Galactic Bar. Astrophys. J. Lett. 1994, 429, 73. [Google Scholar] [CrossRef]
- Alcock, C.; Allsman, R.A.; Alves, D.R.; Axelrod, T.S.; Becker, A.C.; Bennett, D.P.; Cook, K.H.; Drake, A.J.; Freeman, K.C.; Geha, M.; et al. Calibration of the MACHO Photometry Database. Publ. Astron. Soc. Pac. 1999, 111, 1539–1558. [Google Scholar] [CrossRef]
- Szymański, M.; Udalski, A.; Soszyxnxski, I.; Kubiak, M.; Pietrzyxnxski, G.; Poleski, R.; Wyrzykowski, L.; Ulaczyk, K. The Optical Gravitational Lensing Experiment. OGLE-III Photometric Maps of the Galactic Bulge Fields. Acta Astron. 2011, 61, 83–102. [Google Scholar]
- Contreras Ramos, R.; Minniti, D.; Gran, F.; Zoccali, M.; Alonso-García, J.l.; Huijse, P.; Navarro, M.G.; Rojas-Arriagada, A.; Valenti, E. The VVV Survey RR Lyrae Population in the Galactic Center Region. Astrophys. J. 2018, 863, 79. [Google Scholar] [CrossRef]
- Soszyński, I.; Dziembowski, W.A.; Udalski, A.; Poleski, R.; Szymański, M.K.; Kubiak, M.; Pietrzyński, G.; Wyrzykowski, L.; Ulaczyk, K.; Kozłowski, S.; et al. The Optical Gravitational Lensing Experiment. The OGLE-III Catalog of Variable Stars. XI. RR Lyrae Stars in the Galactic Bulge. Acta Astron. 2011, 61, 1. [Google Scholar]
- Dékány, I.; Hajdu, G.; Grebel, E.K.; Catelan, M.; Elorrieta, F.; Eyheramendy, S.; Majaess, D.; Jordxaxn, A. A Near-infrared RR Lyrae Census along the Southern Galactic Plane: The Milky Way’s Stellar Fossil Brought to Light. Astrophys. J. 2018, 857, 54. [Google Scholar] [CrossRef]
- Dékány, I.; Grebel, E.K. Near-infrared Search for Fundamental-mode RR Lyrae Stars toward the Inner Bulge by Deep Learning. Astrophys. J. 2020, 898, 46. [Google Scholar] [CrossRef]
- Kunder, A.; Pérez-Villegas, A.; Rich, R.M.; Ogata, J.; Murari, E.; Boren, E.; Johnson, C.I.; Nataf, D.; Walker, A.; Bono, G.; et al. The Bulge Radial Velocity Assay for RR Lyrae Stars (BRAVA-RR) DR2: A Bimodal Bulge? Astron. J. 2020, 159, 270. [Google Scholar] [CrossRef]
- Alonso-García, J.; Dékány, I.; Catelan, M.; Ramos, R.C.; Gran, F.; Amigo, P.; Leyton, P.; Minniti, D. Variable Stars in the VVV Globular Clusters. I. 2MASS-GC 02 and Terzan 10. Astron. J. 2015, 149, 99. [Google Scholar] [CrossRef]
- Cardelli, J.A.; Clayton, G.C.; Mathis, J.S. The Relationship between Infrared, Optical, and Ultraviolet Extinction. Astrophys. J. 1989, 345, 245. [Google Scholar] [CrossRef]
- Queiroz, A.B.A.; Anders, F.; Chiappini, C.; Khalatyan, A.; Santiago, B.X.; Steinmetz, M.; Valentini, M.; Miglio, A.; Bossini, D.; Barbuy, B.; et al. From the bulge to the outer disc: StarHorse stellar parameters, distances, and extinctions for stars in APOGEE DR16 and other spectroscopic surveys. Astron. Astrophys. 2020, 638, 76. [Google Scholar] [CrossRef]
- Pérez-Villegas, A.; Portail, M.; Gerhard, O. The stellar halo in the inner Milky Way: Predicted shape and kinematics. Mon. Not. R. Astron. Soc. 2017, 464, 80–84. [Google Scholar] [CrossRef]
- Minkowski, R. The Sub-System of Planetary Nebulae. Publ. Astron. Soc. Pac. 1964, 76, 197. [Google Scholar] [CrossRef]
- Catchpole, R.M. Rotation of the galactic bulge In Bulges of galaxies, ESO Conference and Workshop Proceedings, La Serena, Chile, 1990; Jarvis, B.J., Terndrup, D.M., Eds. 111. Astrophys. J. 2004, 1, 409–418. [Google Scholar]
- Minniti, D.; White, S.D.M.; Olszewski, E.W.; Hill, J.M. Rotation of the Galactic Bulge. Astrophys. J. Lett. 1992, 393, 47. [Google Scholar] [CrossRef]
- Beaulieu, S.F.; Freeman, K.C.; Kalnajs, A.J.; Saha, P.; Zhao, H. Dynamics of the Galactic Bulge Using Planetary Nebulae. Astron. J. 2000, 120, 855–871. [Google Scholar] [CrossRef]
- Rich, R.M.; Reitzel, D.B.; Howard, C.D.; Zhao, H. The Bulge Radial Velocity Assay: Techniques and a Rotation Curve. Astrophys. J. 2007, 658, 29. [Google Scholar] [CrossRef]
- Kunder, A.; Koch, A.; Rich, R.M.; de Propris, R.; Howard, C.D.; Stubbs, S.A.; Johnson, C.I.; Shen, J.; Wang, Y.; Robin, A.C.; et al. The Bulge Radial Velocity Assay (BRAVA). II. Complete Sample and Data Release. Astron. J. 2012, 143, 57. [Google Scholar] [CrossRef]
- Howard, C.D.; Rich, R.M.; Clarkson, W.; Mallery, R.; Kormendy, J.; De Propris, R.; Robin, A.C.; Fux, R.; Reitzel, D.B.; Zhao, H.S.; et al. Kinematics at the Edge of the Galactic Bulge: Evidence for Cylindrical Rotation. Astrophys. J. Lett. 2009, 702, 153–157. [Google Scholar] [CrossRef]
- Molaeinezhad, A.; Falcón-Barroso, J.; Martínez-Valpuesta, I.; Khosroshahi, H.G.; Balcells, M.; Peletier, R.F. Establishing the level of cylindrical rotation in boxy/peanut bulges. Mon. Not. R. Astron. Soc. 2016, 456, 692. [Google Scholar] [CrossRef]
- Shen, J.; Rich, R.M.; Kormendy, J.l.; Howard, C.D.; De Propris, R.; Kunder, A. Our Milky Way as a Pure-disk Galaxy—A Challenge for Galaxy Formation. Astrophys. J. Lett. 2010, 720, 72–76. [Google Scholar] [CrossRef]
- Ness, M.; Freeman, K.; Athanassoula, E.; Wylie-de-Boer, E.; Bland-Hawthorn, J.; Asplund, M.; Lewis, G.F.; Yong, D.; Lane, R.R.; Kiss, L.L. ARGOS–III. Stellar populations in the Galactic bulge of the Milky Way. Mon. Not. R. Astron. Soc. 2013, 430, 836–857. [Google Scholar] [CrossRef]
- Ness, M.; Freeman, K.; Athanassoula, E.; Wylie-de-Boer, E.; Bland-Hawthorn, J.; Asplund, M.; Lewis, G.F.; Yong, D.; Lane, R.R.; Kiss, L.L.; et al. ARGOS—IV. The kinematics of the Milky Way bulge. Mon. Not. R. Astron. Soc. 2013, 432, 2092–2103. [Google Scholar] [CrossRef]
- Salaris, M.; Girardi, L. Population effects on the red giant clump absolute magnitude: The K band. Mon. Not. R. Astron. Soc. 2002, 337, 332–340. [Google Scholar] [CrossRef]
- Zoccali, M.; Gonzalez, O.A.; Vasquez, S.; Hill, V.; Rejkuba, M.; Valenti, E.; Renzini, A.; Rojas-Arriagada, A.; Martinez-Valpuesta, I.; Babusiaux, C.; et al. The GIRAFFE Inner Bulge Survey (GIBS). I. Survey description and a kinematical map of the Milky Way bulge. Astron. Astrophys. 2014, 562, 66. [Google Scholar] [CrossRef]
- Ness, M.; Zasowski, G.; Johnson, J.A.; Athanassoula, E.; Majewski, S.R.; García Pérez, A.E.; Bird, J.; Nidever, D.; Donald, P.S.; Sobeck, J.; et al. APOGEE Kinematics. I. Overview of the Kinematics of the Galactic Bulge as Mapped By APOGEE. Astrophys. J. 2016, 819, 2–18. [Google Scholar] [CrossRef]
- Zasowski, G.; Ness, M.K.; Pérez, A.E.G.; Martinez-Valpuesta, I.; Johnson, J.A.; Majewski, S.R. Kinematics in the Galactic Bulge with APOGEE. II. High-Order Kinematic Moments and Comparison to Extragalactic Bar Diagnostics. Astrophys. J. 2016, 832, 132–146. [Google Scholar] [CrossRef]
- Rojas-Arriagada, A.; Recio-Blanco, A.; Hill, V.; de Laverny, P.; Schultheis, M.; Babusiaux, C.; Zoccali, M.; Minniti, D.; Gonzalez, O.A.; Feltzing, S.; et al. The Gaia-ESO Survey: Metallicity and kinematic trends in the Milky Way bulge. Astron. Astrophys. 2014, 569, 103. [Google Scholar] [CrossRef]
- Rojas-Arriagada, A.; Recio-Blanco, A.; de Laverny, P.; Mikolaitis, S.; Matteucci, F.; Spitoni, E.; Schultheis, M.; Hayden, M.; Hill, V.; Zoccali, M.; et al. The Gaia-ESO Survey: Exploring the complex nature and origins of the Galactic bulge populations. Astron. Astrophys. 2017, 601, 140. [Google Scholar] [CrossRef]
- Zoccali, M.; Valenti, E.; Gonzalez, O.A. Weighing the two stellar components of the Galactic bulge. Astron. Astrophys. 2018, 618, 147–153. [Google Scholar] [CrossRef]
- Wegg, C.; Gerhard, O. Mapping the three-dimensional density of the Galactic bulge with VVV red clump stars. Mon. Not. R. Astron. Soc. 2013, 435, 1874–1887. [Google Scholar] [CrossRef]
- Kormendy, J.; Kennicutt, R.C. Secular Evolution and the Formation of Pseudobulges in Disk Galaxies. Annu. Rev. Astron. Astrophys. 2004, 42, 603–683. [Google Scholar] [CrossRef]
- Combes, F.; Debbasch, F.; Friedli, D.; Pfenniger, D. Box and peanut shapes generated by stellar bars. Astron. Astrophys. 1990, 233, 82. [Google Scholar]
- Zhao, H.; Rich, R.M.; Biello, J. Proper-Motion Anisotropy, Rotation, and the Shape of the Galactic Bulge. Astrophys. J. 1996, 470, 506. [Google Scholar] [CrossRef]
- Athanassoula, E. On the nature of bulges in general and of box/peanut bulges in particular: Input from N-body simulations. Mon. Not. R. Astron. Soc. 2005, 358, 1477–1488. [Google Scholar] [CrossRef]
- Raha, N.; Sellwood, J.A.; James, R.A.; Kahn, F.D. A dynamical instability of bars in disk galaxies. Nature 1991, 352, 411–412. [Google Scholar] [CrossRef]
- Martinez-Valpuesta, I.; Gerhard, O. Metallicity Gradients Through Disk Instability: A Simple Model for the Milky Way’s Boxy Bulge. Astrophys. J. 2013, 766, 3. [Google Scholar] [CrossRef]
- Horta, D.; Schiavon, R.P.; Mackereth, J.T.; Pfeffer, J.; Mason, A.C.; Kisku, S.; Fragkoudi, F.; Allende Prieto, C.; Cunha, K.; Hasselquist, S.; et al. Evidence from APOGEE for the presence of a major building block of the halo buried in the inner Galaxy. Mon. Not. R. Astron. Soc. 2021, 500, 1385–1403. [Google Scholar] [CrossRef]
- Kruijssen, D.J.M.; Pfeffer, J.L.; Reina-Campos, M.; Crain, R.A.; Bastian, N. The formation and assembly history of the Milky Way revealed by its globular cluster population. Mon. Not. R. Astron. Soc. 2019, 486, 3180. [Google Scholar] [CrossRef]
- Belokurov, V.; Erkal, D.; Evans, N.W.; Koposov, S.E.; Deason, A.J. Co-formation of the disc and the stellar halo. Mon. Not. R. Astron. Soc. 2018, 478, 611. [Google Scholar] [CrossRef]
- Ibata, R.A.; Gilmore, G.; Irwin, M.J. A dwarf satellite galaxy in Sagittarius. Nature 1994, 370, 194. [Google Scholar] [CrossRef]
- Schultheis, M.; Cunha, K.; Zasowski, G.; García Pérez, A.E.; Sellgren, K.; Smith, V.; García-Hernández, D.A.; Zamora, O.; Fritz, T.K.; Anders, F.; et al. Evidence for a metal-poor population in the inner Galactic bulge. Astron. Astrophys. 2015, 584, 45. [Google Scholar] [CrossRef]
- Rich, R.M.; Origlia, L.; Valenti, E. The First Detailed Abundances for M Giants in the Inner Bulge from Infrared Spectroscopy. Astrophys. J. 2007, 665, 119–122. [Google Scholar] [CrossRef]
- Cunha, K.; Sellgren, K.; Smith, V.V.; Ramirez, S.V.; Blum, R.D.; Terndrup, D.M. Chemical Abundances of Luminous Cool Stars in the Galactic Center from High-Resolution Infrared Spectroscopy. Astrophys. J. 2007, 669, 1011–1023. [Google Scholar] [CrossRef]
- Howes, L.M.; Asplund, M.; Casey, A.R. The Gaia-ESO Survey: The most metal-poor stars in the Galactic bulge. Mon. Not. R. Astron. Soc. 2014, 445, 4241. [Google Scholar] [CrossRef]
- Howes, L.M.; Casey, A.R.; Asplund, M.; Keller, S.C.; Yong, D.; Nataf, D.M.; Poleski, R.; Lind, K.; Kobayashi, C.; Owen, C.I.; et al. Extremely metal-poor stars from the cosmic dawn in the bulge of the Milky Way. Nature 2015, 527, 484. [Google Scholar] [CrossRef]
- Howes, L.M.; Asplund, M.; Keller, S.C.; Casey, A.R.; Yong, D.; Lind, K.; Frebel, A.; Hays, A.; Alves-Brito, A.; Bessell, M.S.; et al. The EMBLA survey—Metal-poor stars in the Galactic bulge. Mon. Not. R. Astron. Soc. 2016, 460, 884–901. [Google Scholar] [CrossRef]
- Arentsen, A.; Starkenburg, E.; Martin, N.F.; Hill, V.; Ibata, R.; Kunder, A.; Schultheis, M.; Venn, K.A.; Zucker, D.B.; Aguado, D.; et al. The Pristine Inner Galaxy Survey (PIGS) I: Tracing the kinematics of metal-poor stars in the Galactic bulge. Mon. Not. R. Astron. Soc. 2020, 491, 11–16. [Google Scholar] [CrossRef]
- Di Matteo, P. The Disc Origin of the Milky Way Bulge. Publ. Astron. Soc. Aust. 2016, 33, 27. [Google Scholar] [CrossRef]
- Debattista, B.P.; Ness, M.; Gonzalez, O.A.; Freeman, K.; Zoccali, M.; Minniti, D. Separation of stellar populations by an evolving bar: Implications for the bulge of the Milky Way. Mon. Not. R. Astron. Soc. 2017, 469, 1587–1611. [Google Scholar] [CrossRef]
- Arentsen, A.; Starkenburg, E.; Aguado, D.S.; Martin, N.F.; Placco, V.M.; Carlberg, R.; González Hernández, J.I.; Hill, V.; Jablonka, P.; Kordopatis, G.; et al. The Pristine Inner Galaxy Survey (PIGS) III: Carbon-enhanced metal-poor stars in the bulge. Mon. Not. R. Astron. Soc. 2021, 505, 1239–1253. [Google Scholar] [CrossRef]
- Kunder, A.; Rich, R.M.; Koch, A.; Storm, J.; Nataf, D.M.; De Propris, R.; Walker, A.R.; Bono, G.; Johnson, C.I.; Shen, J.; et al. Before the Bar: Kinematic Detection of a Spheroidal Metal-poor Bulge Component. Astrophys. J. Lett. 2016, 821, 25–31. [Google Scholar] [CrossRef]
- Du, H.; Mao, S.; Athanassoula, E.; Shen, J.; Pietrukowicz, P. Kinematics of RR Lyrae stars in the Galactic bulge with OGLE-IV and Gaia DR2. Mon. Not. R. Astron. Soc. 2020, 498, 5629–5642. [Google Scholar] [CrossRef]
- Kunder, A.; Rich, R.M.; Hawkins, K.; Poleski, R.; Storm, J.; Johnson, C.I.; Shen, J.; Li, Z.-Y.; Cordero, M.J.; Nataf, D.M.; et al. A High-velocity Bulge RR Lyrae Variable on a Halo-like Orbit. Astrophys. J. Lett. 2015, 808, 12–18. [Google Scholar] [CrossRef]
- Miyamoto, M.; Nagai, R. Three-dimensional models for the distribution of mass in galaxies. Publ. Astron. Soc. Jpn. 1975, 27, 533–543. [Google Scholar]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Wegg, C.; Gerhard, O.; Portail, M. The structure of the Milky Way’s bar outside the bulge. Mon. Not. R. Astron. Soc. 2015, 450, 4050–4069. [Google Scholar] [CrossRef]
- Tumlinson, J. Chemical Evolution in Hierarchical Models of Cosmic Structure. II. The Formation of the Milky Way Stellar Halo and the Distribution of the Oldest Stars. Astrophys. J. 2010, 708, 1398–1418. [Google Scholar] [CrossRef]
- Martinez-Valpuesta, I.; Gerhard, O. Unifying A Boxy Bulge and Planar Long Bar in the Milky Way. Astrophys. J. 2011, 734, 20. [Google Scholar] [CrossRef]
- Buck, T.; Ness, M.K.; Macció, A.V.; Obreja, A.; Dutton, A.A. Stars Behind Bars. I. The Milky Way’s Central Stellar Populations. Astrophys. J. 2018, 861, 88. [Google Scholar] [CrossRef]
- Saha, K.; Gerhard, O.; Martinez-Valpuesta, I. Spin-up of massive classical bulges during secular evolution. Astron. Astrophys. 2016, 588, 42. [Google Scholar] [CrossRef]
- Saha, K.; Martinez-Valpuesta, I.; Gerhard, O. Spin-up of low-mass classical bulges in barred galaxies. Astron. Astrophys. 2012, 421, 333. [Google Scholar] [CrossRef]
- Prudil, Z.; Dékány, I.; Grebel, E.K.; Kunder, A. On the Oosterhoff dichotomy in the Galactic bulge—II. Kinematical distribution. Mon. Not. R. Astron. Soc. 2020, 492, 3408. [Google Scholar] [CrossRef]
- Schiavon, R.P.; Zamora, O.; Carrera, R.; Lucatello, S.; Robin, A.C.; Ness, M.; Martell, S.L.; Smith, V.V.; García-Hernández, D.A.; Manchado, A.; et al. Chemical tagging with APOGEE: Discovery of a large population of N-rich stars in the inner Galaxy. Mon. Not. R. Astron. Soc. 2017, 465, 501–524. [Google Scholar] [CrossRef]
- Fernández-Trincado, J.G.; Zamora, O.; García-Hernández, D.A.; Souto, D.; Dell’Agli, F.; Schiavon, R.P.; Geisler, D.; Tang, B.; Villanova, S.; Hasselquist, S.; et al. Atypical Mg-poor Milky Way Field Stars with Globular Cluster Second-generation-like Chemical Patterns. Astrophys. J. 2017, 846, 2. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).