1. Introduction
The standard model of particle physics (SM) and our basic theories, quantum field theory (QFT) and quantum mechanics (QM) are extremely successful. A comparison, excellently suited to demonstrate the high accuracy of these theories, leads to the astonishing agreement between theory and experiment for the gyromagnetic ratio of the electron with a precision of better than 12 digits [
1].
On the other hand, there are intensive discussions about the interpretation of QM [
2,
3,
4] and about the mechanisms in nature explaining the phenomena excellently described by the SM. I do not need to repeat here the well-known quote of Feynman about QM. If one reads carefully between the lines of articles and talks of the main builders of the SM, see e.g., the quotes of Veltman and ’t Hooft below, one realizes that they know very well about the interesting open questions. The SM has about 20 real and 10 integer parameters. One cannot expect that these numbers can be explained within the SM.
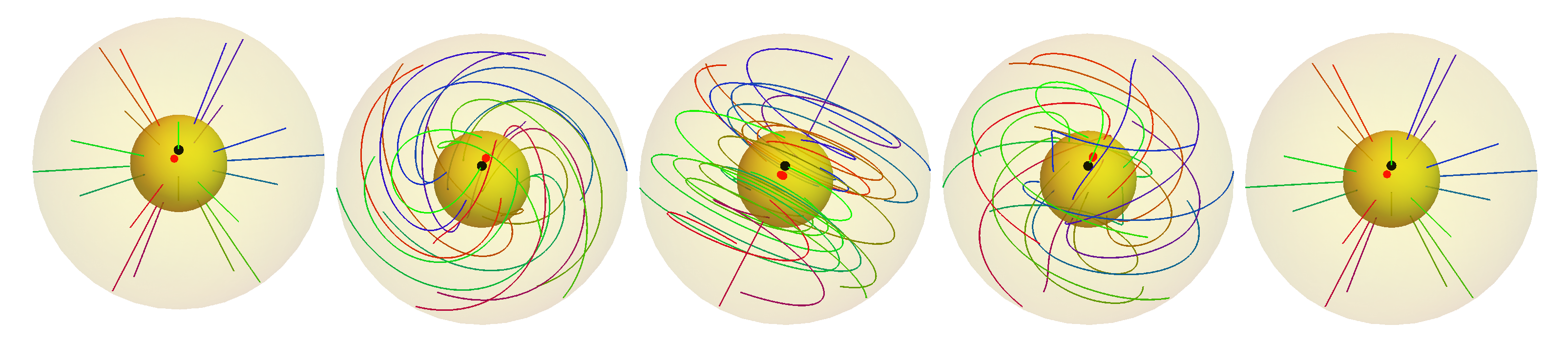
Galileo has shown us, how to learn from nature, by experiments analyzed with efficient mathematical tools and not by philosophical considerations. There are experiments that may give us some hints in which directions we could try to proceed. Within QM we can describe the properties of spin perfectly, its quantization, and its contribution to angular momentum. It is astonishing, how well we can describe transitions in rotational-vibrational spectra of molecules. But QM does not tell us what is really rotating. The belt-trick and the sphere-trick, see Figure 3 fascinate us with their strange rotation properties which can be mathematically well-understood within the group of rotations SO(3) and may be related to the properties of spin, see
Section 3.2.3.
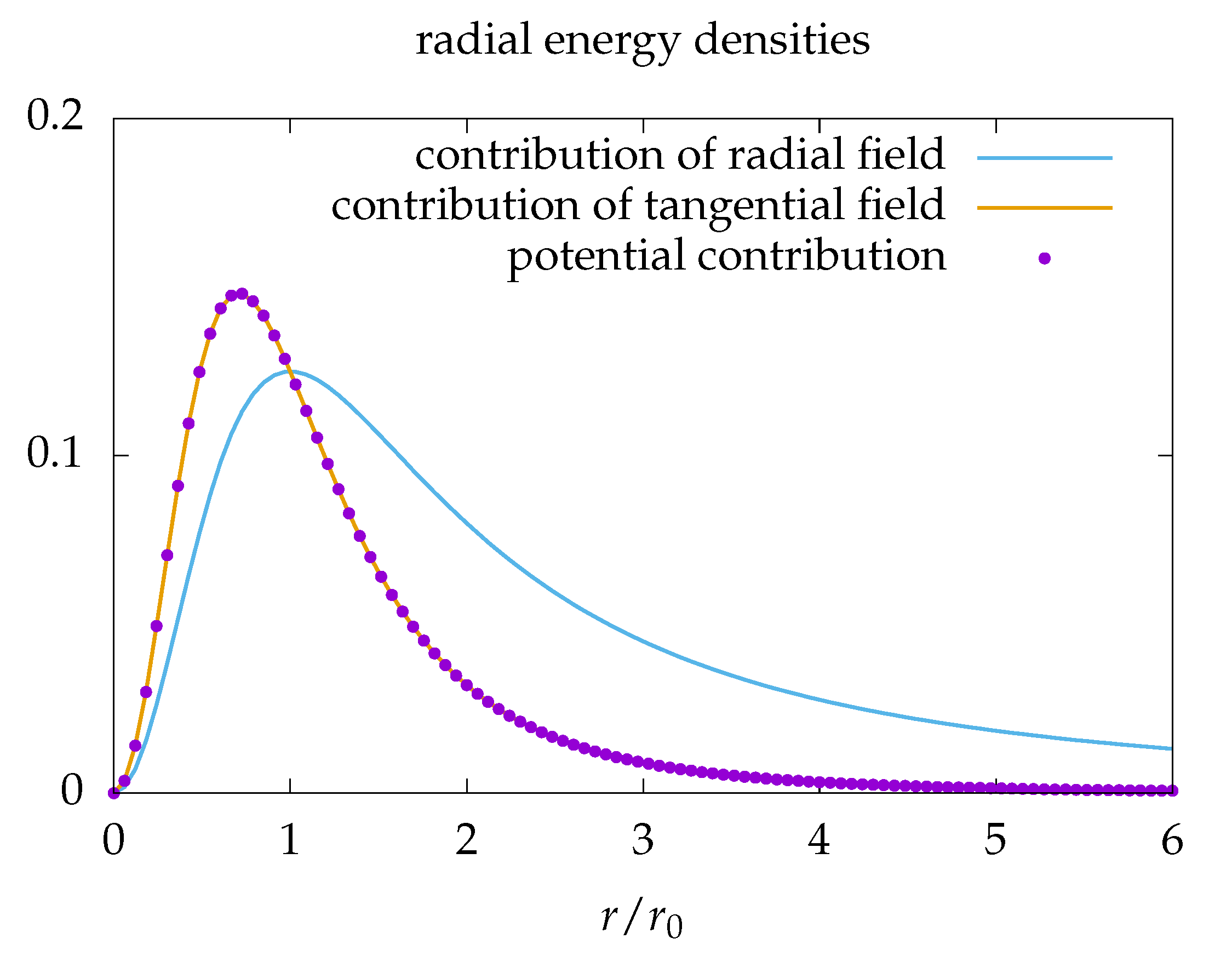
The Sine-Gordon model and its mechanical pendulum models are inspiring since they have solitons, characterized by the topological quantum number
. These solitons behave like particles. Their mass is realized by three contributions to the energy densities of the field: potential, torsion, and kinetic energy. There is a signal velocity
c corresponding to the velocity of light. For the mechanical system, it is in the order of m/s. Since the Lagrangian is Lorentz invariant with respect to
c we can directly observe Lorentz contraction, in a certain sense making the laws of special relativity visible. The sum of the three energy contributions increases with the gamma-factor corresponding to
c, as expected for the mass of a relativistic particle. There are two types of solitons interacting like charges. Solitons and antisolitons have exactly the same properties besides their chirality, resembling the charges of electrons and positrons. Experimentally no differences were found between electrons and positrons, besides the opposite charge. Recent sophisticated experiments show this impressive agreement also for protons and antiprotons [
5] with “A 16-parts-per-trillion measurement of the antiproton-to-proton charge–mass ratio”. The Sine-Gordon model [
6] gives the inspiration that particles may be characterized by topological quantum numbers, leading to the quantization of charge and to such mirror properties of particles and antiparticles. Even experts in particle physics [
7,
8,
9] raise philosophical questions about the basic entities of QM and QFT. One may see this as an indication that particle physics does not tell us comprehensively enough what particles are. The Sine-Gordon model may give a hint, understandable also for physics laymen.
The interference of electrons in double-slit experiments and of neutrons in interferometers is excellently described by QM. But QM does not give us any understandable idea of how objects, registered in electronic detectors as point-like objects, can interfere with each other. To my knowledge, there is only one experiment that may give us the first idea of how to solve this puzzle, the experiment on bouncing oil-drops invented by Yves Couder [
10].
To get a deeper understanding of the phenomena in nature, we can try to construct mathematical models reflecting some of the properties of the above-mentioned experiments. A simple mathematical model of this type I try to discuss in this article. Its main predictions are condensed in
Section 5.1. Some of the items mentioned there agree with the experiment and some of them may disagree. Such a disagreement should motivate modifications improving the applicability of the model.
A further aim of this article is to vote for a possible alternative paradigm of particle physics. It is going back to Einstein, who originally tried to unify gravitation and electromagnetism. This philosophy is summarised in the Aftermath.
In his article “More is Different” Philip Anderson [
11] remarked that physical sciences can be ordered according to the degree of their fundamentality. The fundamental theory of matter, the Standard Model of Particle Physics, is a complex theory of many fields and their degrees of freedom. One of its cornerstones is quantum chromodynamics with
gluon field degrees of freedom (dofs) and 4 complex fields for every quark type. History taught us that we can describe electromagnetic phenomena with 4 components of the photon field and 4 complex fields for every fundamentally charged particle with coupled linear equations, with Maxwell and Dirac equations. From mathematics, we know that some non-linear equations can be linearized by introducing more dofs. This may lead to the conjecture that the Maxwell-Dirac theory is a clever linearization of a non-linear theory with a smaller number of fields. The disadvantage of linearization may be that they hide the real dynamics.
A problem which bothered electrodynamics for a long time was the infinity of the self-energy of the electron, as was nicely described by Martinus Veltman in a talk at the 65th Lindau Nobel Laureate Meeting in Konstanz, 2 January 2022 fascinate in
https://www.mediatheque.lindau-nobel.org/videos/34703/martinus-veltman-discovery-higgs-particle accessed on 2 December 2021. The problem was finally solved by Hendrik Anthony Kramer’s idea of renormalization, by the absorption of infinities in free parameters of the theory. In his talk Veltman commented on the subtraction of two infinities, the bare mass of the electron and the electric self-energy of the electron by the belief of the community: “Maybe at some future time we know more and we know how to deal with these infinities. Maybe we find a better theory, where you go to small distances, maybe something happens there, but we postpone that problem. All we are going to say is whatever we do, the result for the mass of the electron is what we observe and how that comes about, who cares.” A similar statement of Gerard’t Hooft one can read in Ref. [
12]: “It was something of a shock to realize that renormalization can end up as an infinite correction to the theory—and yet, it works”. As these statements indicate it may be worthwhile to think about models which give finite results already at the classical level.
One of the big problems of the present status of particle physics is the unification of the interactions. The overwhelming majority of the community thinks that gravitation should be quantized. This article tries to argue for the opposite direction, for a geometrical formulation of electrodynamics moving electrodynamics closer to general relativity. This might lead to a geometrical motivation of charge quantization, similar to the quantization of Dirac monopoles, and reveal a geometrical origin of spin and its quantization. A model of this type was formulated in 1999 [
13], but besides an almost one-to-one copy [
14] that article was almost completely ignored by the community. Since the author understood since that time several new aspects of the model and since the original presentation was possibly not so easily readable it is time to include the old and new aspects in a revised presentation of the model and compare it to inspiring experiments that have been performed in the last two decades [
10,
15].
In
Section 2 we give the basic definitions of the model, the degrees of freedom (dofs) of the model, and the Lagrangian. In
Section 3 we derive the four types of soliton solutions and calculate their energies. These solitons can be characterized by two topological quantum numbers corresponding to charge and spin quantum numbers. In
Section 4 we derive the general equations of motion and the energy-momentum tensor.
Section 5 separates charges and their fields, compares their relations to Maxwell equations, derives Coulomb and Lorentz forces, demonstrates the geometrical origin of the U(1) gauge invariance, and interprets photons as Goldstone bosons, characterized by a further topological quantum number. Critical questions are asked in
Section 6 and some conjectures added. The conclusion starts with short comparisons to related models and enumerates several agreements and differences to Maxwell’s electrodynamics (MEdyn). In the aftermath, the author tries to summarize his understanding in short statements controversial to the present paradigms.
4. General Equations of Motion
Equation (
30) is the differential equation which results from the Lagrangian (
19) for a static spherical symmetric configuration. For a general field configuration we get the momentum density (
52) and the Euler-Lagrange Equation (
53) by a variation of the soliton field
QWe get up to first order in
From
follows for the square of the curvature
From the variation of the Lagrange density (
19)
we read the momentum density
The last expression for
shows that
can be regarded as generalised velocity. Further we get the general equation of motion
describing that the variation of the potential is the source of the momentum current. With
and
we can get another form of the equation of motion
A consequence of the equation of motion is
In
Section 5 we will separate the system into point-like sources and their fields. This should allow some checks whether these equations describe the dynamics of these solitons and their interactions with electromagnetic fields correctly.
Using the generalised velocity
it is easy to derive the energy momentum tensor
In distinction to the energy momentum tensor in Maxwell’s theory, it is automatically symmetric. Its trace is determined by the potential energy
The force density is given by the divergence of the energy momentum tensor
where we used
. It is finally not astonishing that the force density vanishes in a classical closed system.
To identify the forces between particles and their fields one has to separate artificially particles from fields. This will be done in the next section.
5. Electrodynamic Limit
In the limit
the energy of solitons approaches infinity, we dubbed it the electrodynamic limit [
29]. It suffers from the problem of infinities of the selfenergy of point-like charges, well-known from Maxwell’s electrodynamics. Within these models, the only known solution is Kramers suggestion to subtract compensating infinities. In this limit, we do not care about these infinities and arrive at the Wu-Yang formulation of Dirac monopoles [
22,
23]
with values of the soliton field
on
. We use the singularities of the
-field at given time
t to identify the position of solitons. Since these singularities have no chirality there are only two types of singularities, sources (particles) and sinks (antiparticles) of the
-field, with different charge number
and with singularities from the homotopy class
.
5.1. Comparison to Maxwell Equations
The singular lines of the sources are related to the properties of the connection and the curvature field
The modulus
defines a dual abelian field strength tensor which reads in SI units
In this limit the Lagrange density reduces to
Up to the sign it has the same form as the Lagrangian of Maxwell’s electrodynamics. In order to compare the dynamics resulting from this Lagrangian to Maxwell equations we relate the world-lines of the singularities with the properties of the
-field. The singularities are located in infinitesimal space-like three dimensional volumes, the centers of hedgehog configurations of the
-field. We describe them by
N time-like world-lines of singularities
evolving in time with velocities smaller than
from
to
, or meeting with lines of opposite charge, where particle pairs are created or annihilated. This allows to define for each
-field configuration a singular vector current along the above world-lines
For a single soliton resting at the origin with
both sides reduce to a three-dimensional delta-function at the origin
for the time-component of the singular vector current. Multiplying with
we get the current density
of point-like charges
. A further multiplication by
leads to
and therefore to the inhomogeneous Maxwell equations
These equations are a result of the separation of the soliton field
in singular point-like charges and the surrounding
-field describing electromagnetic fields.
The second set of equation follows from the general equations of motion (
53)
This is a condition for magnetic currents
We conclude, that in this dual formulation we have soft Dirac monopoles and conserved magnetic currents
which are not quantised. Since
has only two dofs there are only two independent equations in Equation (
68). Extending
by appropriate factors to the dual field strength tensor we get the equations
The spatial components of these equations we read as dual transformations of a vanishing Lorentz force on magnetic currents. The appearance of these currents is a consequence of the topological restrictions to the
-field. This is the price we have to pay for the quantisation of electric charges on a classical basis. Solutions of the (linear) Maxwell equations are also solutions of the equations of motion (
67) and (
71). But the two dofs of the
-field are not sufficient to fulfill the homogeneous Maxwell equations exactly and lead to small deviations, to small non-linearities, to magnetic currents. These deviations should remain small for field configurations of minimal energy, which have to respect the topological restrictions and the boundary conditions. It will be interesting to investigate whether the prediction of these magnetic currents is in contradiction to experimental observations. We will see that these magnetic currents do not lead to additional forces acting on electric currents besides the well known Coulomb and Lorentz forces from electric and magnetic field strengths.
5.2. Coulomb and Lorentz Forces
Due to the joint description of charges and electromagnetic fields by
, the interaction of solitons is a consequence of topology [
30]. The forces between charges and electromagnetic fields are internal forces and the total force density is vanishing, see Equation (
58). The electrodynamic limit provides the possibility to separate charges and their fields.
In the electrodynamic limit the energy-momentum tensor (
56) tends to
with components of the same form as the symmetrised energy-momentum tensor in Maxwell’s theory
We can use Newton’s third axiom where the reaction to the force density of electromagnetic fields is the force density
on charges. Then charges appear as external sources
The components of the force density on charges read
Equation (
77) describes the loss of power density of the field and the corresponding increase for charges. The spatial force density (
78) includes Coulomb- and Lorentz forces acting on point-like electric charges.
The above relations show that the electrodynamic limit of the soliton model corresponds to Maxwell’s electrodynamics (MEdyn), with the distinction that only integer multiples of the electric charge unit are allowed. This restriction leads to the appearance of magnetic currents which do not directly contribute to the forces on electric currents and thus are only internal currents. They are not quantized and influence electric charges only via their electric and magnetic fields.
From MEdyn we know that conserved electric currents are related to a U(1)-gauge invariance.
5.3. U(1) Gauge Invariance
According to Equation (
61),
is a vector in the SU(2) algebra, parallel to
. This gives rise to the emergence of a local U(1) gauge symmetry. A gauge transformation corresponds to a x-dependent rotation of the three basis vectors
of the SU(2) algebra under rotations
around
by an arbitrary angle
For infinitesimal coordinate shifts these transformations read
They have to be compensated by an additional rotation of
vectors. The affine connection (
4) is the rotational angle transforming
to
Comparing the two equations, we see that
has to respect
Equation (
60) satisfies this condition. But
is fixed by Equation (
82) up to a component parallel to
only. This freedom offers the possibility to compensate the basis transformation (
80) by the shift
With this transformation, algebra valued fields get invariant under basis transformations.
As Equation (
83) reminds us the affine connection is not a tensor.
According to the above derivation, the
-field and therefore the coordinates (
61) of the curvature tensor
are invariant under local gauge transformations, realized in this model as basis transformations in the tangential space of
. This
is the parameter space of the soliton field
in the electrodynamic limit (
59).
A further important application of the electrodynamic limit is the sector where only electromagnetic waves are present.
5.4. Goldstone Bosons
The minimum
of the potential in the Lagrangian (
19) is degenerate at a two-dimensional manifold. Thus, the vacuum has broken symmetry and the model has two types of Goldstone bosons. The Lagrangian reduces to the form (
63). Up to the different sign, this Lagrangian is formally identical to the Lagrangian of Maxwell’s electrodynamics with 2*4 physical dofs of the wave-field in radiation gauge when the time component and the longitudinal component of the gauge field are removed. In distinction, in the present model, the
-field has two dofs only. We describe them by two spherical angles
and
. In the electrodynamic limit and in the absence of singularities of the
-field there are no charged particles present and we can assume that the field at spatial infinity “
∞” is independent of the direction. The vacuum has broken symmetry. As a consequence of the Hobart-Derrick theorem [
18,
19], pure regular
-field configurations moving with velocities smaller than the velocity of light
are unstable. For velocities
they have constant action in time and one can try to describe electromagnetic waves [
31]. Due to the isomorphism
and the topological relation
there is an additional quantum number for the
-field, the Hopf number or Gauß linking number
v of fibres
defined by
const, thus by certain values
and
. Fibers are in general closed lines and for different fibers
and
we can determine a linking number
v by the famous double integral of Carl Friedrich Gauß
With
we identify right and left polarised photons.
v can be modified by the interaction of photons with solitons. The physical equivalent of
v is the number of photons
in a field configuration.
As described in Refs. [
32,
33]
v can be computed also by one-dimensional integrals from the behavior of neighboring fibers. In such a determination enters the geometry of
in an interesting way.
Crossing solitons in arbitrary direction rotates the spatial Dreibein by
with left or right chirality as depicted in
Table 1. Scattering, emission, and absorption processes of photons by solitons are able to modify the chiralities of both types of particles. These geometrical processes need detailed investigations.
Much work on
-fields with different Lagrangians has already been done by Ferreira et al., see e.g., [
34] and references therein. A recent article about the closely related field of Topological photonics is [
35].
6. Open Questions and Conjectures
In this section, we discuss some features of the model which need future detailed investigations or where, at the moment, we can rely on speculations only.
6.1. Running of the Coupling
The usual conclusion from high-energy scattering experiments is that electrons are point-like. This could counteract this model, since this model suggests a finite size of static electrons of the order of the classical electron radius .
In order to learn from experiments about the property of electrons at distances of and smaller we need high energies. A characteristic relation between radius and energy is . 200 MeV electrons are sensible at distances of fm, the 100 GeV electrons of LEP up to distances of 2 attometers.
The solitons of this model are relativistically covariant. A moving soliton is Lorentz compressed. At LEP, electrons reached a factor of and therefore could approach another electron in a head-on collision up to distances of am. The analogous behavior one can study in the analytical two-particle solutions of the Sine-Gordon model. For to infinity, the distance of the closest approach of two solitons approaches zero.
The finite size of solitons of this model leads to a modification of Coulomb’s law at distances of the order of the soliton radius. This effect is known in quantum field theories as running of the coupling. The result of the perturbative calculations in QED is the Uehling potential [
36]. It predicts a strong rise of the effective charge of electrons at the order of a few fm. Since nothing in nature seems to be infinitely large or infinitely small, one can see this rise as an indication for an effective size of electrons at this order of magnitude.
The model discussed in this article gets a running of the coupling at the classical level. In due course, we will publish a paper about this effect. The numerical calculations were prepared in a paper published recently in Few-Body systems [
28].
6.2. Orthogonality of and
We have seen in Equation (
44) that the conservation of topological charge leads to
. In the electrodynamic limit we have
and therefore also
, as is also implied by Equation (
71) for non-vanishing magnetic currents. This seems to contradict the experimental situation, where we have no problems producing parallel electric and magnetic fields. There is possibly a way out of this problem, see also the discussion in Ref. [
29]. In the electrodynamic limit, the basic field is the unit-vector field
. A constant
-field corresponds to zero-field strength. One can get the electric field by an
-field rotating in space. Due to the topological restriction, a homogeneous electric field can be produced only in a finite spatial region. The solution, given in Ref. [
29] looks more complicated than in Maxwell’s theory, but it agrees better to the experimental situation with capacitor plates of finite size and finite charge and fields whose homogeneity is only approximate. Magnetic fields originate from non-vanishing time components of the connection and thus from the rotations of
-vectors in time. Electric currents in a wire, the source of magnetic fields, correspond to hoppings of electrons from one ion to the next in a very short time, a strong time-dependence of
-fields is necessary to produce a reasonable magnetic field.
The orthogonality of
and
follows from the interpretation of the field strength as the curvature of the unit vector field
, see Equation (
61). It is not derived from the Lagrangian and thus not a consequence of the dynamics. It is valid at the level of distances between elementary charges. This leads to the idea, that the orthogonality is present on a microscopic level and parallelity may be achieved on a macroscopic time-averaged level.
6.3. Quantum Effects
The model formulated in
Section 2 is a classical model. For around 100 years, we have known that nature in atomic and subatomic physics is dominated by quantum effects. Under the present paradigm of the quantum field theory, one would include quantum effects by integrations over all possible quantum fluctuations. In Ref. [
37] it was shown that such integrations lead to diverging integrals. In distinction to Maxwell’s electrodynamics (MEdyn) the presented model is from the beginning finite. Therefore, there seems no need for regularization and renormalization. If the model is of some applicability, there must be another method to include quantum fluctuations and interference, encoded in the path integral formulation of quantum mechanics and quantum field theory by its complex Boltzmann factor
, where
S is the action attributed to field configurations. There is some freedom to achieve this goal since nobody knows how nature does, in order to produce the effects which are perfectly described by quantum mechanics.
There are hundreds of books and thousands of articles about the riddles and the philosophical implications of quantum mechanics, but there are only a few ideas suggesting mechanisms. I know of only one experiment which may give an idea for a mechanism. This is Couder’s experiment [
10] of bouncing oil drops which, as I think, supports De Broglie’s idea [
38] of pilot waves. The bouncing drops are interacting with waves and produce waves themselves [
15]. In the critical double-slit experiments, the waves pass both slits, whereas every particle passes only one slit. The particle trajectories are influenced by the interfering waves and lead to an interference pattern at the detectors.
Can we find such a mechanism in our model? Quantum mechanical fluctuations are action fluctuations and not energy fluctuations. This could mean, the energy is transferred for a short moment and then again subtracted. Some types of waves, unknown in MEdyn, passing a particle could possibly provide such a phenomenon.
There are two types of fields in our model which are unknown in MEdyn, magnetic currents
and waves in the angular parameter
of the
Q-field
is related to the rotational angle
of Dreibeins in space by
. Magnetic currents are non-vanishing sources of magnetic fields [
29]. As was discussed in
Section 5.2 magnetic currents do not contribute to Coulomb and Lorentz forces, see Equation (
78) and therefore do not directly influence the motion of charged particles. The appearance of magnetic currents is a result of the non-Abelian nature of the soliton field. Due to the topological restrictions, electromagnetic waves may be accompanied by magnetic currents, which in the vacuum propagate with the velocity of light in the direction given by the Poynting vector. The magnetic currents coming from the soliton description are different from the Dirac magnetic currents because they are not quantized and cannot be associated with massive magnetic charges. They are suppressed by the request of minimal energy and seem rather tiny deviations from the solutions of the homogeneous Maxwell equations, in case these can not be fulfilled due to the topological restrictions of the
-field. Since magnetic currents seem not to have measurable consequences, they should be ruled out as guiding waves.
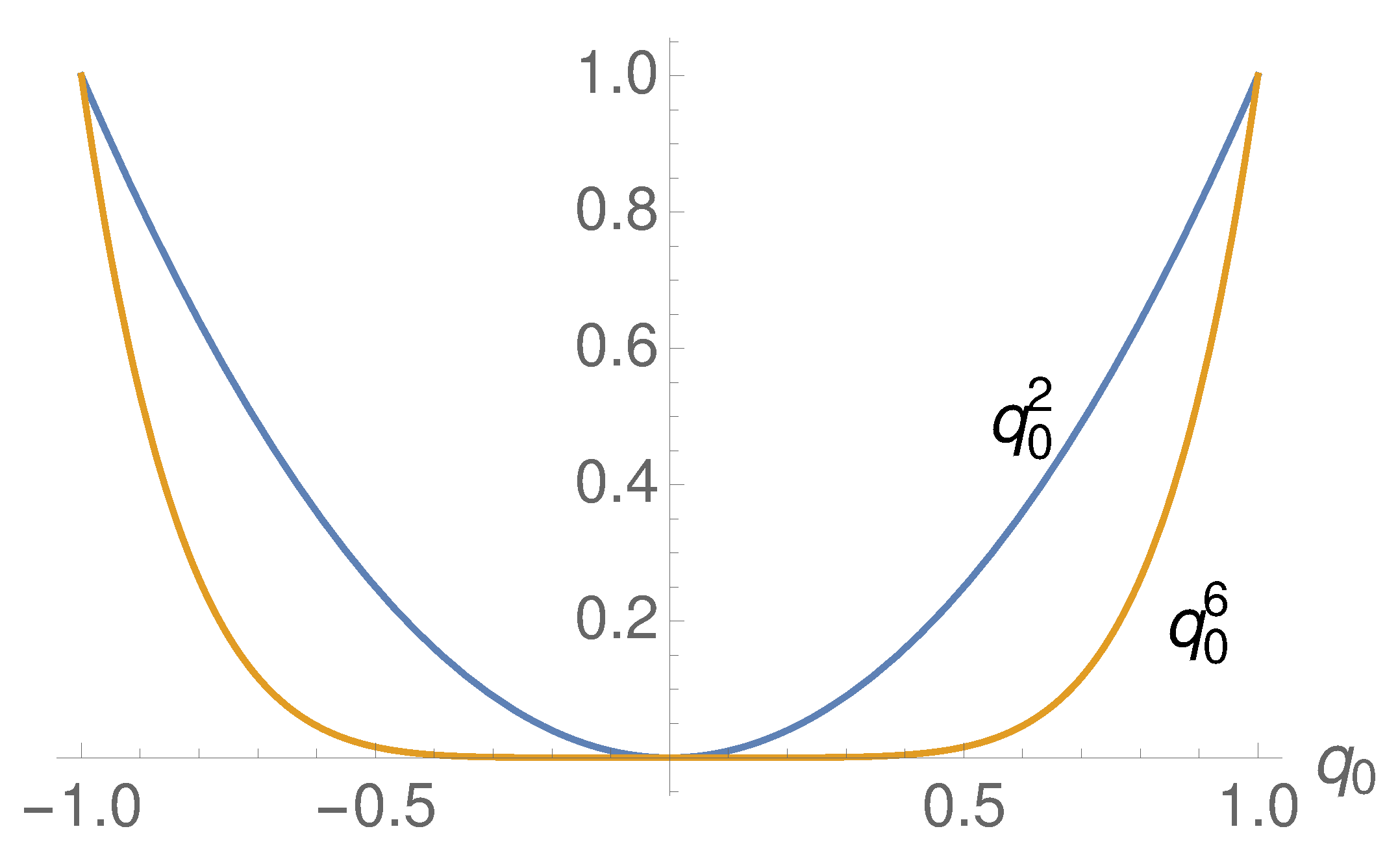
-waves are governed by the shape of the potential term
in the Lagrangian (
19) with its unusual power
, see
Figure 6. In Ref. [
37] it was shown that a
dependence of the potential term would lead to vibrational excitations of solitons. The aim to compare solitons with the lightest charged fermions is to rule out such excitations. Higher even powers in
do not show such vibrations but allow for waves in
. For radial waves a Schrödinger-type equation
with the potential
was derived which is repulsive everywhere and has no bound states. The spectrum of spherical waves
is continuous.
In scattering processes between photons lumps of non-vanishing
are produced. As mentioned in
Section 5.4 photons are characterized by a field of purely imaginary unit quaternions, see Equation (
59). In scattering processes two such fields
and
have to be multiplied
leading to a non-vanishing real part
and therefore to a small contribution to the potential energy, to a tiny massive lump acting like a small particle.
An oscillation of non-vanishing
in some direction
could bounce way and back in the flat region of the
-potential. If such an oscillation approaches a soliton, due to its tiny mass contributions it should shift the soliton center depending on the angle between
and the solitons
-vector in this spatial region. Due to the above-mentioned oscillation in the
-potential the soliton center should move alternating in forward and backward direction, i.e., adding and subtracting energy and momentum in short sequence. This would maintain energy and momentum constant, but increase the action. It will be interesting to investigate in more detail whether such
-waves could provide a model for the physical nature of a guiding field. In diffraction experiments, the diffracted field would exist independent of the presence of solitons and the solitons could maintain their corpuscular nature all along with the experiment as the authors of Ref. [
39] expect for the zero-point fluctuations as guiding field.
-waves could be a candidate for dark matter. Most of the community is looking for dark particles. Up to now, nobody has found dark particles. I think, dark matter escapes our detectors since it does not have the form of particles and it does not modify the kinetic energy of particles. -waves do not have particle structure. Due to their contribution to the potential, they are rather tiny lumps of not quantized mass.
6.4. A Possible Mechanism of Cosmic Inflation
Some cosmological models assume an inflationary epoch [
40] in the early universe, a very short period of exponential expansion of the cosmos, explaining the large-scale structures of our universe, its flatness, and the relative homogeneity and isotropy of the cosmic microwave background. Our model provides a possible mechanism for inflation. A transition from an initial field configuration in the early universe from an initial stationary state with positive energy density
to a stable vacuum with vanishing energy density
after inflation. This transition would have released the energy density
Despite the vanishing energy-momentum tensor in the absence of solitons, see Equation (
91), there is a running of the coupling due to the modification of Coulomb’s law at distances of the order of the soliton radius, as will be discussed in detail in a forthcoming article. This is in contradistinction to quantum electrodynamics, where quantum corrections lead to a running coupling described by a non-vanishing beta-function. There, due to the proportionality between beta-function and the value of the trace of the energy-momentum tensor, see Eq. (19.157) of Peskin-Schröder [
36], a vanishing trace would prevent the running of the coupling.
6.5. Cosmological Constant
1917 Einstein has introduced a cosmological constant in general relativity to compensate for the attractive interaction of the mass density and to get stationary solutions of the field equations. In cosmological models, like the
CDM model [
41], the cosmological constant is related to an energy density of the vacuum explaining the observed cosmic expansion. The Planck collaboration gives in its 2018 results [
42] a cosmological energy density of
, where the critical energy density is
.
The potential term
in the Lagrangian (
19) acts as a cosmological function, contributing to the energy density of the universe. Due to the application of the Hobart-Derrick theorem a quarter of the rest energy of solitons is contributed from the potential energy
, see Equation (
23). If this ratio would also be valid for nucleons an average density of nucleons of 14.5 nucleons per m
would agree with the measured energy density. In comparison, the prediction of field theory deviates many orders of magnitude—a still unsolved problem.
As discussed in
Section 6.3, due to their contributions to the potential energy
-waves would also participate in the cosmological constant, the average of the cosmological function.
7. Conclusions
7.1. Comparison to Other Models
The model discussed in this article has many features in common with other well-known models. The Lagrangian defined in Equation (
19) can be seen as a generalization of the Sine-Gordon model [
6], a model in 1+1D with one field degree of freedom (dof), generalized to a field in 3+1D with three dofs.
Up to the difference between the groups, SU(2) and SO(3) the dofs are the same as those of the Skyrme model [
16,
17]. The difference is in the terms compressing solitons, in the Skyrme model the compressing term has two derivatives, in the Lagrangian (
19) it is substituted by the term
without derivatives.
Dirac [
20,
21] suggested introducing magnetic monopoles in Maxwell’s electrodynamics (MEdyn) by defining a line-like singularity, the well-known Dirac string. Wu and Yang [
22,
23] succeeded in removing this singular line using a normalized three-component scalar field
to describe the field of monopoles, but they did not remove the singularity in the center of the monopoles.
’T Hooft [
43] and Polyakov [
44] investigated monopoles in gauge field theories and identified monopoles in the Georgi-Glashow model. This model has a triplet of gauge fields with
dofs and a triplet of scalar (Higgs) fields, in summary, 15 dofs. The energy of these monopoles was estimated with the order of the mass of the W-boson multiplied with the inverse of Sommerfeld’s fine structure constant. As was shown in [
45,
46,
47] in the so-called BPS-limit [
48,
49] of the massless Higgs boson, monopoles and antimonopoles keep interacting with each other Coulomb-like. However, the force between two monopoles or two antimonopoles vanishes, whereas the interaction strength between a monopole and an antimonopole doubles in comparison with the limit where the Higgs boson is much heavier than the W-bosons of the 3D Georgi-Glashow model.
An attempt to construct the Standard Model with Monopoles was undertaken by Vachaspati [
50]. However, in that article, which is aimed at discussing the algebraic properties of possible mappings between particles and monopoles, dynamical features were set aside.
We describe particles and their fields with the same dofs, in analogy to the Sine-Gordon and the Skyrme model. Only three dofs of an SO(3)-field are necessary to describe charges and their fields. Since these three dofs can be interpreted as orientations of spatial Dreibeins we can ascribe these properties to space-time. In this way, we would succeed to describe the two long-range interactions, electrodynamics, and gravitation, by the properties of space-time only.
An important test of the applicability of this model is an investigation of the differences to MEdyn.
7.2. Comparison to Maxwell’s Electrodynamics
The model describes charges with long-range forces as we have in Maxwell’s electrodynamics (MEdyn). As already mentioned, this model can not substitute Maxwell’s electrodynamics and the SM. The purpose of this chapter is to try to enumerate where this model differs from these theories, where it may be successful, and where it may fail.
Particles are characterized by topological quantum numbers, only artificially they can be separated from their fields. Such separation leads to the well-known singularities of point-like charges.
The following properties agree with MEdyn:
The Lagrangian (
19) is Lorentz covariant, thus the laws of special relativity are respected.
Charges have Coulombic fields fulfilling Gaußes law (
67).
Charges interact via
electric fields (
27), they feel Coulomb and Lorentz forces, see
Section 5.2.
A local U(1) gauge invariance is respected, see
Section 5.3.
There are two dofs of massless excitations for photons, see
Section 5.4.
The critical questions concern the differences to MEdyn. Several differences agree with the experiment, others have to be investigated in detail, whether they differ only superficially or concern deep discrepancies. In distinction to MEdyn we find the following properties:
The following properties differing from MEdyn need deeper investigation and may possibly differ from experiments with electrons and photons.
Spin and magnetic moment are dynamical properties. They are consequences of movements of solitons or time-dependent field variations in their surroundings.
Electric and magnetic field vectors are perpendicular to each other, see
Section 6.2. This is in obvious contradiction to experimental realizations of parallel electric and magnetic fields. An excuse may be, that this property may be realized on a microscopic level and allows for parallelity of these fields on a macroscopic level.
The existence of unquantized magnetic currents is allowed. These currents do not directly appear in Lorentz forces. They contribute only via their magnetic fields.
-waves with oscillating values of
feel non-vanishing values of the potential energy density and contribute therefore to matter density. Such non-topological excitations were not directly detected. If they exist, they contribute to dark matter, see
Section 6.3.
-waves lead to additional forces on particles and are a possible origin of quantum fluctuations.
The potential term allows for a mechanism of cosmic inflation.
The potential term contributes to dark energy.
This model tries to give an idea about a possible direction of future investigations. One should not assume that it can provide a final answer to all questions which are left open by quantum theory and quantum field theory. Both theories have a tremendous success. It is obvious that the model cannot compete with their excellent and precise predictions and the century-long efforts of numerous scientists to describe the properties of nature in the most fundamental domain. But this does not mean that one should not think about scenarios that finally could lead to a deeper understanding of the mechanisms in nature. This could allow us to answer some questions, left open by quantum mechanics and quantum field theory. It could help to answer how nature works to produce the interesting riddles which we could not solve yet.
Some of the questions posed by this model concerning electrodynamics, quantum theory, and quantum field theory are enumerated in the section with critical remarks. Many may still be missing. Essential open problems are also those related to the three other fundamental forces, gravitational, strong, and weak interactions.
If an extension of this model is of some relevance for describing the properties of nature, one could summarise its philosophy in: Particles are properties of regions of space, characterized by topological quantum numbers. Therefore I would like to call it: “Model of topological particles”.
8. Aftermath
In its fundaments, physics is measurements of distances of objects and times of events, and an explanation of their relations.
This may indicate, that
Physics is geometry and not algebra.
Finally, one should use algebra to describe the geometry.
General Relativity:
Wheeler: “Spacetime tells matter how to move;
matter tells spacetime how to curve”. [
51]
My addition for Electrodynamics:
⋯ Charges and electromagnetic fields tell space how to rotate.