Polynomial Affine Model of Gravity in Three-Dimensions
Abstract
:1. Introduction
2. What Is the Polynomial Affine Model of Gravity?
3. Building the Ansätze
3.1. Isotropic Connection
3.2. Isotropic and Homogeneous Connection
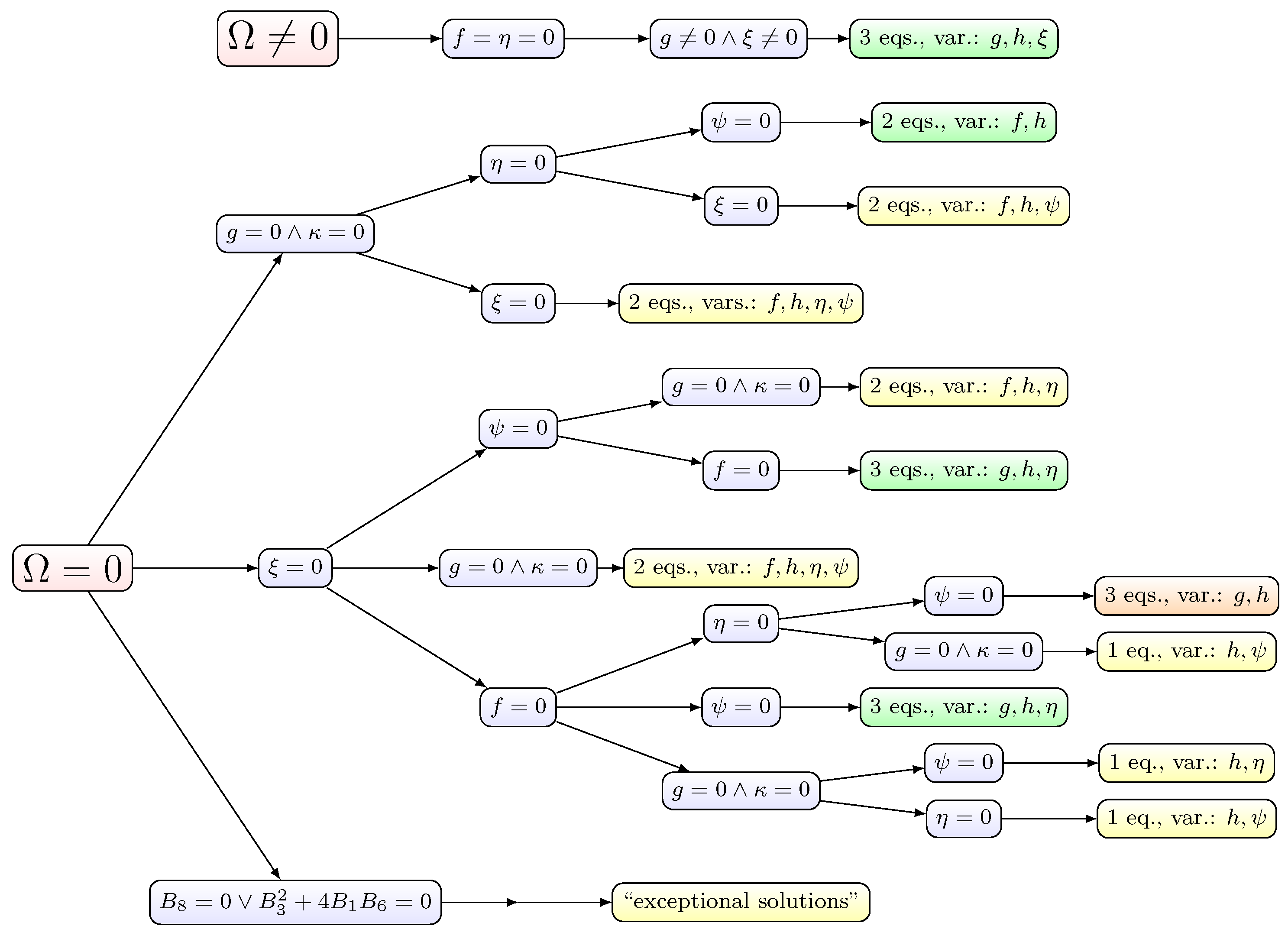
4. Cosmological Solutions
5. Discussion and Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | In general relativity, the role of the metric is two-fold: it is not only the geometric object that defines distances but the field is also responsible for the mediation of gravitational interactions. |
| 2 | In the words of Schrödinger, “For all that I know, no special solution has yet been found which suggests an application to anything that might interest us …” [19]. |
| 3 | We also refer to these metrics as emergent metrics. |
| 4 | An update on the original ideas in this paper can be found in Ref. [46]. |
| 5 | In previous articles, we refer to this as dimensional analysis. |
| 6 | We shall denote the Popławski metric by Popl or . |
| 7 | Note that once the metric is included, as in general relativity, the number of possible terms is naturally unbound, since we allow the contraction of the indices that are initially on the same footing. As an example of these terms, we have the scalar curvature, , and its powers, , opening the window to the -models. |
References
- Will, C.M. Theory and Experiment in Gravitational Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Zwicky, F. On the Masses of Nebulae and of Clusters of Nebulae. Astrophys. J. 1937, 86, 217. [Google Scholar] [CrossRef]
- Rubin, V.C.; Kent, W.; Ford, J. Rotation of the Andromeda Nebula From a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Sofue, Y.; Rubin, V. Rotation Curves of Spiral galaxies. Ann. Rev. Astron. Astrophys. 2001, 39, 137. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence From Supernovae for an Accelerating Universe and a Cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ From 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum Theory of Gravity. 1. The Canonical Theory. Phys. Rev. 1967, 160, 1113. [Google Scholar] [CrossRef] [Green Version]
- DeWitt, B.S. Quantum Theory of Gravity. 2. The Manifestly Covariant Theory. Phys. Rev. 1967, 162, 1195. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum Theory of Gravity. 3. Applications of the Covariant Theory. Phys. Rev. 1967, 162, 1239. [Google Scholar] [CrossRef]
- Deser, S.; van Nieuwenhuizen, P. One Loop Divergences of Quantized Einstein-Maxwell Fields. Phys. Rev. D 1974, 10, 401. [Google Scholar] [CrossRef] [Green Version]
- Deser, S.; van Nieuwenhuizen, P. Nonrenormalizability of the Quantized Dirac-Einstein System. Phys. Rev. D 1974, 10, 411. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M.J.G. One Loop Divergencies in the Theory of gravitation. Ann. Poincare Phys. Theor. A 1974, 20, 69. [Google Scholar]
- Ashtekar, A. New Variables for Classical and Quantum Gravity. Phys. Rev. Lett. 1986, 57, 2244–2247. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A. New Hamiltonian Formulation of General Relativity. Phys. Rev. D 1987, 36, 1587. [Google Scholar] [CrossRef] [PubMed]
- Eisenhart, L. Non-Riemannian Geometry; American Mathematical Society: New York, NY, USA, 1927. [Google Scholar]
- Einstein, A. Zur Affinen Feldtheorie. Sitzungsber. Preuss. Akad. Wiss. 1923, 137–140. [Google Scholar] [CrossRef]
- Einstein, A. Theory of the Affine Field. Nature 1923, 112, 448–449. [Google Scholar] [CrossRef] [Green Version]
- Eddington, A.S. The Mathematical Theory of Relativity; Cambridge University Press: Cambridge, UK, 1923. [Google Scholar]
- Schrödinger, E. Space-Time Structure; Cambridge University Press: Cambridge, UK, 1950. [Google Scholar]
- Kijowski, J. On a New Variational Principle in General Relativity and the Energy of the Gravitational Field. Gen. Rel. Grav. 1978, 9, 857. [Google Scholar] [CrossRef]
- Ferraris, M.; Kijowski, J. General Relativity Is a Gauge Type Theory. Lett. Math. Phys. 1981, 5, 127. [Google Scholar] [CrossRef]
- Ferraris, M.; Kijowski, J. On the Equivalence of the Relativistic Theories of Gravitation. Gen. Rel. Grav. 1982, 14, 165. [Google Scholar] [CrossRef]
- Kijowski, J.; Werpachowski, R. Universality of Affine Formulation in General Relativity. Rept. Math. Phys. 2007, 59, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Popławski, N.J. On the Nonsymmetric Purely Affine gravity. Mod. Phys. Lett. A 2007, 22, 2701. [Google Scholar] [CrossRef] [Green Version]
- Popławski, N.J. A Unified, Purely Affine Theory of Gravitation and Electromagnetism. arXiv 2007, arXiv:0705.0351. [Google Scholar]
- Poplawski, N.J. Gravitation, Electromagnetism and the Cosmological Constant in Purely Affine gravity. Int. J. Mod. Phys. D 2009, 18, 809–829. [Google Scholar] [CrossRef] [Green Version]
- Popławski, N.J. Affine Theory of gravitation. Gen. Rel. Grav. 2014, 46, 1625. [Google Scholar] [CrossRef] [Green Version]
- Krasnov, K. Non-Metric Gravity: A Status report. Mod. Phys. Lett. A 2007, 22, 3013–3026. [Google Scholar] [CrossRef] [Green Version]
- Krasnov, K. Non-Metric Gravity. I. Field Equations. Class. Quant. Grav. 2008, 25, 025001. [Google Scholar] [CrossRef]
- Krasnov, K.; Shtanov, Y. Non-Metric Gravity. II. Spherically Symmetric Solution, Missing Mass and Redshifts of Quasars. Class. Quant. Grav. 2008, 25, 025002. [Google Scholar] [CrossRef] [Green Version]
- Krasnov, K. Pure Connection Action Principle for General Relativity. Phys. Rev. Lett. 2011, 106, 251103. [Google Scholar] [CrossRef] [Green Version]
- Delfino, G.; Krasnov, K.; Scarinci, C. Pure Connection Formalism for Gravity: Linearized Theory. J. High Energy Phys. 2015, 3, 118. [Google Scholar] [CrossRef] [Green Version]
- Delfino, G.; Krasnov, K.; Scarinci, C. Pure Connection Formalism for Gravity: Feynman Rules and the Graviton-Graviton scattering. J. High Energy Phys. 2015, 3, 119. [Google Scholar] [CrossRef] [Green Version]
- Castillo-Felisola, O.; Skirzewski, A. A Polynomial Model of Purely Affine Gravity. Rev. Mex. Fis. 2015, 61, 421. [Google Scholar]
- Castillo-Felisola, O.; Skirzewski, A. Einstein’s Gravity From a Polynomial Affine Model. Class. Quant. Grav. 2018, 35, 055012. [Google Scholar] [CrossRef] [Green Version]
- Krasnov, K. Formulations of General Relativity: Gravity, Spinors and Differential Forms, 1st ed.; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Castillo-Felisola, O.; Perdiguero, J.; Orellana, O. Chapter Cosmological Solutions to Polynomial Affine Gravity in the Torsion-Free Sector. In Redefining Standard Model Cosmology; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Castillo-Felisola, O.; Perdiguero, J.; Orellana, O.; Zerwekh, A.R. Emergent Metric and Geodesic Analysis in Cosmological Solutions of (torsion-Free) Polynomial Affine Gravity. Class. Quant. Grav. 2020, 37, 075013. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. Chapter Critical Phenomena for Field Theorists. In Undertanding the Fundamental Constituents of Matter; The Subnuclear Series; Springer: Berlin/Heidelberg, Germany, 1976; Volume 14. [Google Scholar]
- Staruszkiewicz, A. Gravitation Theory in Three-Dimensional Space. Acta Phys. Pol. 1963, 24, 735–740. [Google Scholar]
- Deser, S.; Jackiw, R.; Templeton, S. Three-Dimensional Massive Gauge Theories. Phys. Rev. Lett. 1982, 48, 975–978. [Google Scholar] [CrossRef] [Green Version]
- Deser, S.; Jackiw, R.; Templeton, S. Topologically Massive Gauge Theories. Ann. Phys. 1982, 140, 372–411, Erratum in Ann. Phys. 1988, 185, 406. [Google Scholar] [CrossRef]
- Deser, S.; Jackiw, R. Three-Dimensional Cosmological Gravity: Dynamics of Constant Curvature. Ann. Phys. 1984, 153, 405–416. [Google Scholar] [CrossRef] [Green Version]
- Deser, S.; Jackiw, R.; ’t Hooft, G. Three-Dimensional Einstein Gravity: Dynamics of Flat Space. Ann. Phys. 1984, 152, 220. [Google Scholar] [CrossRef] [Green Version]
- Witten, E. (2+1)-Dimensional Gravity As an Exactly Soluble System. Nucl. Phys. B 1988, 311, 46. [Google Scholar] [CrossRef]
- Witten, E. Three-Dimensional Gravity Revisited. arXiv 2007, arXiv:0706.3359. [Google Scholar]
- Bañados, M.; Teitelboim, C.; Zanelli, J. The Black Hole in Three-Dimensional space-Time. Phys. Rev. Lett. 1992, 69, 1849–1851. [Google Scholar] [CrossRef] [Green Version]
- García-Díaz, A.A. Exact Solutions in Three-Dimensional Gravity; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Carlip, S. Quantum Gravity in 2 + 1 Dimensions, 1st ed.; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 2010. [Google Scholar]
- Schouten, J.A. Ricci-Calculus: An Introduction to Tensor Analysis and Its Geometrical Applications; Springer: Berlin/Heidelberg, Germany, 2013; Volume 10. [Google Scholar]
- Lovelock, D.; Rund, H. Tensors, Differential Forms, and Variational Principles; Courier Dover Publications: Mignola, NY, USA, 1989. [Google Scholar]
- Ortín, T. Gravity and Strings, 2nd ed.; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Carlip, S. Quantum Gravity in 2 + 1 Dimensions: The Case of a Closed Universe. Living Rev. Relativ. 2005, 8, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zanelli, J.; Hassaine, M. Chern-Simons (Super)Gravity (100 Years of General Relativity); World Scientific: Singapore, 2016; Volume 2. [Google Scholar]
- Castillo-Felisola, O. Chapter Beyond Einstein: A Polynomial Affine Model of Gravity. In Gravity; IntechOpen: London, UK, 2018; pp. 183–201. [Google Scholar] [CrossRef] [Green Version]
- Castillo-Felisola, O.; Orellana, O.; Perdiguero, J.; Ramírez, F.; Skirzewski, A.; Zerwekh, A.R. Aspects of the Polynomial Affine Model of Gravity in Three Dimensions. Eur. Phys. J. C 2022, 82, 8. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo-Felisola, O.; Grez, B.; Orellana, O.; Perdiguero, J.; Ramirez, F.; Skirzewski, A.; Zerwekh, A.R. Polynomial Affine Model of Gravity in Three-Dimensions. Universe 2022, 8, 68. https://doi.org/10.3390/universe8020068
Castillo-Felisola O, Grez B, Orellana O, Perdiguero J, Ramirez F, Skirzewski A, Zerwekh AR. Polynomial Affine Model of Gravity in Three-Dimensions. Universe. 2022; 8(2):68. https://doi.org/10.3390/universe8020068
Chicago/Turabian StyleCastillo-Felisola, Oscar, Bastian Grez, Oscar Orellana, Jose Perdiguero, Francisca Ramirez, Aureliano Skirzewski, and Alfonso R. Zerwekh. 2022. "Polynomial Affine Model of Gravity in Three-Dimensions" Universe 8, no. 2: 68. https://doi.org/10.3390/universe8020068
APA StyleCastillo-Felisola, O., Grez, B., Orellana, O., Perdiguero, J., Ramirez, F., Skirzewski, A., & Zerwekh, A. R. (2022). Polynomial Affine Model of Gravity in Three-Dimensions. Universe, 8(2), 68. https://doi.org/10.3390/universe8020068





