Observe Gamma-Rays and Neutrinos Associated with Ultra-High Energy Cosmic Rays
Abstract
1. Introduction
2. Physical Picture and Assumption
2.1. UHECR Sources as Gamma-Ray and Neutrino Sources
2.2. Spatial and Temporal Association of UHECRs with Gamma-Ray/Neutrino Signals
3. Method and Formula
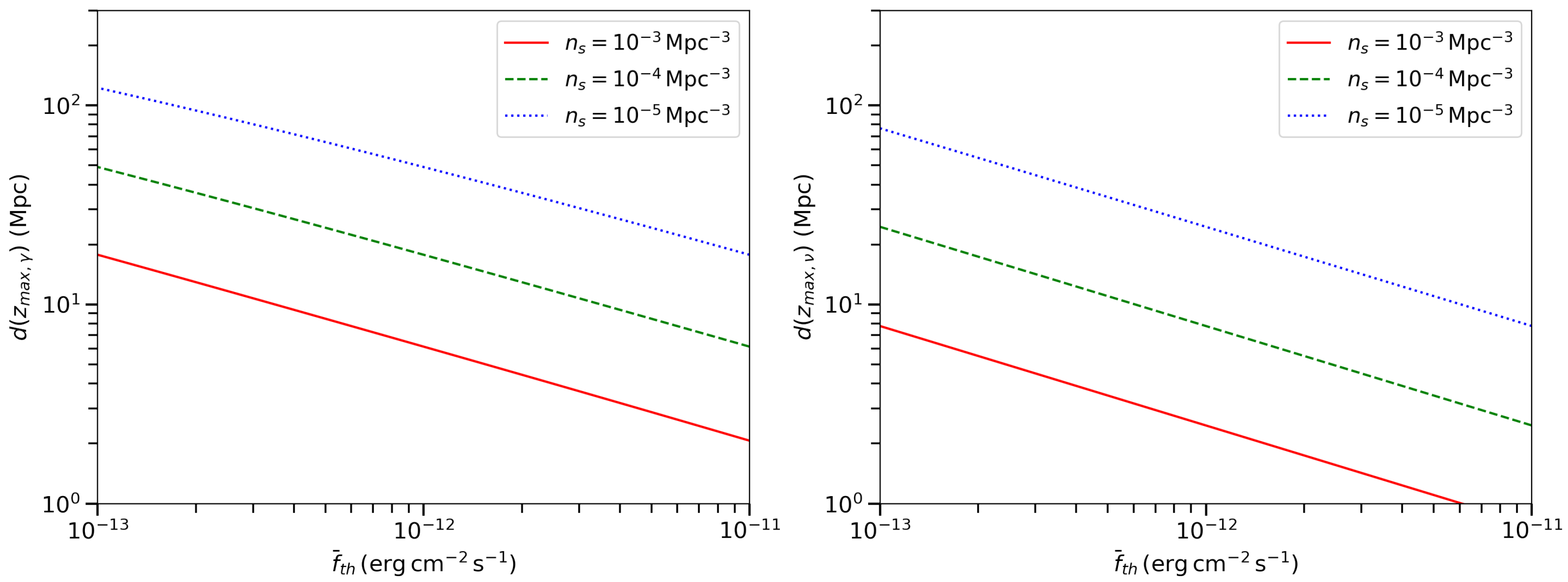
3.1. Horizon for Gamma-Ray and Neutrino Sources
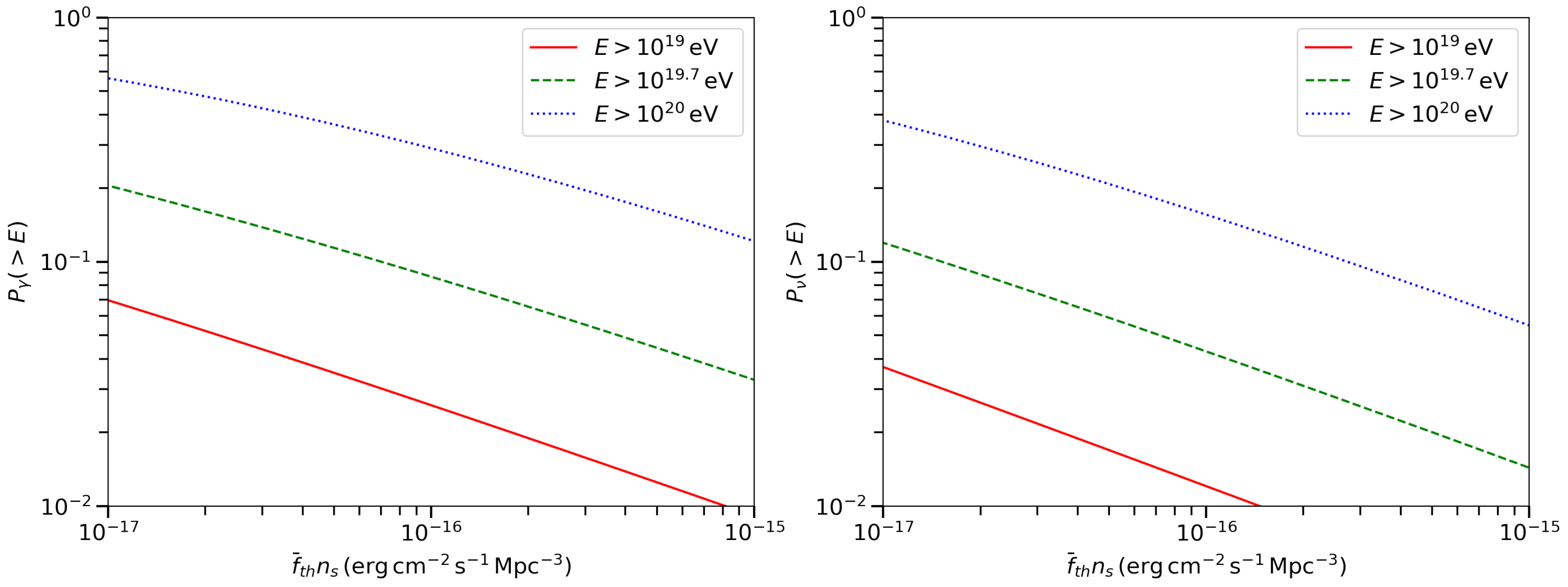
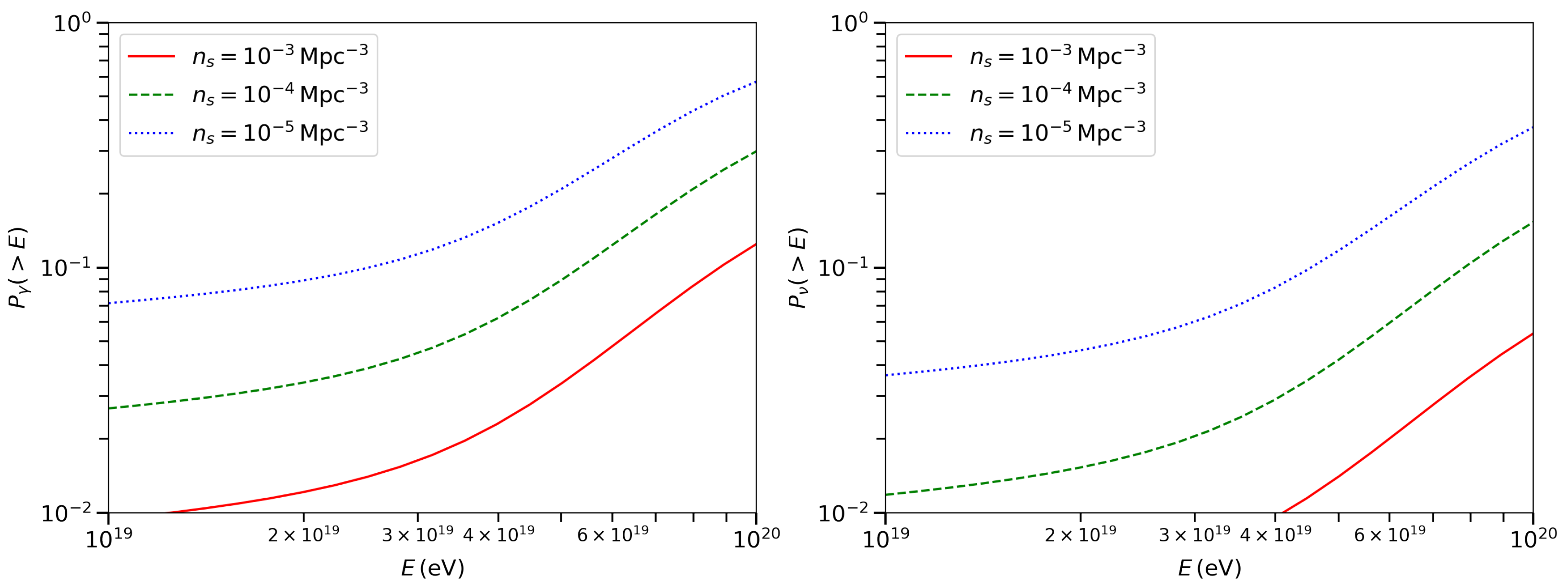
3.2. Detection Probability
4. Results
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nagano, M.; Watson, A.A. Observations and implications of the ultrahigh-energy cosmic rays. Rev. Mod. Phys. 2000, 72, 689–732. [Google Scholar] [CrossRef]
- Kotera, K.; Olinto, A.V. The Astrophysics of Ultrahigh-Energy Cosmic Rays. ARA&A 2011, 49, 119–153. [Google Scholar] [CrossRef]
- Abbasi, R.U.; Abu-Zayyad, T.; Allen, M.; Amman, J.F.; Archbold, G.; Belov, K.; Belz, J.W.; Ben Zvi, S.Y.; Bergman, D.R.; Blake, S.A.; et al. First Observation of the Greisen-Zatsepin-Kuzmin Suppression. Phys. Rev. Lett. 2008, 100, 101101. [Google Scholar] [CrossRef]
- Abraham, J.; Abreu, P.; Aglietta, M.; Aguirre, C.; Allard, D.; Allekotte, I.; Allen, J.; Allison, P.; Alvarez-Muñiz, J.; Ambrosio, M.; et al. Observation of the Suppression of the Flux of Cosmic Rays above 4 × 1019 eV. Phys. Rev. Lett. 2008, 101, 061101. [Google Scholar] [CrossRef] [PubMed]
- Allard, D.; Parizot, E.; Olinto, A.V. On the transition from galactic to extragalactic cosmic-rays: Spectral and composition features from two opposite scenarios. Astropart. Phys. 2007, 27, 61–75. [Google Scholar] [CrossRef]
- Katz, B.; Budnik, R.; Waxman, E. The energy production rate & the generation spectrum of UHECRs. J. Cosmology Astropart. Phys. 2009, 2009, 020. [Google Scholar] [CrossRef]
- Berezinsky, V.; Gazizov, A.; Grigorieva, S. On astrophysical solution to ultrahigh energy cosmic rays. Phys. Rev. D 2006, 74, 043005. [Google Scholar] [CrossRef]
- Greisen, K. End to the Cosmic-Ray Spectrum? Phys. Rev. Lett. 1966, 16, 748–750. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuz’min, V.A. Upper Limit of the Spectrum of Cosmic Rays. Sov. J. Exp. Theor. Phys. Lett. 1966, 4, 78. [Google Scholar]
- Hillas, A.M. The Origin of Ultra-High-Energy Cosmic Rays. ARA&A 1984, 22, 425–444. [Google Scholar] [CrossRef]
- Halzen, F.; Hooper, D. High-energy neutrino astronomy: The cosmic ray connection. Rep. Prog. Phys. 2002, 65, 1025–1078. [Google Scholar] [CrossRef]
- Waxman, E. High energy cosmic ray and neutrino astronomy. arXiv 2011, arXiv:1101.1155. [Google Scholar]
- Aartsen, M.G.; Abbasi, R.; Abdou, Y.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Auffenberg, J.; Bai, X.; et al. First Observation of PeV-Energy Neutrinos with IceCube. Phys. Rev. Lett. 2013, 111, 021103. [Google Scholar] [CrossRef] [PubMed]
- IceCube Collaboration. Evidence for High-Energy Extraterrestrial Neutrinos at the IceCube Detector. Science 2013, 342, 1242856. [Google Scholar] [CrossRef]
- Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Alves, A.A.; Amin, N.M.; Andeen, K.; et al. IceCube high-energy starting event sample: Description and flux characterization with 7.5 years of data. Phys. Rev. D 2021, 104, 022002. [Google Scholar] [CrossRef]
- Waxman, E.; Bahcall, J. High energy neutrinos from astrophysical sources: An upper bound. Phys. Rev. D 1998, 59, 023002. [Google Scholar] [CrossRef]
- Bahcall, J.; Waxman, E. High energy astrophysical neutrinos: The upper bound is robust. Phys. Rev. D 2001, 64, 023002. [Google Scholar] [CrossRef]
- Katz, B.; Waxman, E.; Thompson, T.; Loeb, A. The energy production rate density of cosmic rays in the local universe is ∼1044–45 erg Mpc−3 yr−1 at all particle energies. arXiv 2013, arXiv:1311.0287. [Google Scholar]
- Blandford, R.; Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 1987, 154, 1–75. [Google Scholar] [CrossRef]
- Waxman, E. Cosmological Gamma-Ray Bursts and the Highest Energy Cosmic Rays. Phys. Rev. Lett. 1995, 75, 386–389. [Google Scholar] [CrossRef]
- Stettner, J. Measurement of the diffuse astrophysical muon-neutrino spectrum with ten years of IceCube data. In Proceedings of the 36th International Cosmic Ray Conference (ICRC2019), Madison, Wisconsin, 24 July–1 August 2019; Volume 36, p. 1017. [Google Scholar]
- Franceschini, A.; Rodighiero, G. The extragalactic background light revisited and the cosmic photon-photon opacity. A&A 2017, 603, A34. [Google Scholar] [CrossRef]
- Waxman, E. Cosmological Origin for Cosmic Rays above 1019 eV. ApJ 1995, 452, L1. [Google Scholar] [CrossRef]
- Boyle, B.J.; Terlevich, R.J. The cosmological evolution of the QSO luminosity density and of the star formation rate. MNRAS 1998, 293, L49–L51. [Google Scholar] [CrossRef]
- Abraham, J.; Abreu, P.; Aglietta, M.; Ahn, E.J.; Allard, D.; Allekotte, I.; Allen, J.; Alvarez-Muñiz, J.; Ambrosio, M.; Anchordoqui, L.; et al. Trigger and aperture of the surface detector array of the Pierre Auger Observatory. Nucl. Instruments Methods Phys. Res. A 2010, 613, 29–39. [Google Scholar] [CrossRef]
- Cao, Z.; della Volpe, D.; Liu, S.; Bi, X.; Chen, Y.; D’Ettorre Piazzoli, B.; Feng, L.; Jia, H.; Li, Z.; Ma, X.; et al. The Large High Altitude Air Shower Observatory (LHAASO) Science Book (2021 Edition). arXiv 2019, arXiv:1905.02773. [Google Scholar]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Andeen, K.; Anderson, T.; Ansseau, I.; et al. Time-Integrated Neutrino Source Searches with 10 Years of IceCube Data. Phys. Rev. Lett. 2020, 124, 051103. [Google Scholar] [CrossRef]
- He, H.N.; Kusenko, A.; Nagataki, S.; Zhang, B.B.; Yang, R.Z.; Fan, Y.Z. Monte Carlo Bayesian search for the plausible source of the Telescope Array hotspot. Phys. Rev. D 2016, 93, 043011. [Google Scholar] [CrossRef]
- Murase, K.; Ioka, K.; Nagataki, S.; Nakamura, T. High-energy cosmic-ray nuclei from high- and low-luminosity gamma-ray bursts and implications for multimessenger astronomy. Phys. Rev. D 2008, 78, 023005. [Google Scholar] [CrossRef]
- Vietri, M. The Acceleration of Ultra-High-Energy Cosmic Rays in Gamma-Ray Bursts. ApJ 1995, 453, 883. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Tian, X.; Li, Z. Observe Gamma-Rays and Neutrinos Associated with Ultra-High Energy Cosmic Rays. Universe 2022, 8, 560. https://doi.org/10.3390/universe8110560
Zhang Q, Tian X, Li Z. Observe Gamma-Rays and Neutrinos Associated with Ultra-High Energy Cosmic Rays. Universe. 2022; 8(11):560. https://doi.org/10.3390/universe8110560
Chicago/Turabian StyleZhang, Qinyuan, Xishui Tian, and Zhuo Li. 2022. "Observe Gamma-Rays and Neutrinos Associated with Ultra-High Energy Cosmic Rays" Universe 8, no. 11: 560. https://doi.org/10.3390/universe8110560
APA StyleZhang, Q., Tian, X., & Li, Z. (2022). Observe Gamma-Rays and Neutrinos Associated with Ultra-High Energy Cosmic Rays. Universe, 8(11), 560. https://doi.org/10.3390/universe8110560







