Nuclear Bubble Configuration in Heavy-Ion Collisions
Abstract
1. Introduction
2. Bubble Structure in Heavy-Ion Collisions
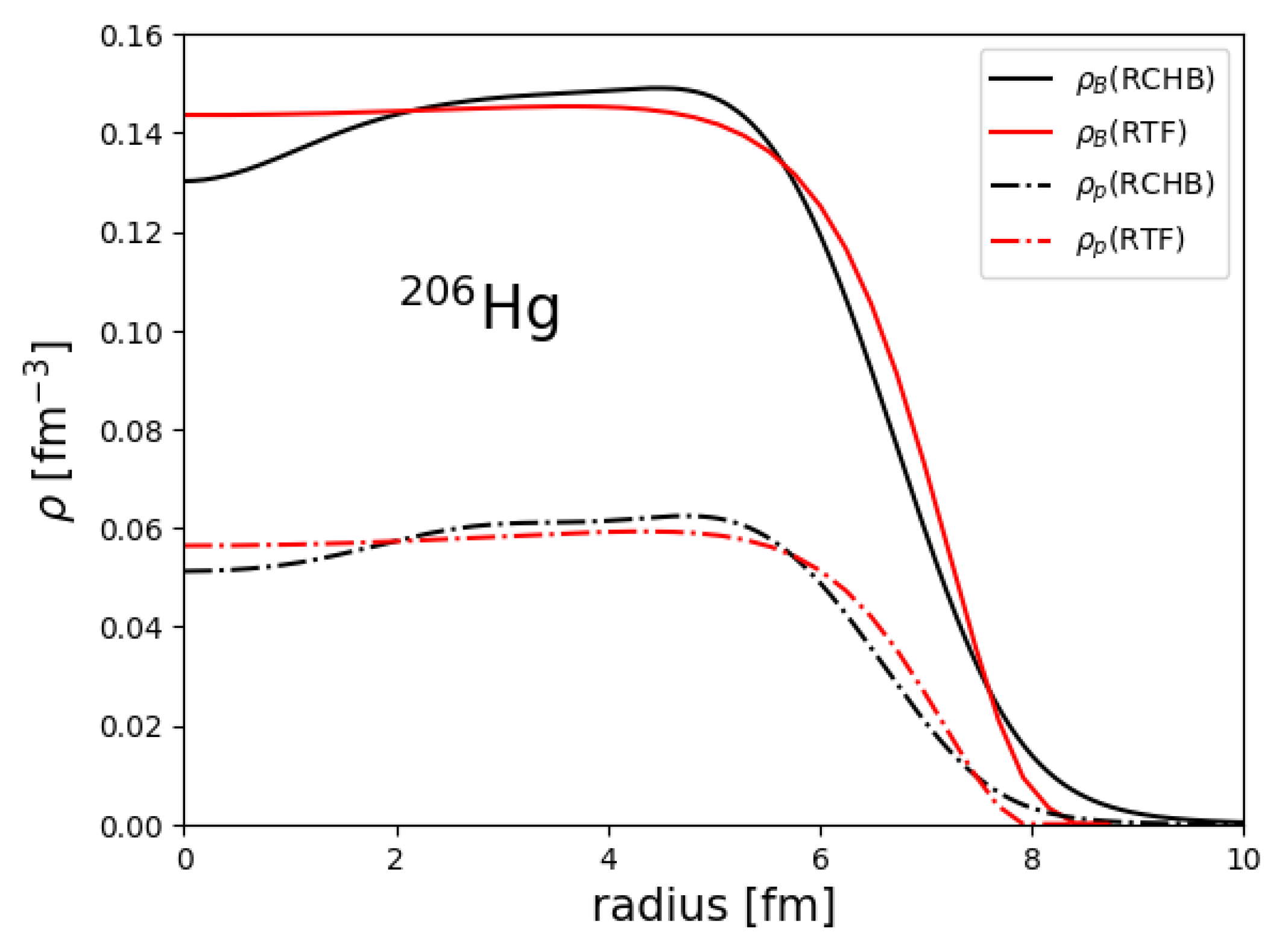
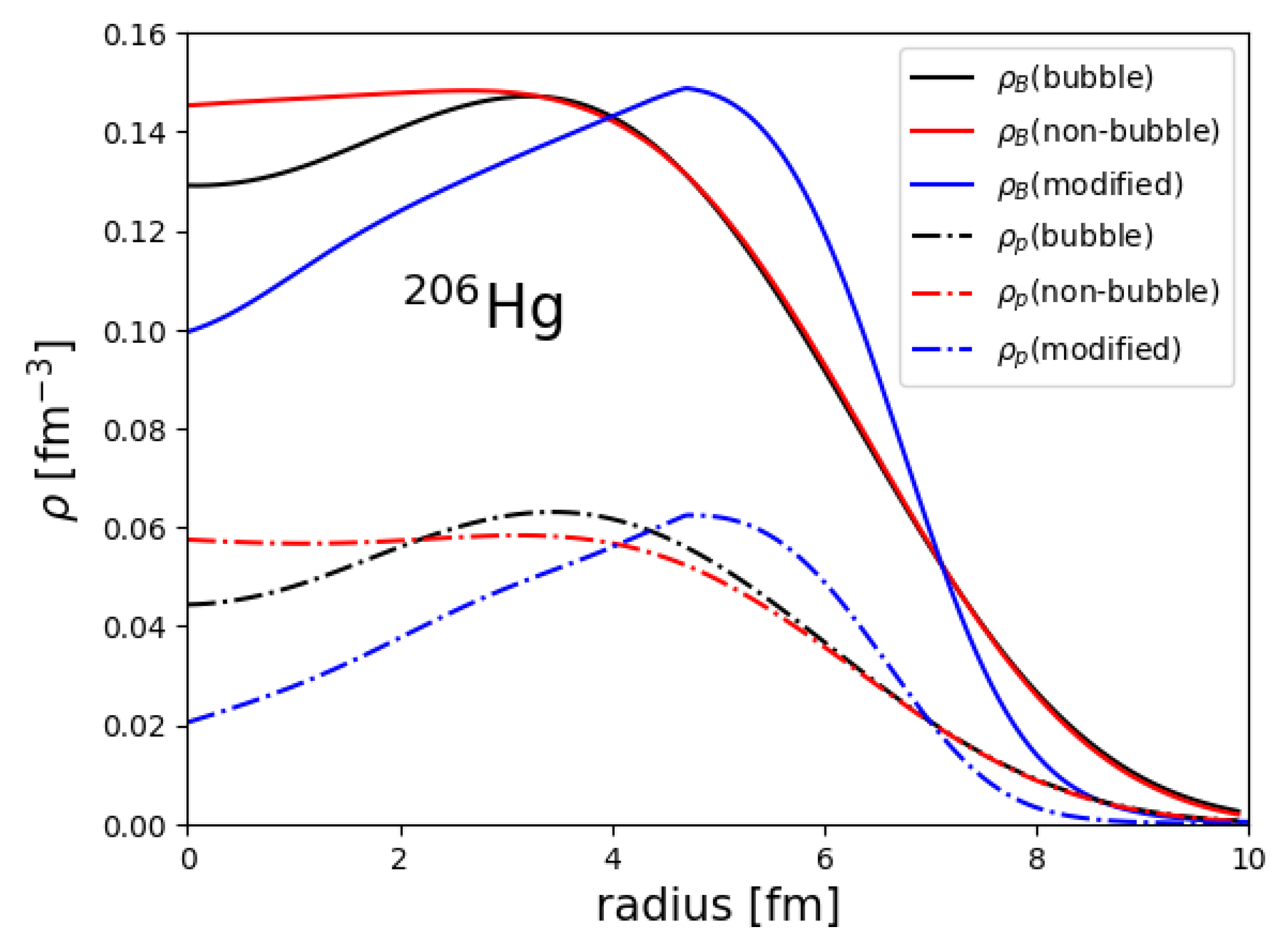
2.1. Bubble Nuclei in RCHB Theory
2.2. DJBUU
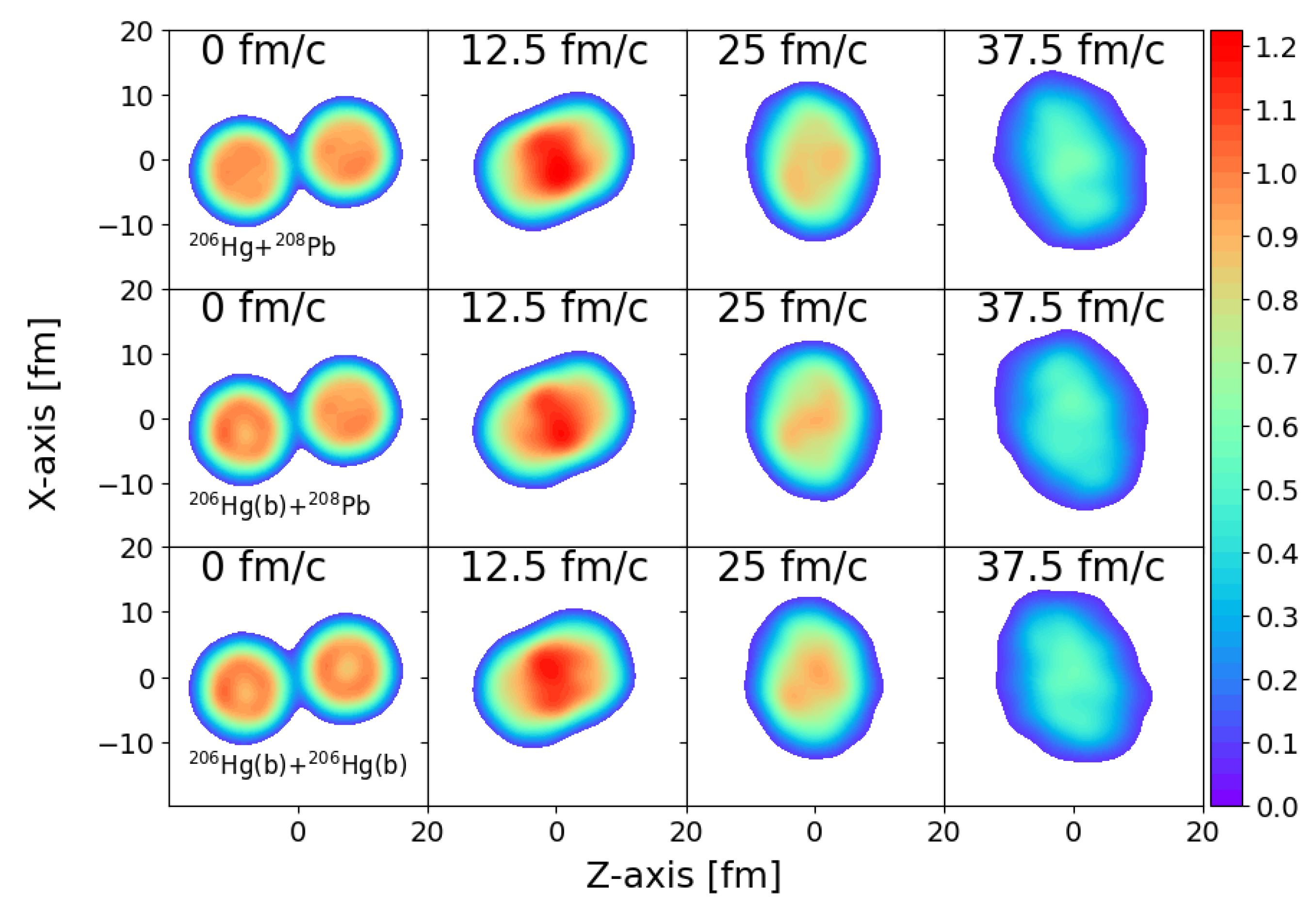
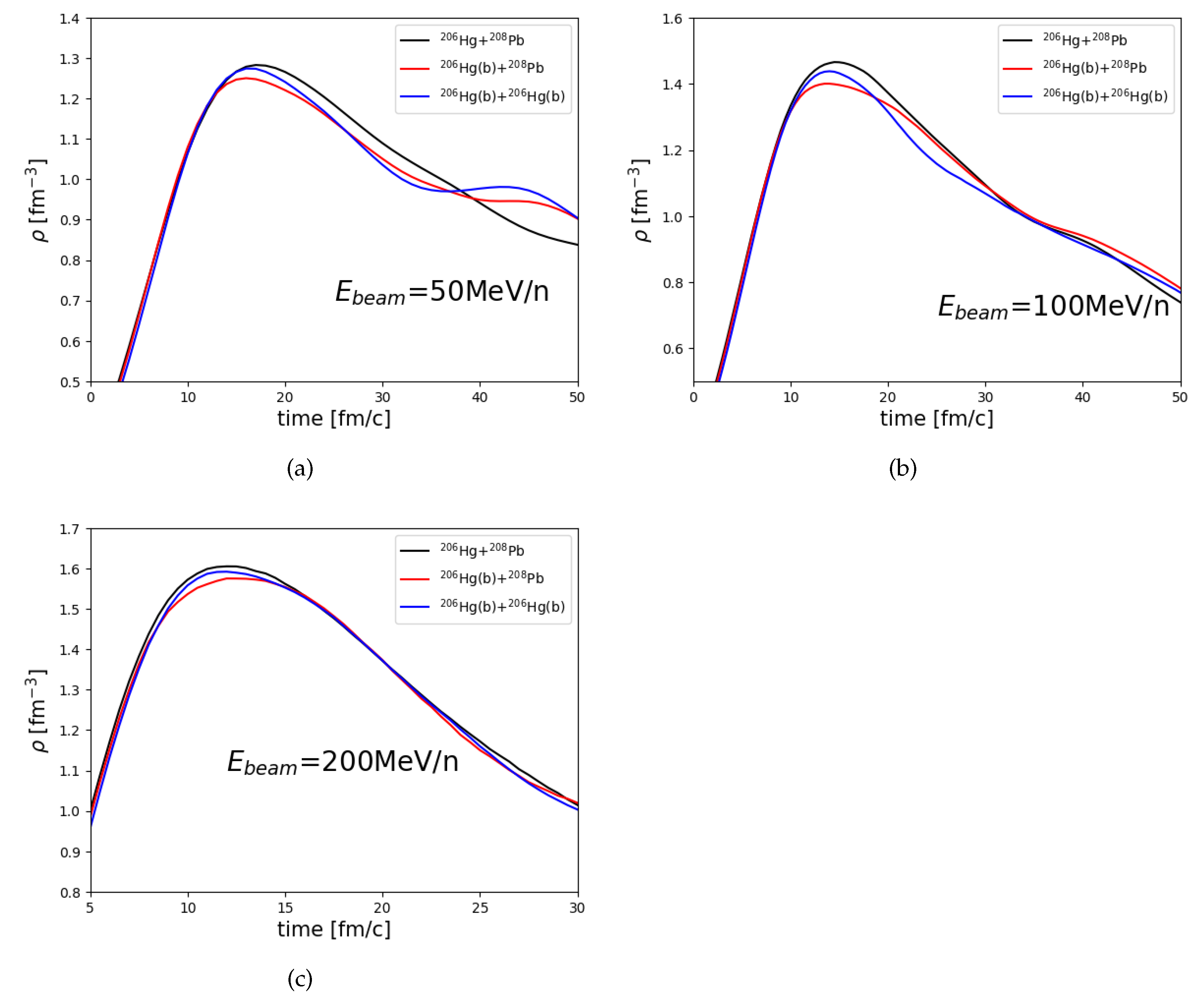
3. Results
4. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
| 1 | In principle, one can obtain different sets of the coupling constants that can equally well describe the nuclear properties. If this new set of coupling constants predicts a different bubble structure, then our results may change accordingly. |
References
- Wolter, H.; [TMEP Collaboration]. Transport model comparison studies of intermediate-energy heavy-ion collisions. Prog. Part. Nucl. Phys. 2022, 125, 103962. [Google Scholar] [CrossRef]
- Yong, G.C. Probing nuclear bubble configuration by the π-/π+ ratio in heavy-ion collisions. Eur. Phys. J. A 2016, 52, 118. [Google Scholar] [CrossRef][Green Version]
- Fan, X.H.; Yong, G.C.; Zuo, W. Probing nuclear bubble configuration by proton induced reaction. Phys. Rev. C 2019, 99, 041601. [Google Scholar] [CrossRef]
- Wilson, H.A. A Spherical Shell Nuclear Model. Phys. Rev. 1946, 69, 538. [Google Scholar] [CrossRef]
- Wong, C.Y. Bubble nuclei. Phys. Lett. B 1972, 41, 451. [Google Scholar] [CrossRef]
- Borunda, M.; Lopez, J.A. On the formation of hollow configurations in heavy-ion collisions. Il Nuovo Cimento A (1965-1970) 1994, 107, 2773–2787. [Google Scholar] [CrossRef]
- Todd-Rutel, B.G.; Piekarewicz, J.; Cottle, P.D. Spin orbit splitting in low j neutron orbits and proton densities in the nuclear interior. Phys. Rev. C 2004, 69, 021301. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Song, J.L.; Zhao, Q. Pseudospin–orbit splitting and its consequences for the central depression in nuclear density. Phys. Rev. C 2016, 93, 054312. [Google Scholar] [CrossRef]
- Yong, G.C. Hollow nuclear matter. Phys. Rev. C 2016, 93, 014602. [Google Scholar] [CrossRef]
- Schuetrumpf, B.; Nazarewicz, W.; Reinhard, P.G. Central depression in nucleonic densities: Trend analysis in the nuclear density functional theory approach. Phys. Rev. C 2017, 96, 024306. [Google Scholar] [CrossRef]
- Arthuis, P.; Barbieri, C.; Vorabbi, M.; Finelli, P. AbInitio Computation of Charge Densities for Sn and Xe Isotopes. Phys. Rev. Lett. 2020, 125, 182501. [Google Scholar] [CrossRef]
- Choi, Y.B.; Lee, C.H.; Mun, M.H.; Kim, Y. Bubble nuclei with shape coexistence in even-even isotopes of Hf to Hg. Phys. Rev. C 2022, 105, 024306. [Google Scholar] [CrossRef]
- Mutschler, A.; Lemasson, A.; Sorlin, O.; Bazin, D.; Borcea, C.; Borcea, R.; Dombrádi, Z.; Ebran, J.P.; Gade, A.; Iwasaki, H.; et al. A proton density bubble in the doubly magic 34Si nucleus. Nat. Phys. 2017, 13, 152. [Google Scholar] [CrossRef]
- Zhan, W.L.; [HIRFL-CSR Group]. Progress in HIRFL-CSR. Nucl. Phys. A 2010, 834, 694c–700c. [Google Scholar] [CrossRef]
- Motobayashi, T. RIKEN RI Beam Factory–Recent Results and Perspectives. Nucl. Phys. A 2010, 834, 707c. [Google Scholar] [CrossRef]
- Jeong, S.; Papakonstantinou, P.; Ishiyama, H.; Kim, Y. A Brief Overview of RAON Physics. J. Korean Phys. Soc. 2018, 73, 516. [Google Scholar] [CrossRef]
- Goutte, H.; Navin, A. Microscopes for the Physics at the Femtoscale: GANIL-SPIRAL2. Nucl. Phys. News 2021, 31, 5. [Google Scholar] [CrossRef]
- Ostroumov, P.N.; Hausmann, M.; Fukushima, K.; Maruta, T.; Plastun, A.S.; Portillo, M.; Wei, J.; Zhang, T.; Zhao, Q. Heavy ion beam physics at Facility for Rare Isotope Beams. JINST 2020, 15, P12034. [Google Scholar] [CrossRef]
- Kim, M.; Lee, C.; Kim, Y.; Jeon, S. Postscript on the indexing of the journal New Physics: Sae Mulli in Scopus. Sci. Ed. 2016, 3, 53–56. [Google Scholar]
- Kim, M.; Jeon, S.; Kim, Y.M.; Kim, Y.; Lee, C.H. Extended parity doublet model with a new transport code. Phys. Rev. C 2020, 101, 064614. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zhou, S.G.; Zhang, S.Q.; Long, W.H.; Geng, L.S. Relativistic Continuum Hartree Bogoliubov theory for ground state properties of exotic nuclei. Prog. Part. Nucl. Phys. 2006, 57, 470. [Google Scholar] [CrossRef]
- Meng, J. Relativistic continuum Hartree-Bogoliubov theory with both zero range and finite range Gogny force and their application. Nucl. Phys. A 1998, 635, 3. [Google Scholar] [CrossRef]
- Xia, X.W.; Lim, Y.; Zhao, P.W.; Liang, H.Z.; Qu, X.Y.; Chen, Y.; Liu, H.; Zhang, L.F.; Zhang, S.Q.; Kim, Y.; et al. The limits of the nuclear landscape explored by the relativistic continuum Hartree–Bogoliubov theory. Atom. Data Nucl. Data Tabl. 2018, 121–122, 1. [Google Scholar] [CrossRef]
- Meng, J.; Ring, P. Relativistic Hartree-Bogoliubov Description of the Neutron Halo in 11Li. Phys. Rev. Lett. 1996, 77, 3963. [Google Scholar] [CrossRef] [PubMed]
- Meng, J.; Ring, P. A Giant halo at the neutron dripline. Phys. Rev. Lett. 1998, 80, 460. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zeng, J.Y.; Zhang, S.Q.; Zhou, S.G. Giant halo at the neutron dripline in Ca isotopes in relativistic continuum Hartree-Bogoliubov theory. Phys. Rev. C 2002, 65, 041302. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Meng, J.; Toki, H.; Tanihata, I.; Zhou, S.G. Study of proton magic even even isotopes and giant halos of Ca isotopes with relativistic continuum Hartree-Bogoliubov theory. Sci. China Phys. Mech. Astron. 2003, 46, 632. [Google Scholar]
- Qu, X.; Chen, Y.; Zhang, S.; Zhao, P.; Shin, I.J.; Lim, Y.; Kim, Y.; Meng, J. Extending the nuclear chart by continuum: From oxygen to titanium. Sci. China Phys. Mech. Astron. 2013, 56, 2031. [Google Scholar] [CrossRef]
- Zhao, P.W.; Li, Z.P.; Yao, J.M.; Meng, J. New parametrization for the nuclear covariant energy density functional with point-coupling interaction. Phys. Rev. C 2010, 82, 054319. [Google Scholar] [CrossRef]
- Liu, B.; Greco, V.; Baran, V.; Colonna, M.; Toro, M.D. Asymmetric nuclear matter: The Role of the isovector scalar channel. Phys. Rev. C 2002, 65, 045201. [Google Scholar] [CrossRef]
- Motohiro, Y.; Kim, Y.; Harada, M. Asymmetric nuclear matter in a parity doublet model with hidden local symmetry. Phys. Rev. C 2015, 92, 025201. [Google Scholar] [CrossRef]
- Shin, I.J.; Paeng, W.G.; Harada, M.; Kim, Y. Nuclear structure in Parity Doublet Model. arXiv 2018, arXiv:1805.03402. [Google Scholar]
- Xu, J.; Chen, L.W.; Tsang, M.B.; Wolter, H.; Zhang, Y.X.; Aichelin, J.; Colonna, M.; Cozma, D.; Danielewicz, P.; Feng, Z.Q.; et al. Understanding transport simulations of heavy-ion collisions at 100A and 400A MeV: Comparison of heavy-ion transport codes under controlled conditions. Phys. Rev. C 2016, 93, 044609. [Google Scholar] [CrossRef]
- Ono, A.; Xu, J.; Colonna, M.; Danielewicz, P.; Ko, C.M.; Tsang, M.B.; Wang, Y.J.; Wolter, H.; Zhang, Y.X.; Chen, L.W.; et al. Comparison of heavy-ion transport simulations: Collision integral with pions and Δ resonances in a box. Phys. Rev. C 2019, 100, 044617. [Google Scholar] [CrossRef]
- Colonna, M.; Zhang, Y.X.; Wang, Y.J.; Cozma, D.; Danielewicz, P.; Ko, C.M.; Ono, A.; Tsang, M.B.; Wang, R.; Wolter, H.; et al. Comparison of heavy-ion transport simulations: Mean-field dynamics in a box. Phys. Rev. C 2021, 104, 024603. [Google Scholar] [CrossRef]
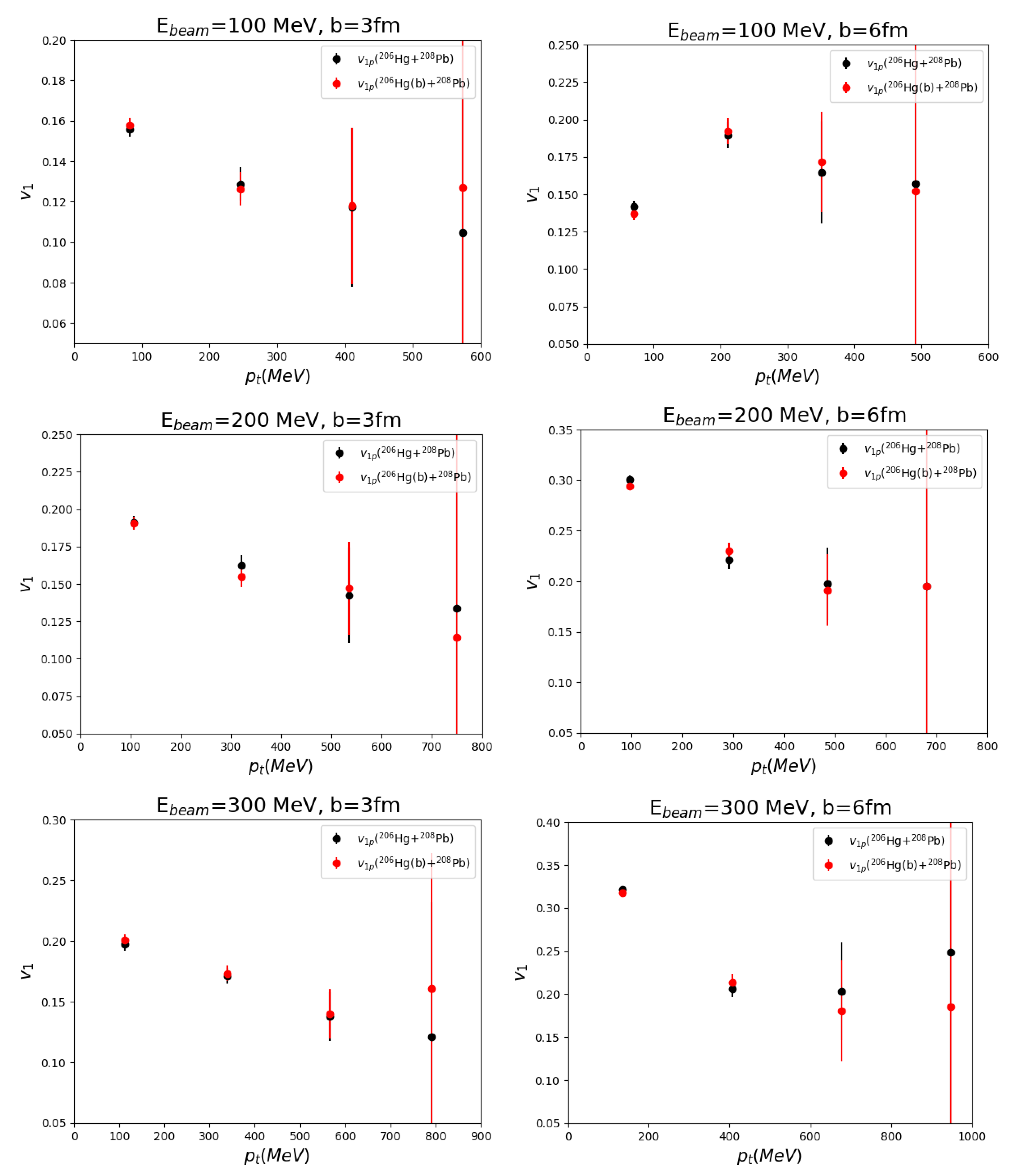
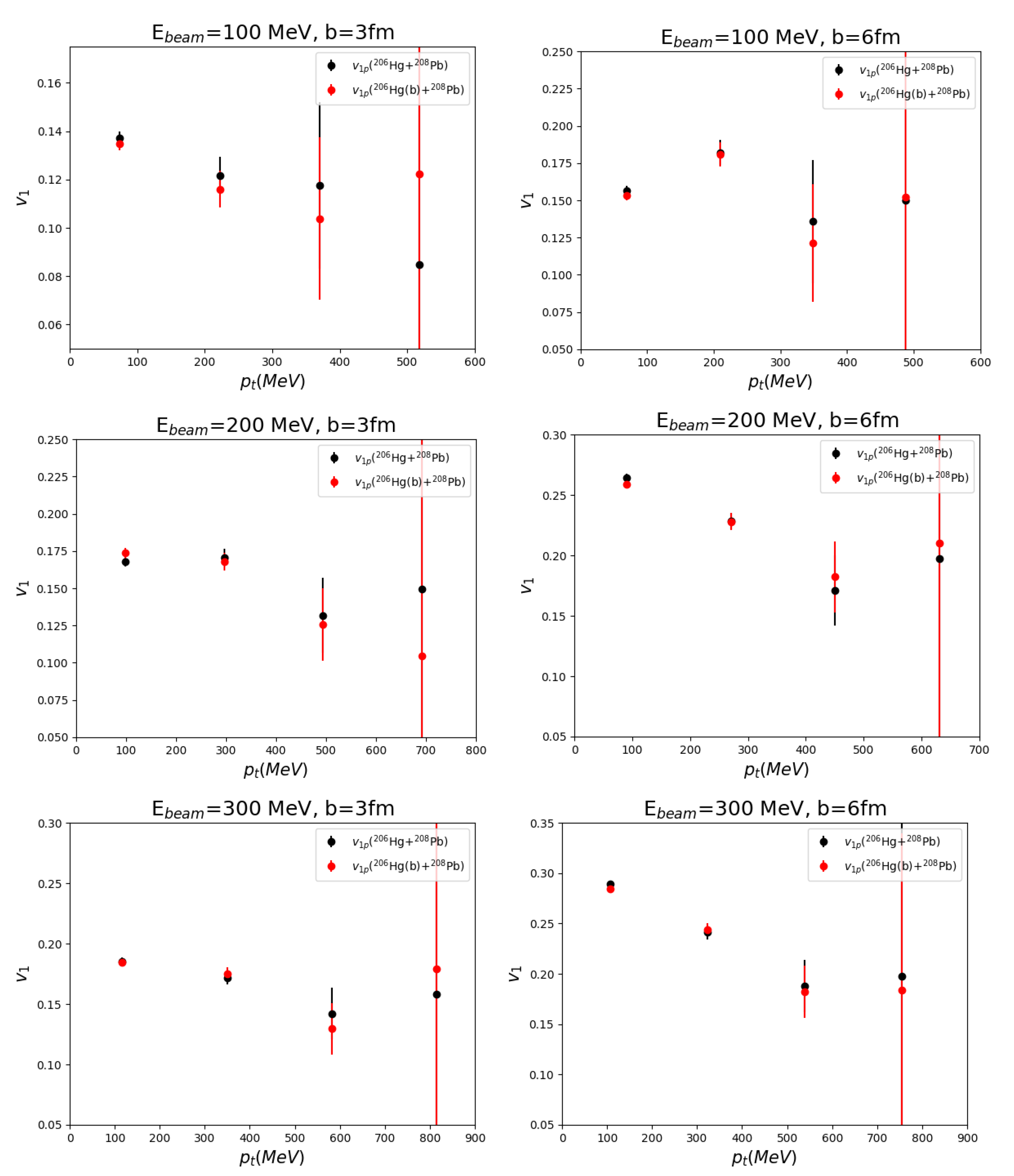
| b | Hg + Pb | Hg (Bubble) + Pb | Hg (Bubble) + Hg (Bubble) |
|---|---|---|---|
| 0 fm | 3.18 (±0.11) | 3.10 (±0.08) | 3.30 (±0.10) |
| 3 fm | 3.18 (±0.11) | 3.22 (±0.06) | 3.23 (±0.07) |
| 6 fm | 3.32 (±0.10) | 3.08 (±0.16) | 3.37 (±0.17) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Jeon, S.; Lee, C.-H.; Kim, Y. Nuclear Bubble Configuration in Heavy-Ion Collisions. Universe 2022, 8, 499. https://doi.org/10.3390/universe8100499
Kim K, Jeon S, Lee C-H, Kim Y. Nuclear Bubble Configuration in Heavy-Ion Collisions. Universe. 2022; 8(10):499. https://doi.org/10.3390/universe8100499
Chicago/Turabian StyleKim, Kyungil, Sangyong Jeon, Chang-Hwan Lee, and Youngman Kim. 2022. "Nuclear Bubble Configuration in Heavy-Ion Collisions" Universe 8, no. 10: 499. https://doi.org/10.3390/universe8100499
APA StyleKim, K., Jeon, S., Lee, C.-H., & Kim, Y. (2022). Nuclear Bubble Configuration in Heavy-Ion Collisions. Universe, 8(10), 499. https://doi.org/10.3390/universe8100499








