Abstract
Several approaches to quantum gravity imply the presence of a minimal measurable length at high energies. This is in tension with the Heisenberg Uncertainty Principle. Such a contrast is then considered in phenomenological approaches to quantum gravity by introducing a minimal length in quantum mechanics via the Generalized Uncertainty Principle. Several features of the standard theory are affected by such a modification. For example, position eigenstates are no longer included in models of quantum mechanics with a minimal length. Furthermore, while the momentum-space description can still be realized in a relatively straightforward way, the (quasi-)position representation acquires numerous issues. Here, we will review such issues, clarifying aspects regarding models with a minimal length. Finally, we will consider the effects of such models on simple quantum mechanical systems.
1. Introduction
Candidate theories of quantum gravity and thought experiments in black hole physics predict the existance of a minimal measurable length [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. The nature of such a minimal length typically depends on the theory from which it is predicted. For example, it can be considered as a structural property of spacetime or a minimal uncertainty in the position. Whatever its nature, from a phenomenological perspective, considered in this work, one of the most interesting aspects is that it is in strong contrast with the Heisenberg Uncertainty Principle. Such a tension led to the low-energy implementation of a minimal measurable length in quantum mechanics via adequate modifications. Models that include such a minimal length are generically referred to as Generalized Uncertainty Principle (GUP). In the past, models of minimal length have been proposed featuring different approaches and characteristics. For example, a minimal length can be implemented by smearing the classical background considering a superposition of geometries [16,17], or by considering models with curved momentum space [18]. Furthermore, GUP can be introduced by modifying the bound for the product of the uncertainties in position and momentum, making such a bound momentum dependent [12,19,20]; or it can be cast by modifying the commutation relation between position and momentum, thus as a particular subgroup of models of Generalized Uncertainty Relations (GUR) [8,21,22,23]. Here, we will consider this last perspective by using a modified commutation relation of the form
For simplicity, we will assume a function for every value of p. The more general case allowing has been considered in [24].
The main objective of the present work is to study the action of the position operator in models with a minimal length described above. In doing so, we will use [21] as a guideline. This first comment to make is that, since a minimal uncertainty is introduced, position eigenstates cannot be included in such a model. Therefore, a position representation, in which states are expanded on a complete set of position eigenstates, is not possible and we will thus start from a description in momentum space. Furthermore, here we will consider for simplicity a model in one dimension. Models with more dimensions have been considered in the literature, showing interesting features [18].
2. Quasi-Position Representation
As mentioned in the introduction, let us start with a description in momentum-space. In this case, we will consider that the momentum operator acts on a wavefunction as in the ordinary quantum mechanics, that is as a multiplicative operator, while the position operator involves the modification function in Equation (1) and a derivative operator
Such expression guarantees that the commutator between position and momentum is of the form presented in Equation (1). However, it is worth noticing that, given the ordering ambiguity of the scalar function and the derivative in Equation (2), other expressions are possible [25]. Nonetheless, all ordering prescriptions are equivalent.
One of the problems in models of quantum mechanics with a minimal length is the lack of a configuration-space description, as mentioned in the introduction. One possibility, introduced in [21], is that of expanding quantum states in terms of a set of states characterized by a minimal uncertainty in position allowed by the model. Such states, named maximally localized states, can be found as the solution of the following equation
Here, the expectation values , as well as the uncertainty , are to be considered as parameters to be fixed in order to select states with the minimal uncertainty in position. Such states have position expectation value . The solution of this equation is
where we have introduced the function
and the auxiliary variable as
It is worth noticing that, in terms of such new variable, we can rewrite the position operator as
This allows us to interpret as the momentum conjugate to the physical position q.
We will now introduce the new representation induced by the maximally localized states. To do so, we will first consider the wave functions in Equation (4) as functions of p and . Then, we will consider the integral transforms using such wavefunctions as kernel, thus generalizing the Fourier transform compatibly with GUP
In this way, the function produced by the anti-transform in Equation (8) is a function of the new variable , corresponding to the position expectation value of maximally localized states. Therefore, a wave function can be thought of as a superposition of maximally localized states of different position expectation values. Such a new representation is commonly referred to as “quasi-position” representation [21,24,26]. Furthermore, it is possible to use the transforms in Equations (8) and () to define a probability density, associated with the wavefunction , as a function of the quasi-position variable, that is
As a special but relevant case, we can find the quasi-position representation of momentum eigenstates of momentum eigenvalue , that is
We thus obtain a plane of wave number
That is, introducing a minimal length modifies the momentum-wavenumber de Broglie relation. It is worth highlighting that, in the current framework, is an auxiliary variable introduced in Equation (6). However, the result above allows us to interpret the variable as the wavenumber associated with a free particle. The same quantity can be also interpreted as the conjugate momentum to q in models with a minimal length [24,27]. Particular attention must be given to models in which is not an even function, and thus the relation between and p is not odd. In such a case, states described by opposite momentum eigenvalues, and , are characterized by different values for the wavenumbers for the left- and right-moving waves. In other words, left- and right-moving particles are characterized by different dispersion relations.
We conclude this section by observing that, using the transformation in Equation (8), we can obtain the quasi-position representation of the position and momentum operators, that is
We can observe that in this case, the position operator is not a multiplicative operator. The additional derivative term in Equation (13), although not contributing to the position-momentum commutator, is essential to make the position a Hermitian operator.
An Alternative Construction
In ref. [28], the author suggests a different method to find states corresponding to a minimal uncertainty product. The analytic method, as it is called in [28], aims towards states, denoted critical states in the same work, relative to which the uncertainty product is stationary. Such a method is particularly relevant in cases in which the uncertainty product is state-dependent, as in the present case. Adapting such a direct method to our case, the critical state is described by the following second order differential equation
in which the expectation values and , as well as the uncertainties and , are parameters to be chosen so that the right hand side of the uncertainty relation obtained from Equation (1), that is
is stationary. In the present case, by introducing the function
and introducing the operator , the Equation (15) can be written as
that corresponds to the harmonic oscillator Schrödinger equation with mass, frequency, and energy terms respectively given by
Thus, for every value of the uncertainty , there may be several values for such that the uncertainty product is stationary, but only the ground state obtained from Equation (18), if it exists, corresponds to a minimum of the uncertainty product. An analysis of the harmonic oscillator with GUP can be found, for example, in [21,25].
3. Examples
The results introduced above, and in particular the modified de Broglie relation Equation (12), can be used to study the effects of a minimal length on particular quantum systems. Below, we will see two such systems.
For sake of clarity, we will consider a particular GUP model in which the function appearing in Equation (1) is a second degree polynomial in p, that is
Here, the parameters and can be cast as
with and two dimensionless parameters, the Planck mass, and c the speed of light in vacuum. Such parameters are related with the expectation values and uncertainty of for a maximally localized states via Equation (4). In particular, one can show that a state of minimal uncertainty requires [24]
With the parametrization in Equation (20), the relation between and p becomes
thus resulting in a limited interval on which can acquire values
It is worth noticing that the relation between and p is not odd when , meaning . As a consequence, the image of the function is not symmetric around 0. As mentioned in Section 2, this implies that left- and right-moving plane waves with the same magnitude of momentum have different magnitudes for the wavenumbers. Furthermore, when the limit for small values of p compared to the Planck momentum is taken in Equation (23), we see that we obtain the standard result . Finally, another interesting observation concernes the case for . Although it will not be treated here, it is worth pointing out that such case exhibits a limited interval on which the physical momentum p can acquire values, whereas the case does not present such constraint. Specifically, when , the variable p is bounded both on the left and on the right, while the auxiliary variable is not [24]. A similar case, with a modified momentum operator expressed as an arctangent of the ordinary one, has been consider in [29].
In quasi-position representation, by using Equations (13), (14) and (22), the position reads
while the momentum operator is obtained by inverting Equation (23) and using , that is
As expected, using the value and substituting , one obtains the results of [21]. Finally, it is worth observing that the commutator between the position and momentum operators presented above returns the expression in Equation (1) with the choice of the modification function made in this section. To see this, it is enough considering the momentum operator as a function of , noticing that , and using the results in Appendix A of [25]. We then find
3.1. Particle in a Box
Here, we will consider the case of a particle bounded in an infinite potential well, i.e., a box. Let use call L the width of the box. We will proceed as customary in quantum mechanics by considering a superposition of left- and right-moving plane waves inside the box. Such waves are characterized by the same magnitude of the momentum eigenvalue, as obtained by the Schrödinger equation for the system, and by the relevant boundary conditions. Differently from the standard case, however, the fact that left- and right-moving waves have different wavenumbers does not allow concluding that an energy eigenfunction is described by a standing wave. This would be true only when is an even function, for example, when . Therefore, in general we find that the quantization condition for an energy eigenfunction in a one-dimensional box is that the sum of the wavelengths of the left- and right-moving plane waves divides the length of the box, that is
where is the momentum eigenvalue of the n’s energy state. Since acquires values on a limited interval, as shown in Equation (24), the integer n is limited as well. Specifically, the largest value for n, and thus the maximum number of energy eigenstates in th box, is given by
where is the Planck length.
The results above are presented in Figure 1. Here, the standard case and two different parametrizations for the model in Equation (20) are compared for the case of a box of width m. The vertical dashed lines signal the highest energy state allowed in the box for each model. It is clear that, the narrower the box, the smaller the number of allowed states. It is then possible finding the largest width of the box so that no state is allowed. Such width is given by
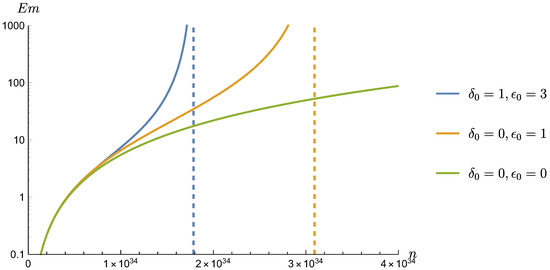
Figure 1.
Energy, multiplied by mass, of a particle in a box of width m. The green solid line corresponds to the standard case, while the blue and orange solid lines correspond to two different parametrizations for the model in Equation (20). The dashed vertical lines correspond to the maximum integer n allowed by the particular parametrization [24].
It is worth observing that only , that is the parameter associated with the quadratic term in Equation (20), affects such a minimal width. The existence of a minimal width is consistent with the introduction of a minimal length in quantum mechanics.
3.2. Potential Barrier
A similar analysis can be carried on for the case of a potential barrier. In this case, we will consider a potential barrier of width L and height . Specifically, we will assume the barrier to be between and . The procedure follows that of ordinary quantum mechanics: a superposition of right-moving (the incoming particle) and left-moving (the reflected particle) is considered on the left of the barrier; in the region of the barrier, a superposition of left- and right-moving waves is considered with a particular value of the wavenumbers, in general complex; a right-moving wave (the transmitted particle) is considered on the right of the barrier. With the usual boundary condition, one can study the various aspect of such a system. For example, we can find that resonances in the transmission amplitude are characterized by different values of energy compared to the standard case. In particular, one can find the following relation between the momentum , related to the wavenumber via Equation (12), and the width of the barrier
where is the momentum eigenvalues of the waves through the barrier corresponding to a resonance. Moreover, since acquires values on a limited interval, only a finite number of resonances are possible. Such a number can be expressed in terms of the barrier width as
Specifically, one can find values for the width L such that no resonance is allowed. Furthermore, when this happens, the transmission coefficient is appreciably different from one even in the case the energy E of the incoming wave is smaller than the barrier energy , as shown in Figure 2.
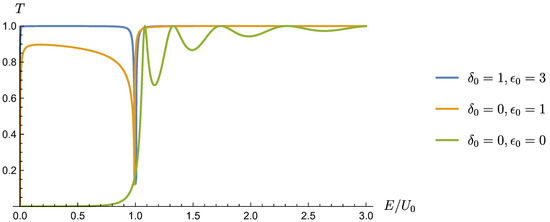
Figure 2.
Transmission coefficient for a barrier of width and height = 120 /mL. In green is the standard case, while the blue and orange lines correspond to two different parametrizations of the model in Equation (20). It is worth observing that, while the standard case predicts a vanishing transmission coefficient at an energy below , this is not the case in models with a minimal length.
4. Conclusions
Phenomenological studies of a minimal measurable length in quantum mechanics are motivated by a large fraction of quantum approaches to gravity and black hole physics. Here, we focused on a particular realization of such a minimal measurable length via the Generalized Uncertainty Principle modifying the position-momentum commutation relation. This modification presents several changes and subtleties. For example, by the very same idea of minimal uncertainty in position, position eigenstates cannot be introduced, with the consequence, that a position representation cannot be introduced. Therefore, we resorted to a description in momentum space and an alternative position based on states of minimal position uncertainty. This last choice, introducing the quasi-position representation, introduces new issues requiring clarification. Specifically, the position operator in the quasi-position representation is not a multiplicative operator. Furthermore, although momentum eigenstates in such a representation can still be described as plane waves, the corresponding wavenumber is not simply proportional to the momentum eigenvalue. De Broglie’s relation between momentum and wavenumber is thus modified. Moreover, depending on the particular model under consideration, left- and right-moving waves referring to the same momentum eigenvalue may be characterized by different magnitudes of the wavenumber. In addition, the wavenumber may acquire values on a limited interval. We thus have a maximum value of the wavenumber magnitude or, equivalently, a minimum value of the wavelength of plane waves.
As we have seen for the particular case of a particle in a box and a potential barrier, such features have interesting implications, strongly differentiating minimal length models from ordinary quantum mechanics. For example, we have found that a box of a given length can host only a finite number of energy eigenstates. Furthermore, when boxes are too narrow, no energy eigenstate can be defined, thus resulting in necessarily empty boxes. In the case of a potential barrier, we obtained that transmission resonance energies are finite in number. Specifically, since such a number depends on the width of the barrier, thin barriers may present no resonance. In such a case, the reflection coefficient may be strongly suppressed even for energies below the potential energy of the barrier, as if the wave was not affected by the barrier. The results obtained for a particle in a box and a potential barrier are compatible with the existence of a minimal length.
The scope of the present work has been that of presenting issues and the proper description of quantum mechanics with a minimal length. The relevance of such an analysis is in the fact that GUP is often used for phenomenological studies in quantum gravity [30,31,32]. Approaching carefully such a topic is thus necessary for a comparison between the predicted features and potential experimental observations.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mead, C.A. Possible Connection Between Gravitation and Fundamental Length. Phys. Rev. 1964, 135, B849–B862. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Superstring collisions at planckian energies. Phys. Lett. B 1987, 197, 81–88. [Google Scholar] [CrossRef] [Green Version]
- Gross, D.J.; Mende, P.F. String theory beyond the Planck scale. Nucl. Phys. B 1988, 303, 407–454. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Can spacetime be probed below the string size? Phys. Lett. B 1989, 216, 41–47. [Google Scholar] [CrossRef] [Green Version]
- Rovelli, C.; Smolin, L. Discreteness of area and volume in quantum gravity. Nucl. Phys. B 1995, 442, 593–619. [Google Scholar] [CrossRef] [Green Version]
- Konishi, K.; Paffuti, G.; Provero, P. Minimum physical length and the generalized uncertainty principle in string theory. Phys. Lett. B 1990, 234, 276–284. [Google Scholar] [CrossRef]
- Maggiore, M. A generalized uncertainty principle in quantum gravity. Phys. Lett. B 1993, 304, 65–69. [Google Scholar] [CrossRef] [Green Version]
- Maggiore, M. The algebraic structure of the generalized uncertainty principle. Phys. Lett. B 1993, 319, 83–86. [Google Scholar] [CrossRef] [Green Version]
- Garay, L.J. Quantum gravity and minimum length. Int. J. Mod. Phys. A 1994, 10, 145–165. [Google Scholar] [CrossRef] [Green Version]
- Adler, R.J.; Santiago, D.I. On gravity and the uncertainty principle. Mod. Phys. Lett. A 1999, 14, 1371–1381. [Google Scholar] [CrossRef]
- Capozziello, S.; Lambiase, G.; Scarpetta, G. Generalized Uncertainty Principle from Quantum Geometry. Int. J. Theor. Phys. 2000, 39, 15–22. [Google Scholar] [CrossRef]
- Scardigli, F. Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment. Phys. Lett. B 1999, 452, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Magueijo, J.; Smolin, L. String theories with deformed energy-momentum relations, and a possible nontachyonic bosonic string. Phys. Rev. D 2005, 71, 026010. [Google Scholar] [CrossRef] [Green Version]
- Amelino-Camelia, G. Quantum-Spacetime Phenomenology. Living Rev. Relativ. 2013, 16, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amelino-Camelia, G. Doubly-Special Relativity: Facts, Myths and Some Key Open Issues. Symmetry 2009, 2, 123–170. [Google Scholar] [CrossRef] [Green Version]
- Lake, M.J.; Miller, M.; Ganardi, R.; Liu, Z.; Liang, S.; Paterek, T. Generalised uncertainty relations from superpositions of geometries. Class. Quantum Gravity 2019, 36, 155012. [Google Scholar] [CrossRef] [Green Version]
- Lake, M.; Miller, M.; Liang, S. Generalised uncertainty relations for angular momentum and spin in quantum geometry. Universe 2020, 6, 56. [Google Scholar] [CrossRef] [Green Version]
- Wagner, F. Generalized uncertainty principle or curved momentum space? Phys. Rev. D 2021, 104, 126010. [Google Scholar] [CrossRef]
- Scardigli, F.; Casadio, R. Gravitational tests of the generalized uncertainty principle. Eur. Phys. J. C 2015, 75, 425. [Google Scholar] [CrossRef] [Green Version]
- Casadio, R.; Scardigli, F. Generalized Uncertainty Principle, Classical Mechanics, and General Relativity. Phys. Lett. B 2020, 807, 135558. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 1995, 52, 1108–1118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ali, A.F.; Das, S.; Vagenas, E.C. Proposal for testing quantum gravity in the lab. Phys. Rev. D 2011, 84, 044013. [Google Scholar] [CrossRef] [Green Version]
- Bosso, P. Generalized Uncertainty Principle and Quantum Gravity Phenomenology. Ph.D. Thesis, University of Lethbridge, Lethbridge, AB, Canada, 2017. [Google Scholar]
- Bosso, P. On the quasi-position representation in theories with a minimal length. Class. Quantum Gravity 2021, 38, 075021. [Google Scholar] [CrossRef]
- Bosso, P.; Luciano, G.G. Generalized Uncertainty Principle: From the harmonic oscillator to a QFT toy model. Eur. Phys. J. C 2021, 81, 982. [Google Scholar] [CrossRef]
- Bosso, P. Position in Models of Quantum Mechanics with a Minimal Length. Phys. Sci. Forum 2021, 2, 35. [Google Scholar] [CrossRef]
- Bosso, P. Rigorous Hamiltonian and Lagrangian analysis of classical and quantum theories with minimal length. Phys. Rev. D 2018, 97, 126010. [Google Scholar] [CrossRef] [Green Version]
- Jackiw, R. Minimum Uncertainty Product, Number-Phase Uncertainty Product, and Coherent States. J. Math. Phys. 1968, 9, 339–346. [Google Scholar] [CrossRef]
- Bishop, M.; Contreras, J.; Lee, J.; Singleton, D. Reconciling a quantum gravity minimal length with lack of photon dispersion. Phys. Lett. B 2021, 816, 136265. [Google Scholar] [CrossRef]
- Jizba, P.; Kleinert, H.; Scardigli, F. Uncertainty relation on a world crystal and its applications to micro black holes. Phys. Rev. D 2010, 81, 084030. [Google Scholar] [CrossRef] [Green Version]
- Ong, Y.C. Generalized uncertainty principle, black holes, and white dwarfs: A tale of two infinities. J. Cosmol. Astropart. Phys. 2018, 2018, 015. [Google Scholar] [CrossRef] [Green Version]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L.; Scardigli, F. Heuristic derivation of Casimir effect in minimal length theories. Int. J. Mod. Phys. D 2020, 29, 2050011. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).