Abstract
The origin of the baryon asymmetry of the Universe (BAU) and the nature of dark matter are two of the most challenging problems in cosmology. We propose a scenario in which the gravitational collapse of large inhomogeneities at the quark-hadron epoch generates both the baryon asymmetry and most of the dark matter in the form of primordial black holes (PBHs). This is due to the sudden drop in radiation pressure during the transition from a quark-gluon plasma to non-relativistic hadrons. The collapse to a PBH is induced by fluctuations of a light spectator scalar field in rare regions and is accompanied by the violent expulsion of surrounding material, which might be regarded as a sort of “primordial supernova". The acceleration of protons to relativistic speeds provides the ingredients for efficient baryogenesis around the collapsing regions and its subsequent propagation to the rest of the Universe. This scenario naturally explains why the observed BAU is of order the PBH collapse fraction and why the baryons and dark matter have comparable densities. The predicted PBH mass distribution ranges from subsolar to several hundred solar masses. This is compatible with current observational constraints and could explain the rate, mass and low spin of the black hole mergers detected by LIGO-Virgo. Future observations will soon be able to test this scenario.
1. Introduction
The LIGO-Virgo detections [1,2,3,4] of gravitational waves from the coalescence of massive black holes has triggered renewed interest in primordial black holes (PBHs) as dark matter (DM) [5,6,7]. Their abundance and mass distribution has intrigued both cosmologists and particle physicists [8,9]. If the PBHs were generated in the early radiation-dominated Universe from the gravitational collapse of large curvature fluctuations, then they would have formed shortly after falling within the Hubble horizon with a mass
Here, is the fraction of the Hubble horizon mass ending up in the black hole (with 1 in general and 0.2 in a simplified analysis [10]), T is the temperature of the background Universe and is the number of degrees of freedom then. is of order the Chandrasekhar mass, , for PBHs forming at the Quantum Chromodynamics (QCD) scale, MeV. At this temperature, quarks and gluons form baryons (protons and neutrons) and mesons (pions) and the number of relativistic degrees of freedom drops abruptly. Moreover, the sound speed dips, exponentially enhancing the collapse probability for any large curvature fluctuation that enters the horizon then [11,12,13]. The fraction of domains undergoing collapse is necessarily tiny, even if the PBHs provide all the DM. However, because they are non-relativistic, their density dilutes more slowly than the surrounding radiation until they dominate the expansion of the Universe at matter-radiation equality.
The sudden gravitational collapse of the mass within the Hubble horizon at the QCD epoch releases a large amount of entropy and generates a relativistically expanding shock-wave, with an effective temperature well above that of the surrounding plasma. Such high density hot spots might be regarded as primordial supernovae and provide the out-of-equilibrium conditions required to generate a baryon asymmetry through the well-known electroweak sphaleron transitions responsible for Higgs windings around the electroweak (EW) vacuum [14]. In this process, the charge-parity (CP) symmetry violation of the standard model of particle physics suffices to generate a local baryon-to-photon ratio of order one or larger. The hot spots are separated by many horizon scales at the time of PBH formation and any matter–antimatter asymmetry in the background Universe, such as may have been generated by baryogenesis at an earlier epoch, is assumed to be much smaller than that currently observed. However, since the baryons are relativistic at formation, they propagate away from the hot spots at the speed of light and become homogeneously distributed well before big bang nucleosynthesis. The large initial local baryon asymmetry is thus diluted to the tiny observed global BAU.
The ratio of the energy densities of matter and radiation (relativistic species) at any time is
where is the ratio of the DM and baryonic densities. At PBH formation, the fraction of domains that collapse is
where is the fraction of the DM in PBHs and is the observed BAU. Therefore, for PBH formation at the QCD epoch, we have ∼∼ if PBHs constitute all the DM. This relationship suggests that baryogenesis is somehow linked with PBH formation and that the smallness of the BAU reflects the rarity of the Hubble domains that collapse.
Here, we present a brief outline of a scenario with these features and derive the expected PBH mass distribution. Another important prediction of this scenario is that the ratio of the PBH and baryon densities is naturally of order one, the precise value depending on . This coincidence is unexplained in particle dark matter scenarios. A more detailed description of our proposal—including the mechanism for generating curvature fluctuations via a spectator field and the various fine-tunings involved—can be found in a companion paper [15]. Here, we mainly focus on the generation of the baryon asymmetry.
2. The Quark-Hadron Transition
In order for PBHs to form at the QCD epoch, one needs large curvature fluctuations to enter the horizon at the right time for relativistic particles to undergo gravitational collapse. One might fine-tune the inflationary dynamics (e.g., using the late plateau arising in critical Higgs inflation [16,17]) to produce a peak in the power spectrum of curvature fluctuations at the solar-mass scale with an amplitude several orders of magnitude larger than at the CMB scale [18]. Large non-Gaussianity might further enhance the probability of gravitational collapse [19,20]. However, such a fine-tuned peak is not required in our scenario because the sound speed drops abruptly by 30% during the QCD transition due to the creation of non-relativistic protons and neutrons from quarks and gluons [21]. This means that the radiation pressure, which usually prevents the collapse of mild inhomogeneities, suddenly drops, lowering the critical curvature needed for PBH formation. Since the probability of collapse is exponentially sensitive to [10], they can form more easily. We need just a billionth of the domains to collapse to PBHs to explain all the DM. As explained later, this condition could be met in our Universe without enhancing the power spectrum of curvature fluctuations or any other parameter fine-tuning.
3. Electroweak Baryogenesis at the QCD Epoch
The gravitational collapse at the QCD epoch of a horizon-sized ball of radiation into a solar-mass black hole would be an extremely violent process, with particles acquiring energies a thousand times their rest mass from the gravitational potential energy released by the collapse. As shown by simulations of PBH formation in spherical symmetry by Musco et al. [22], energy and momentum conservation imply that particles which do not fall into the black hole are driven out as a shock-wave toward the surrounding plasma. This is similar to the shock-wave that ejects the outer layers of a star when it explodes as a supernova, except that the surrounding plasma is much denser in the early Universe context, allowing higher energy interactions. In particular, the effective temperature of the “hot spot" is above that of EW sphaleron transitions, inducing local windings of the Higgs field around the EW vacuum. Through the chiral anomaly, such topological configurations are equivalent to the creation of baryon number [23]. Since the surrounding plasma (initially beyond the Hubble domain that collapsed to form a PBH) is much cooler, the far-from-equilibrium conditions ensure that further sphaleron transitions cannot wash out the local baryon asymmetry.
This means that all of the Sakharov conditions [24] for producing the matter–antimatter asymmetry are met. However, the asymmetry generated can be much larger than in the usual cosmological scenario. This is because the effective CP violation in the standard model (SM) is strongly temperature dependent (), and the amount coming from the CKM matrix [25] is enough for the local baryon-to-photon ratio to exceed one. Subsequently, the impulse of the shock-wave will drive baryons from the hot spot around each PBH to the rest of the Universe, thereby diluting the global baryon-to-photon ratio to the observed value, ∼.
Let us estimate the energy available for the process of hot spot electroweak baryogenesis (HSEWB). Energy conservation implies that the change in kinetic energy due to the collapse of matter within the Hubble radius, , down to the Schwarzschild radius of the PBH, , is
Note that the smaller the value of , the more compact the resulting PBH and the larger the kinetic energy of ejected particles. To estimate the energy acquired per proton in the expanding shell, we note that the number density of protons between the QCD transition and proton freeze-out () is that of a non-relativistic species,
with . Therefore
where is the difference between the Hubble and PBH volumes. We have used as a conservative estimate but note that scales as . At the same time, the density of the relativistic plasma surrounding the collapse horizon is huge, , so it behaves like a wall for the escaping relativistic protons.
One might expect the protons and neutrons to carry much less energy from the collapse than the electrons and positrons since they are much less abundant in thermal equilibrium. However, they acquire significantly more energy per nucleon than a thermal bath could provide because gravitational collapse is a very violent non-equilibrium process. Some of protons acquire enough energy to induce the sphaleron transitions which violate baryon conservation.
For a PBH formed at , the energy released and thus effective temperature is given by
which is well above the sphaleron barrier and thus the sphaleron transition rate per unit volume at this temperature is ∼ [23]. The ultra-relativistic partons (here mainly protons) produce jets that heat up the surrounding plasma and induce a baryon asymmetry [14]
where is the number density of the partons (here protons and antiprotons), ∼ is the duration of the sphaleron process and the standard model CP violation parameter is [23]
The entropy density in the thermalized plasma surrounding each PBH is at temperatures ; this quenches the sphaleron transitions and prevents baryon washout. The production of baryons is thus very efficient for 5, giving or locally. Note, however, that one cannot produce significantly more baryons
than photons since they are soon brought into equilibrium with the rest of the plasma via
standard model interactions. The dynamical process is actually rather complicated [26] and
will require further investigation.
This maximal BAU is then diluted as the protons propagate from the hot spots to the rest of the Universe. If the PBHs provide all the dark matter (), one requires ∼, and the distance between hot spots is then d∼∼3000 km, or 0.01 light-seconds. Moving at the speed of light, protons uniformly distribute the original baryon asymmetry to the rest of the Universe well before big bang nucleosynthesis (∼1–180 s), thus diluting the initial baryon asymmetry and explaining the relation ∼.
It might be argued that the relativistic protons and neutrons would be stopped immediately by electromagnetic interactions with the background electrons and positrons [27], but this assumes they are in thermal equilibrium with the plasma and this does not apply. In particular, the neutrons (which also carry baryon number) interact much more weakly than the protons, because they are neutral and their interactions are sufficiently weak for them to reach the next PBH before interacting. Moreover, the large cross-sections of protons and neutrons with the electron-photon plasma are quenched by the rapid cosmic expansion, so these particles do not lose significant energy before nucleosynthesis.
The DM-to-baryon ratio, ∼5, can also be explained in this scenario: most PBHs are formed during or after the sudden drop of the sound-speed during the QCD transition, when the parton energies are high enough to produce a strong baryon asymmetry. is thus given by the ratio of the black hole mass and the ejected mass, which is if . Lower values of could, nevertheless, be accommodated if the temperature below which protons acquire enough energy to drive the baryon-producing sphaleron transitions is reduced, 100 MeV, so that only the massive PBHs formed at a later time contribute to the BAU. The scenario is represented qualitatively in Figure 1.
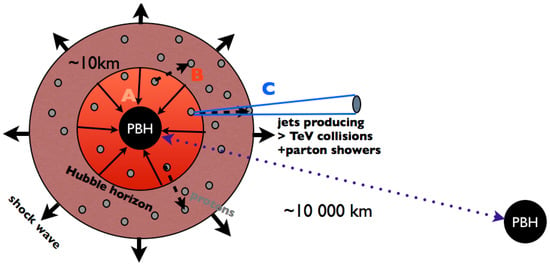
Figure 1.
Qualitative representation of the three steps in our scenario. (A) Gravitational collapse to a PBH of the curvature fluctuation at horizon re-entry. (B) Sphaleron transition in hot spot around the PBH, producing locally through EW baryogenesis. (C) Propagation of baryons to rest of Universe through jets, resulting in the observed BAU with ∼.
4. The Origin of the Large Curvature Fluctuations
The softening of the equation of state during the quark-hadron transition boosts the formation of stellar-mass PBHs but does not alleviate the need for large curvature fluctuations. We stress that the HSEWB scenario does not assume any particular origin for these primordial fluctuations. Nevertheless, inflation is the most studied mechanism, and we give two concrete examples of inflationary models. These are used to compute the PBH mass distribution in Figure 2, and both have a peak at around a solar mass.
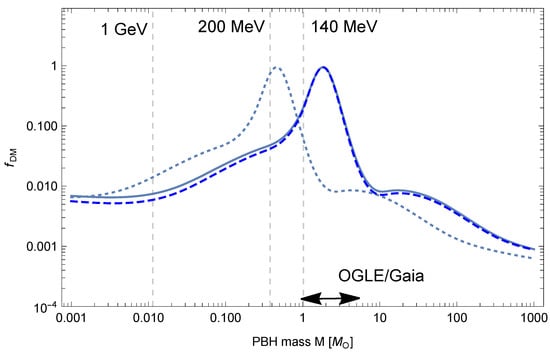
Figure 2.
PBH mass functions, , for different curvaton models and for a collapse efficiency (dotted) and (solid), the integrated PBH abundance corresponding to the dark matter density in all cases. The vertical (grey) lines correspond to the temperature at PBH formation (assuming ). It is comparable to the mass function for a nearly flat spectrum of Gaussian curvature fluctuations with spectral index (dashed blue line). The double arrow indicates the peak in the number of dark lenses from combined OGLE and Gaia microlensing observations [28].
The simplest idea is to invoke a quasi-inflection point during the inflationary phase [16,17], leading on small scales to an enhanced but still nearly scale-invariant power spectrum of curvature fluctuations, with a spectral index close to . However, one still requires some parameter fine-tuning to obtain the correct PBH abundance. In an alternative scenario, one could imagine that before or during the QCD epoch, a light stochastic spectator field [29] induces in rare regions an extra curvature fluctuation above the threshold required for PBH formation.
The spectator field is a curvaton; its quantum fluctuations during inflation permeate all space but its energy density is subdominant during both inflation and the period after reheating. This field remains frozen during the radiation era () until its potential energy density (at the top of its potential) starts to dominate the total density of the Universe. At this point, the spectator field in the still super-horizon regions triggers a second brief period of inflation, generating local non-linear curvature fluctuations which later re-enter the horizon and collapse to form PBHs.
In the rest of the Universe, the field rolls quickly toward the bottom of the potential and its fluctuations do not significantly impact the expansion. This means that the curvature fluctuations remain Gaussian, at the same level as those observed in the CMB, unaffected by the dynamics of the spectator field, and do not form PBHs. There are no isocurvature modes on cosmological scales, because the quantum fluctuations of both the inflaton and spectator fields scale with the Hubble rate during inflation, thereby correlating the large-scale curvature fluctuations with the PBH and baryon fluctuations.
We have envisaged the QCD axion as a natural candidate in this model, but subsequent field oscillations at the bottom of the potential would induce a matter-dominated era if the axion did not rapidly decay into other particles. More general decaying axion-like fields or other light scalar fields could also play this role, possibly even the Brout-Englert-Higgs field if it develops flat regions of the potential at high temperature.
5. The PBH Mass Distribution
This is shown in Figure 2 and is a concrete prediction of our scenario. In the general curvaton case, shown by the lower curves for (dotted lines) and (solid lines), the largest density is associated with the horizon mass when protons become non-relativistic at T∼ and we have seen that this is of order the Chandrasekhar mass (). Then, there is a small plateau associated with the temperature T∼ at which pions become non-relativistic. This also slightly changes the sound-speed and corresponds to M∼, which may explain why LIGO-Virgo finds so many black holes with that mass. At later times, the relativistic degrees of freedom again dominate the expansion of the Universe, so the PBH mass distribution declines quickly at larger masses, evading all of the present constraints [30,31,32,33,34].
The second peak in the distribution might explain the mass, rates and low spins of the black hole mergers detected so far by LIGO-Virgo. This is very different than the distribution expected for stellar black holes, which should exhibit a gap in the range and be suppressed above [35]. It is intriguing that an excess of dark microlensing events in this mass range has recently been reported from OGLE and Gaia observations of the Galactic bulge [28]. In the recent GWTC-3 catalog [4], a series of black hole merger progenitors have masses above , which is in the pair-instability mass gap. In the near future, further LIGO-Virgo observations, upcoming microlensing and supernova lensing surveys and a series of other electromagnetic probes [36] should determine the mass spectrum of coalescing black holes sufficiently well to test our scenario. In particular, LIGO-Virgo might confirm both the “proton" peak and the “pion" plateau at tens of solar masses.
6. Addressing the Fine-Tunings
Our scenario naturally links the PBH abundance to the baryon abundance and the BAU to the PBH collapse fraction (∼). The spectator field mechanism for producing the required curvature fluctuations also avoids the need for a fine-tuned peak in the power spectrum, which has long been considered a major drawback of PBH scenarios. One still needs fine-tuning of the mean field value to produce the observed values of and (i.e., ∼). However, the stochasticity of the field during inflation (if it lasted for more than 60 e-folds) ensures that Hubble volumes exist with all possible field values and this means that one can explain the fine-tuning by invoking a single anthropic selection argument. The argument is discussed in Reference [15] and depends on the fact that only a small fraction of patches will have the PBH and baryon abundance required for galaxies to form. In most others, the field is too far from the slow-roll region to produce either PBHs or baryons. Such patches lead to radiation universes without any DM or matter–antimatter asymmetry. In other (much rarer) patches, PBHs are produced too copiously, leading to rapid accretion of most of the baryons, as might have happened in ultra-faint-dwarf galaxies. This anthropic selection effect may therefore explain the observed value of and . The connection between the rareness of the PBHs, responsible for later matter-domination, and subsequent structure formation is an important feature of our scenario.
7. Conclusions
It is well known that the early Universe can be used as a probe of fundamental physics at very high energies. The production of the BAU through CP-violating processes is one example of this, the usual assumption being that new high-energy physics generates the baryon asymmetry everywhere simultaneously via out-of-equilibrium particle decays or first-order phase transitions. However, in our scenario, the BAU is generated in local hot spots through the violent process of PBH formation at the QCD transition, this being triggered by the sudden drop in the radiation pressure and the presence of large amplitude curvature fluctuations. The only CP violation needed is that of the standard model and the same regions which generate the baryon asymmetry also produce PBHs with a density comparable to that of the baryons.
A full analysis of the non-linear dynamics of gravitational collapse and out-of-equilibrium baryogenesis will require detailed numerical simulations. Future particle physics experiments with ultra-high-density heavy ion collisions in the 100 TeV range [37] may be able to explore the high-energy sphaleron transitions invoked by our proposal. Note that our model does not preclude some baryogenesis occurring at an earlier epoch, providing the associated value of is much less than [38].
Although our model suggests that most of the dark matter (e.g., in galactic halos) comprises PBHs, this does not preclude some fraction of it also being in elementary particles. However, it is unlikely that both candidates have a significant density because the annihilations of the particles accumulated around the PBHs would then produce more -rays than is consistent with observation [39,40]. The PBH mass distribution is expected to be quite broad—extending from subsolar to several hundred solar masses—but it should peak at around a solar mass. This passes the current observational constraints on the PBH abundance, once the large uncertainties on lensing constraints are taken into account. However, accurate predictions of the PBH mass function will require numerical investigations of the stochastic dynamics of the curvaton, both during and after inflation, for different spectator fields. If, over the next few years, LIGO-Virgo-KAGRA interferometers can determine the mass distribution of the coalescing black holes, this will allow a comparison with the predictions of Figure 2 used to derive the results that appear in this letter and can be traced to the longer paper [15].
Author Contributions
Conceptualization, J.G.-B., B.C. and S.C.; methodology, J.G.-B., B.C. and S.C.; investigation, J.G.-B., B.C. and S.C.; writing—original draft preparation, J.G.-B.; writing—review and editing, J.G.-B., B.C. and S.C.; project administration, J.G.-B.; funding acquisition, J.G.-B., B.C. and S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MINECO-FEDER grant number PGC2018-094773-B-C32 and SEV-2016-0597, as well as RESCEU at the University of Tokyo, and by the Belgian Fund for Research F.R.S.-FNRS.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank Misha Shaposhnikov, Chris Byrnes, Karsten Jedamzik, Jane MacGibbon, Ilia Musco and Ester Ruiz Morales for useful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Properties of the Binary Black Hole Merger GW150914. Phys. Rev. Lett. 2016, 116, 241102. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Population Properties of Compact Objects from the Second LIGO-Virgo Gravitational-Wave Transient Catalog. Astrophys. J. Lett. 2021, 913, L7. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Bird, S.; Cholis, I.; Muñoz, J.B.; Ali-Haïmoud, Y.; Kamionkowski, M.; Kovetz, E.D.; Raccanelli, A.; Riess, A.G. Did LIGO Detect Dark Matter? Phys. Rev. Lett. 2016, 116, 201301. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. The clustering of massive Primordial Black Holes as Dark Matter: Measuring their mass distribution with Advanced LIGO. Phys. Dark Univ. 2016, 10, 2. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914. Phys. Rev. Lett. 2016, 117, 061101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carr, B.J.; Kühnel, F.; Sandstat, M. Constraints on primordial black holes from the Galactic gamma-ray background. Phys. Rev. D 2016, 94, 044029. [Google Scholar] [CrossRef] [Green Version]
- García-Bellido, J. Massive Primordial Black Holes as Dark Matter and their detection with Gravitational Waves. J. Phys. Conf. Ser. 2017, 840, 012032. [Google Scholar] [CrossRef]
- Carr, B.J. The primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1. [Google Scholar] [CrossRef]
- Jedamzik, K. Primordial black hole formation during the QCD epoch. Phys. Rev. D 1997, 55, 5871. [Google Scholar] [CrossRef] [Green Version]
- Byrnes, C.T.; Hindmarsh, M.; Young, S.; Hawkins, M.R.S. Primordial black holes with an accurate QCD equation of state. JCAP 2018, 1808, 041. [Google Scholar] [CrossRef] [Green Version]
- Carr, B.; Clesse, S.; García-Bellido, J.; Kühnel, F. Cosmic Conundra Explained by Thermal History and Primordial Black Holes. Phys. Dark Univ. 2021, 31, 100755. [Google Scholar] [CrossRef]
- Asaka, T.; Grigoriev, D.; Kuzmin, V.; Shaposhnikov, M. Late Reheating, Hadronic Jets, and Baryogenesis. Phys. Rev. Lett. 2004, 92, 101303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carr, B.; Clesse, S.; García-Bellido, J. Primordial black holes from the QCD epoch: Linking dark matter, baryogenesis, and anthropic selection. Mon. Not. Roy. Astron. Soc. 2021, 501, 1426. [Google Scholar] [CrossRef]
- García-Bellido, J.; Ruiz Morales, E. Primordial black holes from single field models of inflation. Phys. Dark Univ. 2018, 18, 47. [Google Scholar] [CrossRef] [Green Version]
- Ezquiaga, J.M.; García-Bellido, J.; Ruiz Morales, E. Primordial Black Hole production in Critical Higgs Inflation. Phys. Lett. B 2018, 776, 345. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. Massive primordial black holes from hybrid inflation as dark matter and the seeds of galaxies. Phys. Rev. D 2015, 92, 023524. [Google Scholar] [CrossRef] [Green Version]
- Ezquiaga, J.M.; García-Bellido, J. Quantum diffusion beyond slow-roll: Implications for primordial black-hole production. JCAP 2018, 1808, 018. [Google Scholar] [CrossRef] [Green Version]
- Ezquiaga, J.M.; García-Bellido, J.; Vennin, V. The exponential tail of inflationary fluctuations: Consequences for primordial black holes. JCAP 2020, 2003, 029. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, T.; Buchoff, M.I.; Christ, N.H.; Ding, H.-T.; Gupta, R.; Jung, C.; Karsch, F.; Lin, Z.; Mawhinney, R.; McGlynn, G.; et al. QCD Phase Transition with Chiral Quarks and Physical Quark Masses. Phys. Rev. Lett. 2014, 113, 082001. [Google Scholar] [CrossRef] [PubMed]
- Musco, I.; Miller, J.C. Primordial black hole formation in the early universe: Critical behaviour and self-similarity. Class. Quant. Grav. 2013, 30, 145009. [Google Scholar] [CrossRef] [Green Version]
- Shaposhnikov, M. Baryogenesis. NATO Sci. Ser. C 2000, 555, 397. [Google Scholar]
- Sakharov, A.D. Violation of CP Invariance, C asymmetry, and baryon asymmetry of the universe. JETP Sov. Phys. Lett. 1967, 5, 24. [Google Scholar]
- Yao, W.M.; Amsler, C.D.; Asner, D.M.; Bamett, R.M.; Beringer, J.; Burchat, P.R.; Carone, C.D.; Caso, C.; Dahl, O.I.; D’Ambrosio, G.; et al. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar]
- Kurkela, A.; Moore, G.D. Thermalization and non-equilibrium evolution in heavy-ion collisions. JHEP 2011, 1112, 044. [Google Scholar] [CrossRef] [Green Version]
- Reno, M.H.; Seckel, D. Primordial nucleosynthesis: The effects of injecting hadrons. Phys. Rev. D 1988, 37, 3441. [Google Scholar] [CrossRef]
- Wyrzykowski, L.; Mandel, I. Constraining the masses of microlensing black holes and the mass gap with Gaia DR2. Astron. Astrophys. 2020, 636, A20. [Google Scholar] [CrossRef] [Green Version]
- Hardwick, R.J.; Vennin, V.; Byrnes, C.T.; Torrado, J.; Wands, D. The stochastic spectator. JCAP 2017, 1710, 018. [Google Scholar] [CrossRef] [Green Version]
- Calcino, J.; García-Bellido, J.; Davis, T.M. Updating the MACHO fraction of the Milky Way dark halowith improved mass models. Mon. Not. Roy. Astron. Soc. 2018, 479, 2889. [Google Scholar] [CrossRef] [Green Version]
- García-Bellido, J.; Clesse, S. Constraints from microlensing experiments on clustered primordial black holes. Phys. Dark Univ. 2018, 19, 144. [Google Scholar] [CrossRef] [Green Version]
- Green, A.M. Astrophysical uncertainties on stellar microlensing constraints on multisolar mass primordial black hole dark matter. Phys. Rev. D 2017, 96, 043020. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, M.R.S. The case for primordial black holes as dark matter. Mon. Not. Roy. Astron. Soc. 2011, 415, 2744. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, M.R.S. A new look at microlensing limits on dark matter in the Galactic halo. Astron. Astrophys. 2015, 575, A107. [Google Scholar] [CrossRef] [Green Version]
- Belczynski, K.; Holz, D.E.; Bulik, T.; O’Shaughnessy, R. The first gravitational-wave source from the isolated evolution of two 40–100 Msun stars. Nature 2016, 534, 512. [Google Scholar] [CrossRef] [Green Version]
- Kashlinsky, A.; Ali-Haïmoud, Y.; Clesse, S.; Garcia-Bellido, J.; Wyrzykowski, L.; Achucarro, A.; Amendola, L.; Annis, J.; Arbey, A.; Arendt, R.G.; et al. Electromagnetic probes of primordial black holes as dark matter. Bull. Am. Astron. Soc. 2019, 51, 003. [Google Scholar]
- Ellis, J.; Sakurai, K.; Spannowsky, M. Search for Sphalerons: IceCube vs. LHC. JHEP 2016, 1605, 085. [Google Scholar] [CrossRef] [Green Version]
- Carr, B.J.; Turner, M.S. Does Explaining S Need More than Guts. Comm. Astrophys. 1981, 9, 63. [Google Scholar]
- Lacki, B.C.; Beacom, J.F. Primordial black holes as dark matter: Almost all or almost nothing. Astrophys. J. 2010, 720, L67. [Google Scholar] [CrossRef] [Green Version]
- Carr, B.J.; Kuhnel, F.; Visinelli, L. Black holes and WIMPs: All or nothing or something else. Mon. Not. Roy. Astron. Soc. 2021, 506, 3648. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).