Abstract
Sixty years of study of energetic particle abundances have made a major contribution to our understanding of the physics of solar energetic particles (SEPs) or solar cosmic rays. An early surprise was the observation in small SEP events of huge enhancements in the isotope 3He from resonant wave–particle interactions, and the subsequent observation of accompanying enhancements of heavy ions, later found to increase 1000-fold as a steep power of the mass-to-charge ratio A/Q, right across the elements from H to Pb. These “impulsive” SEP events have been related to magnetic reconnection on open field lines in solar jets; similar processes occur on closed loops in flares, but those SEPs are trapped and dissipate their energy in heat and light. After early controversy, it was established that particles in the large “gradual” SEP events are accelerated at shock waves driven by wide, fast coronal mass ejections (CMEs) that expand broadly. On average, gradual SEP events give us a measure of element abundances in the solar corona, which differ from those in the photosphere as a classic function of the first ionization potential (FIP) of the elements, distinguishing ions and neutrals. Departures from the average in gradual SEPs are also power laws in A/Q, and fits of this dependence can determine Q values and thus estimate source plasma temperatures. Complications arise when shock waves reaccelerate residual ions from the impulsive events, but excess protons and the extent of abundance variations help to resolve these processes. Yet, specific questions about SEP abundances remain.
1. Introduction
Differential rotation of the ionized plasma in the Sun generates the solar magnetic field, and solar activity is driven by energy released in sudden changes and reconnections of that field. This energy release appears in the form of solar flares and jets, and in the detachment of coronal mass ejections (CMEs) that expand into interplanetary space. Solar cosmic rays or solar energetic particles (SEPs), as they are commonly known, can be associated with all of these processes, from the direct reconnection and wave–particle resonances in flares and jets to the shock waves driven by fast CMEs. The largest events contain of a burst of SEPs up to GeV energies lasting several days and spanning nearly 360° in solar longitude. SEPs threaten Mars-bound astronauts with hazardous radiation.
The physical processes that accelerate SEPs are of general astrophysical interest and, at a minimum, they apply to most stars in the universe. While we can see evidence for some of these processes elsewhere, only the Sun also provides us with a direct physical sample of the energetic particles themselves, allowing the observation of their spectra and abundances in addition to the radio, optical, X-ray, and γ-ray photons they emit, thus providing a multi-messenger view of the physics. In recent years, as the study of SEPs has advanced, we have found that the particles themselves carry information on conditions in their coronal source in addition to the physical processes of their acceleration.
The purpose of this article is to acknowledge sixty years of progress in this field, to review the controversies and accomplishments, and to highlight remaining questions.
2. The First SEPs
SEPs were first observed by Scott Forbush [1] in Cheltenham, Maryland using ground-based ion chambers which measured ionization of the cascade of secondary particles produced when GeV protons strike the upper atmosphere. This system measured ionization, proportional to the number of arriving galactic cosmic rays (GCRs), and its decrease when GCRs were screened out by magnetic fields in the structures we now call coronal mass ejections (CMEs). Forbush observed sharp increases in particle intensity from SEPs, accompanied by solar flares, which preceded these “Forbush decreases” in February and March 1942, and again in July 1946. These SEP increases were also seen simultaneously in Greenland and New Zealand. Thus, the study of SEPs began with these ground-level events (GLEs), the largest, most energetic SEP events we see. It would be many years before Kahler et al. [2] began to firmly establish that the SEPs in these large “gradual” or long-duration events were actually accelerated, with a 96% association, at shock waves driven by wide, fast CMEs similar to those that produced the Forbush decreases. The obvious, bright flares that were observed by optical instruments were a consequence of regions of energy containment on closed loops in the huge magnetic reconnections involved.
The first measurement of the abundances of chemical elements in SEP events was made by Fichtel and Guss [3] using nuclear emulsions on a 4 min sounding rocket flight from Ft. Churchill, Manitoba into the SEP event of 3 September 1960. They observed C, N, O, Ne, Mg, Si, and S, beginning a sixty-year effort to compare these SEP abundances with those of the solar photosphere and corona, where element abundance measurements were also slowly improving.
The quality and quantity of measurements improved greatly once Si solid-state telescopes were flown regularly on satellites. A review of these measurements by Meyer [4] and observations by Breneman and Stone [5] established that the relative abundances of elements in these large gradual events consist of two factors: (1) average abundances that differed from solar photospheric abundances as a function of the first ionization potential (FIP) of the elements, and (2) additional element enhancements that depend upon a power law in the mass-to-change ratio, A/Q. For element abundances compared at a single velocity, A/Q represents the effects that depend upon an ion’s magnetic rigidity. This second factor could vary from event to event and even with time during events. A modern version of the “FIP effect” is shown in Figure 1 and represents the abundances in the SEP-determined corona, relative to the two measurements of the solar photosphere. SEP abundances in Figure 1 [6,7,8] provide the reference for all subsequent discussions below of abundance enhancements or suppressions.
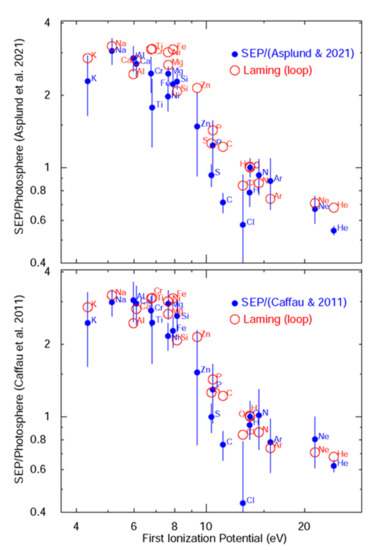
Figure 1.
Average SEP abundances [6,7,8], relative to O, divided by the corresponding solar photospheric abundances [13,14] are plotted vs. FIP (blue filled circles) and compared with theoretical calculations [12] for closed loops (open red circles). Points are labeled by element names.
In the current theory by Laming, the low-FIP (<10 eV) elements which are ionized in the photosphere are subject to ponderomotive force of Alfvén waves, while the neutral high-FIP elements are not [9]. The forces differ for closed magnetic loops, near active regions, where the Alfvén waves can resonate with the loop length. Differences in the FIP pattern between SEPs and the solar wind are seen [10,11], and have been explained theoretically by closed and open field lines [9,12]. The two different photospheric abundance sets depend upon the choice of spectral lines used for the measurement.
3. Electrons
An important source of early information on particles from the Sun was obtained from radio observations. As electrons of 10–100 keV stream out from the Sun along the interplanetary field lines, they excite waves at the local plasma frequency, which decreases as the square root of the local plasma density. Thus, electrons streaming from sources near the Sun produce radio type III bursts, which drift rapidly to a lower frequency as the electrons traverse rapidly decreasing plasma density, while similar electrons at coronal or interplanetary shock waves produce type II bursts, which move out more slowly at the speed of the shock. The classic review by Wild, Smerd, and Weiss [15] initiated the idea of two solar particle sources, associating type III bursts with sources of electrons near the Sun, and type II bursts with shock waves that accelerated primarily protons. Subsequent early observations of electrons in space seemed to confirm this idea [16]. The type III bursts were thought to involve “pure” electron events, without ions, but that was before the measurements of 3He.
4. 3He-Rich Events
Nearly every scientist observing SEPs in the early days had previous experience with GCRs. After acceleration from supernovae, GCRs spend ~107 years in space, where they fragment against interstellar H to produce significant abundances of secondary 2H and 3He ions as well as isotopes of Li, Be, and B. When Hsieh and Simpson [17] measured 3He in the SEPs at a ratio of 3He/4He = (2.1 ± 0.4) × 10−2, the automatic reaction was that SEPs had fragmented during traversal of a small amount of matter.
Then, even higher abundances of 3He began to appear. Serlemitsos and Balasubrahmanyan [18] found a SEP event with 3He/4He = 1.52 ± 0.10 but with 3He/2H > 300. More 3He than 4He but no 2H? This was not fragmentation. Then, there were limits established on Be/O and B/O in SEP events that were found to be <2 × 10−4 [19,20]. This was not fragmentation; this was a completely new resonance phenomenon drastically and selectively enhancing the 3He.
These 3He-rich events would soon be shown to have increased abundances of heavy elements as well, such as a ~10-fold increase in Fe/O [21]. This was soon to be perceived as a power law increase in A/Q [22] and, when measurements of heavy elements became available [23,24,25,26], would rise as the 3.64 ± 0.15 power [26] across the periodic table to become a factor of ~900 increase in (76 ≤ Z ≤ 82)/O, with the Q-values of the elements being determined at a temperature of ~3 MK, where the elements He, C and even O are fully ionized. In the solar corona, the pattern of ionization states determines the temperature, and conversely, the abundances based upon power laws in A/Q require changes in A/Q for relative enhancements.
A sample of 3He-rich events of increasing intensity is shown in Figure 2. 3He equals or exceeds 4He in the first three events, but is smaller (or unmeasurable) in the larger events. 3He is found to be limited, as if all the 3He in the acceleration volume is depleted in large events [27,28]. Except in the smallest event where it is unmeasured, we find that Fe/O ≈ 1, vs. 0.131 ± 0.006 in the reference gradual SEP abundances. When the intensities become large enough, heavy elements begin to appear. See the review by Mason [29] for more information.
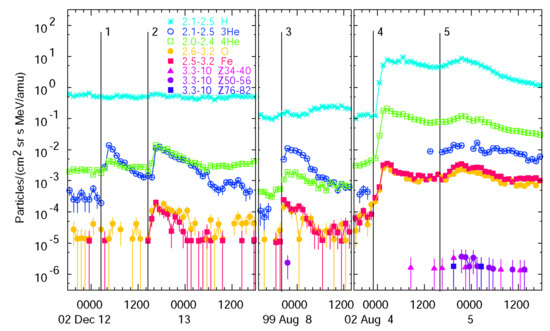
Figure 2.
Element intensities at the indicated MeV amu−1 are shown in a sample of 3He-rich or “impulsive” SEP events of increasing intensity. 3He exceeds 4He in Events 1 and 3. Fe and O are below the background level in Event 1, but Fe/O ≈ 1 in the remaining events. H is below the background level in Events 1–3. 3He/4He < 0.1 in Event 4 and is not plotted because it falls below the possible resolution error; it is ≈ 0.1 in Event 5 and high-Z heavy elements are beginning to appear [24]. Other properties of the last four of these events are listed [26].
As measurements improved, the 3He-rich events were associated with the 10–100 keV electron events [30] that produce the radio type III bursts [31], once thought to be “pure” electron events. Many of the theories to explain 3He enhancements invoked preheating of the ions by selective absorption of various wave modes at the 3He gyrofrequency [8,32,33,34,35,36,37,38,39] and acceleration by an unspecified mechanism. However, Temerin and Roth [40] suggested full acceleration of the 3He by resonant absorption of electromagnetic ion cyclotron (EMIC) waves produced by the observed electron beams, while the ions were mirrored in the magnetic field.
However, all of the resonance theories attempting to explain the sharp increase in 3He failed to explain the smoothly increasing enhancements of heavy elements. These enhancements were explained by simulations that showed the scattering of ions back and forth in the collapsing islands of magnetic reconnection [41], which predicted the power law dependence on A/Q. Similar considerations even apply to electron acceleration [42], but reconnection calculations have not yet explained 3He.
Measurements of the SEP ionization states of the elements up to Fe were possible below ~2 MeV amu−1, and early measurements [43,44] showed average values of QSi = 11.0 ± 0.3 and QFe = 14.1 ± 0.2 for large gradual events to be obtained, suggesting a source temperatures of ≈ 2 MK. 3He-rich events, however, showed QSi ≈ 14 and QFe = 20.5 ± 1.2. Either, this source was very hot, >10 MK, or the ions were stripped after acceleration. Unfortunately, the first interpretation, suggesting a hot flare origin, was generally accepted for many years; then, it was found by DiFabio et al. [45] that the ionization states of Fe increased with ion energy, as would be expected if the ions passed through enough material after acceleration to attain a velocity-dependent equilibrium charge state. This would occur if the ions had been accelerated at a height of ~1.5 solar radii in impulsive events. The amount of material required to strip Fe is too small to cause nuclear fragmentation or energy loss of high-Z ions that would disrupt A/Q power laws.
The result of DiFabio et al. [45] was important, because, otherwise, the highly ionized ions were not compatible with the abundances. If all the elements up to Si were fully ionized, with A/Q = 2, how could Ne, Mg, and Si be enhanced by a factor of ~2.5 relative to C, N, and O, while Fe was enhanced by a factor of ~7 [22]? This pattern was interpreted as suggesting that He, C, N, and O were fully ionized, and Ne, Mg, and Si were in especially stable configurations with two orbital electrons. This pattern occurred in a temperature range of 3–5 MK [22]. It also meant that a best fit to the power-law of abundance enhancements vs. A/Q could be used to determine a likely source temperature. Just try many temperatures and choose the best fit. This was a powerful new idea; abundances could determine a source temperature even after electrons are later stripped off the ions.
5. The Solar-Flare Myth
The small 3He-rich, Fe-rich “impulsive events” were clearly different from the large “proton events” or “gradual” events that lasted for days and spanned nearly 360° in solar longitude [8]. This spread of particles was once explained by the “bird cage” model [46], where particles followed arcades of magnetic loops seen in active regions spreading like the wires of a bird cage, somehow allowing SEPs to hop from structure to structure at the footpoints of the loops and so on across the face of the Sun. Then, Kahler et al. [2] found a 96% correlation between large gradual SEP events and wide, fast CMEs. The shock waves driven by CMEs could easily cross field lines, accelerating particles as they went. Mason, Gloeckler, and Hovestadt [47] said the SEP abundance variations showed none of the magnetic rigidity dependence that a bird cage model required; they supported large-scale shock acceleration. The distribution of abundances of Fe/O showed a bipolar distribution [48]; the Fe-rich branch was 3He-rich, electron-rich, and proton-poor in comparison with the Fe-poor branch. Gradual events were associated with shock waves, while impulsive events were associated first with flares, and much later, with solar jets, as we will see below [49].
By the 1990s, the bird cage model seemed to have lost credence and impulsive and gradual SEP events were often distinguished in the literature, but Gosling’s review article entitled “The Solar Flare Myth” [50,51], describing the ascendance of CMEs, caused widespread controversy. For example, it was found to “wage an assault on the last 30 years of solar-flare research” [52]. If flares did not accelerate astronaut-threatening radiation, perhaps flare research would not even be funded! In a subsequent discussion, commissioned by Eos, Hudson [53] argued that the term “flare” should be broadened to include CMEs and related shocks and SEPs; Miller [54] argued that, since flares were more numerous, they were better subjects for acceleration studies; and Reames [55,56] argued that all SEP sources were interesting, but for SEPs, it was very important to know the spatial extent of a source. Subsequently, the importance of CME-driven shock waves received wider recognition.
Nevertheless, the distinction of sources using abundances was not complete. Shock waves in gradual SEP events were quite able to reaccelerate residual suprathermal ions left over from previous impulsive SEP events [57], sometimes even preferentially, as when the fast pre-accelerated impulsive ions were better able to overtake the shock from downstream, e.g., when the magnetic field was quasi-perpendicular to the shock normal [58,59,60]. It became necessary to discuss the seed population of ions available for shock acceleration, residual impulsive suprathermal ions in addition to ambient coronal plasma. In addition, pools of impulsive suprathermal ions seemed to collect quite often from many small impulsive events that were much more numerous than the larger events we could resolve [61,62,63,64,65,66].
6. Jets
Thus, it once seemed possible to distinguish impulsive and gradual SEP events by abundances. An event with enhanced 3He and Fe was impulsive, was it not? However, as we have just seen, it is not so simple, since shocks can accelerate residual suprathermal ions, sometimes preferentially.
In the next shock to simplicity, we found that impulsive events can also have associated CMEs, even fast CMEs that drive shocks [67]. These seemed to be narrow CMEs associated with solar jets. Separately, the non-relativistic electron events that produce type III radio bursts had also been associated with solar jets [68]. Electrons and type III bursts had long been associated with impulsive SEP events [30,31]. Jets involve magnetic reconnection on open field lines, so the SEPs easily escape without significant heating. In contrast, flares actually require the plasma and SEPs to be trapped on closed loops where they produce the heating and X-ray Bremstrahlung that drive the sudden burst of photons where only neutrals can escape. Measurements of γ-ray lines in large flares [69] have shown that the accelerated “beam” is both 3He-rich [70,71] and Fe-rich [72], similarly to impulsive SEPs in space.
SEP events can now be traced to their sources [26,73,74,75] and impulsive SEP events are routinely associated with individual solar jets [76,77,78]. See the review by Bučík [79] for more information. Impulsive SEP source regions often have characteristics of both flares and jets when the reconnection involves both open and closed field regions, as jet models predict. In these cases, the open regions can be ~2.5 MK and emit in the EUV, while the nearby closing field regions trap SEPs, heating to >10 MK and emitting X-rays. As event size increases, both SEPs and X-rays increase, but they involve different spatial regions in the source.
The CMEs from jets that are fast enough to drive shock waves can reaccelerate the SEPs produced in the reconnection event, essentially maintaining much of the increase in heavy-ion abundance with A/Q that is in the impulsive component, but these shock waves can also sample the ambient coronal plasma. It turns out that the largest impulsive events, usually with fast CMEs, have an extra component of protons, a “proton excess”, as seen in the comparative samples in Figure 3.
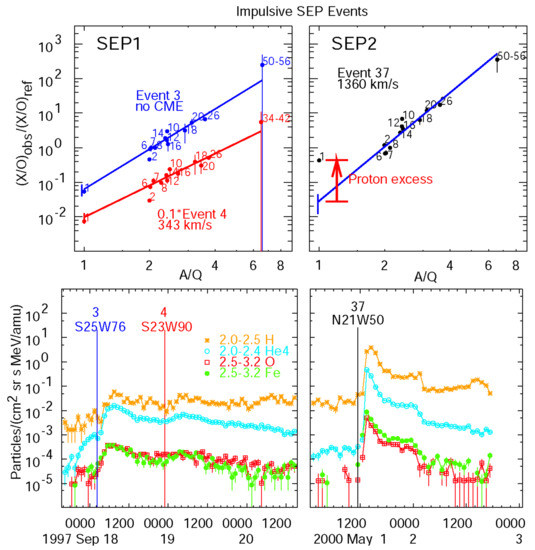
Figure 3.
The lower panels show time histories of H, 4He, O and Fe, at the indicated MeV amu−1, for three impulsive SEP events, two small SEP1 events on the left and a larger SEP2 event on the right. Event numbers shown above source coordinates refer to the event list [26]. Power-law fits to the abundance enhancements, noted by Z, in each event, are shown in the upper panels and CME speeds are listed when CMEs are seen. The right-hand Event 37 is an SEP2 class event because of its large proton excess noted. For the SEP1 events on the left, the protons abundances lie on the extrapolated power-law fits [82,83].
Here, the power law fits of the event-averaged enhancements in abundance, relative to the SEP reference abundances (Figure 1), are fit vs. A/Q of the elements 6 ≤ Z ≤ 56. For each event, fits are obtained using Q values at several temperatures, and the temperature providing the best fit is selected, although it has been shown that most impulsive events have a limited range of T ≈ 2.5–3.2 MK [80,81]. When this best-fit line is extended down to protons at A/Q = 1, the fit at H is good in many small events; Reames [82] labeled these SEP1 events. Other, larger events show a large proton excess and are distinguished as SEP2 events. Samples of each are shown in Figure 3 with the associated CME speeds listed, if any.
For a large sample of impulsive SEP events, Figure 4a shows how the distribution of event size and CME speed depends upon the measured proton excess. Figure 4b shows a probable explanation; when a fast shock wave is present, protons from the ambient coronal plasma may dominate, while heavy ions are dominated by SEP1 ions pre-accelerated and pre-enhanced at the magnetic-reconnection site, i.e., a complex seed population.
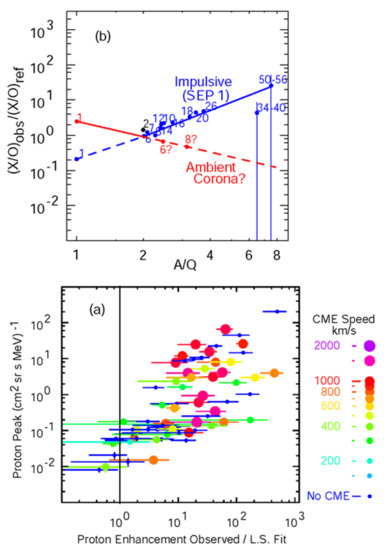
Figure 4.
Panel (a) shows the peak proton intensity at 2–2.5 MeV vs. the proton excess relative to the Z > 2 power-law fit for 90 impulsive SEP events with the symbol size and color determined by CME speed as shown. Panel (b) suggests two possible contributions, impulsive SEP1 seed particles (blue) and ambient coronal seed particles (red), to the plot of enhancement vs. A/Q for the shock-enhanced SEP2 impulsive events [82,83].
Recently, Bučík et al. [78] found source temperatures of 2–2.5 MK, using the differential emission measure technique on the extreme ultraviolet (EUV) images of coronal source regions of 24 solar jets associated with 3He-rich events. This agrees quite well with the dominant 2.5 and 3.2 MK source temperatures found from impulsive SEP abundances by Reames et al. [80,84], and tends to confirm the use of best-fit power laws of abundance enhancements vs. A/Q to estimate source temperatures.
7. Gradual SEP Events
Shock acceleration in gradual SEP events has received considerable attention historically [85,86,87,88,89,90,91,92], and many reviews are available [8,27,93,94,95]. Many advances in our understanding come from features other than element abundances, including the spatial distributions of protons [96,97,98,99,100], the correlations of SEP and CME properties [101,102], onset timing [103,104,105,106], electron/proton ratios [107,108] or GLE events and spectral breaks [109,110,111]. Gradual events have also provided a basis for studies of the coronal FIP effect described above.
Departures from the coronal abundances behave as power laws in A/Q in gradual SEP events, as was found in 1985 by Breneman and Stone [5]. In some events, pitch-angle scattering of particles during transport can change the powers to enhance heavy elements early in events and suppress them later. For example, if Fe scatters less than O, Fe/O may be enhanced early in an event, as Fe preferentially arrives early, but will be depressed later as more O arrives while Fe has been depleted. Solar rotation can spread this temporal behavior into a longitude dependence. Figure 5 shows an analysis of the gradual SEP event of 23 January 2012 [112].
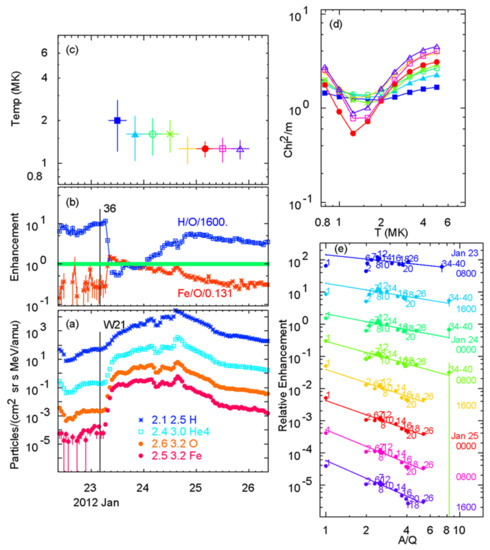
Figure 5.
(a) Intensities of H, He, O, and Fe vs. time. (b) Normalized abundance enhancements H/O and Fe/O vs. time. (c) Best-fit temperatures vs. time for the 23 January 2012 SEP event. (d) χ2/m vs. T for each 8 h interval. (e) Enhancements, labeled by Z, v vs. A/Q for each 8 h interval shifted ×0.1, with best-fit power law for elements with Z ≥ 6 extrapolated down to H at A/Q = 1. Colors correspond for the eight intervals in (c–e) and symbols in (c,d); times are also listed in (e). Event onset is flagged with solar longitude in (a) and the event number from the list of 45 events [113] in (b) [112].
Figure 5a shows the general time behavior of the event, while Figure 5b shows the variation of normalized Fe/O and H/O ratios. Figure 5c identifies the analyzed time intervals and shows the resulting best-fit temperatures for each. Figure 5d shows how the quality of the least-squares fit to enhancement vs. A/Q varies with temperature for each time interval. The temperatures in Figure 5c are chosen at the minima in Figure 5d. The best-fit power laws for each time interval are shown in Figure 5e, passing through element enhancements, labeled by Z.
For the first few intervals in Figure 5e, the A/Q dependences are very flat, so the assigned values of A/Q for each ion make little difference, and hence the curves in Figure 5d are very shallow and the temperatures are poorly determined and have large errors. Later on, the slopes steepen. When the power law dependences are steeper (either positive or negative), the A/Q-values matter, and temperatures are better determined. However, temperatures usually remain consistent during gradual events, even though the slopes of the power law fits often vary. Note in Figure 5e that the protons fit reasonably well on each of the fit lines determined from the elements with 6 ≤ Z ≤ 56.
Reames [113] found that in a list of 45 gradual SEP events, 69% had 0.8 ≤ T ≤ 1.6 MK and no significant proton excess, while 24% had 2 ≤ T ≤ 4 MK with enhancements rising with A/Q, similarly to impulsive events, and also had substantial proton excesses. For these latter events, called SEP3 events [82], impulsive suprathermal seed ions, with enhancements rising with A/Q, dominated the enhancements for Z > 2, while protons from the ambient coronal plasma dominated H. In these events, shocks of moderate strength apparently traversed pools of impulsive suprathermal ions. Overall, 69% of the SEP4 events were accelerated by strong shocks traversing ambient coronal plasma and any impulsive suprathermals present might be included, but were overwhelmed.
The impulsive SEP2 events and the gradual SEP3 events seem similar in temperature range and proton excess. How can we distinguish them? The SEP2 events involve a single jet source with a fast CME-driven shock where there are local abundance variations, e.g., from the local plasma conditions, that are found to have ~30% variations from event to event. In the SEP3 events, the fast shock waves traverse the accumulated pools of impulsive suprathermal ions where the abundances are averaged over many jets and variations are seen to be more like ~10%. If these pools average over N jets, we might expect the variations be reduced by a factor of √N, so we estimate N ~10. As stated previously, there is considerable observational evidence that 3He-rich, Fe-rich pools of suprathermal ions are common [61,62,63,64,65,66], suggesting that there are many small jets (nanojets?) occurring with high frequency, producing small SEP1 events that we are unable to resolve individually. Figure 6 compares the spread in normalized abundance ratios O/C vs. C/4He for these two sources that are relatively hot, where He, C, and O are most likely to be fully ionized. Impulsive events with large statistical errors have been omitted; the large spread of the remaining events is not due to their statistical errors.
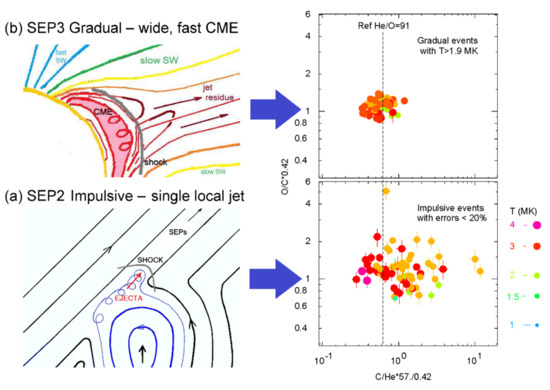
Figure 6.
(a) Cartoon on the left shows SEP2 acceleration from magnetic reconnection in one of the individual jets leading to non-statistical spread in local abundances in O/C vs. C/He at T > 2 MK for various events on the right. (b) Cartoon on the left shows a shock traversing a pool of multi-jet residue producing an SEP3 event with T >2 MK with average abundances of O/C vs. C/He in each event as shown on the right (82, 8). The spread in abundance is reduced by pre-event averaging in multi-jet pools of SEP1 seed particles.
Abundance patterns in SEP events can be affected by seed populations, by acceleration, and by scattering during transport [114]. For impulsive events, it has been found [115] that transport is nearly scatter free, i.e., the scattering mean free path is >1 AU, in most events. In impulsive and small gradual events [114], the ions stream outward, as focusing on the divergent magnetic field overcomes scattering. In gradual events of moderate size, abundances tend to retain the character of the source, or of the seed population in SEP3 events, only weakly modified by transport, e.g., minimal changes of power-law slope with time [114]. However, in large SEP events, wave amplification by the streaming protons [116] becomes a significant factor. As proton intensities increase, wave growth increases until the scattering reduces the streaming to produce equilibrium at the “streaming limit” that modifies abundances, limits intensities, and flattens spectra early in large SEP4 events [117,118,119,120,121,122,123,124,125]. These events can causes dramatic changes in the power law slope, with time or spurious variations in the proton excess [114,125]. Since scattering depends upon past and present proton intensities, it can become a strong function of space, time, and particle rigidity [120,121,122]. The wave number of the resonant waves k ≈ B/μP, where B is the field strength, P is the particle rigidity and μ is its pitch-angle cosine [119,120,121]. Other particle species or energies resonate with waves generated by protons at the same k.
For the SEP3 events, the power law of abundances is determined by the seed population and the energy spectral indices by the shock wave, so these parameters are unrelated. However, for the SEP4 events, the shock determines both the abundances and the spectra, and they are roughly related [114,125]. If the power law of abundance enhancements is (A/Q)x and the ion spectrum is Ey, then we find that y = x/2 − 2. The derivation of this numerical relationship is not clear. However, it specifies how shocks select ions of different A/Q from the coronal plasma and relates to the “injection problem” of shock acceleration [126].
Energy spectral breaks [111] are an important feature of large gradual SEP events that also depend strongly upon A/Q [59,60,127,128,129] and provide a different way to study abundances.
8. Conclusions and Questions
The study of particle abundance in SEP events began sixty years ago and has expanded to a complete field of study in its own right. Progress in this field must speak for itself. Perhaps the most significant conclusions relate to the nature of the sources. We now understand the importance of CME-driven shock waves for acceleration in the large SEP events, and we have recently begun to associate the impulsive SEP events with magnetic reconnection on open field lines in solar jets. Solar flares also involve magnetic reconnection, but closed field lines prevent them from making any significant contribution to the SEPs we see in space. We are beginning to untangle the complexity of the seed population in shock acceleration, and we hope that added measurements by new spacecraft nearer to the Sun will better distinguish the effects of acceleration and transport.
Along with the progress, however, new questions have arisen:
- Some variations in the abundance of He are not understood. SEP3 events have an average source He/O ≈ 91 (e.g., Figure 6), while SEP4 events tend to have He/O ≈ 55 [130]. This is usually attributed to the uniquely high FIP of He (24.6 eV), which can make He slow to ionize and enter the corona. Perhaps, but where is this low-He plasma located that is sampled for SEP4 events?
- About ~6% of impulsive SEP events are He-poor, where 4He/O is suppressed a factor of ~10 from the power-law fit line, even when H lies on that fit line [131]. Why?
- The overall C abundance, i.e., C/O = 0.420 ± 0.010, in SEPs is uniquely far below the theoretical value, as shown in Figure 1, and far below the latest photospheric value of C/O = 0.589 ± 0.054 [14]. Event-to-event variations are small. The photospheric value was C/O = 0.479 ± 0.055 in 1996 [132], but has been rising ever since, while the SEPs have changed little. What is wrong with carbon? Is C/O suppressed in SEPs (see Figure 1) or is the photospheric C/O too high? The FIP of C is not extreme, as with He.
- Impulsive SEPs show enhancements of 3He and of heavy elements, each large and each with its own mechanism. How and where do these mechanisms fit together in a jet, and how do they merge with jet models that do not yet consider SEP acceleration at all?
- What is the origin of the relationship between power law element abundances and energy spectral indices in SEP4 shock events? Present SEP models treat source abundances as adjustable parameters, unrelated to the SEP reference abundances.
Funding
No institutional funding was provided for this work.
Conflicts of Interest
The author declares that this research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Forbush, S.E. Three unusual cosmic ray increases possibly due to charged particles from the Sun. Phys. Rev. 1946, 70, 771. [Google Scholar] [CrossRef]
- Kahler, S.W.; Sheeley, N.R., Jr.; Howard, R.A.; Koomen, M.J.; Michels, D.J.; McGuire, R.E.; von Rosenvinge, T.T.; Reames, D.V. Associations between coronal mass ejections and solar energetic proton events. J. Geophys. Res. 1984, 89, 9683. [Google Scholar] [CrossRef]
- Fichtel, C.E.; Guss, D.E. Heavy nuclei in solar cosmic rays. Phys. Rev. Lett. 1961, 6, 495. [Google Scholar] [CrossRef]
- Meyer, J.P. The baseline composition of solar energetic particles. Astrophys. J. 1985, 57, 151. [Google Scholar] [CrossRef]
- Breneman, H.H.; Stone, E.C. Solar coronal and photospheric abundances from solar energetic particle measurements. Astrophys. J. Lett. 1985, 299, L57. [Google Scholar] [CrossRef]
- Reames, D.V. Coronal Abundances determined from energetic particles. Adv. Space Res. 1995, 15, 41. [Google Scholar] [CrossRef]
- Reames, D.V. Element abundances in solar energetic particles and the solar corona. Solar Phys. 2014, 289, 977. [Google Scholar] [CrossRef]
- Reames, D.V. Solar Energetic Particles, 2nd ed.; Open access; Springer Nature: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Laming, J.M. The FIP and inverse FIP effects in solar and stellar coronae. Living Rev. Sol. Phys. 2015, 12, 2. [Google Scholar] [CrossRef]
- Mewaldt, R.A.; Cohen, C.M.S.; Leske, R.A.; Christian, E.R.; Cummings, A.C.; Stone, E.C.; von Rosenvinge, T.T.; Wiedenbeck, M.E. Fractionation of solar energetic particles and solar wind according to first ionization potential. Advan. Space Res. 2002, 30, 79. [Google Scholar] [CrossRef]
- Reames, D.V. The "FIP effect" and the origins of solar energetic particles and of the solar wind. Solar Phys. 2018, 293, 47. [Google Scholar] [CrossRef]
- Laming, J.M.; Vourlidas, A.; Korendyke, C. Element abundances: A new diagnostic for the solar wind. Astrophys. J. 2019, 879, 124. [Google Scholar] [CrossRef]
- Caffau, E.; Ludwig, H.-G.; Steffen, M.; Freytag, B.; Bonofacio, P. Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Solar Phys. 2011, 268, 255. [Google Scholar] [CrossRef]
- Asplund, M.; Amarsi, A.M.; Grevesse, N. The chemical make-up of the Sun: A 2020 vision, Astron. arXiv 2021, arXiv:2105.01661. (in press)
- Wild, J.P.; Smerd, S.F.; Weiss, A.A. Solar Bursts. Annu. Rev. Astron. Astrophys. 1963, 1, 291. [Google Scholar] [CrossRef]
- Lin, R.P. The emission and propagation of 40 keV solar flare electrons. I: The relationship of 40 keV electron to energetic proton and relativistic electron emission by the sun. Sol. Phys. 1970, 12, 266. [Google Scholar] [CrossRef]
- Hsieh, K.C.; Simpson, J.A. Galactic 3He above 10 MeV per nucleon and the solar contributions of hydrogen and helium. Astrophys. J. Lett. 1970, 162, L197. [Google Scholar] [CrossRef]
- Serlemitsos, A.T.; Balasubrahmanyan, V.K. Solar particle events with anomalously large relative abundance of 3He. Astrophys. J. 1975, 198, 195. [Google Scholar] [CrossRef]
- McGuire, R.E.; von Rosenvinge, T.T.; McDonald, F.B. A survey of solar cosmic ray composition. Int. Cosm. Ray Conf. Tokyo 1979, 5, 61. [Google Scholar]
- Cook, W.R.; Stone, E.C.; Vogt, R.E. Elemental composition of solar energetic particles. Astrophys. J. 1984, 279, 827. [Google Scholar] [CrossRef]
- Mason, G.M.; Reames, D.V.; Klecker, B.; Hovestadt, D.; von Rosenvinge, T.T. The heavy-ion compositional signature in He-3-rich solar particle events. Astrophys. J. 1986, 303, 849. [Google Scholar] [CrossRef]
- Reames, D.V.; Meyer, J.P.; von Rosenvinge, T.T. Energetic-particle abundances in impulsive solar flare events. Astrophys. J. Suppl. 1994, 90, 649. [Google Scholar] [CrossRef]
- Reames, D.V. Abundances of trans-iron elements in solar energetic particle events. Astrophys. J. Lett. 2000, 540, L111. [Google Scholar] [CrossRef]
- Reames, D.V.; Ng, C.K. Heavy-element abundances in solar energetic particle events. Astrophys. J. 2004, 610, 510. [Google Scholar] [CrossRef]
- Mason, G.M.; Mazur, J.E.; Dwyer, J.R.; Jokippi, J.R.; Gold, R.E.; Krimigis, S.M. Abundances of heavy and ultraheavy ions in 3He-rich solar flares. Astrophys. J. 2004, 606, 555. [Google Scholar] [CrossRef]
- Reames, D.V.; Cliver, E.W.; Kahler, S.W. Abundance enhancements in impulsive solar energetic-particle events with associated coronal mass ejections. Solar Phys. 2014, 289, 3817. [Google Scholar] [CrossRef]
- Reames, D.V. Particle acceleration at the Sun and in the heliosphere. Space Sci. Rev. 1999, 90, 413. [Google Scholar] [CrossRef]
- Ho, G.C.; Roelof, E.C.; Mason, G.M. The upper limit on 3He fluence in solar energetic particle events. Atrophys. J. Lett. 2005, 621, L141. [Google Scholar] [CrossRef]
- Mason, G.M. 3He-rich solar energetic particle events. Space Sci. Rev. 2007, 130, 231. [Google Scholar] [CrossRef]
- Reames, D.V.; von Rosenvinge, T.T.; Lin, R.P. Solar 3He-rich events and nonrelativistic electron events—A new association. Astrophys. J. 1985, 292, 716. [Google Scholar] [CrossRef]
- Reames, D.V.; Stone, R.G. The identification of solar 3He-rich events and the study of particle acceleration at the sun. Astrophys. J. 1986, 308, 902. [Google Scholar] [CrossRef]
- Ibragimov, I.A.; Kocharov, G.E. Possible mechanism for enrichment of solar cosmic rays by helium-three and heavy nuclei. Int. Conf. Cosm. Rays 1977, 11, 340. [Google Scholar]
- Kocharov, G.E.; Kocharov, L.G. Present state of experimental and theoretical investigations of solar events enriched by helium-3. Cosmophysics 1978, 37, 37–72. [Google Scholar]
- Kocharov, G.E.; Kocharov, L.G. 3He-rich solar flares. Space Science Rev. 1984, 38, 89. [Google Scholar] [CrossRef]
- Weatherall, J. Turbulent heating in solar cosmic-ray theory. Astrophys. J. 1984, 281, 468. [Google Scholar] [CrossRef]
- Fisk, L.A. 3He-rich flares—A possible explanation. Astrophys. J. 1978, 224, 1048. [Google Scholar] [CrossRef]
- Varvoglis, H.; Papadopoulis, K. Selective nonresonant acceleration of He-3(2+) and heavy ions by H(+) cyclotron waves. Astrophys. J. Lett. 1983, 270, L95. [Google Scholar] [CrossRef]
- Winglee, R.M. Heating and acceleration of heavy ions during solar flares. Astrophys. J. 1989, 343, 511. [Google Scholar] [CrossRef]
- Riyopoulos, S. Subthreshold stochastic diffusion with application to selective acceleration of 3He in solar flares. Astrophys. J. 1991, 381, 578. [Google Scholar] [CrossRef]
- Temerin, M.; Roth, I. The production of 3He and heavy ion enrichment in 3He-rich flares by electromagnetic hydrogen cyclotron waves. Astrophys. J. Lett. 1992, 391, L105. [Google Scholar] [CrossRef]
- Drake, J.F.; Cassak, P.A.; Shay, M.A.; Swisdak, M.; Quataert, E. A magnetic reconnection mechanism for ion acceleration and abundance enhancements in impulsive flares. Astrophys. J. Lett. 2009, 700, L16. [Google Scholar] [CrossRef]
- Arnold, H.; Drake, J.; Swisdak, M.; Guo, F.; Dahlin, J.; Chen, B.; Fleishman, G.; Glesener, L.; Kontar, E.; Phan, T.; et al. Electron acceleration during macroscale magnetic reconnection. arXiv 2011, arXiv:2011.01147. [Google Scholar]
- Luhn, A.; Klecker, B.; Hovestadt, D.; Gloeckler, G.; Ipavich, F.M.; Scholer, M.; Fan, C.Y.; Fisk, L.A. Ionic charge states of N, Ne, Mg, Si and S in solar energetic particle events. Adv. Space Res. 1984, 4, 161. [Google Scholar] [CrossRef]
- Luhn, A.; Klecker, B.; Hovestadt, D.; Möbius, E. The mean ionic charge of silicon in He-3-rich solar flares. Astrophys. J. 1987, 317, 951. [Google Scholar] [CrossRef]
- DiFabio, R.; Guo, Z.; Möbius, E.; Klecker, B.; Kucharek, H.; Mason, G.M.; Popecki, M. Energy-dependent charge states and their connection with ion abundances in impulsive solar energetic particle events. Astrophys. J. 2008, 687, 623. [Google Scholar] [CrossRef]
- Newkirk, G., Jr.; Wenzel, D.G. Rigidity-independent propagation of cosmic rays in the solar corona. J. Geophys. Res. 1978, 83, 2009. [Google Scholar] [CrossRef]
- Mason, G.M.; Gloeckler, G.; Hovestadt, D. Temporal variations of nucleonic abundances in solar flare energetic particle events. II—Evidence for large-scale shock acceleration. Astrophys. J. 1984, 280, 902. [Google Scholar] [CrossRef]
- Reames, D.V. Bimodal abundances in the energetic particles of solar and interplanetary origin. Astrophys. J. Lett. 1988, 330, L71. [Google Scholar] [CrossRef]
- Reames, D.V. Magnetic topology of impulsive and gradual solar energetic particle events. Astrophys. J. Lett. 2002, 571, L63. [Google Scholar] [CrossRef]
- Gosling, J.T. The solar flare myth. J. Geophys. Res. 1993, 98, 18937. [Google Scholar] [CrossRef]
- Gosling, J.T. Corrections to “The solar flare myth”. J. Geophys. Res. 1994, 99, 4259. [Google Scholar] [CrossRef]
- Zirin, H. Solar storminess, Sky and Telescope. 9 November 1994. [Google Scholar]
- Hudson, H.S. Solar flares: No “myth”. Eos Trans. 1995, AGU 76, 405. [Google Scholar] [CrossRef]
- Miller, J.A. Much ado about nothing. Eos Trans. 1995, AGU 76, 401. [Google Scholar] [CrossRef]
- Reames, D.V. The dark side of the solar flare myth. Eos Trans. 1995, AGU 76, 401. [Google Scholar] [CrossRef]
- Reames, D.V. Solar energetic particles: A paradigm shift. Revs. Geophys. Suppl. 1995, 33, 585. [Google Scholar] [CrossRef]
- Mason, G.M.; Mazur, J.E.; Dwyer, J.R. 3He enhancements in large solar energetic particle events. Astrophys. J. Lett. 1999, 525, L133. [Google Scholar] [CrossRef] [PubMed]
- Tylka, A.J.; Cohen, C.M.S.; Dietrich, W.F.; Maclennan, C.G.; McGuire, R.E.; Ng, C.K.; Reames, D.V. Evidence for remnant flare suprathermals in the source population of solar energetic particles in the 2000 bastille day event. Astrophys. J. Lett. 2001, 558, L59. [Google Scholar] [CrossRef][Green Version]
- Tylka, A.J.; Cohen, C.M.S.; Dietrich, W.F.; Lee, M.A.; Maclennan, C.G.; Mewaldt, R.A.; Ng, C.K.; Reames, D.V. Shock geometry, seed populations, and the origin of variable elemental composition at high energies in large gradual solar particle events. Astrophys. J. 2005, 625, 474. [Google Scholar] [CrossRef]
- Tylka, A.J.; Lee, M.A. Spectral and compositional characteristics of gradual and impulsive solar energetic particle events. Astrophys. J. 2006, 646, 1319. [Google Scholar] [CrossRef]
- Richardson, I.G.; Reames, D.V.; Wenzel, K.P.; Rodriguez-Pacheco, J. Quiet-time properties of <10 MeV/n interplanetary ions during solar maximum and minimum. Astrophys. J. Lett. 1990, 363, L9. [Google Scholar] [CrossRef]
- Desai, M.I.; Mason, G.M.; Dwyer, J.R.; Mazur, J.E.; Gold, R.E.; Krimigis, S.M.; Smith, C.W.; Skoug, R.M. Evidence for a suprathermal seed population of heavy ions accelerated by interplanetary shocks near 1 AU. Astrophys. J. 2003, 588, 1149. [Google Scholar] [CrossRef]
- Wiedenbeck, M.E.; Cohen, C.M.S.; Cummings, A.C.; de Nolfo, G.A.; Leske, R.A.; Mewaldt, R.A.; Stone, E.C.; von Rosenvinge, T.T. Persistent energetic 3He in the inner heliosphere. Int. Cosm. Ray Conf. 2008, 1, 91. [Google Scholar]
- Bučík, R.; Innes, D.E.; Mall, U.; Korth, A.; Mason, G.M.; Gómez-Herrero, R. Multi-spacecraft observations of recurrent 3He-rich solar energetic particles. Astrophys. J. 2014, 786, 71. [Google Scholar] [CrossRef]
- Bučík, R.; Innes, D.E.; Chen, N.H.; Mason, G.M.; Gómez-Herrero, R.; Wiedenbeck, M.E. Long-lived energetic particle source regions on the Sun. J. Phys. Conf. Ser. 2015, 642, 012002. [Google Scholar] [CrossRef]
- Chen, N.H.; Bučík, R.; Innes, D.E.; Mason, G.M. Case studies of multi-day 3He-rich solar energetic particle periods. Astron. Astrophys. 2015, 580, 16. [Google Scholar] [CrossRef][Green Version]
- Kahler, S.W.; Reames, D.V.; Sheeley, N.R., Jr. Coronal mass ejections associated with impulsive solar energetic particle events. Astrophys. J. 2001, 562, 558. [Google Scholar] [CrossRef]
- Shimojo, M.; Shibata, K. Physical parameters of solar X-ray jets. Astrophys. J. 2000, 542, 1100. [Google Scholar] [CrossRef]
- Ramaty, R.; Murphy, R.J. Nuclear processes and accelerated particles in solar flares. Space Sci. Rev. 1987, 45, 213. [Google Scholar] [CrossRef]
- Mandzhavidze, N.; Ramaty, R.; Kozlovsky, B. Determination of the abundances of subcoronal 4He and of solar flare-accelerated 3He and 4He from gamma-ray spectroscopy. Astrophys. J. 1999, 518, 918. [Google Scholar] [CrossRef]
- Murphy, R.J.; Kozlovsky, B.; Share, G.H. Evidence for enhanced 3He in flare-accelerated particles based on new calculations of the gamma-ray line spectrum. Astrophys. J. 2016, 833, 166. [Google Scholar] [CrossRef]
- Murphy, R.J.; Ramaty, R.; Kozlovsky, B.; Reames, D.V. Solar abundances from gamma-ray spectroscopy: Comparisons with energetic particle, photospheric, and coronal abundances. Astrophys. J. 1991, 371, 793. [Google Scholar] [CrossRef]
- Nitta, N.V.; Reames, D.V.; DeRosa, M.L.; Yashiro, S.; Gopalswamy, N. Solar sources of impulsive solar energetic particle events and their magnetic field connection to the earth. Astrophys. J. 2006, 650, 438. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Pick, M.; Mason, G.M. Coronal holes, jets, and the origin of 3He-rich particle events. Astrophys. J. 2006, 639, 495. [Google Scholar] [CrossRef]
- Ko, Y.-K.; Tylka, A.J.; Ng, C.K.; Wang, Y.-M.; Dietrich, W.F. Source regions of the interplanetary magnetic field and variability in heavy-ion elemental composition in gradual solar energetic particle events. Astrophys. J. 2013, 776, 92. [Google Scholar] [CrossRef][Green Version]
- Bučík, R.; Innes, D.E.; Mason, G.M.; Wiedenbeck, M.E.; Gómez-Herrero, R.; Nitta, N.V. 3He-rich solar energetic particles in helical jets on the Sun. Astrophys. J. 2018, 852, 76. [Google Scholar] [CrossRef]
- Bučík, R.; Wiedenbeck, M.E.; Mason, G.M.; Gómez-Herrero, R.; Nitta, N.V.; Wang, L. 3He-rich solar energetic particles from sunspot jets. Astrophys. J. Lett. 2018, 869, L21. [Google Scholar] [CrossRef]
- Bučík, R.; Mulay, S.M.; Mason, G.M.; Nitta, N.V.; Desai, M.I.; Dayeh, M.A. Temperature in solar sources of 3He-rich solar energetic particles and relation to ion abundances. Astrophys. J. 2021, 908, 243. [Google Scholar] [CrossRef]
- Bučík, R. 3He-rich solar energetic particles: Solar sources. Space Sci. Rev. 2020, 216, 24. [Google Scholar] [CrossRef]
- Reames, D.V.; Cliver, E.W.; Kahler, S.W. Variations in abundance enhancements in impulsive solar energetic-particle events and related CMEs and flares. Solar Phys. 2014, 289, 4675. [Google Scholar] [CrossRef]
- Reames, D.V. Abundances, ionization states, temperatures, and FIP in solar energetic particles. Space Sci. Rev. 2018, 214, 61. [Google Scholar] [CrossRef]
- Reames, D.V. Four distinct pathways to the element abundances in solar energetic particles. Space Sci. Rev. 2020, 216, 20. [Google Scholar] [CrossRef]
- Reames, D.V. Hydrogen and the abundances of elements in impulsive solar energetic-particle events. Solar Phys. 2019, 294, 37. [Google Scholar] [CrossRef]
- Reames, D.V.; Cliver, E.W.; Kahler, S.W. Temperature of the source plasma for impulsive solar energetic particles. Sol. Phys. 2015, 290, 1761. [Google Scholar] [CrossRef]
- Lee, M.A. Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks. J. Geophys. Res. 1983, 88, 6109. [Google Scholar] [CrossRef]
- Lee, M.A. Coupled hydromagnetic wave excitation and ion acceleration at an evolving coronal/interplanetary shock. Astrophys. J. Suppl. 2005, 158, 38. [Google Scholar] [CrossRef]
- Jones, F.C.; Ellison, D.E. The plasma physics of shock acceleration. Space Sci. Rev. 1991, 58, 259. [Google Scholar] [CrossRef]
- Zank, G.P.; Rice, W.K.M.; Wu, C.C. Particle acceleration and coronal mass ejection driven shocks: A theoretical model. J. Geophys. Res. 2000, 105, 25079. [Google Scholar] [CrossRef]
- Zank, G.P.; Li, G.; Verkhoglyadova, O. Particle Acceleration at Interplanetary Shocks. Space Sci. Rev. 2007, 130, 255. [Google Scholar] [CrossRef]
- Cliver, E.W.; Kahler, S.W.; Reames, D.V. Coronal shocks and solar energetic proton events. Astrophys. J. 2004, 605, 902. [Google Scholar] [CrossRef]
- Sandroos, A.; Vainio, R. Simulation results for heavy ion spectral variability in large gradual solar energetic particle events. Astrophys. J. 2007, 662, L127. [Google Scholar] [CrossRef]
- Ng, C.K.; Reames, D.V. Shock acceleration of solar energetic protons: The first 10 minutes. Astrophys. J. Lett. 2008, 686, L123. [Google Scholar] [CrossRef]
- Reames, D.V. The two sources of solar energetic particles. Space Sci. Rev. 2013, 175, 53. [Google Scholar] [CrossRef]
- Lee, M.A.; Mewaldt, R.A.; Giacalone, J. Shock acceleration of ions in the heliosphere. Space Sci. Rev. 2012, 173, 247. [Google Scholar] [CrossRef]
- Desai, M.I.; Giacalone, J. Large gradual solar energetic particle events. Living Rev. Sol. Phys. 2016, 13, 1–32. [Google Scholar] [CrossRef]
- Reames, D.V.; Barbier, L.M.; Ng, C.K. The spatial distribution of particles accelerated by coronal mass ejection-driven shocks. Astrophys. J. 1996, 466, 473. [Google Scholar] [CrossRef]
- Reames, D.V.; Kahler, S.W.; Ng, C.K. Spatial and temporal invariance in the spectra of energetic particles in gradual solar events. Astrophys. J. 1997, 491, 414. [Google Scholar] [CrossRef]
- Rouillard, A.C.; Odstrčil, D.; Sheeley, N.R., Jr.; Tylka, A.J.; Vourlidas, A.; Mason, G.; Wu, C.-C.; Savani, N.P.; Wood, B.E.; Ng, C.K.; et al. Interpreting the properties of solar energetic particle events by using combined imaging and modeling of interplanetary shocks. Astrophys. J. 2011, 735, 7. [Google Scholar] [CrossRef]
- Rouillard, A.; Sheeley, N.R., Jr.; Tylka, A.; Vourlidas, A.; Ng, C.K.; Rakowski, C.; Cohen, C.M.S.; Mewaldt, R.A.; Mason, G.M.; Reames, D.; et al. The longitudinal properties of a solar energetic particle event investigated using modern solar imaging. Astrophys. J. 2012, 752, 44. [Google Scholar] [CrossRef]
- Rouillard, A.P.; Plotnikov, I.; Pinto, R.F.; Tirole, M.; Lavarra, M.; Zucca, P.; Vainio, R.; Tylka, A.J.; Vourlidas, A.; De Rosa, M.L.; et al. Deriving the properties of coronal pressure fronts in 3D: Application to the 2012 May 17 ground level enhancement. Astrophys. J. 2016, 833, 45. [Google Scholar] [CrossRef]
- Kahler, S.W. The correlation between solar energetic particle peak intensities and speeds of coronal mass ejections: Effects of ambient particle intensities and energy spectra. J. Geophys. Res. 2001, 106, 20947. [Google Scholar] [CrossRef]
- Kouloumvakos, A.; Rouillard, A.P.; Wu, Y.; Vainio, R.; Vourlidas, A.; Plotnikov, I.; Afanasiev, A.; Önel, H. Connecting the properties of coronal shock waves with those of solar energetic particles. Astrophys. J. 2019, 876, 80. [Google Scholar] [CrossRef]
- Kahler, S.W. Injection profiles of solar energetic particles as functions of coronal mass ejection heights. Astrophys. J. 1994, 428, 837. [Google Scholar] [CrossRef]
- Tylka, A.J.; Cohen, C.M.S.; Dietrich, W.F.; Krucker, S.; McGuire, R.E.; Mewaldt, R.A.; Ng, C.K.; Reames, D.V.; Share, G.H. Contributed papers v. 6 (SH sessions 1.1-2.3). In Proceedings of the 28th International Cosmic Ray Conference (Tsukuba) 6 3305 (2003), Tsukuba, Japan, 31 July–7 August 2003. [Google Scholar]
- Reames, D.V. Solar release times of energetic particles in ground-level events. Astrophys. J. 2009, 693, 812. [Google Scholar] [CrossRef]
- Reames, D.V. Solar energetic-particle release times in historic ground-level events. Astrophys. J. 2009, 706, 844. [Google Scholar] [CrossRef]
- Cliver, E.W.; Ling, A.G. Electrons and protons in solar energetic particle events. Astrophys. J. 2007, 658, 1349. [Google Scholar] [CrossRef]
- Cliver, E.W. Flare vs. shock acceleration of high-energy protons in solar energetic particle events. Astrophys. J. 2016, 832, 128. [Google Scholar] [CrossRef]
- Tylka, A.J.; Dietrich, W.F. A New and Comprehensive Analysis of Proton Spectra in Ground-Level Enhanced (GLE) Solar Particle Events. In Proceedings of the 31st International Cos. Ray Conference Lódz, Lódz, Poland, 8 July 2009; Available online: http://icrc2009.uni.lodz.pl/proc/pdf/icrc0273.pdf (accessed on 7 August 2021).
- Gopalswamy, N.; Xie, H.; Yashiro, S.; Akiyama, S.; Mäkelä, P.; Usoskin, I.G. Properties of Ground level enhancement events and the associated solar eruptions during solar cycle 23. Space Sci. Rev. 2012, 171, 23. [Google Scholar] [CrossRef]
- Mewaldt, R.A.; Looper, M.D.; Cohen, C.M.S.; Haggerty, D.K.; Labrador, A.W.; Leske, R.A.; Mason, G.M.; Mazur, J.E.; von Rosenvinge, T.T. Energy spectra, composition, other properties of ground-level events during solar cycle 23. Space Sci. Rev. 2012, 171, 97. [Google Scholar] [CrossRef]
- Reames, D.V. Hydrogen and the abundances of elements in gradual solar energetic-particle events. Solar Phys. 2019, 294, 69. [Google Scholar] [CrossRef]
- Reames, D.V. Temperature of the source plasma in gradual solar energetic particle events. Solar Phys. 2016, 291, 911. [Google Scholar] [CrossRef]
- Reames, D.V. Distinguishing the rigidity dependences of acceleration and transport in solar energetic particles. Solar Phys. 2020, 295, 113. [Google Scholar] [CrossRef]
- Mason, G.M.; Ng, C.K.; Klecker, B.; Green, G. Impulsive acceleration and scatter-free transport of about 1 MeV per nucleon ions in 3He-rich solar particle events. Astrophys. J. 1989, 339, 529. [Google Scholar] [CrossRef]
- Stix, T.H. Waves in Plasmas; AIP: New York, NY, USA, 1992. [Google Scholar]
- Reames, D.V. Acceleration of energetic particles by shock waves from large solar flares. Astrophys. J. Lett. 1990, 358, L63. [Google Scholar] [CrossRef]
- Reames, D.V.; Ng, C.K.; Tylka, A.J. Initial time dependence of abundances in solar particle events. Astrophys. J. Lett. 2000, 531, L83. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ng, C.K.; Reames, D.V. Focused interplanetary transport of approximately 1 MeV solar energetic protons through self-generated Alfven waves. Astrophys. J. 1994, 424, 1032. [Google Scholar] [CrossRef]
- Ng, C.K.; Reames, D.V.; Tylka, A.J. Effect of proton-amplified waves on the evolution of solar energetic particle composition in gradual events. Geophys. Res. Lett. 1999, 26, 2145. [Google Scholar] [CrossRef]
- Ng, C.K.; Reames, D.V.; Tylka, A.J. Modeling shock-accelerated solar energetic particles coupled to interplanetary Alfvén waves. Astrophys. J. 2003, 591, 461. [Google Scholar] [CrossRef]
- Ng, C.K.; Reames, D.V.; Tylka, A.J. Solar energetic particles: Shock acceleration and transport through self-amplified waves. AIP Conf. Proc. 2012, 1436, 212. [Google Scholar] [CrossRef]
- Reames, D.V.; Ng, C.K. Streaming-limited intensities of solar energetic particles. Astrophys. J. 1998, 504, 1002. [Google Scholar] [CrossRef]
- Reames, D.V.; Ng, C.K. Streaming-limited intensities of solar energetic particles on the intensity plateau. Astrophys. J. 2010, 723, 1286. [Google Scholar] [CrossRef]
- Reames, D.V. The correlation between energy spectra and element abundances in solar energetic particles. Sol. Phys. 2021, 296, 24. [Google Scholar] [CrossRef]
- Zank, G.P.; Rice, W.K.M.; le Roux, J.A.; Cairns, I.H.; Webb, G.M. The “injection problem” for quasiparallel shocks. Phys. Plasmas 2001, 8, 4560. [Google Scholar] [CrossRef]
- Li, G.; Zank, G.P.; Rice, W.K.M. Acceleration and transport of heavy ions at coronal mass ejection-driven shocks. J. Geophys. Res. 2005, 110, A06104. [Google Scholar] [CrossRef]
- Li, G.; Zank, G.P.; Verkhoglyadova, O.; Mewaldt, R.A.; Cohen, C.M.S.; Mason, G.M.; Desai, M.I. Shock geometry and spectral breaks in large SEP events. Astrophys. J. 2009, 702, 998. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, M.; Rassoul, H. Double power laws in the event-integrated solar energetic particle spectrum. Astrophys. J. 2016, 821, 62. [Google Scholar] [CrossRef]
- Reames, D.V. The abundance of helium in the source plasma of solar energetic particles. Solar Phys. 2017, 292, 156. [Google Scholar] [CrossRef][Green Version]
- Reames, D.V. Helium suppression in impulsive solar energetic-particle events. Sol. Phys. 2019, 294, 32. [Google Scholar] [CrossRef]
- Grevesse, N.; Noels, A.; Sauval, A.J. Standard Abundances. Astron. Soc. Pacif. Conf. Ser. 1996, 99, 117. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).