Supermassive Black Holes from Bose-Einstein Condensed Dark Matter—Or Black and Dark Separation by Angular Momentum

Abstract

Many supermassive black holes (SMBH) of mass ${10}^{6\sim 9}{M}_{\odot }$ are observed at the center of each galaxy even in the high redshift ($z\approx 7$) Universe. To explain the early formation and the common existence of SMBH, we previously proposed the SMBH formation scenario by the gravitational collapse of the coherent dark matter (DM) composed from the Bose-Einstein Condensed (BEC) objects. A difficult problem in this scenario is the inevitable angular momentum which prevents the collapse of BEC. To overcome this difficulty, in this paper, we consider the very early Universe when the BEC-DM acquires its proper angular momentum by the tidal torque mechanism. The balance of the density evolution and the acquisition of the angular momentum determines the mass of the SMBH as well as the mass ratio of BH and the surrounding dark halo (DH). This ratio is calculated as $M_{BH}/M_{DH}\approx {10}^{-3\sim -5}{(M_{tot}/{10}^{12}{\mathrm{M}}_{\odot })}^{-1/2}$ assuming simple density profiles of the initial DM cloud. This result turns out to be consistent with the observations at $z\approx 0$ and $z\approx 6$, although the data scatter is large. Thus, the angular momentum determines the separation of black and dark, i.e., SMBH and DH, in the original DM cloud.

1. Introduction

Recent observations have revealed a tremendous number of supermassive black holes (SMBH) of mass ${10}^6$–${10}^{10}{M}_{\odot }$ in the wide range of redshift up to $z\approx 7.642$ [1,2,3]. SMBH seems to be a common astronomical species everywhere in the Universe from the very early stage. Most of the galaxies have SMBH in their center as if the SMBH even defines the center of the galaxy. Furthermore, several universal correlations of SMBH with the galactic properties are widely reported so far [4]. Thus, SMBH must be a crucial component in the galaxies and deeply connected with their evolution. The remarkable properties of SMBH are their very early formation and their common existence associated with galaxies: both of them are still not yet well understood. We would like to consider the fundamental origin of such SMBH.

It will be natural to consider that SMBH may be formed from massive primordial stars or directly from the gas clouds [5,6]. For example, the model of a direct collapse of a gas cloud assuming subsequent steady gas accretion with the Eddington limiting rate can explain the early formation of huge SMBH [7,8]. However, such ideal conditions, strong ambient radiation, low metallicity, steady high accretion, etc. [9], are considered to be rare and, therefore, the early stage SMBH should not be common. However, it may happen in the future that much more SMBHs are commonly observed in the early Universe; therefore, we need to consider their universal formation mechanisms. Furthermore, we may need to explore a general model of SMBH formation for explaining the universal association and correlation of SMBH with galaxies.

Thus, we have developed an alternative model of SMBH formation from the coherent Bose-Einstein Condensed (BEC) matter which is supposed to compose the dark matter (DM) [10,11]. This BEC-DM model belongs to the category of the scalar-field DM model families studied for many years [12,13,14]. The BEC-DM model is now actively studied, which is partially summarized in the references in [15]. Since BEC is coherent and has almost no velocity dispersion, it can naturally collapse toward SMBH very quickly in isolated ideal cases. This model of BEC-DM arises from a simple idea that DM and dark energy (DE) are the same boson field but their phases are different for DM and DE [16]. In the original model, the uniform coherent condensation of some low-mass boson is supposed to form global DE, which causes the exponential cosmic expansion. On the other hand, the non-uniform condensation and the boson in the normal gas-phase form local DM. Then, it will be natural to consider that the locally coherent component BEC collapses into black holes of arbitrary mass. Thus, all the dark and black species DE, DM, and SMBH are considered to be, or originated from, the same boson field in this mode, but only their phases are different from each other.

However, in the actual Universe, we encountered a serious problem of the angular momentum, which strongly prevents the SMBH formation even for the coherent BEC-DM. Previously in [11], we have assumed a special DM Axion which has a sufficiently small mass and is supposed to form BEC. In this case, the trigonometric potential of the Axion yields a tiny attractive self-interaction force. Even if it were small, this attractive self-interaction can dominate the angular momentum barrier and allow the BEC-DM to collapse to form SMBH. In this case, the Axion mass parameter should have an appropriate value for the successful description for the observed ratio of DM and dark halo (DH) surrounding the galaxy. It may be favorable if there were a more general and common mechanism to avoid this angular momentum barrier, because SMBH is considered to be a common structure in our Universe.

Therefore, in this article, we consider another approach to solve the angular momentum problem without assuming undiscovered fields such as Axion. We do not attempt to overcome the angular momentum barrier as in the case of the Axion model, but we focus on a special epoch appropriate for SMBH formation. We consider the very early stage of the Universe when each DM mass clump was just acquiring first angular momentum by the tidal torque effect [17,18]. The increase in the angular momentum tends to prevent the SMBH formation but the increase in the mass enhancement promotes the SMBH formation. Then, the balance of these two effects should determine the mass of the SMBH as a function of the clump mass.

In this context, the angular momentum does not prevent the structure formation but adjusts the size of the structures. In our context, the angular momentum adjusts the separation of the central SMBH and the surrounding DH, both of which are essential for the galaxy formation. Furthermore, the angular momentum guarantees the stability of astronomical objects as well. This can be clarified if we estimate the angular momentum in various mass scales in the Universe. Then, we will find the scaling relation $J\approx {10}^{4}G{M}^2/c$ over 30 digits of objects composed from dust, Hydrogen gas, and DM. This further motivates the formation of SMBH from DM.

We first consider the present cosmic angular momentum on various scales in Section 2. The angular momentum in the wide range of scales provides us with a rough estimate of time scales for the formation of BH and other compact structures. Then, in Section 3, we study the SMBH formation from BEC-DM. Effective potential and the BH formation conditions are discussed in the non-relativistic approximation. In Section 4, we consider how the SMBH and DH are separated by the balance of the angular momentum acquisition and the density enhancement in the early stage of the Universe. In Section 5, we describe the verification of our analysis comparing with the observational data. In the last Section 6, we summarize our argument showing further developments for future work.

2. Angular Momentum

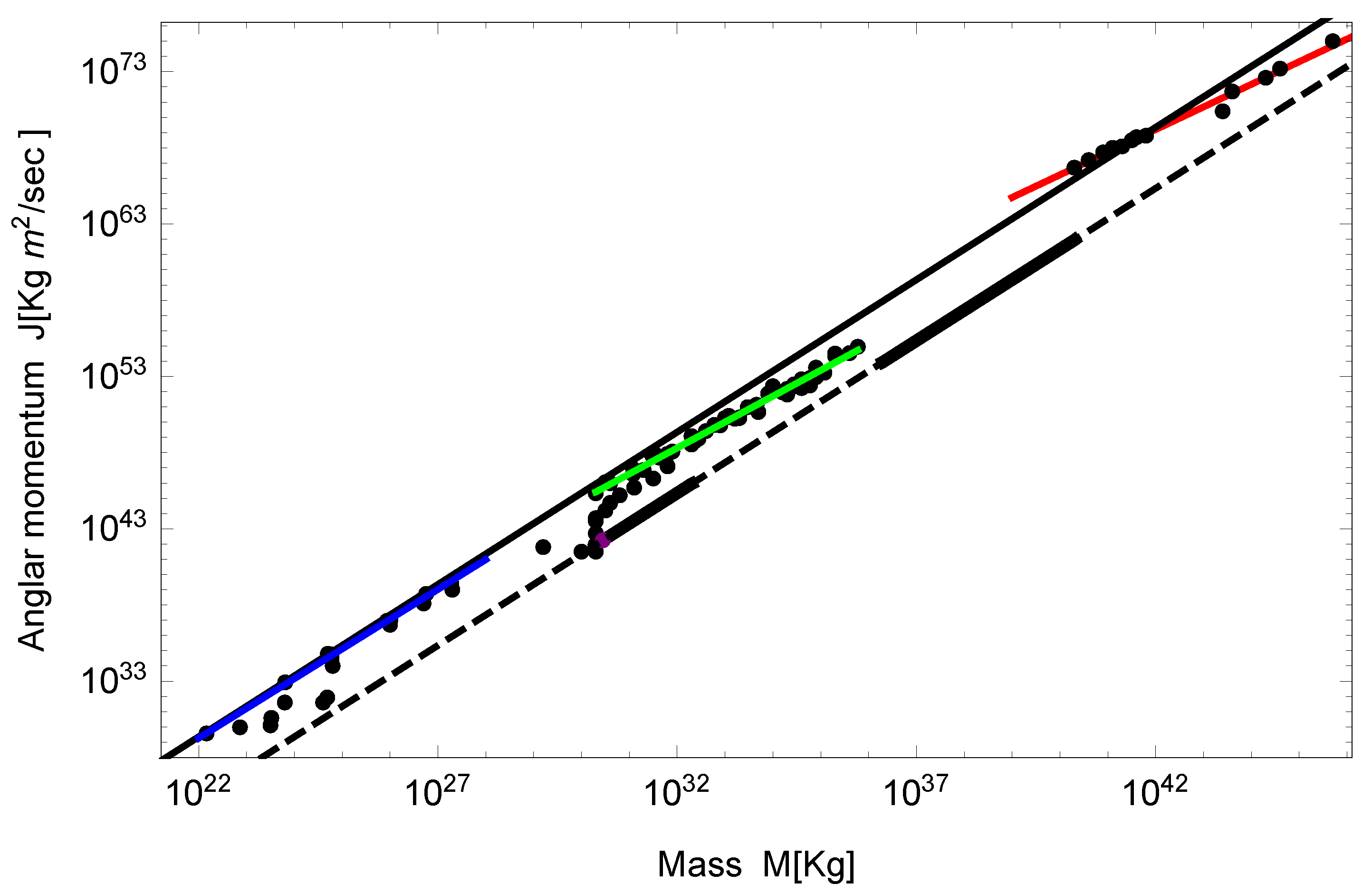
All the structures in the present Universe are rotating. They may collide with each other and the entire rotation may not be apparent. Even in those cases, objects inherit the angular momentum to smaller or larger scales from the original scale. The angular momentum J associated with astronomical objects in the Universe shows a conspicuous scaling relation in the wide range of mass scales M from the planets to the galaxy clusters. This scaling is shown in Figure 1 by the black solid line,

$$J=\kappa \frac{G}{c}{M}^2,$$

(1)

where $\kappa \approx {10}^4$ is a constant. All the dots represent observational data for individual astronomical objects. In the figure, the dashed line represents the critical angular momentum, Equation (1) with $\kappa =1,$ above which the black holes cannot exist. On this dashed line, the observed black hole ranges are marked by thick solid lines.

According to Figure 1, the observed data points seem to separate into three classes, structures made from dust, gas, and DM, from small to large scales. The structures made from dust, classified as metal in astronomy, are rocky planets and smaller substructures such as satellites (class 1). The structures made from the gas of Hydrogen and Helium, classified as non-metal in astronomy, are the interstellar gas and the stars (class 2). The structures made from DM, as well as a small fraction of Baryon, are the galaxies and their clusters (class 3). In between these three classes, there seem to be two ranges of BH: stellar scale BH ($1-{10}^2{M}_{\odot }$) and SMBH (${10}^6-{10}^{10}{M}_{\odot }$).

These scaling relations may be produced by simple physics [22]. We shall regard the objects, dust, gas, and DM, as fluids. Then, the turbulence of those fluids, as well as self-gravity, may yield the scaling relation. The Kolmogorov model of turbulence [23] describes the hierarchical steady flow of energy, in the wavenumber space, from large to small scales, and at the smallest scale, the energy dissipates into heat. The only relevant parameter in this picture is the dissipation speed at the smallest scale, or equivalently, the steady energy flow per unit mass $ϵ$ in the whole scaling range of the fluid.

In the self-gravitating case of the Universe, the energy flow may be steady but the direction would be small to large scale, opposite to the usual three-dimensional fluid case. However, the material flows from large toward small scale, and at the smallest scale, they sediment to form compact objects. This design of hierarchy yields the typical relative velocity $\sigma$, at two positions separated by r, as

$$\sigma ={\left(rϵ\right)}^{1/3}.$$

(2)

where $ϵ$ represents the energy flow per mass in the wavenumber space. Further, in the present cosmic case, a self-gravitating system of mass M and size r in the virial equilibrium is characterized by the relation

$${\sigma }^2=\frac{G{M}^2}{r},$$

(3)

where G is the gravitational constant. Combining these Equations (2) and (3), we can estimate the mass of the object as [22]

$$M=G^{-1}{ϵ}^{2/3}{r}^{5/3},$$

(4)

and the angular momentum as

$$J=\frac{2}{5}{G}^{4/5}{ϵ}^{-1/5}{M}^{9/5}.$$

(5)

This Equation (5) yields the power index $9/5=1.8$ in Figure 1, although the actual indices are slightly different from each other: 1.95 for class 1, 1.70 for class 2, and 1.48 for class 3, and the overall slope is 2. These slightly different indices may reflect (a) the huge compressible nature of the fluids, and (b) the effect of the prevailing magnetic field which locally enhances the flow of energy and angular momentum. Note that Equation (2) can be obtained only for the non-compressible fluid.

If we regard that the above scaling law reflects the hierarchical turbulent structure in each class of ingredient, the parameter $ϵ$ determines the steady flow of energy, angular momentum, as well as the ingredient object. However, in the self-gravitating system, what the parameter $ϵ$ determines is not literal ‘dissipation’, but the sedimentation of the material which finally forms compact structures at the smallest scale in each class. All the compact structures in the Universe may be formed in this flow as stagnation mainly at the smallest scales in each class.

According to this picture, we may naturally expect that the dust forms planets, the gas forms stars as well as stellar size BH, and in particular, the DM forms galaxies as well as SMBH. Thus, this hierarchical turbulent picture naturally motivates us to examine the scenario of SMBH formation from DM [22]. However, Figure 1 tells us more. In the case of class 2, the route from gas to the stellar size BH seems apparent: large-scale interstellar gas continuously connects down to the stars and BHs as the data points show. On the other hand, in the case of class 3, the route from DM to the SMBH cannot be observed. This discontinuity may indicate that the SMBH cannot be formed in the steady process of the hierarchical turbulent scenario. This is another motivation for us to consider the dynamical stage of galaxy formation in the early Universe. Let us continue the argument of the hierarchical turbulent scenario for a while.

The standard Kolmogorov dissipation time scale would correspond to the structure formation time scale in our cosmic case. The ordinary turbulent fluid dissipates its energy into heat mainly at the low-end of the Kolmogorov scaling. In the cosmic case, since the gravity confines such drop-out material into compact objects, the structure formation must be taking place at each smallest end of the class. This stagnation in the steady turbulent flow may be the general origin of astronomical structures such as planets, stars, and galaxies.

We now estimate the time scales of such compact structure formations. In each class, the actual mass density scaling is different. Best-fitting the observed densities of astronomical objects in each class, the mass densities are given by ([19,20,21]), in the unit $\mathrm{Kg}/{\mathrm{Meter}}^3$,

$$\begin{array}{cc}\hfill {\rho }_d& =6.8\times {10}^5{\left(\frac{r}{\mathrm{Meter}}\right)}^{-0.35},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\rho }_g& =6.3\times {10}^{16}{\left(\frac{r}{\mathrm{Meter}}\right)}^{-1.75},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\rho }_D& =1.6\times {10}^9{\left(\frac{r}{\mathrm{Meter}}\right)}^{-1.33},\hfill \end{array}$$

(8)

for each class: dust, gas, and DM, respectively. If we adopt this phenomenology, then the best fit of the angular momentum J in Figure 1 yields the approximate Kolmogorov parameters as,

$${ϵ}_d={10}^{-4}{ϵ}_D,{ϵ}_g={10}^{-2}{ϵ}_D,{ϵ}_D=3.0\times {10}^{-5},$$

(9)

in the unit ${\mathrm{Meter}}^2{\mathrm{Sec}}^{-3}$. They determine the steady energy flow, from small scale to larger scale, per mass per time. Thus, it may be possible to estimate the time scales for the formation in each scale. During the formation time $\tau$, the total amount of energy flow out is the gravitational potential of the compact object $G{M}^2/r$, and the flow speed per mass is $ϵ$. Therefore, the formation time scale $\tau$ of this compact object is estimated as

$$\tau =G\rho r^2{ϵ}^{-1}.$$

(10)

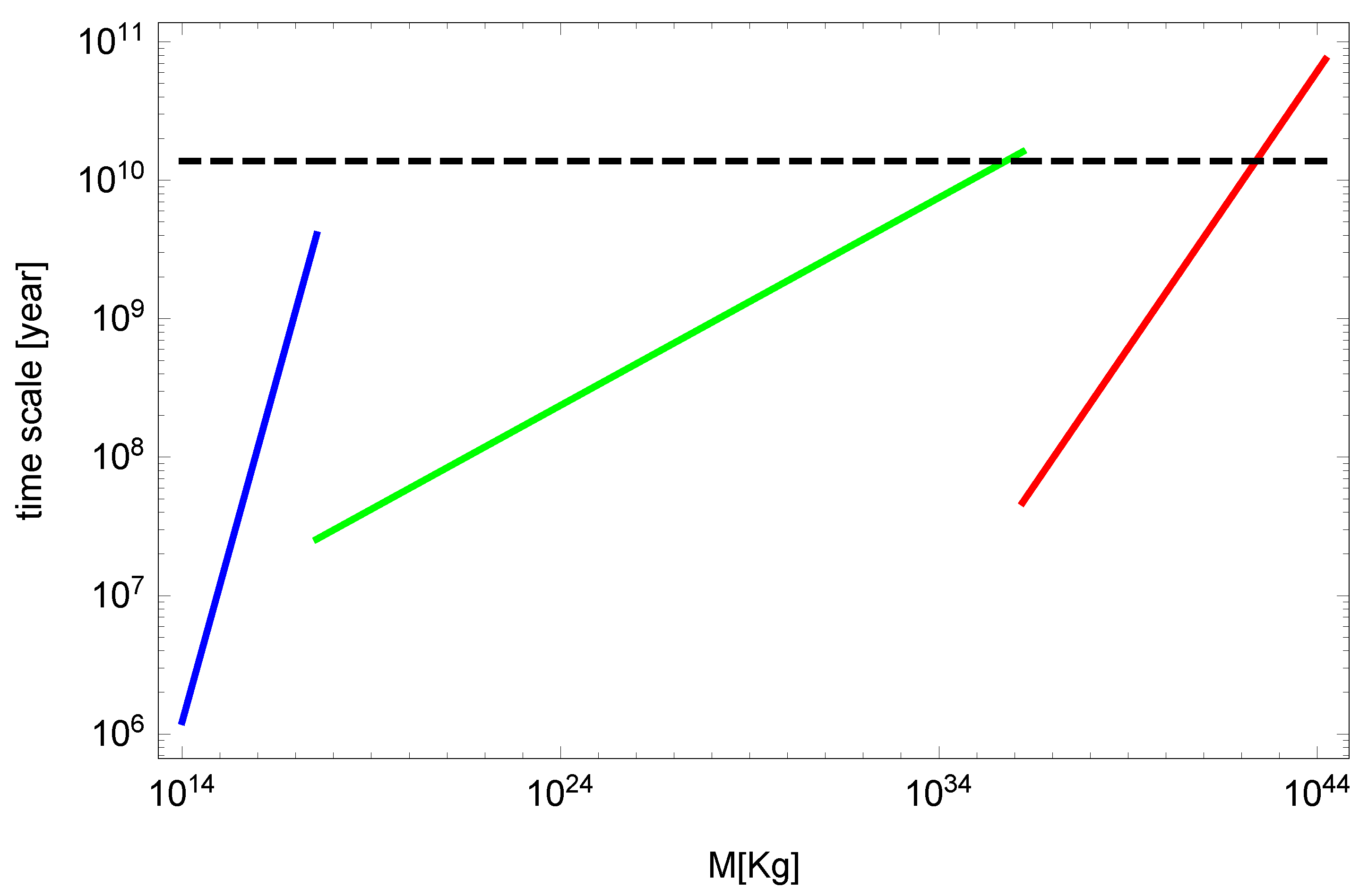
The estimated time scales are expressed in Figure 2.

According to Figure 2, the formation time scale of the object of mass ${10}^9{M}_{\odot }\approx 2\times {10}^{39}$ Kg reads about ${10}^9$ years, corresponding to the redshift $4.8$, which is marginal or ruled out by observations. Further, the large-scale region of this diagram will not be appropriate since the estimated time scale is based on the steady process for structure formation. The Universe evolves from the initial condition and, therefore, the structures are not at all steady. Moreover, the right end of the time scale exceeds the age of the universe. We need to consider the dynamical origin of SMBH going back to much earlier stages in the Universe. We will discuss this issue in the subsequent sections.

3. Supermassive Black Hole from Bose-Einstein Condensed Dark Matter

The standard DM in the gas phase induces velocity dispersion and cannot easily collapse to a BH. On the other hand, if the bosonic DM were in the quantum condensed phase, or Bose-Einstein condensed (BEC) phase, it behaves as a classical scalar field without dispersion. Thus, DM in the form of BEC can collapse to form a BH. We consider this possibility in this Section [11].

BEC becomes possible when the wave functions of atoms overlap with each other, or the thermal de-Broglie length ${\lambda }_{dB}\equiv {\left(2\pi {\hslash }^2/\left(mkT\right)\right)}^{1/2}$ exceeds the mean separation of atoms $r\equiv n_{}^{-1/3}$, where n is the boson number density, m is the boson mass, and k is the Boltzmann constant [24,25]. This gives the BEC condition and defines the critical temperature $T_c\equiv 2\pi {\hslash }^2{n}^{2/3}/\left(mk\right)$. This temperature dependence on n is the same as the cosmic number density $T\propto n^{2/3}$. Therefore, once the cosmic gas cools below the BEC critical temperature, it keeps the BEC phase all later times [16]. This guarantees the robustness of the BEC phase in the Universe although the BEC phase will be destroyed by non-adiabatic processes such as violent collisions.

The BEC is the macroscopic coherent wave and is described by the classical wave $\psi \left(t,\mathbf{x}\right)$ which evolves as

$$i\hslash \frac{\partial \psi \left(t,\mathbf{x}\right)}{\partial t}=\left(-\frac{{\hslash }^2}{2m}\Delta +m\varphi +g{\left|\psi \right|}^2\right)\psi ,$$

(11)

where $\varphi \left(t,\mathbf{x}\right)$ is the gravitational potential field, and generated by BEC,

$$\Delta \varphi =4\pi Gm{\left|\psi \right|}^2.$$

(12)

This is the non-relativistic approximation of BEC and is widely studied for describing DM for many years [26,27,28,29].

Within this non-relativistic approach, the BH formation will be described by the condition that the portion of DM enters inside the corresponding Schwarzschild radius. However, there is another necessary condition for BH formation for the boson case. For the boson system, the structure is supported by the quantum pressure against its gravity. A BH is formed when this balance is no longer sustained, i.e., when the Schwarzschild radius $r_s=2$ GM/c${}^2$ exceeds the boson Compton wavelength ${\lambda }_c=2\pi \hslash /\left(mc\right)$, ($r_S>{\lambda }_c$),

$$M>M_K\approx \pi \frac{m_P^2}{m},$$

(13)

where $m_P={(c\hslash /G)}^{1/2}$ is the Planck mass. This limiting mass $M_K$ is called the Kaup mass, and the exact value $M_K=0.633$ m${}_P^2$/m is derived from numerical calculations based on general relativity [30]. This mass is far smaller than the popular limiting mass for Baryons m${}_P^3$/m${}^2$. However, this Kaup mass sets the lower bound of the BH formed from bosonic DM. For example, if the boson mass is ${10}^{-16}\mathrm{eV}$, then the BH of mass lower than $0.84\times {10}^6{M}_{\odot }$ cannot be formed.

The above set of non-linear Equations (11) and (12) is still difficult to solve and to obtain a general insight, although numerical calculations themselves would be relatively easy. In order to be analytical as much as possible, let us assume that the self-interaction is very small and that the anisotropic back reaction from BEC field to gravity is negligible. These approximations will be justified since we do not rely upon the self-interaction and the acquired angular momentum turns out to be very small in our subsequent calculations. Then, Equation (11) allows the separation of variables,

$$\psi \left(t,\mathit{x}\right)=\phi (t,r)Y_l^m(\theta ,\phi ),$$

(14)

where $Y_l^m(\theta ,\phi )$ is the spherical harmonics. Now, the Lagrangian for the fields $\phi (t,r)$ and $\varphi \left(t,r\right)$ becomes,

$$\begin{array}{cc}L=& \frac{\mathrm{i}\hslash }{2}({\phi }^{†}\dot{\phi }-{\dot{\phi }}^{†}\phi )-\frac{{\hslash }^2}{2m}(\partial {\phi }^{†}/\partial r)(\partial \phi /\partial r)-\frac{g}{2}{\left({\phi }^{†}\phi \right)}^2\\ & -\frac{1}{8\pi G}(\partial \varphi /\partial r)(\partial \varphi /\partial r)-\frac{A^2}{m{r}^2}{\phi }^{†}\phi -m\varphi {\phi }^{†}\phi ,\end{array}$$

(15)

where A is the separation constant or the angular momentum.

Further, we use the Gaussian approximation for the semi-analytic calculations which has been introduced by [29],

$$\phi \left(t,r\right)=N{e}^{-r^2/{\left(2\sigma \left(t\right)\right)}^2+i{r}^2\alpha \left(t\right)},\varphi \left(t,\mathit{x}\right)=\mathsf{\mu }\left(t\right)e^{-r^2/{\left(2\tau \left(t\right)\right)}^2}$$

(16)

where N is the number density of the boson particles. The next step is to integrate the Lagrangian Equation (15), inputting Equation (16), on the entire space. This yields

$$\begin{array}{cc}\hfill L=& -\frac{N\left(8A^2+6\hslash \sigma {\left(t\right)}^4\left(m{\alpha }^{\prime }\left(t\right)+2\hslash \alpha {\left(t\right)}^2\right)+3{\hslash }^2\right)}{4m\sigma {\left(t\right)}^2}-\frac{\sqrt{2}g{N}^2}{8{\pi }^{3/2}\sigma {\left(t\right)}^3}-\frac{3\sqrt{\pi }\mathsf{\mu }{\left(t\right)}^2\tau \left(t\right)}{16G}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & +\frac{2\sqrt{2}mN\mathsf{\mu }\left(t\right)\sigma \left(t\right)\tau {\left(t\right)}^4\sqrt{\frac{2}{\sigma {\left(t\right)}^2}+\frac{1}{\tau {\left(t\right)}^2}}}{{\left(\sigma {\left(t\right)}^2+2\tau {\left(t\right)}^2\right)}^2},\hfill \end{array}$$

(18)

from which we obtain the equations of motion for the variables $\sigma \left(t\right),\alpha \left(t\right),\mathsf{\mu }\left(t\right), \mathrm{and} \tau \left(t\right).$ The equations for the last three variables $\alpha \left(t\right),\mathsf{\mu }\left(t\right), \mathrm{and} \tau \left(t\right)$ are all algebraically solved. Putting them back to the above Lagrangian, we obtain the reduced Lagrangian for the single variable $\sigma \left(t\right)$,

$$L_{\mathrm{eff}}=-\frac{N\left(8A^2+3{\hslash }^2\right)}{4m\sigma {\left(t\right)}^2}-\frac{g{N}^2}{4\sqrt{2}{\pi }^{3/2}\sigma {\left(t\right)}^3}+\frac{25\sqrt{\frac{5}{2\pi }}G{m}^2{N}^2}{81\sigma \left(t\right)}+\frac{3}{4}mN{\sigma }^{\prime }{\left(t\right)}^2.$$

(19)

These ugly numerical coefficients come from the Gaussian approximation and their values are of order 1. Therefore, we simply analyze the Lagrangian setting all the coefficients as 1. In particular, the effective potential becomes

$$V_{\mathrm{eff}}=\frac{g{N}^2}{\sigma {\left(t\right)}^3}-\frac{G{M}^2}{\sigma \left(t\right)}+\frac{J^2}{M\sigma {\left(t\right)}^2},$$

(20)

where $M=mN$ and $J^2=N^2\left(2A^2+(3/4){\hslash }^2\right)$.

The last term of Equation (20) comes from the angular momentum and prevents the collapse of the system. In our previous study [11], we assumed the Axion DM and its inevitable self-interaction naturally yields $g<0$. This tiny attractive self-interaction, the first term in Equation (20), can dominate the angular momentum for a massive system and allows the SMBH formation. On the other hand, in this article, we try to avoid the angular momentum problem from a general point of view not specifying DM species and not utilizing self-interaction.

Another necessary condition, on top of Equation (13), for the BH formation is given by considering this effective potential $V_{\mathrm{eff}}$ Equation (20) without the first term. A BH is formed when the radius which gives the minimum of this potential is inside the corresponding Schwarzschild radius. This condition yields

$$\mathsf{\mu }\le 1,\mathrm{where}\mathsf{\mu }\equiv \frac{cJ}{G{M}^2},$$

(21)

where $\mathsf{\mu }$ is also known as the spin parameter of a BH. This parameter $\mathsf{\mu }$ can be understood as the ratio of the surface velocity to the light velocity of a BH in the non-relativistic sense.

In order to achieve this condition $\mathsf{\mu }\le 1$ for SMBH formation, we need to go back to the early stage of the Universe when J was small. This is because the present value of $\mathsf{\mu }$ is too large $\mathsf{\mu }\approx {10}^4$, as we have observed in Equation (1) and in Figure 1. SMBH cannot be expected to form at the present stage even for the coherent BEC-DM. This amount of angular momentum should be acquired in the early stage of the evolution in the Universe. Therefore, if we go back to the early stage of the first acquisition of the angular momentum, we have a chance to fulfill the condition $\mathsf{\mu }\le 1$, and SMBH can be formed.

4. Tidal Torque Acquisition of Angular Momentum and BEC Collapse

The angular momentum of any astronomical object will originate from the tidal torque exerted in the early stage of the Universe. This general process is precisely described by the tidal torque theory [31,32]. Suppose some portion of density fluctuation in the uniform background starts to evolve, and deviates from the uniform cosmic expansion. Then, this portion is necessarily exerted torque from its nearby region. It acquires the angular momentum of the amount

$$\mathit{J}\left(t\right)={\int }_{a^{3}V}{d}^{3}x\rho \mathit{x}\times \dot{\mathit{x}}={\rho }_b{a}^5{\int }_V{d}^{3}r(1+\delta )\mathit{r}\times \dot{\mathit{r}},$$

(22)

where the physical scale $\mathit{x}$ is expressed by the comoving scale $\mathit{r}$ as $\mathit{x}=a\left(t\right)\mathit{r}$ and ${\rho }_b$ is the background uniform density after removing the density fluctuation factor $1+\delta$ [31,32]. Zel’dovich approximation [33] $\mathit{r}=\mathit{q}-D\left(t\right)\nabla \psi$ greatly reduces the above expression, where $\nabla \psi$ is the peculiar gravitational potential and $D\left(t\right)$ is the fluctuation growing factor. Further, the density enhancement $\delta$ can be expressed by the Jacobian $(1+\delta )=\left|\partial \mathit{q}/\partial \mathit{r}\right|$. Then, the standard $\Lambda$CDM cosmology predicts the evolution of the angular momentum in the lowest order as

$$\mathit{J}\left(t\right)={\rho }_b{a}_0^{3}a\left(t\right)\dot{D}\left(t\right){\int }_{V}dq\mathit{q}\times \nabla \psi \left(\mathit{q}\right).$$

(23)

In fact, this theory is well verified by the numerical simulations [18].

We simply try the singular isothermal distribution for the above over-density region in BEC-DM as

$$\rho \left(t\right)=\frac{\beta \left(t\right){\rho }_0}{{\left(r/r_0\right)}^2},$$

(24)

where r is the comoving length scale and $r_0$, ${\rho }_0$ are the constants although redundant. The time dependent factor $\beta \left(t\right)$ represents the development of the density enhancement in the early Universe. We further assume the rigid rotation of this region and the rotation velocity at the distance r from the center is written as

$$v\left(t\right)=\alpha \left(t\right)\Omega r,$$

(25)

where $\alpha \left(t\right)\Omega$ represents the increasing angular momentum and $\Omega$ is a constant parameter.

The density increases by more inside but the angular momentum increases by more outside. Then, we expect a BH to be formed at the inner central region. Thus, we consider the spherical region around the center with the radius r. The total angular momentum inside the radius r is given by

$$J\left(r\right)=\frac{4}{3}\pi \alpha \left(t\right)\beta \left(t\right){\rho }_0{r}_0^2{r}^3\Omega ,$$

(26)

and the mass inside the radius r by

$$M\left(r\right)=4\pi \beta \left(t\right){\rho }_0{r}_0^{2}r.$$

(27)

The necessary conditions for the BH formation are $\mathsf{\mu }\le 1$, Equation (21), and $M\ge M_K$, Equation (13). Using Equations (26) and (27), the central region inside the radius r turns out to have the following $\mathsf{\mu }$ parameter,

$$\mathsf{\mu }\left(r\right)\equiv \frac{cJ\left(r\right)}{GM{\left(r\right)}^2}=\frac{9\alpha \left(t\right)c{r}^2\Omega }{20\pi \beta \left(t\right)G{\rho }_0{r}_0^{2}r}.$$

(28)

If this condition is satisfied once, as well as $M\left(r\right)\ge M_K$, then there is no preventing factor for this region to collapse to a BH.

According to the standard CDM model, the density enhancement evolves as $\propto t^{2/3}$, and the factor $a{\left(t\right)}^2\dot{D}\left(t\right)$ in Equation (23) is proportional to time t. We use the time evolution of the angular momentum and the mass enhancement numerically analyzed in the reference [18]. According to this analysis, the typical time scale of the angular momentum acquisition is about 3 gigayears. Therefore, we may set

$$J\left(t\right)\propto \alpha \left(t\right)\beta \left(t\right)\propto t,$$

(29)

$$M\left(t\right)\propto \beta \left(t\right)={\left(\frac{t}{3G\mathrm{year}}\right)}^{2/3}.$$

(30)

Further, since the matter collapses to form BH without any resistance if $\mathsf{\mu }\le 1$, the time needed to form BH can be estimated simply by the free fall time of this matter,

$$t_{\mathrm{ff}}=G^{-1/2}{\left(\frac{M\left(r\right)}{\frac{4\pi }{3}{r}^3}\right)}^{-1/2}.$$

(31)

Therefore, the maximum mass BH will be formed at the free fall time when the $\mathsf{\mu }$ parameter becomes critical, and we have the condition for the maximum SMBH formation,

$$t_{\mathrm{ff}}(t,r)=t\mathrm{and}\mathsf{\mu }(t,r)=1.$$

(32)

After the collapse of the central region, the remaining outside part will further acquire angular momentum and the SMBH formation may back react to the outer region to increase the velocity dispersion there. This outer part will be thus stabilized and forms DH surrounding the central SMBH. Although this dynamical process is relevant to determine the properties of the produced SMBH and the detail of DH, the necessary calculation goes beyond the scope of this paper. This interesting problem will be discussed in a separate report shortly, possibly including general relativistic numerical calculations.

Thus, if we solve Equation (32), we can estimate the radius r inside of it forms the maximum mass BH at that time. Consequently, the SMBH formation time scale is given by

$$t_{\mathrm{BH}}=\frac{2\sqrt{6\pi }}{c\Omega }{\left(\frac{G{M}_{\mathrm{tot}}}{R_{\mathrm{tot}}}\right)}^{1/2},$$

(33)

and the region which collapses into SMBH has the radius

$$r_{\mathrm{BH}}=\frac{6{\left(3\pi \right)}^{1/6}}{c^{4/3}{t}_{\mathrm{J}}^{1/3}{\Omega }^{4/3}}{\left(\frac{G{M}_{\mathrm{tot}}}{R_{\mathrm{tot}}}\right)}^{7/6}.$$

(34)

Therefore, the mass of the SMBH is given by

$$M_{\mathrm{BH}}=\frac{12\sqrt{3\pi }}{c^{2}G{t}_J{\Omega }^2}{\left(\frac{G{M}_{\mathrm{tot}}}{R_{\mathrm{tot}}}\right)}^{5/2}.$$

(35)

Setting typical values, for example,

$$M_{tot}={10}^{12}{\mathrm{M}}_{\odot },R_{tot}=10\mathrm{kpc},\Omega =\frac{200}{R_{tot}}\frac{\mathrm{km}}{\mathrm{Sec}},t_J=3\mathrm{Giga}\mathrm{year},$$

(36)

we have the SMBH formation time scale, the size which turns into SMBH, and the resultant mass of SMBH as,

$$\begin{array}{c}{t}_{\mathrm{BH}}=0.9\times {10}^6\mathrm{years},\hfill \\ r_{\mathrm{BH}}=20\mathrm{pc},\hfill \\ M_{\mathrm{BH}}=0.94\times {10}^7{M}_{\odot }.\hfill \end{array}$$

(37)

Thus, the mass ratio of SMBH and dark halo (DH) $M_{DH}$ around it is given by

$$\frac{M_{BH}}{M_{DH}}\approx {10}^{-5}.$$

(38)

Further, we can consider various sizes of the over-density regions in BEC-DM. For this purpose, we tentatively assume a simple relation for mass and size $M_{\mathrm{tot}}\propto R_{\mathrm{tot}}$for those regions. Then, the virial relation $v^2\sim GM/R$ yields almost non-varying velocity and the assumption of the rigid rotation yields $\Omega \propto v/R\propto v/M$. If we further assume that the typical time scale of the object follows the evolution law for the linear perturbation, then the mass ratio of SMBH and DH is given by the expression

$$\frac{M_{BH}}{M_{DH}}\approx {10}^{-5}{\left(\frac{M_{tot}}{{10}^{12}{\mathrm{M}}_{\odot }}\right)}^{-1/2},$$

(39)

as a function of the total mass $M_{tot}$.

However, these values strongly depend on the shape of the cluster we assume as Equation (24). If we have chosen a different density profile

$$\rho \left(\mathrm{t}\right)=\frac{\beta \left(t\right){\rho }_0}{{\left(r/r_0\right)}^{5/2}},$$

(40)

with slightly steep configuration, then we have, under the same condition Equation (36),

$$\begin{array}{c}{t}_{\mathrm{BH}}=3.7\times {10}^6\mathrm{years},\hfill \\ r_{\mathrm{BH}}=309\mathrm{pc},\hfill \\ M_{\mathrm{BH}}=2.02\times {10}^9{M}_{\odot }.\hfill \end{array}$$

(41)

The mass ratio of SMBH and DH is given, with the same assumption for Equation (39), by

$$\frac{M_{BH}}{M_{DH}}\approx 2\times {10}^{-3}{\left(\frac{M_{tot}}{{10}^{12}{\mathrm{M}}_{\odot }}\right)}^{-1/2},$$

(42)

which is much larger than the previous isothermal case Equation (39). On the other hand, if we have chosen the density profile of shallower configuration, then the formed SMBH mass and the ratio are much smaller. The above estimates are based on bold analytic approximations. For serious verification of our model and for the proper comparison with observations, we need reliable numerical calculations based on general relativity.

5. Observational Verification

We now turn our attention to the possible verification of our calculations. Our main estimate has been the mass ratio of SMBH and DH. We examine the observation of 49 QSO data around $z\approx 6$ [34] and the local data $z\approx 0$ [35] quoted in [34]. The authors of [34] estimate $M_{DH}$ of a QSO by measuring the CII velocity-width and assuming it as the circular velocity of DH. Then, they obtain the mass ratio of SMBH and DH $M_{BH}/M_{DH}$ as a function of $M_{DH}$. 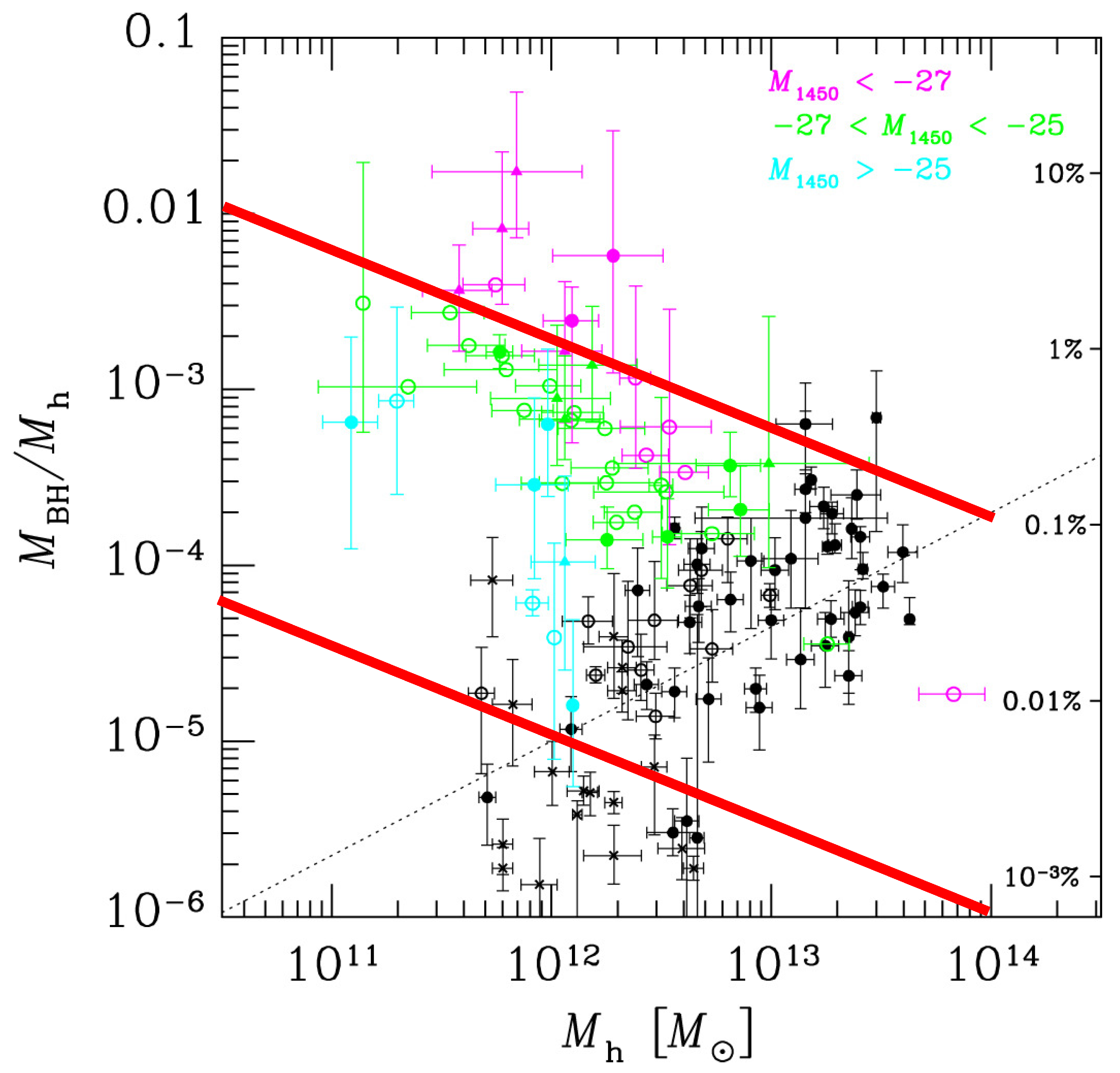Their result Figure 3b is quoted in our paper as Figure 3. On top of the observational data, we superposed our results Equations (39) and (42) by red lines. We describe the verification of our results.

All the observational data has great scatter and, therefore, there may be no definite tendency in $M_{BH}/M_{DH}$. However, it is apparent that the ratio $M_{BH}/M_{DH}$ of galaxies at high redshift $z\approx$ 6–7 is about two orders of magnitude larger than that of present galaxies $z\approx 0$. This fact may indicate that the evolution efficiency of DH is far larger than that of SMBH for $z\le$ 6–7. On the other hand, this result may by caused simply by the bias effect to select luminous QSOs and, therefore, $M_{BH}$ may be overestimated compared to the average.

In the same way, our estimate of $M_{BH}/M_{DH}$ has large variation mainly depending on the choice of the density profile. This is indicated by the wide separation of the two red lines in Figure 3. However, if the density profile, as well as other values assumed, were not actually unique, then we may need to observe more detail and find possible correlations in the data for the verification of our model.

Since our estimate of the ratio $M_{BH}/M_{DH}$ is for the SMBH-DH system just formed in the high redshift era, our result should be compared more with objects at redshift $z\approx$ 6–7 rather than that at $z\approx 0$. Further, our detailed dynamical analysis for the evolution of SMBH and DH, in the near future, may reveal the reason for the large reduction of the rate from $z\approx$ 6–7 to $z\approx 0$.

Overall comparison of our estimate and the observational data are not so different from each other and it does not exclude our model. In the comparison, the slope $-1/2$ for the ratio should not be taken seriously since the slope $-1/2$ is the consequence of our naive assumption $M_{\mathrm{tot}}\propto R_{\mathrm{tot}}$in our calculations. The validity of this assumption as well as others should be checked in the next step of our research.

The authors of [34] quote several other observational results for the ratio $M_{BH}/M_{DH}$ in different redshift $z\approx$ 2–3, 4–5 (Figure 5 in [34]). They also show large data range ${10}^{-5}\le M_{BH}/M_{DH}\le {10}^{-2}$. Our estimates Equations (39) and (42) are not excluded by the comparison with these data. We would like to explore our calculations to find other possible correlations than $M_{BH}/M_{DH}$ for further verification in the future.

6. Conclusions and Discussions

We have discussed the origin of SMBH formed from the BEC-DM, solving the angular momentum problem. This scenario has been needed to guarantee the very early formation and the common existence of SMBH suggested from recent observations. We first examined the prevailing angular momentum associated with all astronomical objects. The angular momentum turns out to follow the scaling law in the wide mass range and the amount of it is about ${10}^4$ times larger than the critical value for black hole formation. However, we obtained a good motivation that the SMBH may be formed from DM. We applied the self-gravitating-turbulence picture and tentatively estimated the time scale for the structure formation at each mass scale. For example, the formation of SMBH of mass ${10}^9{M}_{\odot }$ needs ${10}^9$ years, which does not meet observations. Furthermore, these arguments only apply to the steady stationary processes and, therefore, cannot be applied to much larger scales where the dynamical evolution effect dominates.

Therefore, we proceed to consider the dynamical formation of SMBH based on BEC-DM which is described by non-relativistic approximation (GP and Poisson equations). After a brief introduction of the BEC-DM scenario of SMBH formation, we applied the variable separation method and the Gaussian approximation to obtain the effective action, which yields the approximate BH formation condition within the non-relativistic calculations.

Then, estimating the tidal torque acquisition of the angular momentum and setting appropriate density profiles, we obtain the time scale of SMBH formation and the collapsing scale as well as the maximum mass of SMBH. Then, simply assuming the relation between the mass and the length of the initial DM cluster, we obtain the mass ratio of the SMBH formed and the remaining DH as a function of the total initial mass. The range of the estimated mass ratio widely varies, ${10}^{-5\sim -3}$ at the mass scale ${10}^{12}{M}_{\odot }$, for different density profiles of the initial DM cluster.

Finally, these estimates were compared with the recent observations of the SMBH/DH ratio. We compare our results with the high redshift data and the local data. It turns out that our estimate is not excluded by the observations although the observational data has a large scatter and therefore allows a wide range of predictions. Moreover, the mass ratio is reported to have a huge evolution effect and reduces 1–2 orders of magnitude from $z\approx 6$ to $z\approx 0$.

We found that only a small central portion of the DM cloud can form SMBH and the rest of the cluster simply becomes DH in the very early stage when the cluster is formed and the tidal torque accumulates its angular momentum. Thus, the angular momentum controls the separation of the original DM cluster into the central SMBH and the surrounding DH. If there were no angular momentum, then the whole DM cluster collapses to form an extremely huge BH. Subsequent galaxy, if formed around it, would be quite peculiar and fully different from what we observe today. Thus, our model, angular momentum controlled SMBH/DH formation from BEC-DM, guarantees the rapid formation and the common existence of SMBH at the center of DH, in which many stars and a galaxy are going to evolve. However, we have used several analytic approximations without fully examining their validity. In fact, the assumption of the density profile has drastically changed the mass of the formed SMBH. It is apparent that we need much elaboration on our model in the future.

We have proposed the scenario of the early formation of SMBH from BEC-DM avoiding the angular momentum problem. The present calculation can be improved, the scenario can be much more precise, and the detailed comparison with observations can be possible if we further consider general relativity and numerical methods. Although we have assumed the BH formation proceeds only at the center of the cluster, many smaller BHs may be formed in the other regions of the cluster as well if we assume the quiet acquisition of angular momentum. However, when the central SMBH is formed, a strong shock wave may heat up the surrounding DH region and disturb the formation of those smaller BHs. A numerical calculation of this complicated process would be interesting to obtain the mass distribution function of BHs. Further, the first formed SMBH in our scenario determines the center of the galaxy. It may promote star formation by the shock wave associated with the BH jet. Eventually, the bulge mass and the SMBH mass may establish the observed universal correlation. This process has been partially analyzed before [36], but has not been well analyzed so far. We hope to report all of these calculation results in our subsequent publications soon.