Next Article in Journal
Application of Neural Networks to Classification of Data of the TUS Orbital Telescope
Next Article in Special Issue
Studying Cosmic Ray Sources Using Intergalactic Electromagnetic Cascades
Previous Article in Journal
Time and Evolution in Quantum and Classical Cosmology
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Universe
Volume 7
Issue 7
10.3390/universe7070220
universe-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modeling Gamma-Ray SEDs and Angular Extensions of Extreme TeV Blazars from Intergalactic Proton-Initiated Cascades in Contemporary Astrophysical EGMF Models

by
Emil Khalikov
Skobeltsyn Institute of Nuclear Physics (SINP MSU), Federal State Budget Educational Institution of Higher Education, M.V. Lomonosov Moscow State University, 1(2), Leninskie Gory, GSP-1, 119991 Moscow, Russia
Universe 2021, 7(7), 220; https://doi.org/10.3390/universe7070220
Submission received: 14 May 2021 / Revised: 15 June 2021 / Accepted: 26 June 2021 / Published: 30 June 2021
(This article belongs to the Special Issue Astroparticle Physics)
Browse Figures
Review Reports Versions Notes

Abstract

The intrinsic spectra of some distant blazars known as “extreme TeV blazars” have shown a hint at an anomalous hardening in the TeV energy region. Several extragalactic propagation models have been proposed to explain this possible excess transparency of the Universe to gamma-rays starting from a model which assumes the existence of so-called axion-like particles (ALPs) and the new process of gamma-ALP oscillations. Alternative models suppose that some of the observable gamma-rays are produced in the intergalactic cascades. This work focuses on investigating the spectral and angular features of one of the cascade models, the Intergalactic Hadronic Cascade Model (IHCM) in the contemporary astrophysical models of Extragalactic Magnetic Field (EGMF). For IHCM, EGMF largely determines the deflection of primary cosmic rays and electrons of intergalactic cascades and, thus, is of vital importance. Contemporary Hackstein models are considered in this paper and compared to the model of Dolag. The models assumed are based on simulations of the local part of large-scale structure of the Universe and differ in the assumptions for the seed field. This work provides spectral energy distributions (SEDs) and angular extensions of two extreme TeV blazars, 1ES 0229+200 and 1ES 0414+009. It is demonstrated that observable SEDs inside a typical point spread function of imaging atmospheric Cherenkov telescopes (IACTs) for IHCM would exhibit a characteristic high-energy attenuation compared to the ones obtained in hadronic models that do not consider EGMF, which makes it possible to distinguish among these models. At the same time, the spectra for IHCM models would have longer high energy tails than some available spectra for the ALP models and the universal spectra for the Electromagnetic Cascade Model (ECM). The analysis of the IHCM observable angular extensions shows that the sources would likely be identified by most IACTs not as point sources but rather as extended ones. These spectra could later be compared with future observation data of such instruments as Cherenkov Telescope Array (CTA) and LHAASO.

1. Introduction

Besides having many features that attract scientific interest and prompt their continuous study, blazars are also used as standard probes to determine the opacity of the Universe to gamma-rays. Gamma-rays from distant blazars are subject to absorption on the photons of Extragalactic Background Light (EBL) through the pair production process. This means that the observable Spectral Energy Distributions (SEDs) of gamma-rays from such sources would be attenuated and that one can obtain the intrinsic SEDs of the sources by correcting for the gamma-ray absorption. In this work extreme TeV blazars are defined as blazars, which have intrinsic SEDs peaking at TeV energies. By now, approximately 10 extreme TeV blazars have been registered [1]. Extreme TeV blazars, as compared to such blazars as Mkn 501 and Mkn 421, typically show weak and slow variability for the high energy and very high energy bands, which makes them suitable for studying the effects of intergalactic magnetic and photon fields.
Authors of [2] have obtained intrinsic SEDs for blazars of various classes (some of which were extreme TeV blazars) and found that for a number of sources there is an apparent excess of gamma-rays in the optically thick region of the spectra. The authors of [3] have also conducted a search for this anomaly, favoring its presence with a significance of ∼ 2 σ .
Several gamma-ray propagation models have been developed to account for the possible hardening of the intrinsic spectra. One of such models introduces the so-called axion-like particles (ALPs) which are assumed to be pseudoscalar bosons with extremely low masses that oscillate into photons and vice versa in a similar way to how different flavors of neutrinos oscillate [4,5,6,7,8,9,10,11]. The theory of gamma-ALP mixing was first described in [12] and later developed in [13,14,15,16,17,18]. The authors of [2] credited ALPs as one of the possible explanations to their high energy anomaly. Indeed, if gamma-rays convert to ALPs in the presence of Extragalactic Magnetic Field (EGMF) and propagate an appreciable distance as ALPs (which are not absorbed on EBL photons) before converting back into gamma-rays near the observer, these gamma-rays experience a lesser degree of absorption on EBL photons, which can explain the hardening of the intrinsic blazar spectra. ALPs are characterized by two parameters: their mass m A L P and the gamma-ALP coupling constant g γ − A L P . The latest existing constraints on these parameters are described in [19] (see also [20,21,22,23]).
Alternatively, the excess of photons could be accounted for in the so-called cascade models. These models presuppose that a part of gamma-rays is produced not inside the source but rather in the intergalactic cascades as secondary particles [24,25,26,27]. In the Electromagnetic Cascade Model (ECM) [28,29] gamma-rays are considered to be the primary particles, and the cascades are initiated by the inverse Compton scattering of electrons produced in primary gamma-ray interactions with EBL photons on the photons of Cosmic Microwave Background (CMB). The other type of cascade models, Intergalactic Hadronic Cascade Model (IHCM) [30,31], assumes Ultra-High Energy Cosmic Rays (UHECR) as primary particles that initiate cascades via Bethe–Heitler pair production and photohadronic processes on various photon fields (CMB, EBL, Universal Radio Background (URB)).
For cascade models the account of state-of-the-art models of EGMF is vital because in these models stronger magnetic fields deflect primary CRs and electrons of intergalactic cascades, which has a considerable impact on both SED and angular extension of the source. Without the account of EGMF, the observable SEDs in the IHCM (in this case called “basic hadronic cascade model”) inside a typical IACT PSF would have longer high energy tails because in this case primary protons and cascade electrons would not be deflected by the EGMF. An extensive research of basic hadronic cascade model has been done by the author of this paper and his co-authors in [32]. For this work I use and compare several of the latest EGMF models based on MHD simulations following the large-scale structure of the Universe [33,34] in the IHCM. For ALP models stronger magnetic fields mean smaller values of the mixing constant g γ − A L P and, thus, higher sensitivities to ALPs. Thus, the use of astrophysically accurate EGMF models could help constrain the parameter space of g γ − A L P and facilitate the search for gamma-ALP oscillations. This work does not consider the ALP models, although a similar simulation of these models would be beneficial.
In this work I provide model SEDs and angular extensions of observable gamma-rays from two extreme TeV blazars in the IHCM using several models of EGMF. Since the possible excess of observable gamma-rays in the TeV region of blazar spectra is one of the problems that will be investigated by the soon-to-be-operational Cherenkov Telescope Array (CTA) [35], these results would provide a valuable model comparison to the future CTA observations of such sources. The collaboration of the LHAASO particle detector [36] has also included some extreme TeV blazars in its scientific program.
The paper is organized as follows. In Section 2 the contemporary models of EGMF are discussed and the choice of models used for this work is specified. In Section 3 the simulation methods are described, including the choice of modeling codes, photon field models, and sources. In Section 4 the main results of this paper are presented and discussed. Finally, in Section 5 the main conclusions of this paper are drawn, its limitations are outlined, and prospects for future research are discussed.

2. EGMF Models

There have been several works that model the EGMF with different assumptions for the seed magnetic field [33,34,37,38,39,40,41]. Most of these models are assume that the seed magnetic fields were generated during the formation of the large-scale structure (i.e., astrophysical models) and use magneto-hydrodynamical simulations to model the evolution of these fields.
Three of these models, Refs. [33,34,39] are being frequently used for various astrophysical research, such as extragalactic CR propagation and deflection studies. An important difference between the models of Sigl et al. [39] and Dolag et al. [34] (hereafter named D05 for simplicity) is that in [39] the seed magnetic field is generated from a zero field through the Biermann battery, while in [34] it is assumed as a uniform field with strength B s e e d ∼ 10 − 9 G. Moreover, Ref. [34] is a model of the local part of the large-scale structure with Milky Way in the center constrained by the astrophysical data.
The models of Hackstein et al. [33] (hereafter named H18 for simplicity) improve on the D05 by using more advanced numerical methods and initial conditions of [42], which are based on more contemporary observational constraints. H18 include six different models of EGMF: three primordial ones (i.e., models in which the seed magnetic field is introduced in the early Universe, e.g., during the inflation or phase transition epochs) and three astrophysical ones. The astrophysical models assume a seed magnetic field of B s e e d ∼ 10 − 11 nG and impulsive thermal and magnetic feedback in haloes as the mechanism of EGMF generation. These models differ in the energy budget assumptions with astrophysical model assuming the release of 5 × 10 58 erg per feedback episode starting from redshift z = 4 , astrophysical R model— 10 60 erg per feedback episode from z = 4 , and astrophysical 1R model—an energy budget changing from 10 60 to 5 × 10 58 per feedback episode starting from z = 1 . A recent work by [43] has revealed that astrophysical R and astrophysical 1R show almost the same dependence of mean deflections of CRs on their rigidity. For these models the deflections are strongest among all considered astrophysical models expect [39], followed closely by D05. The astrophysical model demonstrates the lowest mean deflection values.
This work considers three astrophysical EGMF models: D05, and astrophysical and astrophysical R of H18.

3. Simulation Methods

The simulation was done in several steps.
Firstly, the publicly available CRPropa3 simulation framework [44] was used to model the propagation of primary protons and their deflection on the filaments of EGMF. CRPropa3 allows to load the local cubic volumes of D05 and H18 magnetic fields with edge lengths of 132 Mpc and 249 Mpc respectively. For the simulations 10 5 protons with primary energies 30 EeV were isotropically emitted from random points throughout the simulated EGMF volume. The replication of the EGMF volume allowed for propagating these protons to large distances (up to 1200 Mpc) and tracking their energies, positions, and directions every 5 Mpc of the way. Throughout the proton propagation the code accounted for adiabatic as well as interaction losses. The interactions included Bethe–Heitler pair production on CMB and EBL (using the model by Gilmore et al. [45]) photon fields and pion production on CMB, EBL, and URB (using the model by Protheroe et al. [46]) photon fields. As a result, the deflections of 10 5 protons were calculated for every 5 Mpc of their way.
The next step of the simulation was to calculate the observable spectra for gamma-rays produced in the intergalactic cascades. For that the underlying assumption of the so-called weak universality was used as introduced in [47] and previously used by the author of this paper in [32]. As explained in [32], weak universality means that “the spectrum of observable gamma-rays is practically independent of the energy and the type, photon/electron, of the primary particle but depends on the redshift of the source”. Thus, observable cascade gamma-ray spectra could be calculated for a range of redshifts, and an SED of a source with redshift z s could be obtained by summing the cascade SEDs from all the intermediary redshifts from 0 to z s .
To this end the publicly available ELMAG 2.03 code [48] was used to compute a database of the universal EM cascade spectra with primary photon energy 1 PeV and redshift z distributed randomly and uniformly varying from 0 to 0.30. The EBL model [45] was used for these calculations. This code was used in the previous works of this author, and its applicability and sensitivity of the results to the choice of EBL models are discussed in [32]. In this work the deflections of secondary particles in voids were neglected. If they were taken into account, it would broaden the observable angular extensions of the sources as compared to the results below.
The final step of the simulation utilized an improved version of the hybrid code developed by the author of this paper and his colleagues and used previously in [32]. This code propagated the protons from the source to the observer using semi-analytic formulas that calculate adiabatic losses of protons, their pair production losses on CMB [49], and pion production losses on both CMB and EBL [50] and combining them with Monte Carlo simulations of precomputed cascade spectra and proton deflections in EGMF described above. As an output, this code produced a file with coordinates, directions, energies, and observable cascade spectra of 10 4 protons on every redshift step d z = 10 − 4 . This file was then used to produce the averaged SEDs and model angular extensions of the sources shown in the next section.
Two extreme TeV blazars were chosen as sources for this work because of their low variability. They were 1ES 0229+200 with redshift z = 0.14 and 1ES 0414+009 with redshift z = 0.287 . The spectrum of the first source was measured by both the H.E.S.S. Collaboration [51] (with threshold energy E t h r = 580 GeV, total exposure time 41.8 h, and mean zenith angle Z m e a n = 46 ∘ ) and the VERITAS Collaboration [52] (with threshold energy E t h r = 300 GeV and total exposure time 54.3 h). The spectrum of the second source was measured by H.E.S.S. [53] (with threshold energy E t h r = 200 GeV, total exposure time 73.7 h, and zenith angles varying between 22 ∘ and 41 ∘ with a mean value of Z m e a n = 26 ∘ ).

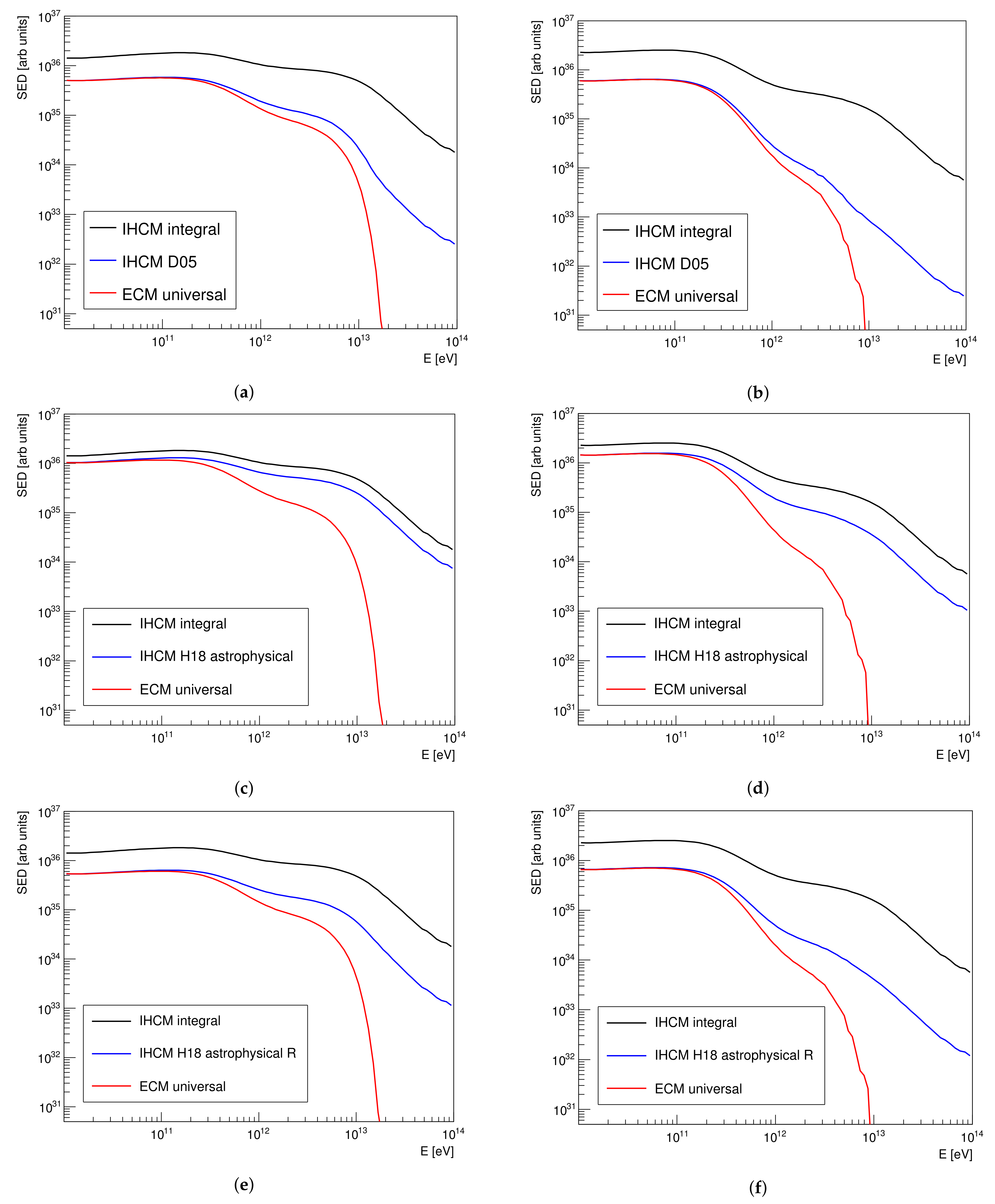
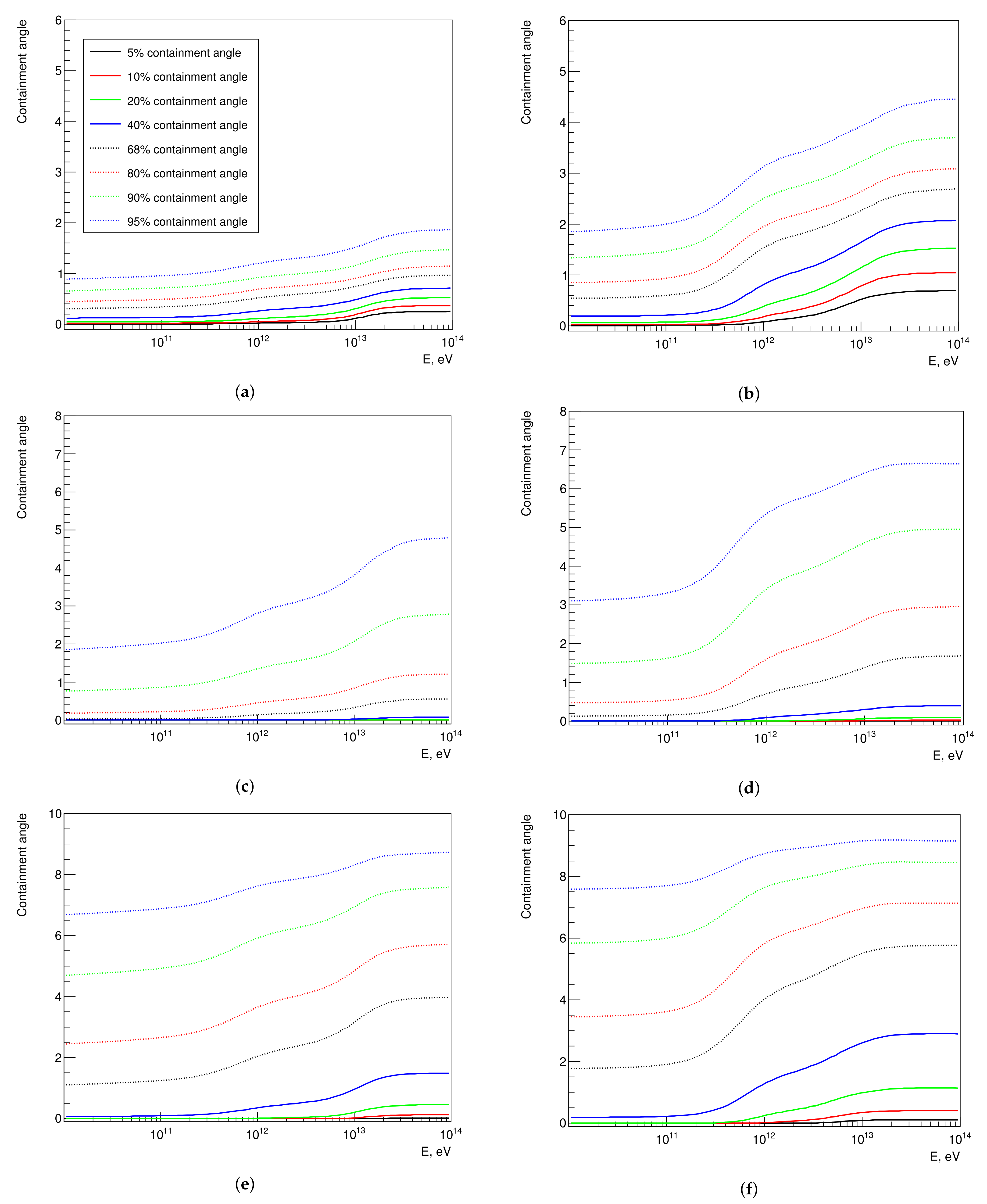
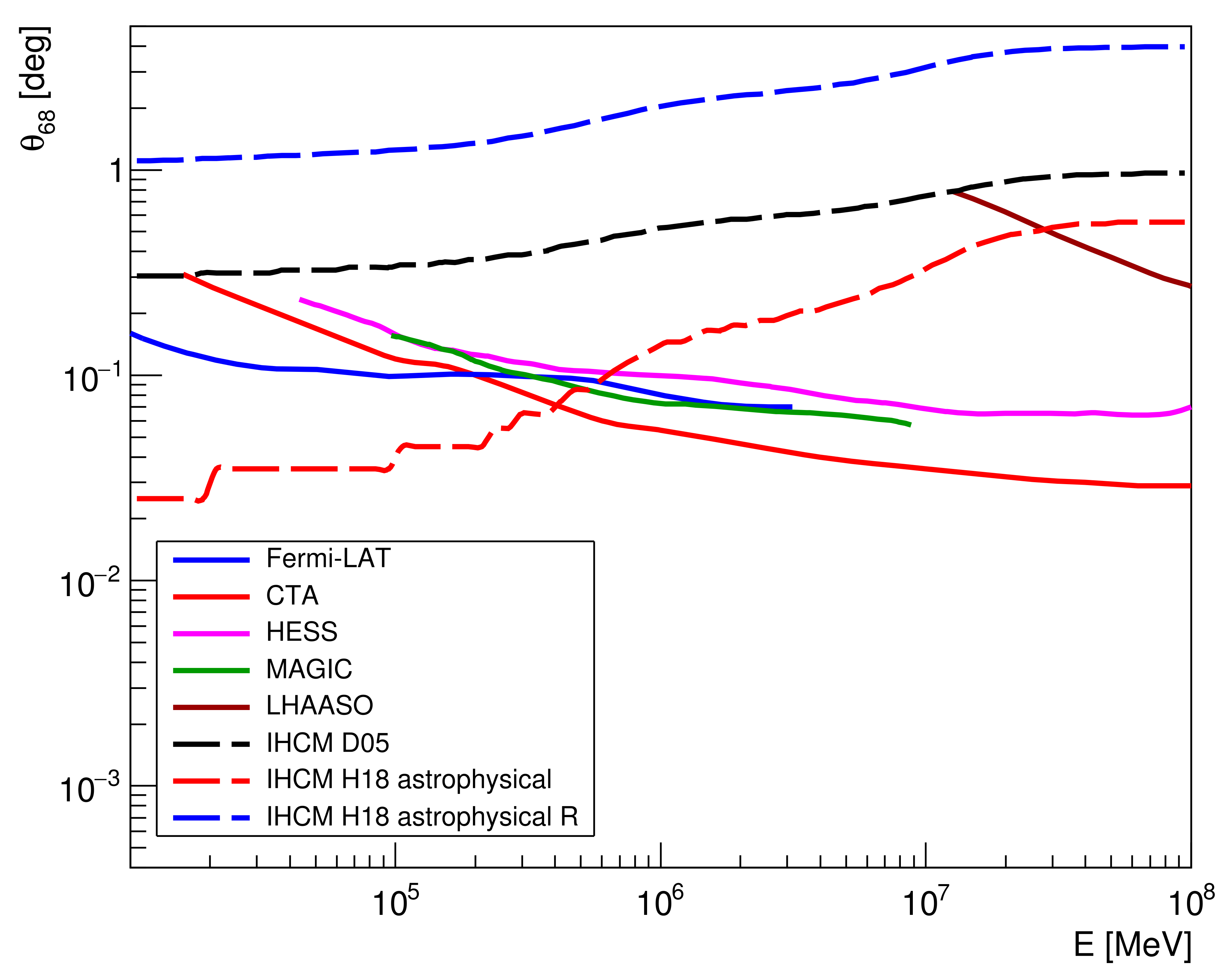
4. Results

In order to see how the observable SEDs in the framework of the IHCM would look like inside the Point Spread function (PSF) of observing gamma-ray telescopes the following cut was applied to the value of the observable angle (i.e., the angle between the direction of an incident cascade gamma-ray and the line source-observer): θ o b s < 0 . 1 ∘ . The value 0 . 1 ∘ represents a typical average value of PSFs of IACTs like H.E.S.S.
Figure 1 shows these observable SEDs (denoted as blue curves) in comparison with the integral observable SEDs (black curves), for which no cuts on the observable angles were applied (these SEDs correspond to the basic hadronic cascade model, which assumes a zero EGMF), and the universal SEDs of ECM, where gamma-rays were the primary particles (red curves). One can see that the model SEDs from D05 and astrophysical R EGMF models demonstrated a significant attenuation in comparison with the integral spectra, especially towards the higher energies. This attenuation was the strongest for the D05 model and the weakest for the astrophysical model.
Figure 2 demonstrates a comparison between IHCM model SEDs for the source 1ES 0229+200 ( z = 0.14 ) and all considered EGMF models and ALP model SEDs obtained in [14] for a similar z = 0.116 , ALP masses m A L P = 10 − 10 eV and two EBL options: Primack et al. [54] (P05) and Kneiske et al. [55] (K04). All IHCM models were normalized at 1 TeV. It can be seen that IHCM SEDs in this case had longer high energy tails than ALP SEDs. However, this result was strongly dependent on the assumed parameters of the ALPs. A more thorough study examining different ALP models with varied parameters is underway and will be published elsewhere.
Figure 3 demonstrates the observable angular extensions of sources in the framework of the IHCM in the form of containment angle dependence on observable energy. Different curves denote different quantiles or containment angle vs. observable energy dependences for different containment values (e.g., black solid curve denotes an angle, inside which 5% of the observable spectrum was contained). One can see two distinct patterns in these graphs. For the D05 model, all the values of containment angles increased substantially with energy for E > 10 12 eV so that 68 % of all observable angles were greater than 0 . 73 ∘ at E = 10 TeV for the source 1ES 0229+200 ( z = 0.14 ) and 2 . 35 ∘ for the source 1ES 0414+009 ( z = 0.287 ) and the same energy.
A different pattern was noticeable for H18 models. While the upper quantiles of containment angles rose rather quickly with energy, the lower ones (less than 40 % for the astrophysical model and less than 10 % for the astrophysical R model) showed only a very slight increase in the values of containment angles. This could mean that in these models a sizeable part of protons did not encounter any filaments on their way and, thus, did not experience strong deflections. So, the deflection effect of filaments for the H18 models was stronger, while at the same time the filaments themselves could be thinner or more far between in comparison with the D05 model.
It can also be said that the characteristic angular extension of these sources (for instance, the value of θ 68 ) mostly fell outside the PSFs of the gamma-ray telescopes, which is clearly seen in Figure 4 (showing PSFs of Fermi-LAT, CTA, H.E.S.S., MAGIC, and LHAASO). For this figure angular resolutions for Fermi-LAT were taken from [56], for H.E.S.S., MAGIC and CTA—from [35], for LHAASO—from [57]. The angular resolution for VERITAS [58,59] was similar to that of H.E.S.S. and MAGIC. The results show that these telescopes would see these sources as extended ones as compared to point sources. Only for the astrophysical model of EGMF and the source 1ES 0229+200 ( z = 0.14 ) the value of θ 68 is lower than the PSFs of these telescopes for energies E < 0.7 TeV. Given that the source 1ES 0229+200 has been reported as a point source based on IACT observations [51], the angular extension predicted by the IHCM diminished this model’s plausibility. Further statistical analysis is required to constrain or possibly disfavor the intergalactic hadronic cascade model.
These SEDs and angular extensions could later be compared with future observation data by imaging atmospheric Cherenkov telescopes (IACTs) such as CTA or particle detectors such as LHAASO. For example, Figure 5 shows the SEDs measured by H.E.S.S. and VERITAS with the model SEDs of the three models of EGMF considered in this paper inside the PSF of the LHAASO particle detector (normalized to fit the data using the same normalization constant) as well as the 1-year and 5-year sensitivity plots of LHAASO obtained in [36] with statistical significance of 5 standard deviations. The PSF of the LHAASO detector was taken from [57]. Since the PSF was available only for energies E > 10 TeV, an integral SED was used for lower energies. It can be seen that LHAASO particle detector had an outstanding sensitivity at energies > 10 TeV allowing it to register the hard tails in the SEDs of certain blazars like 1ES 0229+200, which were included in its scientific program.

5. Discussion and Conclusions

This work presents SEDs and angular extensions of observable gamma-rays from two extreme TeV blazars, 1ES 0229+200 ( z = 0.14 ) and 1ES 0414+009 ( z = 0.287 ), in the framework of the Intergalactic Hadronic Cascade Model for several contemporary models of EGMF (astrophysical and astrophysical R of H18) and D05.
There is a number of features that the observable SEDs and angular extensions demonstrate, which could be used to distinguish between different propagation models. In the IHCM there is a visible attenuation of observable SEDs inside the PSF of observing instruments revealing itself at higher energies (as compared to hadronic models neglecting the EGMF). This attenuation is more pronounced for D05, where at E = 100 TeV the difference between the integral SEDs and the SEDs inside a PSF of 0 . 1 ∘ has a factor of ∼80 for the source 1ES 0229+200 and ∼220 for the source 1ES 0414+009. The ALP models exhibit one important feature: a step-like irregularity at lower energies corresponding to a sizeable drop in the intensity of photons (which could be up to 1/3 of its value) related to two photon polarization states attaining equipartition with one polarization state of ALP above a certain critical energy [14]. As of yet, this irregularity has not been observed in the spectra of several sources [20,21], which led to some of the constraints on the mixing parameters. In comparison with the ALP model SEDs from [14] the IHCM SEDs showed longer high energy tails. Further comparative analysis of these models including ALP models with varied parameter values is necessary for determining the discrimination criteria between the SEDs in IHCM and ALP models.
The analysis of angular extensions of extreme TeV blazars in the framework of IHCM demonstrated clear distinctions between D05 and H18 models with H18 models having fewer or thinner but at the same time more deflective filaments than D05. It has also shown that these sources would be mostly identified by the gamma-ray telescopes as extended sources, not the point ones. The only sources that could in principle be identified as point sources are near sources in the astrophysical model of EGMF. Since this kind of angular extension has not been supported by the IACT observational data, the author of this paper concludes that a thorough statistical analysis of angular extension is crucial for constraining or disfavoring the IHCM.
These SEDs and angular extensions could be compared with future IACT and particle detector observations. For example, the characteristics of CTA allow this telescope to investigate the gamma-ray signal from distant extreme TeV blazars with its angular resolution improving from ∼ 0 . 3 ∘ at 20 GeV to ∼ 0 . 03 ∘ at 100 GeV. Moreover, LHAASO’s outstanding sensitivity at energies >10 TeV allows it to observe the high-energy part in the blazar SEDs as well.
A part of cascade energy can be lost due to plasma beam instabilities [60]. There have been many works modeling these collective plasma losses using Particle-In-Cell simulation methods (they are listed and reviewed in relation to cascade pair beams in Section 4.3 of [61]). However, as of yet there is no clear consensus on the extent of these losses in the context of extragalactic gamma-ray propagation from distant blazars. Such losses are not accounted for in this work; if they are present and appreciable, they could further attenuate the observable gamma-ray spectra.
The consideration of other EBL models, primary proton energies, source redshifts, primary proton angular distributions as well as the account of electron deflection and “additional” processes such as triplet pair production and double pair production could also change the observable SEDs and angular extensions. The effects of these changes are discussed in detail in [62].

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

Author is indebted to T. Dzhatdoev for providing invaluable guidance and assistance throughout all the stages of this work. Author is also grateful to S. Hackstein for clarifying the specifics of the CRPropa3 simulations and pointing out the relevant works connected to EGMF models.

Conflicts of Interest

Author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Biteau, J.; Prandini, E.; Costamante, L.; Lemoine, M.; Padovani, P.; Pueschel, E.; Resconi, E.; Tavecchio, F.; Taylor, A.; Zech, A. Progress in unveiling extreme particle acceleration in persistent astrophysical jets. Nat. Astron. 2020, 4, 124–131. [Google Scholar] [CrossRef]
  2. Horns, D.; Meyer, M. Indications for a pair-production anomaly from the propagation of VHE gamma-rays. J. Cosmol. Astropart. Phys. 2012, 2012, 033. [Google Scholar] [CrossRef][Green Version]
  3. Korochkin, A.; Rubtsov, G.; Troitsky, S. Search for anomalous features in gamma-ray blazar spectra corrected for the absorption on the extragalactic background light. J. Cosmol. Astropart. Phys. 2019, 2019, 002. [Google Scholar] [CrossRef]
  4. Pontecorvo, B. Mesonium and anti-mesonium. Sov. Phys. Jetp 1957, 6, 429. [Google Scholar]
  5. Pontecorvo, B. Inverse beta processes and nonconservation of lepton charge. Zh. Eksp. Teor. Fiz. 1957, 34, 247. [Google Scholar]
  6. Pontecorvo, B. Neutrino Experiments and the Problem of Conservation of Leptonic Charge. Zh. Eksp. Teor. Fiz. 1967, 26, 1717–1725. [Google Scholar]
  7. Wolfenstein, L. Neutrino oscillations in matter. Phys. Rev. D 1978, 17, 2369–2374. [Google Scholar] [CrossRef]
  8. Wolfenstein, L. Neutrino oscillations and stellar collapse. Phys. Rev. D 1979, 20, 2634–2635. [Google Scholar] [CrossRef]
  9. Mikheyev, S.P.; Smirnov, A.Y. Resonance enhancement of oscillations in matter and solar neutrino spectroscopy. Yad. Fiz. 1985, 42, 1441–1448. [Google Scholar]
  10. Mikheyev, S.P.; Smirnov, A.Y. Resonant amplification of ν oscillations in matter and solar-neutrino spectroscopy. Il Nuovo Cim. C 1986, 9, 17–26. [Google Scholar] [CrossRef]
  11. Mikheev, S.P.; Smirnov, A.I. Neutrino oscillations in a medium with variable density and θ-flares from gravitational collapses of stars. Zhurnal Eksperimentalnoi I Teor. Fiz. 1986, 91, 7–13. [Google Scholar]
  12. Raffelt, G.; Stodolsky, L. Mixing of the photon with low-mass particles. Phys. Rev. D 1988, 37. [Google Scholar] [CrossRef]
  13. De Angelis, A.; Roncadelli, M.; Mansutti, O. Evidence for a new light spin-zero boson from cosmological gamma-ray propagation? Phys. Rev. D 2007, 76. [Google Scholar] [CrossRef]
  14. Sánchez-Conde, M.A.; Paneque, D.; Bloom, E.; Prada, F.; Domínguez, A. Hints of the existence of axionlike particles from the gamma-ray spectra of cosmological sources. Phys. Rev. D 2009, 79. [Google Scholar] [CrossRef]
  15. Kartavtsev, A.; Raffelt, G.; Vogel, H. Extragalactic photon-ALP conversion at CTA energies. J. Cosmol. Astropart. Phys. 2017, 2017, 024. [Google Scholar] [CrossRef]
  16. Montanino, D.; Vazza, F.; Mirizzi, A.; Viel, M. Enhancing the Spectral Hardening of Cosmic TeV Photons by Mixing with Axionlike Particles in the Magnetized Cosmic Web. Phys. Rev. Lett. 2017, 119. [Google Scholar] [CrossRef]
  17. Galanti, G.; Roncadelli, M. Behavior of axionlike particles in smoothed out domainlike magnetic fields. Phys. Rev. D 2018, 98. [Google Scholar] [CrossRef]
  18. Galanti, G.; Tavecchio, F.; Roncadelli, M.; Evoli, C. Blazar VHE spectral alterations induced by photon–ALP oscillations. Mon. Not. R. Astron. Soc. 2019, 487, 123–132. [Google Scholar] [CrossRef]
  19. Dessert, C.; Long, A.J.; Safdi, B.R. No evidence for axions from Chandra observation of magnetic white dwarf. arXiv 2021, arXiv:2104.12772. [Google Scholar]
  20. Abramowski, A.; Acero, F.; Aharonian, F.; Benkhali, F.A.; Akhperjanian, A.G. Constraints on axionlike particles with H.E.S.S. from the irregularity of the PKS2155-304energy spectrum. Phys. Rev. D 2013, 88. [Google Scholar] [CrossRef]
  21. Ajello, M.; Albert, A.; Anderson, B.; Baldini, L.; Barbiellini, G. Search for Spectral Irregularities due to Photon–Axionlike-Particle Oscillations with the Fermi Large Area Telescope. Phys. Rev. Lett. 2016, 116. [Google Scholar] [CrossRef] [PubMed]
  22. Libanov, M.; Troitsky, S. On the impact of magnetic-field models in galaxy clusters on constraints on axion-like particles from the lack of irregularities in high-energy spectra of astrophysical sources. Phys. Lett. B 2020, 802, 135252. [Google Scholar] [CrossRef]
  23. The CAST Collaboration. New CAST limit on the axion–photon interaction. Nat. Phys. 2017, 13, 584–590. [Google Scholar] [CrossRef]
  24. Berezinsky, V.S.; Smirnov, A.Y. Cosmic neutrinos of ultra-high energies and detection possibility. Astrophys. Space Sci. 1975, 32, 461–482. [Google Scholar] [CrossRef]
  25. Protheroe, R.J. Effect of electron-photon cascading on the observed energy spectra of extragalactic sources of ultra-high-energy -rays. Mon. Not. R. Astron. Soc. 1986, 221, 769–788. [Google Scholar] [CrossRef]
  26. Protheroe, R.J.; Stanev, T. Electron-photon cascading of very high-energy gamma-rays in the infrared background. Mon. Not. R. Astron. Soc. 1993, 264, 191–200. [Google Scholar] [CrossRef][Green Version]
  27. Aharonian, F.A.; Coppi, P.S.; Voelk, H.J. Very high energy gamma rays from active galactic nuclei: Cascading on the cosmic background radiation fields and the formation of pair halos. Astrophys. J. 1994, 423, L5. [Google Scholar] [CrossRef]
  28. Aharonian, F.A.; Akhperjanian, A.G.; Barrio, J.A.; Bernlöhr, K.; Bojahr, H. The time averaged TeV energy spectrum of MKN 501 of the extraordinary 1997 outburst as measured with the stereoscopic Cherenkov telescope system of HEGRA. Astron. Astrophys. 1999, 349, 11–28. [Google Scholar]
  29. Aharonian, F.A.; Timokhin, A.N.; Plyasheshnikov, A.V. On the origin of highest energy gamma-rays from Mkn 501. Astron. Astrophys. 2002, 384, 834–847. [Google Scholar] [CrossRef][Green Version]
  30. Waxman, E.; Coppi, P. Delayed GeV-TeV Photons from Gamma-Ray Bursts Producing High-Energy Cosmic Rays. Astrophys. J. 1996, 464, L75. [Google Scholar] [CrossRef]
  31. Uryson, A.V. Possible observation of electromagnetic cascades in extragalactic space. J. Exp. Theor. Phys. 1998, 86, 213–219. [Google Scholar] [CrossRef]
  32. Dzhatdoev, T.A.; Khalikov, E.V.; Kircheva, A.P.; Lyukshin, A.A. Electromagnetic cascade masquerade: A way to mimicγ-axion-like particle mixing effects in blazar spectra. Astron. Astrophys. 2017, 603, A59. [Google Scholar] [CrossRef]
  33. Hackstein, S.; Vazza, F.; Brüggen, M.; Sorce, J.G.; Gottlöber, S. Simulations of ultra-high energy cosmic rays in the local Universe and the origin of cosmic magnetic fields. Mon. Not. R. Astron. Soc. 2018, 475, 2519–2529. [Google Scholar] [CrossRef]
  34. Dolag, K.; Grasso, D.; Springel, V.; Tkachev, I. Constrained simulations of the magnetic field in the local Universe and the propagation of ultrahigh energy cosmic rays. J. Cosmol. Astropart. Phys. 2005, 2005, 009. [Google Scholar] [CrossRef]
  35. The CTA Consortium. Science with the Cherenkov Telescope Array; World Scientific: Singapore, 2018. [Google Scholar] [CrossRef]
  36. Bai, X.; Bi, B.Y.; Bi, X.J.; Cao, Z.; Chen, S.Z. The Large High Altitude Air Shower Observatory (LHAASO) Science White Paper. arXiv 2019, arXiv:1905.02773. [Google Scholar]
  37. Kulsrud, R.M.; Cen, R.; Ostriker, J.P.; Ryu, D. The Protogalactic Origin for Cosmic Magnetic Fields. Astrophys. J. 1997, 480, 481–491. [Google Scholar] [CrossRef]
  38. Ryu, D.; Kang, H.; Biermann, P.L. Cosmic magnetic fields in large scale filaments and sheets. arXiv 1998, arXiv:astro-ph/astro-ph/9803275. [Google Scholar]
  39. Sigl, G.; Miniati, F.; Enßlin, T.A. Ultrahigh energy cosmic ray probes of large scale structure and magnetic fields. Phys. Rev. D 2004, 70. [Google Scholar] [CrossRef]
  40. Das, S.; Kang, H.; Ryu, D.; Cho, J. Propagation of Ultra–High-Energy Protons through the Magnetized Cosmic Web. Astrophys. J. 2008, 682, 29–38. [Google Scholar] [CrossRef]
  41. Hackstein, S.; Vazza, F.; Brüggen, M.; Sigl, G.; Dundovic, A. Propagation of ultrahigh energy cosmic rays in extragalactic magnetic fields: A view from cosmological simulations. Mon. Not. R. Astron. Soc. 2016, 462, 3660–3671. [Google Scholar] [CrossRef]
  42. Sorce, J.G.; Gottlöber, S.; Yepes, G.; Hoffman, Y.; Courtois, H.M.; Steinmetz, M.; Tully, R.B.; Pomarède, D.; Carlesi, E. Cosmicflows Constrained Local UniversE Simulations. Mon. Not. R. Astron. Soc. 2015, 455, 2078–2090. [Google Scholar] [CrossRef][Green Version]
  43. Eichmann, B. High Energy Cosmic Rays from Fanaroff-Riley radio galaxies. J. Cosmol. Astropart. Phys. 2019, 2019, 009. [Google Scholar] [CrossRef]
  44. Alves Batista, R.; Dundovic, A.; Erdmann, M.; Kampert, K.H.; Kuempel, D.; Müller, G.; Sigl, G.; van Vliet, A.; Walz, D.; Winchen, T. CRPropa 3-a public astrophysical simulation framework for propagating extraterrestrial ultra-high energy particles. J. Cosmol. Astropart. Phys. 2016, 2016, 038. [Google Scholar] [CrossRef]
  45. Gilmore, R.C.; Somerville, R.S.; Primack, J.R.; Domínguez, A. Semi-analytic modelling of the extragalactic background light and consequences for extragalactic gamma-ray spectra. Mon. Not. R. Astron. Soc. 2012, 422, 3189–3207. [Google Scholar] [CrossRef]
  46. Protheroe, R.; Biermann, P. A new estimate of the extragalactic radio background and implications for ultra-high-energy γ-ray propagation. Astropart. Phys. 1996, 6, 45–54. [Google Scholar] [CrossRef]
  47. Berezinsky, V.; Kalashev, O. High-energy electromagnetic cascades in extragalactic space: Physics and features. Phys. Rev. D 2016, 94. [Google Scholar] [CrossRef]
  48. Kachelrieß, M.; Ostapchenko, S.; Tomàs, R. ELMAG: A Monte Carlo simulation of electromagnetic cascades on the extragalactic background light and in magnetic fields. Comput. Phys. Commun. 2012, 183, 1036–1043. [Google Scholar] [CrossRef]
  49. Kelner, S.R.; Aharonian, F.A. Energy spectra of gamma rays, electrons, and neutrinos produced at interactions of relativistic protons with low energy radiation. Phys. Rev. D 2008, 78. [Google Scholar] [CrossRef]
  50. Berezinsky, V.; Gazizov, A.; Grigorieva, S. On astrophysical solution to ultrahigh energy cosmic rays. Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
  51. Aharonian, F.; Akhperjanian, A.G.; de Almeida, U.B.; Bazer-Bachi, A.R.; Behera, B. New constraints on the mid-IR EBL from the HESS discovery of VHE γ-rays from 1ES 0229+200. Astron. Astrophys. 2007, 475, L9–L13. [Google Scholar] [CrossRef]
  52. Aliu, E.; Archambault, S.; Arlen, T.; Aune, T.; Behera, B. A three-year multi-wavelength study of the very-high-energy γ-ray blazar 1ES 0229+200. Astrophys. J. 2014, 782, 13. [Google Scholar] [CrossRef]
  53. Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G. Discovery of hard-spectrumγ-ray emission from the BL Lacertae object 1ES 0414+009. Astron. Astrophys. 2012, 538, A103. [Google Scholar] [CrossRef]
  54. Primack, J.R. Observational Gamma-ray Cosmology. In Proceedings of the AIP Conference Proceedings, Salt Lake City, UT, USA, 10–11 August 2005. [Google Scholar] [CrossRef]
  55. Kneiske, T.M.; Bretz, T.; Mannheim, K.; Hartmann, D.H. Implications of cosmological gamma-ray absorption. Astron. Astrophys. 2004, 413, 807–815. [Google Scholar] [CrossRef]
  56. Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B. The Large area telescope on thefermi gamma-ray space telescopemission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
  57. Aharonian, F.; An, Q.; Axikegu; Bai, L.X.; Bai, Y.W.; Bao, D.; Bastieri, X.J.; Bi, Y.J.; Bi, H.; Cai, J.T.; et al. The observation of the Crab Nebula with LHAASO-KM2A for the performance study. arXiv 2021, arXiv:2010.06205. [Google Scholar]
  58. Krennrich, F.; Bond, I.; Boyle, P.; Bradbury, S.; Buckley, J. VERITAS: The Very Energetic Radiation Imaging Telescope Array System. New Astron. Rev. 2004, 48, 345–349. [Google Scholar] [CrossRef]
  59. Park, N. Performance of the VERITAS experiment. In Proceedings of the 34th International Cosmic Ray Conference—PoS(ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015. [Google Scholar] [CrossRef]
  60. Broderick, A.E.; Chang, P.; Pfrommer, C. The cosmological impact of luminous Tev blazars. I. implications of plasma instabilities for the intergalactic magnetic field and extragalactic gamma-ray background. Astrophys. J. 2012, 752, 22. [Google Scholar] [CrossRef]
  61. Pohl, M.; Hoshino, M.; Niemiec, J. PIC simulation methods for cosmic radiation and plasma instabilities. Prog. Part. Nucl. Phys. 2020, 111, 103751. [Google Scholar] [CrossRef]
  62. Khalikov, E.V.; Dzhatdoev, T.A. Observable spectral and angular distributions of γ-rays from extragalactic ultrahigh energy cosmic ray accelerators: The case of extreme TeV blazars. Mon. Not. R. Astron. Soc. 2021, 505, 1940–1953. [Google Scholar] [CrossRef]
Universe 07 00220 g001
Figure 1. Observable Spectral Energy Distributions (SEDs) for intergalactic cascade models. Blue curves denote the SEDs in the framework of the Intergalactic Hadronic Cascade Model (IHCM) inside the Point Spread Function (PSF) of 0.1°. Black curves denote the integral SEDs or SEDs for the basic hadronic cascade model (i.e., SEDs, for which no cuts on the observable angles have been applied). Red curves denote the universal spectra in the framework of the Electromagnetic Cascade Model (ECM). (a,c,e) demonstrate the results for the source 1ES 0229+200 (z = 0.14) and D05, astrophysical (H18), and astrophysicalR (H18) models of Extragalactic Magnetic Field (EGMF) respectively; (b,d,f)—for the source 1ES 0414+009 (z = 0.287) and D05, astrophysical (H18), and astrophysical R (H18) models of EGMF respectively.
Figure 1. Observable Spectral Energy Distributions (SEDs) for intergalactic cascade models. Blue curves denote the SEDs in the framework of the Intergalactic Hadronic Cascade Model (IHCM) inside the Point Spread Function (PSF) of 0.1°. Black curves denote the integral SEDs or SEDs for the basic hadronic cascade model (i.e., SEDs, for which no cuts on the observable angles have been applied). Red curves denote the universal spectra in the framework of the Electromagnetic Cascade Model (ECM). (a,c,e) demonstrate the results for the source 1ES 0229+200 (z = 0.14) and D05, astrophysical (H18), and astrophysicalR (H18) models of Extragalactic Magnetic Field (EGMF) respectively; (b,d,f)—for the source 1ES 0414+009 (z = 0.287) and D05, astrophysical (H18), and astrophysical R (H18) models of EGMF respectively.
Universe 07 00220 g001
Universe 07 00220 g002
Figure 2. Comparison of IHCM model SEDs of the blazar 1ES 0229+200 ( z = 0.14 ) with ALP SEDs from [14] ( z = 0.116 ) and IACT measurements. Solid lines denote IHCM model SEDs: black line corresponds to astrophysical R (H18) model of EGMF, magenta line—to astrophysical (H18), and olive line—to D05. Green dashed curve corresponds to ALP model SEDs assuming P05 EBL model [54], blue dashed curve—to ALP model SEDs assuming K04 EBL model [55]. Dotted lines represent primary spectra in ALP models. Finally, symbols with error bars denote IACT measurements of the observable SEDs of 1ES 0229+200: red dots correspond to VERITAS measurements, red triangles—H.E.S.S. measurements.
Figure 2. Comparison of IHCM model SEDs of the blazar 1ES 0229+200 ( z = 0.14 ) with ALP SEDs from [14] ( z = 0.116 ) and IACT measurements. Solid lines denote IHCM model SEDs: black line corresponds to astrophysical R (H18) model of EGMF, magenta line—to astrophysical (H18), and olive line—to D05. Green dashed curve corresponds to ALP model SEDs assuming P05 EBL model [54], blue dashed curve—to ALP model SEDs assuming K04 EBL model [55]. Dotted lines represent primary spectra in ALP models. Finally, symbols with error bars denote IACT measurements of the observable SEDs of 1ES 0229+200: red dots correspond to VERITAS measurements, red triangles—H.E.S.S. measurements.
Universe 07 00220 g002
Universe 07 00220 g003
Figure 3. Containment angle vs. observable energy dependences for different containment values in the framework of the IHCM. Black solid curve denotes a 5% containment angle, red solid curve—10% containment angle, green solid curve—20%, blue solid curve—40%, black dashed curve—68%, red dashed curve—80%, green dashed curve—90%, and blue dashed curve—95%. (a,c,e) demonstrate the results for the source 1ES 0229+200 and D05, astrophysical (H18), and astrophysicalR (H18) models of EGMF respectively; (b,d,f)—for the source 1ES 0414+009 and D05, astrophysical (H18), and astrophysical R (H18) models of EGMF respectively.
Figure 3. Containment angle vs. observable energy dependences for different containment values in the framework of the IHCM. Black solid curve denotes a 5% containment angle, red solid curve—10% containment angle, green solid curve—20%, blue solid curve—40%, black dashed curve—68%, red dashed curve—80%, green dashed curve—90%, and blue dashed curve—95%. (a,c,e) demonstrate the results for the source 1ES 0229+200 and D05, astrophysical (H18), and astrophysicalR (H18) models of EGMF respectively; (b,d,f)—for the source 1ES 0414+009 and D05, astrophysical (H18), and astrophysical R (H18) models of EGMF respectively.
Universe 07 00220 g003
Universe 07 00220 g004
Figure 4. Angular resolution (68% containment angle) of various gamma-ray instruments (solid curves: blue curve denotes Fermi-LAT, red curve—CTA, magenta curve—H.E.S.S., green curve—MAGIC, brown curve—LHAASO) vs. the 68% containment angle of the observable emission in the framework of IHCM assuming different EGMF models (dashed curves: black curve denotes D05 model, red curve—astrophysical model (H18), blue curve—astrophysical R model (H18)).
Figure 4. Angular resolution (68% containment angle) of various gamma-ray instruments (solid curves: blue curve denotes Fermi-LAT, red curve—CTA, magenta curve—H.E.S.S., green curve—MAGIC, brown curve—LHAASO) vs. the 68% containment angle of the observable emission in the framework of IHCM assuming different EGMF models (dashed curves: black curve denotes D05 model, red curve—astrophysical model (H18), blue curve—astrophysical R model (H18)).
Universe 07 00220 g004
Universe 07 00220 g005
Figure 5. Comparison of IHCM model SEDs of the blazar 1ES 0229+200 inside the PSF of LHAASO experiment (the PSF was taken from [57] for energies E > 10 TeV; for lower energies an integral SED is used) with SEDs measured by H.E.S.S. [51] and VERITAS [52] as well as LHAASO sensitivity curves. Solid lines denote model SEDs: blue line corresponds to astrophysical R (H18) model of EGMF, cyan line—to astrophysical (H18), and black line—to D05. Dashed lines denote 1-year (green line) and 5-year (magenta line) sensitivities of the LHAASO experiment particle detector. Finally, symbols with error bars denote IACT measurements of the observable SEDs of 1ES 0229+200: red dots correspond to VERITAS measurements, red triangles—H.E.S.S. measurements.
Figure 5. Comparison of IHCM model SEDs of the blazar 1ES 0229+200 inside the PSF of LHAASO experiment (the PSF was taken from [57] for energies E > 10 TeV; for lower energies an integral SED is used) with SEDs measured by H.E.S.S. [51] and VERITAS [52] as well as LHAASO sensitivity curves. Solid lines denote model SEDs: blue line corresponds to astrophysical R (H18) model of EGMF, cyan line—to astrophysical (H18), and black line—to D05. Dashed lines denote 1-year (green line) and 5-year (magenta line) sensitivities of the LHAASO experiment particle detector. Finally, symbols with error bars denote IACT measurements of the observable SEDs of 1ES 0229+200: red dots correspond to VERITAS measurements, red triangles—H.E.S.S. measurements.
Universe 07 00220 g005
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Khalikov, E. Modeling Gamma-Ray SEDs and Angular Extensions of Extreme TeV Blazars from Intergalactic Proton-Initiated Cascades in Contemporary Astrophysical EGMF Models. Universe 2021, 7, 220. https://doi.org/10.3390/universe7070220

AMA Style

Khalikov E. Modeling Gamma-Ray SEDs and Angular Extensions of Extreme TeV Blazars from Intergalactic Proton-Initiated Cascades in Contemporary Astrophysical EGMF Models. Universe. 2021; 7(7):220. https://doi.org/10.3390/universe7070220

Chicago/Turabian Style

Khalikov, Emil. 2021. "Modeling Gamma-Ray SEDs and Angular Extensions of Extreme TeV Blazars from Intergalactic Proton-Initiated Cascades in Contemporary Astrophysical EGMF Models" Universe 7, no. 7: 220. https://doi.org/10.3390/universe7070220

APA Style

Khalikov, E. (2021). Modeling Gamma-Ray SEDs and Angular Extensions of Extreme TeV Blazars from Intergalactic Proton-Initiated Cascades in Contemporary Astrophysical EGMF Models. Universe, 7(7), 220. https://doi.org/10.3390/universe7070220

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop