New Black Hole Solutions in
Abstract
1. Introduction
Gauged Supergravities and Black Holes
2. The Model
2.1. Single-Dilaton Truncation

 can be expressed as the gradient with respect to the upper entries of the prepotential function,
can be expressed as the gradient with respect to the upper entries of the prepotential function,  . The Kähler potential is expressed as
. The Kähler potential is expressed as
2.1.1. Vacua
2.1.2. Redefinitions
3. Results
3.1. Hairy Black Hole Solutions
3.1.1. Family 1 – Electric Solutions
- Boundary conditions, mass and thermodynamics for the electric solutions.
3.1.2. Family 2 – Magnetic Solutions
- Boundary conditions, mass and thermodynamics for the magnetic solutions.
3.1.3. Case or
4. Discussion
4.1. Duality Relation between the Two Families of Solutions
4.2. Supersymmetric Solutions
4.2.1. Family 1
4.2.2. Family 2
4.3. Old and New Solutions
4.3.1. Duff–Liu
4.3.2. Cacciatori–Klemm
4.4. New BPS Black Holes with Finite Area
4.4.1. Family 1: BPS Electric Black Holes
- k = 0:
- in the flat case the location of the horizon is very simple (see the above (91)) and it follows that and , so we conclude that only exists;
- k = −1:
- in the hyperbolic case, always exists while the solution exists provided ;
- k = +1:
- for spherical black hole only exists, provided .
4.4.2. Family 2: BPS Magnetic Black Holes
4.5. Hamilton–Jacobi Formulation
Flow equations
4.6. Truncations
4.6.1. Uncharged Case
4.6.2. Charged Case
- case.
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Supersymmetric Black Hole Solutions
| 1 | The boundary theory is located at the UV critical point and is it possible to employ a UV/IR connection, which relates gravity degrees of freedom at large (small) radius with the corresponding counterparts in the dual field theory at high (low) energy regime. |
| 2 | Scalar self-interactions could be relevant for dynamic and thermodynamic stability of the configuration: naively, we can imagine the condition for the existence of hairy solutions as if the self-interaction of the scalar and the gravitational interaction were to combine such that the near-horizon hair did not collapse into the black hole, while the far-region hair did not escape to infinity. |
| 3 | |
| 4 | The STU model [62,63,64] is a supergravity coupled to vector multiplets and characterized, in a suitable symplectic frame, by the prepotential , together with symmetric scalar manifold of the form spanned by the three complex scalars (); this model is in turn a consistent truncation of the maximal theory in four dimensions with gauge group [65,66,67,68]. |
| 5 | The conditions come from the consistency of the axion field equations after the truncation. |
| 6 | The explicit form of the solution makes the uncharged limit well-defined, giving the hairy black hole configurations of [47]; the result should be not taken for granted, since in the standard literature the uncharged limit gives either Schwarzschild or Schwarzschild–AdS spacetime. |
| 7 | |
| 8 | |
| 9 | This particular class of solutions is noteworthy as it can be embedded in gauged supergravity [74]. |
| 10 | |
| 11 | The construction of these models was carried out by exploiting the freedom in the initial choice of the symplectic frame of the maximal theory, that is, gauging a group in different symplectic frames by rotating the original one [44,80] making use of a suitable symplectic matrix, thus obtaining a one-parameter class of inequivalent theories (-deformed models). |
| 12 | , label the 28 vectors of the maximal theory, while m, n are the symplectic indices of the 56 electric and magnetic charges. |
| 13 | We explicitly have , , [55]. |
| 14 | For the gamma-matrices we can use the conventions of App. A of [83]. |
References
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Susskind, L. The World as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Peet, A.W.; Polchinski, J. UV/IR relations in AdS dynamics. Phys. Rev. D 1999, 59, 065011. [Google Scholar] [CrossRef]
- Susskind, L.; Witten, E. The Holographic bound in anti-de Sitter space. arXiv 1998, arXiv:hep-th/9805114. [Google Scholar]
- de Boer, J.; Verlinde, E.P.; Verlinde, H.L. On the holographic renormalization group. JHEP 2000, 08, 003. [Google Scholar] [CrossRef]
- de Boer, J. The Holographic renormalization group. Fortsch. Phys. 2001, 49, 339–358. [Google Scholar] [CrossRef]
- Hawking, S.; Page, D.N. Thermodynamics of Black Holes in anti-De Sitter Space. Commun. Math. Phys. 1983, 87, 577. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. D 1999, 60, 064018. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Holography, thermodynamics and fluctuations of charged AdS black holes. Phys. Rev. D 1999, 60, 104026. [Google Scholar] [CrossRef]
- Cvetic, M.; Gubser, S.S. Phases of R charged black holes, spinning branes and strongly coupled gauge theories. JHEP 1999, 04, 024. [Google Scholar] [CrossRef]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quant. Grav. 2000, 17, 399–420. [Google Scholar] [CrossRef]
- Anabalón, A.; Astefanesei, D.; Gallerati, A.; Trigiante, M. Instability of supersymmetric black holes via quantum phase transitions. arXiv 2021, arXiv:hep-th/2105.08771. [Google Scholar]
- Strominger, A.; Vafa, C. Microscopic origin of the Bekenstein-Hawking entropy. Phys. Lett. 1996, B379, 99–104. [Google Scholar] [CrossRef]
- Cacciatori, S.L.; Klemm, D. Supersymmetric AdS(4) black holes and attractors. JHEP 2010, 01, 085. [Google Scholar] [CrossRef]
- Hristov, K.; Looyestijn, H.; Vandoren, S. BPS black holes in N = 2 D = 4 gauged supergravities. JHEP 2010, 08, 103. [Google Scholar] [CrossRef]
- Hristov, K.; Vandoren, S. Static supersymmetric black holes in AdS4 with spherical symmetry. JHEP 2011, 04, 047. [Google Scholar] [CrossRef][Green Version]
- Hristov, K.; Toldo, C.; Vandoren, S. On BPS bounds in D = 4 N = 2 gauged supergravity. JHEP 2011, 12, 014. [Google Scholar] [CrossRef]
- Toldo, C.; Vandoren, S. Static nonextremal AdS4 black hole solutions. JHEP 2012, 09, 048. [Google Scholar] [CrossRef]
- Chow, D.D.K.; Compère, G. Dyonic AdS black holes in maximal gauged supergravity. Phys. Rev. D 2014, 89, 065003. [Google Scholar] [CrossRef]
- Gnecchi, A.; Hristov, K.; Klemm, D.; Toldo, C.; Vaughan, O. Rotating black holes in 4d gauged supergravity. JHEP 2014, 01, 127. [Google Scholar] [CrossRef]
- Gnecchi, A.; Halmagyi, N. Supersymmetric black holes in AdS4 from very special geometry. JHEP 2014, 04, 173. [Google Scholar] [CrossRef]
- Lü, H.; Pang, Y.; Pope, C. An ω deformation of gauged STU supergravity. JHEP 2014, 04, 175. [Google Scholar] [CrossRef][Green Version]
- Faedo, F.; Klemm, D.; Nozawa, M. Hairy black holes in N=2 gauged supergravity. JHEP 2015, 11, 045. [Google Scholar] [CrossRef]
- Klemm, D.; Marrani, A.; Petri, N.; Santoli, C. BPS black holes in a non-homogeneous deformation of the stu model of N = 2, D = 4 gauged supergravity. JHEP 2015, 09, 205. [Google Scholar] [CrossRef]
- Chimento, S.; Klemm, D.; Petri, N. Supersymmetric black holes and attractors in gauged supergravity with hypermultiplets. JHEP 2015, 06, 150. [Google Scholar] [CrossRef][Green Version]
- Hristov, K.; Katmadas, S.; Toldo, C. Rotating attractors and BPS black holes in AdS4. JHEP 2019, 01, 199. [Google Scholar] [CrossRef]
- Daniele, N.; Faedo, F.; Klemm, D.; Ramírez, P.F. Rotating black holes in the FI-gauged N = 2, D = 4 ℂPn model. JHEP 2019, 03, 151. [Google Scholar] [CrossRef]
- Hertog, T. Towards a Novel no-hair Theorem for Black Holes. Phys. Rev. 2006, D74, 084008. [Google Scholar] [CrossRef]
- Hertog, T.; Maeda, K. Stability and thermodynamics of AdS black holes with scalar hair. Phys. Rev. 2005, D71, 024001. [Google Scholar] [CrossRef]
- Anabalon, A.; Astefanesei, D.; Martinez, C. Mass of asymptotically anti–de Sitter hairy spacetimes. Phys. Rev. 2015, D91, 041501. [Google Scholar] [CrossRef]
- Anabalon, A.; Astefanesei, D.; Choque, D.; Martinez, C. Trace Anomaly and Counterterms in Designer Gravity. JHEP 2016, 03, 117. [Google Scholar] [CrossRef]
- Lu, H.; Pope, C.N.; Wen, Q. Thermodynamics of AdS Black Holes in Einstein-Scalar Gravity. JHEP 2015, 03, 165. [Google Scholar] [CrossRef]
- Hertog, T.; Hollands, S. Stability in designer gravity. Class. Quant. Grav. 2005, 22, 5323–5342. [Google Scholar] [CrossRef]
- Amsel, A.J.; Hertog, T.; Hollands, S.; Marolf, D. A Tale of two superpotentials: Stability and instability in designer gravity. Phys. Rev. 2007, D75, 084008. [Google Scholar] [CrossRef]
- Faulkner, T.; Horowitz, G.T.; Roberts, M.M. New stability results for Einstein scalar gravity. Class. Quant. Grav. 2010, 27, 205007. [Google Scholar] [CrossRef][Green Version]
- Dall’Agata, G.; Inverso, G.; Trigiante, M. Evidence for a family of SO(8) gauged supergravity theories. Phys. Rev. Lett. 2012, 109, 201301. [Google Scholar] [CrossRef]
- Borghese, A.; Dibitetto, G.; Guarino, A.; Roest, D.; Varela, O. The SU(3)-invariant sector of new maximal supergravity. JHEP 2013, 1303, 082. [Google Scholar] [CrossRef]
- Tarrio, J.; Varela, O. Electric/magnetic duality and RG flows in AdS4/CFT3. JHEP 2014, 1401, 071. [Google Scholar] [CrossRef]
- Gallerati, A.; Samtleben, H.; Trigiante, M. The > 2 supersymmetric AdS vacua in maximal supergravity. JHEP 2014, 12, 174. [Google Scholar] [CrossRef][Green Version]
- Borghese, A.; Guarino, A.; Roest, D. All G2 invariant critical points of maximal supergravity. JHEP 2012, 1212, 108. [Google Scholar] [CrossRef]
- Kodama, H.; Nozawa, M. Classification and stability of vacua in maximal gauged supergravity. JHEP 2013, 01, 045. [Google Scholar] [CrossRef]
- Guarino, A. On new maximal supergravity and its BPS domain-walls. JHEP 2014, 02, 026. [Google Scholar] [CrossRef][Green Version]
- Guarino, A. CSOc superpotentials. Nucl. Phys. 2015, B900, 501–516. [Google Scholar] [CrossRef]
- De Wit, B.; Nicolai, H. N = 8 Supergravity. Nucl. Phys. 1982, B208, 323. [Google Scholar] [CrossRef]
- Dall’Agata, G.; Inverso, G. On the Vacua of N = 8 Gauged Supergravity in 4 Dimensions. Nucl. Phys. 2012, B859, 70–95. [Google Scholar] [CrossRef]
- Dall’Agata, G.; Inverso, G. De Sitter vacua in N = 8 supergravity and slow-roll conditions. Phys. Lett. B 2013, 718, 1132–1136. [Google Scholar] [CrossRef][Green Version]
- Anabalón, A.; Astefanesei, D.; Gallerati, A.; Trigiante, M. Hairy Black Holes and Duality in an Extended Supergravity Model. JHEP 2018, 04, 058. [Google Scholar] [CrossRef]
- Henneaux, M.; Martinez, C.; Troncoso, R.; Zanelli, J. Black holes and asymptotics of 2+1 gravity coupled to a scalar field. Phys. Rev. 2002, D65, 104007. [Google Scholar] [CrossRef]
- Martinez, C.; Troncoso, R.; Zanelli, J. Exact black hole solution with a minimally coupled scalar field. Phys. Rev. 2004, D70, 084035. [Google Scholar] [CrossRef]
- Hertog, T.; Maeda, K. Black holes with scalar hair and asymptotics in N = 8 supergravity. JHEP 2004, 07, 051. [Google Scholar] [CrossRef]
- Anabalon, A. Exact Black Holes and Universality in the Backreaction of non-linear Sigma Models with a potential in (A)dS4. JHEP 2012, 06, 127. [Google Scholar] [CrossRef]
- Feng, X.H.; Lu, H.; Wen, Q. Scalar Hairy Black Holes in General Dimensions. Phys. Rev. 2014, D89, 044014. [Google Scholar] [CrossRef]
- Dall’Agata, G.; Gnecchi, A. Flow equations and attractors for black holes in N = 2 U(1) gauged supergravity. JHEP 2011, 03, 037. [Google Scholar] [CrossRef]
- Gnecchi, A.; Toldo, C. On the non-BPS first order flow in N = 2 U(1)-gauged Supergravity. JHEP 2013, 03, 088. [Google Scholar] [CrossRef]
- Anabalon, A.; Astefanesei, D.; Gallerati, A.; Trigiante, M. New non-extremal and BPS hairy black holes in gauged N = 2 and N = 8 supergravity. JHEP 2021, 04, 047. [Google Scholar] [CrossRef]
- Anabalon, A.; Astefanesei, D. Black holes in ω-defomed gauged N = 8 supergravity. Phys. Lett. B 2014, 732, 137–141. [Google Scholar] [CrossRef]
- Anabalon, A.; Astefanesei, D.; Choque, D.; Gallerati, A.; Trigiante, M. Exact holographic RG flows in extended SUGRA. JHEP 2021, 04, 053. [Google Scholar] [CrossRef]
- Witten, E. Multitrace operators, boundary conditions, and AdS/CFT correspondence. arXiv 2001, arXiv:hep-th/0112258. [Google Scholar]
- Strominger, A. Special Geometry. Commun. Math. Phys. 1990, 133, 163–180. [Google Scholar] [CrossRef]
- Bagger, J.; Witten, E. Matter Couplings in N = 2 Supergravity. Nucl. Phys. B 1983, 222, 1–10. [Google Scholar] [CrossRef]
- Lauria, E.; Van Proeyen, A. = 2 Supergravity in D = 4, 5, 6 Dimensions; Springer: Berlin/Heidelberg, Germany, 2020; Volume 966. [Google Scholar] [CrossRef]
- Duff, M.J.; Liu, J.T.; Rahmfeld, J. Four-dimensional string-string-string triality. Nucl. Phys. B 1996, 459, 125–159. [Google Scholar] [CrossRef]
- Behrndt, K.; Kallosh, R.; Rahmfeld, J.; Shmakova, M.; Wong, W.K. STU black holes and string triality. Phys. Rev. D 1996, 54, 6293–6301. [Google Scholar] [CrossRef]
- Behrndt, K.; Lust, D.; Sabra, W.A. Stationary solutions of N = 2 supergravity. Nucl. Phys. B 1998, 510, 264–288. [Google Scholar] [CrossRef]
- Duff, M.; Liu, J.T. Anti-de Sitter black holes in gauged N = 8 supergravity. Nucl. Phys. B 1999, 554, 237–253. [Google Scholar] [CrossRef]
- Andrianopoli, L.; D’Auria, R.; Gallerati, A.; Trigiante, M. Extremal Limits of Rotating Black Holes. JHEP 2013, 1305, 071. [Google Scholar] [CrossRef][Green Version]
- Andrianopoli, L.; Gallerati, A.; Trigiante, M. On Extremal Limits and Duality Orbits of Stationary Black Holes. JHEP 2014, 01, 053. [Google Scholar] [CrossRef][Green Version]
- Andrianopoli, L.; D’Auria, R.; Gallerati, A.; Trigiante, M. On D = 4 Stationary Black Holes. J. Phys. Conf. Ser. 2013, 474, 012002. [Google Scholar] [CrossRef]
- Gallerati, A.; Trigiante, M. Introductory Lectures on Extended Supergravities and Gaugings. Springer Proc. Phys. 2016, 176, 41–109. [Google Scholar] [CrossRef]
- Trigiante, M. Gauged Supergravities. Phys. Rept. 2017, 680, 1–175. [Google Scholar] [CrossRef]
- Henneaux, M.; Martinez, C.; Troncoso, R.; Zanelli, J. Asymptotic behavior and Hamiltonian analysis of anti-de Sitter gravity coupled to scalar fields. Annals Phys. 2007, 322, 824–848. [Google Scholar] [CrossRef]
- Myers, R.C. Stress tensors and Casimir energies in the AdS / CFT correspondence. Phys. Rev. D 1999, 60, 046002. [Google Scholar] [CrossRef]
- Anabalon, A.; Andrade, T.; Astefanesei, D.; Mann, R. Universal Formula for the Holographic Speed of Sound. Phys. Lett. B 2018, 781, 547–552. [Google Scholar] [CrossRef]
- Luciani, J.F. Coupling of O(2) Supergravity with Several Vector Multiplets. Nucl. Phys. B 1978, 132, 325–332. [Google Scholar] [CrossRef]
- Gallerati, A. Constructing black hole solutions in supergravity theories. Int. J. Mod. Phys. 2020, A34, 1930017. [Google Scholar] [CrossRef]
- Ferrara, S.; Gibbons, G.W.; Kallosh, R. Black holes and critical points in moduli space. Nucl. Phys. 1997, B500, 75–93. [Google Scholar] [CrossRef]
- Andrianopoli, L.; D’Auria, R.; Ferrara, S.; Trigiante, M. Extremal black holes in supergravity. Lect. Notes Phys. 2008, 737, 661–727. [Google Scholar]
- Dall’Agata, G.; Inverso, G.; Marrani, A. Symplectic Deformations of Gauged Maximal Supergravity. JHEP 2014, 07, 133. [Google Scholar] [CrossRef]
- Inverso, G. Electric-magnetic deformations of D = 4 gauged supergravities. JHEP 2016, 03, 138. [Google Scholar] [CrossRef][Green Version]
- De Wit, B.; Nicolai, H. N=8 Supergravity with Local SO(8) x SU(8) Invariance. Phys. Lett. B 1982, 108, 285. [Google Scholar] [CrossRef]
- Cvetic, M.; Gubser, S.; Lu, H.; Pope, C. Symmetric potentials of gauged supergravities in diverse dimensions and Coulomb branch of gauge theories. Phys. Rev. D 2000, 62, 086003. [Google Scholar] [CrossRef]
- Cvetic, M.; Lu, H.; Pope, C.; Sadrzadeh, A. Consistency of Kaluza-Klein sphere reductions of symmetric potentials. Phys. Rev. D 2000, 62, 046005. [Google Scholar] [CrossRef]
- Andrianopoli, L.; Cerchiai, B.L.; D’Auria, R.; Gallerati, A.; Noris, R.; Trigiante, M.; Zanelli, J. N-extended D = 4 supergravity, unconventional SUSY and graphene. JHEP 2020, 01, 084. [Google Scholar] [CrossRef]
- Gaillard, M.K.; Zumino, B. Duality Rotations for Interacting Fields. Nucl. Phys. 1981, B193, 221. [Google Scholar] [CrossRef]
- Romans, L. Supersymmetric, cold and lukewarm black holes in cosmological Einstein-Maxwell theory. Nucl. Phys. B 1992, 383, 395–415. [Google Scholar] [CrossRef]
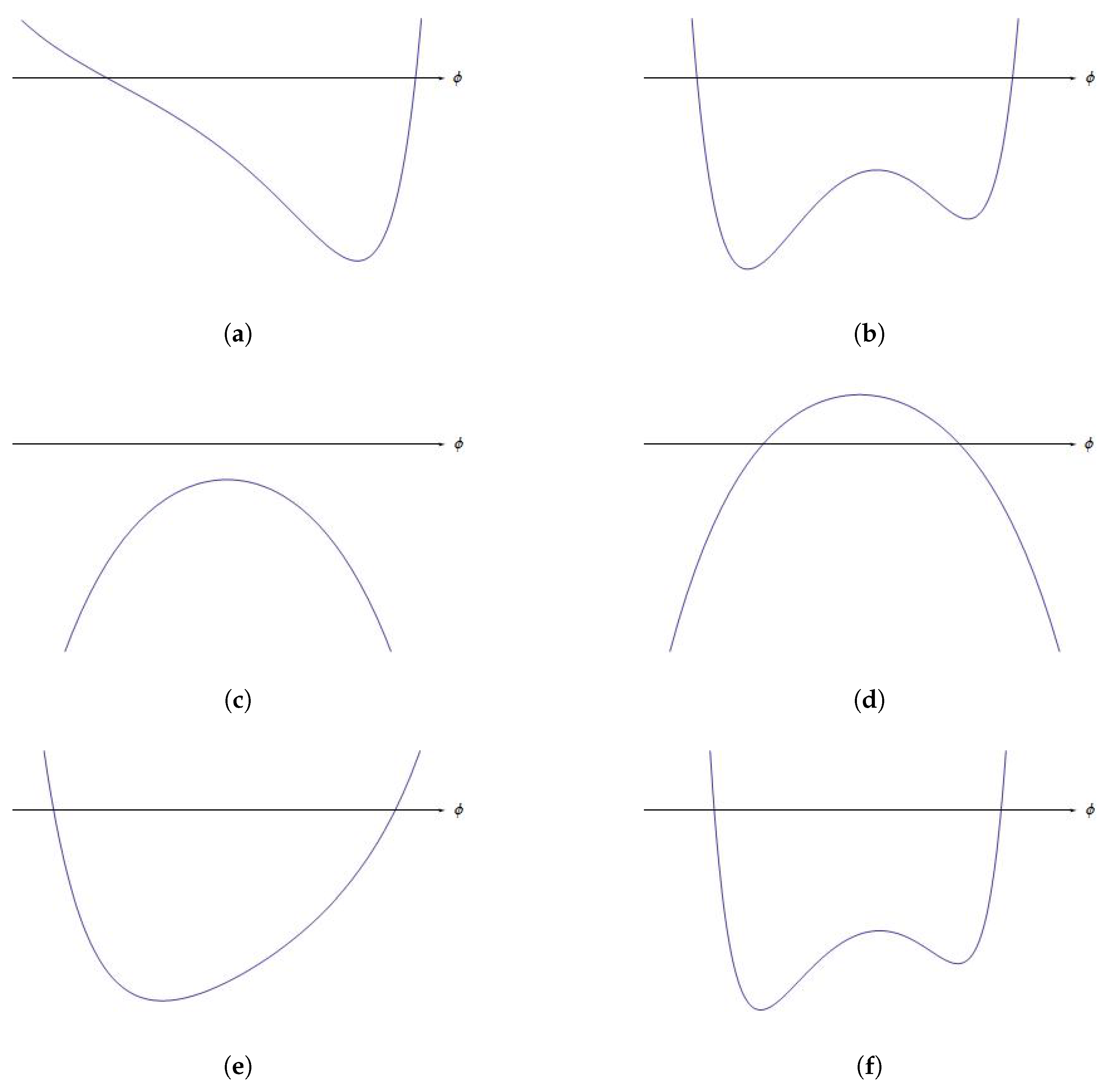
| 1 Anti-de Sitter 3 Anti-de Sitter | Figure 1a Figure 1b | |||
| 1 Anti-de Sitter | Figure 1c | |||
| 1 de Sitter 1 Anti-de Sitter | Figure 1d Figure 1c | |||
| 1 Anti-de Sitter | Figure 1c | |||
| 1 de Sitter 1 Anti-de Sitter | Figure 1d Figure 1c | |||
| 1 Anti-de Sitter | Figure 1c | |||
| 1 Anti-de Sitter 3 Anti-de Sitter | Figure 1e Figure 1f |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallerati, A.
New Black Hole Solutions in
Gallerati A.
New Black Hole Solutions in
Gallerati, Antonio.
2021. "New Black Hole Solutions in
Gallerati, A.
(2021). New Black Hole Solutions in






