Global Portraits of Nonminimal Teleparallel Inflation
Abstract
1. Introduction
2. Scalar-Curvature vs. Scalar-Torsion Cosmology
2.1. Action and Cosmological Equations
2.2. “Effective Potential” and “Effective Mass”
2.3. Slow Roll
3. Dynamical System
4. Quadratic Potential
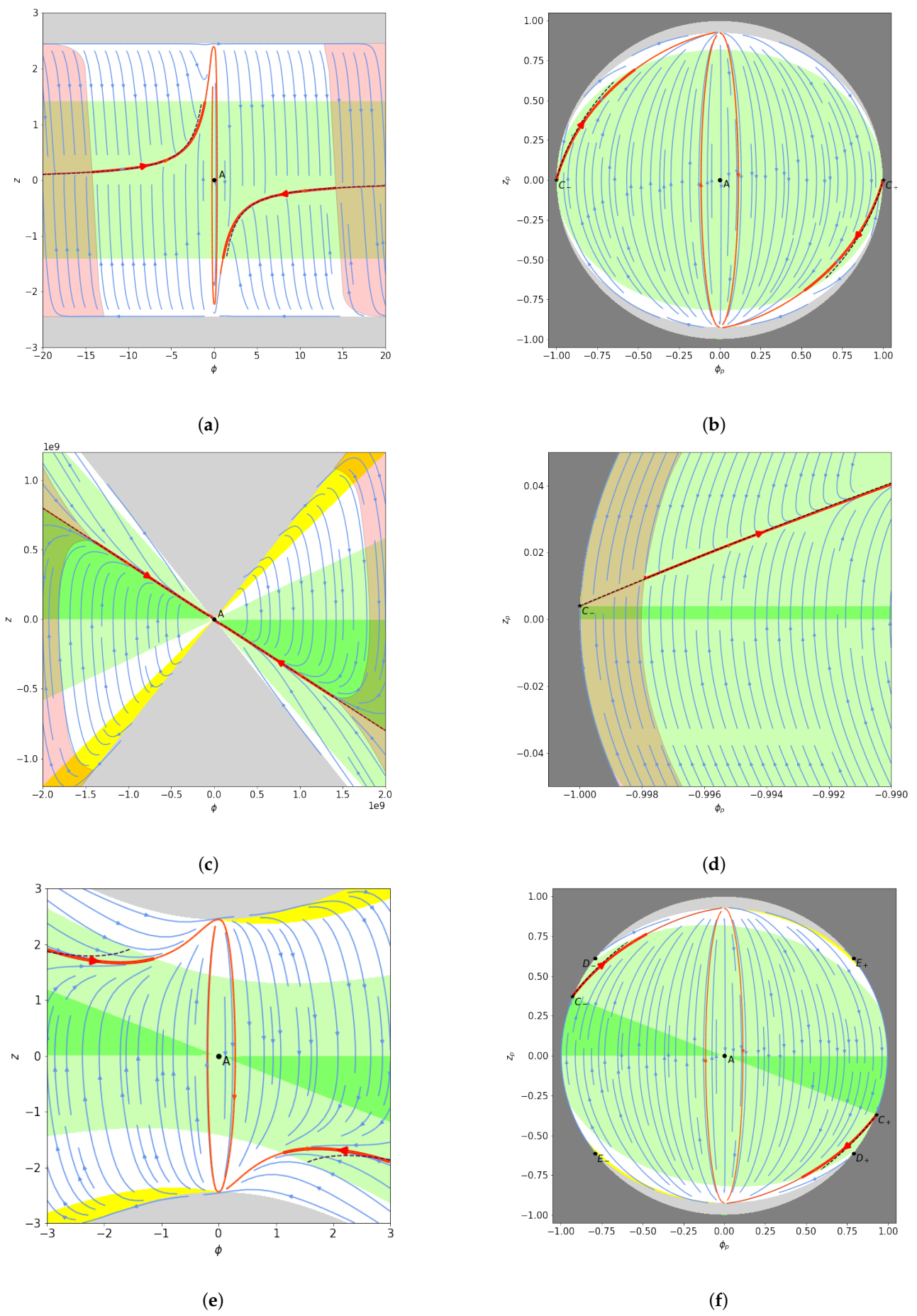
4.1. Finite Analysis
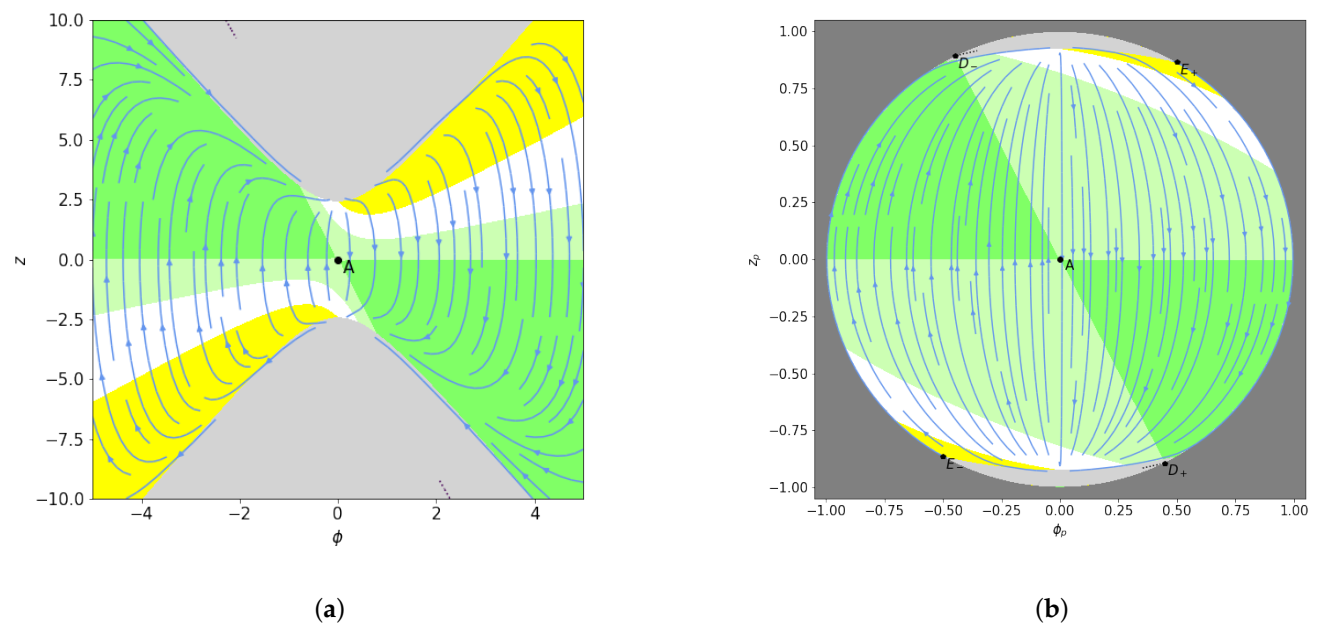
4.2. Infinite Analysis
5. Quartic Potential
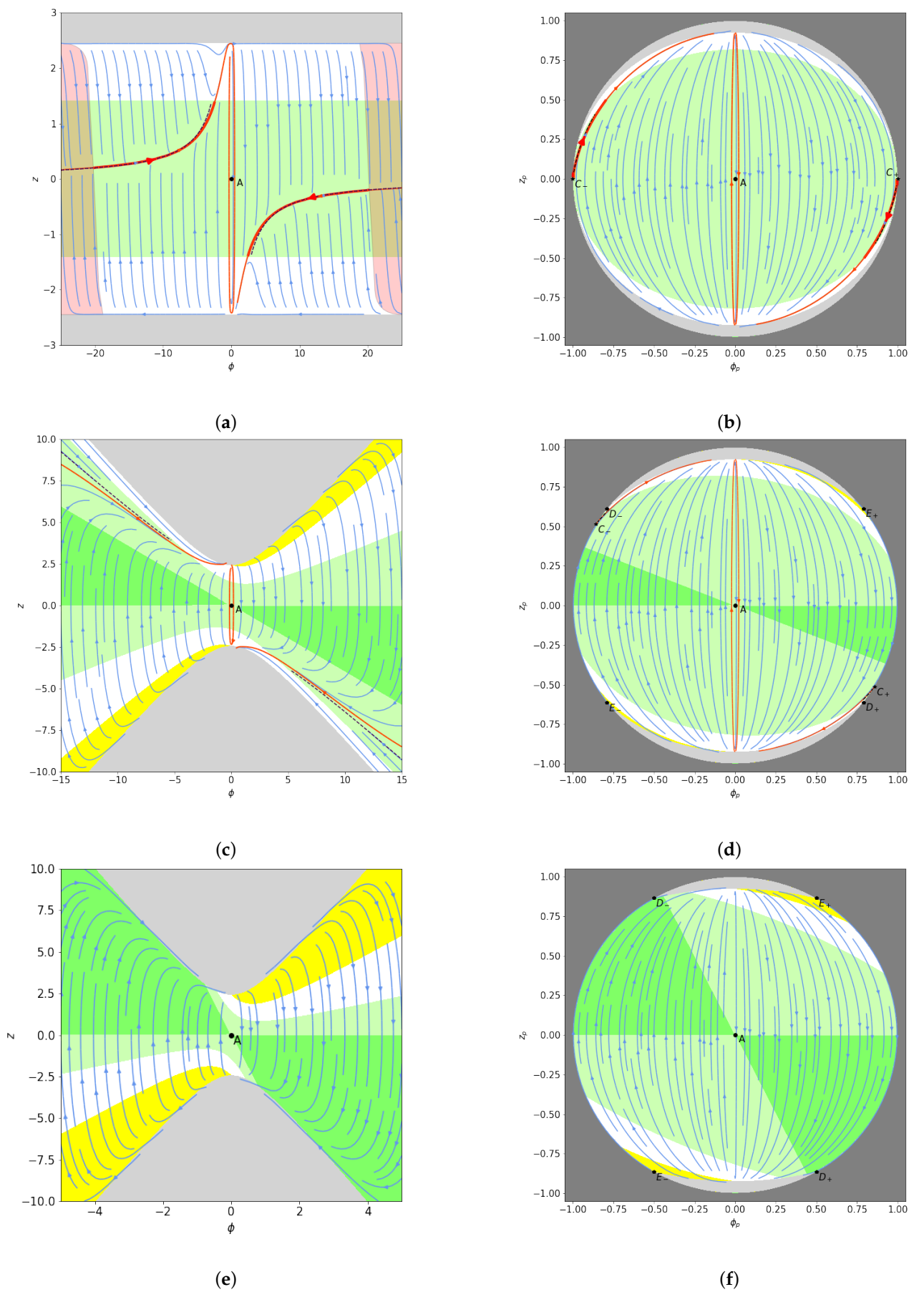
5.1. Finite Analysis
5.2. Infinite Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FLRW | Friedmann–Lemaître–Robertson–Walker |
References
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Chernikov, N.A.; Tagirov, E.A. Quantum theory of scalar fields in de Sitter space-time. Ann. Inst. H. Poincare Phys. Theor. A 1968, 9, 109. [Google Scholar]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge Monographs on Mathematical Physics, Cambridge Univ. Press: Cambridge, UK, 1984. [Google Scholar] [CrossRef]
- Overduin, J.M.; Wesson, P.S. Kaluza-Klein gravity. Phys. Rep. 1997, 283, 303–380. [Google Scholar] [CrossRef]
- Nǎstase, H. Cosmology and String Theory; Fundamental Theories of Physics; Springer: Berlin/Heidelberg, Germany, 2019; Volume 197. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Esposito-Farese, G.; Polarski, D. Scalar tensor gravity in an accelerating universe. Phys. Rev. 2001, D63, 063504. [Google Scholar] [CrossRef]
- Bahamonde, S.; Böhmer, C.G.; Carloni, S.; Copeland, E.J.; Fang, W.; Tamanini, N. Dynamical systems applied to cosmology: Dark energy and modified gravity. Phys. Rep. 2018, 775–777, 1–122. [Google Scholar] [CrossRef]
- Bezrukov, F.L.; Shaposhnikov, M. The Standard Model Higgs boson as the inflaton. Phys. Lett. 2008, B659, 703–706. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Heisenberg, L.; Koivisto, T.S. The Geometrical Trinity of Gravity. Universe 2019, 5, 173. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity; Springer: Dordrecht, The Netherlands, 2013; Volume 173. [Google Scholar] [CrossRef]
- Krssak, M.; van den Hoogen, R.; Pereira, J.; Böhmer, C.; Coley, A. Teleparallel theories of gravity: Illuminating a fully invariant approach. Class. Quant. Grav. 2019, 36, 183001. [Google Scholar] [CrossRef]
- Geng, C.Q.; Lee, C.C.; Saridakis, E.N.; Wu, Y.P. “Teleparallel” dark energy. Phys. Lett. B 2011, 704, 384–387. [Google Scholar] [CrossRef]
- Geng, C.Q.; Luo, L.W.; Tseng, H.H. Teleparallel Gravity in Five Dimensional Theories. Class. Quant. Grav. 2014, 31, 185004. [Google Scholar] [CrossRef][Green Version]
- Geng, C.Q.; Lai, C.; Luo, L.W.; Tseng, H.H. Kaluza–Klein theory for teleparallel gravity. Phys. Lett. B 2014, 737, 248–250. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without inflaton. Phys. Rev. 2007, D75, 084031. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. 2009, D79, 124019. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s Other Gravity and the Acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Yang, R.J. Conformal transformation in f(T) theories. EPL 2011, 93, 60001. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Sáez-Gómez, D. Conformal symmetry and accelerating cosmology in teleparallel gravity. Phys. Rev. D 2013, 88, 084042. [Google Scholar] [CrossRef]
- Wright, M. Conformal transformations in modified teleparallel theories of gravity revisited. Phys. Rev. D 2016, 93, 103002. [Google Scholar] [CrossRef]
- Hohmann, M.; Pfeifer, C. Scalar-torsion theories of gravity II: L(T,X,Y,ϕ) theory. Phys. Rev. D 2018, 98, 064003. [Google Scholar] [CrossRef]
- Chen, Z.C.; Wu, Y.; Wei, H. Post-Newtonian Approximation of Teleparallel Gravity Coupled with a Scalar Field. Nucl. Phys. B 2015, 894, 422–438. [Google Scholar] [CrossRef]
- Mohseni Sadjadi, H. Parameterized post-Newtonian approximation in a teleparallel model of dark energy with a boundary term. Eur. Phys. J. C 2017, 77, 191. [Google Scholar] [CrossRef][Green Version]
- Emtsova, E.D.; Hohmann, M. Post-Newtonian limit of scalar-torsion theories of gravity as analogue to scalar-curvature theories. Phys. Rev. D 2020, 101, 024017. [Google Scholar] [CrossRef]
- Järv, L. Effective Gravitational “Constant” in Scalar-(Curvature)Tensor and Scalar-Torsion Gravities. Universe 2017, 3, 37. [Google Scholar] [CrossRef]
- Izumi, K.; Gu, J.A.; Ong, Y.C. Acausality and Nonunique Evolution in Generalized Teleparallel Gravity. Phys. Rev. D 2014, 89, 084025. [Google Scholar] [CrossRef]
- Li, M.; Miao, R.X.; Miao, Y.G. Degrees of freedom of f(T) gravity. J. High Energy Phys. 2011, 7, 108. [Google Scholar] [CrossRef]
- Ferraro, R.; Guzmán, M.J. Hamiltonian formalism for f(T) gravity. Phys. Rev. 2018, D97, 104028. [Google Scholar] [CrossRef]
- Ferraro, R.; Guzmán, M.J. Quest for the extra degree of freedom in f(T) gravity. Phys. Rev. 2018, D98, 124037. [Google Scholar] [CrossRef]
- Ferraro, R.; Guzmán, M.J. Pseudoinvariance and the extra degree of freedom in f(T) gravity. Phys. Rev. D 2020, 101, 084017. [Google Scholar] [CrossRef]
- Blagojević, M.; Nester, J.M. Local symmetries and physical degrees of freedom in f(T) gravity: A Dirac Hamiltonian constraint analysis. Phys. Rev. D 2020, 102, 064025. [Google Scholar] [CrossRef]
- Blixt, D.; Guzmán, M.J.; Hohmann, M.; Pfeifer, C. Review of the Hamiltonian analysis in teleparallel gravity. arXiv 2020, arXiv:2012.09180. [Google Scholar]
- Beltrán Jiménez, J.; Heisenberg, L.; Koivisto, T.S. Teleparallel Palatini theories. J. Cosmol. Astropart. Phys. 2018, 8, 39. [Google Scholar] [CrossRef]
- Hohmann, M.; Järv, L.; Ualikhanova, U. Covariant formulation of scalar-torsion gravity. Phys. Rev. 2018, D97, 104011. [Google Scholar] [CrossRef]
- Krššák, M.; Saridakis, E.N. The covariant formulation of f(T) gravity. Class. Quant. Grav. 2016, 33, 115009. [Google Scholar] [CrossRef]
- Golovnev, A.; Koivisto, T.; Sandstad, M. On the covariance of teleparallel gravity theories. Class. Quant. Grav. 2017, 34, 145013. [Google Scholar] [CrossRef]
- Hohmann, M.; Järv, L.; Krššák, M.; Pfeifer, C. Modified teleparallel theories of gravity in symmetric spacetimes. Phys. Rev. D 2019, 100, 084002. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Non trivial frames for f(T) theories of gravity and beyond. Phys. Lett. B 2011, 702, 75–80. [Google Scholar] [CrossRef]
- Tamanini, N.; Boehmer, C.G. Good and bad tetrads in f(T) gravity. Phys. Rev. 2012, D86, 044009. [Google Scholar] [CrossRef]
- Hohmann, M. Complete classification of cosmological teleparallel geometries. arXiv 2020, arXiv:2008.12186. [Google Scholar]
- Geng, C.Q.; Lee, C.C.; Saridakis, E.N. Observational Constraints on Teleparallel Dark Energy. J. Cosmol. Astropart. Phys. 2012, 1, 2. [Google Scholar] [CrossRef]
- Xu, C.; Saridakis, E.N.; Leon, G. Phase-Space analysis of Teleparallel Dark Energy. J. Cosmol. Astropart. Phys. 2012, 7, 5. [Google Scholar] [CrossRef]
- Jamil, M.; Momeni, D.; Myrzakulov, R. Stability of a non-minimally conformally coupled scalar field in F(T) cosmology. Eur. Phys. J. C 2012, 72, 2075. [Google Scholar] [CrossRef]
- Kucukakca, Y. Scalar tensor teleparallel dark gravity via Noether symmetry. Eur. Phys. J. C 2013, 73, 2327. [Google Scholar] [CrossRef]
- Jarv, L.; Toporensky, A. General relativity as an attractor for scalar-torsion cosmology. Phys. Rev. D 2016, 93, 024051. [Google Scholar] [CrossRef]
- Wei, H. Dynamics of Teleparallel Dark Energy. Phys. Lett. B 2012, 712, 430–436. [Google Scholar] [CrossRef]
- Otalora, G. Scaling attractors in interacting teleparallel dark energy. J. Cosmol. Astropart. Phys. 2013, 7, 44. [Google Scholar] [CrossRef]
- Bahamonde, S.; Wright, M. Teleparallel quintessence with a nonminimal coupling to a boundary term. Phys. Rev. D 2015, 92, 084034. [Google Scholar] [CrossRef]
- Skugoreva, M.A.; Toporensky, A.V. Asymptotic cosmological regimes in scalar–torsion gravity with a perfect fluid. Eur. Phys. J. C 2016, 76, 340. [Google Scholar] [CrossRef][Green Version]
- Mohseni Sadjadi, H. Onset of acceleration in a universe initially filled by dark and baryonic matters in a nonminimally coupled teleparallel model. Phys. Rev. D 2015, 92, 123538. [Google Scholar] [CrossRef]
- Mohseni Sadjadi, H. Symmetron and de Sitter attractor in a teleparallel model of cosmology. J. Cosmol. Astropart. Phys. 2017, 1, 31. [Google Scholar] [CrossRef]
- D’Agostino, R.; Luongo, O. Growth of matter perturbations in nonminimal teleparallel dark energy. Phys. Rev. D 2018, 98, 124013. [Google Scholar] [CrossRef]
- Bahamonde, S.; Marciu, M.; Rudra, P. Generalised teleparallel quintom dark energy non-minimally coupled with the scalar torsion and a boundary term. J. Cosmol. Astropart. Phys. 2018, 4, 56. [Google Scholar] [CrossRef]
- Gonzalez-Espinoza, M.; Otalora, G. Cosmological dynamics of dark energy in scalar-torsion f(T,ϕ) gravity. arXiv 2020, arXiv:2011.08377. [Google Scholar]
- Bahamonde, S.; Marciu, M.; Odintsov, S.D.; Rudra, P. String-inspired Teleparallel cosmology. Nucl. Phys. B 2021, 962, 115238. [Google Scholar] [CrossRef]
- Skugoreva, M.A.; Saridakis, E.N.; Toporensky, A.V. Dynamical features of scalar-torsion theories. Phys. Rev. D 2015, 91, 044023. [Google Scholar] [CrossRef]
- Skugoreva, M.A. Late-time power-law stages of cosmological evolution in teleparallel gravity with nonminimal coupling. Grav. Cosmol. 2018, 24, 103–111. [Google Scholar] [CrossRef]
- Geng, C.Q.; Wu, Y.P. Density Perturbation Growth in Teleparallel Cosmology. J. Cosmol. Astropart. Phys. 2013, 4, 33. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.P. Inflation with teleparallelism: Can torsion generate primordial fluctuations without local Lorentz symmetry? Phys. Lett. B 2016, 762, 157–161. [Google Scholar] [CrossRef]
- Abedi, H.; Capozziello, S.; D’Agostino, R.; Luongo, O. Effective gravitational coupling in modified teleparallel theories. Phys. Rev. D 2018, 97, 084008. [Google Scholar] [CrossRef]
- Golovnev, A.; Koivisto, T. Cosmological perturbations in modified teleparallel gravity models. J. Cosmol. Astropart. Phys. 2018, 1811, 12. [Google Scholar] [CrossRef]
- Raatikainen, S.; Rasanen, S. Higgs inflation and teleparallel gravity. J. Cosmol. Astropart. Phys. 2019, 12, 21. [Google Scholar] [CrossRef]
- Gonzalez-Espinoza, M.; Otalora, G.; Videla, N.; Saavedra, J. Slow-roll inflation in generalized scalar-torsion gravity. J. Cosmol. Astropart. Phys. 2019, 8, 29. [Google Scholar] [CrossRef]
- Gonzalez-Espinoza, M.; Otalora, G.; Saavedra, J. Stability of scalar perturbations in scalar-torsion f(T,ϕ) gravity theories in presence of a matter fluid. arXiv 2021, arXiv:2101.09123. [Google Scholar]
- Järv, L.; Toporensky, A. Global portraits of nonminimal inflation. arXiv 2021, arXiv:2104.10183. [Google Scholar]
- Felder, G.N.; Frolov, A.V.; Kofman, L.; Linde, A.D. Cosmology with negative potentials. Phys. Rev. D 2002, 66, 023507. [Google Scholar] [CrossRef]
- Urena-Lopez, L.A. Unified description of the dynamics of quintessential scalar fields. J. Cosmol. Astropart. Phys. 2012, 03, 035. [Google Scholar] [CrossRef]
- Alho, A.; Uggla, C. Global dynamics and inflationary center manifold and slow-roll approximants. J. Math. Phys. 2015, 56, 012502. [Google Scholar] [CrossRef]
- Alho, A.; Hell, J.; Uggla, C. Global dynamics and asymptotics for monomial scalar field potentials and perfect fluids. Class. Quant. Grav. 2015, 32, 145005. [Google Scholar] [CrossRef]
- Alho, A.; Uggla, C. Inflationary α-attractor cosmology: A global dynamical systems perspective. Phys. Rev. 2017, D95, 083517. [Google Scholar] [CrossRef]
- Järv, L.; Rünkla, M.; Saal, M.; Vilson, O. Nonmetricity formulation of general relativity and its scalar-tensor extension. Phys. Rev. D 2018, 97, 124025. [Google Scholar] [CrossRef]
- Beltrán Jiménez, J.; Heisenberg, L.; Koivisto, T. Coincident General Relativity. Phys. Rev. D 2018, 98, 044048. [Google Scholar] [CrossRef]
- Dutta, J.; Järv, L.; Khyllep, W.; Tõkke, S. From inflation to dark energy in scalar-tensor cosmology. arXiv 2020, arXiv:2007.06601. [Google Scholar]
- Chiba, T.; Yamaguchi, M. Extended Slow-Roll Conditions and Rapid-Roll Conditions. J. Cosmol. Astropart. Phys. 2008, 10, 21. [Google Scholar] [CrossRef]
- Skugoreva, M.A.; Toporensky, A.V.; Vernov, S.Y. Global stability analysis for cosmological models with nonminimally coupled scalar fields. Phys. Rev. 2014, D90, 064044. [Google Scholar] [CrossRef]
- Järv, L.; Kannike, K.; Marzola, L.; Racioppi, A.; Raidal, M.; Rünkla, M.; Saal, M.; Veermäe, H. Frame-Independent Classification of Single-Field Inflationary Models. Phys. Rev. Lett. 2017, 118, 151302. [Google Scholar] [CrossRef]
- Järv, L.; Kuusk, P.; Saal, M.; Vilson, O. Invariant quantities in the scalar-tensor theories of gravitation. Phys. Rev. 2015, D91, 024041. [Google Scholar] [CrossRef]
- Pozdeeva, E.O.; Sami, M.; Toporensky, A.V.; Vernov, S.Y. Stability analysis of de Sitter solutions in models with the Gauss-Bonnet term. Phys. Rev. D 2019, 100, 083527. [Google Scholar] [CrossRef]
- Vernov, S.Y.; Pozdeeva, E.O. De Sitter solutions in Einstein-Gauss-Bonnet gravity. arXiv 2021, arXiv:2104.11111. [Google Scholar]
- Mishra, S.S.; Müller, D.; Toporensky, A.V. Generality of Starobinsky and Higgs inflation in the Jordan frame. Phys. Rev. D 2020, 102, 063523. [Google Scholar] [CrossRef]
- Otalora, G. A novel teleparallel dark energy model. Int. J. Mod. Phys. D 2015, 25, 1650025. [Google Scholar] [CrossRef]
- Gecim, G.; Kucukakca, Y. Scalar–tensor teleparallel gravity with boundary term by Noether symmetries. Int. J. Geom. Meth. Mod. Phys. 2018, 15, 1850151. [Google Scholar] [CrossRef]
- Rezaei Akbarieh, A.; Izadi, Y. Tachyon Inflation in Teleparallel Gravity. Eur. Phys. J. C 2019, 79, 366. [Google Scholar] [CrossRef]
- Bahamonde, S.; Dialektopoulos, K.F.; Levi Said, J. Can Horndeski Theory be recast using Teleparallel Gravity? Phys. Rev. D 2019, 100, 064018. [Google Scholar] [CrossRef]
- Hohmann, M. Scalar-torsion theories of gravity I: General formalism and conformal transformations. Phys. Rev. D 2018, 98, 064002. [Google Scholar] [CrossRef]
| 1 |
| Effective Mass | Effective Potential | Fixed Point Condition | Stability Condition | |
|---|---|---|---|---|
| Minimally coupled | 1 | V | ||
| Scalar-curvature | ||||
| Scalar-torsion | F |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Järv, L.; Lember, J. Global Portraits of Nonminimal Teleparallel Inflation. Universe 2021, 7, 179. https://doi.org/10.3390/universe7060179
Järv L, Lember J. Global Portraits of Nonminimal Teleparallel Inflation. Universe. 2021; 7(6):179. https://doi.org/10.3390/universe7060179
Chicago/Turabian StyleJärv, Laur, and Joosep Lember. 2021. "Global Portraits of Nonminimal Teleparallel Inflation" Universe 7, no. 6: 179. https://doi.org/10.3390/universe7060179
APA StyleJärv, L., & Lember, J. (2021). Global Portraits of Nonminimal Teleparallel Inflation. Universe, 7(6), 179. https://doi.org/10.3390/universe7060179






