Abstract
We discuss the possibility that the distribution of relic wormholes may possess fractal properties. Relic wormholes and their fractal distributions are predicted in a natural way by lattice quantum gravity models. This provides a new approach to some long standing problems. That is the nature of dark matter phenomena, the origin of Faber-Jackson and Tully-Fisher relations and the observed deficit of baryons. We derive corrections to the Newton’s potential caused by the presence of relic wormholes and show that the analysis of dark matter distribution in galaxies allows us to fix the parameters of the fractal distribution of wormholes.
1. Introduction
The nature of dark matter represents one of the most challenging problems of modern astrophysics. Particle physics suggests many possible candidates. The most promising are WIMPs (weakly interacting massive particles), which can be both new particles beyond the standard model, or particles composed from already known, for example complexes, composed from neutrons (and even primordial neutron stars). However, such particles can hardly solve the problem. Indeed, experiments at the LHC (large hadron collider) do not show the presence of particles beyond the standard model and, moreover, such particles have to possess very exotic properties. One important feature is that in the early Universe, at the moment of recombination, such particles have a rather high density but do not interact with baryons or radiation, otherwise they would cause too strong fluctuations of CMB temperature and such a possibility is excluded by the observed power spectrum of . Another important feature is that, in the modern Universe in centers of galaxies, dark matter particles have much more modest densities (at least three orders less than at the moment of recombination) but they should possess a sufficiently strong interaction with baryons to form the observed cored distribution of dark matter as , where r is the distance to the center of a galaxy [1,2,3]. We recall that numerical investigations based on DM particles predict the presence of a cusp [4,5] in centers of galaxies, which is the unavoidable consequence of the potential nature of initial velocities and the fact that DM particles interact via gravity only.
In principle, such a difficulty of DM models based on particles may be overcome in some of the modified theories of gravity [6] that have gained popularity during the last decade (e.g., see References [7,8] and references therein). However, any modification should be approved first from the particle physics standpoint and most such modifications can be rejected already at laboratory scales. In other words, most such theories have pure academic interest and have no astrophysical applications.
One of the possible solutions to the problem pointed out was suggested in References [9,10]. It is based on the fact that local topology of space may possess a rather complex or fractal structure. It has two important features. First, it does not require any modification of general relativity or the presence of an additional dark matter component. Secondly, it provides a natural explanation of the empirical Tully-Fisher and Faber-Jackson relations [11,12] for rotation curves in galaxies. We point out that, except for the exotic scheme suggested by Milgrom [13], where such relations were incorporated from the very beginning, the fractal topology provides the only natural explanation of such relations [14].
The origin of fractal topological structure comes directly from predictions of lattice quantum gravity models [15,16,17]. Indeed, lattice models predict that, at Planckian scales, space-time has a foamy structure which possesses fractal properties. In particular, numerical investigations [17] show that the spectral dimension of space–time runs from the value at sub-Planckian scales to the value on macroscopic scales. At very small scales, the space–time foam can be described by a distribution of virtual wormholes [18]. At laboratory scales, the vacuum is stable, which means that all virtual wormholes appear and disappear permanently. However, if we believe that the early Universe underwent an inflationary phase, we should expect that the exponential expansion very rapidly stretches all scales and some virtual wormholes do not decay. They temper and form the initial conditions for the topological structure of space. The subsequent evolution of wormholes is the pure classical process. Spherically symmetric wormholes rapidly collapse, while toroidal or more complex wormholes may survive until the present day [19,20]. In other words, the present topological structure of space represents an instant print of the space–time foam picture existing on Planck scales. Since the vacuum state possesses homogeneity and isotropy properties, it inherits the same properties upon the freezing out at the inflationary stage.
The fractal structure of space can be described as follows: Consider an arbitrary point x in space and fix the geodesic distance R. Then, the volume of space, which gets inside the geodesic ball, that is, all points y which obey the inequality (where is the geodesic distance between x and y), scales with R as , where . The homogeneity and isotropy of space requires that the function and the dimension D do not depend on the initial point x.
The initial point x and omnidirectional geodesic lines, issued from point x, define the extrapolated reference system, which is used in astrophysics. The coordinate volume of such a system always has the dimension , which reflects the fact that locally space is Euclidean with the dimension (i.e., ). We point out that the dependence on the redshift (cosmological evolution) and the choice of the background metric (open, flat, or closed model) somewhat changes the behavior of and the definition of the dimension d, but rough features and the value remains valid.
The situation changes when the space is filled with a distribution of wormholes. A part of geodesics go through wormhole throats and return to the same physical region of space or get into a remote region. Therefore, the behavior of and the dimension d may change essentially. From the pure mathematical standpoint this signals the fact that the extrapolated coordinate system stops working (the same point may have multiple images), which requires the introduction of additional atlases. In general, the dimension evaluated in such a manner may either exceed or be less than the coordinate dimension . What kind of dimension is realized for physical space depends on the properties and the distribution of wormholes.
It is curious that the distribution of galaxies provides roughly the analogous picture. In a homogeneous space, the number of galaxies reflects sufficiently well the behavior of the physical volume of space. The galaxy counts show the fractal behavior with the dimension up to the distances [21,22], where is the number of galaxies within the distance R. The maximal scale changes with the increase of the precision. In Reference [23], the scale upon which the distribution of galaxies switches to the homogeneity had the order . However, more recent observations of SDSS (Sloan Digital Sky Survey) [24] have found the existence of wall-type structures (Sloan Great Wall, etc.) on scales up to , where is the Hubble radius, see also [25]. Such super-large structures have posed a serious problem for the standard scenario of the structure formation. Recall that, according to latter, the largest scale on which inhomogeneities may develop is . Moreover, it is even discussed that such structures are inconsistent with the cosmological principle. We consider such data to be indirect evidence of the fractal (or at least complex) topological structure of space and the existence of relic wormholes. The development of perturbations and the formation of structures in the presence of relic wormholes is a rather complex problem which requires further investigation.
We point out that, in the flat space, the light when passing through a wormhole throat is too scattered and may contribute only to the diffuse background radiation [26]. Most likely, the scattered signal is too dim to observe a separate galaxy through wormhole throats. The exception may be only gigantic throats compared to the void and larger size. This means that the observed dimension counted by galaxies is always less than three . In particular, this may also explain the observed deficit of baryons [27].
The fractal topological structure can be easily obtained in open Friedmann models by means of a specific factorization of the negative curvature (Lobachevsky) space over a discrete subgroup of the group of motion of space [19,20]. We point out that the fractal distribution of baryonic matter does not necessarily indicate the existence of a fractal topological structure. However, such a distribution requires specific initial conditions and, to be consistent with the observed homogeneity of the background, it requires the presence of dark matter, which is dually distributed in space. The fractal topological structure, in turn, is the direct prediction of Lattice quantum gravity models and, therefore, it has the most rigorous theoretical ground.
The advantage of such a factorization is that it completely agrees with the observed homogeneity and isotropy of the Universe. Moreover, such a model easily reproduces dark matter phenomena without any modification of general relativity or the presence of actual dark matter particles. Due to the factorization, every source of gravity (or radiation) has multiple images in the covering of total Lobachevsky space, which automatically restores the homogeneity and isotropy of the background but produces dark matter effects in local inhomogeneous structures (e.g., in galaxies). The absence of particles beyond the standard model in experiments at LHC lets us think that the dark matter phenomenon indeed has the origin from a non-trivial topological structure of space, that is, in the first place, from relic wormholes and black holes.
Fractal structure means that the space contains a distribution of stable torus-shaped or more complex wormholes of different sizes, which may reach gigantic scales. Moreover, in the general case, the factorization may even produce wormholes whose throats are not closed surfaces. The latter should be formally excluded in lattice quantum gravity models. Indeed, before the inflationary stage virtual wormholes do exist at Planck scales and they should be restricted in size. Nevertheless, if the inflationary epoch lasts for a sufficiently long period of time, one may expect the existence of wormholes whose throat size exceeds the Hubble radius, which are indistinguishable from non restricted throats.
At first glance, the basic disadvantage of the factorization is the presence of multiple images. Why do we not see images of the same galaxy? To find the answer is not difficult. First, our Universe has flat space. For small throats of wormholes (of the galaxy size or less), the additional images are very small and cannot be directly observed. Indeed, as demonstrated in Reference [28], in the flat model the intensity of an image I has the order , where R is the characteristic radius of the throat and L is the distance between the throat center and the original source and the ratio . It reaches the order of only for very large throats. Moreover, the position of the image will be seen only in the second entrance into the wormhole and, therefore, the image may have an arbitrary distance from the original. We point out that, for fractal distribution over distances between entrances into the same wormhole the mean distance between entrances diverges. Therefore, different images contribute only to the scattered background radiation. While for gigantic wormholes, all such images are too far from each other and we may see the same galaxy at different stages of its evolution. Therefore, it is impossible to recognize that we indeed see the same galaxy.
Thus, the basic disadvantage is that the factorization requires the negative curvature space only, while the position of Doppler picks in the CMB spectrum favor the flat space. In flat space, such a factorization is impossible, while a fractal structure can be obtained by inserting fractal distribution of wormholes or by means of deforming the metric of the factorized Lobachevsky space. We point out that such a deformation is not an unusual phenomenon. For example, if the inflation starts in an open model, then the factorization actually takes place at sub-Planck scales, while the subsequent particle production may change the value of the mean spatial curvature and produce flat or even closed space, which depends on the rate of particle production. In general, this causes many problems that require further and more deep investigation. For example, whether the particle production may indeed essentially change the mean curvature. Moreover, if in open models relic torus-shaped wormholes are stable, in flat or closed models their stability and the rate of evolution are not properly investigated yet. These problems can be somewhat weakened as is discussed in the next section.
In the flat space, the presence of wormholes was shown to produce a specific modification of the standard Newton’s law [29,30]. If we interpret this as a dark matter phenomenon, then we find the rigid relation between the distribution of visible and dark components in a galaxy in the form , where is the Fourier components for dark and visible matter densities and corresponds to the correction, which depends on the distribution of wormholes around the galaxy. This provides the direct method for determining the correction from observations and the subsequent modeling of the distribution of relic wormholes.
If our Universe is filled with relic wormholes, then how can we recognize this? To provide an answer to such a question is not so easy. Besides the effects of dark matter discussed in the present paper, we should look for some independent tests. The investigation of possible independent effects related to the scattering of radiation on wormholes has revealed that almost all effects are well hidden under analogous effects related to the ordinary matter [28]. Here, we see the two most promising possibilities. The first possibility relates to recently observed unexpected circular radio objects [31] and the possible role of torus-shaped wormholes in their origin [32]. The second relates to gravitational wave Astronomy. In particular, several groups have claimed evidence for repeating echoes in the LIGO/Virgo observations of binary black hole mergers [33,34,35,36]. Such echoes can be generated by the near-horizon or other strong field effects related to black holes or wormholes [37,38,39]. We stress that the scattering of GWs by wormholes produces much stronger effects as compared to the scattering by ordinary matter objects, for example, see discussions in [40], which allows us to disentangle such effects and detect wormholes in the near future.
There is a vast literature on the possible effects of wormholes, for example, see the review [39]. However, the basic effects, considered so far, relate to effects produced by a single wormhole that depends on the exact structure of the wormhole. In our study, we focus on collective effects, which appear due to the presence of a collection of wormholes. In addition to the repeating echoes, the scattering on wormholes produces an essential increase of the background GW radiation. Moreover, the accretion disks around small throats should produce gamma ray bursts distinguishable from the ones from black holes. The absence of such may suggest a constraint on the form of the distribution of these wormholes in general (e.g., low distribution of certain sizes).
2. Stable Wormholes and Factorization of the Open Model
As discussed above, relic wormholes are the remnants of the inflationary stage. A-priori, such wormholes may have an arbitrary form and geometric structure. In particular, they may correspond to traversable and non traversable wormholes, which depends on their exact geometric structure and the subsequent evolution. Here, we define the traversable wormhole as follows. Consider some region of space in which all points are causally connected in the framework of the background Friedman model. If in such a region we place a wormhole, then any two points can be connected by a set of geodesic lines. One unique geodesic does not pass through the throat and it corresponds to the direct propagation in the Friedman model, while there is also a countable set of additional lines that go through the throat. We call the wormhole traversable if for almost all points at least one of such additional geodesic lines has the length less than the horizon size. Therefore, a non-traversable wormhole may have two kinds. The first is a wormhole that collapses and forms a couple of black holes. The second kind is a wormhole that has too long a neck (or whose entrances are too separated in space). In what follows, we consider the stability of such wormholes in the context of the cosmological evolution. We call a wormhole stable if it is not static but evolves sufficiently slowly and does survive up to the present day.
Stable spherically symmetric wormholes cannot exist without an essential modification of general relativity. In general relativity, static spherical wormholes require the presence of exotic matter which does not show up in physical systems and laboratory experiments. The exotic matter can be replaced by a proper modification of theory, for example, see also recent papers [41,42,43] and references therein, but any modification requires first a verification from the particle physics point of view. Any deviation from general relativity is not yet detected. Quantum corrections may stabilize only wormholes of a Planck size [44,45]. Therefore, spherical wormholes collapse very soon upon the inflationary stage and form couples of primordial black holes.
The situation changes when we consider less symmetric configurations. In References [19,20], we have demonstrated that in open Friedman models a collection of stable wormholes can be constructed simply by means of a factorization of space over a discrete subgroup of the group of motions for the Lobachevsky space. The simplest wormhole here has a throat in the form of a torus and in such a scheme, spherical wormholes do not appear at all. Such wormholes expand in agreement with the expansion of space and, in other words, in the expanding co-moving reference frame they are static. This does not mean that they cannot collapse as the spherical configurations do. In particular, the development of density perturbations may enforce the collapse of a whole region of space which contains such a wormhole throat. In what follows, we briefly describe the factorization scheme.
2.1. Factorization of the Open Friedman Model
Consider the open Friedman model with the metric
where the space-like metic corresponds to the Lobachevsky space
For the sake of illustration and simplicity we demonstrate the factorization for 2D sections of the space, which correspond to a plane . Such a plane corresponds to two values of the polar angle and , which can formally be covered by the angles , where the range corresponds to the half-plane . Using the coordinate transformation as
where , we get the realization of the section in the form of the upper complex half-plane , which is the Klein model of the Lobachevsky plane . Consider two particular geodesic lines on the plane which correspond to semicircles and with . Then the factorization can be determined by the map which represents one of the possible motions of the plane. The factorization means that any two points of the plane represent the same point, if they are connected by the relation
The above factorization corresponds to the cut along those two geodesic lines and subsequent gluing along them. The resulting space is a wormhole which connects two independent Lobachevsky planes (regions and , see Figure 1).
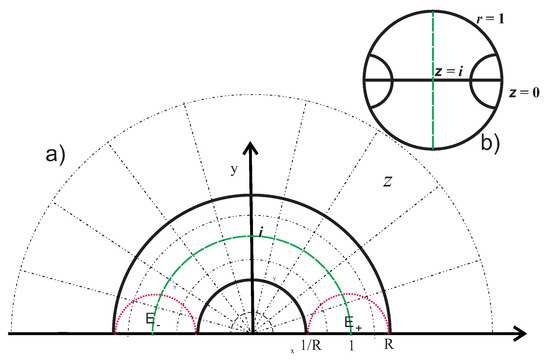
Figure 1.
(a) The Lobachevsky plane. Dashed lines give the polar frame. The stripe between the two geodesic lines and corresponds to the wormhole region. Regions below red dashed geodesics (semi-circles) correspond to two unrestricted Lobschevsky spaces . The point corresponds to the center point of the wormhole throat (). The line corresponds to infinity for the plane. (b) The same plane in coordinates , where .
To understand how such a factorization looks in three dimensions let us return to the initial coordinates , , and . The geodesic lines and are determined by
where and gives the shortest distance to the geodesic lines from the center point . The above equation corresponds to an arbitrary section and describes two lines which can be seen in opposite directions and . Here, the point corresponds to the center of the throat (the point on Figure 1). Using the symmetry with respect to the change of we find that in 3D space the above equation determines two semi-spheres (rigorously speaking they become semi-spheres in terms of the radial variable in which the infinity becomes the sphere ), while the factorization has the same form determined by (3) and (4). In this case, the throat is not restricted. It is important that, from the central point , such semi-spheres occupy the solid angles where can be found from (5) in the limit which gives the asymptotic angles . To get a restricted throat we have to place two more analogous semi-spheres e.g., in the orthogonal to directions at a distance , see Figure 2.
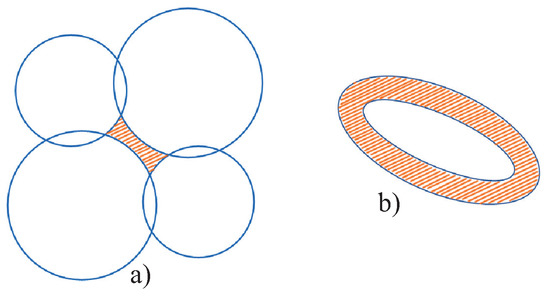
Figure 2.
(a) The form of a throat as it is seen on sky in the open model. It represents the colored curved rectangle. Regions behind the circles are copies of the physical region. All additional images lay within the circles. (b) The form of the throat as it is seen in flat models upon the deformation of the metric from the negative curvature space. The throat has the torus-like form and only part of the throat surface is seen. Additional images lay inside the surface of the torus.
Moreover, the distances should be chosen in such a way that all four semi-spheres restrict a finite minimal section. It is also important that every semi-sphere envelopes a non-physical space, since every point within it represents an image of a point from the corresponding physical space.
Now let us consider how such a wormhole looks for a remote from the center of the throat observer. To this end, we should simply shift the central point from the middle of the throat. From a qualitative standpoint the picture remains the same, every semi-sphere is determined by the same Equation (5) but the distance to it changes. Four such semi-spheres group and if they restrict a finite solid angle they form a remote wormhole. The angle they occupy in the sky is and the throats (minimal sections) are seen as curved rectangles. We point out that, from the topological standpoint, throats are tori but in the open model they will be seen in the sky as rectangles. Such wormholes restore the torus-like form of throats only in the case when the space is additionally deformed or curved in such a way that the mean curvature becomes zero or positive.
Above, we have described the factorization that forms a wormhole that connects two independent (connected only through the throat) Lobachevsky spaces. To obtain a wormhole both entrances of which lay in the same region requires one more analogous map as described in [19]. In this case, we get couples of such throats (groups of semi-spheres) on sky. Now, to obtain a pure fractal picture we may construct a Cantor set on sky by placing such groups of semi-spheres of smaller and smaller solid angles.
2.2. Stability of Wormholes
The factorization described previously requires the negative curvature space, which corresponds to an open Friedman model, while the position of Doppler picks in the power CMB spectrum favor the flat space. In flat space, such a factorization is impossible. However, a fractal structure can be obtained by inserting the fractal distribution of wormholes or by deforming the metric of a factorized Lobachevsky space. The deformation of the Lobachevsky space can be obtained rather naturally during the inflationary stage. Indeed, if the space initially had a negative curvature, then during the inflation stage the production of wormholes and particles took place. Therefore, the particle production process could essentially change the value of spatial curvature and essentially deform the picture described above. In this sense, we may expect to see a distribution of analogous wormholes even in flat space. We point out that, contrary to the open model in flat space, upon the deformation throat sections will look like torus-like shapes. This poses the problem of how such wormholes may evolve in flat space. Spherical wormholes are unstable and collapse very quickly. The stability of torus-like wormholes has not yet been investigated. There are only some encouraging results. For example, the existence and stability of static cylindrical wormholes without exotic matter was demonstrated recently in References [46,47]. We point out that the toroidal wormhole reduces to the cylindrical one in the limit when one of the radii tends to infinity. Though the rigorous investigation of the behavior of toroidal wormholes during the cosmological evolution is not yet completed, we may expect that such wormholes collapse much slower than spherical wormholes do and may survive up to the present day. As a result, we obtain the open or flat Friedman model filled with toroidal wormholes.
When we consider wormhole throats as objects of a finite size (e.g., they occupy a finite solid angle on sky) we may average out over possible random orientations of the throats in space. We point out that there are no strong physical arguments in favor of some particular characteristic size of wormholes; moreover, the fractal structure of space–time at Planck scales predicts analogous fractal distribution over the throat sizes. In the case of the statistical averaging over possible orientations, the spherical symmetry of the wormhole configuration restores and, therefore, estimates based on spherical wormholes should give correct predictions, at least to the leading order. In what follows, we discuss the open Friedman model with almost zero value of the space curvature where wormholes can be considered simply as quasi-static objects expanding only due to the scale factor . The cosmological evolution of follows the standard Friedman equations,
where is the Hubble constant, , and is the matter density (baryons plus radiation). The metric has the standard form , where the space-like part corresponds to the Lobachevsky space.
The behavior of small perturbations in such a model is determined by the standard Lifshitz theory [48], with one exception. The basic equations for perturbations have local character and, therefore, do not depend on the topological structure of space. Possible solutions, however, do. In particular, in comparison to the ordinary Lobachevsky space the space with wormholes represents a space with a specific factorization. For example, in flat space the factorization over translations in one of the directions gives the space which is simply the cylinder and one of the coordinates becomes a periodic one. This means that corresponding modes are classified by discrete wave numbers instead of continuous ones and, therefore, some modes are absent. Analogously, the factorization of the open model selects only particular solutions among all possible solutions for the unrestricted space. Therefore, from qualitative and quantitative standpoints, the evolution of perturbations will show essential deviations from the behavior in standard Friedman models. Analogous deviations are indeed observed and are interpreted as the presence of dark matter, or a modification of general relativity. According to Reference [17], the Hausdorff dimension of space should be . At laboratory scales, we see that and no deviations from the standard Newton’s law are observed. The number of galaxies’ counts show that, starting from galactic scales () at least up to , the Hausdorff dimension is and at those scales we observe the phenomenon of dark matter.
Indeed, the simplest estimate for Newton’s law gives , where M is the mass within the volume (ball of the radius R) and is the square of the sphere surrounding the volume . In the case of a fractal law and . The value is in very good agreement with observations of dark matter in the range of scales . The value gives too strong a gravitational bind and such structures should decouple the cosmological expansion very early, or it should even be suppressed during the inflationary stage.
From one standpoint, stable toroidal wormholes do surely exist in negative curvature spaces (in the open model), while in the flat model, their stability requires additional study. From other points, the position of the Doppler picks in the CMB () spectrum points to the fact that our Universe is very close to the flat space, which means that the matter density is close to the critical value. Here, however, one should be especially careful in making estimates. First, the positions of picks are evaluated on the basis of the standard Friedman models when the possible factorization of the space is not taken into account (i.e., the possible presence of wormholes). Secondly, the presence of fluctuations means that, at the moment of recombination, analogous fluctuations are present in the metric and matter density , where and is the critical density. In other words, the space is split into regions of a positive (, ) and negative (, ) curvature. If in regions where the presence of stable wormholes requires additional study, in the regions where stable wormholes do exist. Moreover, in the fractal Universe, the observed mean value of the spatial curvature is somewhat different from the actual local value. It contains the additional factor , where is the actual physical volume of space, while is the coordinate, or extrapolated volume. In this estimate, one should take the Hubble radius , or the radius of the sphere of last scattering. In accordance with Reference [6], the estimate is in agreement with observations, which means that at the moment of recombination, the local value of the spatial curvature and the Hubble constant may have the same order (). We point out that the same value characterizes the portion of actually observed baryons with respect to the value predicted by nucleosynthesis. Here, we assume estimates of the number of baryons based only on counts of galaxies and discrete sources, while the diffuse background (e.g., the X-ray background) provides a much higher estimate for such a ratio ∼0.4 [49,50,51]. In a fractal picture, the diffuse background does not rigorously reflect the actual number of baryons. It reflects merely the mean homogeneity and isotropy of space and the local density of baryons, while the actual number of baryons is proportional to the physical volume of space . In other words, rigorous estimates require further investigation.
3. Fractal Distribution of Wormholes and Modification of Newton’s Law
The fractality of the topological structure of space requires the analogous fractal distribution of wormholes. At first glance, the fractality is not consistent with the observed homogeneity and isotropy of the Universe. This, however, is not so, for example, the diffuse background which appears due to the scattering on wormholes remains homogeneous and isotropic [28]. The basic feature of the fractal distribution is a scale—dependence of different mean values, such as mean density of wormhole throats n, the mean distance between entrances , the mean radius of the throat , and so forth.
Consider the simplest model suggested by us in Reference [29], which explicitly demonstrates that non-trivial topology can model the effects of dark matter. The model is based on spherical wormholes, while actual stable wormholes should have torus-like throats. We assume that throats are averaged over orientations then the spherical symmetry restores and such wormholes can be considered in the leading order as spherical ones.
In the case of weak gravitational fields and potential perturbations, Einstein’s equations reduce to the Laplace equation for Newton’s potential ()
where a is the scale factor, and are perturbations in density and pressure, respectively. The behavior of perturbations is determined by the Green function (Newton’s law)
In the Euclidean space, Newton’s law gives (in the Fourier representation it gives ). In the presence of wormholes, the Green function changes [29]. It is convenient to describe corrections which appear due to wormholes by the presence of additional sources (fictitious sources). Then, formally, we may think that the space remains Euclidean, while proper periodic conditions on throats are accounted for by the bias of sources
Here, the bias function describes corrections to Newton’s law which appear due to the non-trivial topology of space. Indeed, the presence of the bias gives rise to the transformation
The asymptotically flat rotation curves in galaxies require that the correction to the Newton’s potential should have the logarithmic behavior, that is, the gravitational acceleration should switch from to . The above expression implies that at galaxy scales the bias behaves as with and . When considering a galaxy with surface mass density distribution the bias forms an effective dark matter halo in the form
In particular, for and an infinitely thin disc this expression gives the pseudo-isothermal halo , where is the radius of the core, for example, see [6,14].
For a homogeneous distribution of wormholes, the bias function was first considered in [29] and a more general case was constructed in [18]. The bias is expressed via the distribution of wormholes which in the homogeneous and isotropic case is a function , where n is the density of wormhole throats in space, X is the distance between entrances into a wormhole, and R is the throat radius. In the Fourier representation () it has the form [30]
where we define
and is the Fourier transform for the distribution function over distances. Here and the dependence of the above functions only on k reflects the isotropy of the distribution f. The physical meaning of these two functions and become quite clear in the limit , when throat radii assumed to be small as compared to the characteristic scales. Then we may set and we find which is simply the mean value of the throat radius. We point out that is proportional to the imaginary part of the characteristic function for the distribution over radii (6) (which is ). Analogously the function is the characteristic function for the distribution over the distances between throat entrances. In the most general case the effective radius has the dependence on scales and it admits both signs. Thus, the presence of a distribution of wormholes gives rise to the specific modification of Newton’s law and the true Green function becomes
Consider the simplest particular situation when all distances between throats have the same value and all throat radii are , then we find the homogeneous and isotropic distribution in the form
and the Fourier transform is
The effective radius and the characteristic function, which correspond to such a distribution are
and the bias is
We see that the bias (and, therefore, corrections to the Newton’s potential) alternates the sign with the change of scales. It is completely determined by three typical scales related to wormhole distribution, which are the density , the typical throat radius , and the typical distance between entrances into throats .
In the general case (of the isotropic and homogeneous distributions), the above expressions can be rewritten as follows
where the mean value is determined as . For normal distributions, when all momenta are finite, we may expand the above expressions in series and find
where and the characteristic scales are determined via mean values as follows
The first term here determines the re-normalization of the gravitational constant, while the next terms determine higher order corrections. The above analysis shows that using only normal distributions it is hardly possible to get the desirable form of corrections (observed in galaxies). This is confirmed by estimates presented in Introduction. Indeed, Gaussian distribution of wormholes is described by three typical scales those are , which characterizes the absolute value of corrections, , and . Starting from a typical scale and all corrections reduce to a some renormalization of gravitational constant, while at smaller intermediate scales (), corrections have more complex behavior (partial screening, e.g., see [29]). This indicates that we should consider more general fractal distributions.
In the case of fractal distributions, such an expansion does not work since all momenta may diverge, while the density of wormholes n is badly determined (its value also depends on scales). In this case, we should directly work with characteristic functions () and . Indeed, consider the simplest example when and are independent. Then, every function can be expressed as
where determines an asymmetry of the distribution e.g., see Ref. [52]. Analogously,
with its own parameters L, , and . The last equation defines the effective radius as
In the case , the above characteristic functions corresponds to the standard Gaussian distribution, while for the dispersion which corresponds to such a distribution diverges as
as well as all higher momenta. The parameters relate to the Hausdorff dimension of space D and it characterizes the fractal structure of . To avoid misunderstanding, we also point out that the scales do not characterize the mean value between entrances into throats, or the mean radius, since for fractal distributions such moments diverge. In such a case the decomposition in series presented above (8) does not work. In this case, we should expand directly the characteristic functions (9) and (11) themselves. In the region of sufficiently small scales (i.e., at very small distances) the function quickly oscillates and vanishes . In this region of scales the standard Newton’s law does work. At sufficiently big scales, that is, in the limit , we find the first leading term as
where and
Corrections to the empirical Green function can be restored directly from observations and by relations (6) and (7) they determine the distribution of wormholes. In the present paper, we do not analyze any actual data, since it requires an independent study. However, some rough estimates can be obtained. Indeed, the first correction for the empirical Green function, which follows from rotation curves [14], behaves roughly as with , which determines parameters in (12) as (), , and . As was discussed in Reference [14], the value of the parameter may somewhat change from a galaxy to a galaxy that reflects the presence of the initial inhomogeneities of the metric at the moment of recombination.
As demonstrated in [14], the bias in the form (12) and the homogeneity of total matter (baryon plus dark matter components) [6] straightforwardly lead to the origin of Tully-Fisher and Faber-Jackson relations. Therefore, this can also be considered an indirect indication of the fractal topological structure of space. Moreover, the recent SDSS data [24,25] show the traces of the fractal distribution of baryons up to scales ∼0.1R.
4. Concluding Remarks
As concluding remarks, we point out the basic results of this paper. First, we have demonstrated that the most natural origin of dark matter phenomena relates to the existence of a locally complex or fractal topological structure of our Universe. At extremely small (sub-Planckian) distances, such a fractal structure is predicted by lattice quantum gravity models. It is widely accepted that, in the past, the Universe underwent the stage of exponential expansion, that is, the inflationary stage. Exactly in this period, the topological fractal structure tempers and it forms the initial conditions for the actual structure of space in Friedman models. One may imagine such a process as an instant enormous increase of a small (of the Planckian order) portion of space filled with virtual wormholes up to macroscopic scales. The stretched wormholes become real and form the initial topological structure, while their subsequent evolution is already governed by classical gravity (general relativity). Spherical wormholes collapse very quickly and form primordial black holes. Toroidal wormholes do not require exotic matter for their stability and they may survive until the present day.
Secondly, the fractal structure is consistent with the apparent homogeneity and isotropy of space. The simplest rigorous model is the Lobachevsky space factorized over a discrete subgroup of the group of motion (of the group of the symmetry). The resulting space has a constant spatial curvature and it locally cannot be distinguished from the Friedman model. However, it is not a homogeneous space anymore and, in general, it possesses a complex topological structure. The flat model can be obtained by a deformation (due to particle production) of the factorized Lobachevsky space. In this case, the fractal topological structure will correspond to a specific distribution of relic wormholes that possesses fractal properties.
Finally, we have demonstrated that when the distribution of wormholes possesses fractal properties, corrections to the standard Newton’s law have the necessary form to imitate rather carefully the presence of dark matter in galaxies. Moreover, the empirical Green function restored from the analysis of rotation curves in galaxies allows us to directly restrict some of the parameters of the fractal distribution of wormholes.
We also indicate that the complex topological structure of space does not assume any modification of general relativity. However it results in a strong modification of gravity predictions, for example, it changes the behavior of perturbations and even the rate of expansion of space changes with the development of perturbations. Besides, it is much more flexible as compared to different modified theories that have been suggested in the last decade [7,8].
Author Contributions
These authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We acknowledge valuable comments and the advice of referees which helped us to essentially improve the presentation of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- De Blok, W.J.G.; Bosma, A. High-resolution rotation curves of low surface brightness galaxies. Astron. Astrophys. 2002, 385, 816–846. [Google Scholar] [CrossRef]
- Gentile, G.; Salucci, P.; Klein, U.; Vergani, D.; Kalberla, P. The cored distribution of dark matter in spiral galaxies. Mon. Not. R. Astron. 2004, 351, 903–922. [Google Scholar] [CrossRef]
- Salucci, P. The distribution of dark matter in galaxies. Astron. Astrophys. Rev. 2019, 27, 2. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563–575. [Google Scholar] [CrossRef]
- Diem, J.; Zemp, M.; Moore, B.; Stadel, J.; Carollo, M. Cusps in cold dark matter haloes. Mon. Not. R. Astron. 2005, 364, 665–673. [Google Scholar]
- Kirillov, A.A. The nature of dark matter. Phys. Lett. B 2006, 632, 453–462. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Relativ. 2018, 21, 2. [Google Scholar] [CrossRef] [PubMed]
- Harko, T.; Lobo, F. Extensions of f(R) Gravity: Curvature-Matter Couplings and Hybrid Metric-Palatini Theory; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P. Astrophysical effects of spacetime foam. Gravit. Cosmol. 2008, 14, 256–261. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Turaev, D. Foam-like structure of the Universe. Phys. Lett. B 2007, 656, 1–8. [Google Scholar] [CrossRef]
- Tully, R.B.; Fisher, J.R. A new method of determining distances to galaxies. Astron. Astrophys. 1977, 54, 661–673. [Google Scholar]
- Faber, S.M.; Jackson, R.E. Velocity dispersions and mass-to-light ratios for elliptical galaxies. Astrophys. J. 1976, 206, 668–683. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Turaev, D. The Universal rotation curve of spiral galaxies. Mon. Not. RAS. L 2006, 371, 31–35. [Google Scholar] [CrossRef]
- Knizhnik, V.; Polyakov, A.; Zamolodchikov, A. Fractal structure of 2D quantum gravity. Mod. Phys. Lett. A 1988, 3, 819. [Google Scholar] [CrossRef]
- Kawai, H.; Kawamoo, N.; Mogami, T.; Watabiki, Y. Transfer matrix formalism for twodimensional quantum gravity and fractal structures of space-time. Phys. Lett. B 1993, 306, 19–26. [Google Scholar] [CrossRef]
- Ambjorn, J.; Jurkiewicz, J.; Loll, R. Spectral dimension of the Universe. Phys. Rev. Lett. 2005, 95, 171301. [Google Scholar] [CrossRef] [PubMed]
- Savelova, E.P. Gas of wormholes in Euclidean quantum field theory. Grav. Cosmol. 2015, 21, 48–56. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P. Cosmological wormholes. Int. J. Mod. Phys. D 2016, 25, 1650075. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P. Wormhole as a possible accelerator of high-energy cosmic-ray particles. Eur. Phys. J. C 2020, 80, 45. [Google Scholar] [CrossRef]
- Coleman, P.H.; Pietronero, L. The fractal structure of the Universe. Phys. Rep. 1992, 213, 311–389. [Google Scholar] [CrossRef]
- Baryshev, Y.; Teerikorpi, P. Discovery of Cosmic Fractals; World Scientific: London, UK, 2002; p. 408. [Google Scholar]
- Geller, M.J.; Huchra, J.P. Mapping the Universe. Science 1989, 246, 897–903. [Google Scholar] [CrossRef] [PubMed]
- SDSS Collaboration. The Thirteenth data release of the SDSS: First Spectroscopic data from the SDSS-IV Survey Mapping nearby galaxies at Apache point observatory. Astrophys. J. Suppl. Ser. 2017, 233, 25. [Google Scholar] [CrossRef]
- Horvath, I.; Bagoly, Z.; Hakkila, J.; Toth, L.V. New data support the existence of the Hercules-Corona Borealis Great Wall. Astron. Astrophys. 2015, 584, A48. [Google Scholar] [CrossRef][Green Version]
- Planck Collaboration. Planck 2018 results—IV. Diffuse component separation. Astron. Astrophys. 2020, 641, A4. [Google Scholar] [CrossRef]
- Fukugitai, M.; Hogan, C.J.; Peebles, P.J.E. The cosmic baryon budget. Astrophys. J. 1998, 503, 518. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P. Effects of scattering of radiation on wormholes. Universe 2018, 4, 35. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P. Dark matter from a gas of wormholes. Phys. Lett. B 2008, 660, 93–99. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P. On Modification of Newton’s Law by a Homogeneous Distribution of Wormholes in Space. Gravit. Cosmol. 2018, 24, 337–343. [Google Scholar] [CrossRef]
- Norris, R.; Intema, H.; Kapińska, A.; Koribalski, B.; Lenc, E.; Rudnick, L.; Whiting, M. Unexpected circular radio objects at high Galactic latitude. Publ. Astron. Soc. Aust. 2021, 38, E003. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P. Possible formation of ring galaxies by torus—Shaped magnetic wormholes. Eur. Phys. J. C 2020, 80, 810. [Google Scholar] [CrossRef]
- Abedi, J.; Dykaar, H.; Afshordi, N. Echoes from the Abyss: Tentative evidence for Planck-scale structure atblack hole horizons. Phys. Rev. D 2017, 96, 082004. [Google Scholar] [CrossRef]
- Conklin, R.S.; Holdom, B.; Ren, J. Gravitational wave echoes through new windows. Phys. Rev. D 2018, 98, 044021. [Google Scholar] [CrossRef]
- Westerweck, J.; Nielsen, A.B.; Fischer-Birnholtz, O.; Cabero, M.; Capano, C.; Dent, T.; Krishnan, B.; Meadors, G.; Nitz, A.H. Low significance of evidence for black hole echoes in gravitational wave data. Phys. Rev. D 2018, 97, 124037. [Google Scholar] [CrossRef]
- Abedi, J.; Afshordi, N. Echoes from the abyss: A highly spinning black hole remnant for the binary neutron star merger GW170817. JCAP 2019, 11, 10. [Google Scholar] [CrossRef]
- Cardoso, V.; Franzin, E.; Pani, P. Is the Gravitational-Wave Ringdown a Probe of the Event Horizon? Phys. Rev. Lett. 2016, 116, 171101. [Google Scholar] [CrossRef]
- Cardoso, V.; Hopper, S.; Macedo, C.F.; Palenzuela, C.; Pani, P. Echoes of ECOs: Gravitational-wave signatures of exotic compact objects and of quantum corrections at the horizon scale. Phys. Rev. D 2016, 94, 084031. [Google Scholar] [CrossRef]
- Cardoso, V.; Pani, P. Testing the nature of dark compact objects: A status report. Living Rev. Rel. 2019, 22, 4. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P.; Lecian, O.M. On generation of a stochastic GW background by the scattering on relic wormholes. Eur. Phys. J. C 2021, 81, 263. [Google Scholar] [CrossRef]
- De Falco, V.; Battista, E.; Capozziello, S.; De Laurentis, M. Reconstructing wormhole solutions in curvature based Extended Theories of Gravity. Eur. Phys. J. C 2021, 81, 157. [Google Scholar] [CrossRef]
- Ashraf, A.; Mustafa, G.; Ahmad, M.; Hussain, I. Lorentz distributed wormhole solutions in f(T) gravity with off-diagonal tetrad under conformal motions. Mod. Phys. Lett. A 2020, 35, 2050240. [Google Scholar] [CrossRef]
- Zubair, M.; Waheed, S.; Mustafa, G.; Rehman, H. Ur Noncommutative inspired wormholes admitting conformal motion involving minimal coupling. Int. J. Mod. Phys. D 2019, 28, 1950067. [Google Scholar] [CrossRef]
- Khatsymovsky, V. Can wormholes exist? Phys. Lett. B 1994, 320, 234–240. [Google Scholar] [CrossRef]
- Hochberg, D.; Popov, A.; Sushkov, S.V. Self-consistent wormhole solutions of semiclassical gravity. Phys. Rev. Lett. 1997, 78, 2050. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Krechet, V.G. Potentially observable cylindrical wormholes without exotic matter in general relativity. Phys. Rev. D 2019, 99, 084051. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Bolokhov, S.V.; Skvortsova, M.V. Cylindrical wormholes: A search for viable phantom-free models in GR. Int. J. Mod. Phys. D 2019, 28, 1941008. [Google Scholar] [CrossRef]
- Lifshitz, E. On the gravitational stability of the expanding universe. J. Phys. (USSR) 1946, 10, 116–129, republication in: Gen. Relativ. Gravit. 2017, 49, 18. [Google Scholar]
- Nicarstro, F.; Mathur, S.; Elvis, M.; Drake, J.; Fiore, F.; Fang, T.; Fruscione, A.; Krongold, Y.; Marshall, H.; Williams, R. Chandra detection of the first X-ray forest along the line of sight to Markarian 421. Astrophys. J. 2005, 629, 700. [Google Scholar] [CrossRef]
- Tripp, T.M.; Sembach, K.R.; Bowen, D.V.; Savage, B.D.; Jenkins, E.B.; Lehner, N.; Richter, P.A. High-resolution survey of low-redshift QSO absorption lines: Statistics and physical conditions of OVI absorbers. Astrophys. J. Suppliment Ser. 2008, 177, 39. [Google Scholar] [CrossRef]
- Buote, D.A.; Zappacosta, L.; Fang, T.; Humphrey, P.J.; Gastaldello, F.; Tagliaferri, G. X-Ray absorption by WHIM in the sculptor wall. Astrophys. J. 2009, 695, 1351. [Google Scholar] [CrossRef]
- Samorodmitzky, G.; Taggy, M.S. Stable Non-Gaussian Random Processes; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).