The Genuine Resonance of Full-Charm Tetraquarks

Abstract

In this work, the genuine resonance states of full-charm tetraquark systems with quantum numbers $J^{PC}=0^{++},1^{+-},2^{++}$ are searched in a nonrelativistic chiral quark model with the help of the Gaussian Expansion Method. In this calculation, two structures, meson-meson and diquark–antidiquark, as well as their mixing with all possible color-spin configurations, are considered. The results show that no bound states can be formed. However, resonances are possible because of the color structure. The genuine resonances are identified by the stabilization method (real scaling method). Several resonances for the full-charm system are proposed, and some of them are reasonable candidates for the full-charm states recently reported by LHCb.

1. Introduction

In the past few decades, many charmonium-like or bottomonium-like $XYZ$ states [1,2,3,4,5,6,7,8,9] have been observed in experiments, which has generated great challenges and opportunities for researchers to study multiquark states.

Recently, the tetraquark of the all-heavy system, such as $cc\overline{c}\overline{c}$ and $bb\overline{b}\overline{b}$, has received considerable attention due to the development of experiments. If the $cc\overline{c}\overline{c}$ or $bb\overline{b}\overline{b}$ states steadily exist, they are most likely to be observed at LHC, Belle II and other facilities. Double $J/\psi$ production becomes possible [10,11,12,13,14] and an enhancement in the differential production cross-section for $J/\psi$ pairs between 6 GeV and 8 GeV can be observed [10,11]. The CMS collaboration measured pair production of $\mathrm{Y}\left(1S\right)$ [15]. There was also a claim for the existence of a full-bottom tetraquark state $bb\overline{b}\overline{b}$ [16], with a global significance of $3.6\sigma$ and a mass of around $18.4$ GeV, almost 500 MeV below the threshold of $\mathrm{Y}\mathrm{Y}$. Very recently, the LHCb collaboration reported their newest finding that the full-charm states have been observed: there is a broad structure in the range 6.2∼6.8 GeV, a narrower structure at 6.9 GeV with a significance of about 5$\sigma$, and a structure around 7.2 GeV [17]. This discovery brought about widespread theoretical attention [18,19,20,21,22,23,24,25].

In fact, whether or not observable states of fully-heavy tetraquarks exist has been debated for more than forty years. Theoretically, various methods are applied to study the full-heavy tetraquark states. Some work has suggested that stable bound states should exist [26,27,28,29,30,31,32,33]. Iwasaki [26] first argued that the bound state of $c^2{\overline{c}}^2$ can exist and estimated its mass to be in the neighborhood of 6 GeV or 6.2 GeV based on a string model. Heller et al. Claimed that the dimensions $cc\overline{c}\overline{c}$ and $bb\overline{b}\overline{b}$ are bound, and that the binding energy ranges from 0.16∼0.22 GeV based on the potential energy arising from the MIT bag model [27]. Lloyd et al. have used a parametrized Hamiltonian to calculate the spectrum of the all-charm tetraquark state and found several close-lying bound states with two sets of parameters based on large but finite oscillator bases. For example, the lowest state with quantum number $J^{PC}=0^{++}$ had a mass below the threshold of two ${\eta }_c\left(1S\right)$, 5967.2 MeV [28]. Berezhnoy et al. showed that the masses of $cc\overline{c}\overline{c}$ and $bb\overline{b}\overline{b}$ states are under the thresholds for $J=1,2$ by taking a diquark and antidiquark as point particles and employing the hyperfine interaction between them [29]. In a moment QCD sum rule approach, Chen et al. studied the fully-heavy tetraquark states, and discovered that the masses of the $bb\overline{b}\overline{b}$ tetraquarks are below the thresholds of $\mathrm{Y}\left(1S\right)\mathrm{Y}\left(1S\right)$ and ${\eta }_b\left(1S\right){\eta }_b\left(1S\right)$, and the masses of the $cc\overline{c}\overline{c}$ tetraquarks are above the threshold [30]. Yang Bai et al. and Esposito et al. calculated the mass of the $bb\overline{b}\overline{b}$ state to be around 100 MeV below the threshold of ${\eta }_b{\eta }_b$ [31,32]. In recent research, Debastiani et al. used a non-relativistic model to study the spectroscopy for a tetraquark composed of $cc\overline{c}\overline{c}$ in a diquark–antidiquark configuration and found that the lowest S-wave $cc\overline{c}\overline{c}$ tetraquarks might exist below their thresholds [33].

On the contrary, in other work, there is no bound full-heavy tetraquark state but resonance states are possible [34,35,36,37,38,39,40,41,42,43]. Chao predicted full-charm diquark–antidiquark states exist with masses in the range of 6.4∼6.8 GeV [34]. Ader et al. investigated the full-heavy tetraquark state in a potential model and found that there no state exists below the corresponding thresholds [35]. Barnea et al. studied a system consisting of quarks and antiquarks of the same flavor within the hyperspherical formalism, and the mass of $cc\overline{c}\overline{c}$ was approximately 6038 MeV, which is above the corresponding threshold [36]. In the QCD sum-rule approach, no bound state was found and several resonances for $cc\overline{c}\overline{c}$ and $bb\overline{b}\overline{b}$ systems were proposed [37]. Karliner et al. have calculated the mass spectrum of $cc\overline{c}\overline{c}$ state and found it unlikely to be less than twice the mass of the lowest charmonium state ${\eta }_c$ [38]. Wu et al. also found no full-heavy tetraquark with the same flavor below the thresholds in a color-magnetic interaction model [39]. Recently in Ref. [40], Liu et al. suggested that no bound states can be formed below the thresholds for meson pairs $\left(\overline{c}c\right)$-$\left(\overline{c}c\right)$ within a potential model by including the linear confining potential, Coulomb potential and spin-spin interactions. The full-bottom tetraquark was also calculated in the chiral quark model with the help of the Gaussian Expansion Method, and no bound states were found and a resonance was proposed [44]. In the framework of a quark delocalization color screening model and chiral quark model with the help of the resonating group method, the reported state $X\left(6900\right)$ can be explained as a compact resonance state with $I{J}^P={00}^{+}$ [45].

Hadron spectroscopy always plays an important role in revealing the properties of the dynamics of the strong interaction. The fully-heavy tetraquark system provides a good chance to test our understanding of hadron structure. To date, most calculations for fully-heavy tetraquarks assume that the system has a given structure, meson-meson, diquark–antidiquark, etc. A few studies have carried out calculations with structure mixing. Such as Ref. [30], the authors calculated the mass spectra for doubly hidden-charm/bottom tetraquark states using only the compact diquark–antidiquark configuration. Now most calculations are usually carried out in a finite space. The finite space will discretize the energy of the system. The bound state or genuine resonance state should have a stable energy against an increasing space and structure mixing. To obtain the genuine resonances, various techniques are available: the real scaling method (stabilization) [46,47,48], complex scaling method [49], phase shift analysis [50,51] and so on. In the present work, we systematically investigate the masses of full-charm tetraquarks with $J^{PC}=0^{++},1^{+-},2^{++}$ in the chiral quark model, which can well describe the properties of hadrons and hadron-hadron interactions. The method of the Gaussian Expansion Method (GEM) is employed to carry out a high precision four-body calculation. The dynamical mixing of the meson-meson configuration with the diquark–antidiquark configuration is also considered. One thing that needs to be specified is that, here, the diquark–antidiquark and meson-meson configuration is just a nomenclature for the color saturation of the system and does not correspond to the compact tetraquark and the meson molecule configurations. For example, color singlet-singlet $1\times 1$ and color octet-octet $8\times 8$ denotes meson-meson structure, and color antitriplet-triplet $\overline{3}\times 3$ and sextet-antisextet $6\times \overline{6}$ denotes diquark–antidiquark structure, and their mixing is taken into account. This mixing occurs via both the spin-independent and the spin-dependent parts of the potential. To obtain the genuine resonances, the real scaling method is employed. In previous work [44], only the lowest resonances of the full-bottom tetraquark were investigated. Inspired by the recent experimental results for the full-charm tetraquark, and unlike our previous work for $bb\overline{b}\overline{b}$, the possible resonance states with higher energies are explored in the present work.

This paper is organized as follows. In Section 2, we briefly discuss the chiral quark model, the wave functions of the full-heavy tetraquark, and the Gaussian Expansion Method. In Section 3, the numerical results and discussion are presented. Some conclusions and a summary are given in Section 4.

2. Quark Model and Wave Functions

2.1. The Chiral Quark Model

The chiral quark model has been applied both in explaining the hadron spectra and hadron-hadron interactions successfully. We can find the details for the model in [52,53]. Three parts of the Hamiltonian are included for the $cc\overline{c}\overline{c}$ fully-heavy system: quark rest mass, kinetic energy, and potential energy:

$$\begin{array}{cc}\hfill H& =\sum _{i=1}^4{m}_i+\frac{p_{12}^2}{2{\mu }_{12}}+\frac{p_{34}^2}{2{\mu }_{34}}+\frac{p_{1234}^2}{2{\mu }_{1234}}\hfill \\ \hfill & +\sum _{i<j=1}^4\left(V_{ij}^C+V_{ij}^G\right),\hfill \end{array}$$

(1)

$m_i$ is the constituent mass of i-th quark/antiquark, and ${\mu }_{ij}$ is the reduced mass of two interacting quarks, with

$$\begin{array}{cc}\hfill {\mu }_{ij}& =\frac{m_i{m}_j}{m_i+m_j},\hfill \\ \hfill {\mu }_{1234}& =\frac{(m_1+m_2)(m_3+m_4)}{m_1+m_2+m_3+m_4},\hfill \\ \hfill {\mathbf{p}}_{ij}& =\frac{m_j{\mathbf{p}}_i-m_i{\mathbf{p}}_j}{m_i+m_j},\hfill \\ \hfill {\mathbf{p}}_{1234}& =\frac{(m_3+m_4){\mathbf{p}}_{12}-(m_1+m_2){\mathbf{p}}_{34}}{m_1+m_2+m_3+m_4}.\hfill \end{array}$$

(2)

$V^C$ and $V^G$ represents the quark confinement and the one-gluon-exchange potential, respectively. The detailed forms for the two potentials are shown below [52]:

$$\begin{array}{cc}\hfill V_{ij}^C& =(-a_c{r}_{ij}^2-\Delta ){\mathit{\lambda }}_i^c·{\mathit{\lambda }}_j^c,\hfill \\ \hfill V_{ij}^G& =\frac{{\alpha }_s}{4}{\mathit{\lambda }}_i^c·{\mathit{\lambda }}_j^c\left[\frac{1}{r_{ij}}-\frac{2\pi }{3m_i{m}_j}{\mathit{\sigma }}_i·{\mathit{\sigma }}_j\delta \left({\mathit{r}}_{ij}\right)\right],\hfill \\ \hfill \delta \left({\mathit{r}}_{ij}\right)& =\frac{e^{-r_{ij}/r_0\left({\mu }_{ij}\right)}}{4\pi r_{ij}{r}_0^2\left({\mu }_{ij}\right)}.\hfill \end{array}$$

(3)

${\mathit{\lambda }}^c$ are the $SU\left(3\right)$ color Gell-Mann matrices and $\mathit{\sigma }$ are the $SU\left(2\right)$ Pauli matrices; $r_0\left({\mu }_{ij}\right)=s_0/{\mu }_{ij}$ and ${\alpha }_s$ is an effective scale-dependent running coupling [53],

$${\alpha }_s\left({\mu }_{ij}\right)=\frac{{\alpha }_0}{ln\left[({\mu }_{ij}^2+{\mu }_0^2)/{\Lambda }_0^2\right]}.$$

(4)

All the model parameters are listed in

Table 1. Model parameters, determined by fitting the meson spectrum from light to heavy.

Quark masses	$m_u=m_d$	313
(MeV)	$m_s$	536
	$m_c$	1728
	$m_b$	5112
Confinement	$a_c$ (MeV fm${}^{-2}$)	101
	$\Delta$ (MeV)	−78.3
OGE	${\alpha }_0$	3.67
	${\Lambda }_0\left({\mathrm{fm}}^{-1}\right)$	0.033
	${\mu }_0$ (MeV)	36.98
	$s_0$ (MeV)	28.17

, which are determined by fitting the light and heavy meson spectra. In

Table 2. The masses of some heavy mesons (unit: MeV). $M_{cal}$ and $M_{exp}$ represent the theoretical and experimental masses, respectively.

Meson	${\mathit{\eta }}_{\mathit{c}}$	$\mathit{J}/\mathit{\psi }$	${\mathit{h}}_{\mathit{c}}$	${\mathit{\chi }}_{\mathit{c}0}$	${\mathit{\chi }}_{\mathit{c}1}$	${\mathit{\chi }}_{\mathit{c}2}$
$M_{cal}$	2986.3	3096.4	3417.3	3416.4	3416.4	3416.4
$M_{exp}$	$2983.4$	$3096.9$	$3525.4$	$3414.8$	$3510.7$	$3556.2$

, the theoretical and experimental masses for the low-lying $c\overline{c}$ are demonstrated in the chiral quark model. Because the orbital-spin interactions are not taken into account in the present calculation, the P-wave states ${\chi }_{cJ}(J=0,1,2)$ have the same mass.

2.2. The Wave Functions of $cc\overline{c}\overline{c}$ System

The wave functions of four-quark states can be constructed in two steps for both the meson-meson and diquark–antidiquark structure. First we obtain the wave functions for two-body sub-clusters, and, then, secondly, couple the wave functions of these two sub-clusters to construct the total wave functions for a four-quark state with exclusive quantum number $I{J}^{PC}$. To save space, only the wave functions for each degree of freedom are shown below.

(1) Diquark–antidiquark structure

We denote $\alpha$ and $\beta$ as the spin-up and spin-down states of the quarks and the spin wave functions for the four-quark states takes the form of

$$\begin{array}{ccc}\hfill {\chi }_{00}^{\sigma 1}& =& \frac{1}{2}(\alpha \beta \alpha \beta -\alpha \beta \beta \alpha -\beta \alpha \alpha \beta +\beta \alpha \beta \alpha ),\hfill \\ \hfill {\chi }_{00}^{\sigma 2}& =& \sqrt{\frac{1}{12}}(2\alpha \alpha \beta \beta -\alpha \beta \alpha \beta -\alpha \beta \beta \alpha \hfill \\ & & -\beta \alpha \alpha \beta -\beta \alpha \beta \alpha +2\beta \beta \alpha \alpha ),\hfill \\ \hfill {\chi }_{11}^{\sigma 3}& =& \sqrt{\frac{1}{2}}(\alpha \beta \alpha \alpha -\beta \alpha \alpha \alpha ),\hfill \\ \hfill {\chi }_{11}^{\sigma 4}& =& \sqrt{\frac{1}{2}}(\alpha \alpha \alpha \beta -\alpha \alpha \beta \alpha ),\hfill \\ \hfill {\chi }_{11}^{\sigma 5}& =& \frac{1}{2}(\alpha \alpha \alpha \beta +\alpha \alpha \beta \alpha -\alpha \beta \alpha \alpha -\beta \alpha \alpha \alpha ),\hfill \\ \hfill {\chi }_{22}^{\sigma 6}& =& \alpha \alpha \alpha \alpha .\hfill \end{array}$$

(5)

There are six spin wave functions for four-quark states in total, which are marked as the superscript $\sigma i$ (i = 1∼6) of $\chi$. The subscripts of $\chi$ represent the total spin and the third projection of total spin of the system, and only one component ($M_S=S$) is needed for a given total spin S.

For the $cc\overline{c}\overline{c}$ system, the flavor wave function reads as follows:

$${\chi }_{d0}^f=\left(cc\right)\left(\overline{c}\overline{c}\right).$$

(6)

The marks $d0$ of $\chi$ represent the diquark–antidiquark structure with an isospin that equals zero.

For the color freedom, we need to obtain the color singlet wave functions for the four-quark states. The detailed coupling pathways can be found in our previous work [54].

$$\begin{array}{cc}\hfill {\chi }_d^{c1}& =\frac{\sqrt{3}}{6}(rg\overline{r}\overline{g}-rg\overline{g}\overline{r}+gr\overline{g}\overline{r}-gr\overline{r}\overline{g}\hfill \\ \hfill & +rb\overline{r}\overline{b}-rb\overline{b}\overline{r}+br\overline{b}\overline{r}-br\overline{r}\overline{b}\hfill \\ \hfill & +gb\overline{g}\overline{b}-gb\overline{b}\overline{g}+bg\overline{b}\overline{g}-bg\overline{g}\overline{b}).\hfill \\ \hfill {\chi }_d^{c2}& =\frac{\sqrt{6}}{12}(2rr\overline{r}\overline{r}+2gg\overline{g}\overline{g}+2bb\overline{b}\overline{b}+rg\overline{r}\overline{g}+rg\overline{g}\overline{r}\hfill \\ \hfill & +gr\overline{g}\overline{r}+gr\overline{r}\overline{g}+rb\overline{r}\overline{b}+rb\overline{b}\overline{r}+br\overline{b}\overline{r}\hfill \\ \hfill & +br\overline{r}\overline{b}+gb\overline{g}\overline{b}+gb\overline{b}\overline{g}+bg\overline{b}\overline{g}+bg\overline{g}\overline{b}).\hfill \end{array}$$

(7)

where, ${\chi }_d^{c1}$ and ${\chi }_d^{c2}$ is the color antitriplet-triplet ($\overline{3}\times 3$) and sextet-antisextet ($6\times \overline{6}$) color configuration, respectively.

(2) Meson-meson structure

For the spin freedom, the wave functions are independent of the structure of the system and they are the same as those for the diquark–antidiquark structure, Equation (5).

For the flavor part, the wave function takes the following form:

$${\chi }_{m0}^f=\left(\overline{c}c\right)\left(\overline{c}c\right).$$

(8)

The marks $m0$ of $\chi$ represent the meson-meson structure and isospin $I=0$.

For the color freedom, the color singlet wave functions for the four-quark states are,

$$\begin{array}{cc}\hfill {\chi }_m^{c1}& =\frac{1}{3}(\overline{r}r+\overline{g}g+\overline{b}b)(\overline{r}r+\overline{g}g+\overline{b}b),\hfill \\ \hfill {\chi }_m^{c2}& =\frac{\sqrt{2}}{12}(3\overline{b}r\overline{r}b+3\overline{g}r\overline{r}g+3\overline{b}g\overline{g}b+3\overline{g}b\overline{b}g+3\overline{r}g\overline{g}r\hfill \\ \hfill & +3\overline{r}b\overline{b}r+2\overline{r}r\overline{r}r+2\overline{g}g\overline{g}g+2\overline{b}b\overline{b}b-\overline{r}r\overline{g}g\hfill \\ \hfill & -\overline{g}g\overline{r}r-\overline{b}b\overline{g}g-\overline{b}b\overline{r}r-\overline{g}g\overline{b}b-\overline{r}r\overline{b}b).\hfill \end{array}$$

(9)

where ${\chi }_m^{c1}$ and ${\chi }_m^{c2}$ represents the color singlet-singlet ($1\times 1$) and color octet-octet ($8\times 8$) configuration, respectively.

The orbital wave functions for the four-quark states can be obtained by coupling the orbital wave function for each relative motion of the system:

$${\Psi }_{L{M}_L}={\left[{\left[{\Psi }_{l_1}\left({\mathbf{r}}_{12}\right){\Psi }_{l_2}\left({\mathbf{r}}_{34}\right)\right]}_{l_{12}}{\Psi }_{L_r}\left({\mathbf{r}}_{1234}\right)\right]}_{L{M}_L},$$

(10)

where ${\Psi }_{l_1}$ and ${\Psi }_{l_2}$ are the orbital wave functions of the two sub-clusters, with an angular momentum of $l_1$ and $l_2$, respectively. ${\Psi }_{L_r}\left({\mathbf{r}}_{1234}\right)$ is the wave function of the relative motion between two sub-clusters with orbital angular momentum $L_r$. The total orbital angular momentum of the four-quark state is L. “[ ]” denotes the Clebsh–Gordan coupling. As a preliminary calculation, here, we take an approximation that all angular momenta ($l_1,l_2,L_r,L$) are set to zero. The Jacobi coordinates used are defined as follows:

$$\begin{array}{cc}\hfill {\mathbf{r}}_{12}& ={\mathbf{r}}_1-{\mathbf{r}}_2,\hfill \\ \hfill {\mathbf{r}}_{34}& ={\mathbf{r}}_3-{\mathbf{r}}_4,\hfill \\ \hfill {\mathbf{r}}_{1234}& =\frac{m_1{\mathbf{r}}_1+m_2{\mathbf{r}}_2}{m_1+m_2}-\frac{m_3{\mathbf{r}}_3+m_4{\mathbf{r}}_4}{m_3+m_4}.\hfill \end{array}$$

(11)

For the diquark–antidiquark structure, the two quarks $cc$ in one cluster are numbered as $1,2$, and the two antiquarks $\overline{c}\overline{c}$ in the other cluster are numbered as $3,4$; for the meson-meson structure, numbers $1,2$ denote the antiquark and quark $\overline{c}c$ in one cluster, and numbers $3,4$ denote the antiquark and quark $\overline{c}c$ in the other cluster. In the mixing calculations for the two structures, the marks of the quarks, antiquarks in the diquark–antidiquark structure are changed to be consistent with the numbering scheme in the meson-meson structure. In GEM, the orbital wave function is expanded by a series of Gaussians [55]:

$$\begin{array}{cc}\hfill {\Psi }_{lm}\left(\mathbf{r}\right)& =\sum _{n=1}^{n_{\max }}{c}_n{\psi }_{nlm}^G\left(\mathbf{r}\right),\hfill \\ \hfill {\psi }_{nlm}^G\left(\mathbf{r}\right)& =N_{nl}{r}^l{e}^{-{\nu }_n{r}^2}{Y}_{lm}\left(\widehat{\mathbf{r}}\right),\hfill \end{array}$$

(12)

where $N_{nl}$ are normalization constants,

$$\begin{array}{c}\hfill N_{nl}={\left[\frac{2^{l+2}{\left(2{\nu }_n\right)}^{l+\frac{3}{2}}}{\sqrt{\pi }(2l+1)}\right]}^{\frac{1}{2}}.\end{array}$$

(13)

$c_n$ are the variational parameters, which are determined dynamically. The Gaussian size parameters are chosen according to the following geometric progression:

$${\nu }_n=\frac{1}{r_n^2},r_n=r_1{a}^{n-1},a={\left(\frac{r_{n_{\max }}}{r_1}\right)}^{\frac{1}{n_{\max }-1}}.$$

(14)

This procedure enables optimized use of Gaussians, with as small a number of Gaussians used as possible.

So, we obtain the final channel wave function for the four-quark system $cc\overline{c}\overline{c}$ in the diquark–antidiquark structure:

$$\begin{array}{cc}\hfill & {\Psi }_{IJ,i,j}^{M_I{M}_J}={\mathcal{A}}_1{\left[{\Psi }_L^{M_L}{\chi }_{S{M}_S}^{\sigma i}\right]}_J^{M_J}{\chi }_{d0}^f{\chi }_d^{cj},\hfill \\ \hfill & (i=1\sim 6;j=1,2;S=0,1,2),\hfill \end{array}$$

(15)

where ${\mathcal{A}}_1$ is the antisymmetrization operator, for the $cc\overline{c}\overline{c}$ system,

$${\mathcal{A}}_1=\frac{1}{2}(1-P_{12}-P_{34}+P_{12}{P}_{34}).$$

(16)

In the meson-meson structure, the final channel wave function for the $cc\overline{c}\overline{c}$ system is written as

$$\begin{array}{cc}\hfill & {\Psi }_{IJ,i,j}^{M_I{M}_J}={\mathcal{A}}_2{\left[{\Psi }_L^{M_L}{\chi }_{S{M}_S}^{\sigma i}\right]}_J^{M_J}{\chi }_{m0}^f{\chi }_m^{cj},\hfill \\ \hfill & (i=1\sim 6;j=1,2;S=0,1,2),\hfill \end{array}$$

(17)

where ${\mathcal{A}}_2$ is the antisymmetrization operator, for the $c\overline{c}c\overline{c}$ system,

$${\mathcal{A}}_2=\frac{1}{2}(1-P_{13}-P_{24}+P_{13}{P}_{24}).$$

(18)

Finally, we obtain the eigenenergies for the $cc\overline{c}\overline{c}$ system by solving a Schrödinger equation:

$$H{\Psi }_{I{M}_{I}J{M}_J}=E_{IJ}{\Psi }_{I{M}_{I}J{M}_J}.$$

(19)

${\Psi }_{I{M}_{I}J{M}_J}$ is the wave function of the four-quark states, which is the linear combinations of the above channel wave functions, Equation (15) in the pure diquark–antidiquark structure or Equation (17) in the pure meson-meson structure, or both wave functions of Equations (15) and (17), respectively.

3. Results and Discussions

In this work, we estimated the masses of the tetraquark states for $cc\overline{c}\overline{c}$ with the quantum numbers $J^{PC}=0^{++},1^{+-},2^{++}$ in the chiral quark model by adopting GEM. The pure meson-meson and the pure diquark–antidiquark structure, along with the dynamical mixing of these two structures are considered, respectively. In our calculations, all possible color, and spin configurations are included, and the approximation that all orbital angular momenta are set to 0 is used. In

Table 3. The possible channels and corresponding wave functions for $cc\overline{c}\overline{c}$ tetraquarks with quantum numbers $J^{PC}=0^{++},1^{+-},2^{++}$. The channels $\left(DA\right)$ represent the diquark–antidiquark structures and the superscripts of the channels represent the total angular momentum J.

${\mathit{J}}^{\mathit{PC}}=0^{++}$		${\mathit{J}}^{\mathit{PC}}=1^{+-}$		${\mathit{J}}^{\mathit{PC}}=2^{++}$
Channels	Wave Functions	Channels	Wave Functions	Channels	Wave Functions
${\left({\eta }_c{\eta }_c\right)}^0$	${\chi }_{00}^{\sigma 1}{\chi }_{m0}^f{\chi }_m^{c1}$	${({\eta }_{c}J/\psi )}^1$	${\chi }_{11}^{\sigma 3}{\chi }_{m0}^f{\chi }_m^{c1}$	${(J/\psi J/\psi )}^2$	${\chi }_{22}^{\sigma 6}{\chi }_{m0}^f{\chi }_m^{c1}$
${\left({\eta }_c^8{\eta }_c^8\right)}^0$	${\chi }_{00}^{\sigma 1}{\chi }_{m0}^f{\chi }_m^{c2}$	${({\eta }_c^{8}J/{\psi }^8)}^1$	${\chi }_{11}^{\sigma 3}{\chi }_{m0}^f{\chi }_m^{c2}$	${(J/{\psi }^{8}J/{\psi }^8)}^2$	${\chi }_{22}^{\sigma 6}{\chi }_{m0}^f{\chi }_m^{c2}$
${(J/\psi J/\psi )}^0$	${\chi }_{00}^{\sigma 2}{\chi }_{m0}^f{\chi }_m^{c1}$	${(J/\psi {\eta }_c)}^1$	${\chi }_{11}^{\sigma 4}{\chi }_{m0}^f{\chi }_m^{c1}$	${\left(DA\right)}^2$	${\chi }_{22}^{\sigma 6}{\chi }_{d0}^f{\chi }_d^{c1}$
${(J/{\psi }^{8}J/{\psi }^8)}^0$	${\chi }_{00}^{\sigma 2}{\chi }_{m0}^f{\chi }_m^{c2}$	${(J/{\psi }^8{\eta }_c^8)}^1$	${\chi }_{11}^{\sigma 4}{\chi }_{m0}^f{\chi }_m^{c2}$
${\left(DA\right)}_1^0$	${\chi }_{00}^{\sigma 2}{\chi }_{d0}^f{\chi }_d^{c1}$	${\left(DA\right)}^1$	${\chi }_{11}^{\sigma 5}{\chi }_{d0}^f{\chi }_d^{c1}$
${\left(DA\right)}_2^0$	${\chi }_{00}^{\sigma 1}{\chi }_{d0}^f{\chi }_d^{c2}$

, we give the possible channels and corresponding wave functions.

The single-channel and channel-coupling calculations are performed in the present work. To determine whether or not any bound states exist,

Table 4. The low-lying energies of the $cc\overline{c}\overline{c}$ states with $J^{PC}=0^{++}$, $1^{+-}$, $2^{++}$ in single channel and full-channel coupling calculations. $E_{\mathrm{th}}^{\mathrm{theo}}$ and $E_{\mathrm{th}}^{\exp }$ represent the theoretical and experimental thresholds, respectively (unit: MeV).

Channel	E	${\mathit{E}}_{\mathit{th}}^{\mathbf{theo}}$	${\mathit{E}}_{\mathit{th}}^{\mathbf{exp}}$
$J^{PC}=0^{++}$
${\left({\eta }_c{\eta }_c\right)}^0$	5973.4	5972.6	5966.8
${\left({\eta }_c^8{\eta }_c^8\right)}^0$	6373.2
${(J/\psi J/\psi )}^0$	6193.7	6192.8	6193.8
${(J/{\psi }^{8}J/{\psi }^8)}^0$	6356.9
${\left(DA\right)}_1^0$	6360.2
${\left(DA\right)}_2^0$	6390.9
full-channel coupling	5973.4	5972.6	5966.8
$J^{PC}=1^{+-}$
${({\eta }_{c}J/\psi )}^1$	6083.6	6082.7	6080.3
${({\eta }_c^{8}J/{\psi }^8)}^1$	6349.8
${(J/\psi {\eta }_c)}^1$	6083.6	6082.7	6080.3
${(J/{\psi }^8{\eta }_c^8)}^1$	6349.8
${\left(DA\right)}^1$	6397.6
full-channel coupling	6083.6	6082.7	6080.3
$J^{PC}=2^{++}$
${(J/\psi J/\psi )}^2$	6193.7	6192.8	6193.8
${(J/{\psi }^{8}J/{\psi }^8)}^2$	6365.3
${\left(DA\right)}^2$	6410.4
full-channel coupling	6193.7	6192.8	6193.8

gives the low-lying energies for $cc\overline{c}\overline{c}$ tetraquarks with quantum numbers $J^{PC}=0^{++},1^{+-},2^{++}$, respectively. From the table, we find that all the energies obtained are above the corresponding theoretical thresholds, so no bound states are formed in our calculations. In addition, the energies of the hidden-color states with color configurations $8\times 8$, $\overline{3}\times 3$ and $6\times \overline{6}$ are higher than those with color $1\times 1$.

Although there is no bound state for the fully-heavy tetraquark system, resonance states with energies higher than the corresponding thresholds are possible because of the color structures of the system. In the present work, we employ the dedicated real scaling (stabilization) method to determine the genuine resonances. Because the calculation is carried out in a finite space, all the energies obtained are discrete. The bound state has a stable energy in the channel coupling calculation, while the resonance has a quasi-stable energy with increasing space after coupling to the scattering states. The real scaling method has been often used for analyzing electron–atom and electron–molecule scattering [46]. In the present approach, the real scaling method is realized by scaling the Gaussian size parameters $r_n$ in Equation (14) just for the meson-meson structure with the $1\times 1$ color configuration, i.e., $r_n\to \alpha r_n$, where $\alpha$ takes values between 0.9 and 1.7.

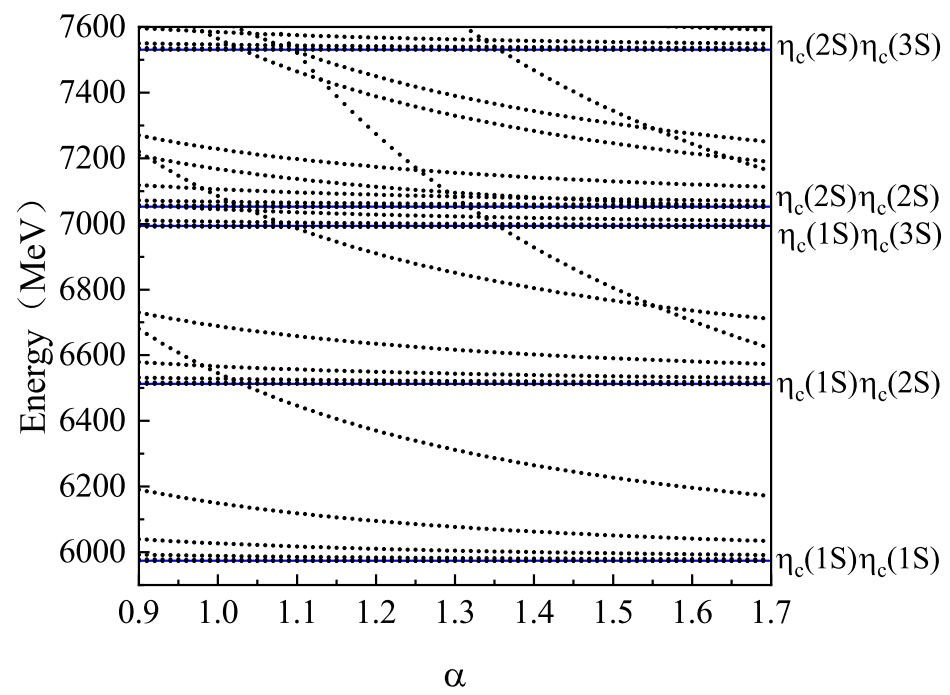
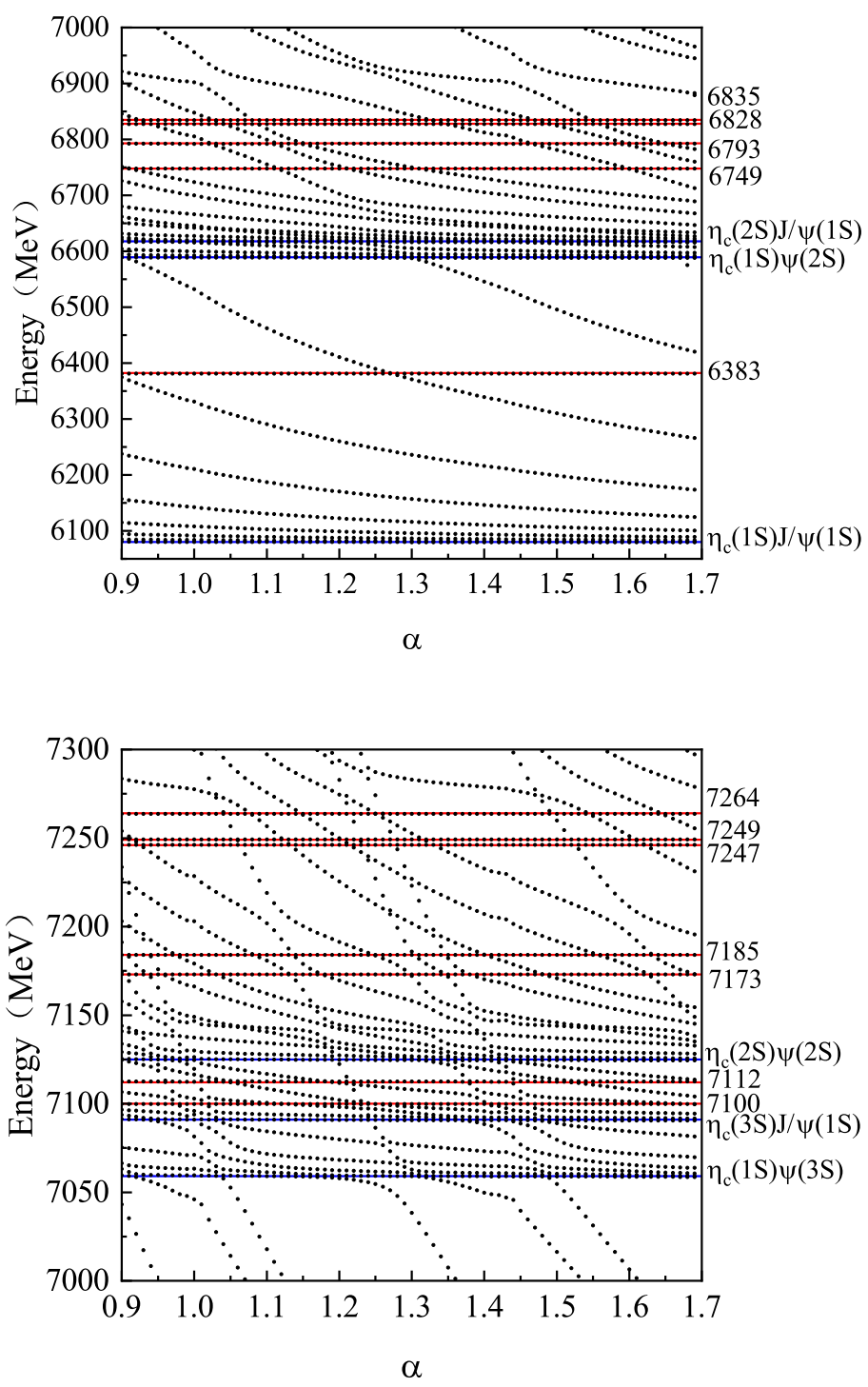
(a) $J^{PC}=0^{++}$: There are six channels in this case. The stabilization plots for some channels are given. The first channel corresponds to the ${\left({\eta }_c{\eta }_c\right)}^0$ configuration. Figure 1 shows the behavior of the energy spectrum of the first channel under the scaling of space. In this figure, most energies for the states decrease with increasing $\alpha$, and they are scattering states. However, there are several horizontal lines, which correspond to the thresholds, ${\eta }_c\left(1S\right){\eta }_c\left(1S\right)$, ${\eta }_c\left(1S\right){\eta }_c\left(2S\right)$, ${\eta }_c\left(1S\right){\eta }_c\left(3S\right)$ and ${\eta }_c\left(2S\right){\eta }_c\left(2S\right)$. The second channel is the hidden-color channel ${\left({\eta }_c^8{\eta }_c^8\right)}^0$. ${\eta }_c^8$ is the color octet state of $c\overline{c}$ with spin 0. To check the $\alpha$ dependence of the energies of the hidden color channel, we also changed $r_n$ to $\alpha r_n$ for the relative motion between two sub-clusters in the hidden color channel. Figure 2 gives a stabilization plot of the second channel, and all the energies are stable against the scaling of space. Figure 3 shows the stabilization plot for the third channel, ${(J/\psi J/\psi )}^0$ configuration. We observe similar behavior as that found for the first channel ${\left({\eta }_c{\eta }_c\right)}^0$ and some thresholds appear. The remaining three channels ${(J/{\psi }^{8}J/{\psi }^8)}^0$, ${\left(DA\right)}_1^0$ and ${\left(DA\right)}_2^0$ show similar behavior as observed for the second channel ${\left({\eta }_c^8{\eta }_c^8\right)}^0$, which is omitted here to save space. From these three figures, we can see that the energies of the hidden-color channels are independent with the scaling of space, but for the $1\times 1$ color configuration.

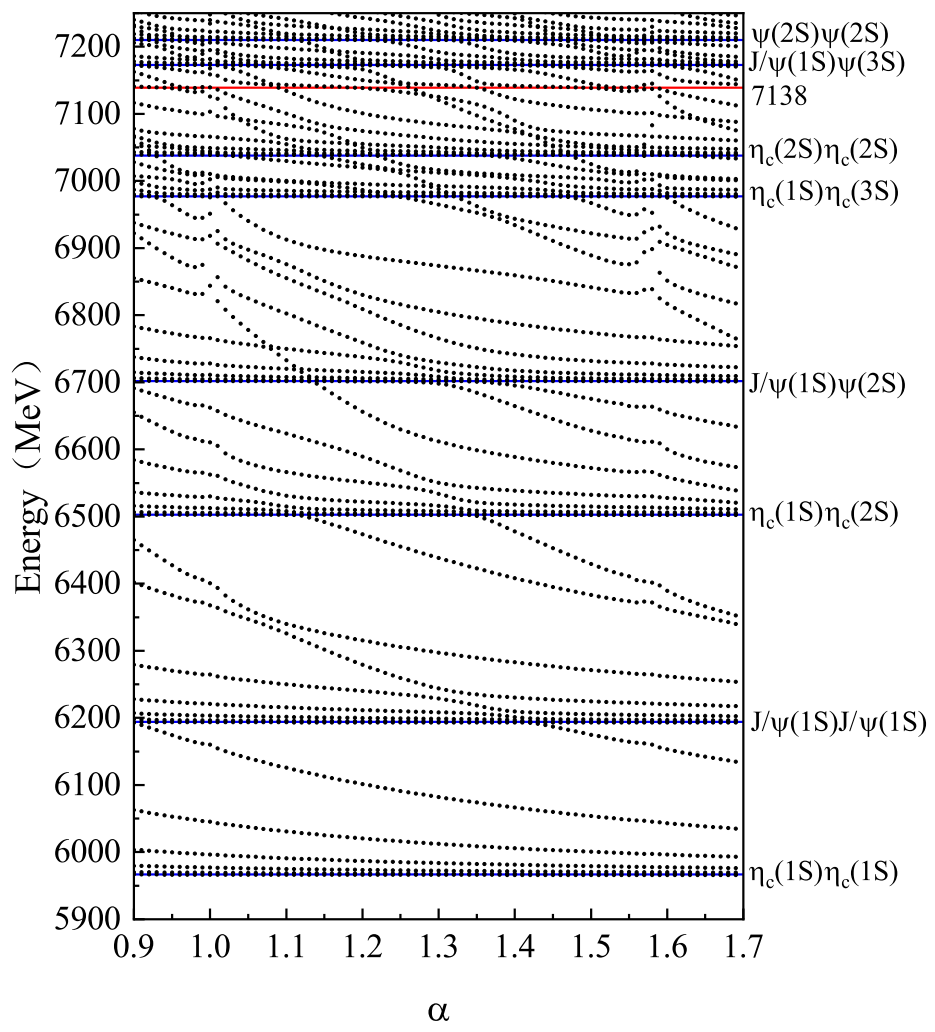
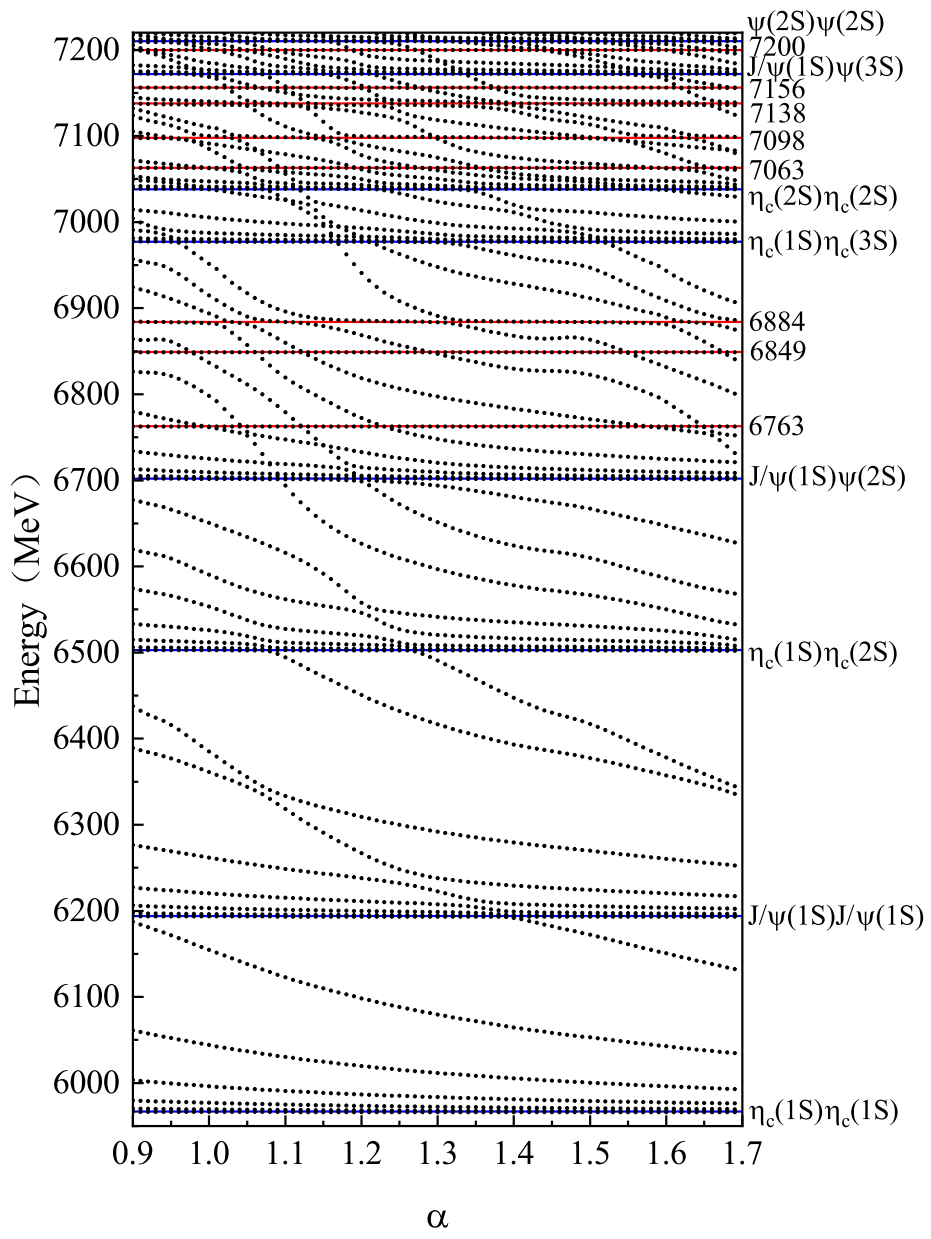
To show the coupling effect, the following calculations were carried out. We first studied the coupling effects between hidden-color channels. In

Table 5. The energy spectra for the $cc\overline{c}\overline{c}$ states with $J^{PC}=0^{++}$ in the single hidden-color channel and hidden-color channels coupling (unit: MeV).

Channel	${\left({\mathit{\eta }}_{\mathit{c}}^8{\mathit{\eta }}_{\mathit{c}}^8\right)}^0$	${(\mathit{J}/{\mathit{\psi }}^8\mathit{J}/{\mathit{\psi }}^8)}^0$	${\left({\mathit{\eta }}_{\mathit{c}}^8{\mathit{\eta }}_{\mathit{c}}^8\right)}^0$+${(\mathit{J}/{\mathit{\psi }}^8\mathit{J}/{\mathit{\psi }}^8)}^0$	${\left(\mathbf{DA}\right)}_1^0$	${\left(\mathbf{DA}\right)}_2^0$	${\left(\mathbf{DA}\right)}_1^0$+${\left(\mathbf{DA}\right)}_2^0$	${\left({\mathit{\eta }}_{\mathit{c}}^8{\mathit{\eta }}_{\mathit{c}}^8\right)}^0$+${(\mathit{J}/{\mathit{\psi }}^8\mathit{J}/{\mathit{\psi }}^8)}^0$+${\left(\mathbf{DA}\right)}_1^0$+${\left(\mathbf{DA}\right)}_2^0$
Energy	6371	6355	6328	6388	6358	6344	6253
	6708	6717	6402	6756	6690	6400	6316
	6973	6951	6657	6841	6763	6683	6528
	7036	7065	6765	6848	6974	6759	6577
	7140	7142	6944	7149	7022	6763	6714
	7301	7258	6978	7196	7063	6840	6763
	7357	7393	6987	7200	7102	6849	6805
	7448	7453	7110	7262	7268	6972	6849
	7507	7490	7130	7266	7326	7021	6877
	7613	7577	7154	7281	7329	7063	6886

, the energies for the single hidden-color channel and hidden-color channels coupling are shown. To save space, only the first ten energies are listed. From the table, we can see that the coupling has important effects on the energy spectrum because all the energies of the hidden-color channels lie in the same energy range. For example, hidden-color meson-meson structure has the lowest energy of 6328 MeV, while the diquark–antidiquark structure has a lowest energy of 6344 MeV, and the coupling between structures reduces this energy to 6253 MeV. The coupling results for all hidden-channels are stable against the scaling of space, which is shown in Figure 4. The energy of the lowest state is 6253 MeV. There is another state close to it with an energy of 6316 MeV. At around 6500 MeV, there are two states, and, in the range of 6700–7000 MeV, 8 resonance states appear. Which resonance states can be observed among these states? A calculation for the coupling of the hidden-color channels to the scattering states is required.

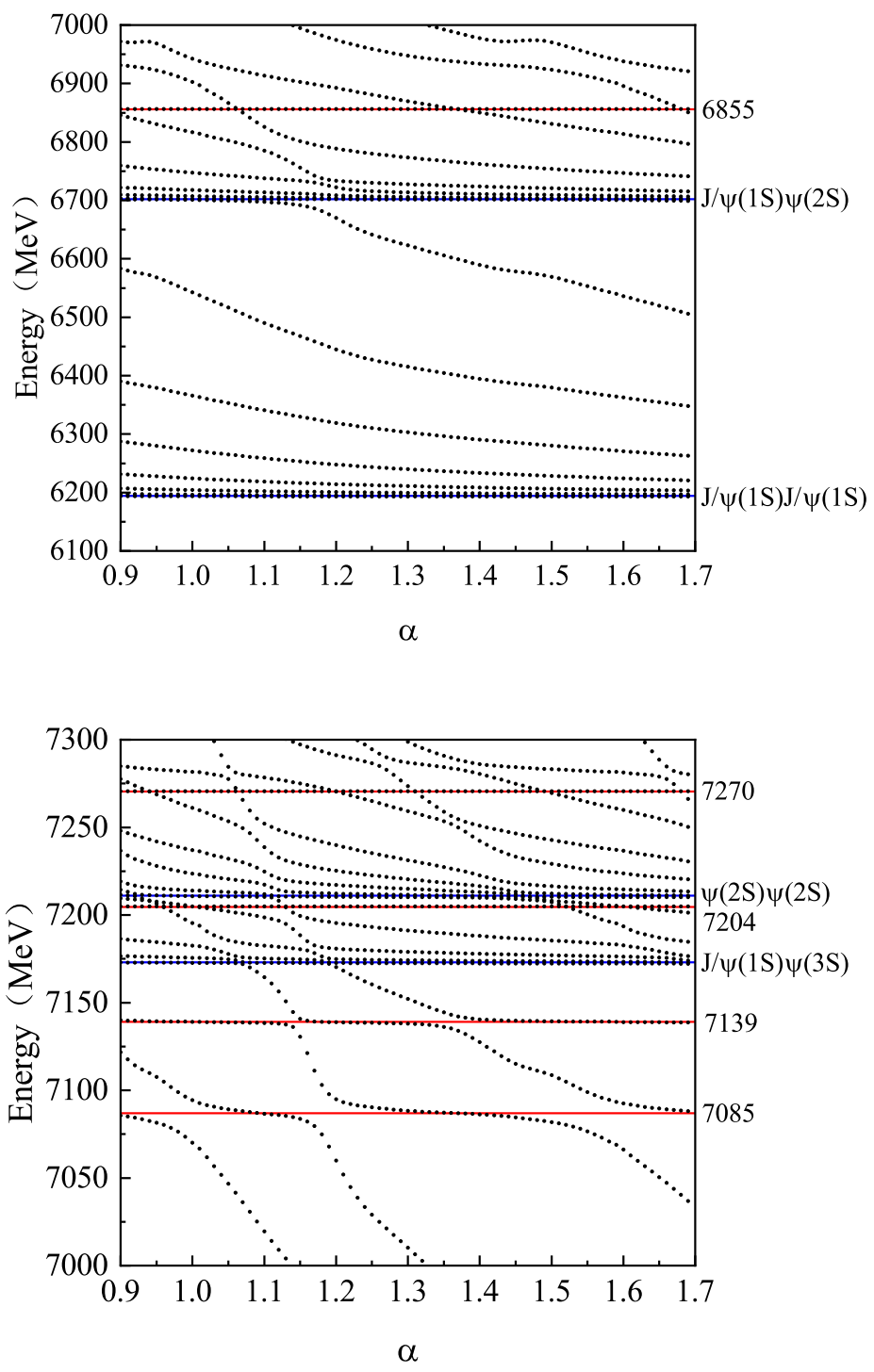
Figure 5 shows the results obtained by considering the coupling between hidden-color channels ${\left({\eta }_c^8{\eta }_c^8\right)}^0$+${(J/{\psi }^{8}J/{\psi }^8)}^0$ and the two scattering states ${\left({\eta }_c{\eta }_c\right)}^0$+${(J/\psi J/\psi )}^0$. One can find that all the resonance states from the hidden color channels (${\left({\eta }_c^8{\eta }_c^8\right)}^0$+${(J/{\psi }^{8}J/{\psi }^8)}^0$) below 7100 MeV are missing. Only one resonance with an energy of 7138 MeV survives the coupling to the scattering states. Because there is no scattering state in the diquark–antidiquark structure, we also perform a channel coupling calculation involving two diquark–antidiquark structures, ${\left(DA\right)}_1^0$+${\left(DA\right)}_2^0$, and the two scattering states, ${\left({\eta }_c{\eta }_c\right)}^0$+${(J/\psi J/\psi )}^0$. The results are displayed in Figure 6. Unlike the channel coupling calculations between the hidden-color channels ${\left({\eta }_c^8{\eta }_c^8\right)}^0$+${(J/{\psi }^{8}J/{\psi }^8)}^0$ and the two scattering states ${\left({\eta }_c{\eta }_c\right)}^0$+${(J/\psi J/\psi )}^0$, several resonance states appear in the spectral region of 6700–7200 MeV. So, to identify the resonance states, full channel-coupling calculations are needed. From these calculations, we also find that the low-lying resonance states in the hidden-color channels are all missing.

To understand the reason behind the missing low-lying resonance states, we carried out the following calculations: Figure 7 illustrates the results obtained for the coupling between all hidden-color channels and the color-singlet channel ${\left({\eta }_c{\eta }_c\right)}^0$. The lowest state with energy of 6253 MeV disappears, which means that the state strongly couples to ${\left({\eta }_c{\eta }_c\right)}^0$. The resonance states around 6500 MeV are also missing in the coupling. Figure 8 gives the results for the coupling between all hidden-color channels and the color-singlet channel ${(J/\psi J/\psi )}^0$. The second lowest state with energy of 6316 MeV disappears, which denotes that this state couples strongly to ${(J/\psi J/\psi )}^0$. So, the resonance states below 6714 MeV are all missing after coupling to the scattering states.

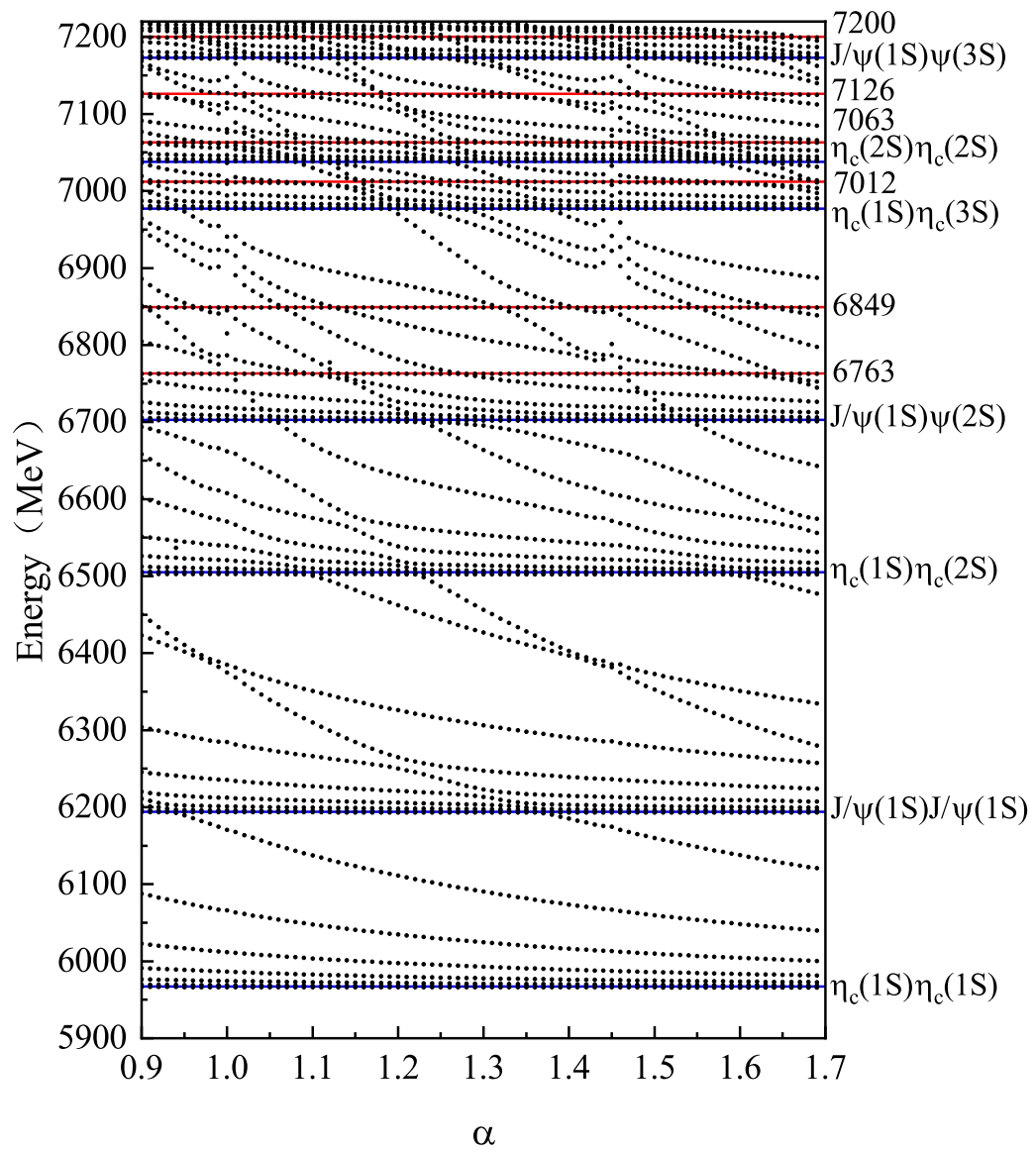
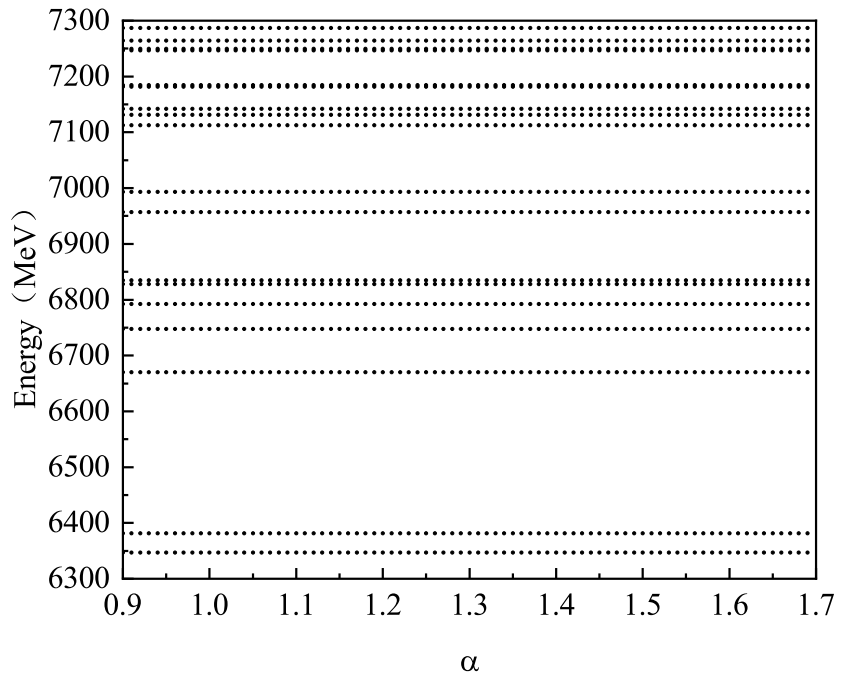
To identify the genuine resonances, the full channel-coupling calculations are performed and the results are shown in Figure 9. The first resonance state $R\left(6763\right)$ appears at an energy of 6763 MeV. There are two other resonances below 7000 MeV, with energies of 6849 MeV and 6884 MeV, which can be good candidates for the narrow structure around 6.9 GeV reported by the LHCb collaboration. The broad structure in the range 6.2∼6.8 GeV is due to the effect of the mixture of scattering channels, $J/\psi J/\psi$, ${\eta }_c\left(1S\right){\eta }_c\left(2S\right)$ and $J/\psi \psi \left(2S\right)$ opening and the resonance $R\left(6763\right)$. As for the structure around 7.2 GeV, there are too many resonances here and our present calculations cannot give a clear picture. More scattering states with non-zero orbital angular momentum are required to be added.

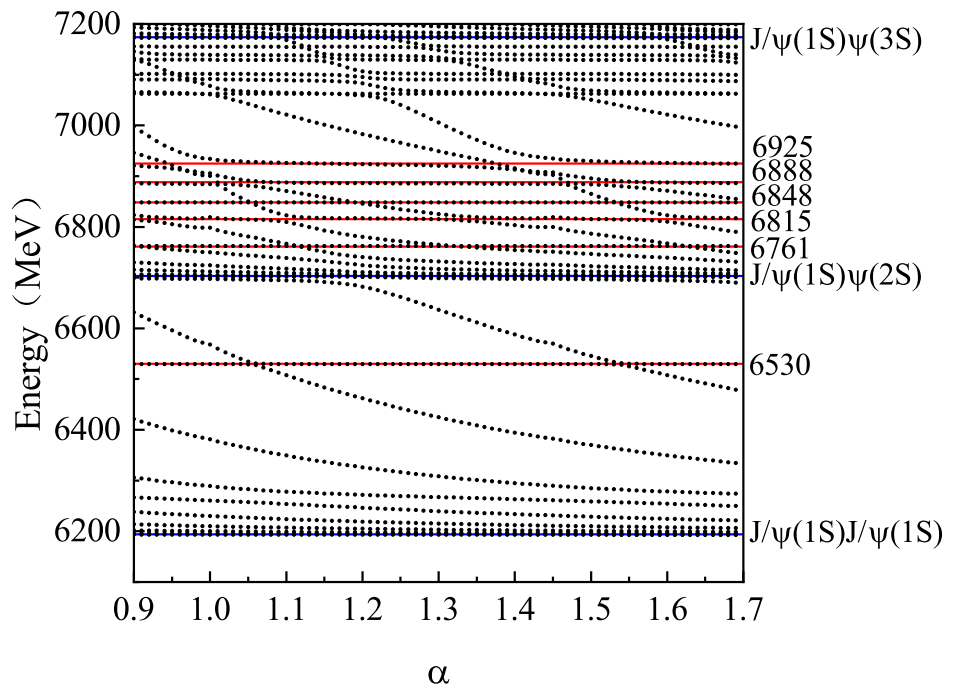
(b) $J^{PC}=1^{+-}$: There are five channels, four with a meson-meson structure and one with a diquark–antidiquark structure. The possible resonances, the results for all hidden-color channels coupling are given in Figure 10. After coupling to the scattering channels, the remaining resonances can be read from Figure 11. From Figure 10, one can see that the energy of the lowest state is 6346 MeV in the hidden-color channels, but this state disappears after coupling the open channel, ${\eta }_c\left(1S\right)J/\psi$. However, the second lowest state survives the coupling (see Figure 11), so we obtain a resonance state with an energy of 6383 MeV. There are several resonance states around 6.8 GeV, $R\left(6749\right)$, $R\left(6793\right)$, $R\left(6828\right)$ and $R\left(6835\right)$. There are also several resonances above 7.0 GeV, $R\left(7100\right)$, $R\left(7112\right)$, $R\left(7173\right)$, $R\left(7173\right)$, $R\left(7185\right)$, $R\left(7247\right)$, $R\left(7249\right)$ and $R\left(7264\right)$. In the meson-meson structure, there are also states with $J^{PC}=1^{++}$. The calculation shows that there are no resonances below 7.3 GeV, and the results are omitted here to save space.

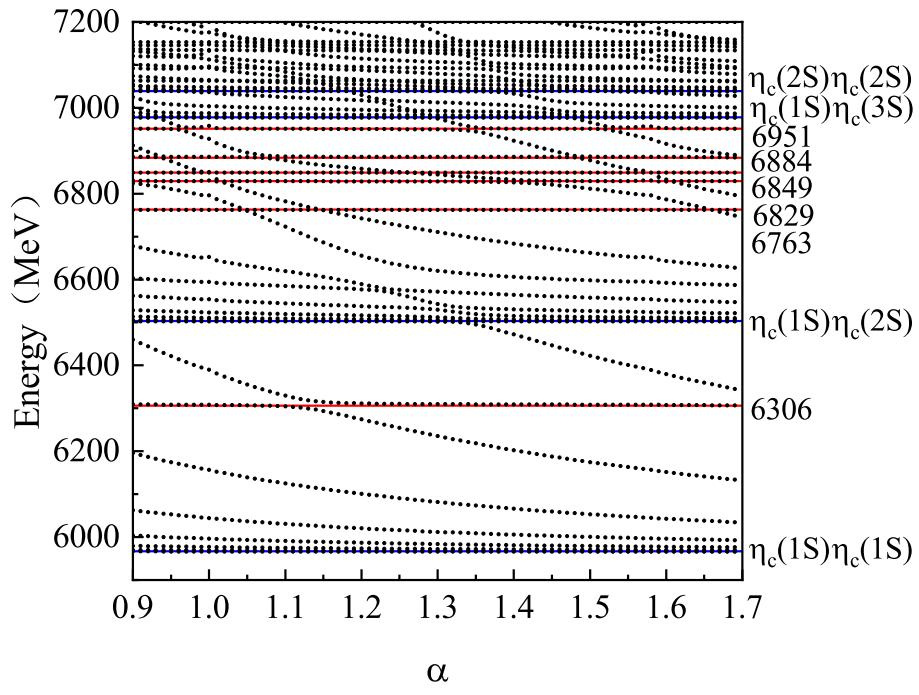
(c) $J^{PC}=2^{++}$: There are three channels, two with a meson-meson structure and one with a diquark–antidiquark structure. The results for the two hidden-color channels coupling are given in Figure 12. After coupling to the scattering channel ${(J/\psi J/\psi )}^2$, the possible resonances can be read from Figure 13. There are three hidden-color states with energies of 6335 MeV, 6590 MeV and 6742 MeV, below 6800 MeV, respectively. However, they all disappear after coupling to the scattering channel ${(J/\psi J/\psi )}^2$. The surviving states after the coupling are shown in Figure 13. These states are $R\left(6855\right)$, $R\left(7085\right)$, $R\left(7139\right)$, $R\left(7204\right)$ and $R\left(7270\right)$.

Table 6. The resonance states with quantum numbers $J^{PC}=0^{++},1^{+-},2^{++}$ for the $cc\overline{c}\overline{c}$ system (unit: MeV).

State	$0^{++}$	$1^{+-}$	$2^{++}$
Energy	6763	6383	6855
	6849	6749	7085
	6884	6793	7139
	7063	6828	7204
	7098	6835	7270
	7138	7100
	7156	7112
	7200	7173
		7185
		7247
		7249
		7264

collects all possible resonance states with quantum numbers $J^{PC}=0^{++},1^{+-},2^{++}$. The lowest observable resonance is the state with energy of 6383 MeV with $J^{PC}=1^{+-}$, and, below 7.0 GeV, there are nine states, which are separated into three groups. The first group has one state with an energy of 6383 MeV; the second group has three states with energies in the range of 6.75∼6.8 GeV, and the final group has five states with energies around 6.85∼6.9 GeV. The broad structure in the region 6.2∼6.8 GeV observed by the LHCb collaboration can be explained by the mixed effects of the resonance states in the first and second groups, and the thresholds for double $J/\psi$ and ${\eta }_c\left(1S\right){\eta }_c\left(2S\right)$. The narrow structure around 6.9 GeV can be well explained by the resonances $R\left(6849\right)$ and $R\left(6884\right)$ with $J^{PC}=0^{++}$ and/or $R\left(6855\right)$ with $J^{PC}=2^{++}$. As for the resonances above 7.0 GeV, we obtain nine states below 7.3 GeV with double $J/\psi$ as the final states ($J^{PC}=0^{++},2^{++}$). Here, we have mentioned that not all the states can be observed, because we have not taken into account angular excited scattering states, such as ${\chi }_{cJ}{\chi }_{cJ}$.

In order to identify the structures of these possible resonances, we calculated the distance between c and $\overline{c}$ quark, denoted as $R_{c\overline{c}}$, as well as the distance between c and c quark, denoted as $R_{cc}$ for the resonance states, respectively, which are shown in

Table 7. The distances between c and $c\left(\overline{c}\right)$ quark for the possible resonance states of the $cc\overline{c}\overline{c}$ system.

State	Resonance (MeV)	${\mathit{R}}_{\mathit{c}\overline{\mathit{c}}}$ (fm)	${\mathit{R}}_{\mathit{cc}}$ (fm)
$0^{++}$	6763	0.68	0.82
	6849	0.66	0.70
	6884	0.80	0.85
	7063	0.80	1.01
	7098	0.84	1.03
	7138	0.96	0.98
	7156	0.88	0.81
	7200	0.83	0.73
$1^{+-}$	6383	0.85	0.88
	6749	1.20	1.39
	6793	0.52	0.48
	6828	0.75	0.97
	6835	1.35	1.31
	7100	1.75	2.42
	7112	1.00	1.26
	7173	1.13	1.51
	7185	1.55	1.66
	7247	1.59	1.54
	7249	1.60	1.50
	7264	1.58	1.49
$2^{++}$	6855	0.66	0.71
	7085	0.94	0.74
	7139	0.88	0.80
	7204	0.84	0.72
	7270	0.76	0.85

. From this table, we can see that for all the states with $J^{PC}=0^{++}$ and $2^{++}$, and some states with $J^{PC}=1^{+-}$, $R_{cc}$ and $R_{c\overline{c}}$ are all in the range of 0.6∼1.0 fm, which means that the states are in the diquark–antidiquark structure. For the other states with $J^{PC}=1^{+-}$, $R_{cc}$ and $R_{c\overline{c}}$ are larger than 1 fm, which means that the states are very likely to be molecular. The large $R_{c\overline{c}}$ is due to the antisymmetrization and it gives the average distance between c and two $\overline{c}$. The distance between c and $\overline{c}$ in one sub-cluster can be extracted from $R_{cc}$ and $R_{c\overline{c}}$, which is round 0.6 fm; this is consistent with the results obtained for charmonium.

4. Summary

In this work, we studied the mass spectra of the fully-charm $cc\overline{c}\overline{c}$ system with quantum numbers $J^{PC}=0^{++},1^{+-},2^{++}$ in the chiral quark model with the help of GEM. The dynamical mixing of the meson-meson structure and the diquark–antidiquark structure, along with all possible color, spin configurations were taken into account. The predicted masses for the lowest-lying $cc\overline{c}\overline{c}$ states are all above the corresponding two meson decay thresholds, leaving no space for bound states. By adopting the real scaling method, we identify the genuine resonance states for the $J^{PC}=0^{++},1^{+-},2^{++}$$cc\overline{c}\overline{c}$ system. The lowest observable resonance state has quantum numbers $J^{PC}=1^{+-}$ with energy 6.38 GeV, and there are several states with quantum numbers $J^{PC}=0^{++},2^{++}$ with energies in the region of 6.85∼6.90 GeV, which can be used to explain the narrow structure around 6.9 GeV in the double $J/\psi$ invariant mass spectrum reported by the LHCb collaboration. There are many resonance states above 7.0 GeV,, which are worth further study by including the angular excited scattering channels.

In general, the $QQ\overline{Q}\overline{Q}$ ($Q=b,c$) resonance states mainly decay into two $Q\overline{Q}$ meson final states by spontaneous dissociation. For the full-charm $cc\overline{c}\overline{c}$ tetraquarks, they can decay via the spontaneous dissociation mechanism since they lie above the two-charmonium thresholds. The doubly hidden-charm tetraquarks can be clearly differentiated in experiments because of their much heavier energies than conventional charmonium mesons $c\overline{c}$. However, it is more difficult to produce $cc\overline{c}\overline{c}$ states because two heavy quark pairs need to be created in vacuum. However, the running of the LHC provides a chance for the observation of double heavy quarkonium. For example, the recent observations of the $J/\psi J/\psi$ [10,11,12,13,14], $J/\psi \mathrm{Y}\left(1S\right)$ [56] and $\mathrm{Y}\left(1S\right)\mathrm{Y}\left(1S\right)$ [15] events, shine a light for the production of $cc\overline{c}\overline{c}$ and $bb\overline{b}\overline{b}$ tetraquarks. With the accumulation of experimental data and the advancement of theoretical work, the nature of the fully-heavy tetraquark states will become more clear.