“In-System” Fission-Events: An Insight into Puzzles of Exoplanets and Stars?
Abstract
1. Introduction
2. The “Fission-Events Framework”
- (1)
- a fission-event may occur in the “interstellar space”—perhaps triggered by perturbations due to encountered variations in interstellar medium/fields or propagating ejecta/shock wave from some other stellar cataclysm—thus enriching the medium (the molecular cloud and subsequent protonebulas) in the vicinity;
- (2)
- a fission-event may occur in a protonebula, thus enriching the nebula (producing either homogeneous or heterogeneous distribution of nuclei) and perhaps serving as the trigger for the nebula’s collapse (as considered for the solar system, suggesting a supernova as the trigger);
- (3)
- a fission-event may occur in a protodisk, injecting new nuclei and abruptly changing disk properties;
- (4)
- a fission-event may occur within an already-formed stellar system, possibly impacting the host–star (its atmosphere and/or interior) and/or the orbital structure and compositions of the planets.
3. Chemical Compositions of Stars
- “Actinide Boost”: About a quarter of strongly r-process enhanced stars shows Th abundances that are higher than expected compared to other stable r-process elemental abundances and the scaled solar r-process pattern. This results in negative stellar ages when using the Th/Eu chronometer. «One explanation may be that these stars show the r-process pattern of two r-process events that occurred at different times—one just prior to the star’s formation and one at a later time in the vicinity of the star» [1].
- «[A]ll the strongly r-process enhanced metal-poor stars found so far exhibit a narrow range in [Fe/H] of 0.3–0.4 dex. If the r-process is universal, why do these stars appear at a certain “chemical time”, as put by [21]? Some propose this signals the start of a new process at work in the chemical evolution of the universe (e.g., [22]), or else that these stars only form from a very special type of supernova in which the neutron-capture elements are released via jets, unlike the other elements [21]» [1].
- «[N]o stars with have yet been discovered that display any known or characteristic neutron-capture abundance pattern. This raises the question of when exactly the very first neutron-capture events took place in the early universe and whether massive Population III stars produced neutron-capture material, and, if so, in what quantities» [1].
- «[A]bundances of neutron-capture elements with 40 < Z < 56, i.e., those between the first and second peak, signal that yet other, unidentified …processes may have been at work in the early universe. In their analysis of silver and palladium in metal-poor stars, Hansen [23] found that the abundance ratios of Pd and Ag (e.g., [Ag/Fe], [Ag/Eu], [Ag/Ba]) did not match the patterns expected if they were produced by the main r, the weak r, or any s-process channel» [1].
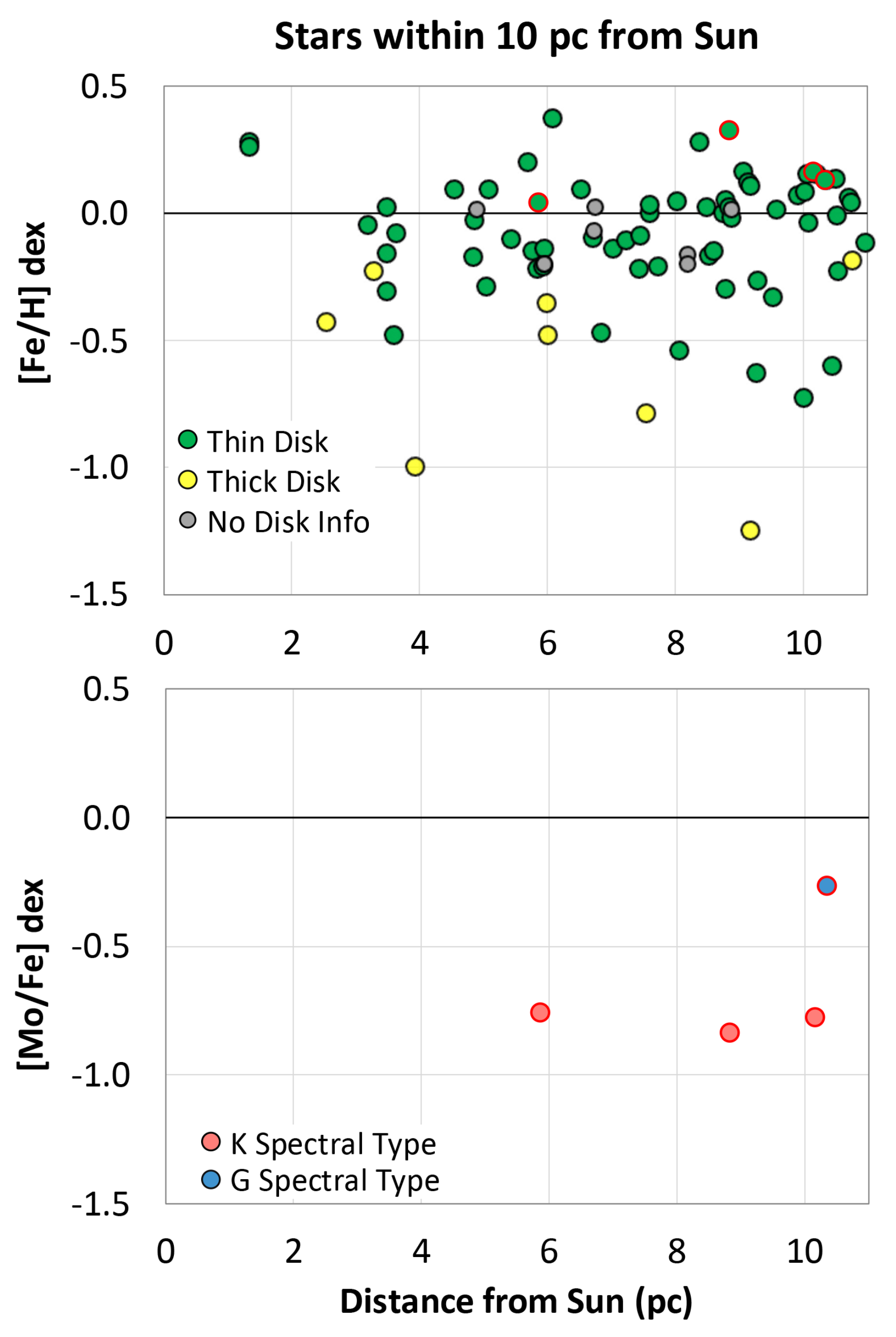
- «[Fe/H]-rich group near the midplane is deficient in Mg, Si, S, Ca, Sc II, Cr II, and Ni as compared to stars farther from the plane» [19].
- Observations of the ratios of [Y/Fe], [Ba/Fe], [La/Fe], and [Eu/Fe] in the stars in the Milky Way dwarf spheroidal satellite galaxies (dSphs) and the stars in the Galaxy indicated that «[Y/Fe] is significantly lower/offset in the dSph stars than in the Galaxy. This includes roughly half of the dSph stars, and suggests the r- and s-process enrichment of this element differs between the galaxies …This result suggests that the site of r-processed Y must differ from that of r-processed Ba, La, and Eu; is there a weak r-process site? In addition, the source that produces Y in the metal-poor Galactic stars must be absent in the dSphs or it must have a different time lag relative to the Ba, La, and Eu enrichments …[N]o population of stars in the Galaxy is representative of stars in the low mass dwarfs» [20].
«We treat these three levels of relative actinide enhancement as three distinct “groups” and assume that each group’s members formed from gas enriched by an individual r-process event. …Within each group, we consider the relative variations among the limited r-elements as well as the actinides as intrinsic to the progenitor r-process event. …«We combine the abundances of stars within [each group] by scaling the individual abundance patterns to the respective average residual obtained from comparison with the Solar r-process pattern between and . After scaling the solar pattern such that the average deviation of the stellar pattern from solar pattern betweenBatoLuis minimized, we find the range of scaled abundances derived for each element …»
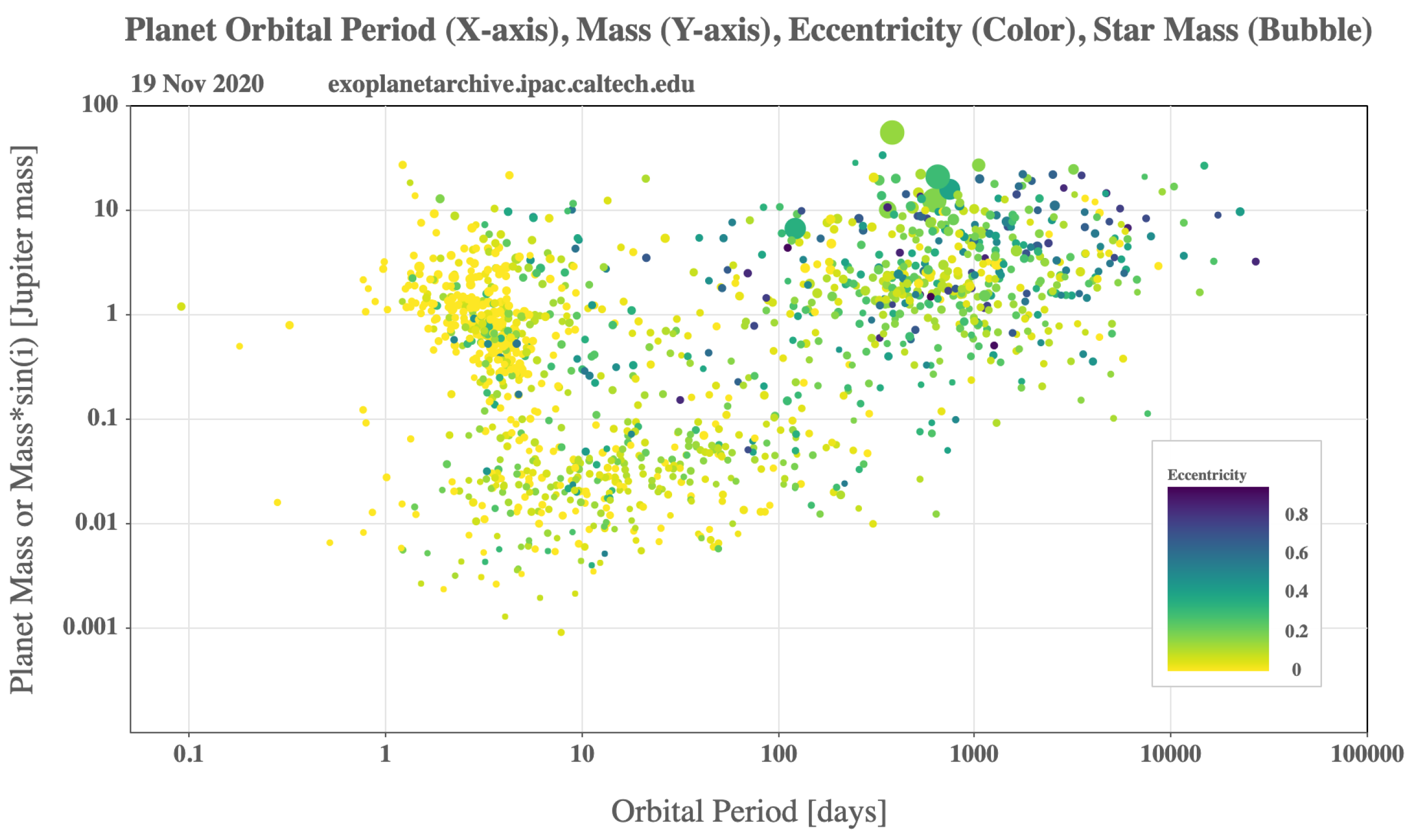
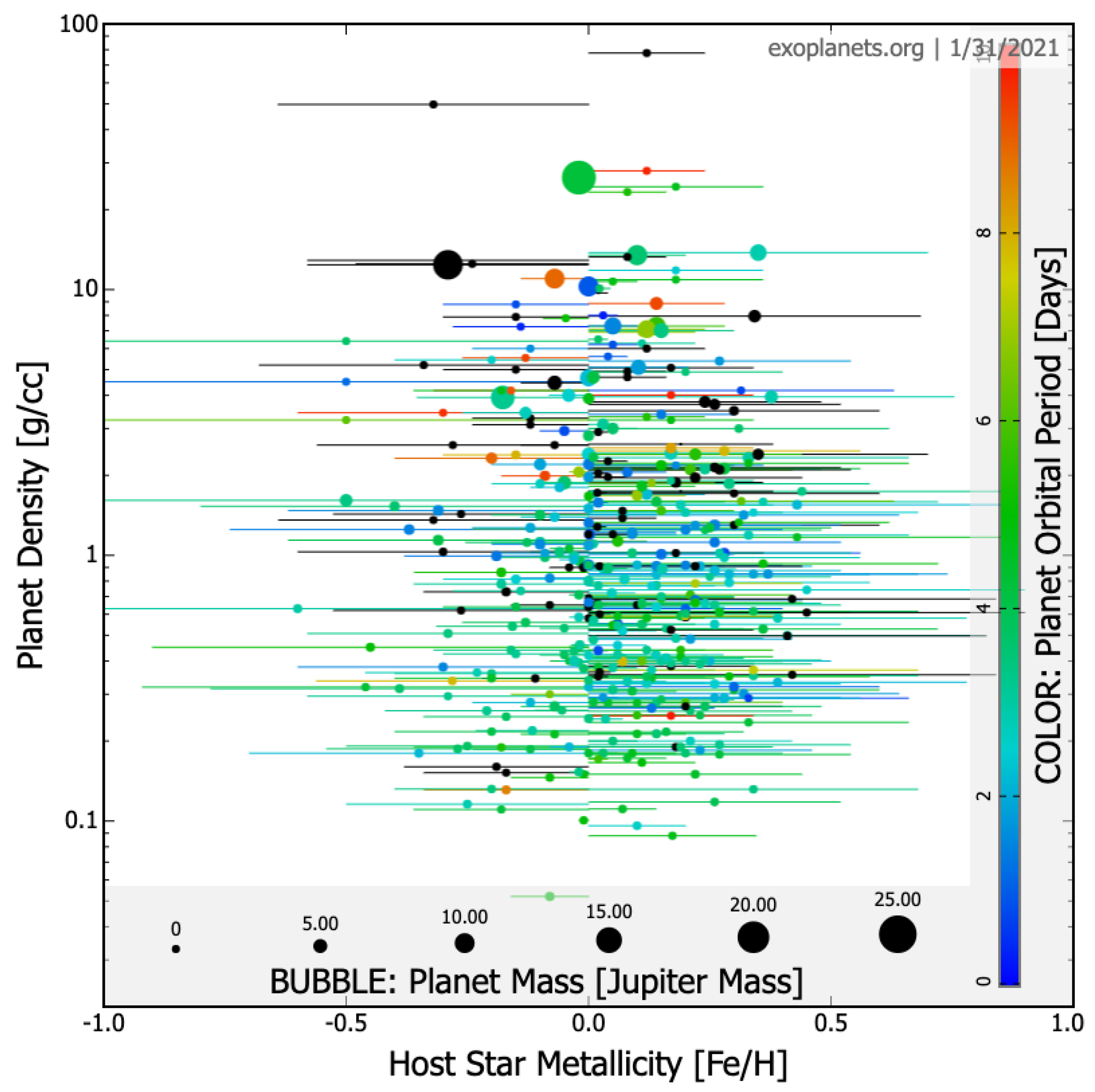
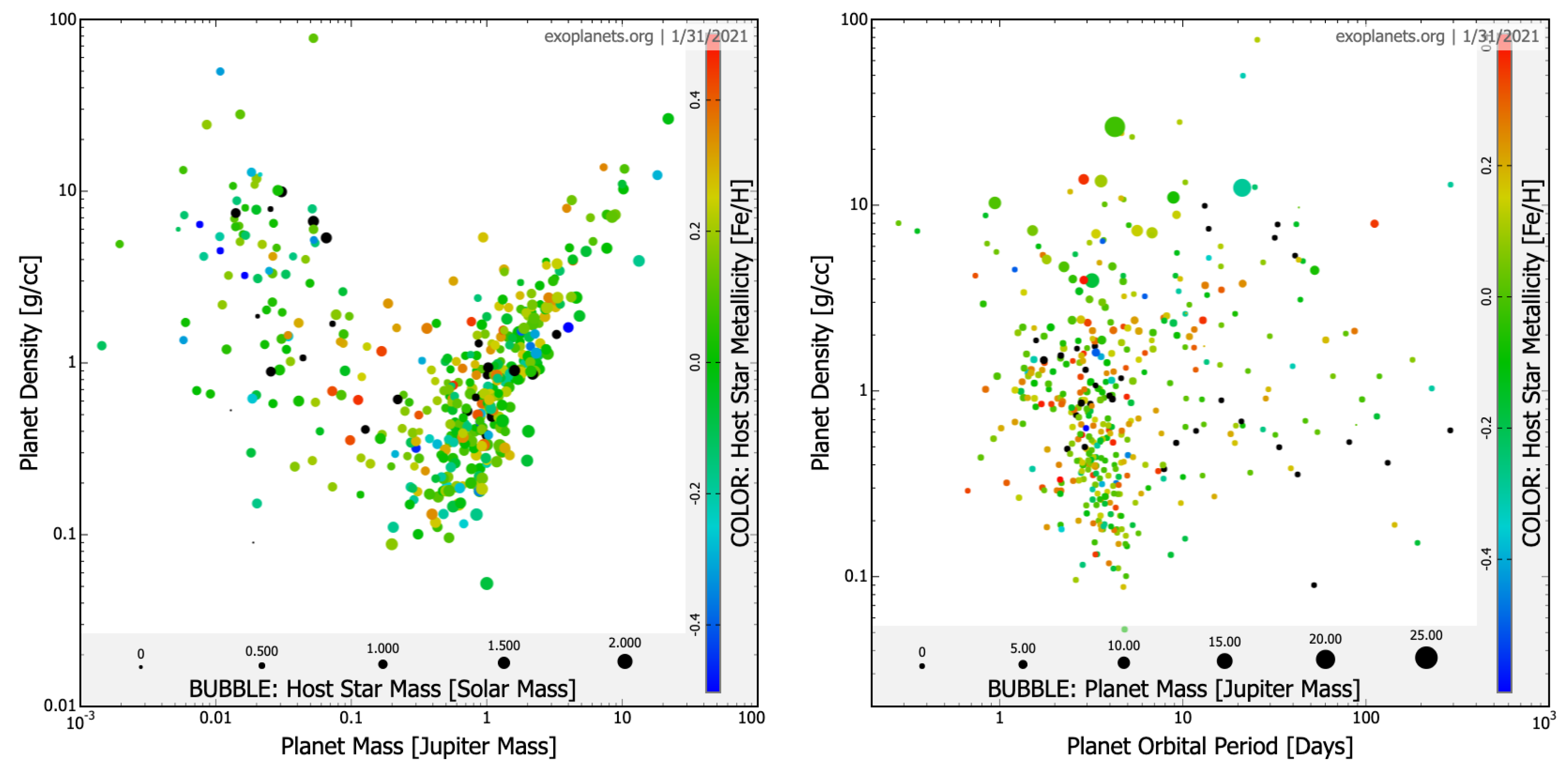
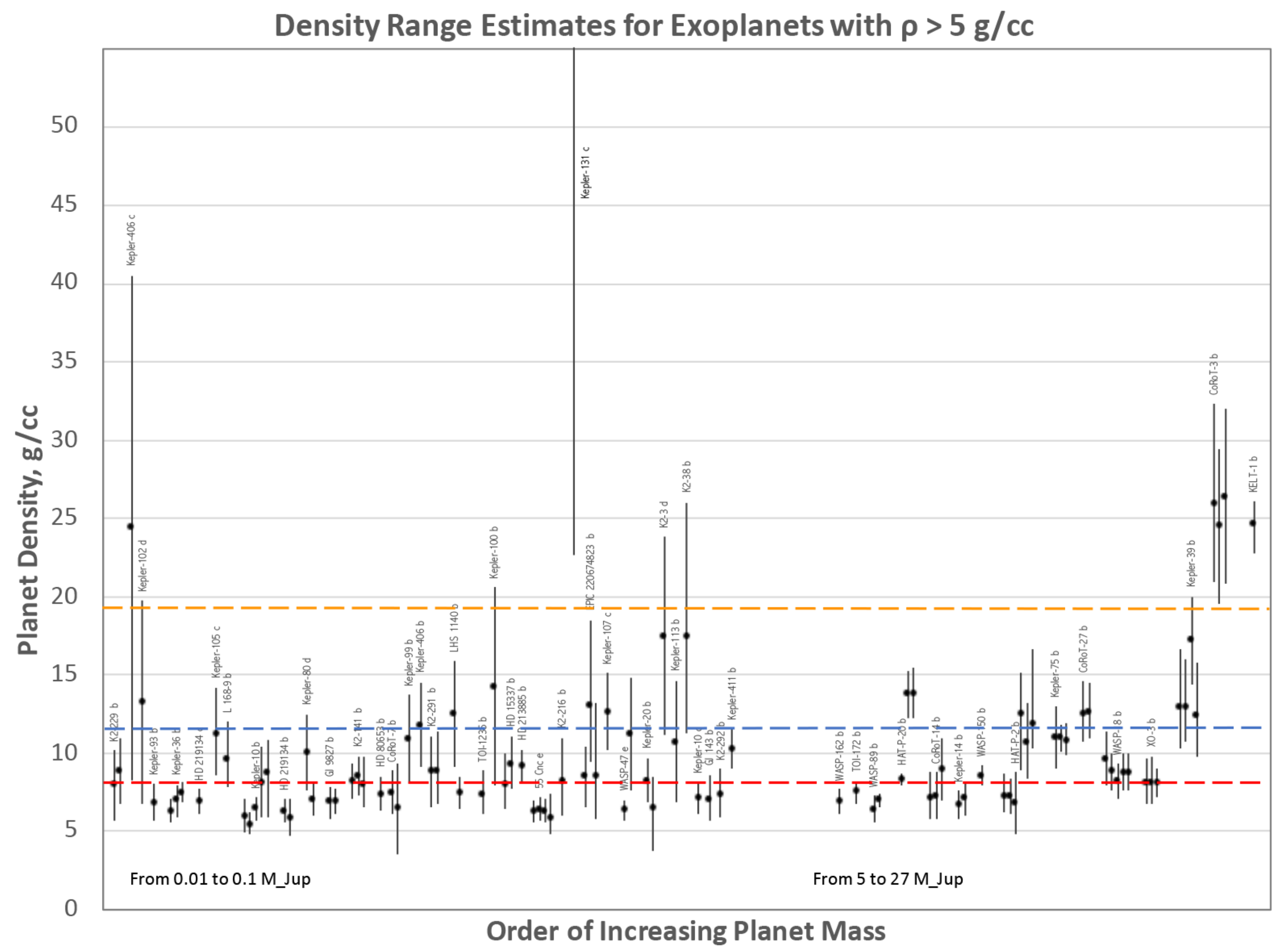
4. Exoplanetary Systems
5. Conclusions
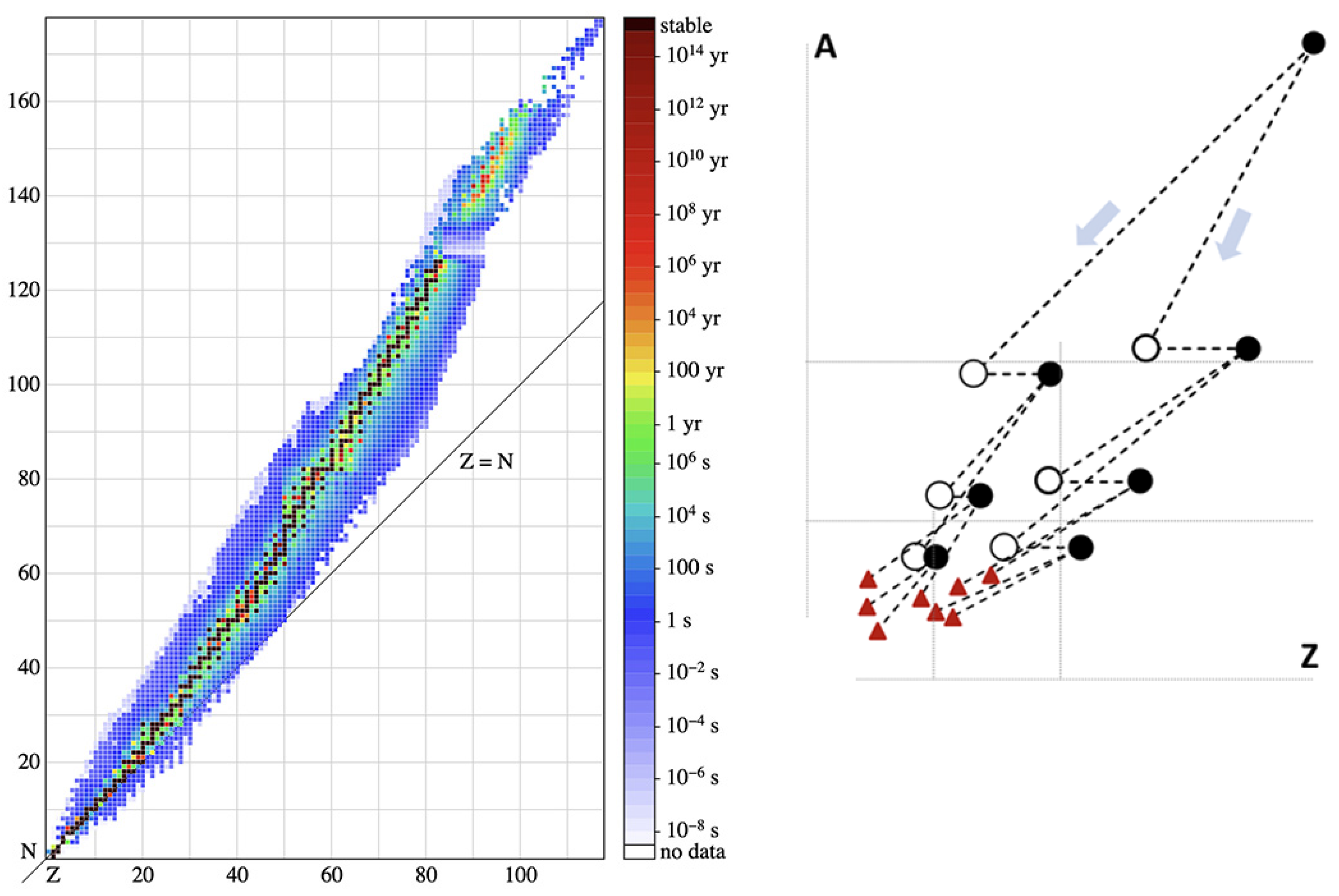
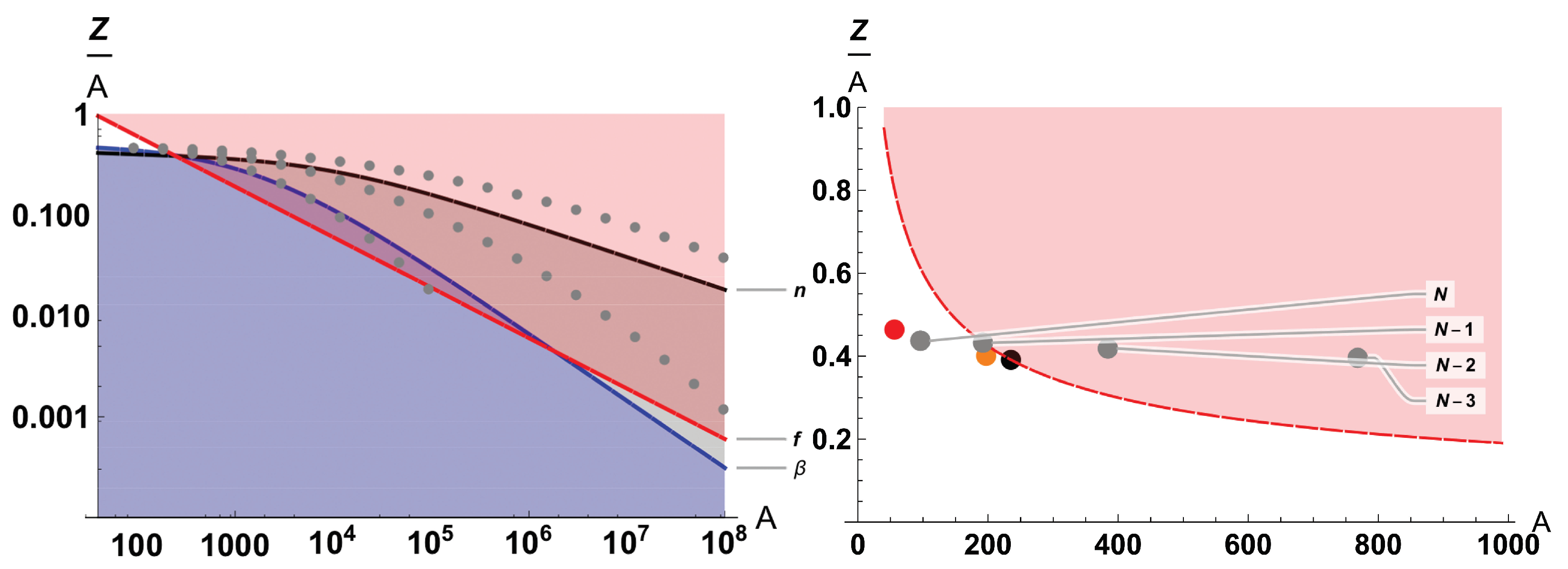
- Traditionally, the nuclei are believed to form via nucleosynthesis (with “add-on” decays and fission-(re)cycling), so the general direction of nuclei-creation is upward (from lower nucleon numbers A to higher A).In the fission-event framework, the direction is reversed: the nuclei are formed via fragmentation and fission-cascades (with “add-on” captures and decays), so the general direction of nuclei-creation is downward. Fission-cascades start from giant nuclei with and include even extremely-short-lived nuclei, and should be distinguished from the upward-nucleosynthesis-driven fission-(re)cycling used in traditional models which operate in a limited A-domain only, disregarding very-short-lived nuclei and nuclei with (currently 320).Nucleogenetic signatures of the processes are different, and, therefore, various detected but not-yet-explained “excesses” in stellar element abundances (relative to the traditional models) may have their origins in the fission-events. Therefore, spectral observations (and derived isotopic abundances) of multiple “impacted” stars may perhaps help nuclear-physics theoreticians by offering factual data for development of constraints for the “production signature” of fission-driven nucleogenesis. See Ref. [7] and references therein, for discussion about the challenges of experimental studies of super-heavy elements in terrestrial conditions.)
- Traditionally, it is believed that the “enrichment material” is (a) first synthesized at the production-site and in the ejecta of some cataclysm (such as supernova, AGB star, neutron star merger), and (b) then it travels some distance in the form of dust gradually polluting interstellar gas and encountered nebulas which later form stars and planets.In the fission-events framework, the order is reversed: the “enrichment material” (a) first travels great distances in the form of a compact drop-like super-dense nuclear-matter object, and (b) it explodes in fission-cascades at the encountered stellar system (“in-system”) or in the interstellar space.This means that the fission-event “enrichment material”—being at first a compact drop-like super-dense “clump” torn away and catapulted by a supermassive black hole—may travel much greater distances than the traditionally presumed supernova-ejected “dust”, thus enriching much more distant regions, not just the local neighborhood of the cataclysm. Furthermore, the dispersion of fission-event debris (post-explosion) naturally has a relatively “localized” character, which may explain some cases of spatial heterogeneity among stars in clusters or individual outliers in neighborhoods.
- high abundances of post-Fe elements (actinides and those called r- or s- process elements);
- high abundances of elements with p-isotopes;
- high bulk densities of exoplanets;
- short orbital periods of exoplanets.
- Protonebula Stage: If the fission-event occurs during the protonebula stage of evolution, besides enriching the nebula, the event may serve as the trigger initiating the nebula’s gravitational collapse. Over the course of subsequent stellar-system evolution, the enrichment is likely to become well-mixed and uniformly distributed, and reveal itself in the spectrum of the eventually-formed host–star and in the composition of the planets.
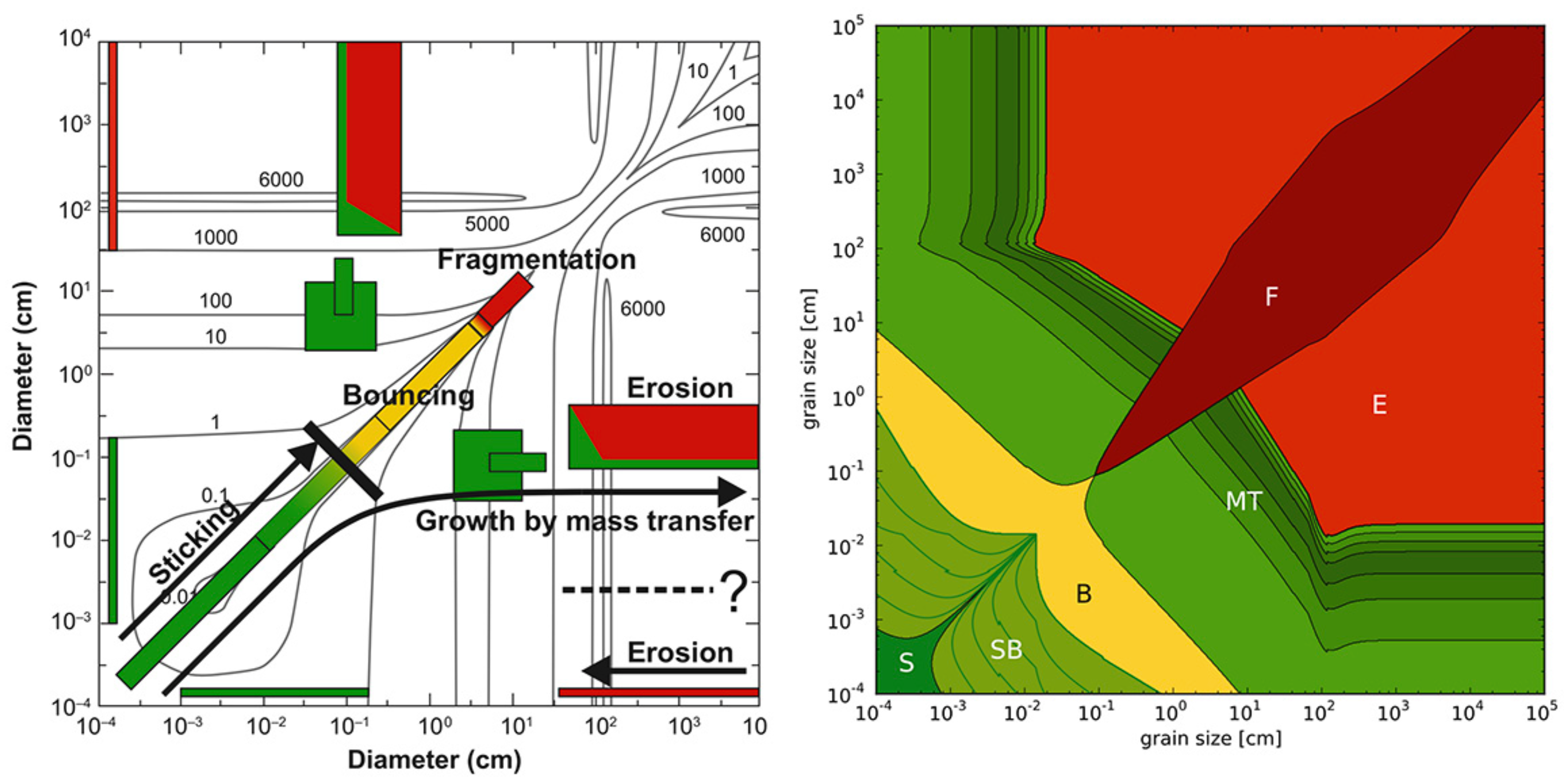
- Protodisk Stage: If the fission-event occurs during the protodisk stage of evolution, disk properties—”dust” sizes and composition, viscosity, opacity, and so on—may increase abruptly but locally, thus creating spatial heterogeneity in the enrichment of the subsequently-formed planets and likely influencing the planets’ growth and orbital dynamics. The content and size distribution of solid particles strongly influence the disk thermal regime, viscous properties, turbulence flow patterns, disk medium opacity, snow-line locations, chemical transformations in gaseous medium and, ultimately, its evolution including the processes’ dependence on the radial distance from the protostar and the early subdisk formation. Numerical simulations can perhaps examine how evolution paths may change for the “t-tau” systems—those suddenly impacted at time t during the protodisk’s lifetime (such as , , and so on, with zero-tau being the nebula-impacted system, and one-tau being the system with fully-formed planets).
- Fully-Formed Stage: If the star and the first-stage planets had already formed, then the fission-event may occur directly within the star, near the star, or farther away from the star. The within-star impact, if meaningful, would reveal itself in the stellar spectrum. If the fission-event occurs not directly in the star, but its debris is spread within the system, then the debris would orbit the star and accrete via collisions without any protodisk-effects (since the protodisk had already dissipated by then). Such event may lead to formation of objects analogous to the solar system’s asteroid belt or its terrestrial planets, the proximity of which to the host star would depend on the location of the “explosion” and the overall dynamics of the combined system’s parts. Highly-dense planets may be the representatives of this type of outcomes. The debris may also enrich the host–star (and thus reveal itself in the stellar spectrum) and the already-existing planets (perhaps altering their orbits in the process). This is what happened in the solar system, as we advocated in Ref. [7].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Brief Overview of Physics of “Fission-Event”
Appendix A.1. Instability of Nuclear Matter: Nuclear-Fog
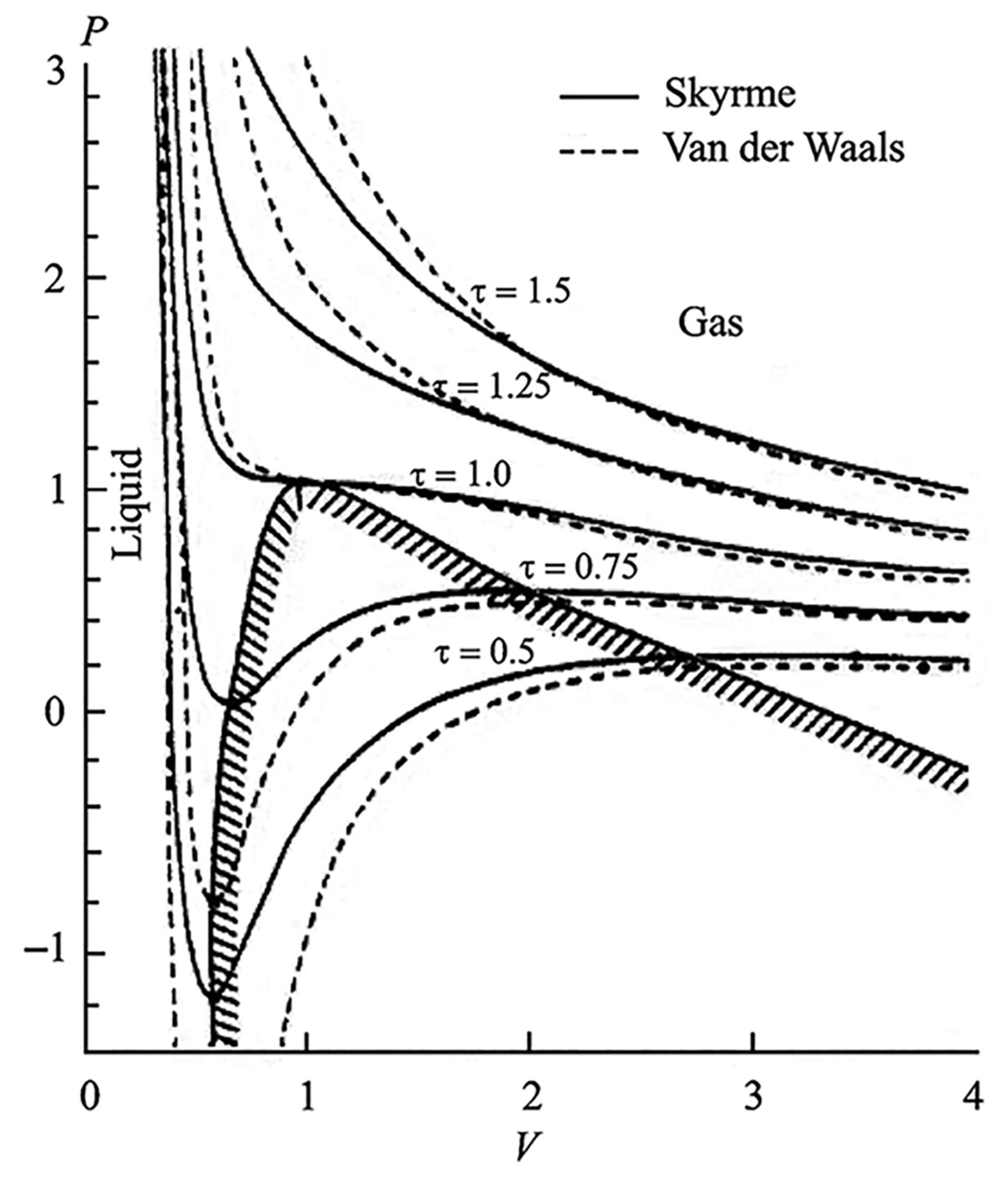
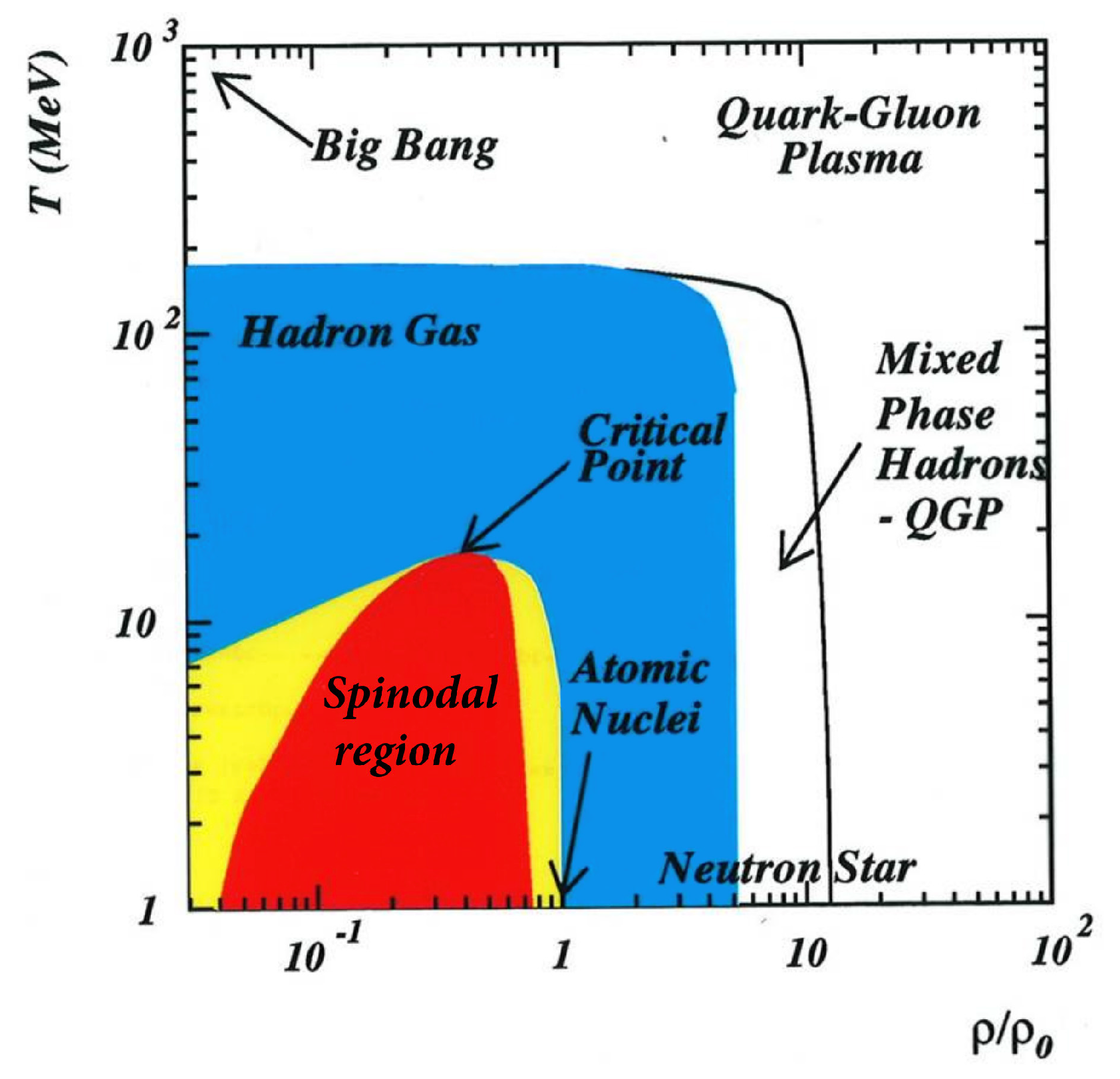
Appendix A.2. Structural Cohesion/Disintegration of Compact Super-Dense Stellar Fragment
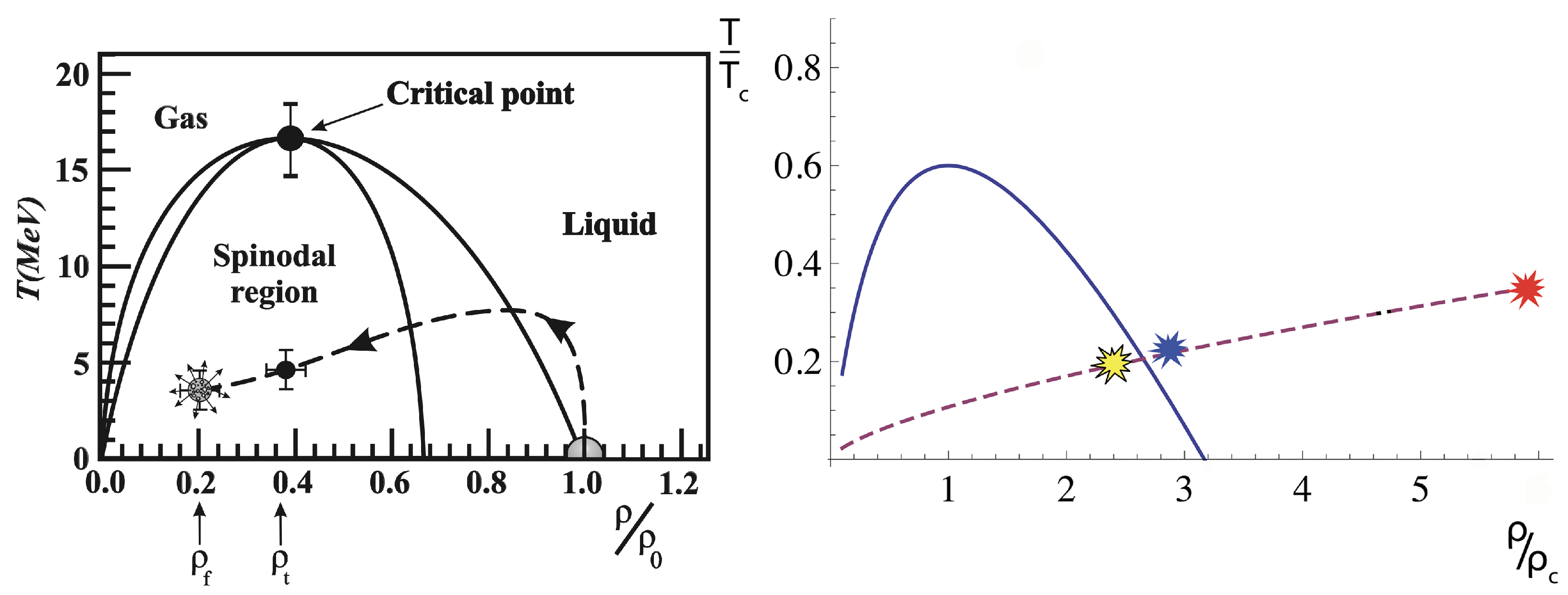
Appendix A.3. Multi-Fragmentation of Giant Nuclei
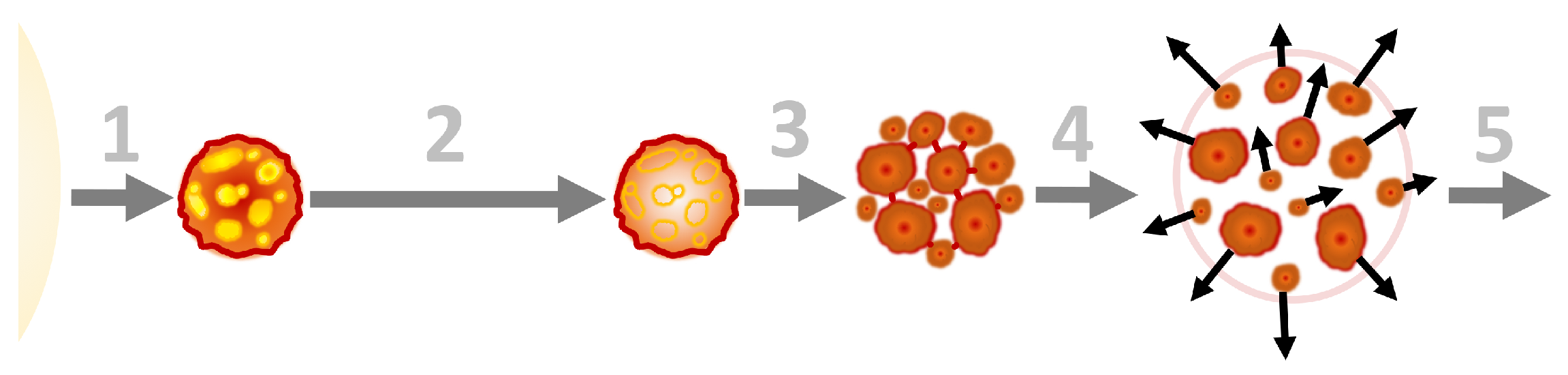
Appendix A.4. Origination of Stellar-Fragments
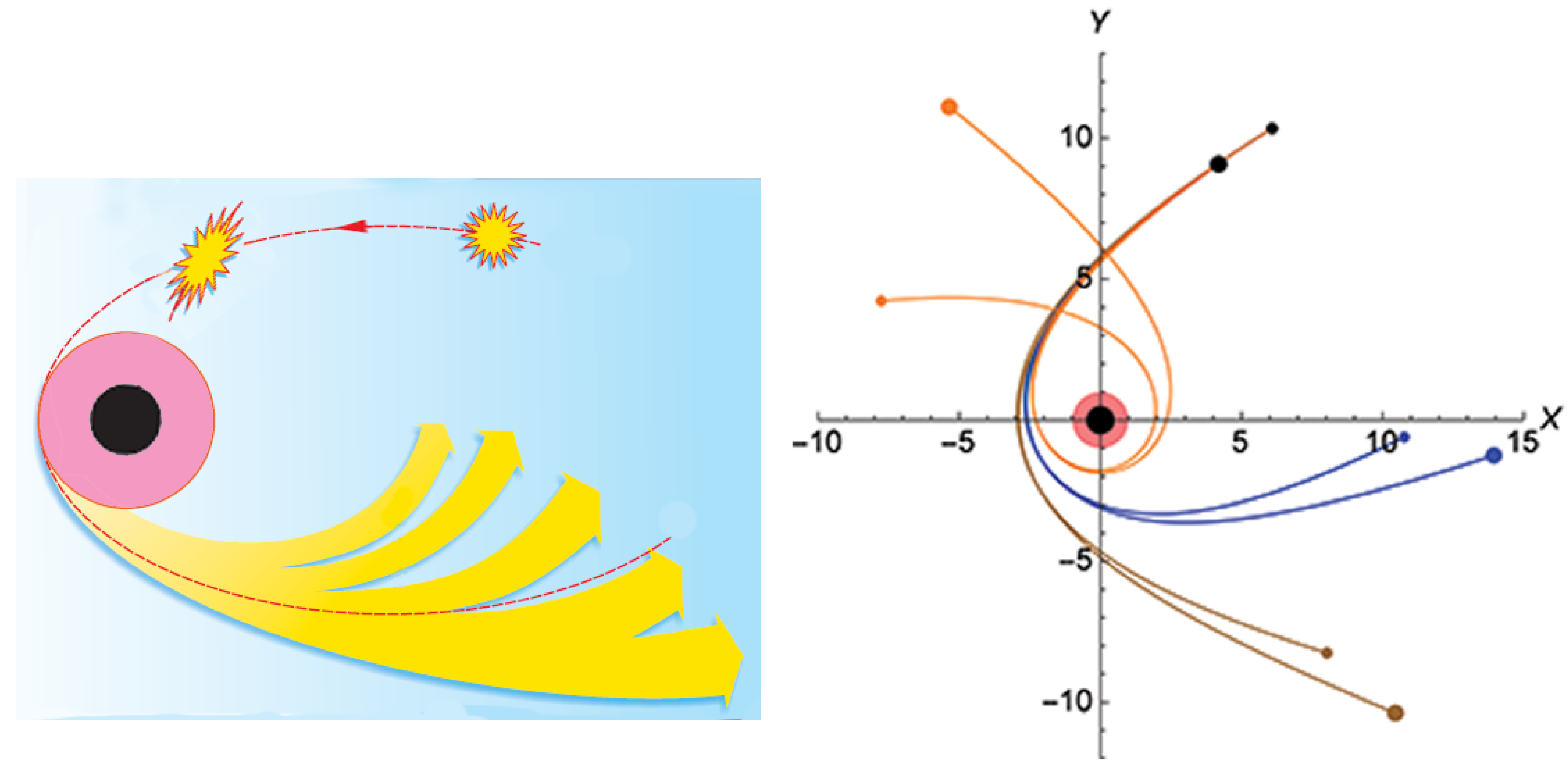
Appendix B. Likelihood of Fission-Event within Individual Planetary Systems
References
- Jacobson, H.R.; Frebel, A. Observational nuclear astrophysics: Neutron-capture element abundances in old, metal-poor stars. J. Phys. G Nucl. Part. Phys. 2014, 41, 044001. [Google Scholar] [CrossRef][Green Version]
- Marov, M.; Shevchenko, I. Exoplanets: Nature and Models. Uspekhi Fiz. Nauk 2020, 190, 897–932. [Google Scholar] [CrossRef]
- Borucki, W.J. Kepler: A Brief Discussion of the Mission and Exoplanet Results. Proc. Am. Philos. Soc. 2017, 161, 38–65. [Google Scholar]
- Raymond, S.N.; Kokubo, E.; Morbidelli, A.; Morishima, R.; Walsh, K.J. Terrestrial Planet Formation at Home and Abroad. In Protostars and Planets VI; Beuther, H., Klessen, R.S., Dullemond, C.P., Henning, T.K., Eds.; University of Arizona Press: Tucson, AZ, USA, 2014; pp. 32–58. [Google Scholar] [CrossRef]
- Cameron, A.G.W. The Formation of the Sun and Planets. Icarus 1962, 1, 13–69. [Google Scholar] [CrossRef]
- Marov, M. The Formation and Evolution of the Solar System. In Oxford Research Encyclopedia (Planetary Science); Oxford University Press: Oxford, UK, 2018; pp. 1–54. [Google Scholar] [CrossRef]
- Tito, E.P.; Pavlov, V.I. Hypothesis about Enrichment of Solar System. Physics 2020, 2, 213–276. [Google Scholar] [CrossRef]
- Imshennik, V.S.; Popov, D. An analytic model for the evolution of a close binary system of neutron (degenerate) stars. Astron. Lett. 1998, 24, 206–221. [Google Scholar]
- Colpi, M.; Wasserman, I. Formation of an Evanescent Proto–Neutron Star Binary and the Origin of Pulsar Kicks. Astrophys. J. 2002, 581, 1271–1279. [Google Scholar] [CrossRef]
- Rees, M.J. “Dead Quasars” in Nearby Galaxies? Science 1990, 247, 817–823. [Google Scholar] [CrossRef] [PubMed]
- Tito, E.P.; Pavlov, V.I. Relativistic Motion of Stars near Rotating Black Holes. Galaxies 2018, 6, 61. [Google Scholar] [CrossRef]
- Hirota, T.; Nagayama, A.T.; Honma, M.; Adachi, Y.; Burns, R.A.; Chibueze, J.O.; Choi, Y.K.; Hachisuka, K.; Hada, K.; Hagiwara, Y.; et al. The First VERA Astrometry Catalog. Publ. Astron. Soc. Jpn. 2020, 72, 50. [Google Scholar] [CrossRef]
- Gillessen, S.; Plewa, P.M.; Eisenhauer, F.; Sari, R.; Waisberg, I.; Habibi, M.; Pfuhl, O.; George, E.; Dexter, J.; von Fellenberg, S.; et al. An Update on Monitoring Stellar Orbits in the Galactic Center. Astrophys. J. 2017, 837, 30. [Google Scholar] [CrossRef]
- Koposov, S.E.; Boubert, D.; Li, T.S.; Erkal, D.; Costa, G.S.D.; Zucker, D.B.; Ji, A.P.; Kuehn, K.; Lewis, G.F.; Mackey, D.; et al. Discovery of a nearby 1700 km/s star ejected from the Milky Way by Sgr A*. Mon. Not. R. Astron. Soc. 2019, 491, 2465–2480. [Google Scholar] [CrossRef]
- Nicholl, M.; Wevers, T.; Oates, S.R.; Alexander, K.D.; Leloudas, G.; Onori, F.; Jerkstrand, A.; Gomez, S.; Campana, S.; Arcavi, I.; et al. An outflow powers the optical rise of the nearby, fast-evolving tidal disruption event AT2019qiz. Mon. Not. R. Astron. Soc. 2020, 499, 482–504. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, D.N.C. Tidal fragmentation as the origin of 1I/2017 U1 (`Oumuamua). Nat. Astron. 2020, 4, 852–860. [Google Scholar] [CrossRef]
- Bodewits, D.; Noonan, J.W.; Feldman, P.D.; Bannister, M.T.; Farnocchia, D.; Harris, W.M.; Li, J.Y.; Mandt, K.E.; Parker, J.W.; Xing, Z.X. The carbon monoxide-rich interstellar comet 2I/Borisov. Nat. Astron. 2020, 4, 867–871. [Google Scholar] [CrossRef]
- Tito, E.P.; Pavlov, V.I. Hot super-dense compact object with particular EoS. Astrophys. Space Sci. 2018, 363, 44. [Google Scholar] [CrossRef]
- Hinkel, N.R.; Timmes, F.; Young, P.A.; Pagano, M.D.; Turnbull, M.C. Stellar Abundances In The Solar Neighborhood: The Hypatia Catalog. Astron. J. 2014, 148, 54. [Google Scholar] [CrossRef]
- Venn, K.A.; Irwin, M.; Shetrone, M.D.; Tout, C.A.; Hill, V.; Tolstoy, E. Stellar Chemical Signatures and Hierarchical Galaxy Formation. Astron. J. 2004, 128, 1177–1195. [Google Scholar] [CrossRef]
- Hansen, T.; Andersen, J.; Nordström, B.; Buchhave, L.A.; Beers, T.C. The Binary Frequency Of r-Process-Element-Enhanced Metal-Poor Stars In addition, Its Implications: Chemical Tagging In The Primitive Halo Of The Milky Way. Astrophys. J. Lett. 2011, 743, L1. [Google Scholar] [CrossRef]
- François, P.; Depagne, E.; Hill, V.; Spite, M.; Spite, F.; Plez, B.; Beers, T.C.; Andersen, J.; James, G.; Barbuy, B.; et al. First stars: VIII. Enrichment of the neutron-capture elements in the early Galaxy. Astron. Astrophys. 2007, 476, 935–950. [Google Scholar] [CrossRef]
- Hansen, C.J.; Primas, F.; Hartman, H.; Kratz, K.L.; Wanajo, S.; Leibundgut, B.; Farouqi, K.; Hallmann, O.; Christlieb, N.; Nilsson, H. Silver and palladium help unveil the nature of a second r-process. Astron. Astrophys. 2012, 545, A31. [Google Scholar] [CrossRef]
- Shibagaki, S.; Kajino, T.; Mathews, G.J.; Chiba, S.; Nishimura, S.; Lorusso, G. Relative contributions of the weak, main and fission-recycling r-process. Astrophys. J. 2016, 816, 79. [Google Scholar] [CrossRef]
- National Nuclear Data Center (NuDat2), Brookhaven National Laboratory, Graphics by Wikimedia Commons/Public Domain. Half-Lives of Isotopes. Available online: https://www.nndc.bnl.gov/nudat2/ (accessed on 1 June 2012).
- Oganessian, Y.T.; Utyonkov, V.K. Super-heavy element research. Rep. Prog. Phys. 2015, 78, 036301. [Google Scholar] [CrossRef]
- Oganessian, Y.T.; Sobiczewski, A.; Ter-Akopian, G.M. Superheavy nuclei: From predictions to discovery. Phys. Scr. 2017, 92, 023003. [Google Scholar] [CrossRef]
- Giuliani, S.; Matheson, Z.; Nazarewicz, W.; Olsen, E.; Reinhard, P.G.; Sadhukhan, J.; Schuetrumpf, B.; Schunck, N.; Schwerdtfeger, P. Colloquium: Superheavy elements: Oganesson and beyond. Rev. Mod. Phys. 2019, 91, 011001. [Google Scholar] [CrossRef]
- Wapstra, A.H. Criteria that must be satisfied for the discovery of a new chemical element to be recognized. Pure Appl. Chem. 1991, 63, 879–886. [Google Scholar] [CrossRef][Green Version]
- Heenen, P.H.; Skalski, J.; Staszczak, A.; Vretenar, D. Shapes and alpha- and beta-decays of superheavy nuclei. Nucl. Phys. A 2015, 944, 415–441. [Google Scholar] [CrossRef]
- Jachimowicz, P.; Kowal, M.; Skalski, J. Adiabatic fission barriers in superheavy nuclei. Phys. Rev. C 2017, 95, 014303. [Google Scholar] [CrossRef]
- Goldanskh, V.I. Modes of Radioactive Decay Involving Proton Emission. Annu. Rev. Nucl. Sci. 1966, 16, 1–30. [Google Scholar] [CrossRef]
- Thoennessen, M. Reaching the limits of nuclear stability. Rep. Prog. Phys. 2004, 67, 1187–1232. [Google Scholar] [CrossRef]
- Holmbeck, E.M.; Frebel, A.; McLaughlin, G.C.; Mumpower, M.R.; Sprouse, T.M.; Surman, R. Actinide-rich and actinide-poor r-process enhanced metal-poor stars do not require separate r-process progenitors. Astrophys. J. 2019, 881, 5. [Google Scholar] [CrossRef]
- Lodders, K.; Palme, H.; Gail, H.P. 4.4 Abundances of the elements in the Solar System. In Solar System; Springer: Berlin/Heidelberg, Germany, 2009; pp. 712–770. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Grevesse, N.; Scott, P.; Asplund, M.; Sauval, A.J. The elemental composition of the Sun-III. The heavy elements Cu to Th. Astron. Astrophys. 2014, 573, A27. [Google Scholar] [CrossRef]
- Scott, P.; Grevesse, N.; Asplund, M.; Sauval, A.J.; Lind, K.; Takeda, Y.; Collet, R.; Trampedach, R.; Hayek, W. The elemental composition of the Sun I. The intermediate mass elements Na to Ca. Astron. Astrophys. 2014, 573, A25. [Google Scholar] [CrossRef]
- Scott, P.; Asplund, M.; Grevesse, N.; Bergemann, M.; Sauval, A.J. The elemental composition of the Sun-II. The iron group elements Sc to Ni. Astron. Astrophys. 2014, 573, A26. [Google Scholar] [CrossRef]
- Lodders, K. Solar Elemental Abundances. In The Oxford Research Encyclopedia of Planetary Science; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Hinkel, N.R.; Young, P.A.; Pagano, M.D.; Desch, S.J.; Anbar, A.D.; Adibekyan, V.; Blanco-Cuaresma, S.; Carlberg, J.K.; Mena, E.D.; Liu, F.; et al. A Comparison of Stellar Elemental Abundance Techniques and Measurements. Astrophys. J. Suppl. Ser. 2016, 22, 4. [Google Scholar] [CrossRef]
- Gehren, T.; Shi, J.R.; Zhang, H.W.; Zhao, G.; Korn, A.J. Na, Mg and Al abundances as a population discriminant for nearby metal-poor stars. Astron. Astrophys. 2006, 451, 1065–1079. [Google Scholar] [CrossRef][Green Version]
- Zhao, G.; Mashonkina, L.; Yan, H.L.; Alexeeva, S.; Kobayashi, C.; Pakhomov, Y.; Shi, J.R.; Sitnova, T.; Tan, K.F.; Zhang, H.W.; et al. Systematic Non-LTE Study of the -.6 ≤ [Fe/H] ≤ 0.2 F and G Dwarfs in the Solar Neighborhood. II. Abundance Patterns from Li to Eu. Astrophys. J. Lett. 2016, 833, 225. [Google Scholar] [CrossRef]
- Serenelli, A.M.; Basu, S.; Ferguson, J.W.; Asplund, M. New Solar Composition: The Problem with Solar Models Revisited. Astrophys. J. Lett. 2009, 705, L123–L127. [Google Scholar] [CrossRef]
- Villante, F.L. Constraints on the Opacity Profile of the Sun from Helioseismic Observables and Solar Neutrino Flux Measurements. Astrophys. J. 2010, 724, 98–110. [Google Scholar] [CrossRef][Green Version]
- Vagnozzi, S.; Freese, K.; Zurbuchen, T.H. Solar Models in Light of New High Metallicity Measurements from Solar Wind Data. Astrophys. J. 2017, 839, 55. [Google Scholar] [CrossRef]
- Vagnozzi, S. New Solar Metallicity Measurements. Atoms 2019, 7, 41. [Google Scholar] [CrossRef]
- Rauscher, T.; Dauphas, N.; Dillmann, I.; Fröhlich, C.; Fülöp, Z.; Gyürky, G. Constraining the astrophysical origin of the p-nuclei through nuclear physics and meteoritic data. Rep. Prog. Phys. 2013, 76, 066201. [Google Scholar] [CrossRef] [PubMed]
- Pignatari, M.; Göbel, K.; Reifarth, R.; Travaglio, C. The production of proton-rich isotopes beyond iron: The γ-process in stars. Int. J. Mod. Phys. E 2016, 25, 1630003. [Google Scholar] [CrossRef]
- Lewis, R.S.; Ming, T.; Wacker, J.F.; Anders, E.; Steel, E. Interstellar diamonds in meteorites. Nature 1987, 326, 160–162. [Google Scholar] [CrossRef]
- Hill, V.; Plez, B.; Cayrel, R.; Beers, T.C.; Nordström, B.; Andersen, J.; Spite, M.; Spite, F.; Barbuy, B.; Bonifacio, P.; et al. First stars. I. The extreme r-element rich, iron-poor halo giant CS 31082-001. Astron. Astrophys. 2002, 387, 560–579. [Google Scholar] [CrossRef]
- Honda, S.; Aoki, W.; Kajino, T.; Ando, H.; Beers, T.C.; Izumiura, H.; Sadakane, K.; Takada-Hidai, M. Spectroscopic Studies of Extremely Metal-Poor Stars with the Subaru High Dispersion Spectrograph. II. The r-Process Elements, Including Thorium. Astrophys. J. 2004, 607, 474–498. [Google Scholar] [CrossRef]
- NASA Exoplanet Archive. Confirmed Planets Table; NASA: Pasadena, CA, USA, 2020. [CrossRef]
- Han, E.; Wang, S.X.; Wright, J.T.; Feng, Y.K.; Zhao, M.; Fakhouri, O.; Brown, J.I.; Hancock, C. Exoplanet Orbit Database. II. Updates to Exoplanets.org. Publ. Astron. Soc. Pac. 2014, 126, 827–837. [Google Scholar] [CrossRef]
- Bonomo, A.S.; Desidera, S.; Benatti, S.; Borsa, F.; Crespi, S.; Damasso, M.; Lanza, A.F.; Sozzetti, A.; Lodato, G.; Marzari, F.; et al. The GAPS Programme with HARPS-N at TNG. Astron. Astrophys. 2017, 602, A107. [Google Scholar] [CrossRef]
- NASA Exoplanet Science Institute. Planetary Systems Table; NASA: Pasadena, CA, USA, 2020. [CrossRef]
- Greiner, W. Nuclei: Superheavy–superneutronic–strange–and of antimatter. J. Phys. Conf. Ser. 2013, 413, 012002. [Google Scholar] [CrossRef]
- Afanasjev, A.; Agbemava, S.; Gyawali, A. Hyperheavy nuclei: Existence and stability. Phys. Lett. B 2018, 782, 533–540. [Google Scholar] [CrossRef]
- Testi, L.; Birnstiel, T.; Ricci, L.; Andrews, S.; Blum, J.; Carpenter, J.; Dominik, C.; Isella, A.; Natta, A.; Williams, J.P.; et al. Dust Evolution in Protoplanetary Disks. In Protostars and Planets VI; University of Arizona Press: Tucson, AZ, USA, 2014. [Google Scholar] [CrossRef]
- Weidenschilling, S.J.; Cuzzi, J.N. Formation of planetesimals in the solar nebula. In Protostars and Planets III; Levy, E.H., Lunine, J.I., Eds.; University of Arizona Press: Tucson, AZ, USA, 1993; pp. 1031–1060. [Google Scholar]
- Zsom, A.; Ormel, C.W.; G'uttler, C.; Blum, J.; Dullemond, C.P. The outcome of protoplanetary dust growth: Pebbles, boulders, or planetesimals? II. Introducing the bouncing barrier. Astrophys. Astron. 2010, 513, A57. [Google Scholar] [CrossRef]
- Windmark, F.; Birnstiel, T.; Ormel, C.W.; Dullemond, C.P. Breaking through: The effects of a velocity distribution on barriers to dust growth. Astrophys. Astron. 2012, 544, L16. [Google Scholar] [CrossRef]
- Scott, E.R.D. Handbook of Iron Meteorites. Meteorit. Planet. Sci. 1975, 48, 2608. [Google Scholar] [CrossRef]
- Caporali, S.; Grazzi, F.; Salvemini, F.; Garbe, U.; Peetermans, S.; Pratesi, G. Structural Characterization of Iron Meteorites through Neutron Tomography. Minerals 2016, 6, 14. [Google Scholar] [CrossRef]
- Plavcan, J.; Hornácková, M.; Grolmusová, Z.; Kociánová, M.; Rakovský, J.; Veis, P. Sikhote-Alin Meteorite, Elemental Composition Analysis Using CF LIBS. 2012. Available online: https://www.semanticscholar.org/paper/Sikhote-Alin-Meteorite%2C-Elemental-Composition-Using-Plavcan-Hor%C5%88%C3%A1%C4%8Dkov%C3%A1/ac8253280505eeebf41fdb388a82097eabb36095 (accessed on 1 June 2020).
- Wolszczan, A.; Frail, D.A. A planetary system around the millisecond pulsar PSR1257+12. Nature 1992, 355, 145–147. [Google Scholar] [CrossRef]
- Martin, R.G.; Livio, M.; Palaniswamy, D. Why are pulsar planets rare? Astrophys. J. 2016, 832, 122. [Google Scholar] [CrossRef]
- Jaqaman, H.; Mekjian, A.Z.; Zamick, L. Nuclear condensation. Phys. Rev. C 1983, 27, 2782–2791. [Google Scholar] [CrossRef]
- Karnaukhov, V.; Oeschler, H.; Avdeyev, S.; Rodionov, V.; Kirakosyan, V.; Simonenko, A.; Rukoyatkin, P.; Budzanowski, A.; Karcz, W.; Skwirczyńska, I.; et al. Spinodal decomposition, nuclear fog and two characteristic volumes in thermal multifragmentation. Nucl. Phys. A 2005, 749, 65–72. [Google Scholar] [CrossRef][Green Version]
- Borderie, B.; Frankland, J. Liquid–Gas phase transition in nuclei. Prog. Part. Nucl. Phys. 2019, 105, 82–138. [Google Scholar] [CrossRef]
- Karnaukhov, V.A. Nuclear multifragmentation and phase transitions in hot nuclei. Phys. Part. Nucl. 2006, 37, 165–193. [Google Scholar] [CrossRef]
- Karnaukhov, V.; Avdeyev, S.; Botvina, A.; Cherepanov, E.; Karzc, W.; Kirakosyan, V.; Kuzmin, E.; Oeschler, H.; Rukoyatkin, P.; Skwirczynska, I. Properties of Hot Nuclei Produced in Relativistic Collisions. 2011. Available online: https://vfs.fias.science/d/4fdd7ba24e/files/?p=/Karna-NUFRA.pdf (accessed on 25 October 2013).
- Karnaukhov, V.; Avdeyev, S.; Botvina, A.; Budzanowski, A.; Chulkov, L.; Czech, B.; Karzc, W.; Kirakosyan, V.; Kuzmin, E.; Norbeck, E.; et al. Nuclear multifragmentation and fission: Similarity and differences. Nucl. Phys. A 2006, 780, 91–99. [Google Scholar] [CrossRef][Green Version]
- Karnaukhov, V.; Avdeyev, S.; Botvina, A.; Kirakosyan, V.; Strekalovsky, O.; Rukoyatkin, P.; Karzc, W.; Norbeck, E.; Oeschler, H. Time scale of nuclear multifragmentation induced by light relativistic ions. J. Phys. G Nucl. Part. Phys. 2012, 39, 125104. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton Univ. Press: Princeton, NJ, USA, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tito, E.P.; Pavlov, V.I. “In-System” Fission-Events: An Insight into Puzzles of Exoplanets and Stars? Universe 2021, 7, 118. https://doi.org/10.3390/universe7050118
Tito EP, Pavlov VI. “In-System” Fission-Events: An Insight into Puzzles of Exoplanets and Stars? Universe. 2021; 7(5):118. https://doi.org/10.3390/universe7050118
Chicago/Turabian StyleTito, Elizabeth P., and Vadim I. Pavlov. 2021. "“In-System” Fission-Events: An Insight into Puzzles of Exoplanets and Stars?" Universe 7, no. 5: 118. https://doi.org/10.3390/universe7050118
APA StyleTito, E. P., & Pavlov, V. I. (2021). “In-System” Fission-Events: An Insight into Puzzles of Exoplanets and Stars? Universe, 7(5), 118. https://doi.org/10.3390/universe7050118





