Blocks Size Frequency Distribution in the Enceladus Tiger Stripes Area: Implications on Their Formative Processes
Abstract
1. Introduction
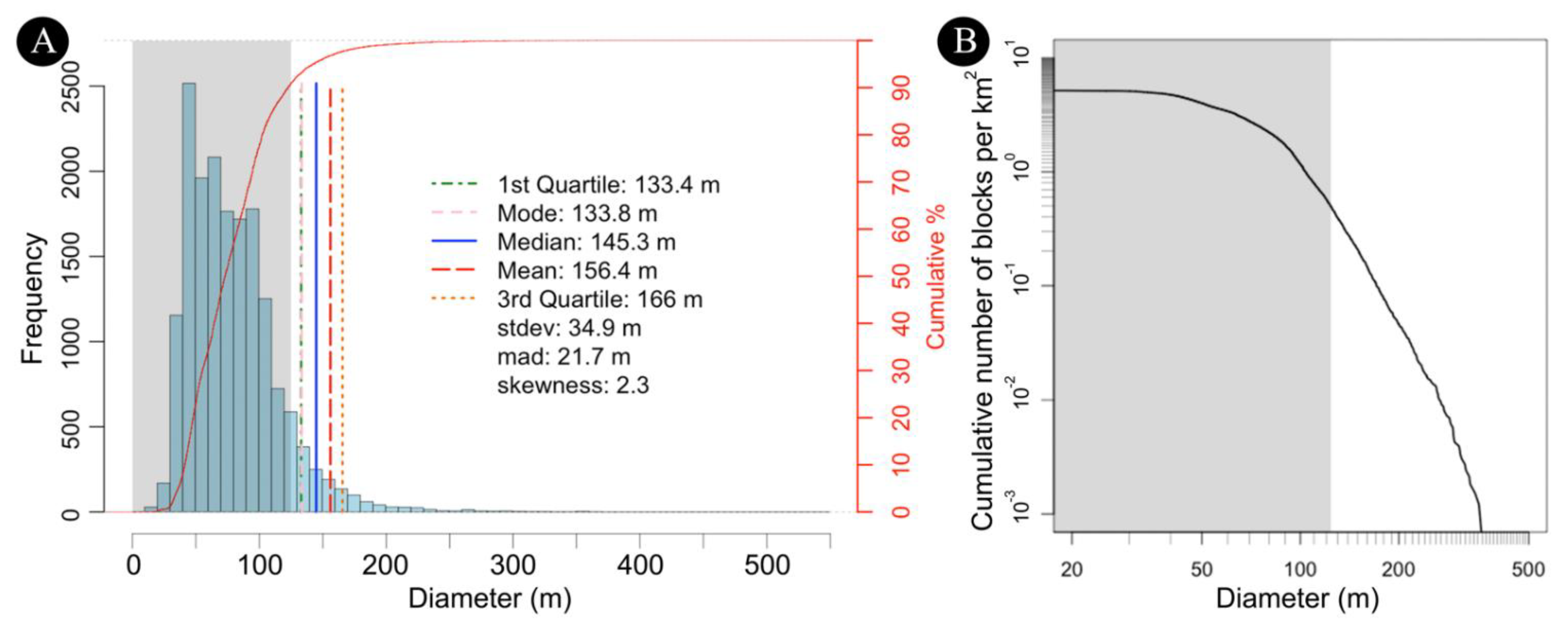
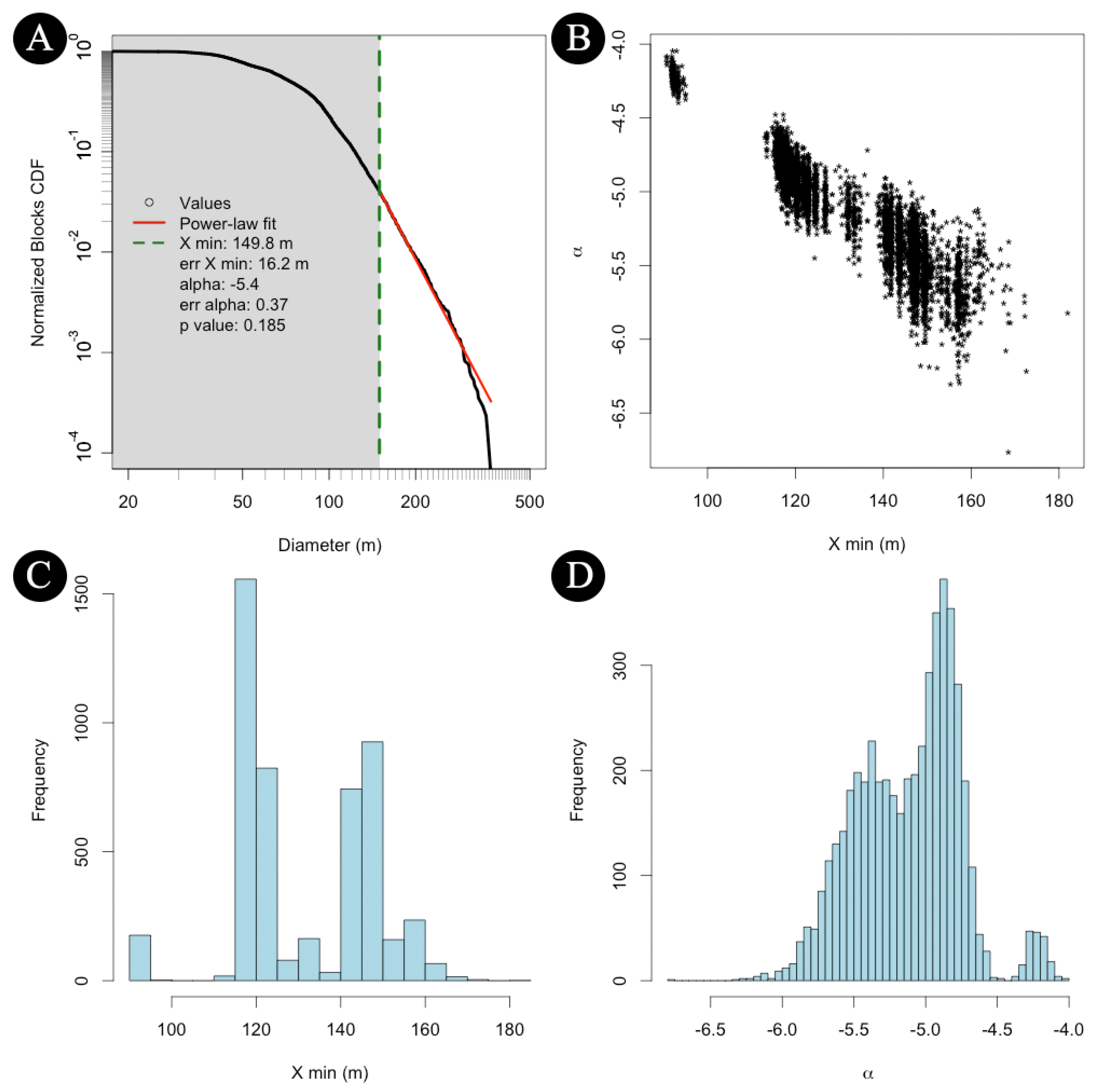
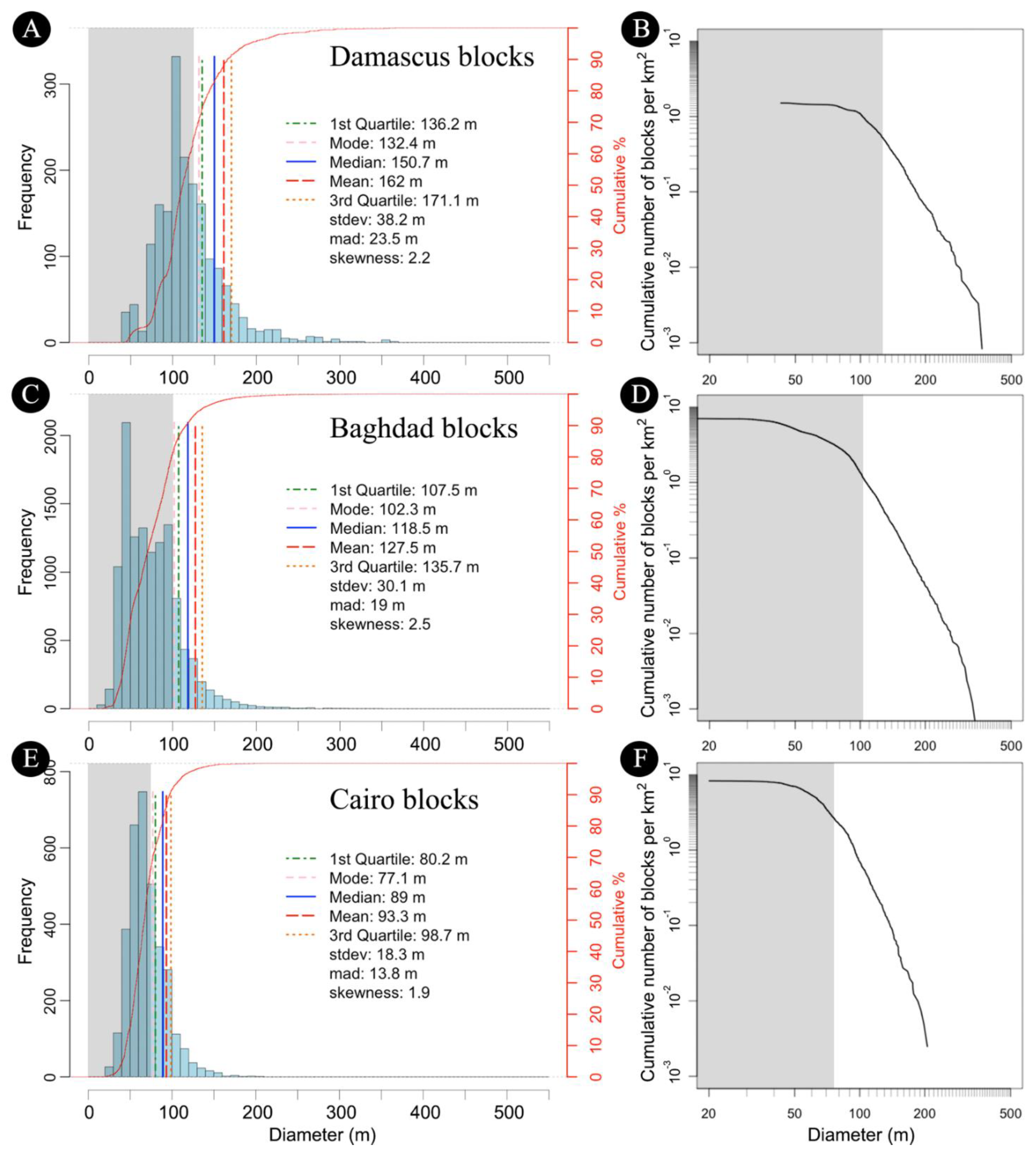
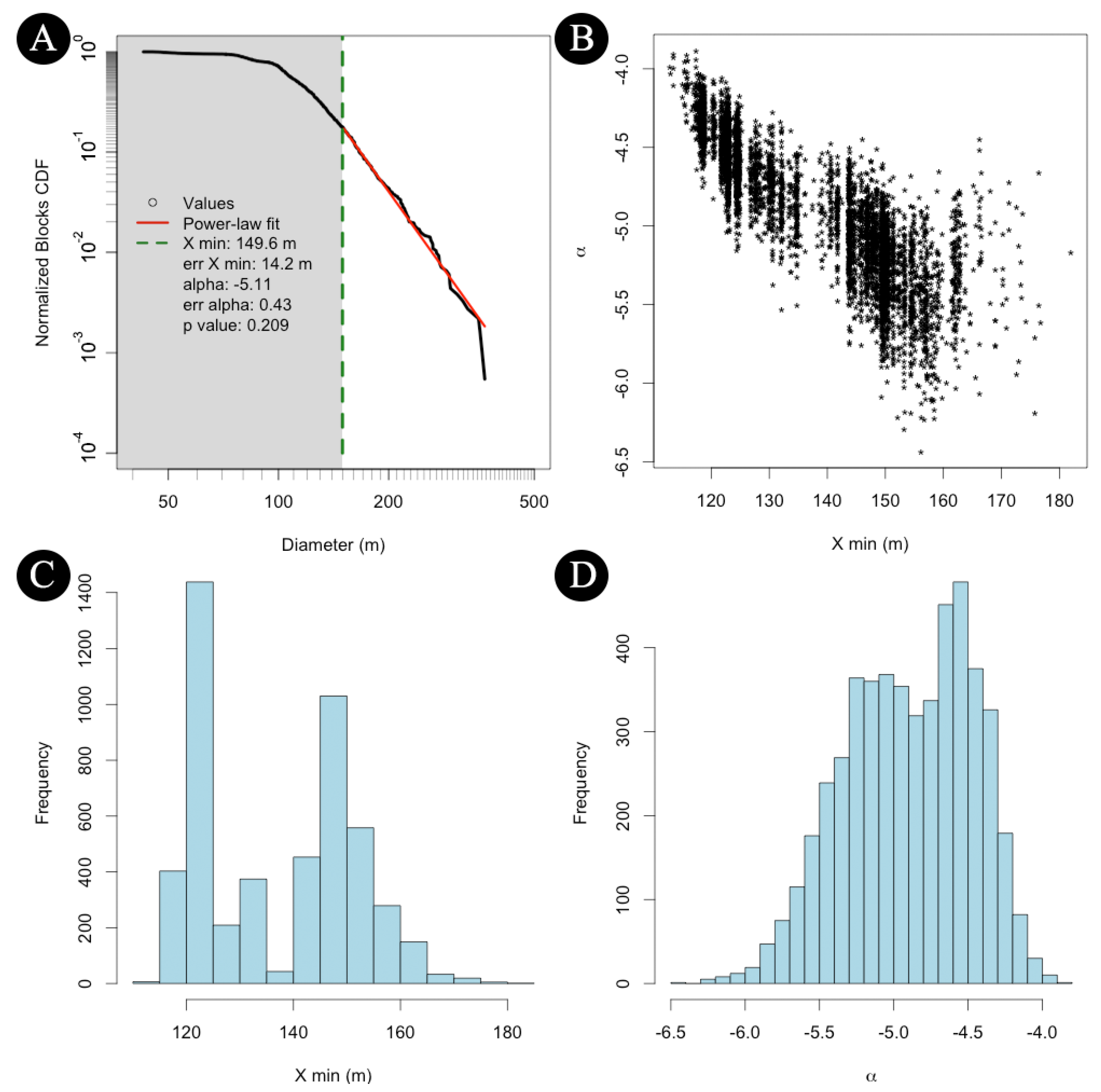
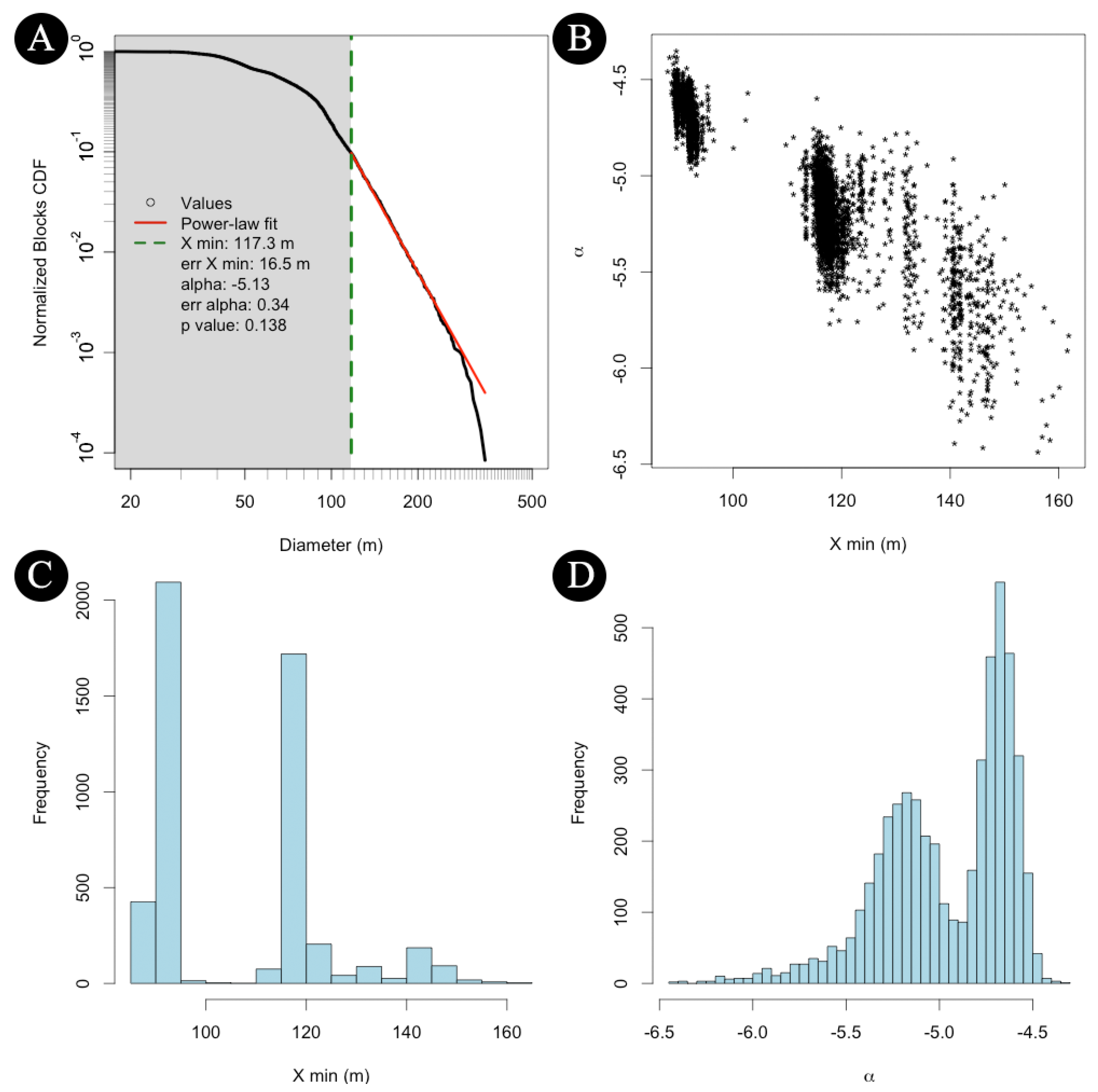
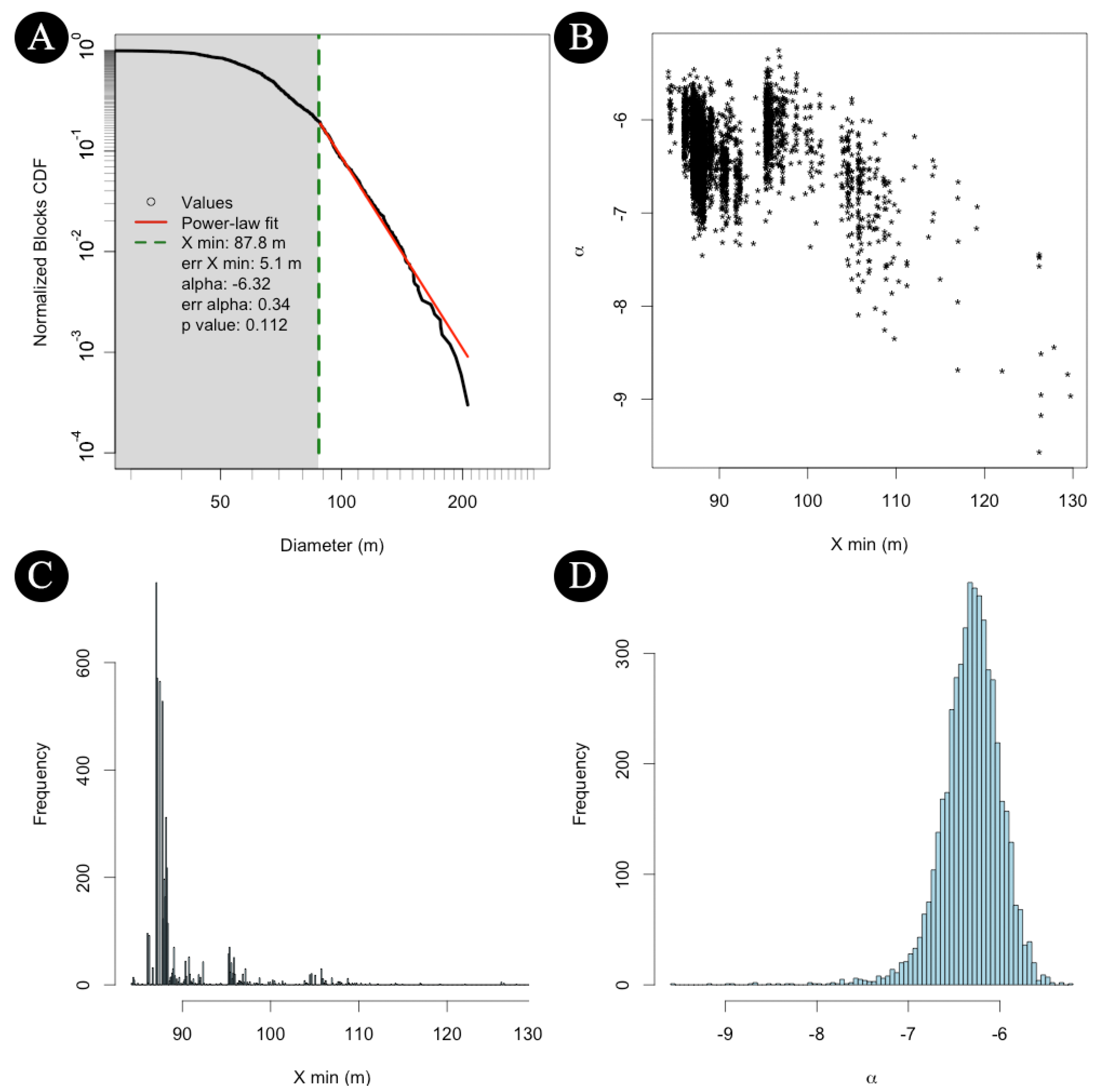
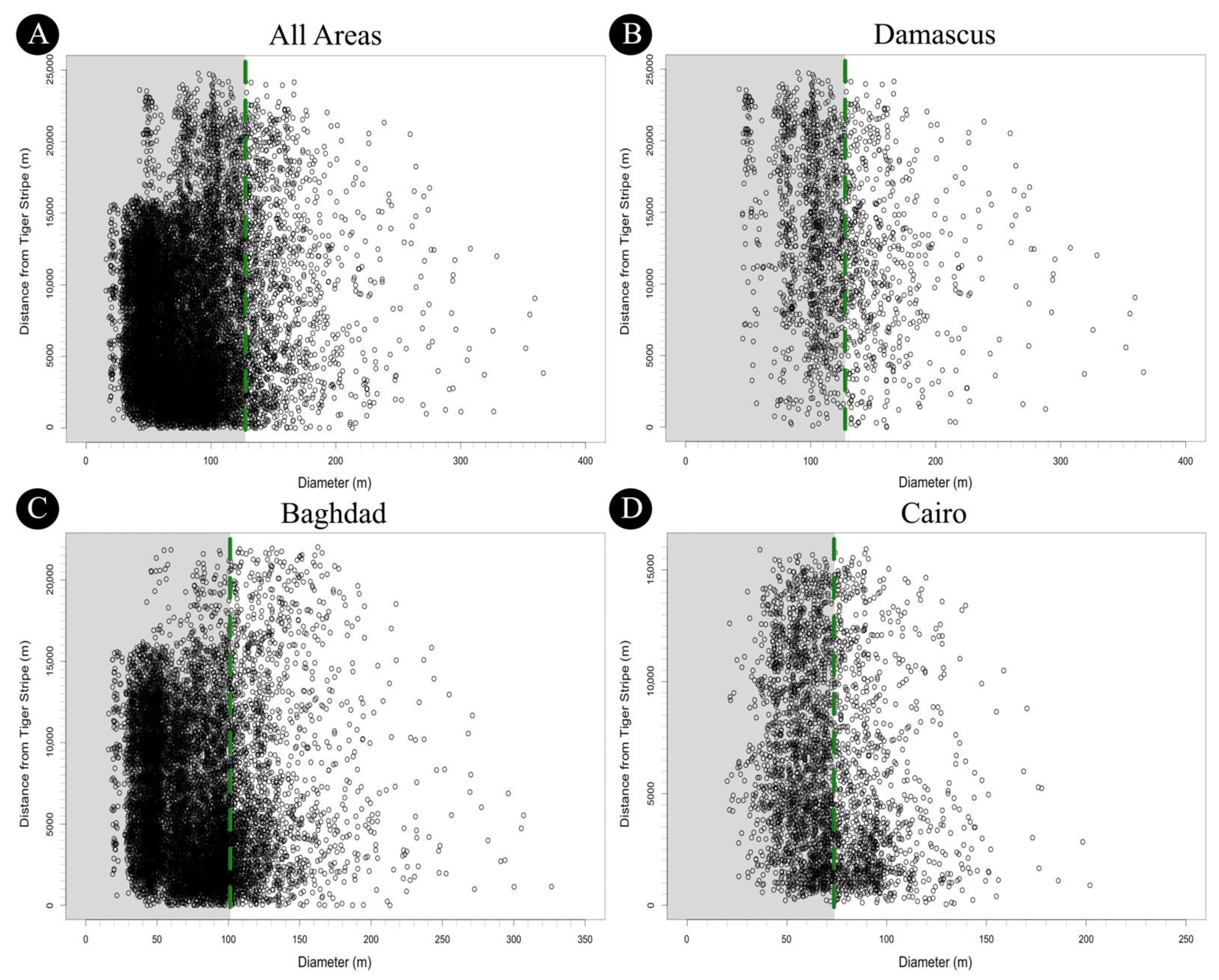
2. Dataset and Methodology
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martens, H.R.; Ingersoll, A.P.; Ewald, S.P.; Helfenstein, P.; Giese, B. Spatial distribution of ice blocks on Enceladus and implications for their origin and emplacement. Icarus 2015, 245, 162–176. [Google Scholar] [CrossRef]
- Verbiscer, A.J.; Peterson, D.E.; Skrutskie, M.F.; Cushing, M.; Helfenstein, P.; Nelson, M.J.; Smith, J.; Wilson, J.C. Near-infrared spectra of the leading and trailing hemispheres of Enceladus. Icarus 2006, 182, 211–223. [Google Scholar] [CrossRef]
- Smith, B.A.; Soderblom, L.; Beebe, R.; Boyce, J.; Briggs, G.; Bunker, A.; Collins, S.A.; Hansen, C.J.; Johnson, T.V.; Mitchell, J.L.; et al. Encounter with Saturn: Voyager 1 Imaging Science Results. Science 1981, 212, 163–191. [Google Scholar] [CrossRef]
- Smith, B.A.; Soderblom, L.; Batson, R.; Bridges, P.; Inge, J.; Masursky, H.; Shoemaker, E.; Beebe, R.; Boyce, J.; Briggs, G.; et al. A New Look at the Saturn System: The Voyager 2 Images. Science 1982, 215, 504–537. [Google Scholar] [CrossRef]
- Porco, C.C.; West, R.A.; Squyres, S.; McEwen, A.; Thomas, P.; Murray, C.D.; DelGenio, A.; Ingersoll, A.P.; Johnson, T.V.; Neukum, G.; et al. Cassini Imaging Science: Instrument Characteristics and Anticipated Scientific Investigations At Saturn. Space Sci. Rev. 2004, 115, 363–497. [Google Scholar] [CrossRef]
- Porco, C.C.; Helfenstein, P.; Thomas, P.C.; Ingersoll, A.P.; Wisdom, J.; West, R.; Neukum, G.; Denk, T.; Wagner, R.; Roatsch, T.; et al. Cassini Observes the Active South Pole of Enceladus. Science 2006, 311, 1393–1401. [Google Scholar] [CrossRef] [PubMed]
- Crow-Willard, E.N.; Pappalardo, R.T. Structural mapping of Enceladus and implications for formation of tectonized regions. J. Geophys. Res. Planets 2015, 120, 928–950. [Google Scholar] [CrossRef]
- Yin, A.; Pappalardo, R.T. Gravitational spreading, bookshelf faulting, and tectonic evolution of the South Polar Terrain of Saturn’s moon Enceladus. Icarus 2015, 260, 409–439. [Google Scholar] [CrossRef]
- Rossi, C.; Cianfarra, P.; Salvini, F.; Bourgeois, O.; Tobie, G. Tectonics of Enceladus’ South Pole: Block Rotation of the Tiger Stripes. J. Geophys. Res. Planets 2020, 125, 006471. [Google Scholar] [CrossRef]
- Porco, C.C.; DiNino, D.; Nimmo, F. How the geysers, tidal stresses, and thermal emission across the south polar terrain of enceladus are related. Astron. J. 2014, 148. [Google Scholar] [CrossRef]
- Hedman, M.M.; Gosmeyer, C.M.; Nicholson, P.D.; Sotin, C.; Brown, R.H.; Clark, R.N.; Baines, K.H.; Buratti, B.J.; Showalter, M.R. An observed correlation between plume activity and tidal stresses on Enceladus. Nat. Cell Biol. 2013, 500, 182–184. [Google Scholar] [CrossRef]
- Iess, L.; Stevenson, D.J.; Parisi, M.; Hemingway, D.; Jacobson, R.A.; Lunine, J.I.; Nimmo, F.; Armstrong, J.W.; Asmar, S.W.; Ducci, M.; et al. The Gravity Field and Interior Structure of Enceladus. Science 2014, 344, 78–80. [Google Scholar] [CrossRef]
- Čadek, O.; Tobie, G.; Van Hoolst, T.; Massé, M.; Choblet, G.; Lefèvre, A.; Mitri, G.; Baland, R.-M.; Běhounková, M.; Bourgeois, O.; et al. Enceladus’s internal ocean and ice shell constrained from Cassini gravity, shape, and libration data. Geophys. Res. Lett. 2016, 43, 5653–5660. [Google Scholar] [CrossRef]
- Lucchetti, A.; Pozzobon, R.; Mazzarini, F.; Cremonese, G.; Massironi, M. Brittle ice shell thickness of Enceladus from fracture distribution analysis. Icarus 2017, 297, 252–264. [Google Scholar] [CrossRef]
- Hemingway, D.; Iess, L.; Tadjeddine, R.; Tobie, G. The Interior of Enceladus. In Enceladus and the Icy Moons of Saturn; University of Arizona: Tucson, AZ, USA, 2018; pp. 57–77. [Google Scholar]
- Spencer, J.R. Cassini Encounters Enceladus: Background and the Discovery of a South Polar Hot Spot. Science 2006, 311, 1401–1405. [Google Scholar] [CrossRef]
- Spitale, J.N.; Porco, C.C. Association of the jets of Enceladus with the warmest regions on its south-polar fractures. Nat. Cell Biol. 2007, 449, 695–697. [Google Scholar] [CrossRef] [PubMed]
- Helfenstein, P.; Porco, C.C. Enceladus’ geysers: Relation to geological features. Astron. J. 2015, 150. [Google Scholar] [CrossRef]
- Cintala, M.J.; McBride, K.M. Block Distributions on the Lunar Surface: A Comparison between Measurements Obtained from Surface and Orbital Photography. In NASA Technical Memorandum 104804. 1995. Available online: https://www.lpi.usra.edu/lunar/documents/NASA_TM_104804_Lunar_blocks.pdf (accessed on 13 July 2020).
- Bart, G.D.; Melosh, H. Distributions of boulders ejected from lunar craters. Icarus 2010, 209, 337–357. [Google Scholar] [CrossRef]
- Krishna, N.; Kumar, P.S. Impact spallation processes on the Moon: A case study from the size and shape analysis of ejecta boulders and secondary craters of Censorinus crater. Icarus 2016, 264, 274–299. [Google Scholar] [CrossRef]
- Pajola, M.; Pozzobon, R.; Lucchetti, A.; Rossato, S.; Baratti, E.; Galluzzi, V.; Cremonese, G. Abundance and size-frequency distribution of boulders in Linné crater’s ejecta (Moon). Planet. Space Sci. 2019, 165, 99–109. [Google Scholar] [CrossRef]
- Garvin, J.B.; Mouginis-Mark, P.J.; Head, J.W. Characterization of rock populations on planetary surfaces: Techniques and a preliminary analysis of Mars and Venus. Earth Moon Planets 1981, 24, 355–387. [Google Scholar] [CrossRef]
- Grant, J.A.; Wilson, S.A.; Ruff, S.W.; Golombek, M.P.; Koestler, D.L. Distribution of rocks on the Gusev Plains and on Husband Hill, Mars. Geophys. Res. Lett. 2006, 33, 16202. [Google Scholar] [CrossRef]
- Golombek, M.P.; Huertas, A.; Marlow, J.; McGrane, B.; Klein, C.; Martinez, M.; Arvidson, R.E.; Heet, T.; Barry, L.; Seelos, K.; et al. Size-frequency distributions of rocks on the northern plains of Mars with special reference to Phoenix landing surfaces. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Pajola, M.; Rossato, S.; Baratti, E.; Pozzobon, R.; Quantin, C.; Carter, J.; Thollot, P. Boulder abundances and size-frequency distributions on Oxia Planum-Mars: Scientific implications for the 2020 ESA ExoMars rover. Icarus 2017, 296, 73–90. [Google Scholar] [CrossRef]
- Mastropietro, M.; Pajola, M.; Cremonese, G.; Munaretto, G.; Lucchetti, A. Boulder Analysis on the Oxia Planum ExoMars 2022 Rover Landing Site: Scientific and Engineering Perspectives. Sol. Syst. Res. 2020, 54, 504–519. [Google Scholar] [CrossRef]
- Geissler, P.; Petit, J.-M.; Durda, D.D.; Greenberg, R.; Bottke, W.; Nolan, M.; Moore, J. Erosion and Ejecta Reaccretion on 243 Ida and Its Moon. Icarus 1996, 120, 140–157. [Google Scholar] [CrossRef]
- Thomas, P.C.; Veverka, J.; Robinson, M.S.; Murchie, S. Shoemaker crater as the source of most ejecta blocks on the asteroid 433 Eros. Nat. Cell Biol. 2001, 413, 394–396. [Google Scholar] [CrossRef]
- Mazrouei, S.; Daly, M.; Barnouin, O.; Ernst, C.; DeSouza, I. Block distributions on Itokawa. Icarus 2014, 229, 181–189. [Google Scholar] [CrossRef]
- DellaGiustina, D.N.; The OSIRIS-REx Team; Emery, J.P.; Golish, D.R.; Rozitis, B.; Bennett, C.A.; Burke, K.N.; Ballouz, R.-L.; Becker, K.J.; Christensen, P.R.; et al. Properties of rubble-pile asteroid (101955) Bennu from OSIRIS-REx imaging and thermal analysis. Nat. Astron. 2019, 3, 341–351. [Google Scholar] [CrossRef]
- Schröder, S.E.; Carsenty, U.; Hauber, E.; Schulzeck, F.; Raymond, C.A.; Russell, C.T. The Boulder Population of Asteroid 4 Vesta: Size-Frequency Distribution and Survival Time. Earth Space Sci. 2021, 8, 000941. [Google Scholar] [CrossRef]
- Pajola, M.; Vincent, J.-B.; Güttler, C.; Lee, J.-C.; Bertini, I.; Massironi, M.; Simioni, E.; Marzari, F.; Giacomini, L.; Lucchetti, A.; et al. Size-frequency distribution of boulders ≥7 m on comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2015, 583, A37. [Google Scholar] [CrossRef]
- Mottola, S.; Arnold, G.; Grothues, H.-G.; Jaumann, R.; Michaelis, H.; Neukum, G.; Bibring, J.-P.; Schroder, S.E.; Hamm, M.; Otto, K.A.; et al. The structure of the regolith on 67P/Churyumov-Gerasimenko from ROLIS descent imaging. Science 2015, 349, aab0232. [Google Scholar] [CrossRef] [PubMed]
- Pajola, M.; Lucchetti, A.; Vincent, J.; Oklay, N.; El-Maarry, M.; Bertini, I.; Naletto, G.; Lazzarin, M.; Massironi, M.; Sierks, H. The southern hemisphere of 67P/Churyumov-Gerasimenko: Analysis of the pre-perihelion size-frequency distribution of boulders >7 m. Astron. Astrophys. 2016, 592, 2. [Google Scholar] [CrossRef][Green Version]
- Pajola, M.; Lucchetti, A.; Bertini, I.; Marzari, F.; A’Hearn, M.F.; La Forgia, F.; Lazzarin, M.; Naletto, G.; Barbieri, C. Size-frequency distribution of boulders ≥10 m on comet 103P/Hartley 2. Astron. Astrophys. 2015, 585, A85. [Google Scholar] [CrossRef]
- Acton, C.H. Ancillary data services of NASA’s Navigation and Ancillary Information Facility. Planet. Space Sci. 1996, 44, 65–70. [Google Scholar] [CrossRef]
- Michikami, T.; Nakamura, A.M.; Hirata, N.; Gaskell, R.W.; Nakamura, R.; Honda, T.; Honda, C.; Hiraoka, K.; Saito, J.; Demura, H.; et al. Size-frequency statistics of boulders on global surface of asteroid 25143 Itokawa. Earth Planets Space 2008, 60, 13–20. [Google Scholar] [CrossRef]
- Küppers, M.; Moissl, R.; Vincent, J.-B.; Besse, S.; Hviid, S.F.; Carry, B.; Grieger, B.; Sierks, H.; Keller, H.U.; Marchi, S. Boulders on Lutetia. Planet. Space Sci. 2012, 66, 71–78. [Google Scholar] [CrossRef]
- Pajola, M.; Höfner, S.; Vincent, J.-B.; Oklay, N.; Scholten, F.; Preusker, F.; Mottola, S.; Naletto, G.; Fornasier, S.; Lowry, S.; et al. The pristine interior of comet 67P revealed by the combined Aswan outburst and cliff collapse. Nat. Astron. 2017, 1, 0092. [Google Scholar] [CrossRef]
- Mohajeri, N.; Gudmundsson, A. Entropies and Scaling Exponents of Street and Fracture Networks. Entropy 2012, 14, 800–833. [Google Scholar] [CrossRef]
- Lucchetti, A.; Rossi, C.; Mazzarini, F.; Pajola, M.; Pozzobon, R.; Massironi, M.; Cremonese, G. Equatorial grooves distribution on Ganymede: Length and self-similar clustering analysis. Planet. Space Sci. 2021, 195, 105140. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Crawford, G.D.; Stevenson, D.J. Gas-driven water volcanism and the resurfacing of Europa. Icarus 1988, 73, 66–79. [Google Scholar] [CrossRef]
- Hansen, C.J.; Shemansky, D.E.; Esposito, L.W.; Stewart, A.I.F.; Lewis, B.R.; Colwell, J.E.; Hendrix, A.R.; West, R.A.; Waite, J.H.; Teolis, B.; et al. The composition and structure of the Enceladus plume. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Abramov, O.; Spencer, J. Endogenic heat from Enceladus’ south polar fractures: New observations, and models of conductive surface heating. Icarus 2009, 199, 189–196. [Google Scholar] [CrossRef]
- Goguen, J.D.; Buratti, B.J.; Brown, R.H.; Clark, R.N.; Nicholson, P.D.; Hedman, M.M.; Howell, R.R.; Sotin, C.; Cruikshank, D.P.; Baines, K.H.; et al. The temperature and width of an active fissure on Enceladus measured with Cassini VIMS during the 14 April 2012 South Pole flyover. Icarus 2013, 226, 1128–1137. [Google Scholar] [CrossRef]
- Keller, H.U.; Barbieri, C.; Lamy, P.; Rickman, H.; Rodrigo, R.; Wenzel, K.-P.; Sierks, H.; A’Hearn, M.F.; Angrilli, F.; Angulo, M.; et al. OSIRIS—The Scientific Camera System Onboard Rosetta. Space Sci. Rev. 2007, 128, 433–506. [Google Scholar] [CrossRef]
- Sierks, H.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; Koschny, D.; Rickman, H.; Keller, H.U.; Agarwal, J.; A’Hearn, M.F.; Angrilli, F.; et al. On the nucleus structure and activity of comet 67P/Churyumov-Gerasimenko. Science 2015, 347, aaa1044. [Google Scholar] [CrossRef]
- Alí-Lagoa, V.; Delbo, M.; Libourel, G. Rapid temperature changes and the early activity on comet 67P/Churyumov–Gerasimenko. Astrophys. J. 2015, 810, L22. [Google Scholar] [CrossRef]
- Thomas, N.; Sierks, H.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; Rickman, H.; Koschny, D.; Keller, H.U.; Agarwal, J.; A’Hearn, M.F.; et al. The morphological diversity of comet 67P/Churyumov-Gerasimenko. Science 2015, 347, aaa0440. [Google Scholar] [CrossRef]
- Pajola, M.; Oklay, N.; La Forgia, F.; Giacomini, L.; Massironi, M.; Bertini, I.; El-Maarry, M.R.; Marzari, F.; Preusker, F.; Scholten, F.; et al. Aswan site on comet 67P/Churyumov-Gerasimenko: Morphology, boulder evolution, and spectrophotometry. Astron. Astrophys. 2016, 592, A69. [Google Scholar] [CrossRef]
- Pajola, M.; Lee, J.-C.; Oklay, N.; Hviid, S.F.; Penasa, L.; Mottola, S.; Shi, X.; Fornasier, S.; Davidsson, B.; Giacomini, L.; et al. Multidisciplinary analysis of the Hapi region located on Comet 67P/Churyumov–Gerasimenko. Mon. Not. R. Astron. Soc. 2019, 485, 2139–2154. [Google Scholar] [CrossRef]
- Le Gall, A.; Leyrat, C.; Janssen, M.A.; Choblet, G.; Tobie, G.; Bourgeois, O.; Lucas, A.; Sotin, C.; Howett, C.; Kirk, R.; et al. Thermally anomalous features in the subsurface of Enceladus’s south polar terrain. Nat. Astron. 2017, 1, 0063. [Google Scholar] [CrossRef]
- Palumbo, P.; Jaumann, R.; Cremonese, G.; Hoffmann, H.; Debei, S.; Della Corte, V.; Holland, A.; Lara, L.M.; Castro, J.M.; Herranz, M.; et al. JANUS: The Visible Camera Onboard the ESA JUICE Mission to the Jovian System. 45th LPSC Meeting. Abstract #2094. 2014. Available online: https://elib.dlr.de/90175/1/2094.pdf (accessed on 4 January 2021).
- Grasset, O.; Dougherty, M.; Coustenis, A.; Bunce, E.; Erd, C.; Titov, D.; Blanc, M.; Coates, A.; Drossart, P.; Fletcher, L.; et al. JUpiter ICy moons Explorer (JUICE): An ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet. Space Sci. 2013, 78, 1–21. [Google Scholar] [CrossRef]
- Turtle, E.P.; McEwen, A.S.; Bland, M.; Collins, G.C.; Daubar, I.J.; Ernst, C.M.; Fletcher, L.; Hansen, C.J.; Hawkins, S.E.; Hayes, A.G.; et al. The Europa Imaging System (EIS): High-Resolution, 3-D Insight into Europa’s Geology, Ice Shell, and Potential for Current Activity. EPSC-DPS Joint Meeting 2019. Volume 13, EPSC-DPS2019–832-2. 2019. Available online: https://meetingorganizer.copernicus.org/EPSC-DPS2019/EPSC-DPS2019-832-2.pdf (accessed on 4 January 2021).
- Pappalardo, R.T.; Senske, D.; Korth, H.; Klima, R.; Vance, S.; Craft, K. The Europa Clipper Mission: Exploring the Habitability of a Unique Icy World. EPSC 2017 Abstracts. 2017, Volume 11–304. 2017. Available online: https://meetingorganizer.copernicus.org/EPSC2017/EPSC2017-304.pdf (accessed on 4 January 2021).
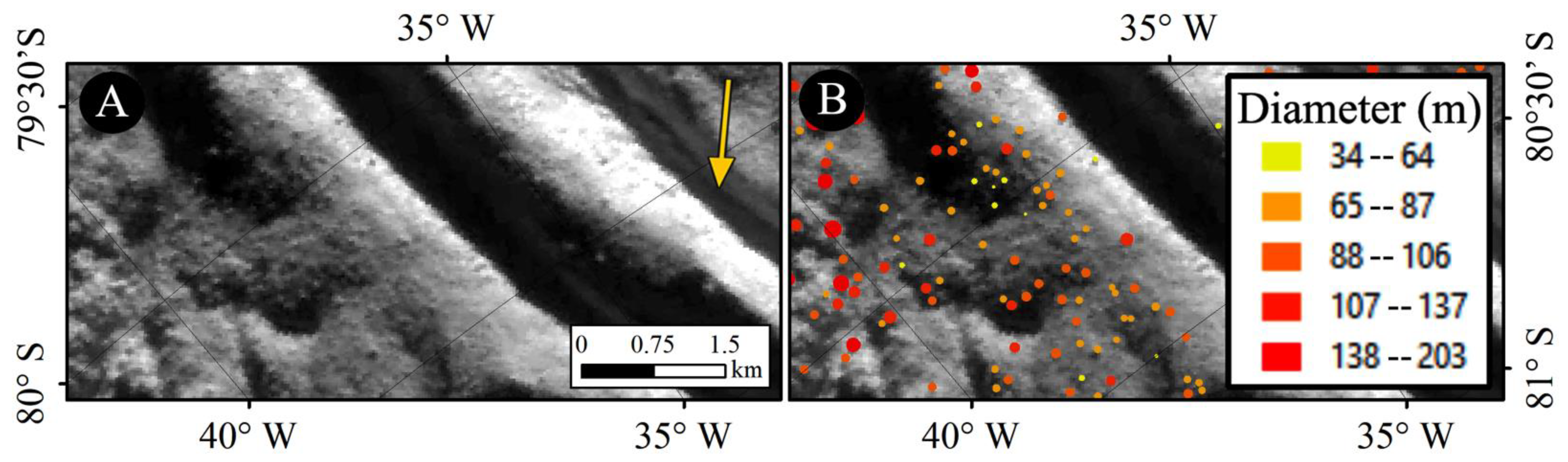
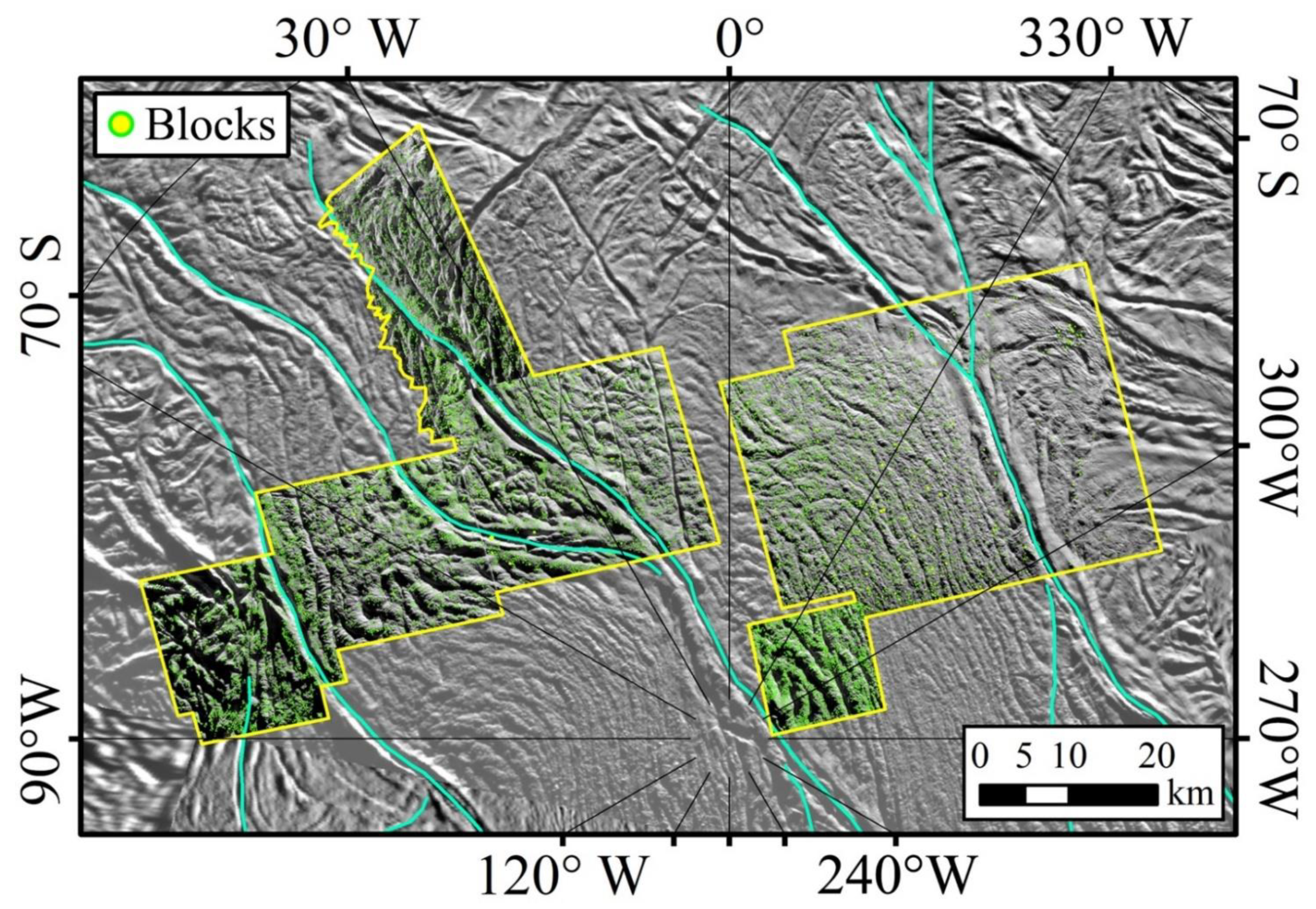
| Image ID | Acquisition Date (DD-MMM-YYYY) | Spatial Scale (m/pixel) |
|---|---|---|
| N1597182401 | 11 August 2008 | 11.5 |
| N1597182434 | 11 August 2008 | 15.0 |
| N1597182467 | 11 August 2008 | 18.4 |
| N1597182500 | 11 August 2008 | 21.8 |
| N1597182533 | 11 August 2008 | 25.3 |
| N1604166970 | 31 October 2008 | 12.1 |
| N1604167158 | 31 October 2008 | 31.9 |
| N1637462964 | 21 November 2009 | 14.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pajola, M.; Lucchetti, A.; Senter, L.; Cremonese, G. Blocks Size Frequency Distribution in the Enceladus Tiger Stripes Area: Implications on Their Formative Processes. Universe 2021, 7, 82. https://doi.org/10.3390/universe7040082
Pajola M, Lucchetti A, Senter L, Cremonese G. Blocks Size Frequency Distribution in the Enceladus Tiger Stripes Area: Implications on Their Formative Processes. Universe. 2021; 7(4):82. https://doi.org/10.3390/universe7040082
Chicago/Turabian StylePajola, Maurizio, Alice Lucchetti, Lara Senter, and Gabriele Cremonese. 2021. "Blocks Size Frequency Distribution in the Enceladus Tiger Stripes Area: Implications on Their Formative Processes" Universe 7, no. 4: 82. https://doi.org/10.3390/universe7040082
APA StylePajola, M., Lucchetti, A., Senter, L., & Cremonese, G. (2021). Blocks Size Frequency Distribution in the Enceladus Tiger Stripes Area: Implications on Their Formative Processes. Universe, 7(4), 82. https://doi.org/10.3390/universe7040082








