AGB Stars and Their Circumstellar Envelopes. I. the VULCAN Code
Abstract
1. Introduction
2. The VULCAN Code
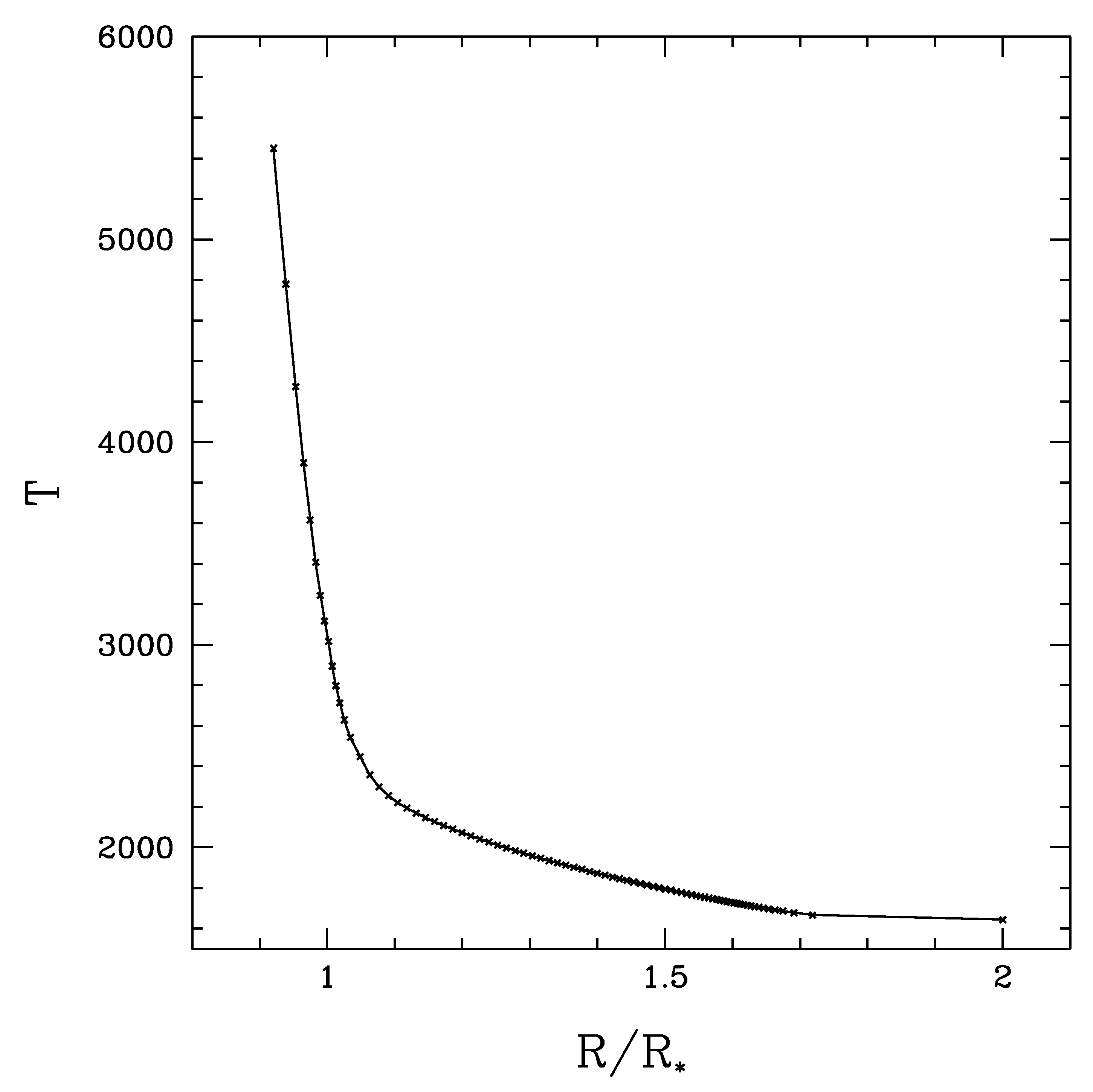
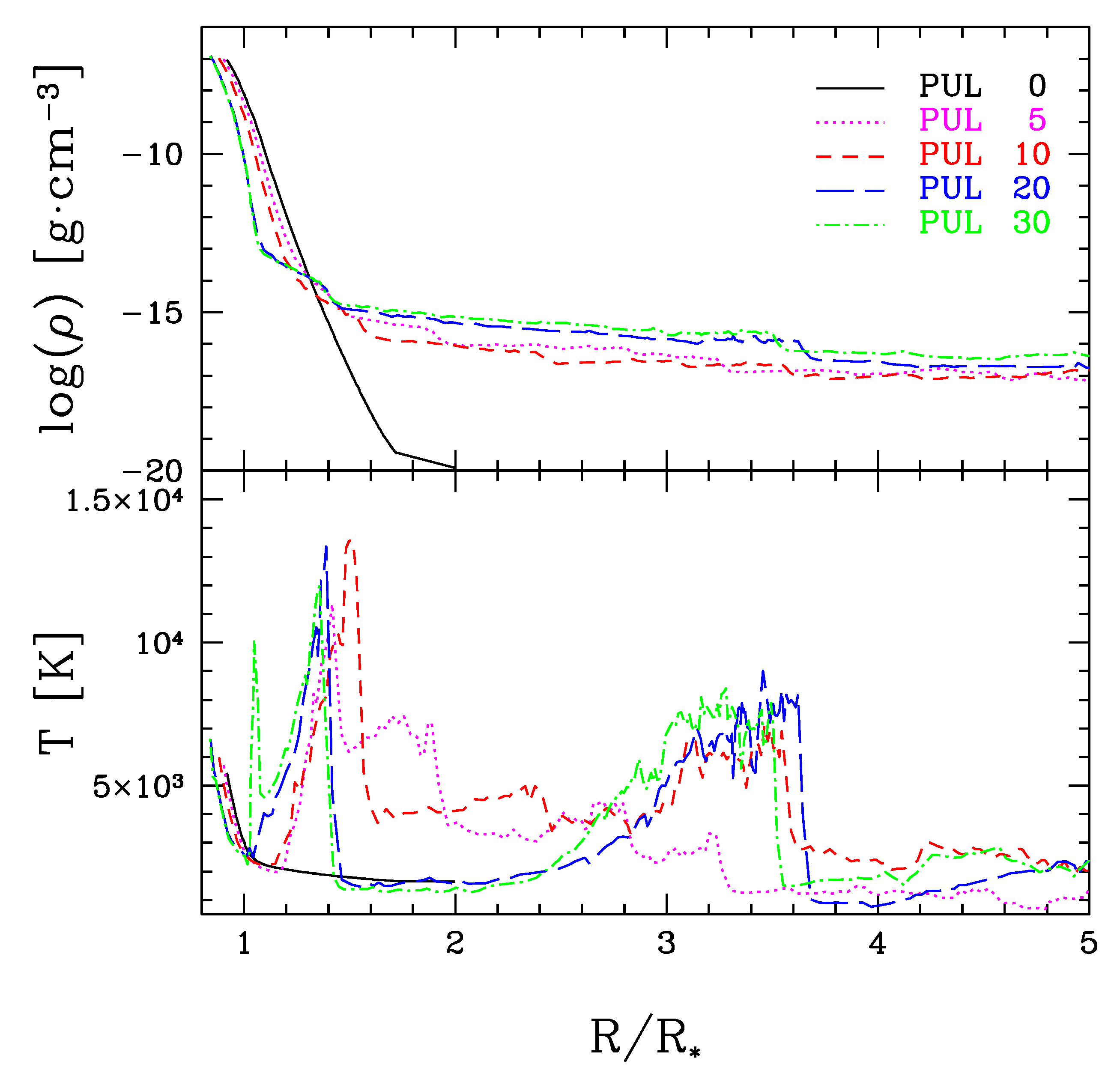
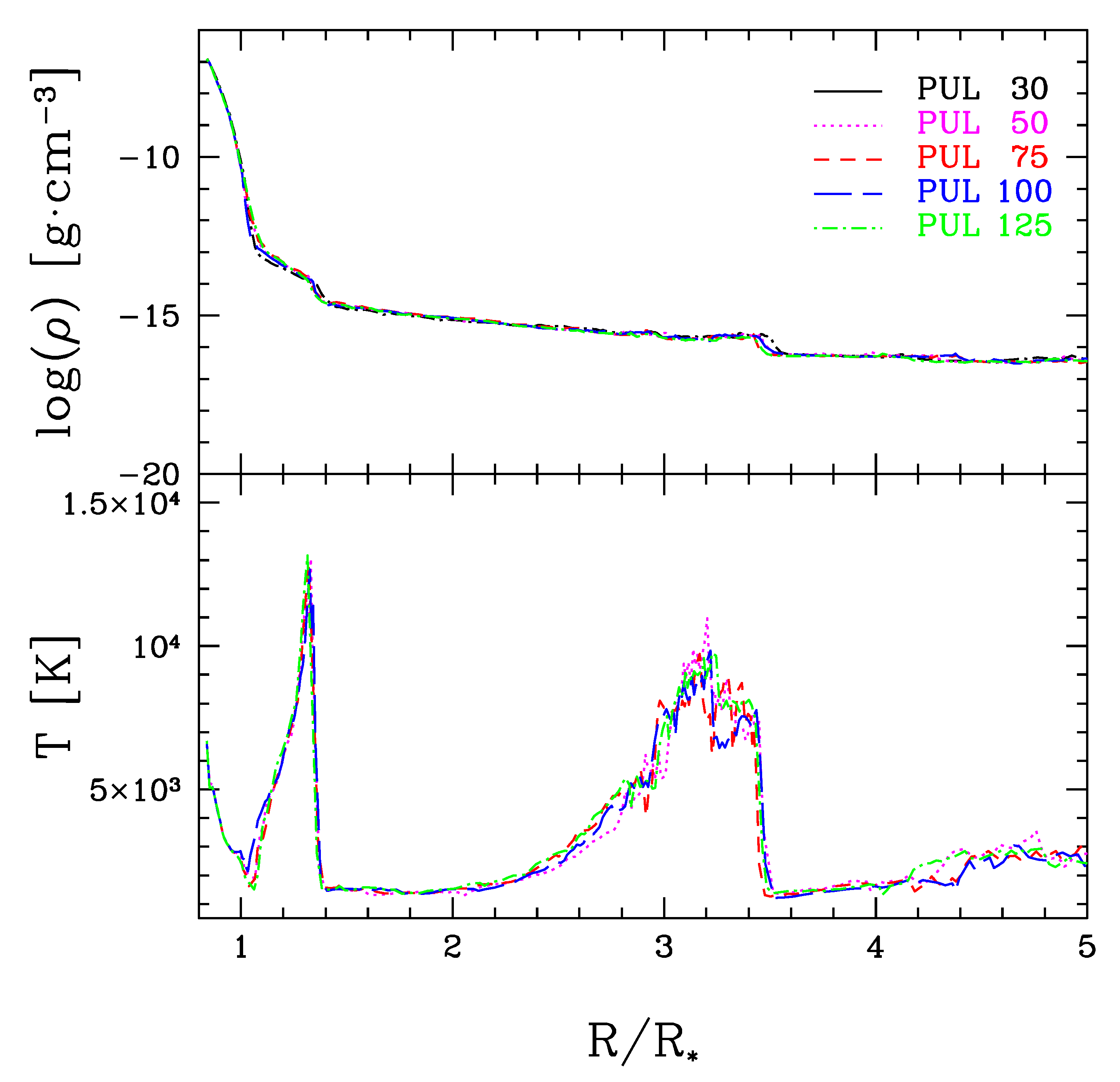
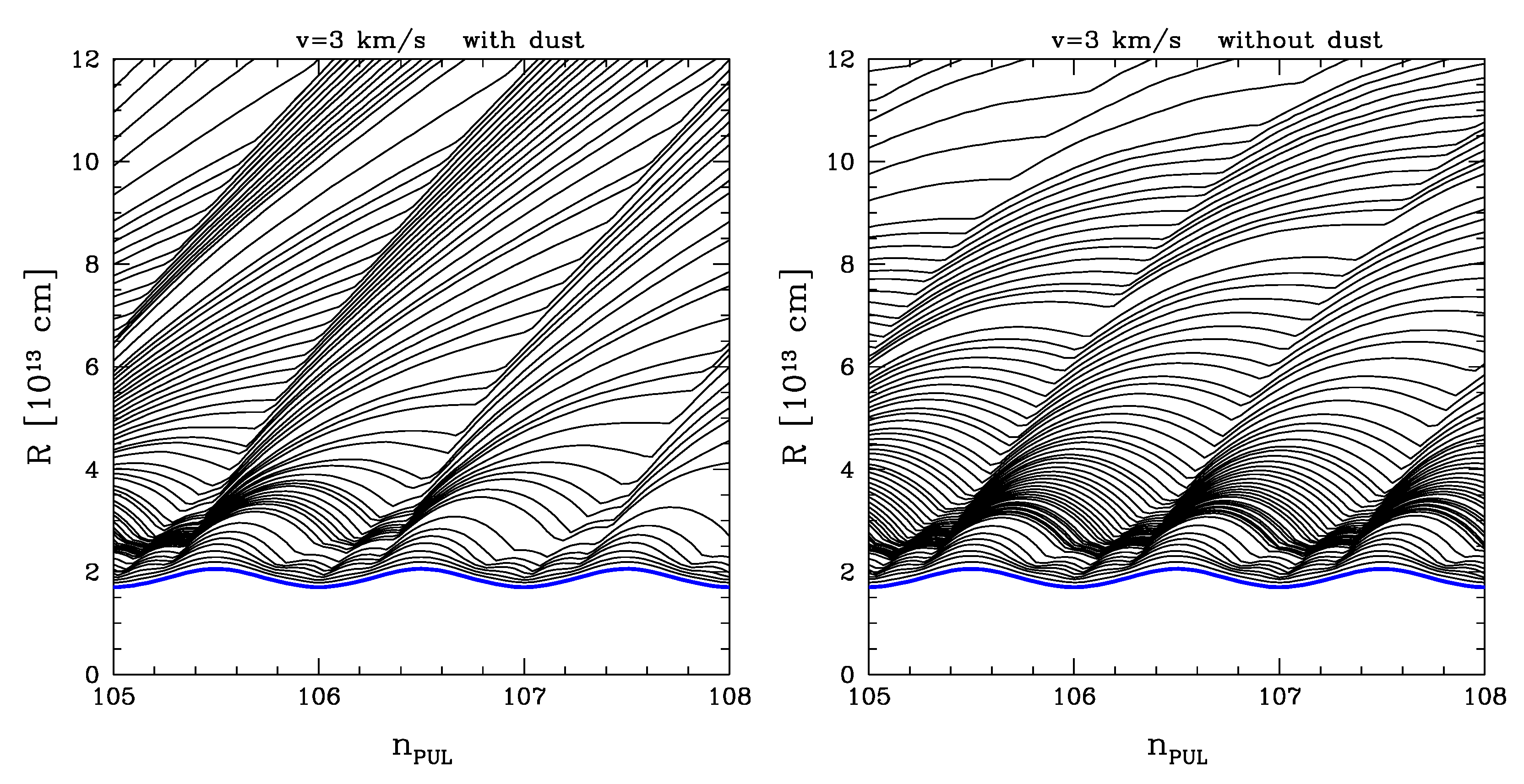
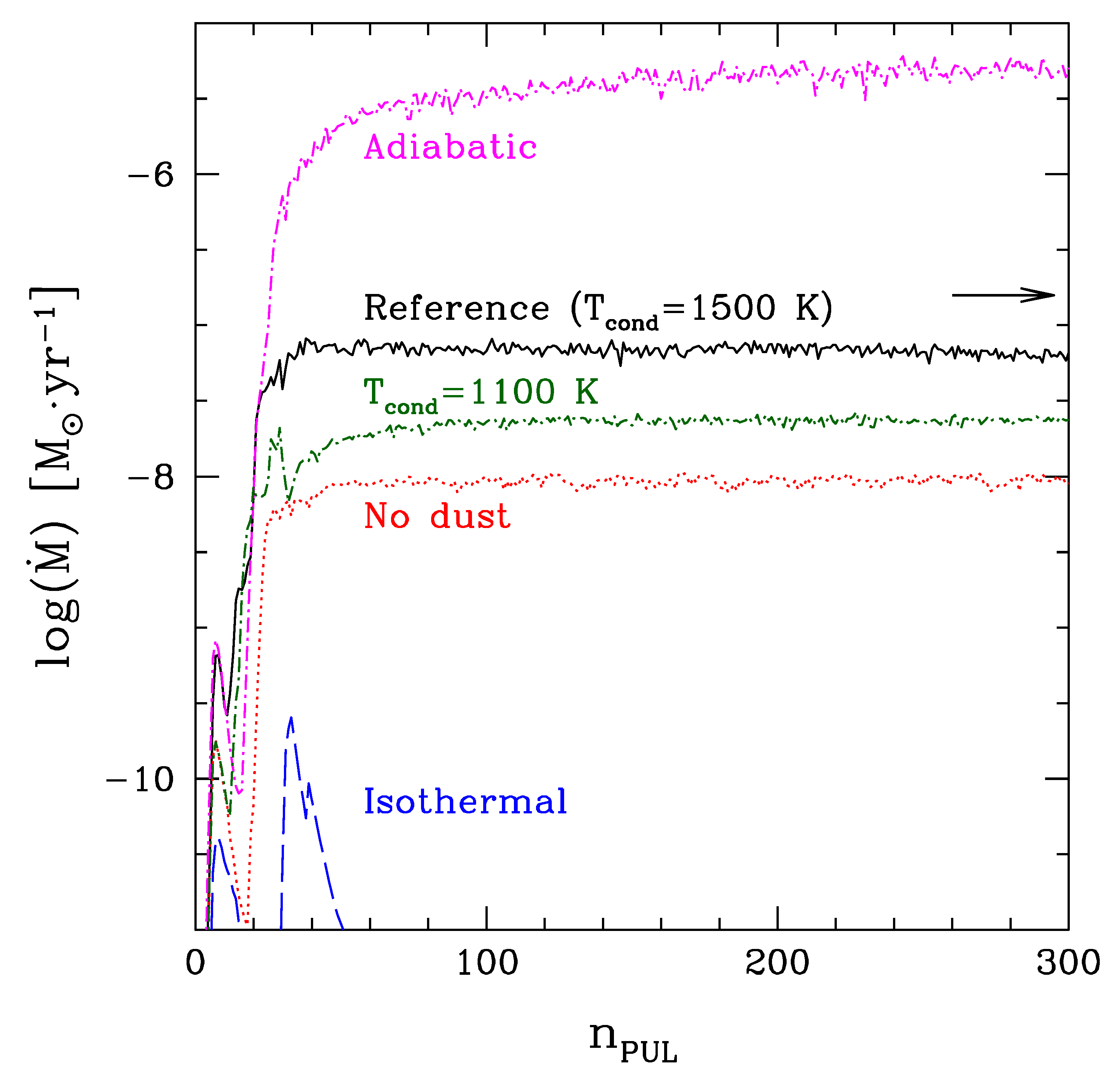
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Herwig, F. Evolution of Asymptotic Giant Branch Stars. ARA&A 2005, 43, 435–479. [Google Scholar] [CrossRef]
- Straniero, O.; Gallino, R.; Cristallo, S. s process in low-mass asymptotic giant branch stars. Nucl. Phys. A 2006, 777, 311–339. [Google Scholar] [CrossRef]
- Karakas, A.I.; Lattanzio, J.C. The Dawes Review 2: Nucleosynthesis and Stellar Yields of Low- and Intermediate-Mass Single Stars. PASA 2014, 31, e030. [Google Scholar] [CrossRef]
- Marigo, P. Asymptotic Giant Branch evolution at varying surface C/O ratio: Effects of changes in molecular opacities. A&A 2002, 387, 507–519. [Google Scholar] [CrossRef]
- Nanni, A.; Bressan, A.; Marigo, P.; Girardi, L. Evolution of thermally pulsing asymptotic giant branch stars-II. Dust production at varying metallicity. MNRAS 2013, 434, 2390–2417. [Google Scholar] [CrossRef]
- Gail, H.P.; Wetzel, S.; Pucci, A.; Tamanai, A. Seed particle formation for silicate dust condensation by SiO nucleation. A&A 2013, 555, A119. [Google Scholar] [CrossRef]
- Gobrecht, D.; Cherchneff, I.; Sarangi, A.; Plane, J.M.C.; Bromley, S.T. Dust formation in the oxygen-rich AGB star IK Tauri. A&A 2016, 585, A6. [Google Scholar] [CrossRef]
- Höfner, S.; Olofsson, H. Mass loss of stars on the asymptotic giant branch. Mechanisms, models and measurements. A&A Rev. 2018, 26, 1. [Google Scholar] [CrossRef]
- Bowen, G.H. Dynamical modeling of long-period variable star atmospheres. ApJ 1988, 329, 299–317. [Google Scholar] [CrossRef]
- Cristallo, S.; Straniero, O.; Lederer, M.T.; Aringer, B. Molecular Opacities for Low-Mass Metal-poor AGB Stars Undergoing the Third Dredge-up. ApJ 2007, 667, 489–496. [Google Scholar] [CrossRef][Green Version]
- Dupree, A.K.; Hartmann, L.; Avrett, E.H. Chromospheres and mass loss in metal-deficient giant stars. ApJ 1984, 281, L37–L39. [Google Scholar] [CrossRef]
- Nowotny, W.; Höfner, S.; Aringer, B. Line formation in AGB atmospheres including velocity effects. Molecular line profile variations of long period variables. A&A 2010, 514, A35. [Google Scholar] [CrossRef]
- Höfner, S. Winds of M-type AGB stars driven by micron-sized grains. A&A 2008, 491, L1–L4. [Google Scholar] [CrossRef]
- Cristallo, S.; Piersanti, L.; Straniero, O.; Gallino, R.; Domínguez, I.; Abia, C.; Di Rico, G.; Quintini, M.; Bisterzo, S. Evolution, Nucleosynthesis, and Yields of Low-mass Asymptotic Giant Branch Stars at Different Metallicities. II. The FRUITY Database. ApJS 2011, 197, 17. [Google Scholar] [CrossRef]
- Piersanti, L.; Cristallo, S.; Straniero, O. The Effects of Rotation on s-process Nucleosynthesis in Asymptotic Giant Branch Stars. ApJ 2013, 774, 98. [Google Scholar] [CrossRef]
- Cristallo, S.; Straniero, O.; Piersanti, L.; Gobrecht, D. Evolution, Nucleosynthesis, and Yields of AGB Stars at Different Metallicities. III. Intermediate-mass Models, Revised Low-mass Models, and the ph-FRUITY Interface. ApJS 2015, 219, 40. [Google Scholar] [CrossRef]
- Cristallo, S.; Karinkuzhi, D.; Goswami, A.; Piersanti, L.; Gobrecht, D. Constraints of the Physics of Low-mass AGB Stars from CH and CEMP Stars. ApJ 2016, 833, 181. [Google Scholar] [CrossRef]
- Freytag, B.; Liljegren, S.; Höfner, S. Global 3D radiation-hydrodynamics models of AGB stars. Effects of convection and radial pulsations on atmospheric structures. A&A 2017, 600, A137. [Google Scholar] [CrossRef]
- Bladh, S.; Höfner, S. Exploring wind-driving dust species in cool luminous giants. I. Basic criteria and dynamical models of M-type AGB stars. A&A 2012, 546, A76. [Google Scholar] [CrossRef]
- Mattsson, L.; Wahlin, R.; Höfner, S. Dust driven mass loss from carbon stars as a function of stellar parameters. I. A grid of solar-metallicity wind models. A&A 2010, 509, A14. [Google Scholar] [CrossRef]
- Sloan, G.C.; Matsuura, M.; Lagadec, E.; van Loon, J.T.; Kraemer, K.E.; McDonald, I.; Groenewegen, M.A.T.; Wood, P.R.; Bernard-Salas, J.; Zijlstra, A.A. Carbon-rich Dust Production in Metal-poor Galaxies in the Local Group. ApJ 2012, 752, 140. [Google Scholar] [CrossRef]
- Eriksson, K.; Nowotny, W.; Höfner, S.; Aringer, B.; Wachter, A. Synthetic photometry for carbon-rich giants. IV. An extensive grid of dynamic atmosphere and wind models. A&A 2014, 566, A95. [Google Scholar] [CrossRef]
- Boyer, M.L.; McQuinn, K.B.W.; Barmby, P.; Bonanos, A.Z.; Gehrz, R.D.; Gordon, K.D.; Groenewegen, M.A.T.; Lagadec, E.; Lennon, D.; Marengo, M.; et al. An Infrared Census of DUST in Nearby Galaxies with Spitzer (DUSTiNGS). II. Discovery of Metal-poor Dusty AGB Stars. ApJ 2015, 800, 51. [Google Scholar] [CrossRef]
- Höfner, S.; Bladh, S.; Aringer, B.; Ahuja, R. Dynamic atmospheres and winds of cool luminous giants. I. Al2O3 and silicate dust in the close vicinity of M-type AGB stars. A&A 2016, 594, A108. [Google Scholar] [CrossRef]
- Gobrecht, D.; Cristallo, S.; Piersanti, L.; Bromley, S.T. Nucleation of Small Silicon Carbide Dust Clusters in AGB Stars. ApJ 2017, 840, 117. [Google Scholar] [CrossRef]
- Boulangier, J.; Gobrecht, D.; Decin, L.; de Koter, A.; Yates, J. Developing a self-consistent AGB wind model - II. Non-classical, non-equilibrium polymer nucleation in a chemical mixture. MNRAS 2019, 489, 4890–4911. [Google Scholar] [CrossRef]
- Winters, J.M.; Le Bertre, T.; Jeong, K.S.; Helling, C.; Sedlmayr, E. A systematic investigation of the mass loss mechanism in dust forming long-period variable stars. A&A 2000, 361, 641–659. [Google Scholar]
- Woitke, P. Too little radiation pressure on dust in the winds of oxygen-rich AGB stars. A&A 2006, 460, L9–L12. [Google Scholar] [CrossRef]
- Dorfi, E.A.; Feuchtinger, M.U. Nonlinear stellar pulsations. I-Numerical methods, basic physics, initial models and first results. A&A 1991, 249, 417–427. [Google Scholar]
- Dorfi, E.A.; Hoefner, S. Dust formation in winds of long-period variables. I - Equations, method of solution, simple examples. A&A 1991, 248, 105–114. [Google Scholar]
- Bravo, E. Nucleosintesis y Curvas de Luz en Supernovas de Tipo Ia. Ph.D. Thesis, Universidad de Barcelona, Barcelona, Spain, 1990. [Google Scholar]
- Tscharnuter, W.M.; Winkler, K.H.A. A method for computing selfgravitating gas flows with radiation. Comput. Phys. Commun. 1979, 18, 171–199. [Google Scholar] [CrossRef]
- Spitzer, L. Physical Processes in the Interstellar Medium; Wiley-Interscience Publication: New York, NY, USA, 1978. [Google Scholar]
- Chandrasekhar, S. The radiative equilibrium of extended stellar atmospheres. MNRAS 1934, 94, 444–458. [Google Scholar] [CrossRef]
- Woitke, P.; Goeres, A.; Sedlmayr, E. On the gas temperature in the shocked circumstellar envelopes of pulsating stars. II. Shock induced condensation around R Coronae Borealis stars. A&A 1996, 313, 217–228. [Google Scholar]
- Nanni, A.; Groenewegen, M.A.T.; Aringer, B.; Rubele, S.; Bressan, A.; van Loon, J.T.; Goldman, S.R.; Boyer, M.L. The mass-loss, expansion velocities, and dust production rates of carbon stars in the Magellanic Clouds. MNRAS 2019, 487, 502–521. [Google Scholar] [CrossRef]
- Gobrecht, D.; Decin, L.; Cristallo, S.; Bromley, S.T. A global optimisation study of the low-lying isomers of the alumina octomer (Al2O3)8. Chem. Phys. Lett. 2018, 711, 138–147. [Google Scholar] [CrossRef]
- Decin, L.; Hony, S.; de Koter, A.; Justtanont, K.; Tielens, A.G.G.M.; Waters, L.B.F.M. Probing the mass-loss history of AGB and red supergiant stars from CO rotational line profiles. I. Theoretical model-Mass-loss history unravelled in VYCMa. A&A 2006, 456, 549–563. [Google Scholar] [CrossRef]
- Ramstedt, S.; Schöier, F.L.; Olofsson, H.; Lundgren, A.A. On the reliability of mass-loss-rate estimates for AGB stars. A&A 2008, 487, 645–657. [Google Scholar] [CrossRef]
- Bains, I.; Cohen, R.J.; Louridas, A.; Richards, A.M.S.; Rosa-González, D.; Yates, J.A. Sub-au imaging of water vapour clouds around four asymptotic giant branch stars. MNRAS 2003, 342, 8–32. [Google Scholar] [CrossRef][Green Version]
- Decin, L.; Montargès, M.; Richards, A.M.S.; Gottlieb, C.A.; Homan, W.; McDonald, I.; El Mellah, I.; Danilovich, T.; Wallström, S.H.J.; Zijlstra, A.; et al. (Sub)stellar companions shape the winds of evolved stars. Science 2020, 369, 1497–1500. [Google Scholar] [CrossRef]
- Lagadec, E.; Zijlstra, A.A.; Mauron, N.; Fuller, G.; Josselin, E.; Sloan, G.C.; Riggs, A.J.E. The low wind expansion velocity of metal-poor carbon stars in the Halo and the Sagittarius stream. MNRAS 2010, 403, 1331–1338. [Google Scholar] [CrossRef][Green Version]
- Ramstedt, S.; Olofsson, H. The 12CO/13CO ratio in AGB stars of different chemical type. Connection to the 12C/13C ratio and the evolution along the AGB. A&A 2014, 566, A145. [Google Scholar] [CrossRef]
- Danilovich, T.; Teyssier, D.; Justtanont, K.; Olofsson, H.; Cerrigone, L.; Bujarrabal, V.; Alcolea, J.; Cernicharo, J.; Castro-Carrizo, A.; García-Lario, P.; et al. New observations and models of circumstellar CO line emission of AGB stars in the Herschel SUCCESS programme. A&A 2015, 581, A60. [Google Scholar] [CrossRef]
- Groenewegen, M.A.T.; Vlemmings, W.H.T.; Marigo, P.; Sloan, G.C.; Decin, L.; Feast, M.W.; Goldman, S.R.; Justtanont, K.; Kerschbaum, F.; Matsuura, M.; et al. The ALMA detection of CO rotational line emission in AGB stars in the Large Magellanic Cloud. A&A 2016, 596, A50. [Google Scholar] [CrossRef]
- Goldman, S.R.; van Loon, J.T.; Zijlstra, A.A.; Green, J.A.; Wood, P.R.; Nanni, A.; Imai, H.; Whitelock, P.A.; Matsuura, M.; Groenewegen, M.A.T.; et al. The wind speeds, dust content, and mass-loss rates of evolved AGB and RSG stars at varying metallicity. MNRAS 2017, 465, 403–433. [Google Scholar] [CrossRef]
- Bladh, S.; Höfner, S.; Aringer, B.; Eriksson, K. Exploring wind-driving dust species in cool luminous giants. III. Wind models for M-type AGB stars: Dynamic and photometric properties. A&A 2015, 575, A105. [Google Scholar] [CrossRef]
- Bladh, S.; Liljegren, S.; Höfner, S.; Aringer, B.; Marigo, P. An extensive grid of DARWIN models for M-type AGB stars. I. Mass-loss rates and other properties of dust-driven winds. A&A 2019, 626, A100. [Google Scholar] [CrossRef]
- Gros, M.; Crivellari, L.; Simonneau, E. An Implicit Integral Method to Solve Selected Radiative Transfer Problems. IV. The Case of Spherical Geometry. ApJ 1997, 489, 331–345. [Google Scholar] [CrossRef]
- Crivellari, L.; Cristallo, S.; Piersanti, L. Universe Letters. In Preparation. Available online: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.108.225301 (accessed on 25 March 2011).
- Ferrarotti, A.S.; Gail, H.P. Composition and quantities of dust produced by AGB-stars and returned to the interstellar medium. A&A 2006, 447, 553–576. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cristallo, S.; Piersanti, L.; Gobrecht, D.; Crivellari, L.; Nanni, A. AGB Stars and Their Circumstellar Envelopes. I. the VULCAN Code. Universe 2021, 7, 80. https://doi.org/10.3390/universe7040080
Cristallo S, Piersanti L, Gobrecht D, Crivellari L, Nanni A. AGB Stars and Their Circumstellar Envelopes. I. the VULCAN Code. Universe. 2021; 7(4):80. https://doi.org/10.3390/universe7040080
Chicago/Turabian StyleCristallo, Sergio, Luciano Piersanti, David Gobrecht, Lucio Crivellari, and Ambra Nanni. 2021. "AGB Stars and Their Circumstellar Envelopes. I. the VULCAN Code" Universe 7, no. 4: 80. https://doi.org/10.3390/universe7040080
APA StyleCristallo, S., Piersanti, L., Gobrecht, D., Crivellari, L., & Nanni, A. (2021). AGB Stars and Their Circumstellar Envelopes. I. the VULCAN Code. Universe, 7(4), 80. https://doi.org/10.3390/universe7040080






