Abstract
It is possible to empirically discriminate between the predictions of orthodox (i.e., Copenhagen) quantum theory and the de Broglie−Bohm theory of quantum mechanics. A practical experiment is proposed in which a single, laser-cooled ion inside an ultra-cold particle trap is either found to be near the trap’s walls or not. Detections of the former kind would support the prediction of orthodox quantum theory and of the latter kind would support the de Broglie−Bohm theory. The outcome of this experiment would show which theory gives the more correct description and, consequently, would have far-reaching implications for our understanding of quantum mechanics.
1. Introduction
The controversy over what quantum mechanics actually tells us about the physical world has been going on for over ninety years. This controversy is on-going because of a continuing dissatisfaction with nonempirical aspects of orthodox (i.e., Copenhagen) quantum mechanics. What has become obvious in the twenty-first century is that arguments over these nonempirical aspects are not going to persuade the majority of the physics community to accept any of the alternatives to orthodox quantum theory (OQT), even if an alternative provides a clearer perspective on the nature of quantum processes. The only way that the majority of physicists will accept an alternative to OQT is if that alternative theory can be shown to be empirically better.
One of the main alternatives to OQT is the de Broglie-Bohm (deBB) Theory of quantum mechanics. Contrary to a common misunderstanding, the deBB alternative is a theory in its own right and not just another interpretation of the quantum formalism. The question of whether deBB Theory or OQT is more correct remains unanswered [1,2,3,4]. If it could be shown that one of these theories is empirically superior to the other then this question would be essentially resolved.
Advances in quantum measurement technologies have rendered possible the realization of experiments that the founders of quantum mechanics would have considered only to be “gedanken-experiments” (e.g., tests of Bell’s Inequalities, detection of gravitational waves). In recent decades, the trapping of single quantum particles has been achieved and this too has greatly extended the scope of possible quantum measurements. These advances have reached a stage where it is possible to conduct a laboratory test which can distinguish between OQT and deBB Theory.
A proposal for an experimental test using the techniques of atom optics that can demonstrate which of these two theories provides better empirical outcomes was made some years ago [5]. The proposed test offers the possibility of delivering results with implications of enormous significance for our understanding of the fundamentals of quantum mechanics. The proposal was based on different predictions made by the two theories when quantum particles are within a sealed particle trap. However, the original testing proposal required a free-fall environment which made it impractical. A feasible version of this test is outlined.
2. Background
Any comparison of OQT and deBB Theory needs to first specify what they predict. The existence of particles is a case in point since some accounts of OQT maintain that a particle does not exist until it is “measured”. In order to ensure the presence of one or more quantum particles in the proposed experiment, it is sufficient that the quantum state inside a sealed particle trap be prepared using the well-known techniques of loading and trapping of quantum particles.
A sealed particle trap is modelled as a three-dimensional “infinite” potential well [6,7] with zero potential inside and “infinite” potential outside the well, i.e., the particle cannot escape. The wavefunction of a particle of mass m inside an “infinite” rectangular well of side lengths Lx, Ly, Lz with one corner taken as the origin of a Cartesian coordinate system has the simple form [6]:
where
is the system’s energy, with nx, ny, nz = 1, 2, 3, ...; ℏ is Planck’s constant divided by 2π; and t is time.
Ψnxnynz = (8/LxLyLz)1/2 sin(nxπx/Lx) sin(nyπy/Ly) sin(nzπz/Lz) exp (–iEt/ℏ)
E = Enxnynz = [(nx2/Lx2) + (ny2/Ly2) + (nz2/Lz2)] (π2ℏ2/2m) > 0
Since ∣Ψnxnynz∣2 > 0 for 0 < x < Lx, 0 < y < Ly, 0 < z < Lz, OQT predicts that there is a nonzero probability of detecting a particle at any position inside the potential well, including near its walls. As the ground state (nx = ny = nz = 1) energy is greater than zero, OQT predicts that a particle in the well will have a nonzero momentum value [8,9]. Nonzero momentum is also required by the Uncertainty Principle as understood in OQT [10].
In deBB Theory, a quantum particle has a definite position and momentum in all circumstances. The particle is guided by its accompanying matter wave, i.e., both wave and particle are accepted as physical entities. When the configuration wavefunction Ψ of a spinless particle is expressed in polar form: Ψ = R exp (iS/ℏ), where R and S are real-valued functions of the space and time coordinates, the momentum p of the particle is given by [11,12,13,14,15,16]:
where v is the particle’s velocity. Equation (3) is a key expression in this experimental proposal and the cited references confirm its validity in deBB Theory. (Note that the expression for the momentum of a nonzero spin particle will have a more complicated form.) The deBB Theory predicts that a spinless particle inside a three-dimensional “infinite” well is at rest (in the laboratory frame of reference). This outcome is found by substituting the S-function from Equation (1) into Equation (3), then:
i.e., the particle’s momentum is zero and therefore it is stationary. This does not violate the Uncertainty Principle as interpreted in deBB Theory [17].
p = mv = ∇S
p = ∇(–Et) = 0 = mv
The particle will be at rest because all of its (initial kinetic) energy has become stored as potential energy in the standing matter wave formed inside the well [17,18,19,20,21]. The particle being stationary is a clear and unambiguous theoretical prediction of deBB Theory (the energy calculation supporting this outcome appears in Appendix A). The zero momentum result holds for a system with many non-interacting, spinless particles and the corresponding relativistic calculation also gives zero momentum [22].
3. Original Testing Proposal
The novel (i.e., nonstandard) design of the proposed experiment is all-important. Standard measurement techniques (e.g., detection by irradiating quantum particles) introduce disturbances to a quantum system and thereby guarantee identical measurement outcomes for the two theories which is why a nonstandard technique is required. The original testing proposal was to use evanescent light on the inside of the transparent walls of a particle trap, generated by projecting laser beams on the outside of the trap’s walls at an angle greater than the critical angle (see Figure 1).
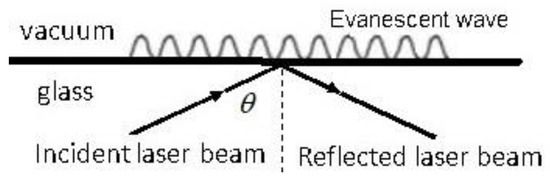
Figure 1.
An evanescent wave is formed on the vacuum side when θ > critical angle.
Neutral atoms in their lowest energy state initially placed in the center of the trap would be repelled if their motion took them into the evanescent waves without reaching the trap’s walls (i.e., the atoms would be reflected elastically). Atoms close to the interior surfaces of the trap would be detectable by small phase shifts in the laser beams reflected from any of the (glass) walls. These relevant phase shifts are due to changes in the refractive index because of the presence of particles near the walls in addition to the usual change of phase on reflection. This usual change of phase (δ) is a function of the angle of incidence θ and for transverse electric (TE) polarized light is given by [23]:
where n is the index of refraction of the glass forming the trap’s walls. The change in phase can be measured by interfering each reflected laser beam with a reference laser (see the extensive references listed in [5]) where the laser beams incident on the trap’s exterior surfaces have well-defined phases.
tan(δ/2) = −(sin2θ − n2)½/cosθ
Aspect et al. calculated for a trap wall forming a glass−vacuum interface, using transverse electric (TE) polarized lasers, the relevant phase shift (φ) of a reflected laser beam is [24]:
where p is the magnitude of the maximum momentum of the atoms, M is the atomic mass, λ is the incident laser wavelength, Γ is the natural linewidth of atomic transition, ρin is the incident density distribution of the “cloud” of atoms, κ = (2π/λ) (n2 sin2θ − 1)1/2, Isat = 2π2ℏΓc/3λ3, Iev = (4n cos2θ) IL/(n2 − 1), with IL being the intensity of the incident laser beam and c is the speed of light in a vacuum.
The results of measurements made on such a quantum system would supply an uncontroversial method of deciding between the theories. A series of measurements would be needed over the lifetime of the trap. Detection of the relevant phase shift (as given by Equation (6)) in one or more of the reflected laser beams would indicate that the OQT prediction is verified whilst an absence of this phase shift would indicate that the deBB Theory prediction is correct. The detection of these relevant phase shifts constitutes a quantum nondemolition measurement where no extra energy is imparted to the atoms, i.e., energy is not gained from the measurement apparatus. This is an instance of an exchange of quantum information between matter and light. The method proposed incorporates a fundamental difference between this experimental test and previous tests of quantum mechanics which have utilized standard quantum measurement techniques.
The original testing proposal also highlighted a number of technical issues. The issues which require addressing in order to successfully conduct the experiment are as follows:
- Effect of GravityGravity will affect an atom’s vertical motion resulting in the matter wave not forming a standing wave pattern. Unless the effects of gravity could be counteracted without affecting the stationary state, the experiment would need to be done in a free-fall environment. Performing the experiment in such an environment would introduce significant practical complications to its conduct and greatly increase its cost.
- Vibration EliminationVibrations of the walls of the particle trap have the tendency to disrupt the standing matter wave and possibly heat the atoms if they approach too near to the walls. This could be eliminated by cooling the trap’s walls close to absolute zero. External sources of vibration would also need to be avoided by acoustically, mechanically, and thermally isolating the apparatus.
- Homodyne DetectionEach of the incident laser beams used to generate the evanescent waves might be split into two parts with one part reflected from a wall of the trap and the other part used as a reference beam. This arrangement will greatly reduce fluctuations over what would result by having the reflected and reference beams produced by separate laser devices [25].
4. Discussion—A Feasible Test
Many complications would be avoided if the experiment was conducted only using a single particle. One reason for the use of neutral atoms in the original proposal was to have particles that do not affect each other. A practical version of the proposed experiment could be done with a single ion rather than a collection of atoms as there will not, obviously, be any interparticle interactions with just a single ion. This is a viable possibility as the methods for creating isolated, trapped, one-particle quantum systems are now firmly established [26,27,28,29,30,31].
A feasible version of the experiment would have a single ion in its lowest energy state placed at the center of a regular, ultra-cold particle trap. The use of a single ion has several advantages. An ion is easier to manipulate than a neutral atom and can be readily prepared in its lowest energy eigenstate. Since ascertaining that the ion is at rest (or not) is the experimental aim, just the detection (or otherwise) of a relevant phase shift would be sufficient. The use of a single ion will not affect the detection of any relevant phase shifts in the reflected laser beams as this only depends on a change in refractive index due to the presence of the ion near one of the trap’s walls. A detailed design of the experimental setup will, however, need to be done by leading experimentalists in the field of quantum/atom optics.
If the OQT prediction is correct, then there will be relevant phase shifts in some of the results obtained in a large series of sensitive measurements showing that the ion was detected near a wall (as this has a nonzero probability in OQT). If the deBB Theory prediction is correct, there will be no relevant phase shift as the ion would be stationary in a region away from the walls of the trap, i.e., there will not be anything to detect. Any doubts about this being the case should be dispelled when it is acknowledged that a faithful measurement and any consistent theory of measurement will both produce a zero result when there is nothing to measure.
The Earth’s gravitational field would not allow the creation of a standing matter wave unless the effects of gravity can be negated. However, as previously noted, the conduct of the experiment in a free-fall environment would render it impractical. The use of a single ion can get around this problem if the particle trap is embedded in a suitably sized and directed electric field. Such an electric field would counteract the force of gravity on the ion allowing a standing matter wave to be formed. Techniques for setting up and maintaining an electric field inside a particle trap are straight-forward [32,33]. The experiment could then be conducted in an ultra-cold particle trap at rest in the laboratory’s frame of reference.
5. Concluding Remarks
An outline of a feasible test of quantum theory using an ultra-cold particle trap has been provided. The use of a single trapped ion would allow for a basic version of the test to be practical where the single ion is either detected or not detected. Nevertheless, the test will be difficult to conduct requiring not only the highest resolution and accuracy available from laser interferometry but also a very specifically controlled environment for the particle trap. If this experiment is properly conducted then its results should empirically refute the prediction made by either OQT or deBB Theory.
Finally, an episode from the history of physics is worth recalling. In respect to the possibility of testing Bell’s Inequalities, it was stated by a prominent physicist in the 1960s that these inequalities were worth taking notice of but that no competent experimentalist would attempt to measure them [34]. Since the proposed test has the possibility of delivering an outcome with wide-ranging repercussions for our comprehension of fundamental quantum processes, quantum experimentalists should take care not to be similarly dissuaded from constructing a working laboratory version and conducting this test.
Funding
This research received no external funding.
Acknowledgments
The author thanks the Editor for the invitation to submit a contribution to this Special Issue of the journal and the reviewers for their comments.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
In deBB Theory: a particle of mass m is described by a quantum version of the Hamilton−Jacobi equation which is derived from the time-dependent Schrödinger equation [17,35]:
where V is any classical potential, and the last term is called the quantum potential energy Q. In the case of a particle inside a three-dimensional “infinite” well, its momentum and kinetic energy are both zero and the quantum potential energy Q corresponding to Equation (1) is found to be:
which is equal in magnitude to the particle’s energy as predicted by OQT (Equation (2)). This shows that, in deBB Theory, the particle’s kinetic energy is zero having been transformed into potential energy that is stored in the standing matter wave within the well and therefore why the particle is stationary.
Q = −(ℏ2/2m) (∇2R)/R = [(nx2/Lx2) + (ny2/Ly2) + (nz2/Lz2)] (π2ℏ2/2m)
References
- Cushing, J.T. Quantum Mechanics: Historical Contingency and the Copenhagen Hegemony; University of Chicago Press: Chicago, IL, USA, 1994; Chapter 9. [Google Scholar]
- Steward, E.G. Quantum Mechanics: Its Early Development and the Road to Entanglement and Beyond; Imperial College Press: London, UK, 2012; Section 12.4. [Google Scholar]
- Bricmont, J. The de Broglie–Bohm Theory as a Rational Completion of Quantum Mechanics. Can. J. Phys. 2018, 96, 379–390. [Google Scholar] [CrossRef]
- Sanz, A.S. Bohm’s Approach to Quantum Mechanics: Alternative Theory or Practical Picture? Front. Phys. 2019, 14, 11301. [Google Scholar] [CrossRef]
- Riggs, P.J. A Proposed Experimental Test of Orthodox Quantum Theory Using the Techniques of Atom Optics. arXiv 2014, arXiv:1411.0464. [Google Scholar]
- Basdevant, J.-L.; Dalibard, J. Quantum Mechanics; Springer: Berlin, Germany, 2002; p. 75. [Google Scholar]
- Rajasekar, S.; Velusamy, R. Quantum Mechanics I: The Fundamentals; CRC Press: Boca Raton, FL, USA, 2014; p. 107. [Google Scholar]
- Greenhow, R.C. Introductory Quantum Mechanics: A Computer Illustrated Text; Institute of Physics Publishing: Bristol, UK, 1990; p. 46. [Google Scholar]
- Green, N.J.B. Quantum Mechanics 1: Foundations; Oxford University Press: Oxford, UK, 2001; p. 40. [Google Scholar]
- Auletta, G.; Fortunato, M.; Parisi, G. Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2009; p. 115. [Google Scholar]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables I. Phys. Rev. 1952, 85, 166–179. [Google Scholar] [CrossRef]
- Holland, P.R. The Quantum Theory of Motion: An Account of the de Broglie-Bohm Causal Interpretation of Quantum Mechanics; Cambridge University Press: Cambridge, UK, 1993; p. 73. [Google Scholar]
- Cushing, J.T. Quantum Mechanics; University of Chicago Press: Chicago, IL, USA, 1994; pp. 61–62. [Google Scholar]
- Wyatt, R.E. Quantum Dynamics with Trajectories: Introduction to Quantum Hydrodynamics; Springer: Berlin, Germany, 2005; p. 48. [Google Scholar]
- Riggs, P.J. Quantum Causality: Conceptual Issues in the Causal Theory of Quantum Mechanics; Springer: Dordrecht, The Netherlands, 2009; p. 54. [Google Scholar]
- Sanz, A.S.; Miret-Artés, S. A Trajectory Description of Quantum Processes I: Fundamentals; Springer: Berlin, Germany, 2012; p. 196. [Google Scholar]
- Holland, P.R. The Quantum Theory of Motion; Cambridge University Press: Cambridge, UK, 1993; p. 365. [Google Scholar]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables II. Phys. Rev. 1952, 85, 180–193. [Google Scholar] [CrossRef]
- Riggs, P.J. Quantum Causality; Springer: Dordrecht, The Netherlands, 2009; pp. 111–112. [Google Scholar]
- Oriols, X.; Mompart, J. (Eds.) Overview of Bohmian Mechanics. In Applied Bohmian Mechanics: From Nanoscale Systems to Cosmology; Pan Stanford Publishing: Singapore, 2012; pp. 99–100. [Google Scholar]
- Benseny, A.; Albareda, G.; Sanz, A.S.; Mompart, J.; Oriols, X. Applied Bohmian Mechanics. Eur. Phys. J. D 2014, 68, 286–328. [Google Scholar] [CrossRef]
- Khodagholizadeh, J.; Kazem, J.; Babazadeh, A. Relativistic Bohmian Mechanics. arXiv 2014, arXiv:1405.3822v2. [Google Scholar]
- Smith, F.G.; King, T.A.; Wilkins, D. Optics and Photonics: An Introduction, 2nd ed.; Wiley: Chichester, UK, 2007; p. 124. [Google Scholar]
- Aspect, A.; Kaiser, R.; Vansteenkiste, N.; Vignolo, P.; Westbrook, C.I. Nondestructive Detection of Atoms Bouncing on an Evanescent Wave. Phys. Rev. A 1995, 52, 4704–4708. [Google Scholar] [CrossRef] [PubMed]
- Welsch, D.-G.; Vogel, W.; Opatrný, T. Homodyne Detection and Quantum State Reconstruction. Prog. Opt. 1999, 39, 63–211. [Google Scholar]
- Roy, A.; Jing, A.B.S.; Barrett, M.D. The Trapping and Detection of Single Atoms Using a Spherical Mirror. New J. Phys. 2012, 14, 093007. [Google Scholar] [CrossRef]
- Carpentier, A.V.; Fung, Y.H.; Sompet, P.; Hilliard, A.J.; Walker, T.G.; Andersen, M.F. Preparation of a Single Atom in an Optical Microtrap. Laser Phys. Lett. 2013, 10, 125501. [Google Scholar] [CrossRef]
- Haroche, S. Nobel Lecture: Controlling Photons in a Box and Exploring the Quantum to Classical Boundary. Rev. Mod. Phys. 2013, 85, 1083–1102. [Google Scholar] [CrossRef]
- Han, H.S.; Yoon, S.; Cho, D. Detection of a Single Lithium Atom in a Magneto-optical Trap. J. Korean Phys. Soc. 2015, 66, 1675. [Google Scholar] [CrossRef]
- Ott, H. Single Atom Detection in Ultracold Quantum Gases: A Review of Current Progress. Rep. Prog. Phys. 2016, 79, 054401. [Google Scholar] [CrossRef] [PubMed]
- Mauranyapin, N.P.; Madsen, L.S.; Taylor, M.A.; Waleed, M.; Bowen, W.P. Evanescent Single-Molecule Biosensing with Quantum-Limited Precision. Nat. Photonics 2017, 11, 477–481. [Google Scholar] [CrossRef]
- Fritioff, T.; Bergström, I.; Nagya, S.; Solders, A.; Suhonen, M.; Schuch, R. Precise measurements of ionic masses for QED tests. IJMS 2006, 251, 281–285. [Google Scholar] [CrossRef]
- Hobein, M.; Solders, A.; Liu, Y.; Ketelaer, J.; Suhonen Linné, M.; Marx, G.; Schuch, R. SMILETRAP II. Hyperfine Interact. 2011, 199, 141–150. [Google Scholar] [CrossRef]
- Wick, D. The Infamous Boundary: Seven Decades of Controversy in Quantum Physic; Birkhäuser: Boston, MA, USA, 1995; p. 105. [Google Scholar]
- Wyatt, R.E. Quantum Dynamics with Trajectories; Springer: Berlin, Germany, 2005; pp. 56–57. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).