Gravitational Interaction in the Chimney Lattice Universe †
Abstract
1. Introduction
2. Methods
The Model and Basic Equations
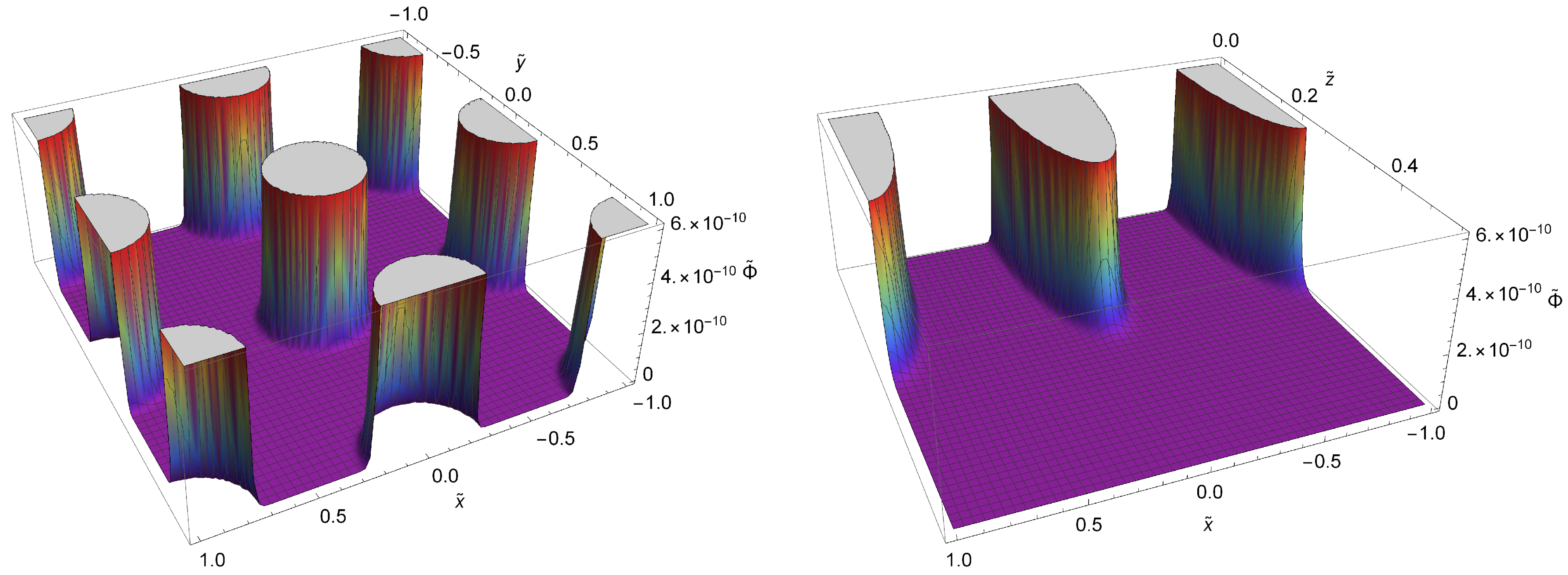
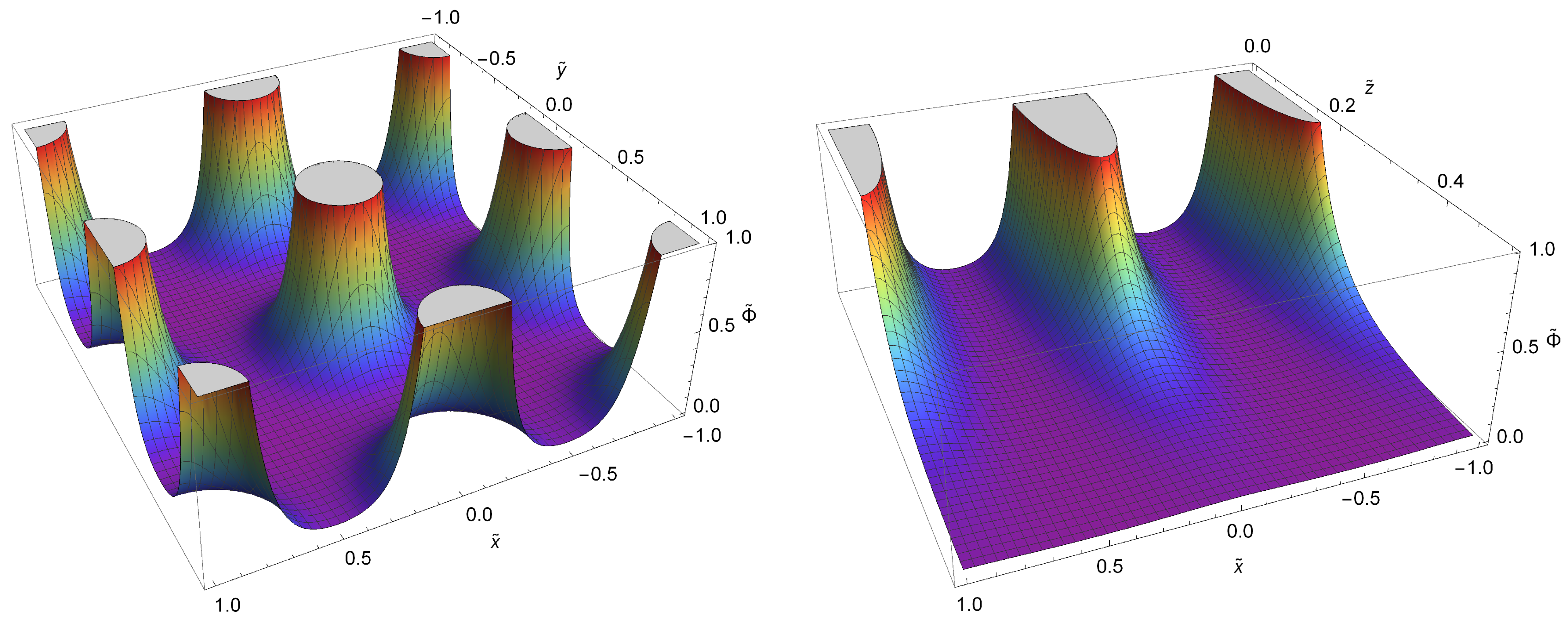
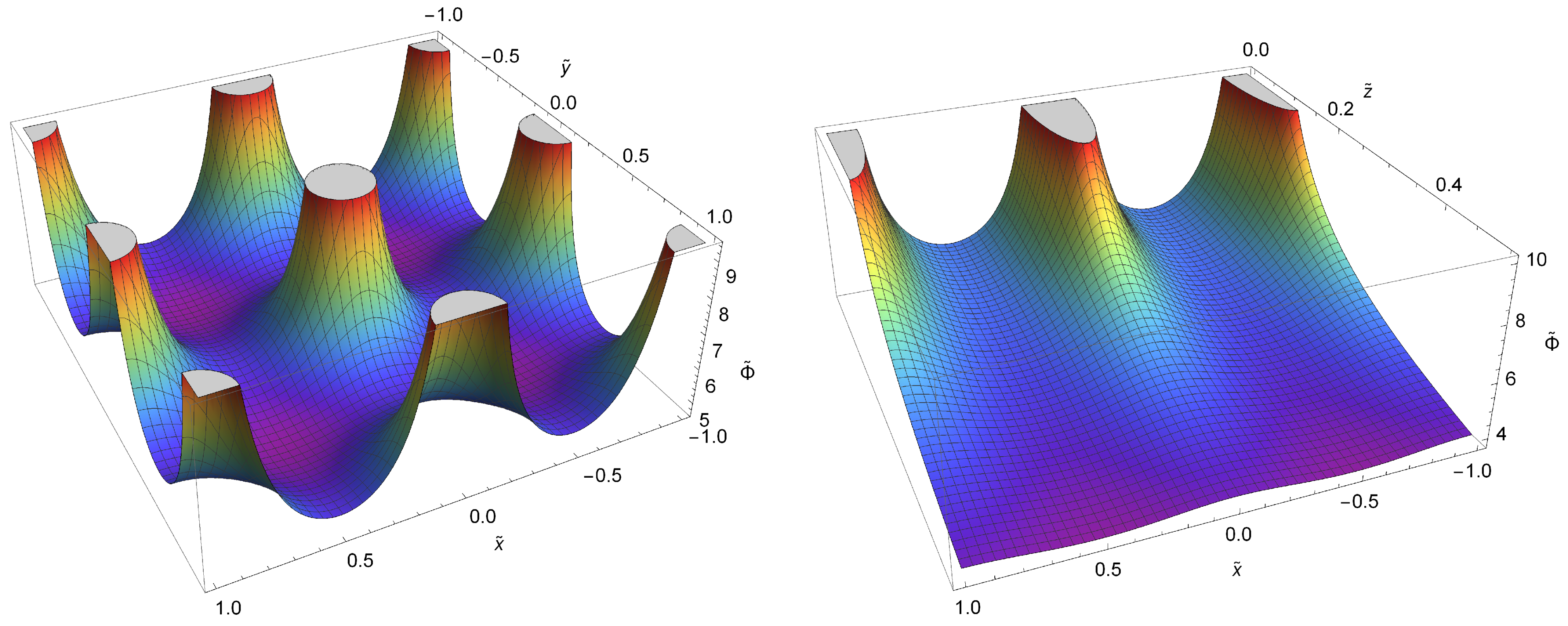
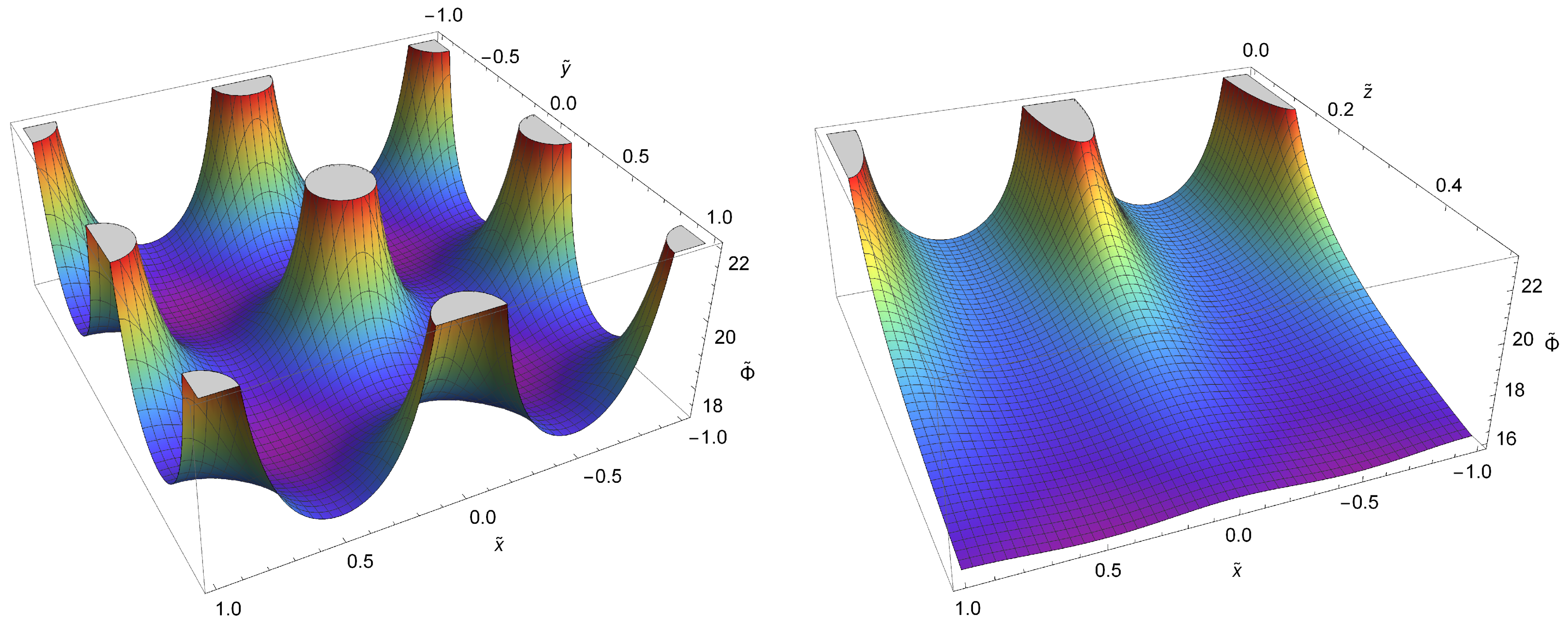
3. Results
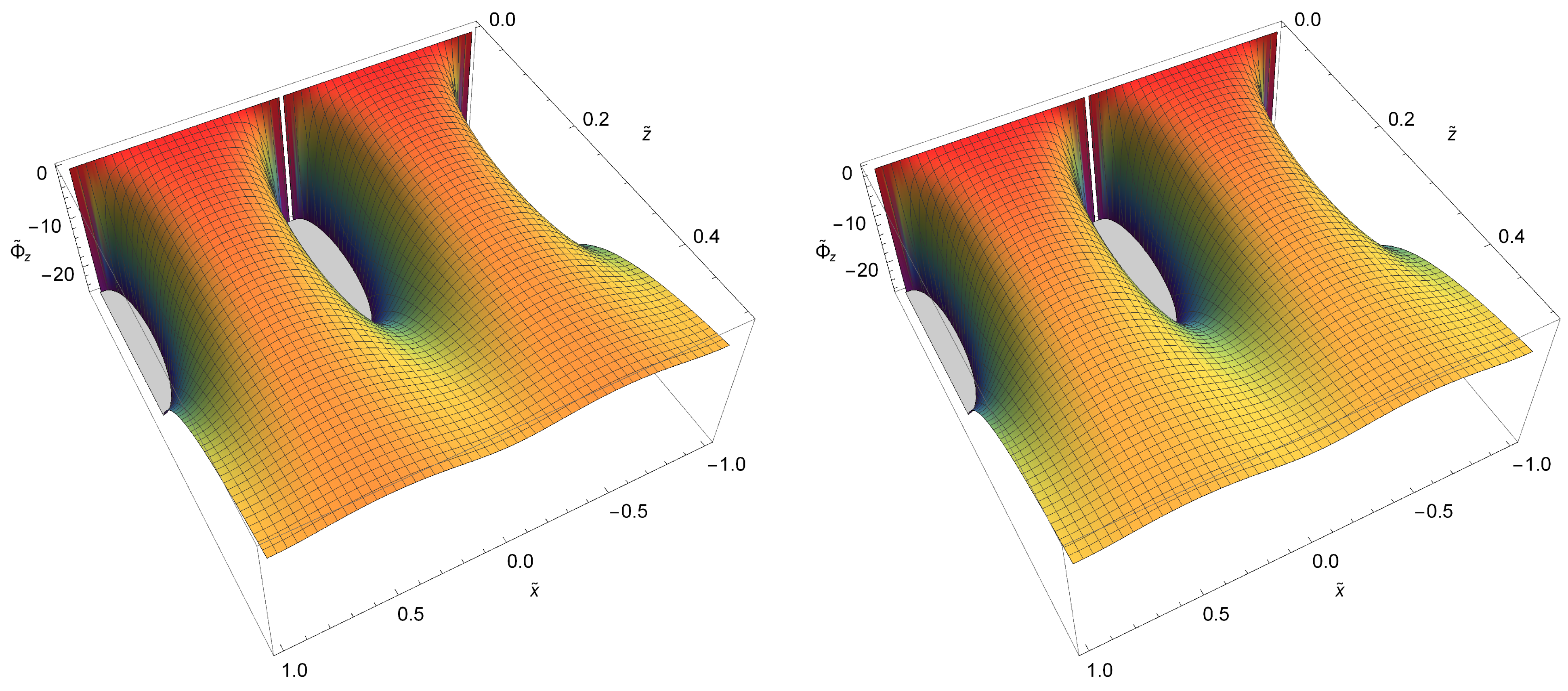
3.1. Gravitational Potentials
3.2. Gravitational Forces
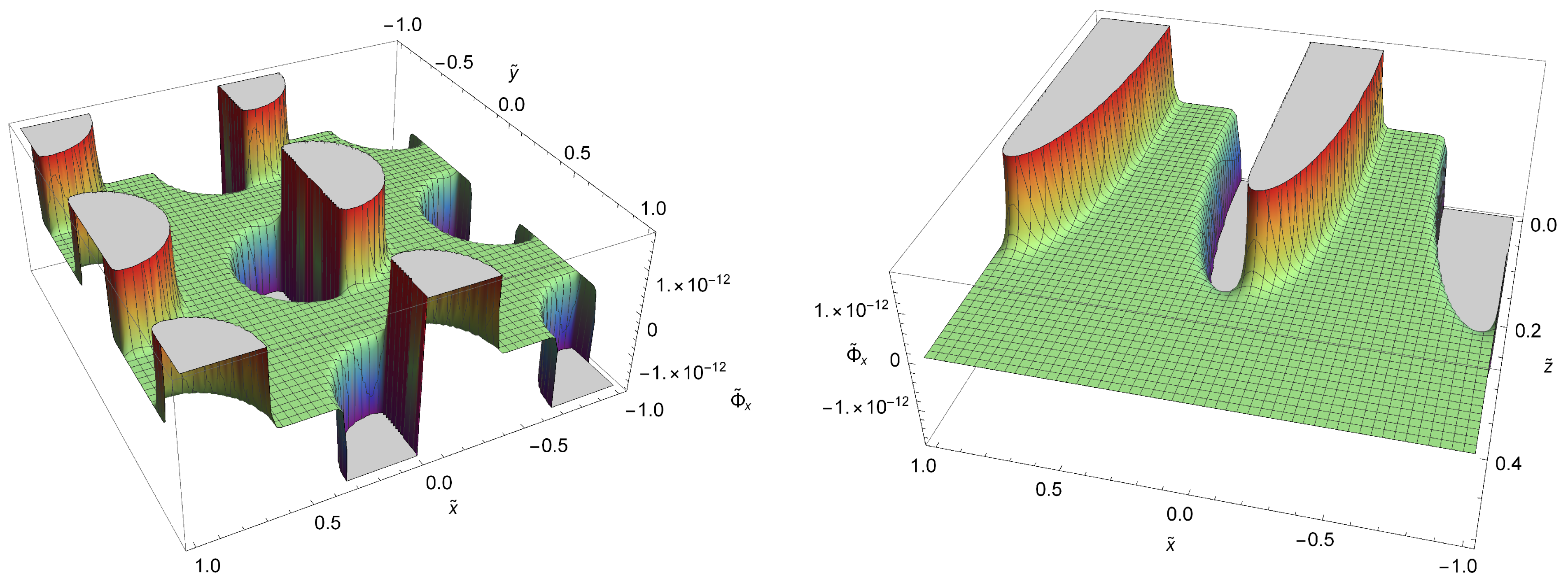
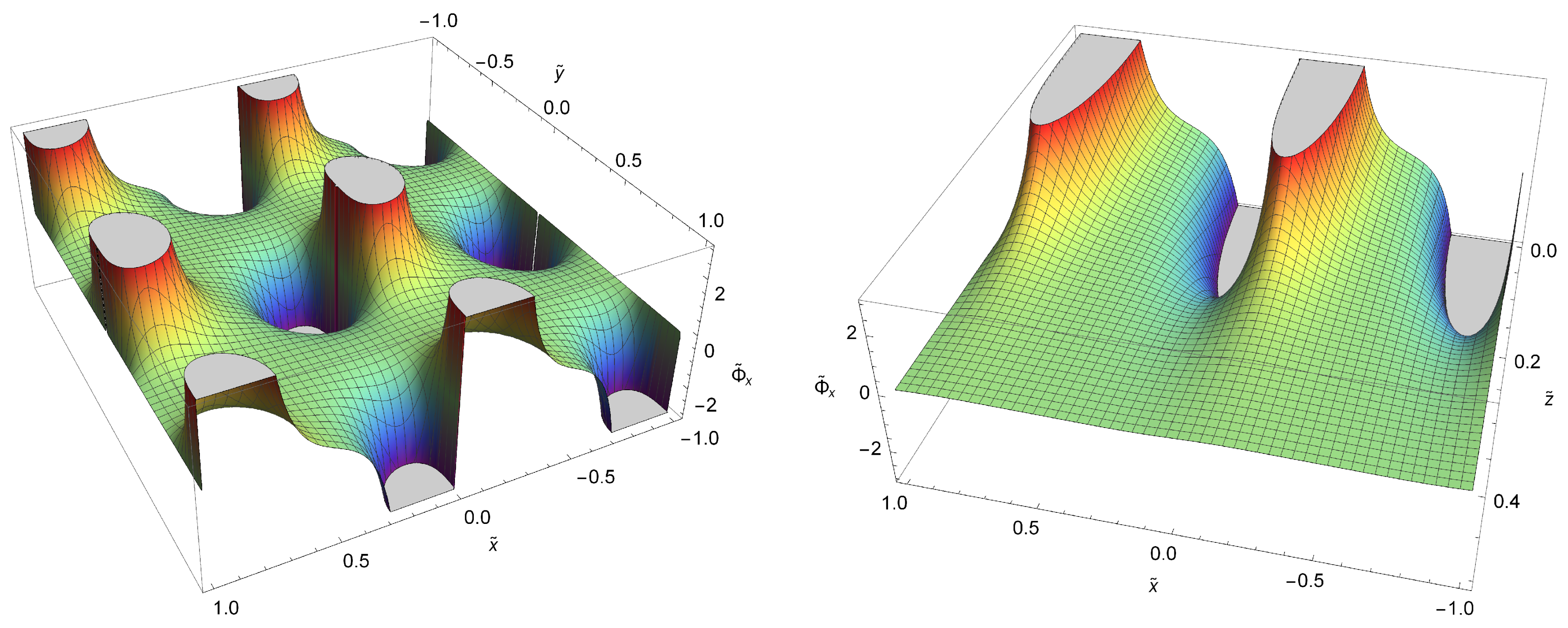
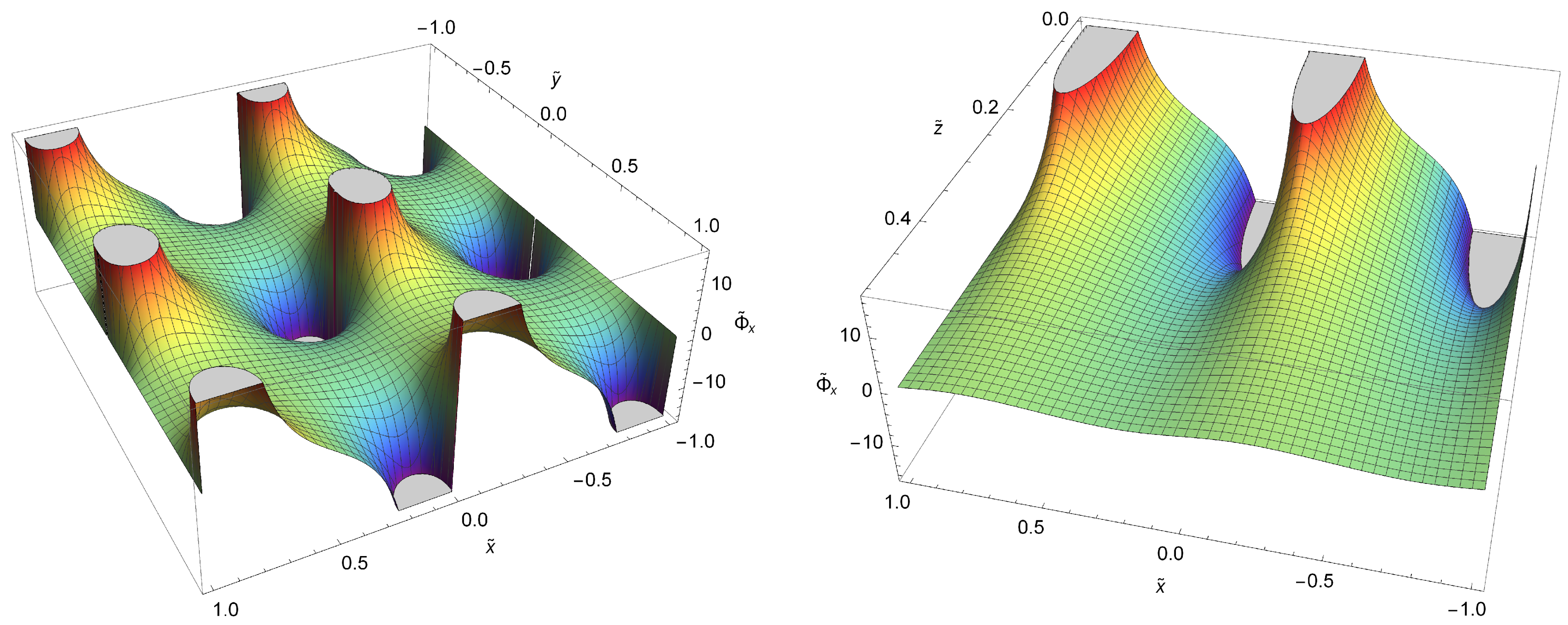
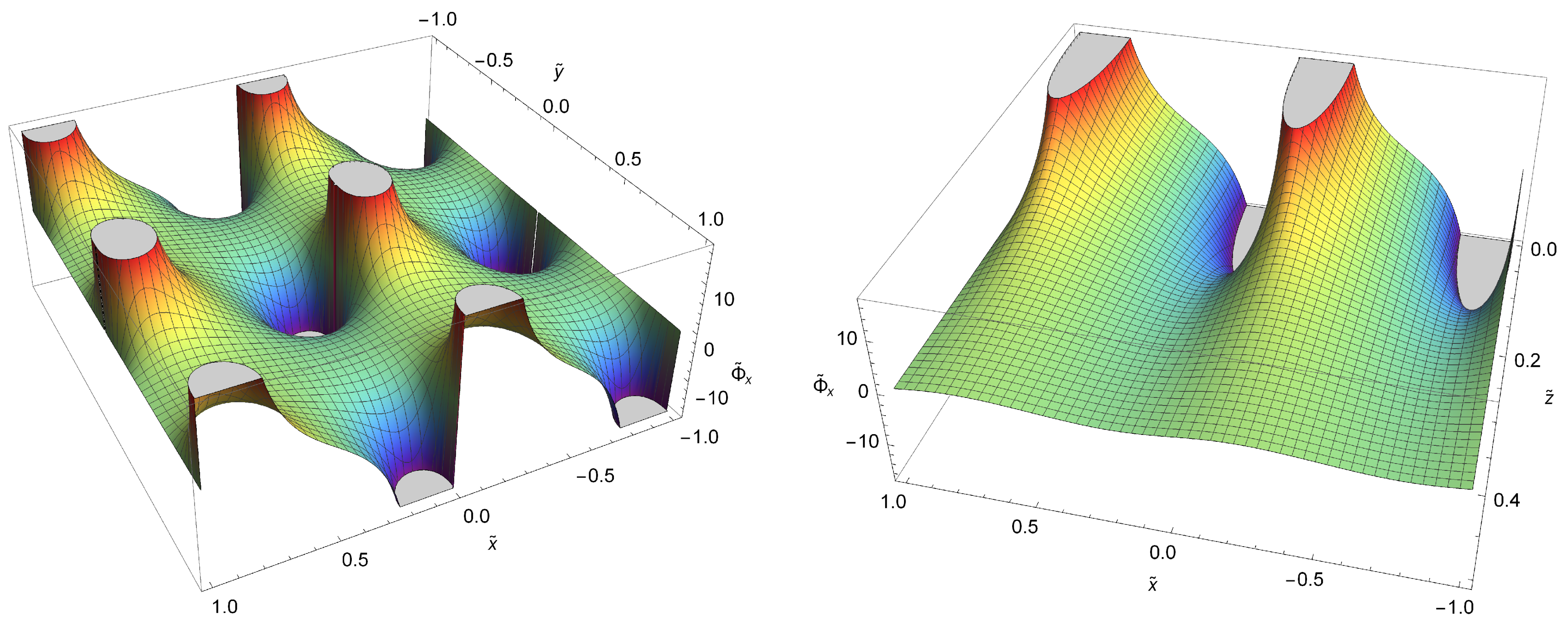
3.2.1. x-Component of the Gravitational Force
3.2.2. z-Component of the Gravitational Force
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gannon, D. Singularities in nonsimply connected space-times. J. Math. Phys. 1975, 16, 2364. [Google Scholar] [CrossRef]
- Ade, P.A.R.; et al. [Planck Collaboration] Planck 2013 results. XXVI. Background geometry and topology of the Universe. Astron. Astrophys. 2014, 571, A26. [Google Scholar]
- Luminet, J.-P. The shape and topology of the Universe. arXiv 2008, arXiv:0802.2236. [Google Scholar]
- Roukema, B.F. Topology of the Universe: Background and recent observational approaches. Pramana 1999, 53, 945–949. [Google Scholar] [CrossRef][Green Version]
- Piechocki, W. Topology of the Universe. arXiv 1999, arXiv:gr-qc/9910055. [Google Scholar]
- Bielewicz, P.; Riazuelo, A. The study of topology of the universe using multipole vectors. Mon. Not. R. Astron. Soc. 2009, 396, 609–623. [Google Scholar] [CrossRef]
- Bielewicz, P.; Banday, A.J.; Gorski, K.M. Constraining the topology of the Universe using the polarized CMB maps. Mon. Not. R. Astron. Soc. 2012, 421, 1064–1072. [Google Scholar] [CrossRef]
- Vaudrevange, P.M.; Starkman, G.D.; Cornish, N.J.; Spergel, D.N. Constraints on the topology of the Universe: Extension to general geometries. Phys. Rev. D 2012, 86, 083526. [Google Scholar] [CrossRef]
- Fabre, O.; Prunet, S.; Uzan, J.-P. Topology beyond the horizon: How far can it be probed? Phys. Rev. D 2015, 92, 043003. [Google Scholar] [CrossRef]
- Bucher, M.; et al. [Planck Collaboration] Planck 2015 results. XVIII. Background geometry and topology. Astron. Astrophys. 2016, 594, A18. [Google Scholar]
- Bielewicz, P.; Banday, A.J. Constraints on the topology of the Universe derived from the 7-year WMAP data. Mon. Not. R. Astron. Soc. 2011, 412, 2104–2110. [Google Scholar] [CrossRef]
- Bielewicz, P.; Banday, A.J.; Gorski, K.M. Constraints on the topology of the Universe derived from the 7-year WMAP CMB data and prospects of constraining the topology using CMB polarization maps. In Proceedings of the XLVIIth Rencontres de Moriond, La Tuile, Italy, 3–10 March 2012; Auge, E., Dumarchez, J., Tran Thanh Van, J., Eds.; ARISF: Paris, France, 2012; p. 91. [Google Scholar]
- Luminet, J.P.; Weeks, J.R.; Riazuelo, A.; Lehoucq, R.; Uzan, J.P. Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background. Nature 2003, 425, 593–595. [Google Scholar] [CrossRef] [PubMed]
- Aslanyan, G.; Manohar, A.V. The topology and size of the Universe from the Cosmic Microwave Background. J. Cosmol. Astropart. Phys. 2012, 06, 003. [Google Scholar] [CrossRef]
- Floratos, E.G.; Leontaris, G.K. On topological modifications of Newton’s law. J. Cosmol. Astropart. Phys. 2012, 2012, 24. [Google Scholar] [CrossRef]
- Aslanyan, G.; Manohar, A.V.; Yadav, A.P.S. The topology and size of the Universe from CMB temperature and polarization data. J. Cosmol. Astropart. Phys. 2013, 2013, 9. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Large-Scale Structure of the Universe; Princeton University Press: Princeton, NJ, USA, 1980. [Google Scholar]
- Brilenkov, M.; Eingorn, M.; Zhuk, A. Lattice Universe: Examples and problems. Eur. Phys. J. C 2015, 75, 217. [Google Scholar] [CrossRef] [PubMed]
- Eingorn, M. First-order cosmological perturbations engendered by point-like masses. Astrophys. J. 2016, 825, 84. [Google Scholar] [CrossRef]
- Eingorn, M.; Kiefer, C.; Zhuk, A. Scalar and vector perturbations in a universe with discrete and continuous matter sources. J. Cosmol. Astropart. Phys. 2016, 2016, 32. [Google Scholar] [CrossRef]
- Eingorn, M.; Kiefer, C.; Zhuk, A. Cosmic screening of the gravitational interaction. Int. J. Mod. Phys. D 2017, 26, 1743012. [Google Scholar] [CrossRef]
- Eingorn, M.; McLaughlin II, A.; Canay, E.; Brilenkov, M.; Zhuk, A. Gravitation in the space with chimney topology. In Proceedings of the 1st Electronic Conference on Universe, online, 22–28 February 2021. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Course of Theoretical Physics Series, V.2; Pergamon Press: Oxford, UK, 2000. [Google Scholar]
- Mukhanov, V.F. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Gorbunov, D.S.; Rubakov, V.A. Introduction to the Theory of the Early Universe: Cosmological Perturbations and Inflationary Theory; World Scientific: Singapore, 2011. [Google Scholar]
- Eingorn, M. Cosmological law of universal gravitation. Int. J. Mod. Phys. D 2017, 26, 1750121. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Volume 2. Special Functions; Gordon and Breach Science Publishers: New York, NY, USA, 1992. [Google Scholar]
- Eingorn, M.; Brilenkov, M.; Vlahovic, B. Zero average values of cosmological perturbations as an indispensable condition for the theory and simulations. Eur. Phys. J. C 2015, 75, 381. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Canay, E.; Eingorn, M. Duel of cosmological screening lengths. Phys. Dark Universe 2020, 29, 100565. [Google Scholar] [CrossRef]
- Mazars, M. Ewald sums for Yukawa potentials in quasi-two-dimensional systems. J. Chem. Phys. 2007, 126, 056101. [Google Scholar] [CrossRef] [PubMed]
- Mazars, M. Yukawa potentials in systems with partial periodic boundary conditions I: Ewald sums for quasi-two dimensional systems. Mol. Phys. 2007, 105, 1909–1925. [Google Scholar] [CrossRef][Green Version]
- Wolfram Research, Inc. Mathematica; Version 11.3; Wolfram Research, Inc.: Champaign, IL, USA, 2018. [Google Scholar]

| 0.5 | 0 | 0.5 | 2 | 1007 | 2 | 0.5 | 0 | 0.5 | 7 | 40 | 7 | ||||
| 0.5 | 0 | 0.1 | 2 | — | 2 | 0.5 | 0 | 0.1 | 6 | 808 | 6 | ||||
| 0.5 | 0 | 0 | 2 | — | 2 | 0.5 | 0 | 0 | 4 | — | 4 | ||||
| 0.1 | 0 | 0.5 | 1 | 187 | 1 | 0.1 | 0 | 0.5 | 4 | 28 | 4 | ||||
| 0.1 | 0 | 0.1 | 1 | 2119 | 1 | 0.1 | 0 | 0.1 | 1 | 380 | 1 | ||||
| 0.1 | 0 | 0 | 1 | — | 1 | 0.1 | 0 | 0 | 1 | — | 1 | ||||
| 0 | 0 | 0.5 | 1 | 236 | 1 | 0 | 0 | 0.5 | 4 | 37 | 4 | ||||
| 0 | 0 | 0.1 | 1 | 1479 | 1 | 0 | 0 | 0.1 | 1 | 490 | 1 |
| 0.5 | 0 | 0.5 | 174 | 9 | 15 | 0.5 | 0 | 0.5 | 1418 | 7 | 6 | ||||
| 0.5 | 0 | 0.1 | 163 | 229 | 15 | 0.5 | 0 | 0.1 | 1379 | 120 | 9 | ||||
| 0.5 | 0 | 0 | 163 | — | 15 | 0.5 | 0 | 0 | 1377 | — | 9 | ||||
| 0.1 | 0 | 0.5 | 171 | 10 | 13 | 0.1 | 0 | 0.5 | 1411 | 8 | 6 | ||||
| 0.1 | 0 | 0.1 | 133 | 164 | 11 | 0.1 | 0 | 0.1 | 1290 | 138 | 9 | ||||
| 0.1 | 0 | 0 | 123 | — | 10 | 0.1 | 0 | 0 | 1242 | — | 9 | ||||
| 0 | 0 | 0.5 | 170 | 13 | 13 | 0 | 0 | 0.5 | 1410 | 8 | 7 | ||||
| 0 | 0 | 0.1 | 123 | 357 | 9 | 0 | 0 | 0.1 | 1243 | 286 | 9 |
| 0.1 | 0 | 0.5 | 1 | 263 | 1 | 0.1 | 0 | 0.5 | 5 | 54 | 5 | ||||
| 0.1 | 0 | 0.1 | 1 | 2448 | 1 | 0.1 | 0 | 0.1 | 1 | 592 | 1 | ||||
| 0.1 | 0 | 0 | 1 | — | 1 | 0.1 | 0 | 0 | 1 | — | 1 |
| 0.1 | 0 | 0.5 | 130 | 38 | 21 | 0.1 | 0 | 0.5 | 862 | 38 | 21 | ||||
| 0.1 | 0 | 0.1 | 20 | 553 | 9 | 0.1 | 0 | 0.1 | 77 | 552 | 13 | ||||
| 0.1 | 0 | 0 | 19 | — | 8 | 0.1 | 0 | 0 | 34 | — | 9 |
| 0.5 | 0 | 0.5 | 2 | 1070 | 2 | 0.5 | 0 | 0.5 | 6 | 47 | 6 | ||||
| 0.5 | 0 | 0.1 | 2 | — | 2 | 0.5 | 0 | 0.1 | 2 | 1647 | 2 | ||||
| 0.1 | 0 | 0.5 | 1 | 187 | 1 | 0.1 | 0 | 0.5 | 2 | 33 | 2 | ||||
| 0.1 | 0 | 0.1 | 1 | 2228 | 1 | 0.1 | 0 | 0.1 | 1 | 649 | 1 | ||||
| 0 | 0 | 0.5 | 1 | 240 | 1 | 0 | 0 | 0.5 | 3 | 44 | 3 | ||||
| 0 | 0 | 0.1 | 1 | 1620 | 1 | 0 | 0 | 0.1 | 1 | 722 | 1 |
| 0.5 | 0 | 0.5 | 85 | 21 | 15 | 0.5 | 0 | 0.5 | 444 | 21 | 11 | ||||
| 0.5 | 0 | 0.1 | 64 | 900 | 15 | 0.5 | 0 | 0.1 | 331 | 863 | 13 | ||||
| 0.1 | 0 | 0.5 | 74 | 20 | 13 | 0.1 | 0 | 0.5 | 397 | 19 | 9 | ||||
| 0.1 | 0 | 0.1 | 15 | 444 | 5 | 0.1 | 0 | 0.1 | 57 | 444 | 8 | ||||
| 0 | 0 | 0.5 | 73 | 26 | 13 | 0 | 0 | 0.5 | 392 | 24 | 12 | ||||
| 0 | 0 | 0.1 | 8 | 678 | 4 | 0 | 0 | 0.1 | 21 | 677 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eingorn, M.; McLaughlin, A., II; Canay, E.; Brilenkov, M.; Zhuk, A. Gravitational Interaction in the Chimney Lattice Universe. Universe 2021, 7, 101. https://doi.org/10.3390/universe7040101
Eingorn M, McLaughlin A II, Canay E, Brilenkov M, Zhuk A. Gravitational Interaction in the Chimney Lattice Universe. Universe. 2021; 7(4):101. https://doi.org/10.3390/universe7040101
Chicago/Turabian StyleEingorn, Maxim, Andrew McLaughlin, II, Ezgi Canay, Maksym Brilenkov, and Alexander Zhuk. 2021. "Gravitational Interaction in the Chimney Lattice Universe" Universe 7, no. 4: 101. https://doi.org/10.3390/universe7040101
APA StyleEingorn, M., McLaughlin, A., II, Canay, E., Brilenkov, M., & Zhuk, A. (2021). Gravitational Interaction in the Chimney Lattice Universe. Universe, 7(4), 101. https://doi.org/10.3390/universe7040101






