Physical Acceptability of the Renyi, Tsallis and Sharma-Mittal Holographic Dark Energy Models in the f(T,B) Gravity under Hubble’s Cutoff
Abstract
1. Introduction
2. The Gravity Field Equations
3. Metric, Friedman-Like Equations and Power Law Expansion Solutions
4. Physical Acceptability of the Gravity Holographic Dark Energy Models
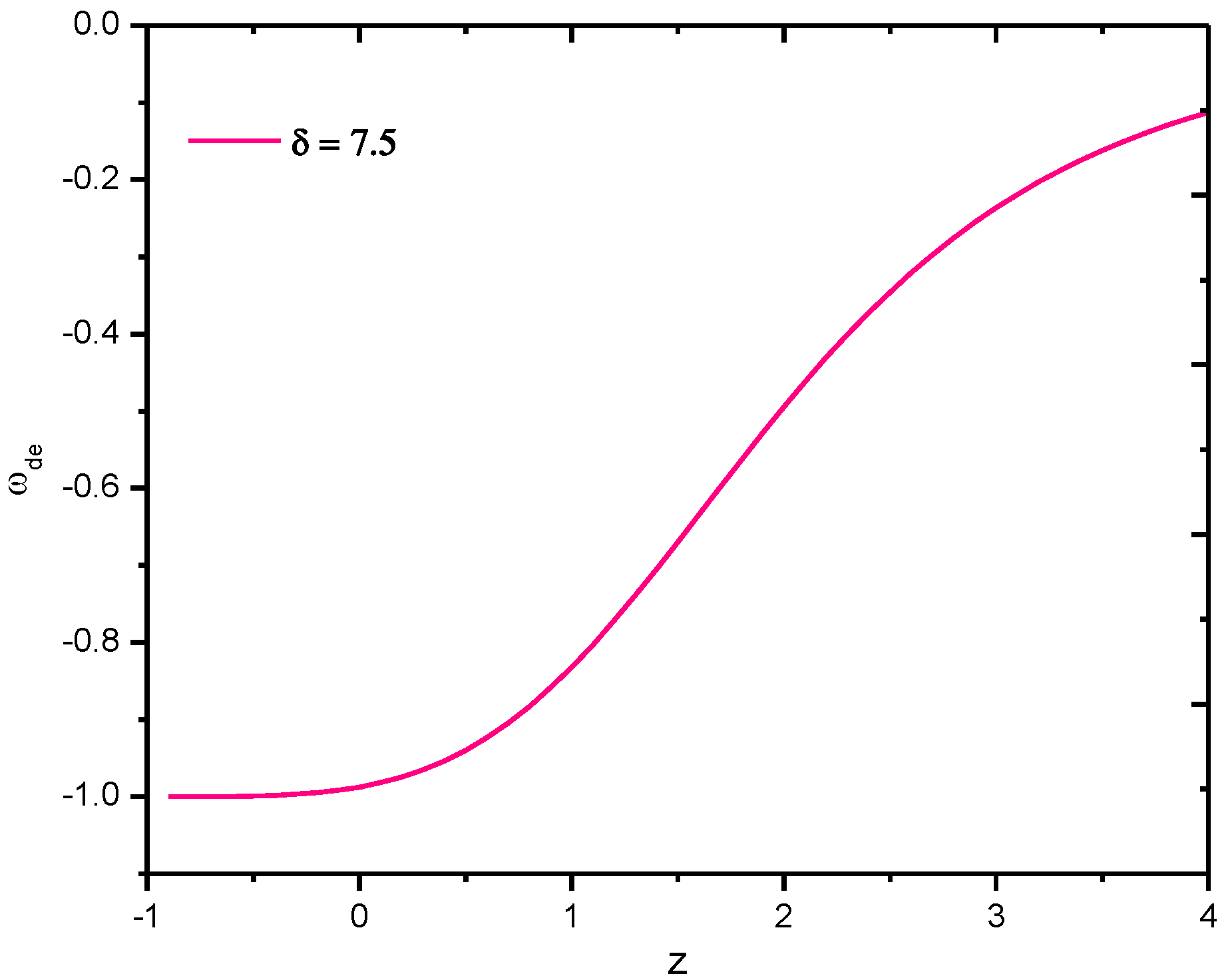
4.1. Renyi Holographic Dark Energy Model with Hubble’s Horizon Cutoff
4.2. Tsallis Holographic Dark Energy Model with Hubble’s Horizon Cutoff
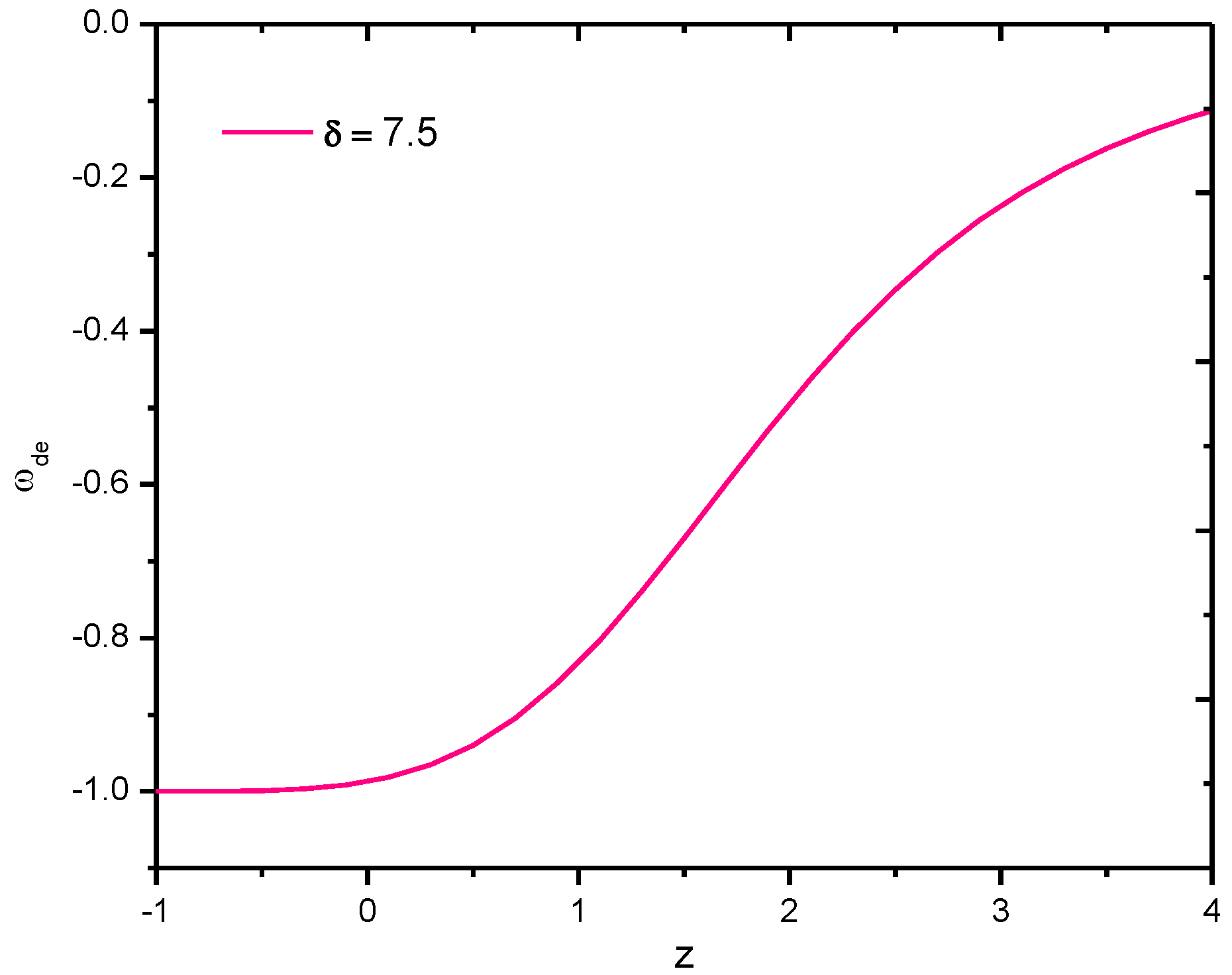
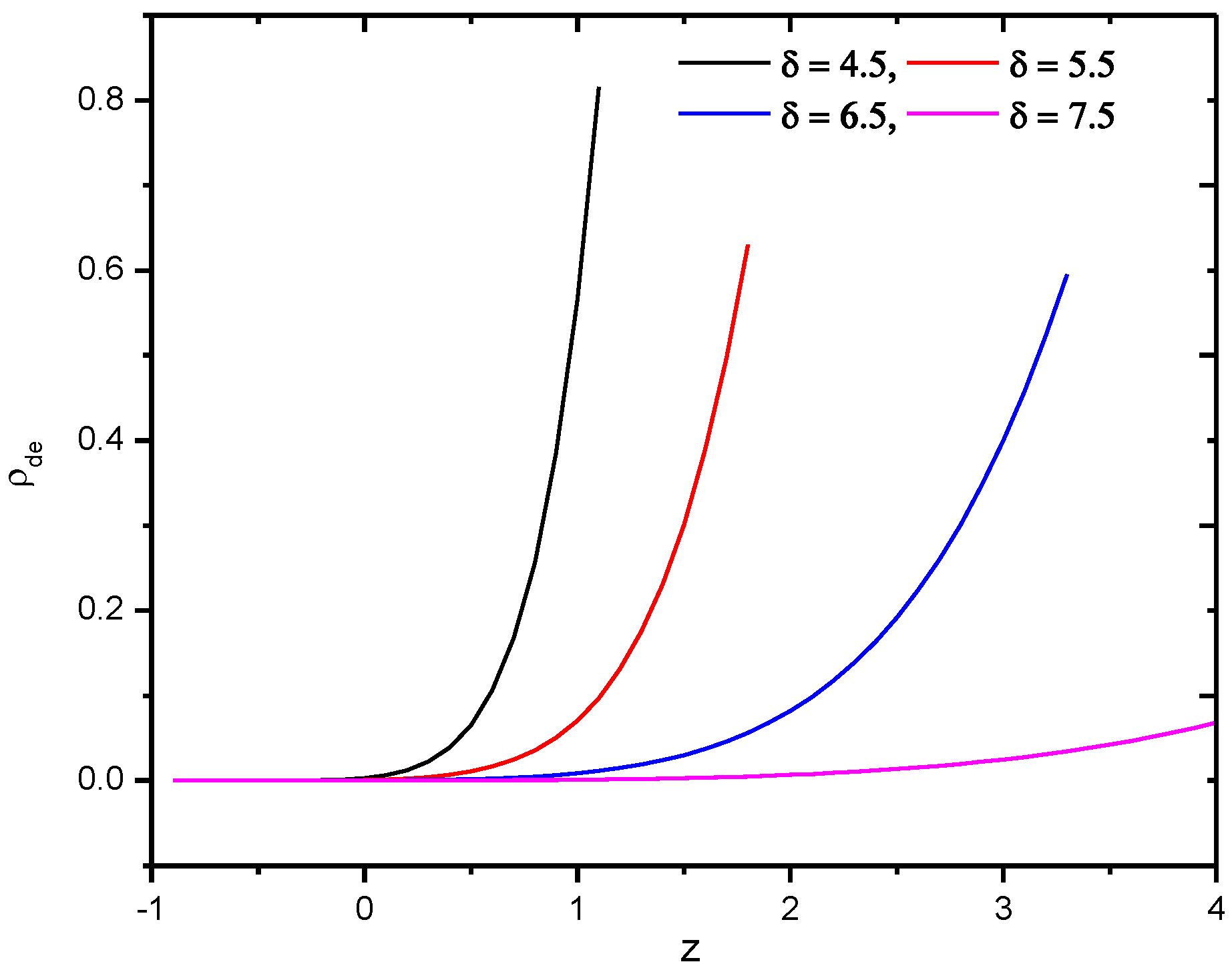
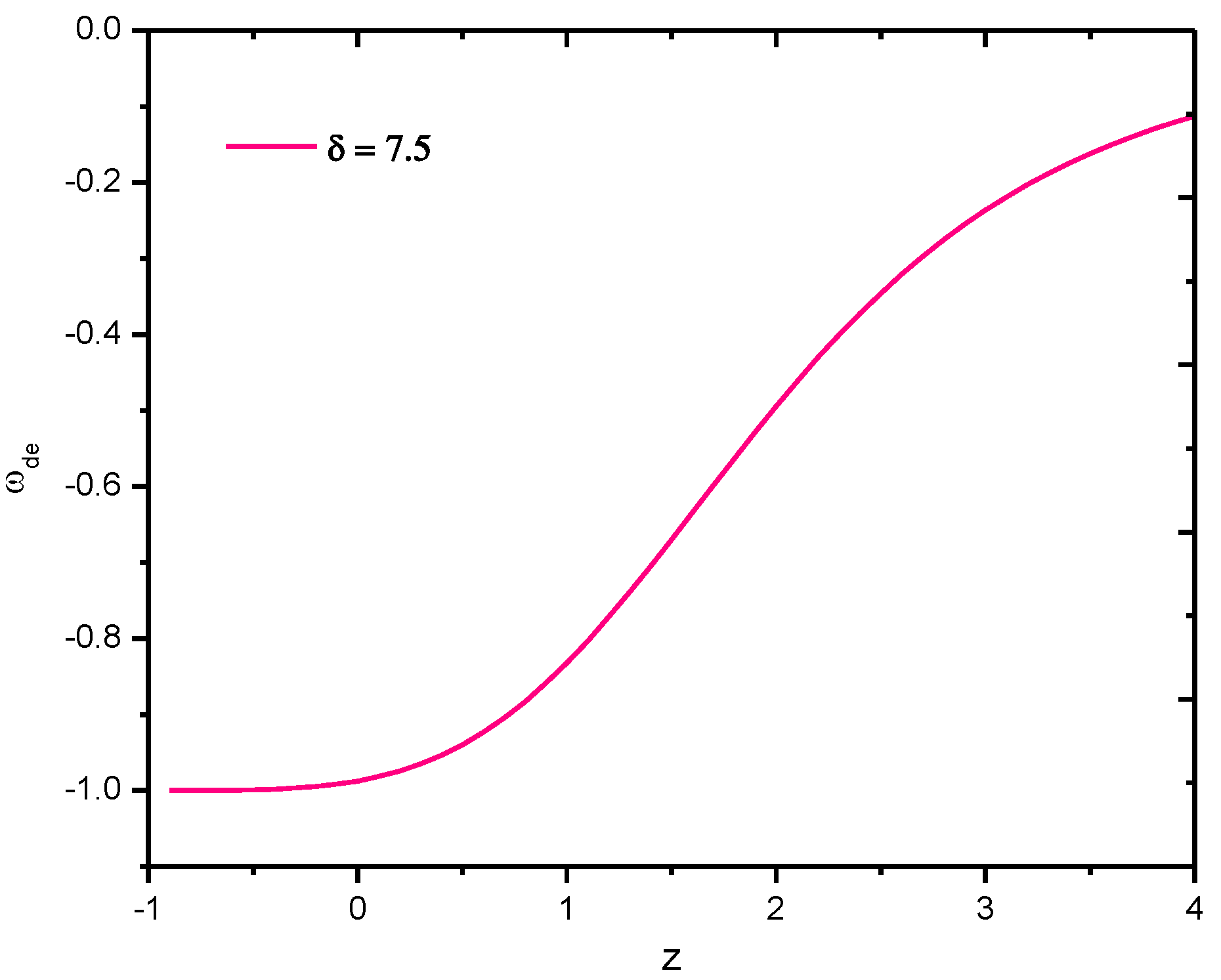
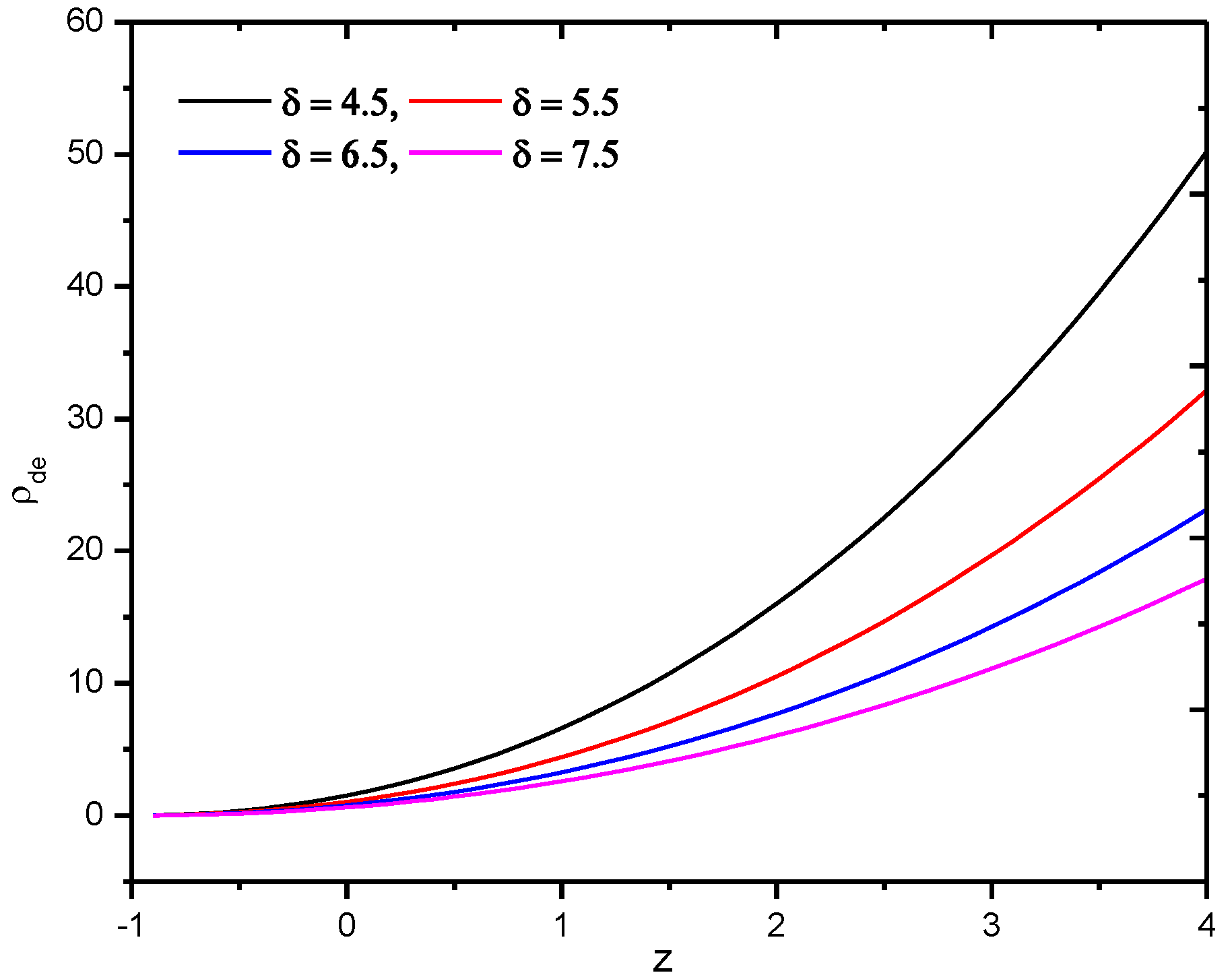
4.3. Sharma–Mittal Holographic Dark Energy Model with Hubble’s Horizon Cutoff
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Riess, A.G.; Strolger, L.-G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia Supernova Discoveries at z>1 from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665. [Google Scholar] [CrossRef]
- Astier, P.; Pain, R. Observational evidence of the accelerated expansion of the universeL’acceleration de l’expansion de l’Univers du point de vue de l’observation. Compt. Rend. Phys. 2012, 13, 521–538. [Google Scholar] [CrossRef]
- Yu, H.-R.; Zhang, T.-J.; Pen, U.-L. Method for Direct Measurement of Cosmic Acceleration by 21-cm Absorption Systems. Phys. Rev. Lett. 2014, 113, 041303. [Google Scholar] [CrossRef] [PubMed]
- Haridasu, B.S.; Luković, V.V.; D’Agostino, R.; Vittorio, N. Strong evidence for an accelerating Universe. Astron. Astrophys. 2017, 600, L1. [Google Scholar] [CrossRef]
- Rubin, D.; Hayden, B. Is the expansion of the universe accelerating? all signs point to yes. Astrophys. J. Lett. 2016, 833, L30. [Google Scholar] [CrossRef]
- Trentham, N. Distance measurements as a probe of cosmic acceleration. Month. Not. Roy. Astron. Soc. 2001, 326, 1328. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Martin, J. The phenomenological approach to modeling the dark energy. Compt. Rend. Phys. 2012, 13, 566. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Chiba, T. Tracking K-essence. Phys. Rev. D 2002, 66, 063514. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom Energy: Dark Energy with ω<1 Causes a Cosmic Doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [PubMed]
- González-Diíaz, P. You need not be afraid of phantom energy. Phys. Rev. D 2003, 68, 021303. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, Cosmic Coincidence, and the Cosmological Constant. Phys. Rev. Lett. 1999, 82, 896. [Google Scholar] [CrossRef]
- Amendola, L.; Finelli, F.; Burigana, C.; Carturan, D. WMAP and the generalized Chaplygin gas. J. Cosm. Astrop. Phys. 2003, 7, 005. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Keresztes, Z.; Gergely, L.A.; Kamenshchik, A.Y.; Gorini, V.; Polarski, D. Soft singularity crossing and transformation of matter properties. Phys. Rev. D 2003, 88, 023535. [Google Scholar] [CrossRef]
- Li, M. A Model of holographic dark energy. Phys. Lett. B 2004, 603, 1. [Google Scholar] [CrossRef]
- Pavón, D.; Zimdahl, W. Holographic dark energy and cosmic coincidence. Phys. Lett. B 2005, 628, 206. [Google Scholar] [CrossRef]
- Huang, Q.G.; Li, M. The holographic dark energy in a Non-flat Universe. J. Cosm. Astrop. Phys. 2004, 8, 013. [Google Scholar] [CrossRef]
- Huang, Q.G.; Gong, Y. Supernova Constraints on a holographic dark energy model. arXiv 2004, arXiv:astro-ph/0403590. [Google Scholar] [CrossRef]
- Gong, Y. Extended holographic dark energy. Phys. Rev. D 2004, 70, 064029. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Comm. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Hooft, G. Dimensional reduction in quantum gravity. arXiv 1993, arXiv:gr-qc/9310026. [Google Scholar]
- Maldacena, J.M. The large-N limit of super conformal field theories and super gravity. Int. J. Theor. Phys. 1999, 38, 1113. [Google Scholar] [CrossRef]
- Liu, H.; Rajagopal, K.; Wiedemann, U.A. Wilson loops in heavy ion collisions and their calculation in AdS/CFTJ. J. High Energy Phys. 2007, 3, 066. [Google Scholar] [CrossRef]
- Strominger, A. The dS/CFT correspondence. J. High Energy Phys. 2001, 10, 034. [Google Scholar] [CrossRef]
- Jawad, A.A. Tsallis, Renyi and Sharma–Mittal holographic dark energy models in DGP brane-world. Phys. Dark Univ. 2019, 26, 100349. [Google Scholar]
- Tavayef, M.; Sheykhi, A.; Bamba, K.; Moradpour, H. Tsallis holographic dark energy. Phys. Lett. B 2018, 781, 195. [Google Scholar] [CrossRef]
- Aditya, Y.; Mandal, S.; Sahoo, P.K.; Reddy, D.R.K. Observational constraint on interacting Tsallis holographic dark energy in logarithmic Brans–Dicke theory. Eur. Phys. J. C 2019, 79, 1020. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Li, M. Holographic dark energy. Phys. Rep. 2017, 696, 1. [Google Scholar] [CrossRef]
- Pourhassan, B.; Bonilla, A.; Faizal, M.; Abreu, E.M.C. Holographic dark energy from fluid/gravity duality constraint by cosmological observations. Phys. Dark Univ. 2018, 20, 41. [Google Scholar] [CrossRef]
- Sharma, U.K.; Dubey, V.C.; Pradhan, A. Diagnosing interacting Tsallis holographic dark energy in the non-flat universe. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050032. [Google Scholar] [CrossRef]
- Shekh, S.H.; Ghaderi, K. Hypersurface-homogeneous space–time with interacting holographic model of dark energy with Hubble’s and Granda–Oliveros IR cut-off. Phys. Dark Univ. 2021, 31, 100785. [Google Scholar] [CrossRef]
- Xu, L. Holographic dark energy model with Hubble horizon as an IR cut-off. J. Cosm. Astrop. Phys. 2009, 9, 016. [Google Scholar] [CrossRef]
- Liu, J.; Gong, Y.; Chen, X. Dynamical behavior of the extended holographic dark energy with the Hubble horizon. Phys. Rev. D 2010, 81, 083536. [Google Scholar] [CrossRef]
- Nomura, Y.; Remmen, G.N. Area law unification and the holographic event horizon. J. High Ener. Phys. 2018, 2018, 063. [Google Scholar] [CrossRef]
- Sadjadi, H.M. The particle versus the future event horizon in an interacting holographic dark energy model. J. Cosm. Astrop. Phys 2007, 2, 026. [Google Scholar] [CrossRef]
- Huang, Z.P.; Wu, Y.L. Holographic dark energy model characterized by the conformal-age-like length. Int. J. Mod. Phys. A 2012, 27, 1250085. [Google Scholar] [CrossRef]
- Huang, Z.P.; Wu, Y.L. Cosmological constraint and analysis on holographic dark energy model characterized by the conformal-age-like length. Int. J. Mod. Phys. A 2012, 27, 1250130. [Google Scholar] [CrossRef]
- Li, E.K.; Zhang, Y.; Geng, J.-L.; Duan, P.-F. Generalized holographic Ricci dark energy and generalized second law of thermodynamics in Bianchi Type I universe. Gen. Rel. Grav. 2015, 47, 136. [Google Scholar] [CrossRef]
- Khodam-Mohammadi, A.; Pasqua, A.; Malekjani, M.; Khomenko, I.; Monshizadeh, M. Statefinder diagnostic of logarithmic entropy corrected holographic dark energy with Granda-Oliveros IR cut-off. Astrophys. Spa. Sci. 2013, 345, 415. [Google Scholar] [CrossRef]
- Renyi, A. Probability Theory; North-Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Stallis, C. Possible generalization of Boltzmann-Gibbs entropy. J. Stat. Phys. 1988, 52, 479. [Google Scholar]
- Moradpour, H.; Moosavi, S.A.; Lobo, I.P.; Morais Graça, J.P.; Jawad, A.; Salako, I.G. Thermodynamic approach to holographic dark energy and the Rényi entropy. Eur. Phys. J. C 2018, 78, 829. [Google Scholar]
- Sayahian, S.J.; Moosavi, S.A.; Moradpour, H.; Morais Graça, J.P.; Lobo, I.P.; Salako, I.G.; Jawad, A. Generalized entropy formalism and a new holographic dark energy model. Phys. Lett. B 2018, 780, 21. [Google Scholar] [CrossRef]
- Dubey, V.C.; Sharma, U.K.; Mamon, A.A. Interacting Rényi holographic dark energy in the Brans-Dicke theory. Adv. High Energy Phys. 2021, 2021, 6658862. [Google Scholar] [CrossRef]
- Zadeh, M.A.; Sheykhi, A.; Moradpour, H.; Bamba, K. Note on Tsallis holographic dark energy. Eur. Phys. J. 2018, 78, 940. [Google Scholar] [CrossRef]
- Sadri, E. Observational constraints on interacting Tsallis holographic dark energy model. Eur. Phys. J. C 2019, 79, 762. [Google Scholar] [CrossRef]
- Sharma, U.K.; Dubey, V.C. Exploring the Sharma–Mittal holographic dark energy models with different diagnostic tools. Eur. Phys. J. Plus 2020, 135, 391. [Google Scholar] [CrossRef]
- Amendola, L.; Polarski, D.; Tsujikawa, S. Are f(R) Dark Energy Models Cosmologically Viable? Phys. Rev. Lett. 2007, 98, 131302. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Reconciling dark energy models with f(R) theories. Phys. Rev. D 2005, 71, 043503. [Google Scholar] [CrossRef]
- Baffou, E.H.; Kpadonou, A.V.; Rodrigues, M.E.; Houndjo, M.J.S.; Tossa, J. Cosmological viable f(R,T) dark energy model: Dynamics and stability. Astrophys. Space Sci. 2015, 356, 173. [Google Scholar] [CrossRef]
- Houndjo, M.J.S. Reconstruction of f(R,T) gravity describing matter dominated and accelerated phases. Int. J. Mod. Phys. D 2012, 21, 1250003. [Google Scholar] [CrossRef]
- Mishra, R.K.; Chand, A.; Pradhan, A. Dark energy models in f(R,T) theory with variable deceleration parameter. Int. J. Theor. Phys. 2016, 55, 1241. [Google Scholar] [CrossRef]
- Amirhashchi, H.; Pradhan, A.; Jaiswal, R. Two-Fluid Dark Energy Models in Bianchi Type-III Universe with Variable Deceleration Parameter. Int. J. Theor. Phys. 2013, 52, 2735. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. The simplest non-minimal matter–geometry coupling in the f(R,T) cosmology. Eur. Phys. J. C 2017, 77, 480. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Sahoo, P.; Bishi, B.K. Anisotropic cosmological models in f(R,T) gravity with variable deceleration parameter. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750097. [Google Scholar] [CrossRef]
- Combi, L.; Romero, G.E. Is Teleparallel gravity really equivalent to reneral relativity? Annal. Phys. 2018, 530, 1700175. [Google Scholar] [CrossRef]
- Arcos, H.I.; Pereira, J.G. Torsion gravity: A Reappraisal. Int. J. Mod. Phys. D 2004, 13, 2193. [Google Scholar] [CrossRef]
- Maluf, J.W. The teleparallel equivalent of general relativity. Annal. Phys. 2013, 525, 339. [Google Scholar] [CrossRef]
- Karami, K.; Abdolmaleki, A. Generalized second law of thermodynamics in f(T) gravity. JCAP 2012, 04, 007. [Google Scholar] [CrossRef]
- Harko, T.; Francisco, F.S.L.; Otalora, G.; Saridakis, E.N. f(T) gravity and cosmology. JCAP 2014, 12, 021. [Google Scholar] [CrossRef]
- Rezaei, T.M.; Amani, A. Stability and interacting f(T) gravity with modified Chaplygin gas. Can. J. Phys. 2017, 95, 1068. [Google Scholar] [CrossRef]
- Bahamonde, S.; Boehmer, C.G.; Wright, M. Modified teleparallel theories of gravity. Phys. Rev. D 2015, 92, 104042. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Sotiriou, T.P.; Barrow, J.D. f(T) gravity and local Lorentz invariance. Phys. Rev. D 2011, 83, 064035. [Google Scholar] [CrossRef]
- Zubair, M.; Waheed, S.; Fayyaz, M.A.; Ahmad, I. Energy constraints and the phenomenon of cosmic evolution in the f(T,B) framework. Eur. Phys. J. Plus 2018, 133, 452. [Google Scholar] [CrossRef]
- Capozziello, S.; Capriolo, M.; Caso, L. Weak field limit and gravitational waves in f(T,B) teleparallel gravity. Eur. Phys. J. C 2020, 80, 156. [Google Scholar] [CrossRef]
- Bahamonde, S.; Capozziello, S. Noether symmetry approach in f(T,B) teleparallel cosmology. Eur. Phys. J. C 2017, 77, 107. [Google Scholar] [CrossRef]
- Bahamonde, S.; Zubair, M.; Abbas, G. Thermodynamics and cosmological reconstruction in f(T,B) gravity. Phys. Dark Univ. 2018, 19, 78. [Google Scholar] [CrossRef]
- Maity, S.; Debnath, U. Tsallis, Rényi and Sharma-Mittal holographic and new agegraphic dark energy models in D-dimensional fractal universe. Eur. Phys. J. Plus 2019, 134, 514. [Google Scholar] [CrossRef]
- Fischler, W.; Susskind, L. Holography and Cosmology. arXiv 1998, arXiv:hep-th/9806038. [Google Scholar]
- Gao, C.; Wu, F.; Chen, X.; Shen, Y.-G. Holographic dark energy model from Ricci scalar curvature. Phys. Rev. D 2009, 79, 043511. [Google Scholar] [CrossRef]
- Del Campo, S.; Fabris, J.C.; Herrera, R.; Zimdahl, W. Holographic dark-energy models. Phys. Rev. D 2011, 83, 123006. [Google Scholar] [CrossRef]
- Setare, M.R. Interacting holographic dark energy model in non-flat universe. Phys. Lett. B 2006, 642, 1. [Google Scholar] [CrossRef]
- Setare, M.R.; Vagenas, E.C. The cosmological dynamics of interacting holographic dark energy model. Int. J. Mod. Phys. D 2009, 18, 147. [Google Scholar] [CrossRef]
- Jamil, M.; Farooq, M.U.; Rashid, M.A. Generalized holographic dark energy model. Eur. Phys. J. C 2009, 61, 471. [Google Scholar] [CrossRef]
- Ito, M. Holographic-dark-energy model with non-minimal coupling. Europhys. Lett. 2005, 71, 712. [Google Scholar] [CrossRef]
- Myung, Y.S.; Seo, M.G. Origin of holographic dark energy models. Phys. Lett. B 2009, 671, 435. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shekh, S.H.; Moraes, P.H.R.S.; Sahoo, P.K. Physical Acceptability of the Renyi, Tsallis and Sharma-Mittal Holographic Dark Energy Models in the f(T,B) Gravity under Hubble’s Cutoff. Universe 2021, 7, 67. https://doi.org/10.3390/universe7030067
Shekh SH, Moraes PHRS, Sahoo PK. Physical Acceptability of the Renyi, Tsallis and Sharma-Mittal Holographic Dark Energy Models in the f(T,B) Gravity under Hubble’s Cutoff. Universe. 2021; 7(3):67. https://doi.org/10.3390/universe7030067
Chicago/Turabian StyleShekh, Salim Harun, Pedro H. R. S. Moraes, and Pradyumn Kumar Sahoo. 2021. "Physical Acceptability of the Renyi, Tsallis and Sharma-Mittal Holographic Dark Energy Models in the f(T,B) Gravity under Hubble’s Cutoff" Universe 7, no. 3: 67. https://doi.org/10.3390/universe7030067
APA StyleShekh, S. H., Moraes, P. H. R. S., & Sahoo, P. K. (2021). Physical Acceptability of the Renyi, Tsallis and Sharma-Mittal Holographic Dark Energy Models in the f(T,B) Gravity under Hubble’s Cutoff. Universe, 7(3), 67. https://doi.org/10.3390/universe7030067







