Cosmological Constraints on the Coupling Model from Observational Hubble Parameter and Baryon Acoustic Oscillation Measurements

Abstract

In the paper, we consider two models in which dark energy is coupled with either dust matter or dark matter, and discuss the conditions that allow more time for structure formation to take place at high redshifts. These models are expected to have a larger age of the universe than that of $\mathsf{\Lambda }$CDM [universe consists of cold dark matter (CDM) and dark energy (a cosmological constant, $\mathsf{\Lambda }$)], so it can explain the formation of high redshift gravitationally bound systems which the $\mathsf{\Lambda }$CDM model cannot interpret. We use the observational Hubble parameter data (OHD) and Hubble parameter obtained from cosmic chronometers method ($H\left(z\right)$) in combination with baryon acoustic oscillation (BAO) data to constrain these models. With the best-fitting parameters, we discuss how the age, the deceleration parameter, and the energy density parameters evolve in the new universes, and compare them with that of $\mathsf{\Lambda }$CDM.

1. Introduction

The observational developments recently have provided cosmology with a standard model, which describes the universe by the Friedmann–Lemaitre–Robertson–Walker (FLRW) metric, with cold pressureless matter contributing roughly 1/3 and the negative pressure dark energy (DE) contributing the remaining 2/3 of the critical energy density [1,2,3].

Agreeing with most observations, $\mathsf{\Lambda }$CDM [universe consists of cold dark matter (CDM) and dark energy (a cosmological constant, $\mathsf{\Lambda }$)] [4] is accepted by most of the scientists in cosmology. However, recent observations provide some conflicts with $\mathsf{\Lambda }$CDM. For example, over 400 quasars (QSOs) with $z>4$ are found, and the seven highest redshift quasars have $z>5.7$ [5,6]. If their centers are black holes, these black holes must have a scale of ${10}^9{M}_{\odot }$. Whether such supermassive black holes can form in the $\mathsf{\Lambda }$CDM universe with an age less than ${10}^9$ years at $z\sim 6$ [7] remains an open question. Moreover, as stated in [8], the recent discovery of SDSS 010013.02+280225.8 (hereinafter “J0100+2802”), an ultraluminous quasar at redshift $z=6.30$, has aggravated the problem of supermassive black-hole growth and evolution in the early Universe [9]. Not to mention the issues that the 14-Gyr age of the universe obtained by Pont et al. [10], which is in tension with $13.797\pm 0.023$ Gyr [11], the 3.5-Gyr-old radio galaxy 53W091 at $z=1.55$ and 4-Gyr-old radio galaxy 53W069 [12,13]. In addition, the existence of Pop III stars ($z\ge 17$) which may have been responsible for ionizing the universe at lower redshifts is also problematic in the $\mathsf{\Lambda }$CDM [5].

Motivated by the above issues and the works of Hao Wei [14,15,16], here we intend to test a model of dark energy (DE) coupled with matter that ameliorates the aging problem. The coupling between DE and dust matter has been discussed in detail [17,18,19]. In the literature, the coupling between DE and dark matter (DM) has been investigated to explain the Hubble constant ($H_0$) and ${\sigma }_8$ tensions [20,21,22,23,24,25,26], where ${\sigma }_8$ measures the amplitude of the (linear) power spectrum on the scale of 8 h${}^{-1}$ Mpc, with $h=H_0/\left(100\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}\right)$ being the reduced Hubble constant. It would be interesting to also consider a model with DE and DM coupling. Therefore, for comparison purpose, we select three coupling forms of these two models and use observational Hubble parameter data (OHD) and Hubble parameter obtained from cosmic chronometers method (denoted as $H\left(z\right)$) in combination with baryon acoustic oscillation (BAO) data to constrain the cosmological and nuisance parameters in the given models. Finally, we explore the general properties of the best-fitting models and their implications, and determine the most favored model.

This paper is organized as follows: In Section 2, we briefly review the standard cosmology and its challenges. In Section 3, we describe the coupling models in details. The constraints on the models are presented in Section 4. In Section 5, we discuss the properties of the best-fitting models and their merits. Finally, the conclusions and discussions are given in Section 6.

2. The Standard Cosmology and Its Challenges

The current standard cosmology is mainly based on the Einstein’s general relativity, and FLRW metric, where the homogeneous and isotropic solution of Einstein’s field equations, is given by

$$d{s}^2=-d{t}^2+a^2\left(t\right)[\frac{d{r}^2}{1-k{r}^2}+r^{2}d{\theta }^2+r^{2}si{n}^2\theta d\varphi ].$$

(1)

$a\left(t\right)$ is the scale factor, r, $\theta$ and $\varphi$ are dimensionless comoving coordinates, and $k=0,\pm 1$ represent the curvature of the spatial Section [27]. The homogeneous matter in the universe behaves as a tensor

$$T^{\mu \nu }=(\rho +P)U^{\mu }{U}^{\nu }+P{g}^{\mu \nu },$$

(2)

where $\rho$ and P represent the density and the pressure of the matter, and $U^{\mu }$ and $g_{\mu \nu }$ denote the 4-velocity of the matter and space-time metric, respectively. When U=(1, 0, 0, 0), matter is static in the reference coordinate, but comoving with the expanding universe. From Friedmann equations, one can get the the expression of Hubble parameter $H\left(z\right)$ in flat $\mathsf{\Lambda }$CDM,

$$H^2=H_0^2\left({\Omega }_{m_0}{(1+z)}^3+{\Omega }_{r_0}{(1+z)}^3+{\Omega }_{\mathsf{\Lambda }}\right),$$

(3)

where ${\Omega }_{m_0}$, ${\Omega }_{r_0}$, and ${\Omega }_{\mathsf{\Lambda }}$ are current radiation energy, current dust matter, and constant DE density parameters, respectively, and subscript “0” denotes the present value hereafter. Note that ${\Omega }_{r_0}$ is accurately measured, being ${\Omega }_{r_0}=2.47\times {10}^{-5}{h}^{-2}$ [28], and the current neutrino energy density parameter ${\Omega }_{{\nu }_0}$ is given by

$${\Omega }_{{\nu }_0}=\frac{\sum m_{\nu }}{93.14h^2},$$

(4)

where $\sum m_{\nu }=0.06$ eV is the total neutrino mass and the effective number of massless neutrino species $N_{\mathrm{eff}}=3.045$ [28]. Though $\mathsf{\Lambda }$CDM is generally accepted by most scientists and agreed mostly with the observations, it appears that the recent observations at modest redshifts ($6\le z\le 20$) have some surprises in store for $\mathsf{\Lambda }$CDM [5].

In fact, over 400 QSOs with redshifts $z>4$ are known at present, and the seven highest redshift quasars have $z>5.7$. If quasars shine by virtue of an accreting black hole at their centers, then all these QSOs must host $\ge {10}^9{M}_{\odot }$ black holes [7], and it takes at least $7\times {10}^8$ years for such a black hole to form. We define the age of the universe at the redshifts z, $t_z$, as

$$t_z={\int }_z^{\infty }\frac{dz}{(1+z)H\left(z\right)}.$$

(5)

Considering $H_0=67.4$ $\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ and ${\Omega }_{m_0}=0.315$ [11], and substituting Equation (3) into Equation (5), we get the age of universe at $z\sim 6$ as $9.3\times {10}^8$ years which is merely enough for the formation of ${10}^9{M}_{\odot }$ black holes.

The following arguments are summarized by Melia and McClintock [8]. In the standard context, the universe became transparent about 0.4 Myr after the big bang, descending into the so-called Dark Ages, which ended several hundred million years later. After that, density perturbations condensed into stars and early galaxies, producing ionizing radiation and the epoch of re-ionization (EoR) began. Standard astrophysical principles suggest that ionizing radiation was produced by Pop II and III stars. The EoR was constrained by Zaroubi et al. [29] at $6\lesssim z\lesssim 15$. How the universe evolved through the Dark Ages and into the EoR was studied by many detailed simulations (e.g., [30]), which show that primordial gas clouds formed in dark-matter halos with virial temperature 1000 K and mass ${10}^6{M}_{\odot }$ (so-called “minihaloes”; $M_{\odot }$, solar mass). In the standard CDM model, the minihaloes that were the first sites for star formation are expected to be in place at redshift $z\approx 20$, when the age of the universe was just a few hundred million years [31]. After at least 100 Myr, 5–20 $M_{\odot }$ black-hole seeds were created, presumably following the supernova explosion of evolved Pop II (and possibly Pop III) stars. Conventionally, the black-hole mass as a function of time can be expressed by Salpeter relation (see [8] and references therein for more details)

$$M\left(t\right)=M_{\mathrm{seed}}exp\frac{t-t_{\mathrm{seed}}}{45\mathrm{Myr}},$$

(6)

where $M_{\mathrm{seed}}$ is the black-hole seed mass produced at time $t_{\mathrm{seed}}$. Note that $M\left(t\right)$, being a model-dependent quantity, may present dependence on cosmological parameters, especially on $H_0$ [32]. Assuming $M_{\mathrm{seed}}=20M_{\odot }$ (upper bound), the minimal growth time from the Salpeter relation is $t-t_{\mathrm{seed}}\sim 910$ Myr for an inferred mass of approximately 10–12 $\times {10}^9{M}_{\odot }$. Since in $\mathsf{\Lambda }$CDM (with $H_0=67.4$$\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ and ${\Omega }_{m_0}=0.315$ given by [11]), $t(z=6.3)\sim 873$ Myr, not only is this age of quasar J0100+2802 inconsistent with the transition from the Dark Ages to the EoR, but also the quasar would have had to grow beyond the big bang. This is still true even if we are using the lower bounds of $H_0=66.82$ $\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ and ${\Omega }_{m_0}=0.308$ from [11], which result in $t(z=6.3)\sim 891$ Myr.

In order to improve these problems, we aim to test a new model to agree better with the observations. Indeed, a smaller value of $H\left(z\right)$ at high redshifts can result in a larger age of the universe, so can an oscillating $H\left(z\right)$. Note that there also exist other challenges, such as $H_0$ and ${\sigma }_8$ tensions, but here we mainly focus on the aging problems. We will introduce the coupling model in the following section.

3. Coupling between Dark Energy and Dust/Dark Matter

3.1. Dark Energy Coupled with Dust Matter

The standard theory of $\mathsf{\Lambda }$CDM is based on the assumption that all the cosmological compositions evolve independently, while first we assume that the dust matter and DE exchange energy through interaction according to

$${\dot{\rho }}_{\mathrm{X}}+3H(1+w_{\mathrm{X}}){\rho }_{\mathrm{X}}=-3\lambda H{\rho }_m,$$

(7)

and

$${\dot{\rho }}_m+3H{\rho }_m=3\lambda H{\rho }_m,$$

(8)

and the conservation equation for the radiation energy density is

$${\dot{\rho }}_r+4H{\rho }_r=0,$$

(9)

which preserves the total energy conservation equation ${\dot{\rho }}_{\mathrm{tot}}+3H({\rho }_{\mathrm{tot}}+P_{\mathrm{tot}})=0$ [14,15,16], where $\lambda$, ${\rho }_m$, ${\rho }_{\mathrm{X}}$, ${\rho }_r$, and $\dot{\rho }$ denote the coupling coefficient, the matter density, the DE density, the radiation energy density, and their time derivatives. Some researchers use this model to discuss the Chameleon DE and its test of the solar system [17,18,19]. Here, $\lambda$ determines the coupling form between the matter and DE, and the DE equation of state (EoS) $w_{\mathrm{X}}=P_{\mathrm{X}}/{\rho }_{\mathrm{X}}$ is constant. Here we only consider the spatially-flat FLRW universe. With $3\lambda H{\rho }_m$ as the interaction term, here we assume that the coupling coefficient takes the form $\lambda =A_1^{3}cos\left[\frac{ln(1+z)}{A_2}-A_1\pi \right]$ [14], in which $A_1$ and $A_2$ are undetermined constant coefficients. Substituting the expression of $\lambda$ into Equation (8), we can get the expression of ${\rho }_m$,

$${\rho }_m\left(z\right)={\rho }_{m_0}{(1+z)}^{3}exp\left\{-3A_1^3{A}_2\left[sin\left(A_1\pi \right)+sin\left[\frac{ln(1+z)}{A_2}-A_1\pi \right]\right]\right\},$$

(10)

where ${\rho }_{m_0}\equiv {\rho }_m(z=0)$. Substituting Equation (10) into Equation (7), we can obtain the expression of ${\rho }_{\mathrm{X}}$,

$${\rho }_{\mathrm{X}}\left(z\right)={(1+z)}^{3(1+w_{\mathrm{X}})}\left[{\rho }_{{\mathrm{X}}_0}+{\rho }_{m_0}I\left(z\right)\right],$$

(11)

where

$$\begin{array}{cc}\hfill I\left(z\right)=& {\int }_0^z\frac{3A_1^3}{{(1+x)}^{3w_{\mathrm{X}}+1}}cos\left[\frac{ln(1+x)}{A_2}-A_1\pi \right]\hfill \\ & exp\left\{-3A_1^3{A}_2\left[sin\left[\frac{ln(1+x)}{A_2}-A_1\pi \right]+sin\left(\frac{\pi }{A_1}\right)\right]\right\}dx.\hfill \end{array}$$

(12)

Similarly, from Equation (9), we can get

$${\rho }_r\left(z\right)={\rho }_{r_0}{(1+z)}^4.$$

(13)

Therefore in this model, we have

$$\frac{{\rho }_m+{\rho }_{\mathrm{X}}+{\rho }_r}{{\rho }_{\mathrm{crit}}}={\Omega }_m\left(z\right)+{\Omega }_{\mathrm{X}}\left(z\right)+{\Omega }_r\left(z\right)=1,$$

(14)

in which ${\Omega }_m={\rho }_m/{\rho }_{\mathrm{crit}}$, ${\Omega }_{\mathrm{X}}={\rho }_{\mathrm{X}}/{\rho }_{\mathrm{crit}}$, and ${\Omega }_r={\rho }_r/{\rho }_{\mathrm{crit}}$ are the dust matter density, DE density, and radiation energy density parameters, respectively, with ${\rho }_{\mathrm{crit}}\equiv 3H^2/8\pi G$ being the critical density. Furthermore, ${\Omega }_{m_0}+{\Omega }_{{\mathrm{X}}_0}+{\Omega }_{r_0}=1$ is satisfied. Then, the Friedmann equation becomes

$$\begin{array}{cc}\hfill \frac{H^2}{H_0^2}=& {\Omega }_{m_0}{(1+z)}^{3}exp\left\{-3A_1^3{A}_2\left[sin\left(A_1\pi \right)+sin\left[\frac{ln(1+z)}{A_2}-A_1\pi \right]\right]\right\}\hfill \\ & +{(1+z)}^{3(1+w_{\mathrm{X}})}\left\{1-{\Omega }_{{\mathrm{m}}_0}-{\Omega }_{r_0}+{\Omega }_{m_0}I\left(z\right)\right\}+{\Omega }_{r_0}{(1+z)}^4.\hfill \end{array}$$

(15)

This equation is the $H\left(z\right)$ expression of this coupling model (denoted as “Model 1” hereinafter).

We could also simply put $\lambda =$ const. In this case (denoted as “Model 2” hereinafter), the Hubble parameter becomes

$$H\left(z\right)=H_0\sqrt{\frac{w_{\mathrm{X}}{\Omega }_{m_0}}{\lambda +w_{\mathrm{X}}}{(1+z)}^{3(1-\lambda )}+\left(1-{\Omega }_{r_0}-\frac{w_{\mathrm{X}}{\Omega }_{m_0}}{\lambda +w_{\mathrm{X}}}\right){(1+z)}^{3(1+w_{\mathrm{X}})}+{\Omega }_{r_0}{(1+z)}^4}.$$

(16)

3.2. Dark Energy Coupled with Dark Matter

If we consider the coupling between DE and (cold) DM (see [33] for review), the interaction equations read

$${\dot{\rho }}_{\mathrm{X}}+3H(1+w_{\mathrm{X}}){\rho }_{\mathrm{X}}=-3\lambda H{\rho }_X,$$

(17)

and

$${\dot{\rho }}_c+3H{\rho }_c=3\lambda H{\rho }_X,$$

(18)

where ${\rho }_c$ is the energy density for cold DM. Here we also consider $\lambda =$ const. Consequently, we can obtain the expressions of ${\rho }_{\mathrm{X}}$

$${\rho }_{\mathrm{X}}\left(z\right)={\rho }_{{\mathrm{X}}_0}{(1+z)}^{3(1+w_{\mathrm{X}}+\lambda )},$$

(19)

and ${\rho }_c$

$${\rho }_c\left(z\right)={(1+z)}^3\left\{{\rho }_{c_0}+\frac{\lambda }{w_{\mathrm{X}}+\lambda }{\rho }_{{\mathrm{X}}_0}\left[{(1+z)}^{3(w_{\mathrm{X}}+\lambda )}-1\right]\right\},$$

(20)

where ${\rho }_{{\mathrm{X}}_0}\equiv {\rho }_{\mathrm{X}}(z=0)$ and ${\rho }_{c_0}\equiv {\rho }_c(z=0)$. The conservation equation for the energy density of the barynoic matter is

$${\dot{\rho }}_b+3H{\rho }_b=0,$$

(21)

which leads to

$${\rho }_b\left(z\right)={\rho }_{b_0}{(1+z)}^3.$$

(22)

In this case (denoted as “Model 3” hereinafter), the dust matter density becomes ${\rho }_m={\rho }_b+{\rho }_c$. Following the same definitions of the cosmological density parameters as above, ${\Omega }_b$, ${\Omega }_c$, and ${\Omega }_{\mathrm{X}}$ are the baryon, DM, and DE density parameters, respectively, and ${\Omega }_b+{\Omega }_c+{\Omega }_{\mathrm{X}}+{\Omega }_r=1$. The Friedman equation then becomes

$$H\left(z\right)=H_0\sqrt{{(1+z)}^3\left\{{\Omega }_{b_0}+{\Omega }_{c_0}+\frac{{\Omega }_{{\mathrm{X}}_0}}{w_{\mathrm{X}}+\lambda }\left[(w_{\mathrm{X}}+2\lambda ){(1+z)}^{3(w_{\mathrm{X}}+\lambda )}-\lambda \right]+{\Omega }_{r_0}(1+z)\right\}},$$

(23)

where ${\Omega }_{m_0}={\Omega }_{b_0}+{\Omega }_{c_0}$ and ${\Omega }_{m_0}+{\Omega }_{{\mathrm{X}}_0}+{\Omega }_{r_0}=1$.

In the following section, we will constrain these models with OHD and $H\left(z\right)$ + BAO combination.

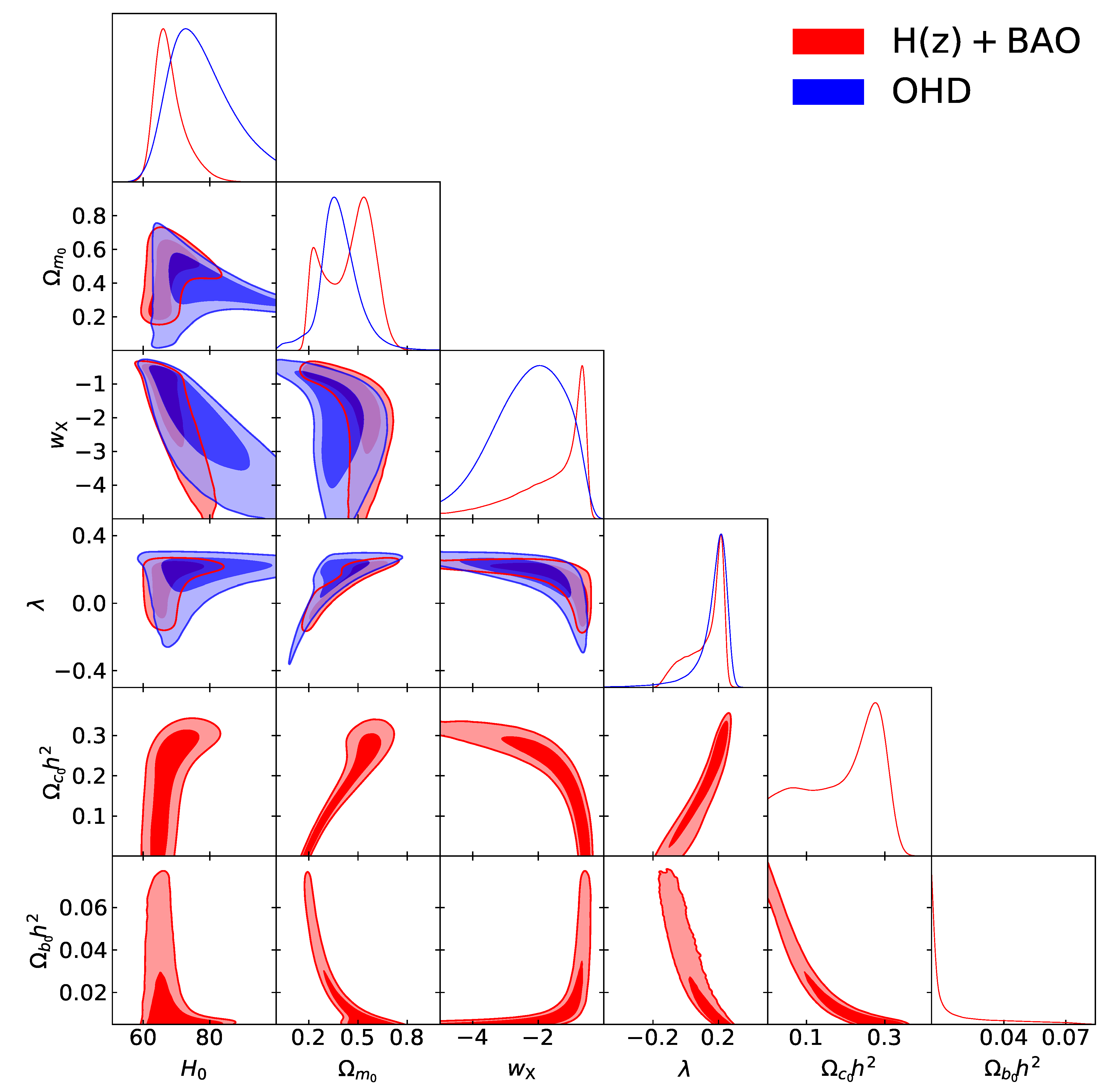
4. Constraints on the Coupling Model with Observational Data

The 40 OHD we used here are based on cosmic chronometers (see [34,35,36,37,38] for the usage of these 31 $H\left(z\right)$ data) and radial BAO size methods, as shown in

Table 1. The current available OHD dataset.

z	$\mathit{H}\left(\mathit{z}\right)$a	Method b	Ref.
$0.0708$	$69.0\pm 19.68$	I	Zhang et al. (2014)-[47]
$0.09$	$69.0\pm 12.0$	I	Jimenez et al. (2003)-[48]
$0.12$	$68.6\pm 26.2$	I	Zhang et al. (2014)-[47]
$0.17$	$83.0\pm 8.0$	I	Simon et al. (2005)-[49]
$0.179$	$75.0\pm 4.0$	I	Moresco et al. (2012)-[50]
$0.199$	$75.0\pm 5.0$	I	Moresco et al. (2012)-[50]
$0.2$	$72.9\pm 29.6$	I	Zhang et al. (2014)-[47]
$0.240$	$79.69\pm 2.65$	II	Gazta$\tilde{\mathrm{n}}$aga et al. (2009)-[51]
$0.27$	$77.0\pm 14.0$	I	Simon et al. (2005)-[49]
$0.28$	$88.8\pm 36.6$	I	Zhang et al. (2014)-[47]
$0.35$	$84.4\pm 7.0$	II	Xu et al. (2013)-[52]
$0.352$	$83.0\pm 14.0$	I	Moresco et al. (2012)-[50]
$0.3802$	$83.0\pm 13.5$	I	Moresco et al. (2016)-[40]
$0.4$	$95\pm 17.0$	I	Simon et al. (2005)-[49]
$0.4004$	$77.0\pm 10.2$	I	Moresco et al. (2016)-[40]
$0.4247$	$87.1\pm 11.2$	I	Moresco et al. (2016)-[40]
$0.43$	$86.45\pm 3.68$	II	Gazta$\tilde{\mathrm{n}}$aga et al. (2009)-[51]
$0.44$	$82.6\pm 7.8$	II	Blake et al. (2012)-[53]
$0.4497$	$92.8\pm 12.9$	I	Moresco et al. (2016)-[40]
$0.47$	$89\pm 50$	I	Ratsimbazafy et al. (2017)-[54]
$0.4783$	$80.9\pm 9.0$	I	Moresco et al. (2016)-[40]
$0.48$	$97.0\pm 62.0$	I	Stern et al. (2010)-[55]
$0.57$	$92.4\pm 4.5$	II	Samushia et al. (2013)-[56]
$0.593$	$104.0\pm 13.0$	I	Moresco et al. (2012)-[50]
$0.6$	$87.9\pm 6.1$	II	Blake et al. (2012)-[53]
$0.68$	$92.0\pm 8.0$	I	Moresco et al. (2012)-[50]
$0.73$	$97.3\pm 7.0$	II	Blake et al. (2012)-[53]
$0.781$	$105.0\pm 12.0$	I	Moresco et al. (2012)-[50]
$0.875$	$125.0\pm 17.0$	I	Moresco et al. (2012)-[50]
$0.88$	$90.0\pm 40.0$	I	Stern et al. (2010)-[55]
$0.9$	$117.0\pm 23.0$	I	Simon et al. (2005)-[49]
$1.037$	$154.0\pm 20.0$	I	Moresco et al. (2012)-[50]
$1.3$	$168.0\pm 17.0$	I	Simon et al. (2005)-[49]
$1.363$	$160.0\pm 33.6$	I	Moresco (2015)-[57]
$1.43$	$177.0\pm 18.0$	I	Simon et al. (2005)-[49]
$1.53$	$140.0\pm 14.0$	I	Simon et al. (2005)-[49]
$1.75$	$202.0\pm 40.0$	I	Simon et al. (2005)-[49]
$1.965$	$186.5\pm 50.4$	I	Moresco (2015)-[57]
$2.34$	$222.0\pm 7.0$	II	Delubac et al. (2015)-[58]
$2.36$	$226.0\pm 8.0$	II	Font-Ribera et al. (2014)-[59]

^a km s⁻¹ Mpc⁻¹. ^b Methods I and II represent the cosmic chronometers and the radial BAO size methods, respectively.

, where we could use them together is because they are statistically-independent (systematic uncertainty of individual data point is accounted for, and in fact, based on the reduced ${\chi }^2$ value listed in

Table 2. Unmarginalized best-fitting parameter values for the coupling models.

Model	Data Set	${\Omega }_{{\mathit{c}}_0}{\mathit{h}}^2$	${\Omega }_{{\mathit{b}}_0}{\mathit{h}}^2$	${\Omega }_{{\mathit{m}}_0}$	${\mathit{w}}_{\mathbf{X}}$	${\mathit{H}}_0$a	${\mathit{A}}_1$	${\mathit{A}}_2$	$\mathit{\lambda }$	${\mathit{\chi }}_{\mathbf{min}}^2$	$\mathit{\nu }$	${\mathit{\chi }}_{\mathbf{min}}^2/\mathit{\nu }$	$\mathit{AIC}$	$\mathit{BIC}$	$\Delta \mathit{AIC}$	$\Delta \mathit{BIC}$
Model 1	OHD	–	–	0.020	$-0.740$	71.34	1.210	0.333	–	15.85	35	0.45	25.85	34.30	0.35	2.04
	$H\left(z\right)$ + BAO	0.0010	0.0742	0.171	$-0.797$	66.64	0.907	0.472	–	17.85	36	0.50	29.85	40.27	1.43	3.16
Model 2	OHD	–	–	0.383	$-1.904$	76.39	–	–	0.167	17.50	36	0.49	25.50	32.26	0.00	0.00
	$H\left(z\right)$ + BAO	0.2598	0.0064	0.579	$-1.973$	67.90	–	–	0.206	18.42	37	0.50	28.42	37.11	0.00	0.00
Model 3	OHD	–	–	0.157	$-1.107$	70.48	–	–	0.112	18.47	36	0.51	26.47	33.23	0.97	0.97
	$H\left(z\right)$ + BAO	0.1330	0.0195	0.361	$-0.607$	65.12	–	–	$-0.088$	19.65	37	0.53	29.65	38.34	1.23	1.23

^a km s⁻¹ Mpc⁻¹. ^b Degrees of freedom.

, the errors are overestimated). Systematic errors that affect $H\left(z\right)$ measurements from cosmic chronometers were studied [39,40], and were recently re-examined in [41,42]. Note that the statistically-dependent (correlated) data [43] has been removed (which is included in BAO measurements) compared with what used in [44] (see also [45,46] for more details regarding OHD).

The 11 BAO data used here are the same as what used in Cao et al. (see [38] for more details). The systematic uncertainties of these BAO data are examined and found to be either negligible compared with the statistical uncertainties or included in the corresponding covariance matrix.

In consideration of the non-Gaussian posterior in parameter space, we perform a full Markov chain Monte Carlo (MCMC) Metropolis-Hastings sampling with emcee [60] and assume flat parameter priors to constrain these parameters, for OHD (or $H\left(z\right)$ data)

$${\chi }^2=\sum _i\frac{{[H_{\mathrm{th}}\left(z_i\right|\mathit{p})-H_{\mathrm{obs}}\left(z_i\right)]}^2}{{\sigma }^2\left(z_i\right)},$$

(24)

in which $H_{\mathrm{th}}\left(z_i\right|\mathit{p})$, $H_{\mathrm{obs}}\left(z_i\right)$, and $\sigma \left(z_i\right)$ are the theoretical Hubble parameter at redshift $z_i$, the OHD (or $H\left(z\right)$ data), and the uncertainty of each $H_{\mathrm{obs}}\left(z_i\right)$, respectively. For BAO, we use the same procedure given in Cao et al. [36]. We show in Table 2 and

Table 3. One-dimensional marginalized best-fitting parameter values and uncertainties ($\pm 1\sigma$ or $2\sigma$ upper limits) for the coupling models.

Model	Data Set	${\Omega }_{{\mathit{c}}_0}{\mathit{h}}^2$	${\Omega }_{{\mathit{b}}_0}{\mathit{h}}^2$	${\Omega }_{{\mathit{m}}_0}$	${\mathit{w}}_{\mathbf{X}}$	${\mathit{H}}_0$a	${\mathit{A}}_1$	${\mathit{A}}_2$	$\mathit{\lambda }$
Model 1	OHD	–	–	$0.{249}_{-0.029}^{+0.042}$	$-1.{077}_{-0.223}^{+0.347}$	$71.{28}_{-5.85}^{+3.95}$	$0.{376}_{-0.243}^{+0.220}$	$4.{521}_{-4.295}^{+1.827}$	–
	$H\left(z\right)$ + BAO	$0.{0832}_{-0.0300}^{+0.0402}$	$0.{0361}_{-0.0163}^{+0.0069}$	$0.{278}_{-0.039}^{+0.045}$	$-0.{734}_{-0.095}^{+0.219}$	$65.{50}_{-2.86}^{+2.20}$	$0.{359}_{-0.215}^{+0.251}$	$4.{771}_{-4.510}^{+2.336}$	–
Model 2	OHD	–	–	$0.{385}_{-0.111}^{+0.093}$	$-2.{298}_{-0.813}^{+1.355}$	$77.{42}_{-11.21}^{+6.66}$	–	–	$0.{158}_{-0.019}^{+0.107}$
	$H\left(z\right)$ + BAO	$0.{1899}_{-0.1371}^{+0.1267}$	$<0.0628$	$0.{444}_{-0.240}^{+0.183}$	$-1.{650}_{-0.396}^{+1.203}$	$68.{04}_{-5.45}^{+2.62}$	–	–	$0.{127}_{-0.049}^{+0.124}$
Model 3	OHD	–	–	$0.{363}_{-0.111}^{+0.255}$	$-0.{754}_{-0.439}^{+0.471}$	$71.{36}_{-4.92}^{+3.93}$	–	–	$-0.{293}_{-0.230}^{+0.529}$
	$H\left(z\right)$ + BAO	$<0.2532$	$0.{0314}_{-0.0264}^{+0.0094}$	$0.{344}_{-0.168}^{+0.065}$	$-0.{629}_{-0.306}^{+0.220}$	$65.{80}_{-2.64}^{+2.38}$	–	–	$-0.{108}_{-0.059}^{+0.235}$

^a km s⁻¹ Mpc⁻¹.

the unmarginalized and marginalized best-fitting results (the marigninalized ones are the posterior means) with 1$\sigma$ confidence regions, and with the best-fitting parameters (details described below), we can substitute Equation (15) into Equation (5) to obtain the age of the universe. Furthermore, panal (a) of Figure 1 shows theoretical curves of $H\left(z\right)$ for the best-fitting models along with the OHD. The 1$\sigma$ and 2$\sigma$ contours are shown in Figure 2, Figure 3 and Figure 4, which are analyzed by using the Python package GetDist [61]. Note that in Model 1, $\mathit{p}=\{H_0,{\Omega }_{m_0},w_{\mathrm{X}},A_1,A_2\}$ for OHD and $\mathit{p}=\{H_0,{\Omega }_{c_0}{h}^2,{\Omega }_{b_0}{h}^2,w_{\mathrm{X}},A_1,A_2\}$ for $H\left(z\right)$ + BAO combination; in Models 2 and 3, $\mathit{p}=\{H_0,{\Omega }_{m_0},w_{\mathrm{X}},\lambda \}$ for OHD and $\mathit{p}=\{H_0,{\Omega }_{c_0}{h}^2,{\Omega }_{b_0}{h}^2,w_{\mathrm{X}},\lambda$} for $H\left(z\right)$ + BAO combination; the priors on $\mathit{p}$ are non-zero and flat over the ranges $0.005\le {\Omega }_{{\mathrm{b}}_0}{h}^2\le 0.1$, $0.001\le {\Omega }_{{\mathrm{c}}_0}{h}^2\le 0.99$, $0.2\le h\le 1.0$, $-5\le w_{\mathrm{X}}\le 0$, $0\le A_1\le 2$, $0.2\le A_2\le 10$, and $-5\le \lambda \le 5$. We also include the Akaike Information Criterion ($AIC$) and the Bayesian Information Criterion ($BIC$) to compare the goodness of fit of these models with different numbers of parameters, where

$$AIC={\chi }_{\min }^2+2n,$$

(25)

and

$$BIC={\chi }_{\min }^2+nlnN,$$

(26)

where n and N are the numbers of free parameters of the given model and of data points. For OHD, $N=40$, and for $H\left(z\right)$ + BAO combination, $N=42$. The degrees of freedom is $\nu =N-n$, which is used to determine the reduced ${\chi }^2$, i.e., ${\chi }_{\min }^2/\nu$ listed in Table 2. We will discuss the details of these best-fitting models in detail in the following section.

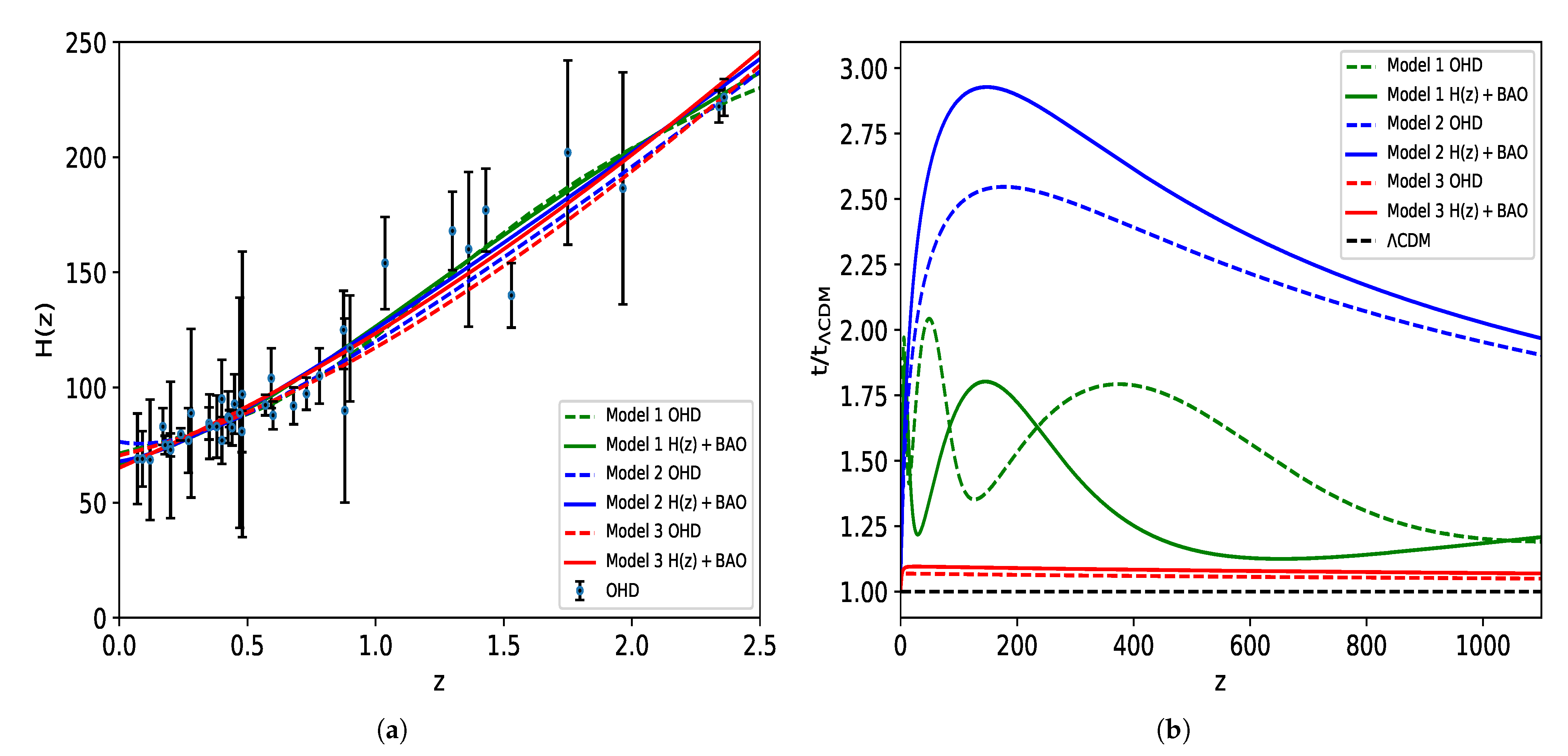
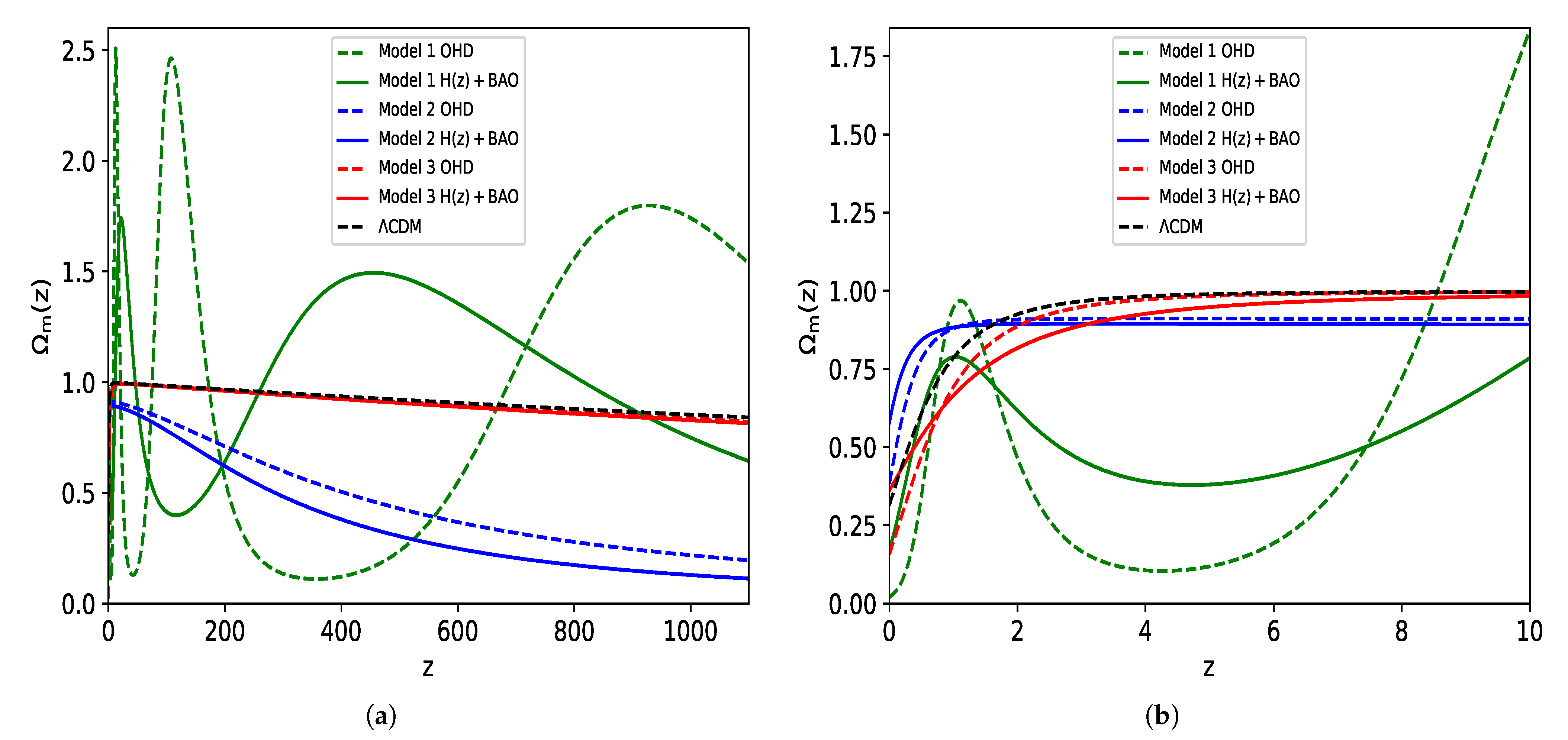
5. Preferred Best-Fitting Models and Their Implications

From Table 2 we can see that although Model 1 has the lowest ${\chi }_{\min }^2$, based on $AIC$ and $BIC$, Model 2 is the best candidate among these three models. The evidence against Model 1 is not strong, so Model 1 is not ruled out from these three candidate models. The values of reduced ${\chi }_{\min }^2\sim 0.5$ suggest that the error bars of these data are overestimated. Below we summarize the main results for the best-fitting models with the unmarginalized best-fitting parameters listed in Table 2 in different data combinations. Note that unmariginalized best-fitting parameters means that the parameters are given by maximizing the full likelihood, while the marginalized likelihood means the likelihood is obtained by marginalizing over one (or some) of the parameters.

Model 1 

With the best-fitting parameters in this model, we have:

• EoR ($6\lesssim z\lesssim 15$), for OHD ($H\left(z\right)$ + BAO), from around 379.9 Myr (402.6 Myr) to 1.825 Gyr (1.718 Gyr), which lasts ∼ 1.445 Gyr (1.315 Gyr);
• The seed redshift of J0100+2802, for OHD ($H\left(z\right)$ + BAO), $z_{\mathrm{seed}}\sim$ 9.74 (11.03);
• If the first star formed at $z\approx 20$, then the age of the universe at that time would be, for OHD ($H\left(z\right)$ + BAO), 272.8 Myr (234.1 Myr);
• Old globular cluster M92 (NGC 6341) would appear at $z\sim 7.53\left(9.27\right)$ with age of 14.0 Gyr for OHD ($H\left(z\right)$ + BAO);
• For OHD ($H\left(z\right)$ + BAO), 3.5-Gyr-old ratio galaxy 53W091 ($z\sim 1.55$) and 4-Gyr-old radio galaxy 53W069 ($z\sim 1.43$) are formed at $z\sim 4.98\left(5.40\right)$ and $z\sim 5.41\left(5.99\right)$, respectively;
• For OHD ($H\left(z\right)$ + BAO), QSO APM 08279+5255 with age around 2.1 Gyr [62] would have formed at $z\sim 9.37\left(12.32\right)$.

Model 2 

With the best-fitting parameters in this Model, we have:

• EoR ($6\lesssim z\lesssim 15$), for OHD ($H\left(z\right)$ + BAO), from around 478.7 Myr (534.1 Myr) to 1.371 Gyr (1.462 Gyr), which lasts ∼ 892.4 Myr (927.8 Myr);
• The seed redshift of J0100+2802, for OHD ($H\left(z\right)$ + BAO), $z_{\mathrm{seed}}\sim 17.75\left(16.46\right)$;
• If the first star formed at $z\approx 20$, then the age of the universe at that time would be, for OHD ($H\left(z\right)$ + BAO), 337.1 Myr (381.4 Myr);
• Old globular cluster M92 (NGC 6341) would appear at $z\sim 18.19\left(18.98\right)$ with age of 14.0 Gyr for OHD ($H\left(z\right)$ + BAO);
• For OHD ($H\left(z\right)$ + BAO), 3.5-Gyr-old ratio galaxy 53W091 ($z\sim 1.55$) and 4-Gyr-old radio galaxy 53W069 ($z\sim 1.43$) are formed at $z\sim 5.95\left(6.20\right)$ and $z\sim 6.85\left(7.22\right)$, respectively;
• For OHD ($H\left(z\right)$ + BAO), QSO APM 08279+5255 with age around 2.1 Gyr would have formed at $z\sim 92.16\left(44.83\right)$. If we consider it to be formed after $z\approx 20$, then its age would be $\sim 1.810\left(1.861\right)$ Gyr for OHD ($H\left(z\right)$ + BAO).

Model 3 

With the best-fitting parameters in this model, we have:

• EoR ($6\lesssim z\lesssim 15$), for OHD ($H\left(z\right)$ + BAO), from around 286.8 Myr (293.9 Myr) to 992.2 Myr (1.011 Gyr), which lasts ∼ 705.4 Myr (716.8 Myr);
• The seed redshift of J0100+2802, for OHD and $H\left(z\right)$ + BAO, $z_{\mathrm{seed}}>20$;
• If the first star formed at $z\approx 20$, then the age of the universe at that time would be, for OHD ($H\left(z\right)$ + BAO), 190.5 Myr (195.3 Myr);
• Old globular cluster M92 (NGC 6341) would appear at $z\sim 71.70(>1100)$ with age of 14.0 Gyr for OHD and $H\left(z\right)$ + BAO;
• addedFor OHD ($H\left(z\right)$ + BAO), 3.5-Gyr-old ratio galaxy 53W091 ($z\sim 1.55$) and 4-Gyr-old radio galaxy 53W069 ($z\sim 1.43$) are formed at $z\sim 6.48\left(6.92\right)$ and $z\sim 7.76\left(8.54\right)$, respectively;
• For OHD and $H\left(z\right)$ + BAO, QSO APM 08279+5255 with age around 2.1 Gyr would have formed at $z>1100$. (ruled out)

Therefore, the Model 1 OHD and $H\left(z\right)$ + BAO cases are the best cases to alleviate the aging problems. In Figure 5, the redshifts when $H\left(z\right)/H_{\mathsf{\Lambda }\mathrm{CDM}}\left(z\right)\sim 1$ are 0.40, 0.91, and 1.99 (Model 1 OHD), 0.30 and 1.96 (Model 1 $H\left(z\right)$ + BAO), 0.40 (Model 2 OHD), 0.04, 0.24, and 1.83 (Model 2 $H\left(z\right)$ + BAO), 0.52 and 725.79 (Model 3 OHD), and 0.16, 1.56, and 984.77 (Model 3 $H\left(z\right)$ + BAO); and the current values of $H/H_{\mathsf{\Lambda }\mathrm{CDM}}$ are 0.49 (Model 1 OHD), 0.33 (Model 1 $H\left(z\right)$ + BAO), 0.49 (Model 2 OHD), 0.47 (Model 2 $H\left(z\right)$ + BAO), 1.03 (Model 3 OHD), and 1.01 (Model 3 $H\left(z\right)$ + BAO). Note that the evolutions of dust matter density parameter ${\Omega }_m$ and DE density parameter ${\Omega }_{\mathrm{X}}$ are shown in Figure 6 and Figure 7 up to $z=1100$, where for Model 1 OHD ($H\left(z\right)$ + BAO), the redshifts when ${\Omega }_m$ have local extrema are 1.11, 4.26, 12.51, 41.89, 107.78, 356.20, and 928.41 (Model 1 OHD); 1.03, 4.72, 21.71, 115.98, and 455.68 (Model 1 $H\left(z\right)$ + BAO); 3.98 (Model 2 OHD); 3.23 (Model 1 $H\left(z\right)$ + BAO); 14.15 (Model 1 OHD); and 24.84 (Model 1 $H\left(z\right)$ + BAO); while the redshifts when ${\Omega }_{\mathrm{X}}$ have local extrema are 1.11, 4.24, 12.51, 40.53, 107.27, 300.45, and 906.09 (Model 1 OHD); 1.03, 4.70, 21.67, 108.17, and 443.89 (Model 1 $H\left(z\right)$ + BAO); and none for the rest cases. Since the universe has a slightly larger age in these best-fitting models, we also care about how it works with the expansion of the universe. The deceleration parameter is

$$q\left(z\right)=-\left(\frac{\ddot{a}}{a}\right)/H^2=\frac{1}{H\left(z\right)}\frac{dH\left(z\right)}{dz}(1+z)-1.$$

(27)

As shown in Figure 8, except for the Model 3 OHD and $H\left(z\right)$ + BAO cases, the deceleration parameter $q\left(z\right)$ for the other four cases are going through transitions from deceleration to acceleration phases. For the Model 1 OHD case, the transition redshifts (for $z\le 1100$) are 8.67, 56.70, and 169.15; for the Model 1 $H\left(z\right)$ + BAO case, the transition redshifts are 8.67, 56.70, and 169.15; for the Model 2 OHD case, the transition redshift is 0.45; and for the Model 2 $H\left(z\right)$ + BAO case, the transition redshift is 0.64; while for the Model 3 OHD and $H\left(z\right)$ + BAO cases, $q\left(z\right)<0$ is satisfied until today.

Although the Model 1 OHD and $H\left(z\right)$ + BAO cases are capable of explaining the aging issues, Model 1 have some strange (non-physical) behaviors due to the unbounded time-dependent choice of $\lambda$, where the matter density parameter ${\Omega }_m$ and the DE density parameter ${\Omega }_{\mathrm{X}}$ oscillate with the value of ${\Omega }_m$ and ${\Omega }_{\mathrm{X}}$ being a high of 2.51 (1.74) and a low of $-1.52$ ($-0.75$) for the Model 1 OHD and $H\left(z\right)$ + BAO cases, respectively. From panel (b) of Figure 1 we see that the Model 2 cases have relatively larger ages during the evolution and find that other than the age of QSO APM 08279+5255, the other age issues are significantly improved. Furthermore, judging from $AIC$ and $BIC$ listed in Table 2, Model 2 is the most favored model among these three models. Therefore, we conclude that Model 2 is the best model.

6. Conclusions and Discussions

By exploring the properties of the coupling models with the best-fitting parameters obtained from constraints over OHD and $H\left(z\right)$ + BAO, we manage to improve the aging problems of the $\mathsf{\Lambda }$CDM model, where four of the six best-fitting models demonstrate good improvements on them. Although the Model 1 OHD and $H\left(z\right)$ + BAO cases have better capability of improving the issues, Model 1 has some strange (non-physical) behaviors (see, e.g., Figure 6 and Figure 7). The Model 2 OHD and $H\left(z\right)$ + BAO cases can alleviate most of the aging problems and based on $AIC$ and $BIC$ listed in Table 2, Model 2 is considered to be the best candidate model amongst these three models. For Model 2 OHD ($H\left(z\right)$ + BAO), the constraints on the parameters are ${\Omega }_{m_0}=0.{385}_{-0.111}^{+0.093}(0.{444}_{-0.240}^{+0.183})$, $w_{\mathrm{X}}=-2.{298}_{-0.813}^{+1.355}(-1.{650}_{-0.396}^{+1.203})$, $H_0=77.{42}_{-11.21}^{+6.66}(68.{04}_{-5.45}^{+2.62})$$\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$, and $\lambda =0.{158}_{-0.019}^{+0.107}(0.{127}_{-0.049}^{+0.124})$. The Model 2 OHD and $H\left(z\right)$ + BAO cases support the currently accelerating expansion of the the Universe with the expansions transitioned from decelerating to accelerating at redshits 0.45 and 0.64, respectively. The ages of the universes are 14.385 Gyr and 14.409 Gyr in the Model 2 OHD and $H\left(z\right)$ + BAO cases, respectively. That Model 3 is ruled out does not convey the idea that the coupling between DE and DM is not worth investigating, because we do not include perturbations in this paper.