Scope Out Multiband Gravitational-Wave Observations of GW190521-Like Binary Black Holes with Space Gravitational Wave Antenna B-DECIGO
Abstract
1. Introduction
Goals and Organization of This Paper
2. Method for Signal-to-Noise Ratio and Fisher Analysis
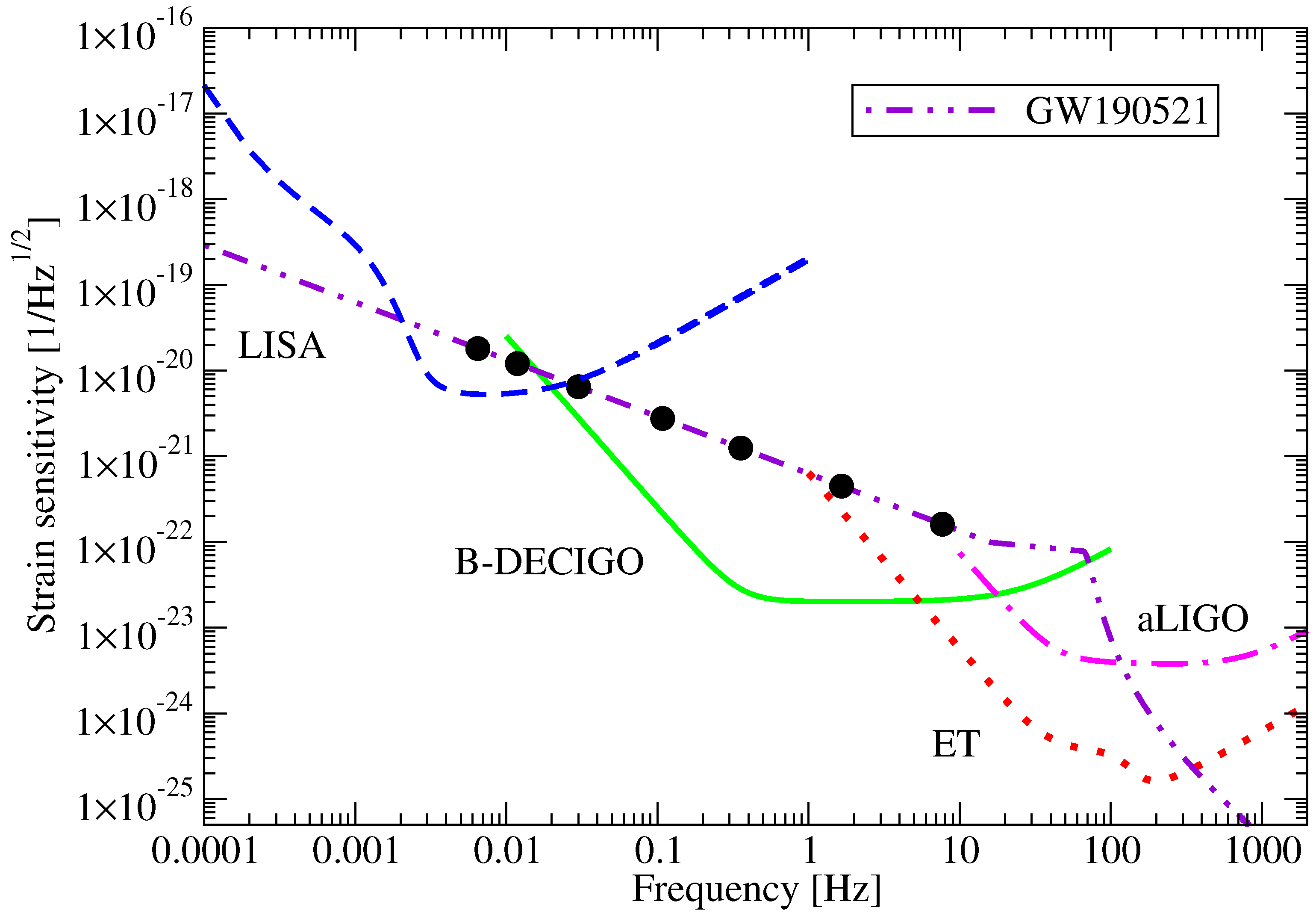
2.1. aLIGO, ET, B-DECIGO and LISA
2.2. Waveform Models
2.3. Signal-to-Noise Ratio
2.4. Multiband Fisher Analysis
3. Parameter Estimation Errors via Multiband Observation
3.1. Setup of Fisher Analysis
3.2. Result: Inspiral Phase
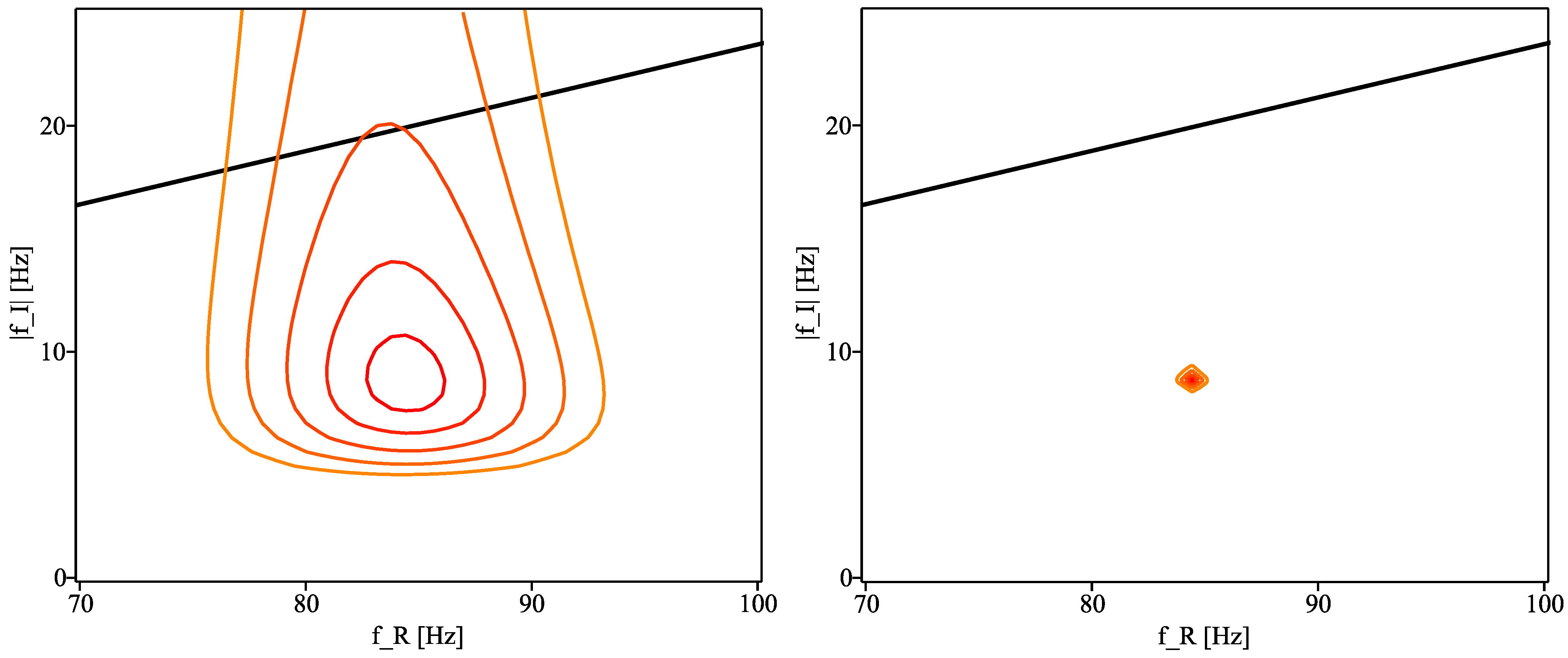
3.3. Result: Ringdown Phase
4. The Implications for Tests of GR via Multiband Observation
4.1. A Consistency test of GR with the Inspiral and Ringdown GW Signals
4.2. A Simple Test of the Remnant Compact Object with Quasinormal Modes
5. Summary and Discussion
Assessment of Prospects
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Signal-to-Noise Ratio of GW190521-Like Eccentric BBH Systems
| SNR and Eccentricity at | |||||
|---|---|---|---|---|---|
| aLIGO | |||||
| ET | |||||
| B-DECIGO | |||||
| LISA | <1.00 | <1.00 | <1.00 | ||
| (0.985) | (>0.999) | (>0.999) | (>0.999) | ||
Appendix B. Some More Noise Power Spectral Densities of (Next-Generation) GW Detectors
- “LIGO O3a-Livingston” rough fitting curve (during the first half of LIGO/Virgo third observing run by using Ref. [157]):
- “CE2” rough fitting curve (for Cosmic Explorer presented in Ref. [21]):
- “DECIGO” (the noise PSD of the L-shaped configuration [161]):with . Note that this expression accounted for the factor of due to DECIGO having arms that make an angle of .
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. arXiv 2010, arXiv:2010.14527. [Google Scholar]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190521: A Binary Black Hole Merger with a Total Mass of 150M⊙. Phys. Rev. Lett. 2020, 125, 101102. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Properties and Astrophysical Implications of the 150 M⊙ Binary Black Hole Merger GW190521. Astrophys. J. Lett. 2020, 900, L13. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi1, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Varma, V.; Field, S.E.; Scheel, M.A.; Blackman, J.; Gerosa, D.; Stein, L.C.; Kidder, L.E.; Pfeiffer, H.P. Surrogate models for precessing binary black hole simulations with unequal masses. Phys. Rev. Res. 2019, 1, 033015. [Google Scholar] [CrossRef]
- Nitz, A.H.; Capano, C.D. GW190521 may be an intermediate mass ratio inspiral. arXiv 2010, arXiv:2010.12558. [Google Scholar]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Nakamura, T.; Ando, M.; Kinugawa, T.; Nakano, H.; Eda, K.; Sato, S.; Musha, M.; Akutsu, T.; Tanaka, T.; Seto, N.; et al. Pre-DECIGO can get the smoking gun to decide the astrophysical or cosmological origin of GW150914-like binary black holes. Prog. Theor. Exp. Phys. 2016, 2016, 093E01. [Google Scholar] [CrossRef]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. arXiv 2020, arXiv:2006.13545. [Google Scholar]
- Ruan, W.H.; Guo, Z.K.; Cai, R.G.; Zhang, Y.Z. Taiji program: Gravitational-wave sources. Int. J. Mod. Phys. A 2020, 35, 2050075. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.-S.; Duan, H.-Z.; Gong, Y.-G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M. TianQin: A space-borne gravitational wave detector. Class. Quant. Grav. 2016, 33, 035010. [Google Scholar] [CrossRef]
- Graham, P.W.; Jung, S. Localizing Gravitational Wave Sources with Single-Baseline Atom Interferometers. Phys. Rev. D 2018, 97, 024052. [Google Scholar] [CrossRef]
- Kuns, K.A.; Yu, H.; Chen, Y.; Adhikari, R.X. Astrophysics and cosmology with a decihertz gravitational-wave detector: TianGO. Phys. Rev. D 2020, 102, 043001. [Google Scholar] [CrossRef]
- Ni, W.T. Gravitational wave detection in space. Int. J. Mod. Phys. D 2016, 25, 1630001. [Google Scholar] [CrossRef]
- Ni, W.T. Mid-frequency gravitational wave detection and sources. Int. J. Mod. Phys. D 2020, 29, 1902005. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Aso, Y.; Bae, S.-W.; Bae, Y.-B.; et al. Overview of KAGRA: Detector design and construction history. arXiv 2020, arXiv:2005.05574. [Google Scholar] [CrossRef]
- Hild, S.; Chelkowski, S.; Freise, A.; Franc, J.; Morgado, N.; Flaminio, R.; DeSalvo, R. A Xylophone Configuration for a third Generation Gravitational Wave Detector. Class. Quant. Grav. 2010, 27, 015003. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quant. Grav. 2010, 27, 194002. [Google Scholar] [CrossRef]
- Reitze, D.; Adhikari, R.X.; Ballmer, S.; Barish, B.; Barsotti, L.; Billingsley, G.; Brown, D.A.; Chen, Y.; Coyne, D.; Eisenstein, R.; et al. Cosmic Explorer: The U.S. Contribution to Gravitational-Wave Astronomy beyond LIGO. Bull. Am. Astron. Soc. 2019, 51, 035. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Sesana, A. Prospects for Multiband Gravitational-Wave Astronomy after GW150914. Phys. Rev. Lett. 2016, 116, 231102. [Google Scholar] [CrossRef]
- Cutler, C.; Berti, E.; Jani, K.; Kovetz, E.D.; Randall, L.; Vitale, S.; Wong, K.W.K.; Holley-Bockelmann, K.; Larson, S.L.; Littenberg, T.; et al. What we can learn from multi-band observations of black hole binaries. arXiv 2019, arXiv:1903.04069. [Google Scholar]
- Vitale, S. Multiband Gravitational-Wave Astronomy: Parameter Estimation and Tests of General Relativity with Space- and Ground-Based Detectors. Phys. Rev. Lett. 2016, 117, 051102. [Google Scholar] [CrossRef] [PubMed]
- Jani, K.; Shoemaker, D.; Cutler, C. Detectability of Intermediate-Mass Black Holes in Multiband Gravitational Wave Astronomy. Nat. Astron. 2019, 4, 260–265. [Google Scholar] [CrossRef]
- Barausse, E.; Yunes, N.; Chamberlain, K. Theory-Agnostic Constraints on Black-Hole Dipole Radiation with Multiband Gravitational-Wave Astrophysics. Phys. Rev. Lett. 2016, 116, 241104. [Google Scholar] [CrossRef]
- Carson, Z.; Yagi, K. Multi-band gravitational wave tests of general relativity. Class. Quant. Grav. 2020, 37, 02LT01. [Google Scholar] [CrossRef]
- Carson, Z.; Yagi, K. Parametrized and inspiral-merger-ringdown consistency tests of gravity with multiband gravitational wave observations. Phys. Rev. D 2020, 101, 044047. [Google Scholar] [CrossRef]
- Toubiana, A.; Marsat, S.; Babak, S.; Barausse, E.; Baker, J. Tests of general relativity with stellar-mass black hole binaries observed by LISA. Phys. Rev. D 2020, 101, 104038. [Google Scholar] [CrossRef]
- Gupta, A.; Datta, S.; Kastha, S.; Borhanian, S.; Arun, K.G.; Sathyaprakash, B.S. Multiparameter tests of general relativity using multiband gravitational-wave observations. Phys. Rev. Lett. 2020, 125, 201101. [Google Scholar] [CrossRef]
- Datta, S.; Gupta, A.; Kastha, S.; Arun, K.G.; Sathyaprakash, B.S. Tests of general relativity using multiband observations of intermediate mass binary black hole mergers. Phys. Rev. D 2021, 103, 024036. [Google Scholar] [CrossRef]
- Gerosa, D.; Ma, S.; Wong, K.W.K.; Berti, E.; O’Shaughnessy, R.; Chen, Y.; Belczynski, K. Multiband gravitational-wave event rates and stellar physics. Phys. Rev. D 2019, 99, 103004. [Google Scholar] [CrossRef]
- Ng, K.K.Y.; Isi, M.; Haster, C.J.; Vitale, S. Multiband gravitational-wave searches for ultralight bosons. Phys. Rev. D 2020, 102, 083020. [Google Scholar] [CrossRef]
- Toubiana, A.; Sberna, L.; Caputo, A.; Cusin, G.; Marsat, S.; Jani, K.; Babak, S.; Barausse, E.; Caprini, C.; Pani, P.; et al. Detectable environmental effects in GW190521-like black-hole binaries with LISA. arXiv 2020, arXiv:2010.06056. [Google Scholar]
- Ewing, B.; Sachdev, S.; Borhanian, S.; Sathyaprakash, B.S. Archival searches for stellar-mass binary black holes in LISA. arXiv 2020, arXiv:2011.03036. [Google Scholar]
- Nair, R.; Jhingan, S.; Tanaka, T. Synergy between ground and space based gravitational wave detectors for estimation of binary coalescence parameters. Prog. Theor. Exp. Phys. 2016, 2016, 053E01. [Google Scholar] [CrossRef]
- Isoyama, S.; Nakano, H.; Nakamura, T. Multiband Gravitational-Wave Astronomy: Observing binary inspirals with a decihertz detector, B-DECIGO. Prog. Theor. Exp. Phys. 2018, 2018, 073E01. [Google Scholar] [CrossRef]
- Nair, R.; Tanaka, T. Synergy between ground and space based gravitational wave detectors. Part II: Localisation. J. Cosmol. Astropart. Phys. 2018, 8, 033. [Google Scholar] [CrossRef]
- Grimm, S.; Harms, J. Multiband gravitational-wave parameter estimation: A study of future detectors. Phys. Rev. D 2020, 102, 022007. [Google Scholar] [CrossRef]
- Liu, C.; Shao, L.; Zhao, J.; Gao, Y. Multiband Observation of LIGO/Virgo Binary Black Hole Mergers in the Gravitational-wave Transient Catalog GWTC-1. Mon. Not. R. Astron. Soc. 2020, 496, 182–196. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Santamaria, L. Detection of IMBHs with ground-based gravitational wave observatories: A biography of a binary of black holes, from birth to death. Astrophys. J. 2010, 722, 1197–1206. [Google Scholar] [CrossRef][Green Version]
- Yagi, K. Gravitational wave observations of galactic intermediate-mass black hole binaries with DECIGO Path Finder. Class. Quant. Grav. 2012, 29, 075005. [Google Scholar] [CrossRef]
- Gayathri, V.; Healy, J.; Lange, J.; O’Brien, B.; Szczepanczyk, M.; Bartos, I.; Campanelli, M.; Klimenko, S.; Lousto, C.; O’Shaughnessy, R. GW190521 as a Highly Eccentric Black Hole Merger. arXiv 2020, arXiv:2009.05461. [Google Scholar]
- Ajith, P. Addressing the spin question in gravitational-wave searches: Waveform templates for inspiralling compact binaries with nonprecessing spins. Phys. Rev. D 2011, 84, 084037. [Google Scholar] [CrossRef]
- Sathyaprakash, B.S.; Schutz, B.F. Physics, Astrophysics and Cosmology with Gravitational Waves. Living Rev. Rel. 2009, 12, 2. [Google Scholar] [CrossRef]
- Robson, T.; Cornish, N.J.; Liu, C. The construction and use of LISA sensitivity curves. Class. Quant. Grav. 2019, 36, 105011. [Google Scholar] [CrossRef]
- Nagar, A.; Bernuzzi, S.; Pozzo, W.D.; Riemenschneider, G.; Akcay, S.; Carullo, G.; Fleig, P.; Babak, S.; Tsang, K.W.; Colleoni, M.; et al. Time-domain effective-one-body gravitational waveforms for coalescing compact binaries with nonprecessing spins, tides and self-spin effects. Phys. Rev. D 2018, 98, 104052. [Google Scholar] [CrossRef]
- Ossokine, S.; Buonanno, A.; Marsat, S.; Cotesta, R.; Babak, S.; Dietrich, T.; Haas, R.; Hinder, I.; Pfeiffer, H.P.; Purrer, M.; et al. Multipolar Effective-One-Body Waveforms for Precessing Binary Black Holes: Construction and Validation. Phys. Rev. D 2020, 102, 044055. [Google Scholar] [CrossRef]
- Khan, S.; Ohme, F.; Chatziioannou, K.; Hannam, M. Including higher order multipoles in gravitational-wave models for precessing binary black holes. Phys. Rev. D 2020, 101, 024056. [Google Scholar] [CrossRef]
- Pratten, G.; Husa, S.; Garcia-Quiros, C.; Colleoni, M.; Ramos-Buades, A.; Estelles, H.; Jaume, R. Setting the cornerstone for a family of models for gravitational waves from compact binaries: The dominant harmonic for nonprecessing quasicircular black holes. Phys. Rev. D 2020, 102, 064001. [Google Scholar] [CrossRef]
- Berti, E.; Buonanno, A.; Will, C.M. Estimating spinning binary parameters and testing alternative theories of gravity with LISA. Phys. Rev. D 2005, 71, 084025. [Google Scholar] [CrossRef]
- Dalal, N.; Holz, D.E.; Hughes, S.A.; Jain, B. Short grb and binary black hole standard sirens as a probe of dark energy. Phys. Rev. D 2006, 74, 063006. [Google Scholar] [CrossRef]
- Mishra, C.K.; Kela, A.; Arun, K.G.; Faye, G. Ready-to-use post-Newtonian gravitational waveforms for binary black holes with nonprecessing spins: An update. Phys. Rev. D 2016, 93, 084054. [Google Scholar] [CrossRef]
- Arun, K.G.; Iyer, B.R.; Sathyaprakash, B.S.; Sundararajan, P.A. Parameter estimation of inspiralling compact binaries using 3.5 post-Newtonian gravitational wave phasing: The Non-spinning case. Phys. Rev. D 2005, 71, 084008, Erratum in 2005, 72, 069903. [Google Scholar] [CrossRef]
- Blanchet, L. Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries. Living Rev. Rel. 2014, 17, 2. [Google Scholar] [CrossRef] [PubMed]
- Bohé, A.; Marsat, S.; Blanchet, L. Next-to-next-to-leading order spin-orbit effects in the gravitational wave flux and orbital phasing of compact binaries. Class. Quant. Grav. 2013, 30, 135009. [Google Scholar] [CrossRef]
- Bohé, A.; Faye, G.; Marsat, S.; Porter, E.K. Quadratic-in-spin effects in the orbital dynamics and gravitational-wave energy flux of compact binaries at the 3PN order. Class. Quant. Grav. 2015, 32, 195010. [Google Scholar] [CrossRef]
- Marsat, S. Cubic order spin effects in the dynamics and gravitational wave energy flux of compact object binaries. Class. Quant. Grav. 2015, 32, 085008. [Google Scholar] [CrossRef]
- Chatziioannou, K.; Poisson, E.; Yunes, N. Improved next-to-leading order tidal heating and torquing of a Kerr black hole. Phys. Rev. D 2016, 94, 084043. [Google Scholar] [CrossRef]
- Isoyama, S.; Nakano, H. Post-Newtonian templates for binary black-hole inspirals: The effect of the horizon fluxes and the secular change in the black-hole masses and spins. Class. Quant. Grav. 2018, 35, 024001. [Google Scholar] [CrossRef]
- Hughes, S.A. Bound orbits of a slowly evolving black hole. Phys. Rev. D 2019, 100, 064001. [Google Scholar] [CrossRef]
- Nakano, H.; Takahashi, H.; Tagoshi, H.; Sasaki, M. An Effective search method for gravitational ringing of black holes. Phys. Rev. D 2003, 68, 102003. [Google Scholar] [CrossRef]
- Nakano, H.; Takahashi, H.; Tagoshi, H.; Sasaki, M. An Improved search method for gravitational ringing of black holes. Prog. Theor. Phys. 2004, 111, 781–805. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Will, C.M. On gravitational-wave spectroscopy of massive black holes with the space interferometer LISA. Phys. Rev. D 2006, 73, 064030. [Google Scholar] [CrossRef]
- Nakano, H.; Tanaka, T.; Nakamura, T. Possible golden events for ringdown gravitational waves. Phys. Rev. D 2015, 92, 064003. [Google Scholar] [CrossRef]
- Mohanty, S.D. Hierarchical search strategy for the detection of gravitational waves from coalescing binaries: Extension to postNewtonian wave forms. Phys. Rev. D 1998, 57, 630–658. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O.; Zlochower, Y. Remnant mass, spin, and recoil from spin aligned black-hole binaries. Phys. Rev. D 2014, 90, 104004. [Google Scholar] [CrossRef]
- Hofmann, F.; Barausse, E.; Rezzolla, L. The final spin from binary black holes in quasi-circular orbits. Astrophys. J. Lett. 2016, 825, L19. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O. Remnant of binary black-hole mergers: New simulations and peak luminosity studies. Phys. Rev. D 2017, 95, 024037. [Google Scholar] [CrossRef]
- Jiménez-Forteza, X.; Keitel, D.; Husa, S.; Hannam, M.; Khan, S.; Pürrer, M. Hierarchical data-driven approach to fitting numerical relativity data for nonprecessing binary black holes with an application to final spin and radiated energy. Phys. Rev. D 2017, 95, 064024. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O. Hangup effect in unequal mass binary black hole mergers and further studies of their gravitational radiation and remnant properties. Phys. Rev. D 2018, 97, 084002. [Google Scholar] [CrossRef]
- Varma, V.; Gerosa, D.; Stein, L.C.; Hébert, F.; Zhang, H. High-accuracy mass, spin, and recoil predictions of generic black-hole merger remnants. Phys. Rev. Lett. 2019, 122, 011101. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Isolated and dynamical horizons and their applications. Living Rev. Rel. 2004, 7, 10. [Google Scholar] [CrossRef]
- Black Hole Perturbation Club (BHPC). Available online: https://sites.google.com/view/bhpc1996/home (accessed on 2 March 2021).
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Emanuele Berti’s Ringdown. Available online: https://pages.jh.edu/eberti2/ringdown/ (accessed on 2 March 2021).
- Cook, G.B.; Zalutskiy, M. Gravitational perturbations of the Kerr geometry: High-accuracy study. Phys. Rev. D 2014, 90, 124021. [Google Scholar] [CrossRef]
- Black Hole Perturbation ToolKit. Available online: https://bhptoolkit.org/ (accessed on 2 March 2021).
- Ajith, P.; Hannam, M.; Husa, S.; Chen, Y.; Bruegmann, B.; Dorband, N.; Muller, D.; Ohme, F.; Pollney, D.; Reisswig, C.; et al. Inspiral-merger-ringdown waveforms for black-hole binaries with non-precessing spins. Phys. Rev. Lett. 2011, 106, 241101. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.J.; Cole, R.H.; Berry, C.P.L. Gravitational-wave sensitivity curves. Class. Quant. Grav. 2015, 32, 015014. [Google Scholar] [CrossRef]
- Finn, L.S. Detection, measurement and gravitational radiation. Phys. Rev. D 1992, 46, 5236. [Google Scholar] [CrossRef]
- Vallisneri, M. Use and abuse of the Fisher information matrix in the assessment of gravitational-wave parameter-estimation prospects. Phys. Rev. D 2008, 77, 042001. [Google Scholar] [CrossRef]
- Babak, S.; Gair, J.; Sesana, A.; Barausse, E.; Sopuerta, C.F.; Berry, C.P.L.; Berti, E.; Amaro-Seoane, P.; Petiteau, A.; Klein, A. Science with the space-based interferometer LISA. V: Extreme mass-ratio inspirals. Phys. Rev. D 2017, 95, 103012. [Google Scholar] [CrossRef]
- Giesler, M.; Isi, M.; Scheel, M.A.; Teukolsky, S. Black Hole Ringdown: The Importance of Overtones. Phys. Rev. X 2019, 9, 041060. [Google Scholar] [CrossRef]
- Poisson, E.; Will, C.M. Gravitational waves from inspiraling compact binaries: Parameter estimation using second postNewtonian wave forms. Phys. Rev. D 1995, 52, 848–855. [Google Scholar] [CrossRef]
- Moore, C.J.; Gerosa, D.; Klein, A. Are stellar-mass black-hole binaries too quiet for LISA? Mon. Not. R. Astron. Soc. 2019, 488, L94–L98. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of general relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101, Erratum in 2018, 121, 129902. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of General Relativity with the Binary Black Hole Signals from the LIGO-Virgo Catalog GWTC-1. Phys. Rev. D 2019, 100, 104036. [Google Scholar] [CrossRef]
- Carson, Z.; Yagi, K. Parameterized and Consistency Tests of Gravity with GravitationalWaves: Current and Future. Proceedings 2019, 17, 5. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Tests of General Relativity with Binary Black Holes from the second LIGO-Virgo Gravitational-Wave Transient Catalog. arXiv 2020, arXiv:2010.14529. [Google Scholar]
- Nakano, H.; Nakamura, T.; Tanaka, T. The detection of quasinormal mode with a/M∼0.95 would prove a sphere 99% soaking in the ergoregion of the Kerr space-time. Prog. Theor. Exp. Phys. 2016, 31E02. [Google Scholar] [CrossRef]
- Pretorius, F. Evolution of binary black hole spacetimes. Phys. Rev. Lett. 2005, 95, 121101. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C.O.; Marronetti, P.; Zlochower, Y. Accurate evolutions of orbiting black-hole binaries without excision. Phys. Rev. Lett. 2006, 96, 111101. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.G.; Centrella, J.; Choi, D.I.; Koppitz, M.; van Meter, J. Gravitational wave extraction from an inspiraling configuration of merging black holes. Phys. Rev. Lett. 2006, 96, 111102. [Google Scholar] [CrossRef] [PubMed]
- Jani, K.; Healy, J.; Clark, J.A.; London, L.; Laguna, P.; Shoemaker, D. Georgia Tech Catalog of Gravitational Waveforms. Class. Quant. Grav. 2016, 33, 204001. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O.; Zlochower, Y.; Campanelli, M. The RIT binary black hole simulations catalog. Class. Quant. Grav. 2017, 34, 224001. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O.; Lange, J.; O’Shaughnessy, R.; Zlochower, Y.; Campanelli, M. Second RIT binary black hole simulations catalog and its application to gravitational waves parameter estimation. Phys. Rev. D 2019, 100, 024021. [Google Scholar] [CrossRef]
- Boyle, M.; Hemberger, D.; Iozzo, D.A.B.; Lovelace, G.; Ossokine, S.; Pfeiffer, H.P.; Scheel, M.A.; Stein, L.C.; Woodford, C.J.; Zimmerman, A.B.; et al. The SXS Collaboration catalog of binary black hole simulations. Class. Quant. Grav. 2019, 36, 195006. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O. Third RIT binary black hole simulations catalog. Phys. Rev. D 2020, 102, 104018. [Google Scholar] [CrossRef]
- Ghosh, A.; Ghosh, A.; Johnson-McDaniel, N.K.; Mishra, C.K.; Ajith, P.; Pozzo, W.D.; Nichols, D.A.; Chen, Y.; Nielsen, A.B.; Berry, C.P.L.; et al. Testing general relativity using golden black-hole binaries. Phys. Rev. D 2016, 94, 021101. [Google Scholar] [CrossRef]
- Ghosh, A.; Johnson-Mcdaniel, N.K.; Ghosh, A.; Mishra, C.K.; Ajith, P.; Pozzo, W.D.; Berry, C.P.L.; Nielsen, A.B.; London, L. Testing general relativity using gravitational wave signals from the inspiral, merger and ringdown of binary black holes. Class. Quant. Grav. 2018, 35, 014002. [Google Scholar] [CrossRef]
- Hughes, S.A.; Menou, K. Golden binaries for LISA: Robust probes of strong-field gravity. Astrophys. J. 2005, 623, 689–699. [Google Scholar] [CrossRef]
- Luna, M.; Sintes, A.M. Parameter estimation of compact binaries using the inspiral and ringdown waveforms. Class. Quant. Grav. 2006, 23, 3763–3782. [Google Scholar] [CrossRef]
- Veitch, J.; Raymond, V.; Farr, B.; Farr, W.; Graff, P.; Vitale, S.; Aylott, B.; Blackburn, K.; Christensen, N.; Coughlin, M.; et al. Parameter estimation for compact binaries with ground-based gravitational-wave observations using the LALInference software library. Phys. Rev. D 2015, 91, 042003. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration. LIGO Algorithm Library—LALSuite. 2018. Available online: https://lscsoft.docs.ligo.org/lalsuite/lalsimulation/index.html (accessed on 2 March 2021).
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Properties of the Binary Black Hole Merger GW150914. Phys. Rev. Lett. 2016, 116, 241102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, T.D.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Improved analysis of GW150914 using a fully spin-precessing waveform Model. Phys. Rev. X 2016, 6, 041014. [Google Scholar] [CrossRef]
- Yang, H.; Yagi, K.; Blackman, J.; Lehner, L.; Paschalidis, V.; Pretorius, F.; Yunes, N. Black hole spectroscopy with coherent mode stacking. Phys. Rev. Lett. 2017, 118, 161101. [Google Scholar] [CrossRef]
- Isoyama, S.; Sturani, R.; Nakano, H. Post-Newtonian templates for gravitational waves from compact binary inspirals. arXiv 2012, arXiv:2012.01350. [Google Scholar]
- Biwer, C.M.; Capano, C.D.; De, S.; Cabero, M.; Brown, D.A.; Nitz, A.H.; Raymond, V. PyCBC Inference: A Python-based parameter estimation toolkit for compact binary coalescence signals. Publ. Astron. Soc. Pac. 2019, 131, 024503. [Google Scholar] [CrossRef]
- Ashton, G.; Hübner, M.; Lasky, P.D.; Talbot, C.; Ackley, K.; Biscoveanu, S.; Chu, Q.; Divakarla, A.; Easter, P.J.; Goncharov, B.; et al. BILBY: A user-friendly Bayesian inference library for gravitational-wave astronomy. Astrophys. J. Suppl. 2019, 241, 27. [Google Scholar] [CrossRef]
- Ireland, B.; Birnholtz, O.; Nakano, H.; West, E.; Campanelli, M. Eccentric Binary Black Holes with Spin via the Direct Integration of the Post-Newtonian Equations of Motion. Phys. Rev. D 2019, 100, 024015. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- London, L.; Khan, S.; Fauchon-Jones, E.; García, C.; Hannam, M.; Husa, S.; Jiménez-Forteza, X.; Kalaghatgi, C.; Ohme, F.; Pannarale, F. First higher-multipole model of gravitational waves from spinning and coalescing black-hole binaries. Phys. Rev. Lett. 2018, 120, 161102. [Google Scholar] [CrossRef]
- Sakai, K.; Oohara, K.I.; Nakano, H.; Kaneyama, M.; Takahashi, H. Estimation of starting times of quasinormal modes in ringdown gravitational waves with the Hilbert-Huang transform. Phys. Rev. D 2017, 96, 044047. [Google Scholar] [CrossRef]
- Carullo, G.; Schaaf, L.V.D.; London, L.; Pang, P.T.H.; Tsang, K.W.; Hannuksela, O.A.; Meidam, J.; Agathos, M.; Samajdar, A.; Ghosh, A.; et al. Empirical tests of the black hole no-hair conjecture using gravitational-wave observations. Phys. Rev. D 2018, 98, 104020. [Google Scholar] [CrossRef]
- Isi, M.; Giesler, M.; Farr, W.M.; Scheel, M.A.; Teukolsky, S.A. Testing the no-hair theorem with GW150914. Phys. Rev. Lett. 2019, 123, 111102. [Google Scholar] [CrossRef]
- Bhagwat, S.; Forteza, X.J.; Pani, P.; Ferrari, V. Ringdown overtones, black hole spectroscopy, and no-hair theorem tests. Phys. Rev. D 2020, 101, 044033. [Google Scholar] [CrossRef]
- Ota, I.; Chirenti, C. Overtones or higher harmonics? Prospects for testing the no-hair theorem with gravitational wave detections. Phys. Rev. D 2020, 101, 104005. [Google Scholar] [CrossRef]
- Nakano, H.; Narikawa, T.; Oohara, K.; Sakai, K.; Shinkai, H.; Takahashi, H.; Tanaka, T.; Uchikata, N.; Yamamoto, S.; Yamamoto, T.S. Comparison of various methods to extract ringdown frequency from gravitational wave data. Phys. Rev. D 2019, 99, 124032. [Google Scholar] [CrossRef]
- Yamamoto, T.S.; Tanaka, T. Use of conditional variational auto encoder to analyze ringdown gravitational waves. arXiv 2012, arXiv:2002.12095. [Google Scholar]
- Carson, Z.; Yagi, K. Testing General Relativity with Gravitational Waves. arXiv 2011, arXiv:2011.02938. [Google Scholar]
- Detweiler, S.L. Black holes and gravitational waves. III. the resonant frequencies of rotating holes. Astrophys. J. 1980, 239, 292–295. [Google Scholar] [CrossRef]
- Dreyer, O.; Kelly, B.J.; Krishnan, B.; Finn, L.S.; Garrison, D.; Lopez-Aleman, R. Black hole spectroscopy: Testing general relativity through gravitational wave observations. Class. Quant. Grav. 2004, 21, 787–804. [Google Scholar] [CrossRef]
- Berti, E.; Sesana, A.; Barausse, E.; Cardoso, V.; Belczynski, K. Spectroscopy of Kerr black holes with Earth- and space-based interferometers. Phys. Rev. Lett. 2016, 117, 101102. [Google Scholar] [CrossRef]
- Baibhav, V.; Berti, E. Multimode black hole spectroscopy. Phys. Rev. D 2019, 99, 024005. [Google Scholar] [CrossRef]
- Gnocchi, G.; Maselli, A.; Abdelsalhin, T.; Giacobbo, N.; Mapelli, M. Bounding alternative theories of gravity with multiband GW observations. Phys. Rev. D 2019, 100, 064024. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, J.; Cardoso, V.; Cavaglia, M. Matched-filtering and parameter estimation of ringdown waveforms. Phys. Rev. D 2007, 76, 104044. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Asada, H.; Aso, Y.; Bae, S.; et al. Overview of KAGRA: KAGRA science. arXiv 2020, arXiv:2008.02921. [Google Scholar] [CrossRef]
- Uchikata, N.; Narikawa, T.; Sakai, K.; Takahashi, H.; Nakano, H. Black hole spectroscopy for KAGRA future prospect in O5. Phys. Rev. D 2020, 102, 024007. [Google Scholar] [CrossRef]
- Tso, R.; Gerosa, D.; Chen, Y. Optimizing LIGO with LISA forewarnings to improve black-hole spectroscopy. Phys. Rev. D 2019, 99, 124043. [Google Scholar] [CrossRef]
- Lousto, C.O. (Rochester Institute of Technology, Rochester, NY, USA). Personal communication, 2020.
- Romero-Shaw, I.M.; Lasky, P.D.; Thrane, E.; Bustillo, J.C. GW190521: Orbital eccentricity and signatures of dynamical formation in a binary black hole merger signal. Astrophys. J. Lett. 2020, 903, L5. [Google Scholar] [CrossRef]
- Bustillo, J.C.; Sanchis-Gual, N.; Torres-Forné, A.; Font, J.A. Confusing head-on and precessing intermediate-mass binary black hole mergers. arXiv 2020, arXiv:2009.01066. [Google Scholar]
- Peters, P.C.; Mathews, J. Gravitational radiation from point masses in a Keplerian orbit. Phys. Rev. 1963, 131, 435–439. [Google Scholar] [CrossRef]
- Peters, P.C. Gravitational Radiation and the Motion of Two Point Masses. Phys. Rev. 1964, 136, B1224. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational Waves. Vol. 1: Theory and Experiments; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Amaro-Seoane, P. Detecting Intermediate-Mass Ratio Inspirals From The Ground And Space. Phys. Rev. D 2018, 98, 063018. [Google Scholar] [CrossRef]
- Holgado, A.M.; Ortega, A.; Rodriguez, C.L. Dynamical Formation Scenarios for GW190521 and Prospects for Decihertz Gravitational-Wave Astronomy with GW190521-Like Binaries. arXiv 2020, arXiv:2012.09169. [Google Scholar]
- Amaro-Seoane, P.; Miller, M.C.; Freitag, M. Gravitational waves from eccentric intermediate-mass black hole binaries. Astrophys. J. Lett. 2009, 692, L50–L53. [Google Scholar] [CrossRef]
- Loutrel, N. Repeated Bursts: Gravitational Waves from Highly Eccentric Binaries. arXiv 2020, arXiv:2009.11332. [Google Scholar]
- Nagar, A.; Bonino, A.; Rettegno, P. All in one: Effective one body multipolar waveform model for spin-aligned, quasi-circular, eccentric, hyperbolic black hole binaries. arXiv 2021, arXiv:2101.08624. [Google Scholar]
- Arredondo, J.N.; Loutrel, N. Neutron Stars in the Effective Fly-By Framework: f-Mode Re-summation. arXiv 2021, arXiv:2101.10963. [Google Scholar]
- Setyawati, Y.; Ohme, F. Adding eccentricity to quasi-circular binary-black-hole waveform models. arXiv 2021, arXiv:2101.11033. [Google Scholar]
- Islam, T.; Varma, V.; Lodman, J.; Field, S.E.; Khanna, G.; Scheel, M.A.; Pfeiffer, H.P.; Gerosa, D.; Kidder, L.E. Eccentric binary black hole surrogate models for the gravitational waveform and remnant properties: Comparable mass, nonspinning case. arXiv 2021, arXiv:2101.11798. [Google Scholar]
- Finn, L.S.; Thorne, K.S. Gravitational waves from a compact star in a circular, inspiral orbit. Phys. Rev. D 2000, 62, 124021. [Google Scholar] [CrossRef]
- Huerta, E.A.; McWilliams, S.T.; Gair, J.R.; Taylor, S.R. Detection of eccentric supermassive black hole binaries with pulsar timing arrays: Signal-to-noise ratio calculations. Phys. Rev. D 2015, 92, 063010. [Google Scholar] [CrossRef]
- Cutler, C.; Kennefick, D.; Poisson, E. Gravitational radiation reaction for bound motion around a Schwarzschild black hole. Phys. Rev. D 1994, 50, 3816–3835. [Google Scholar] [CrossRef]
- Gondán, L.; Kocsis, B.; Raffai, P.; Frei, Z. Accuracy of Estimating Highly Eccentric Binary Black Hole Parameters with Gravitational-Wave Detections. Astrophys. J. 2018, 855, 34. [Google Scholar] [CrossRef]
- Mikoczi, B.; Kocsis, B.; Forgacs, P.; Vasuth, M. Parameter estimation for inspiraling eccentric compact binaries including pericenter precession. Phys. Rev. D 2012, 86, 104027. [Google Scholar] [CrossRef]
- Drasco, S.; Hughes, S.A. Gravitational wave snapshots of generic extreme mass ratio inspirals. Phys. Rev. D 2006, 73, 024027, Erratum in 2013, 88, 109905; Erratum in 2014, 90, 109905. [Google Scholar] [CrossRef]
- Nishizawa, A.; Berti, E.; Klein, A.; Sesana, A. eLISA eccentricity measurements as tracers of binary black hole formation. Phys. Rev. D 2016, 94, 064020. [Google Scholar] [CrossRef]
- Seto, N. Prospects of eLISA for Detecting Galactic Binary Black Holes Similar to GW150914. Mon. Not. R. Astron. Soc. 2016, 460, L1–L4. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Population Properties of Compact Objects from the Second LIGO-Virgo Gravitational-Wave Transient Catalog. arXiv 2020, arXiv:2010.14533. [Google Scholar]
- Kinugawa, T.; Nakamura, T.; Nakano, H. Formation of mass gap compact object and black hole binary from Population III stars. arXiv 2007, arXiv:2007.13343. [Google Scholar]
- KAGRA Collaboration; LIGO Scientific Collaboration; Virgo Collaboration. Prospects for Observing and Localizing Gravitational-Wave Transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2020, 21, 3. [Google Scholar] [CrossRef]
- Hild, S.; Chelkowski, S.; Freise, A. Pushing towards the ET sensitivity using ‘conventional’ technology. arXiv 2008, arXiv:0810.0604. [Google Scholar]
- Mishra, C.K.; Arun, K.G.; Iyer, B.R.; Sathyaprakash, B.S. Parametrized tests of post-Newtonian theory using Advanced LIGO and Einstein Telescope. Phys. Rev. D 2010, 82, 064010. [Google Scholar] [CrossRef]
- ET Sensitivities Page. Available online: http://www.et-gw.eu/index.php/etsensitivities (accessed on 2 March 2021).
- Yagi, K.; Seto, N. Detector configuration of DECIGO/BBO and identification of cosmological neutron-star binaries. Phys. Rev. D 2011, 83, 044011, Erratum in 2017, 95, 109901. [Google Scholar] [CrossRef]
- Hu, X.C.; Li, X.H.; Wang, Y.; Feng, W.F.; Zhou, M.Y.; Hu, Y.M.; Hu, S.C.; Mei, J.W.; Shao, C.G. Fundamentals of the orbit and response for TianQin. Class. Quant. Grav. 2018, 35, 095008. [Google Scholar] [CrossRef]
- Shi, C.; Bao, J.; Wang, H.; Zhang, J.D.; Hu, Y.; Sesana, A.; Barausse, E.; Mei, J.; Luo, J. Science with the TianQin observatory: Preliminary results on testing the no-hair theorem with ringdown signals. Phys. Rev. D 2019, 100, 044036. [Google Scholar] [CrossRef]
| Parameter | Symbol | |
|---|---|---|
| Primary mass [] | ||
| Secondary mass [] | ||
| Primary spin magnitude | ||
| Secondary spin magnitude | ||
| Total mass [] | ||
| Mass ratio | ||
| Luminosity Distance [Gpc] | ||
| Redshift | z |
| GW Detector | SNR | ||||
|---|---|---|---|---|---|
| BD + aLIGO | |||||
| BD | |||||
| aLIGO | ⋯ | ⋯ | ⋯ | ⋯ | |
| BD + aLIGO | |||||
| BD + ET | |||||
| ET | ⋯ | ||||
| BD + ET | |||||
| LISA + BD + ET | |||||
| LISA | ⋯ | ||||
| LISA + BD | |||||
| LISA + BD + ET | |||||
| GW Detector | SNR | ||
|---|---|---|---|
| aLIGO | |||
| ET |
| GW190521-Like BBH | GW150914-Like BBH | |||||
|---|---|---|---|---|---|---|
| GW Detector | SNR | SNR | ||||
| Single band: Ringdown GW signal | ||||||
| aLIGO | ||||||
| ET | ||||||
| Single band: inspiral GW signal | ||||||
| BD | ||||||
| Multiband: inspiral GW signal | ||||||
| BD + ET | ||||||
| LISA + BD | ||||||
| LISA + BD + ET | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakano, H.; Fujita, R.; Isoyama, S.; Sago, N. Scope Out Multiband Gravitational-Wave Observations of GW190521-Like Binary Black Holes with Space Gravitational Wave Antenna B-DECIGO. Universe 2021, 7, 53. https://doi.org/10.3390/universe7030053
Nakano H, Fujita R, Isoyama S, Sago N. Scope Out Multiband Gravitational-Wave Observations of GW190521-Like Binary Black Holes with Space Gravitational Wave Antenna B-DECIGO. Universe. 2021; 7(3):53. https://doi.org/10.3390/universe7030053
Chicago/Turabian StyleNakano, Hiroyuki, Ryuichi Fujita, Soichiro Isoyama, and Norichika Sago. 2021. "Scope Out Multiband Gravitational-Wave Observations of GW190521-Like Binary Black Holes with Space Gravitational Wave Antenna B-DECIGO" Universe 7, no. 3: 53. https://doi.org/10.3390/universe7030053
APA StyleNakano, H., Fujita, R., Isoyama, S., & Sago, N. (2021). Scope Out Multiband Gravitational-Wave Observations of GW190521-Like Binary Black Holes with Space Gravitational Wave Antenna B-DECIGO. Universe, 7(3), 53. https://doi.org/10.3390/universe7030053







