Fundamental Tone and Overtones of Quasinormal Modes in Ringdown Gravitational Waves: A Detailed Study in Black Hole Perturbation
Abstract
1. Introduction
2. Post-Newtonian Initial Conditions in the Close Limit: Head-On Collisions
Model Problem: Head-On Collisions of Two Non-Spinning Black Holes
3. Numerical Method
3.1. Initial Data and Gravitational Waveform in Terms of Master Functions
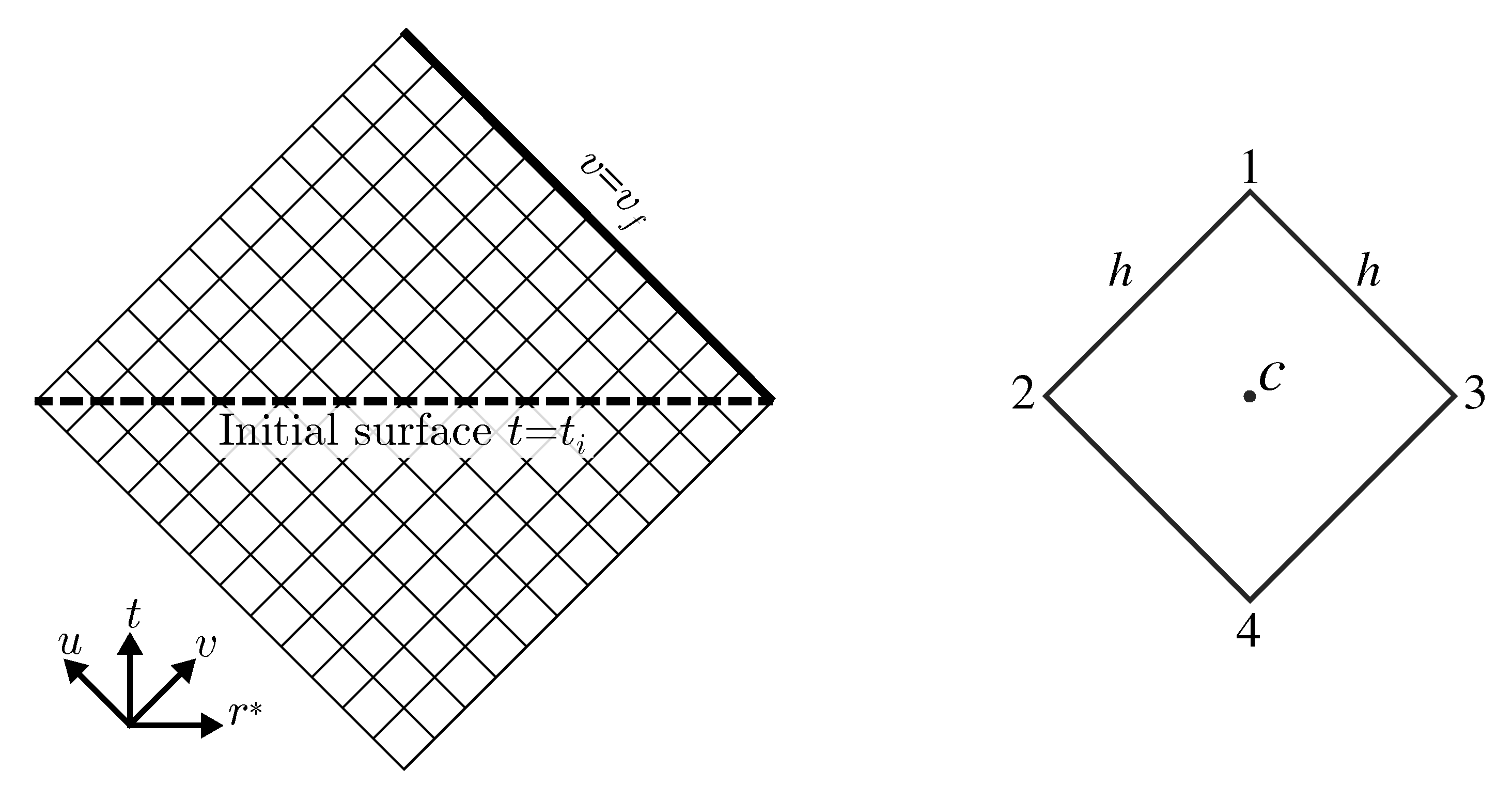
3.2. Time Domain Integration of the Zerilli Equation
3.3. Simulation Parameters
- Case A: an equal mass collision with the initial separation of .
- Case B: an asymmetric mass collision with the mass ratio of and the initial separation of .
3.4. Code Validation
4. Modeling of Ringdown Waveforms
4.1. Standard Quasinormal-Mode Fitting Formula
4.2. Modified Quasinormal-Mode Fitting Formula with an Orthonormal Set of Mode Functions
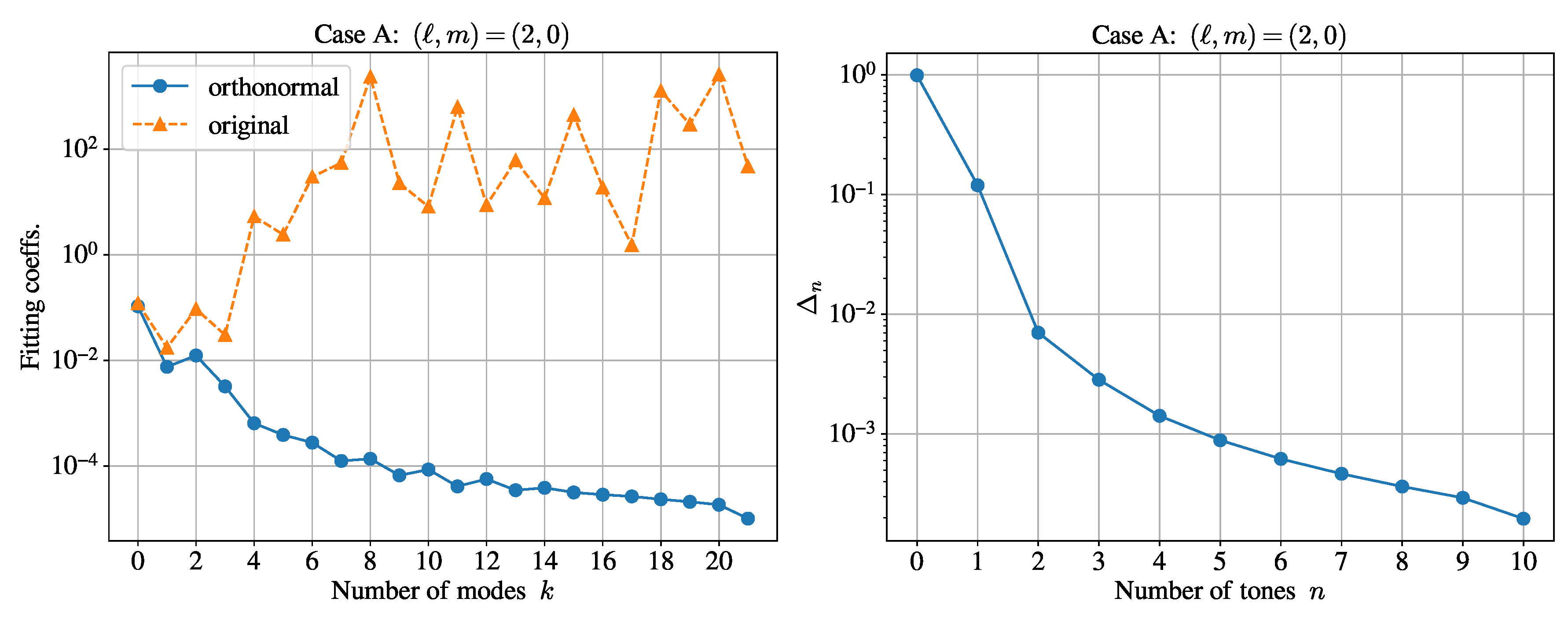
5. Results
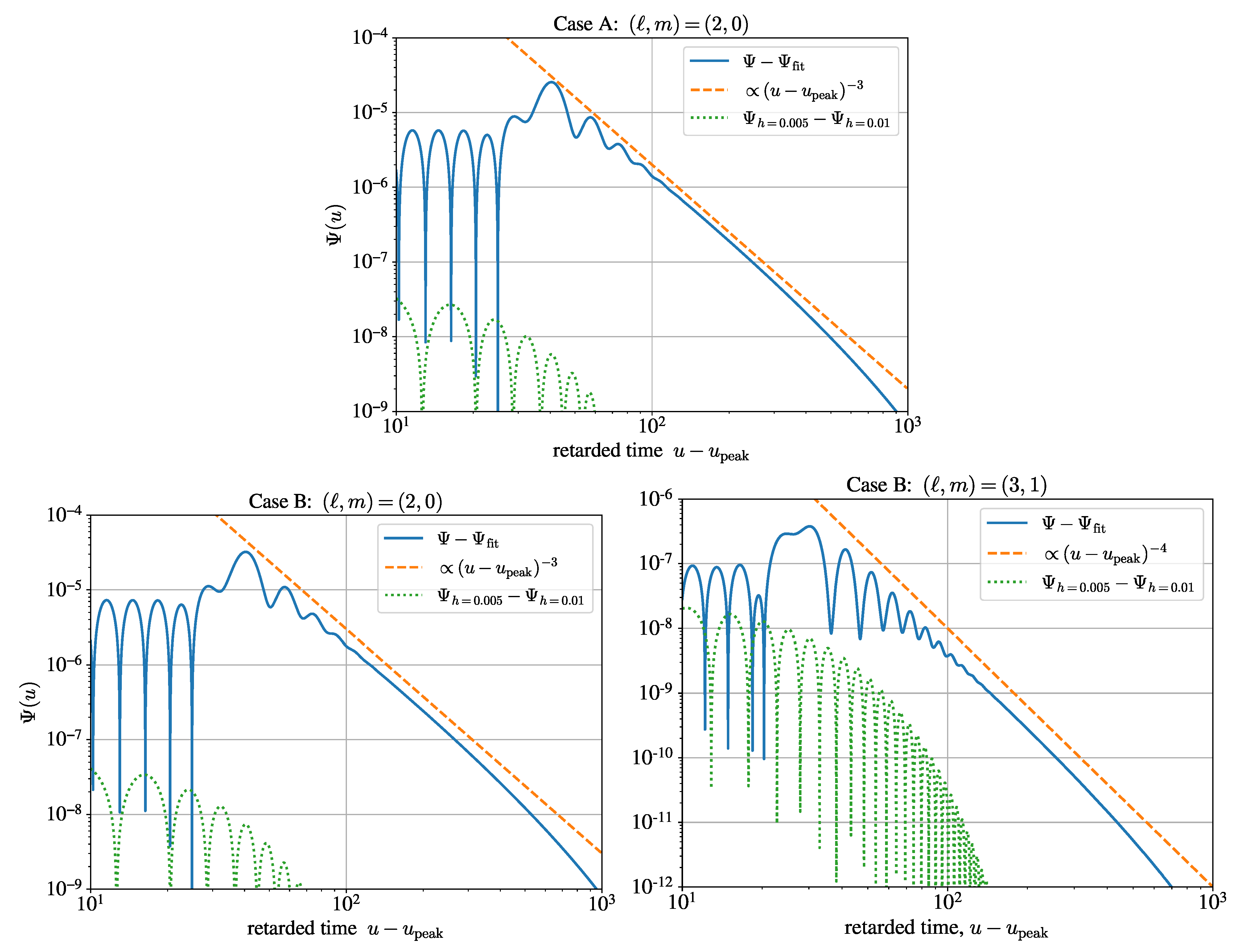
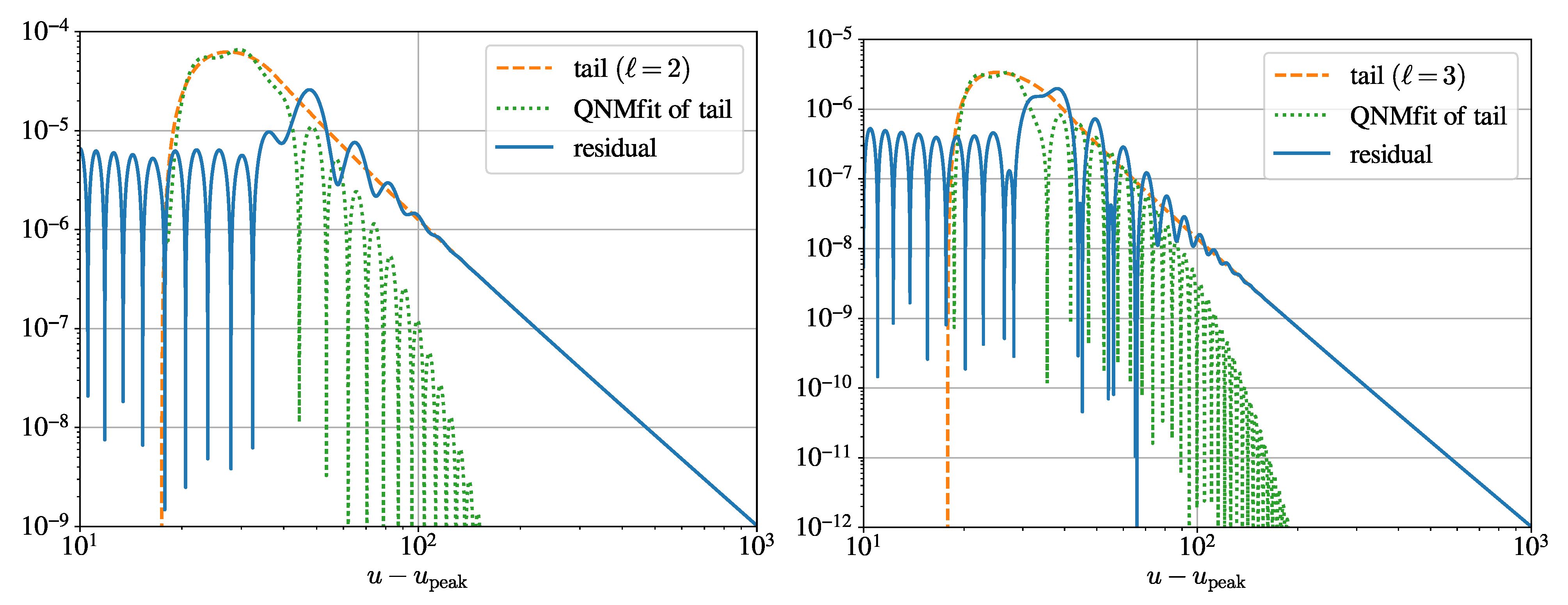
5.1. Quasinormal-Mode Fitting and Residuals
5.2. Convergence of the Fitting Coefficients
6. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
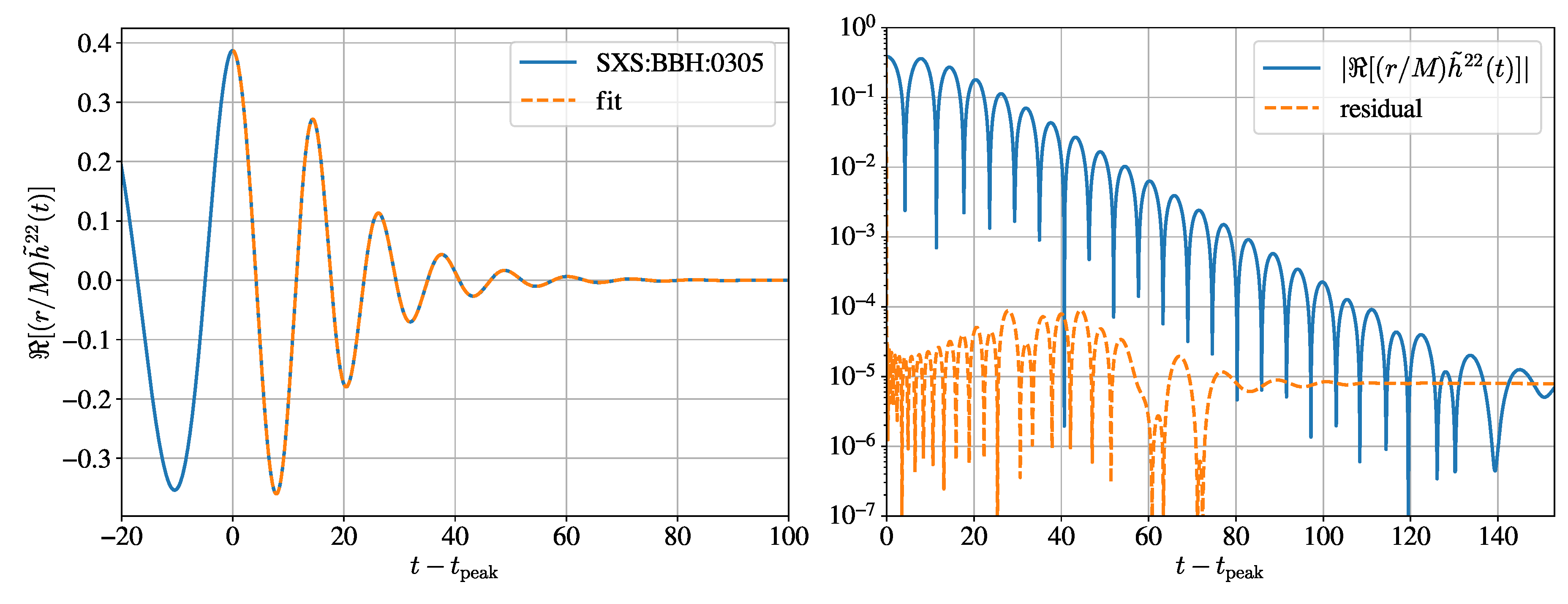
Appendix A. Analysis of Some Numerical-Relativity Waveforms in Time Domain
| ID | Mass () | Spin () | Reference |
|---|---|---|---|
| SXS:BBH:0305 | 0.952032939704 | 0.6920851868180025 | [66,124,125] |
| SXS:BBH:1936 | 0.9851822160611967 | 0.021659378750190413 | [66,125,126] |
| SXS:BBH:0260 | 0.9810057011067479 | 0.12447236057508855 | [66,125,127] |
| SXS:BBH:1501 | 0.93633431069 | 0.8085731624240002 | [66,125,128] |
| SXS:BBH:1477 | 0.911077401717 | 0.907542632208 | [66,125,128] |
| SXS:BBH:0178 | 0.8866898235070239 | 0.9499311295284206 | [66,125,129] |
| SXS:BBH:1124 | 0.8827804590335694 | 0.9506671398803149 | [66,125] |
| RIT:BBH:0062 | 0.9520211506 | 0.6919694604 | [130,131,132] |
| RIT:BBH:0604 | 0.9361520656 | 0.8101416903 | [130,131,132] |
| RIT:BBH:0558 | 0.9108618514 | 0.9077062488 | [130,131,132] |
| RIT:BBH:0767 | 0.9057246958 | 0.9462438132 | [130,131,132] |
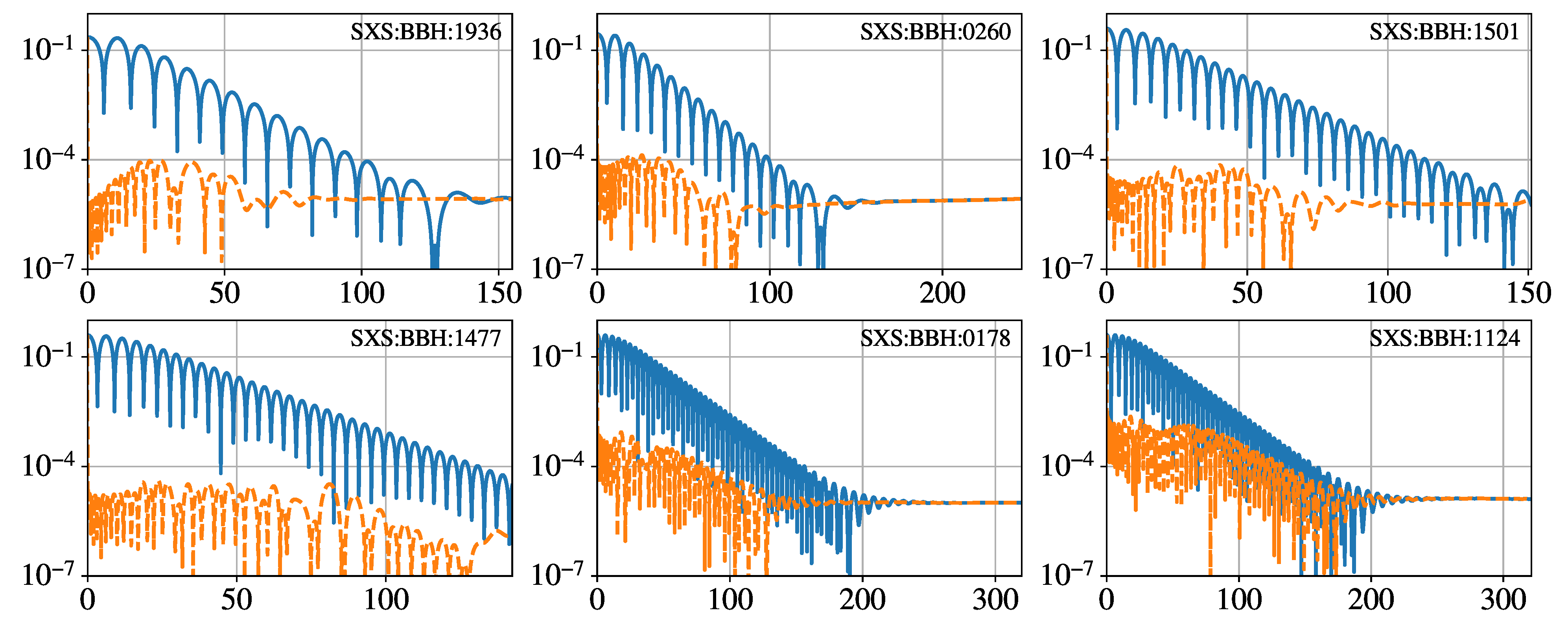
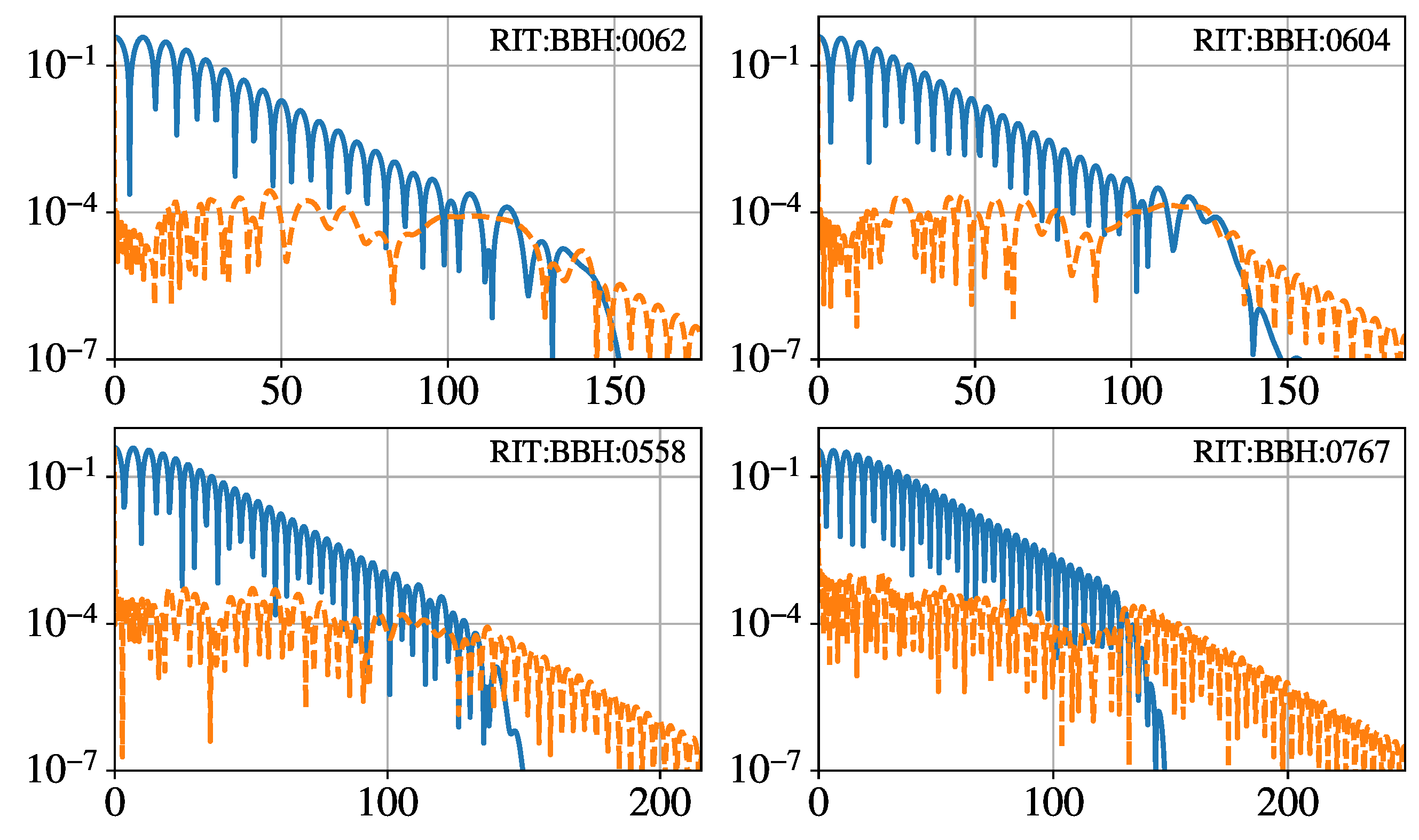
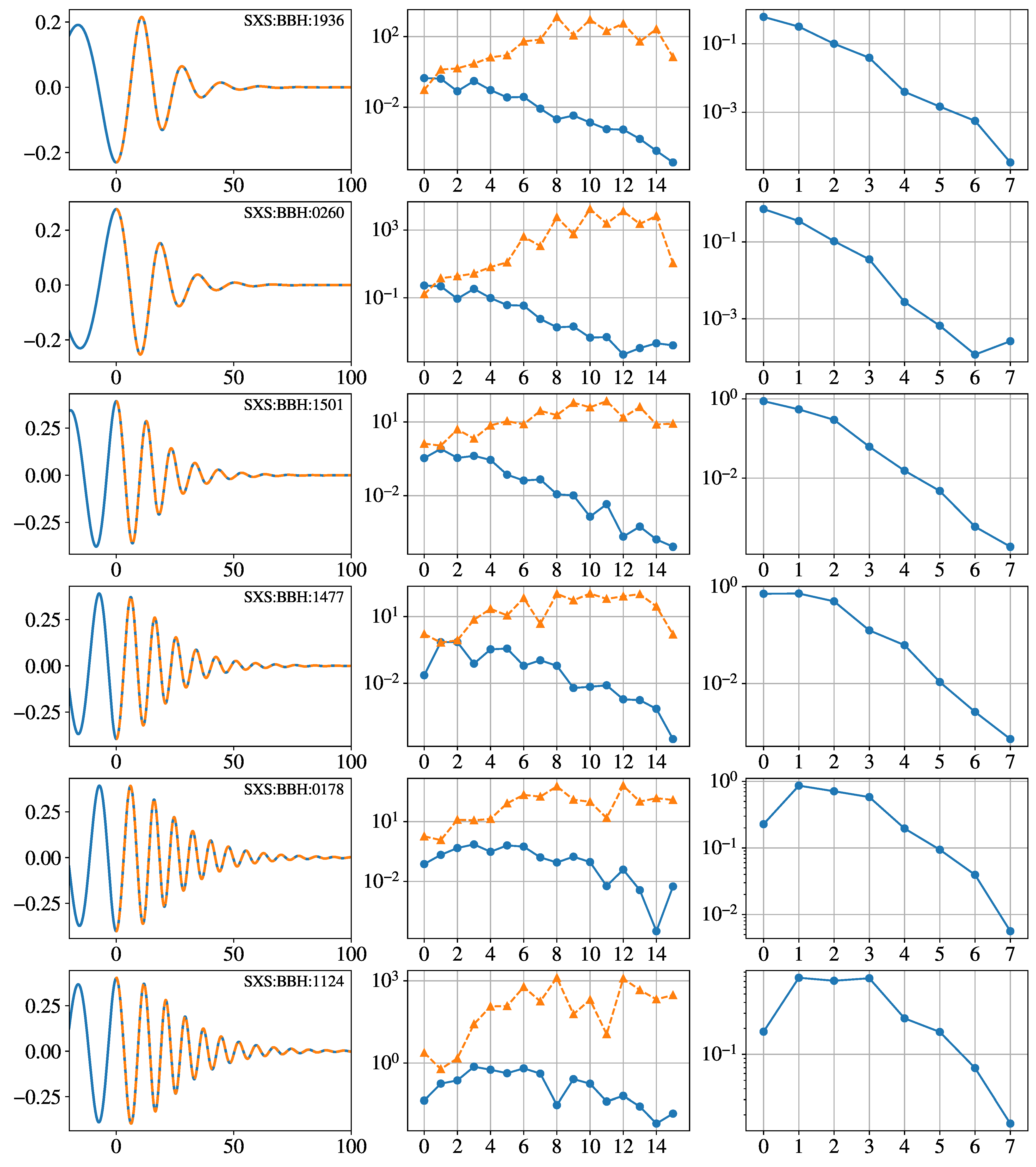
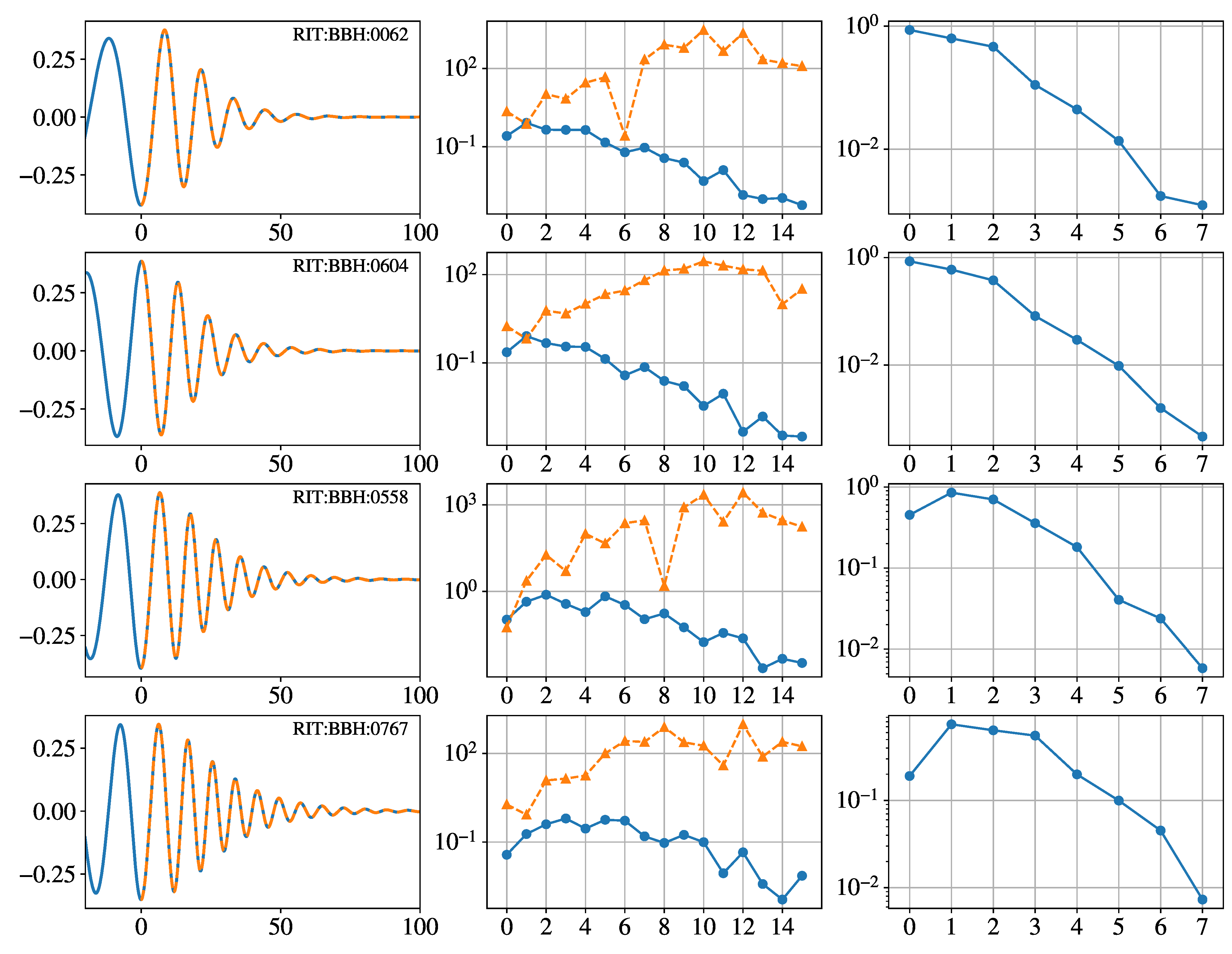
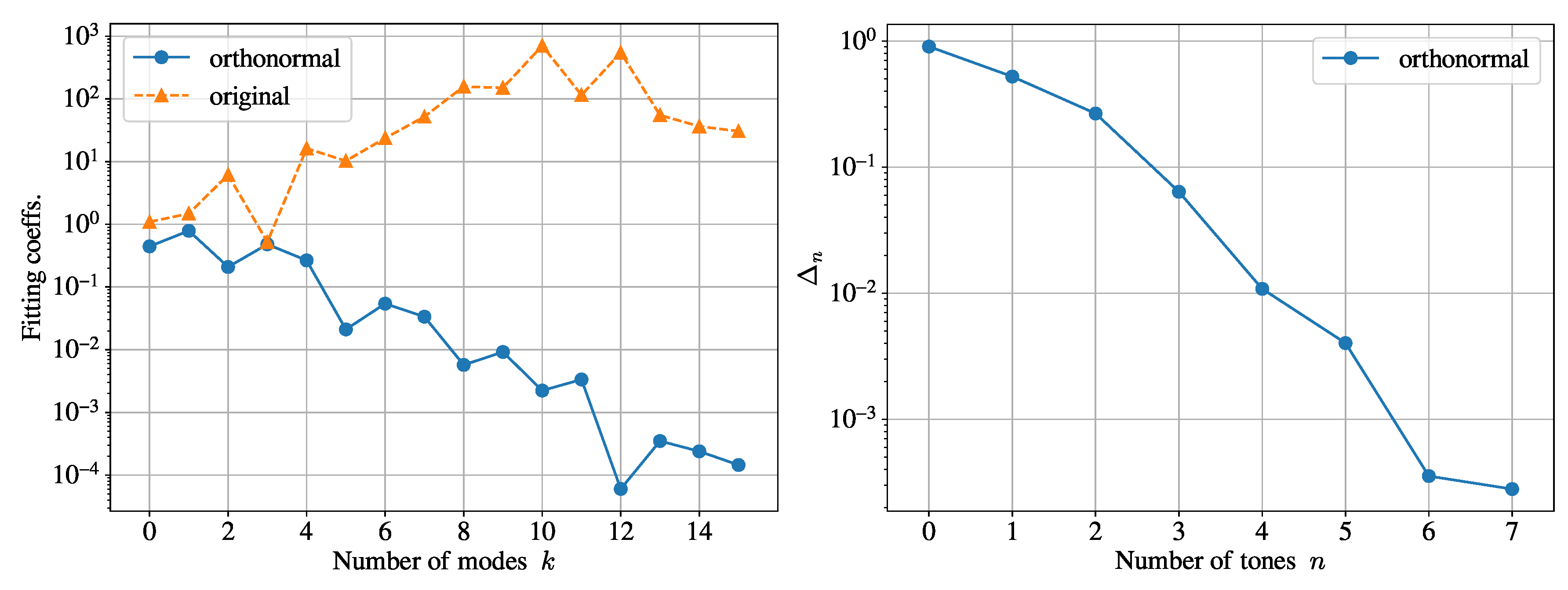
Appendix B. Analysis of the Fitting Coefficients of Some Numerical-Relativity Data
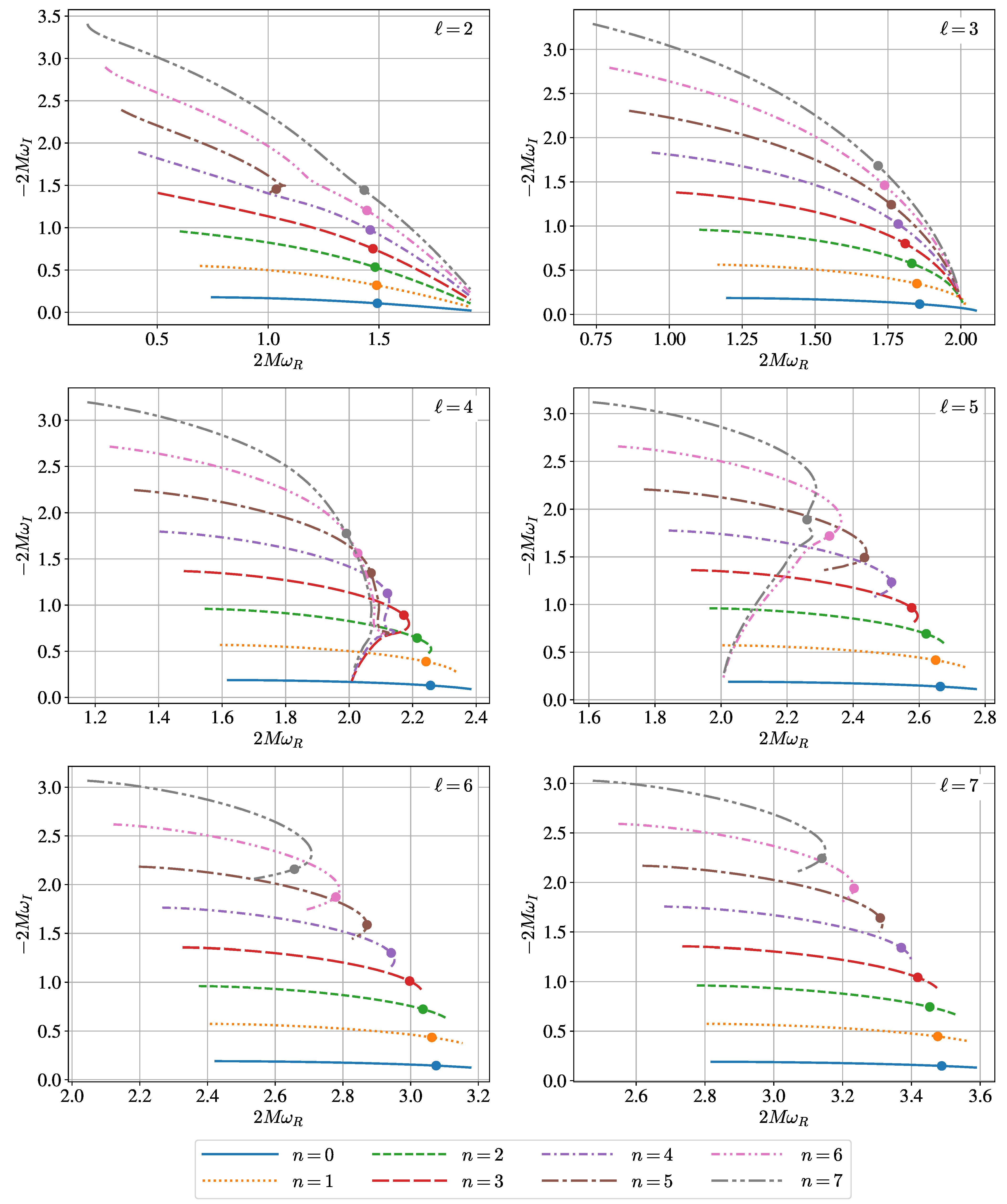
Appendix C. Frequencies of Kerr Quasinormal Modes
References
- Kerr, R.P. Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. GWTC-2.1: Deep Extended Catalog of Compact Binary Coalescences Observed by LIGO and Virgo during the First Half of the Third Observing Run. arXiv 2021, arXiv:2108.01045. [Google Scholar]
- Nakamura, T.; Nakano, H.; Tanaka, T. Detecting quasinormal modes of binary black hole mergers with second-generation gravitational-wave detectors. Phys. Rev. D 2016, 93, 044048. [Google Scholar] [CrossRef]
- Nakamura, T.; Nakano, H. How close can we approach the event horizon of the Kerr black hole from the detection of gravitational quasinormal modes? Prog. Theor. Exp. Phys. 2016, 2016, 041E01. [Google Scholar] [CrossRef]
- Nakano, H.; Nakamura, T.; Tanaka, T. The detection of quasinormal mode with a/M = 0.95 would prove a sphere 99% soaking in the ergoregion of the Kerr space-time. Prog. Theor. Exp. Phys. 2016, 2016, 031E02. [Google Scholar] [CrossRef]
- Nakano, H.; Tanaka, T.; Nakamura, T. Possible golden events for ringdown gravitational waves. Phys. Rev. D 2015, 92, 064003. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quantum Gravity 2009, 26, 163001. [Google Scholar] [CrossRef]
- Berti, E.; Yagi, K.; Yang, H.; Yunes, N. Extreme Gravity Tests with Gravitational Waves from Compact Binary Coalescences: (II) Ringdown. Gen. Relativ. Gravit. 2018, 50, 49. [Google Scholar] [CrossRef]
- Vishveshwara, C.V. Scattering of Gravitational Radiation by a Schwarzschild Black-hole. Nature 1970, 227, 936–938. [Google Scholar] [CrossRef]
- Press, W.H. Long Wave Trains of Gravitational Waves from a Vibrating Black Hole. Astrophys. J. Lett. 1971, 170, L105–L108. [Google Scholar] [CrossRef]
- Teukolsky, S.A.; Press, W.H. Perturbations of a rotating black hole. III—Interaction of the hole with gravitational and electromagnet ic radiation. Astrophys. J. 1974, 193, 443–461. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Detweiler, S.L. The quasi-normal modes of the Schwarzschild black hole. Proc. R. Soc. Lond. A 1975, 344, 441–452. [Google Scholar] [CrossRef]
- Detweiler, S.L. Resonant oscillations of a rapidly rotating black hole. Proc. R. Soc. Lond. A 1977, 352, 381–395. [Google Scholar] [CrossRef]
- Detweiler, S.L. Black holes and gravitational waves. III. The resonant frequencies of rotating holes. Astrophys. J. 1980, 239, 292–295. [Google Scholar] [CrossRef]
- Leaver, E.W. An Analytic representation for the quasi normal modes of Kerr black holes. Proc. R. Soc. Lond. A 1985, 402, 285–298. [Google Scholar] [CrossRef]
- Castro, A.; Lapan, J.M.; Maloney, A.; Rodriguez, M.J. Black Hole Scattering from Monodromy. Class. Quantum Gravity 2013, 30, 165005. [Google Scholar] [CrossRef]
- Casals, M.; Longo Micchi, L.F. Spectroscopy of extremal and near-extremal Kerr black holes. Phys. Rev. D 2019, 99, 084047. [Google Scholar] [CrossRef]
- Hatsuda, Y.; Kimura, M. Semi-analytic expressions for quasinormal modes of slowly rotating Kerr black holes. Phys. Rev. D 2020, 102, 044032. [Google Scholar] [CrossRef]
- Echeverria, F. Gravitational Wave Measurements of the Mass and Angular Momentum of a Black Hole. Phys. Rev. D 1989, 40, 3194–3203. [Google Scholar] [CrossRef]
- Finn, L.S. Detection, measurement and gravitational radiation. Phys. Rev. D 1992, 46, 5236–5249. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Hughes, S.A. Measuring gravitational waves from binary black hole coalescences: 1. Signal-to-noise for inspiral, merger, and ringdown. Phys. Rev. D 1998, 57, 4535–4565. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Hughes, S.A. Measuring gravitational waves from binary black hole coalescences: 2. The Waves’ information and its extraction, with and without templates. Phys. Rev. D 1998, 57, 4566–4587. [Google Scholar] [CrossRef]
- Creighton, J.D.E. Search techniques for gravitational waves from black hole ringdowns. Phys. Rev. D 1999, 60, 022001. [Google Scholar] [CrossRef]
- Arnaud, N.; Barsuglia, M.; Bizouard, M.A.; Brisson, V.; Cavalier, F.; Davier, M.; Hello, P.; Kreckelbergh, S.; Porter, E.K. An Elliptical tiling method to generate a two-dimensional set of templates for gravitational wave search. Phys. Rev. D 2003, 67, 102003. [Google Scholar] [CrossRef]
- Nakano, H.; Takahashi, H.; Tagoshi, H.; Sasaki, M. An Effective search method for gravitational ringing of black holes. Phys. Rev. D 2003, 68, 102003. [Google Scholar] [CrossRef]
- Nakano, H.; Takahashi, H.; Tagoshi, H.; Sasaki, M. An Improved search method for gravitational ringing of black holes. Prog. Theor. Phys. 2004, 111, 781–805. [Google Scholar] [CrossRef][Green Version]
- Tsunesada, Y. Search for gravitational waves from black-hole ringdowns using TAMA300 data. Class. Quantum Gravity 2004, 21, S703–S708. [Google Scholar] [CrossRef]
- Tsunesada, Y.; Kanda, N.; Nakano, H.; Tatsumi, D.; Ando, M.; Sasaki, M.; Tagoshi, H.; Takahashi, H. On detection of black hole quasi-normal ringdowns: Detection efficiency and waveform parameter determination in matched filtering. Phys. Rev. D 2005, 71, 103005. [Google Scholar] [CrossRef]
- Tsunesada, Y.; Tatsumi, D.; Kanda, N.; Nakano, H. Black-hole ringdown search in TAMA300: Matched filtering and event selections. Class. Quantum Gravity 2005, 22, S1129–S1138. [Google Scholar] [CrossRef]
- Ando, M.; Arai, K.; Takahashi, R.; Heinzel, G.; Kawamura, S.; Tatsumi, D.; Kanda, N.; Tagoshi, H.; Araya, A.; Asada, H.; et al. Stable operation of a 300-m laser interferometer with sufficient sensitivity to detect gravitational wave events within our galaxy. Phys. Rev. Lett. 2001, 86, 3950. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Adhikari, R.; Ajith, P.; Allen, B.; Allen, G.; Amin, R.S.; Anderson, S.B.; Anderson, W.G.; Arain, M.A.; et al. Search for gravitational wave ringdowns from perturbed black holes in LIGO S4 data. Phys. Rev. D 2009, 80, 062001. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Search for gravitational wave ringdowns from perturbed intermediate mass black holes in LIGO-Virgo data from 2005–2010. Phys. Rev. D 2014, 89, 102006. [Google Scholar] [CrossRef]
- Goggin, L.M. A Search For Gravitational Waves from Perturbed Black Hole Ringdowns in LIGO Data. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2008. [Google Scholar] [CrossRef]
- Caudill, S.; Field, S.E.; Galley, C.R.; Herrmann, F.; Tiglio, M. Reduced Basis representations of multi-mode black hole ringdown gravitational waves. Class. Quantum Gravity 2012, 29, 095016. [Google Scholar] [CrossRef][Green Version]
- Caudill, S.E. Searches for gravitational waves from perturbed black holes in data from LIGO detectors. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, 2012. [Google Scholar]
- Talukder, D. Multi-Baseline Searches for Stochastic Sources and Black Hole Ringdown Signals in LIGO-Virgo Data. Ph.D. Thesis, Washington State University, Pullman, WA, USA, 2012. [Google Scholar]
- Baker, P.T. Distinguishing Signal from Noise: New Techniques for Gravitational Wave Data Analysis. Ph.D. Thesis, Montana State University, Bozeman, MT, USA, 2013. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of general relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101, Erratum in 2018, 121, 129902. [Google Scholar] [CrossRef]
- Nakano, H.; Fujita, R.; Isoyama, S.; Sago, N. Scope out multiband gravitational-wave observations of GW190521-like binary black holes with space gravitational wave antenna B-DECIGO. Universe 2021, 7, 53. [Google Scholar] [CrossRef]
- Nair, R.; Jhingan, S.; Tanaka, T. Synergy between ground and space based gravitational wave detectors for estimation of binary coalescence parameters. Prog. Theor. Exp. Phys. 2016, 2016, 053E01. [Google Scholar] [CrossRef]
- Nakamura, T.; Ando, M.; Kinugawa, T.; Nakano, H.; Eda, K.; Sato, S.; Musha, M.; Akutsu, T.; Tanaka, T.; Seto, N.; et al. Pre-DECIGO can get the smoking gun to decide the astrophysical or cosmological origin of GW150914-like binary black holes. Prog. Theor. Exp. Phys. 2016, 2016, 093E01. [Google Scholar] [CrossRef]
- Isoyama, S.; Nakano, H.; Nakamura, T. Multiband Gravitational-Wave Astronomy: Observing binary inspirals with a decihertz detector, B-DECIGO. Prog. Theor. Exp. Phys. 2018, 2018, 073E01. [Google Scholar] [CrossRef]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. Prog. Theor. Exp. Phys. 2021, 2021, 05A105. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, J.; Cardoso, V.; Cavaglia, M. Matched-filtering and parameter estimation of ringdown waveforms. Phys. Rev. D 2007, 76, 104044. [Google Scholar] [CrossRef]
- Giesler, M.; Isi, M.; Scheel, M.A.; Teukolsky, S. Black Hole Ringdown: The Importance of Overtones. Phys. Rev. X 2019, 9, 041060. [Google Scholar] [CrossRef]
- Buonanno, A.; Cook, G.B.; Pretorius, F. Inspiral, merger and ring-down of equal-mass black-hole binaries. Phys. Rev. D 2007, 75, 124018. [Google Scholar] [CrossRef]
- Baibhav, V.; Berti, E.; Cardoso, V.; Khanna, G. Black Hole Spectroscopy: Systematic Errors and Ringdown Energy Estimates. Phys. Rev. D 2018, 97, 044048. [Google Scholar] [CrossRef]
- Carullo, G.; van der Schaaf, L.; London, L.; Pang, P.T.H.; Tsang, K.W.; Hannuksela, O.A.; Meidam, J.; Agathos, M.; Samajdar, A.; Ghosh, A.; et al. Empirical tests of the black hole no-hair conjecture using gravitational-wave observations. Phys. Rev. D 2018, 98, 104020. [Google Scholar] [CrossRef]
- Bhagwat, S.; Forteza, X.J.; Pani, P.; Ferrari, V. Ringdown overtones, black hole spectroscopy, and no-hair theorem tests. Phys. Rev. D 2020, 101, 044033. [Google Scholar] [CrossRef]
- Ota, I.; Chirenti, C. Overtones or higher harmonics? Prospects for testing the no-hair theorem with gravitational wave detections. Phys. Rev. D 2020, 101, 104005. [Google Scholar] [CrossRef]
- Cook, G.B. Aspects of multimode Kerr ringdown fitting. Phys. Rev. D 2020, 102, 024027. [Google Scholar] [CrossRef]
- Jiménez Forteza, X.; Bhagwat, S.; Pani, P.; Ferrari, V. Spectroscopy of binary black hole ringdown using overtones and angular modes. Phys. Rev. D 2020, 102, 044053. [Google Scholar] [CrossRef]
- Mitman, K.; Moxon, J.; Scheel, M.A.; Teukolsky, S.A.; Boyle, M.; Deppe, N.; Kidder, L.E.; Throwe, W. Computation of displacement and spin gravitational memory in numerical relativity. Phys. Rev. D 2020, 102, 104007. [Google Scholar] [CrossRef]
- Dhani, A. Importance of mirror modes in binary black hole ringdown waveform. Phys. Rev. D 2021, 103, 104048. [Google Scholar] [CrossRef]
- Jiménez Forteza, X.; Mourier, P. High-overtone fits to numerical relativity ringdowns: Beyond the dismissed n = 8 special tone. arXiv 2021, arXiv:2107.11829. [Google Scholar]
- Dhani, A.; Sathyaprakash, B.S. Overtones, mirror modes, and mode-mixing in binary black hole mergers. arXiv 2021, arXiv:2107.14195. [Google Scholar]
- Pretorius, F. Evolution of binary black hole spacetimes. Phys. Rev. Lett. 2005, 95, 121101. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C.O.; Marronetti, P.; Zlochower, Y. Accurate evolutions of orbiting black-hole binaries without excision. Phys. Rev. Lett. 2006, 96, 111101. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.G.; Centrella, J.; Choi, D.I.; Koppitz, M.; van Meter, J. Gravitational wave extraction from an inspiraling configuration of merging black holes. Phys. Rev. Lett. 2006, 96, 111102. [Google Scholar] [CrossRef]
- Isi, M.; Giesler, M.; Farr, W.M.; Scheel, M.A.; Teukolsky, S.A. Testing the no-hair theorem with GW150914. Phys. Rev. Lett. 2019, 123, 111102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190521: A Binary Black Hole Merger with a Total Mass of 150 M⊙. Phys. Rev. Lett. 2020, 125, 101102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Properties and Astrophysical Implications of the 150 M⊙ Binary Black Hole Merger GW190521. Astrophys. J. Lett. 2020, 900, L13. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Tests of general relativity with binary black holes from the second LIGO-Virgo gravitational-wave transient catalog. Phys. Rev. D 2021, 103, 122002. [Google Scholar] [CrossRef]
- SXS Gravitational Waveform Database. Available online: https://data.black-holes.org/waveforms/index.html (accessed on 24 September 2021).
- CCRG@RIT Catalog of Numerical Simulations. Available online: https://ccrg.rit.edu/numerical-simulations (accessed on 24 September 2021).
- Georgia Tech Catalog of Gravitational Waveforms. Available online: http://www.einstein.gatech.edu/catalog/ (accessed on 24 September 2021).
- SACRA Gravitational Waveform Data Bank. Available online: https://www2.yukawa.kyoto-u.ac.jp/~nr_kyoto/SACRA_PUB/catalog.html (accessed on 24 September 2021).
- Okounkova, M. Revisiting non-linearity in binary black hole mergers. arXiv 2020, arXiv:2004.00671. [Google Scholar]
- Pook-Kolb, D.; Birnholtz, O.; Jaramillo, J.L.; Krishnan, B.; Schnetter, E. Horizons in a binary black hole merger II: Fluxes, multipole moments and stability. arXiv 2020, arXiv:2006.03940. [Google Scholar]
- Mourier, P.; Jiménez Forteza, X.; Pook-Kolb, D.; Krishnan, B.; Schnetter, E. Quasinormal modes and their overtones at the common horizon in a binary black hole merger. Phys. Rev. D 2021, 103, 044054. [Google Scholar] [CrossRef]
- London, L.; Shoemaker, D.; Healy, J. Modeling ringdown: Beyond the fundamental quasinormal modes. Phys. Rev. D 2014, 90, 124032, Erratum in 2016, 94, 069902. [Google Scholar] [CrossRef]
- Ioka, K.; Nakano, H. Second and higher-order quasi-normal modes in binary black hole mergers. Phys. Rev. D 2007, 76, 061503. [Google Scholar] [CrossRef]
- Nakano, H.; Ioka, K. Second Order Quasi-Normal Mode of the Schwarzschild Black Hole. Phys. Rev. D 2007, 76, 084007. [Google Scholar] [CrossRef]
- Okuzumi, S.; Ioka, K.; Sakagami, M.a. Possible Discovery of Nonlinear Tail and Quasinormal Modes in Black Hole Ringdown. Phys. Rev. D 2008, 77, 124018. [Google Scholar] [CrossRef]
- Price, R.H.; Pullin, J. Colliding black holes: The Close limit. Phys. Rev. Lett. 1994, 72, 3297–3300. [Google Scholar] [CrossRef]
- Abrahams, A.M.; Price, R.H. Black hole collisions from Brill-Lindquist initial data: Predictions of perturbation theory. Phys. Rev. D 1996, 53, 1972–1976. [Google Scholar] [CrossRef]
- Anninos, P.; Brandt, S. Headon collision of two unequal mass black holes. Phys. Rev. Lett. 1998, 81, 508–511. [Google Scholar] [CrossRef]
- Sopuerta, C.F.; Yunes, N.; Laguna, P. Gravitational Recoil from Binary Black Hole Mergers: The Close-Limit Approximation. Phys. Rev. D 2006, 74, 124010, Erratum in 2008, 78, 049901. [Google Scholar] [CrossRef]
- Baker, J.G.; Campanelli, M.; Lousto, C.O. The Lazarus project: A Pragmatic approach to binary black hole evolutions. Phys. Rev. D 2002, 65, 044001. [Google Scholar] [CrossRef]
- Annulli, L.; Cardoso, V.; Gualtieri, L. Generalizing the close limit approximation of binary black holes. arXiv 2021, arXiv:2104.11236. [Google Scholar]
- Le Tiec, A.; Blanchet, L. The Close-limit Approximation for Black Hole Binaries with Post-Newtonian Initial Conditions. Class. Quantum Gravity 2010, 27, 045008. [Google Scholar] [CrossRef]
- Price, R.H. Nonspherical perturbations of relativistic gravitational collapse. 1. Scalar and gravitational perturbations. Phys. Rev. D 1972, 5, 2419–2438. [Google Scholar] [CrossRef]
- Gleiser, R.J.; Nicasio, C.O.; Price, R.H.; Pullin, J. Colliding black holes: How far can the close approximation go? Phys. Rev. Lett. 1996, 77, 4483–4486. [Google Scholar] [CrossRef]
- Andrade, Z.; Price, R.H. Headon collisions of unequal mass black holes: Close limit predictions. Phys. Rev. D 1997, 56, 6336–6350. [Google Scholar] [CrossRef]
- Gleiser, R.J.; Nicasio, C.O.; Price, R.H.; Pullin, J. Gravitational radiation from Schwarzschild black holes: The Second order perturbation formalism. Phys. Rep. 2000, 325, 41–81. [Google Scholar] [CrossRef]
- Futamase, T.; Itoh, Y. The post-Newtonian approximation for relativistic compact binaries. Living Rev. Relativ. 2007, 10, 2. [Google Scholar] [CrossRef]
- Blanchet, L. Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries. Living Rev. Relativ. 2014, 17, 2. [Google Scholar] [CrossRef] [PubMed]
- Levi, M. Effective Field Theories of Post-Newtonian Gravity: A comprehensive review. Rep. Prog. Phys. 2020, 83, 075901. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, G.; Jaranowski, P. Hamiltonian formulation of general relativity and post-Newtonian dynamics of compact binaries. Living Rev. Relativ. 2018, 21, 7. [Google Scholar] [CrossRef] [PubMed]
- Le Tiec, A.; Blanchet, L.; Will, C.M. Gravitational-Wave Recoil from the Ringdown Phase of Coalescing Black Hole Binaries. Class. Quantum Gravity 2010, 27, 012001. [Google Scholar] [CrossRef]
- Nichols, D.A.; Chen, Y. A hybrid method for understanding black-hole mergers: Head-on case. Phys. Rev. D 2010, 82, 104020. [Google Scholar] [CrossRef]
- Blanchet, L.; Faye, G.; Ponsot, B. Gravitational field and equations of motion of compact binaries to 5/2 postNewtonian order. Phys. Rev. D 1998, 58, 124002. [Google Scholar] [CrossRef]
- Tagoshi, H.; Ohashi, A.; Owen, B.J. Gravitational field and equations of motion of spinning compact binaries to 2.5 postNewtonian order. Phys. Rev. D 2001, 63, 044006. [Google Scholar] [CrossRef]
- Faye, G.; Blanchet, L.; Buonanno, A. Higher-order spin effects in the dynamics of compact binaries. I. Equations of motion. Phys. Rev. D 2006, 74, 104033. [Google Scholar] [CrossRef]
- Bohe, A.; Marsat, S.; Faye, G.; Blanchet, L. Next-to-next-to-leading order spin-orbit effects in the near-zone metric and precession equations of compact binaries. Class. Quantum Gravity 2013, 30, 075017. [Google Scholar] [CrossRef]
- Pound, A.; Wardell, B. Black hole perturbation theory and gravitational self-force. arXiv 2021, arXiv:2101.04592. [Google Scholar]
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild singularity. Phys. Rev. 1957, 108, 1063–1069. [Google Scholar] [CrossRef]
- Sago, N.; Nakano, H.; Sasaki, M. Gauge problem in the gravitational selfforce. 1. Harmonic gauge approach in the Schwarzschild background. Phys. Rev. D 2003, 67, 104017. [Google Scholar] [CrossRef]
- Brill, D.R.; Lindquist, R.W. Interaction energy in geometrostatics. Phys. Rev. 1963, 131, 471–476. [Google Scholar] [CrossRef]
- Lousto, C.O.; Price, R.H. Understanding initial data for black hole collisions. Phys. Rev. D 1997, 56, 6439–6457. [Google Scholar] [CrossRef]
- Ringdown. Available online: https://pages.jh.edu/eberti2/ringdown/ (accessed on 24 September 2021).
- Black Hole Perturbation Club. 2020. Available online: https://sites.google.com/view/bhpc1996/home (accessed on 9 July 2020).
- Lousto, C.O.; Campanelli, M.; Zlochower, Y.; Nakano, H. Remnant Masses, Spins and Recoils from the Merger of Generic Black-Hole Binaries. Class. Quantum Gravity 2010, 27, 114006. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Leaver, E.W. Spectral decomposition of the perturbation response of the Schwarzschild geometry. Phys. Rev. D 1986, 34, 384–408. [Google Scholar] [CrossRef]
- Ching, E.S.C.; Leung, P.T.; Suen, W.M.; Young, K. Wave propagation in gravitational systems: Late time behavior. Phys. Rev. D 1995, 52, 2118–2132. [Google Scholar] [CrossRef] [PubMed]
- Andersson, N. Evolving test fields in a black hole geometry. Phys. Rev. D 1997, 55, 468–479. [Google Scholar] [CrossRef]
- Krivan, W.; Laguna, P.; Papadopoulos, P.; Andersson, N. Dynamics of perturbations of rotating black holes. Phys. Rev. D 1997, 56, 3395–3404. [Google Scholar] [CrossRef]
- Pazos-Avalos, E.; Lousto, C.O. Numerical integration of the Teukolsky equation in the time domain. Phys. Rev. D 2005, 72, 084022. [Google Scholar] [CrossRef]
- Zenginoglu, A.; Nunez, D.; Husa, S. Gravitational perturbations of Schwarzschild spacetime at null infinity and the hyperboloidal initial value problem. Class. Quantum Gravity 2009, 26, 035009. [Google Scholar] [CrossRef]
- Gundlach, C.; Price, R.H.; Pullin, J. Late time behavior of stellar collapse and explosions: 1. Linearized perturbations. Phys. Rev. D 1994, 49, 883–889. [Google Scholar] [CrossRef] [PubMed]
- Nakano, H.; Narikawa, T.; Oohara, K.i.; Sakai, K.; Shinkai, H.a.; Takahashi, H.; Tanaka, T.; Uchikata, N.; Yamamoto, S.; Yamamoto, T.S. Comparison of various methods to extract ringdown frequency from gravitational wave data. Phys. Rev. D 2019, 99, 124032. [Google Scholar] [CrossRef]
- Uchikata, N.; Narikawa, T.; Sakai, K.; Takahashi, H.; Nakano, H. Black hole spectroscopy for KAGRA future prospect in O5. Phys. Rev. D 2020, 102, 024007. [Google Scholar] [CrossRef]
- Sundararajan, P.A.; Khanna, G.; Hughes, S.A. Towards adiabatic waveforms for inspiral into Kerr black holes. I. A New model of the source for the time domain perturbation equation. Phys. Rev. D 2007, 76, 104005. [Google Scholar] [CrossRef]
- Dolan, S.R.; Barack, L. Self-force via m-mode regularization and 2+1D evolution: III. Gravitational field on Schwarzschild spacetime. Phys. Rev. D 2013, 87, 084066. [Google Scholar] [CrossRef]
- Long, O.; Barack, L. Time-domain metric reconstruction for hyperbolic scattering. Phys. Rev. D 2021, 104, 024014. [Google Scholar] [CrossRef]
- Lousto, C.O.; Nakano, H.; Zlochower, Y.; Campanelli, M. Intermediate-mass-ratio black hole binaries: Intertwining numerical and perturbative techniques. Phys. Rev. D 2010, 82, 104057. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V. Quasinormal ringing of Kerr black holes. I. The Excitation factors. Phys. Rev. D 2006, 74, 104020. [Google Scholar] [CrossRef]
- Zhang, Z.; Berti, E.; Cardoso, V. Quasinormal ringing of Kerr black holes. II. Excitation by particles falling radially with arbitrary energy. Phys. Rev. D 2013, 88, 044018. [Google Scholar] [CrossRef]
- Hughes, S.A.; Apte, A.; Khanna, G.; Lim, H. Learning about black hole binaries from their ringdown spectra. Phys. Rev. Lett. 2019, 123, 161101. [Google Scholar] [CrossRef]
- Lim, H.; Khanna, G.; Apte, A.; Hughes, S.A. Exciting black hole modes via misaligned coalescences: II. The mode content of late-time coalescence waveforms. Phys. Rev. D 2019, 100, 084032. [Google Scholar] [CrossRef]
- Lovelace, G.; Lousto, C.O.; Healy, J.; Scheel, M.A.; Garcia, A.; O’Shaughnessy, R.; Boyle, M.; Campanelli, M.; Hemberger, D.A.; Kidder, L.E.; et al. Modeling the source of GW150914 with targeted numerical-relativity simulations. Class. Quantum Gravity 2016, 33, 244002. [Google Scholar] [CrossRef]
- Boyle, M.; Hemberger, D.; Iozzo, D.A.; Lovelace, G.; Ossokine, S.; Pfeiffer, H.P.; Scheel, M.A.; Stein, L.C.; Woodford, C.J.; Zimmerman, A.B.; et al. The SXS Collaboration catalog of binary black hole simulations. Class. Quantum Gravity 2019, 36, 195006. [Google Scholar] [CrossRef]
- Varma, V.; Field, S.E.; Scheel, M.A.; Blackman, J.; Gerosa, D.; Stein, L.C.; Kidder, L.E.; Pfeiffer, H.P. Surrogate models for precessing binary black hole simulations with unequal masses. Phys. Rev. Res. 2019, 1, 033015. [Google Scholar] [CrossRef]
- Chu, T.; Fong, H.; Kumar, P.; Pfeiffer, H.P.; Boyle, M.; Hemberger, D.A.; Kidder, L.E.; Scheel, M.A.; Szilagyi, B. On the accuracy and precision of numerical waveforms: Effect of waveform extraction methodology. Class. Quantum Gravity 2016, 33, 165001. [Google Scholar] [CrossRef]
- Varma, V.; Field, S.E.; Scheel, M.A.; Blackman, J.; Kidder, L.E.; Pfeiffer, H.P. Surrogate model of hybridized numerical relativity binary black hole waveforms. Phys. Rev. D 2019, 99, 064045. [Google Scholar] [CrossRef]
- Scheel, M.A.; Giesler, M.; Hemberger, D.A.; Lovelace, G.; Kuper, K.; Boyle, M.; Szilágyi, B.; Kidder, L.E. Improved methods for simulating nearly extremal binary black holes. Class. Quantum Gravity 2015, 32, 105009. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O.; Zlochower, Y.; Campanelli, M. The RIT binary black hole simulations catalog. Class. Quantum Gravity 2017, 34, 224001. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O.; Lange, J.; O’Shaughnessy, R.; Zlochower, Y.; Campanelli, M. Second RIT binary black hole simulations catalog and its application to gravitational waves parameter estimation. Phys. Rev. D 2019, 100, 024021. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O. Third RIT binary black hole simulations catalog. Phys. Rev. D 2020, 102, 104018. [Google Scholar] [CrossRef]
- Onozawa, H. A Detailed study of quasinormal frequencies of the Kerr black hole. Phys. Rev. D 1997, 55, 3593–3602. [Google Scholar] [CrossRef]
- Cook, G.B.; Zalutskiy, M. Gravitational perturbations of the Kerr geometry: High-accuracy study. Phys. Rev. D 2014, 90, 124021. [Google Scholar] [CrossRef]
- Kerr Quasinormal Modes: s = −2, n = 0–7. Available online: https://zenodo.org/record/2650358 (accessed on 24 September 2021).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sago, N.; Isoyama, S.; Nakano, H. Fundamental Tone and Overtones of Quasinormal Modes in Ringdown Gravitational Waves: A Detailed Study in Black Hole Perturbation. Universe 2021, 7, 357. https://doi.org/10.3390/universe7100357
Sago N, Isoyama S, Nakano H. Fundamental Tone and Overtones of Quasinormal Modes in Ringdown Gravitational Waves: A Detailed Study in Black Hole Perturbation. Universe. 2021; 7(10):357. https://doi.org/10.3390/universe7100357
Chicago/Turabian StyleSago, Norichika, Soichiro Isoyama, and Hiroyuki Nakano. 2021. "Fundamental Tone and Overtones of Quasinormal Modes in Ringdown Gravitational Waves: A Detailed Study in Black Hole Perturbation" Universe 7, no. 10: 357. https://doi.org/10.3390/universe7100357
APA StyleSago, N., Isoyama, S., & Nakano, H. (2021). Fundamental Tone and Overtones of Quasinormal Modes in Ringdown Gravitational Waves: A Detailed Study in Black Hole Perturbation. Universe, 7(10), 357. https://doi.org/10.3390/universe7100357







