Precision Measurement Noise Asymmetry and Its Annual Modulation as a Dark Matter Signature
Abstract
1. Introduction
2. Results
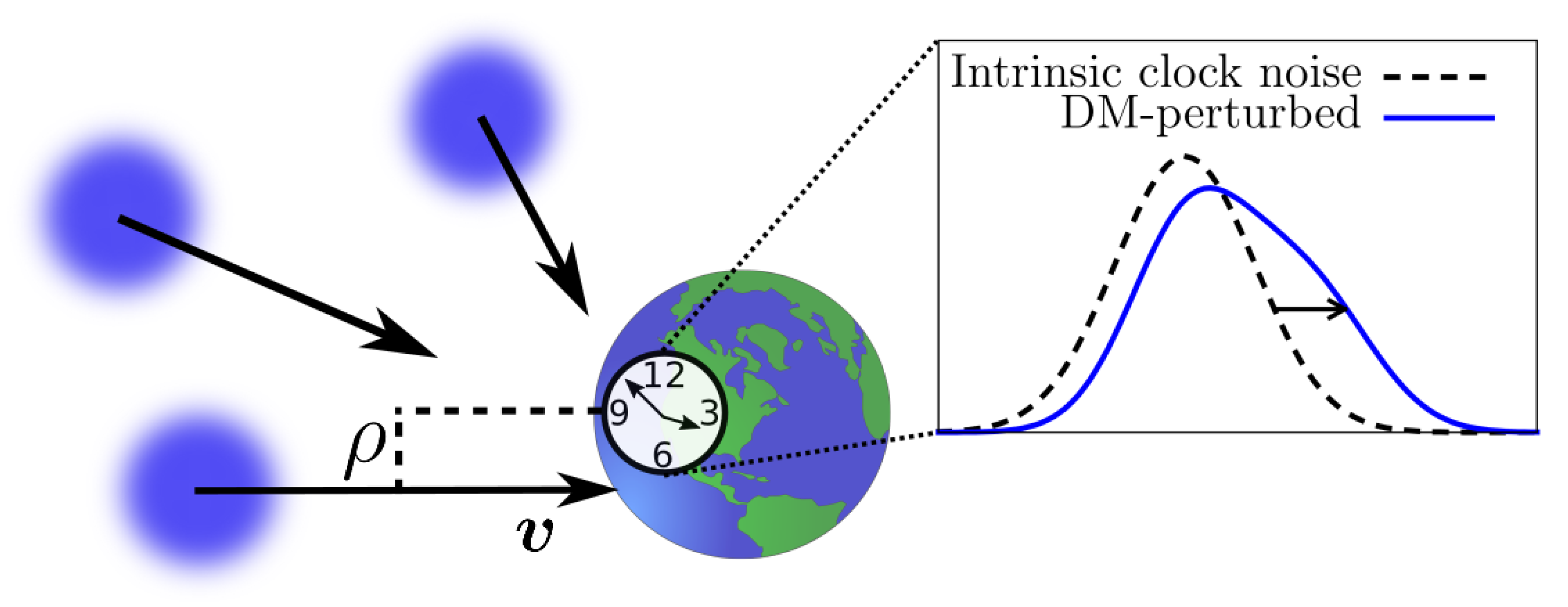
2.1. Dark Matter and Atomic Clocks
2.2. DM-Induced Variation of Fundamental Constants
2.3. DM-Induced Asymmetry and Skewness
2.4. Symmetric Non-Gaussian Signatures
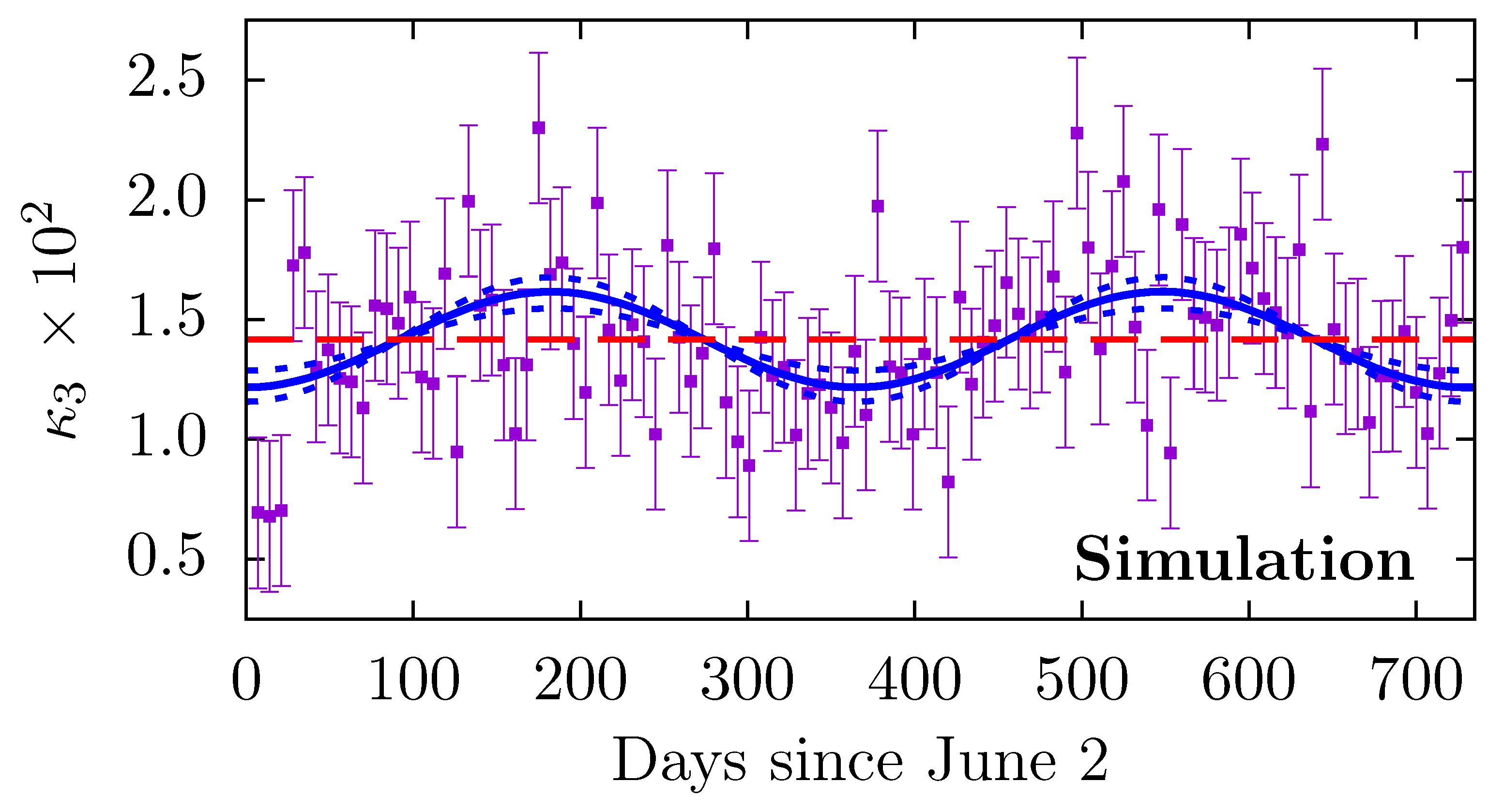
2.5. Annual Modulation
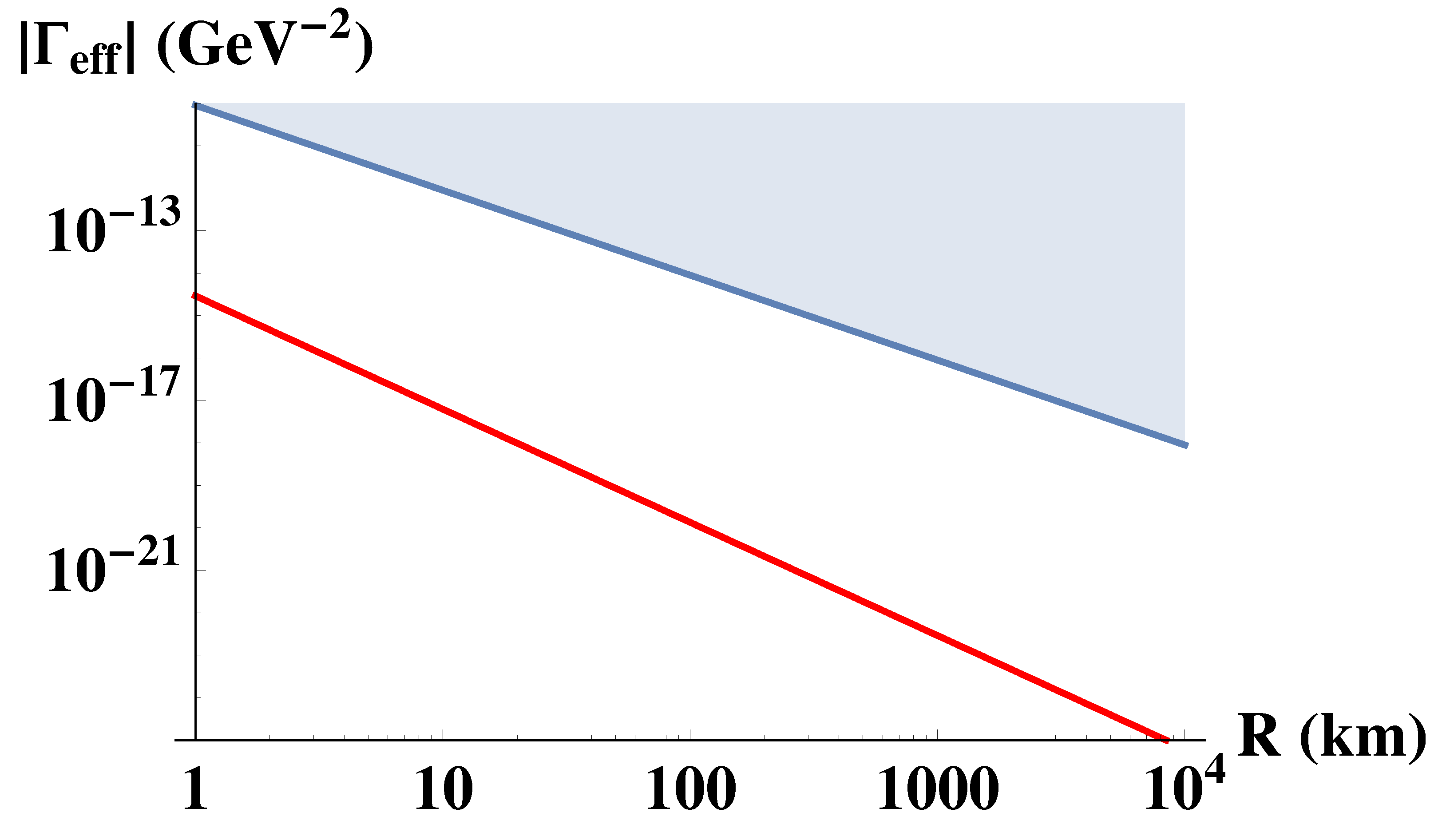
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WIMP | weakly-interacting massive particle |
| DM | dark matter |
| GPS | Global Positioning System |
References
- Weinberg, S. Cosmology; Cosmology, Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Peebles, P.J.E. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Ann. Rev. Astron. Astrophys. 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Matarrese, S.; Colpi, M.; Gorini, V.; Moschella, U. Dark Matter and Dark Energy: A Challenge for Modern Cosmology; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Blumenthal, G.R.; Faber, S.M.; Primack, J.R.; Rees, M.J. Formation of galaxies and large-scale structure with cold dark matter. Nature 1984, 311, 517–525. [Google Scholar] [CrossRef]
- The XENON Collaboration. First Dark Matter Search Results from the XENON1T Experiment. Phys. Rev. Lett. 2017, 119, 181301. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Ji, X. Current status of direct dark matter detection experiments. Nat. Phys. 2017, 13, 212–216. [Google Scholar] [CrossRef]
- Bertone, G.; Tait, T.M.P. A new era in the search for dark matter. Nature 2018, 562, 51–56. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Dokuchaev, V.I.; Eroshenko, Y.N. Small-scale clumps of dark matter. Phys. Uspekhi 2014, 57, 1–36. [Google Scholar] [CrossRef]
- Derevianko, A.; Pospelov, M. Hunting for topological dark matter with atomic clocks. Nat. Phys. 2014, 10, 933–936. [Google Scholar] [CrossRef]
- Safronova, M.S.; Budker, D.; DeMille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Coleman, S. Q-balls. Nucl. Phys. B 1985, 262, 263–283. [Google Scholar] [CrossRef]
- Lee, T.D. Soliton stars and the critical masses of black holes. Phys. Rev. D 1987, 35, 3637–3639. [Google Scholar] [CrossRef] [PubMed]
- Kusenko, A.; Steinhardt, P.J. Q-ball candidates for self-interacting dark matter. Phys. Rev. Lett. 2001, 87, 141301. [Google Scholar] [CrossRef] [PubMed]
- Kimball, D.F.J.; Budker, D.; Eby, J.; Pospelov, M.; Pustelny, S.; Scholtes, T.; Stadnik, Y.V.; Weis, A.; Wickenbrock, A. Searching for axion stars and Q-balls with a terrestrial magnetometer network. Phys. Rev. D 2018, 97, 043002. [Google Scholar] [CrossRef]
- Hogan, C.J.; Rees, M.J. Axion miniclusters. Phys. Lett. B 1988, 205, 228–230. [Google Scholar] [CrossRef]
- Barranco, J.; Monteverde, A.C.; Delepine, D. Can the dark matter halo be a collisionless ensemble of axion stars? Phys. Rev. D 2013, 87, 103011. [Google Scholar] [CrossRef]
- Krippendorf, S.; Muia, F.; Quevedo, F. Moduli stars. J. High Energy Phys. 2018, 2018, 70. [Google Scholar] [CrossRef]
- Kibble, T. Some Implications of a Cosmological Phase Transition. Phys. Rep. 1980, 67, 183–199. [Google Scholar] [CrossRef]
- Vilenkin, A. Cosmic strings and domain walls. Phys. Rep. 1985, 121, 263–315. [Google Scholar] [CrossRef]
- Vilenkin, A.; Shaposhnikov, M. Cosmic Strings and Other Topological Defects; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Ge, S.; Lawson, K.; Zhitnitsky, A. Axion quark nugget dark matter model: Size distribution and survival pattern. Phys. Rev. D 2019, 99, 116017. [Google Scholar] [CrossRef]
- Budker, D.; Flambaum, V.V.; Liang, X.; Zhitnitsky, A. Axion quark nuggets and how a global network can discover them. Phys. Rev. D 2020, 101, 043012. [Google Scholar] [CrossRef]
- Budker, D.; Flambaum, V.V.; Zhitnitsky, A. Axion Quark Nuggets. SkyQuakes and Other Mysterious Explosions. arXiv preprint 2020, arXiv:2003.07363. [Google Scholar]
- Grabowska, D.M.; Melia, T.; Rajendran, S. Detecting dark blobs. Phys. Rev. D 2018, 98, 115020. [Google Scholar] [CrossRef]
- Brax, P.; Valageas, P.; Cembranos, J.A. Nonrelativistic formation of scalar clumps as a candidate for dark matter. Phys. Rev. D 2020, 102, 22–35. [Google Scholar] [CrossRef]
- Niikura, H.; Takada, M.; Yasuda, N.; Lupton, R.H.; Sumi, T.; More, S.; Kurita, T.; Sugiyama, S.; More, A.; Oguri, M.; et al. Microlensing constraints on primordial black holes with Subaru/HSC Andromeda observations. Nat. Astron. 2019, 3, 524–534. [Google Scholar] [CrossRef]
- Nesti, F.; Salucci, P. The Dark Matter halo of the Milky Way, AD 2013. J. Cosmol. Astropart. Phys. 2013, 2013, 16. [Google Scholar] [CrossRef]
- Freese, K.; Lisanti, M.; Savage, C. Colloquium: Annual modulation of dark matter. Rev. Mod. Phys. 2013, 85, 1561–1581. [Google Scholar] [CrossRef]
- Pospelov, M.; Pustelny, S.; Ledbetter, M.P.; Kimball, D.F.J.; Gawlik, W.; Budker, D. Detecting domain walls of axionlike models using terrestrial experiments. Phys. Rev. Lett. 2013, 110, 021803. [Google Scholar] [CrossRef]
- Roberts, B.M.; Blewitt, G.; Dailey, C.; Derevianko, A. Search for transient ultralight dark matter signatures with networks of precision measurement devices using a Bayesian statistics method. Phys. Rev. D 2018, 97, 083009. [Google Scholar] [CrossRef]
- Panelli, G.; Roberts, B.M.; Derevianko, A. Applying the matched-filter technique to the search for dark matter transients with networks of quantum sensors. EPJ Quantum Technol. 2020, 7, 5. [Google Scholar] [CrossRef]
- Masia-Roig, H.; Smiga, J.A.; Budker, D.; Dumont, V.; Grujic, Z.; Kim, D.; Jackson Kimball, D.F.; Lebedev, V.; Monroy, M.; Pustelny, S.; et al. Analysis method for detecting topological defect dark matter with a global magnetometer network. Phys. Dark Universe 2020, 28, 100494. [Google Scholar] [CrossRef]
- Jaeckel, J.; Schenk, S.; Spannowsky, M. Probing Dark Matter Clumps, Strings and Domain Walls with Gravitational Wave Detectors. arXiv preprint 2020, arXiv:2004.13724. [Google Scholar]
- Dailey, C.; Bradley, C.; Jackson Kimball, D.F.; Sulai, I.A.; Pustelny, S.; Wickenbrock, A.; Derevianko, A. Quantum sensor networks as exotic field telescopes for multi-messenger astronomy. Nat. Astron. 2020. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration and Virgo Collaboration. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Arvanitaki, A.; Huang, J.; Van Tilburg, K. Searching for dilaton dark matter with atomic clocks. Phys. Rev. D 2015, 91, 015015. [Google Scholar] [CrossRef]
- Van Tilburg, K.; Leefer, N.; Bougas, L.; Budker, D. Search for Ultralight Scalar Dark Matter with Atomic Spectroscopy. Phys. Rev. Lett. 2015, 115, 011802. [Google Scholar] [CrossRef]
- Hees, A.; Guéna, J.; Abgrall, M.; Bize, S.; Wolf, P. Searching for an Oscillating Massive Scalar Field as a Dark Matter Candidate Using Atomic Hyperfine Frequency Comparisons. Phys. Rev. Lett. 2016, 117, 061301. [Google Scholar] [CrossRef]
- Wcisło, P.; Morzyński, P.; Bober, M.; Cygan, A.; Lisak, D.; Ciuryło, R.; Zawada, M. Experimental constraint on dark matter detection with optical atomic clocks. Nat. Astron. 2016, 1, 0009. [Google Scholar] [CrossRef]
- Roberts, B.M.; Blewitt, G.; Dailey, C.; Murphy, M.; Pospelov, M.; Rollings, A.; Sherman, J.; Williams, W.; Derevianko, A. Search for domain wall dark matter with atomic clocks on board global positioning system satellites. Nat. Commun. 2017, 8, 1195. [Google Scholar] [CrossRef] [PubMed]
- Kalaydzhyan, T.; Yu, N. Extracting dark matter signatures from atomic clock stability measurements. Phys. Rev. D 2017, 96, 075007. [Google Scholar] [CrossRef]
- Wcislo, P.; Ablewski, P.; Beloy, K.; Bilicki, S.; Bober, M.; Brown, R.; Fasano, R.; Ciurylo, R.; Hachisu, H.; Ido, T.; et al. New bounds on dark matter coupling from a global network of optical atomic clocks. Sci. Adv. 2018, 4, eaau4869. [Google Scholar] [CrossRef]
- Savalle, E.; Hees, A.; Frank, F.; Cantin, E.; Pottie, P.E.; Roberts, B.M.; Cros, L.; McAllister, B.T.; Wolf, P. Searching for DArk Matter with a Non-Equal Delay inteferometer: The DAMNED experiment. Phys. Rev. Lett. 2021, accepted. [Google Scholar]
- Roberts, B.M.; Delva, P.; Al-Masoudi, A.; Amy-Klein, A.; Bærentsen, C.; Baynham, C.F.A.; Benkler, E.; Bilicki, S.; Bize, S.; Bowden, W.; et al. Search for transient variations of the fine structure constant and dark matter using fiber-linked optical atomic clocks. New J. Phys. 2020, 22, 093010. [Google Scholar] [CrossRef]
- Stadnik, Y.V.; Flambaum, V.V. Searching for dark matter and variation of fundamental constants with laser and maser interferometry. Phys. Rev. Lett. 2015, 114, 161301. [Google Scholar] [CrossRef] [PubMed]
- Stadnik, Y.V.; Flambaum, V.V. Enhanced effects of variation of the fundamental constants in laser interferometers and application to dark-matter detection. Phys. Rev. A 2016, 93, 063630. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Graham, P.W.; Hogan, J.M.; Rajendran, S.; Van Tilburg, K. Search for light scalar dark matter with atomic gravitational wave detectors. Phys. Rev. D 2018, 97, 075020. [Google Scholar] [CrossRef]
- Hu, W.; Lawson, M.; Budker, D.; Figueroa, N.L.; Kimball, D.F.J.; Mills, A.P.; Voigt, C. A network of precision gravimeters as a detector of matter with feeble nongravitational coupling. Eur. Phys. J. D 2020, 74, 115. [Google Scholar] [CrossRef]
- McNally, R.L.; Zelevinsky, T. Constraining domain wall dark matter with a network of superconducting gravimeters and LIGO. Eur. Phys. J. D 2020, 74, 61. [Google Scholar] [CrossRef]
- Savalle, E.; Roberts, B.M.; Frank, F.; Pottie, P.E.; McAllister, B.T.; Dailey, C.; Derevianko, A.; Wolf, P. Novel approaches to dark-matter detection using space-time separated clocks. arXiv preprint 2019, arXiv:1902.07192. [Google Scholar]
- Baron, J.; Campbell, W.C.; DeMille, D.; Doyle, J.M.; Gabrielse, G.; Gurevich, Y.V.; Hess, P.W.; Hutzler, N.R.; Kirilov, E.; Kozyryev, I.; et al. Order of magnitude smaller limit on the electric dipole moment of the electron. Science 2014, 343, 269–272. [Google Scholar] [CrossRef]
- Roberts, B.M.; Stadnik, Y.V.; Dzuba, V.A.; Flambaum, V.V.; Leefer, N.; Budker, D. Parity-violating interactions of cosmic fields with atoms, molecules, and nuclei: Concepts and calculations for laboratory searches and extracting limits. Phys. Rev. D 2014, 90, 096005. [Google Scholar] [CrossRef]
- Roberts, B.M.; Stadnik, Y.V.; Dzuba, V.A.; Flambaum, V.V.; Leefer, N.; Budker, D. Limiting P-Odd Interactions of Cosmic Fields with Electrons, Protons, and Neutrons. Phys. Rev. Lett. 2014, 113, 81601. [Google Scholar] [CrossRef]
- Abel, C.; Ayres, N.J.; Ban, G.; Bison, G.; Bodek, K.; Bondar, V.; Daum, M.; Fairbairn, M.; Flambaum, V.V.; Geltenbort, P.; et al. Search for Axionlike Dark Matter through Nuclear Spin Precession in Electric and Magnetic Fields. Phys. Rev. X 2017, 7, 041034. [Google Scholar] [CrossRef]
- Bovy, J.; Tremaine, S. On the local dark matter density. Astrophys. J. 2012, 756, 89. [Google Scholar] [CrossRef]
- Hernández, X.; Matos, T.; Sussman, R.A.; Verbin, Y. Scalar field “mini-MACHOs”: A new explanation for galactic dark matter. Phys. Rev. D 2004, 70, 043537. [Google Scholar] [CrossRef]
- González-Morales, A.X.; Valenzuela, O.; Aguilar, L.A. Constraining dark matter sub-structure with the dynamics of astrophysical systems. J. Cosmol. Astropart. Phys. 2013, 2013, 001. [Google Scholar] [CrossRef][Green Version]
- Angstmann, E.J.; Dzuba, V.A.; Flambaum, V.V. Relativistic effects in two valence-electron atoms and ions and the search for variation of the fine-structure constant. Phys. Rev. A 2004, 70, 014102. [Google Scholar] [CrossRef]
- Dinh, T.H.; Dunning, A.; Dzuba, V.A.; Flambaum, V.V. Sensitivity of hyperfine structure to nuclear radius and quark mass variation. Phys. Rev. A 2009, 79, 054102. [Google Scholar] [CrossRef]
- Roberts, B.M. Companion Code 2018. Available online: https://github.com/benroberts999/DM-ClockAsymmetry (accessed on 27 February 2021).
- Jet Propulsion Laboratory. Available online: ftp://sideshow.jpl.nasa.gov/pub/jpligsac/ (accessed on 27 February 2021).
- Jean, Y.; Dach, R. International GNSS Service Technical Report 2015 (IGS Annual Report); IGS Central Bureau and University of Bern, Bern Open Publishing: Bern, Switzerland, 2016. [Google Scholar] [CrossRef]
- Centers, G.P.; Blanchard, J.W.; Conrad, J.; Figueroa, N.L.; Garcon, A.; Gramolin, A.V.; Kimball, D.F.J.; Lawson, M.; Pelssers, B.; Smiga, J.A.; et al. Stochastic amplitude fluctuations of bosonic dark matter and revised constraints on linear couplings. arXiv preprint 2019, arXiv:1905.13650. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roberts, B.M.; Derevianko, A. Precision Measurement Noise Asymmetry and Its Annual Modulation as a Dark Matter Signature. Universe 2021, 7, 50. https://doi.org/10.3390/universe7030050
Roberts BM, Derevianko A. Precision Measurement Noise Asymmetry and Its Annual Modulation as a Dark Matter Signature. Universe. 2021; 7(3):50. https://doi.org/10.3390/universe7030050
Chicago/Turabian StyleRoberts, Benjamin M., and Andrei Derevianko. 2021. "Precision Measurement Noise Asymmetry and Its Annual Modulation as a Dark Matter Signature" Universe 7, no. 3: 50. https://doi.org/10.3390/universe7030050
APA StyleRoberts, B. M., & Derevianko, A. (2021). Precision Measurement Noise Asymmetry and Its Annual Modulation as a Dark Matter Signature. Universe, 7(3), 50. https://doi.org/10.3390/universe7030050





