Bound States for the Spin-1/2 Aharonov-Bohm Problem in a Rotating Frame
Abstract
:1. Introduction
2. The Equation of Motion
3. Self-Adjoint Extensions
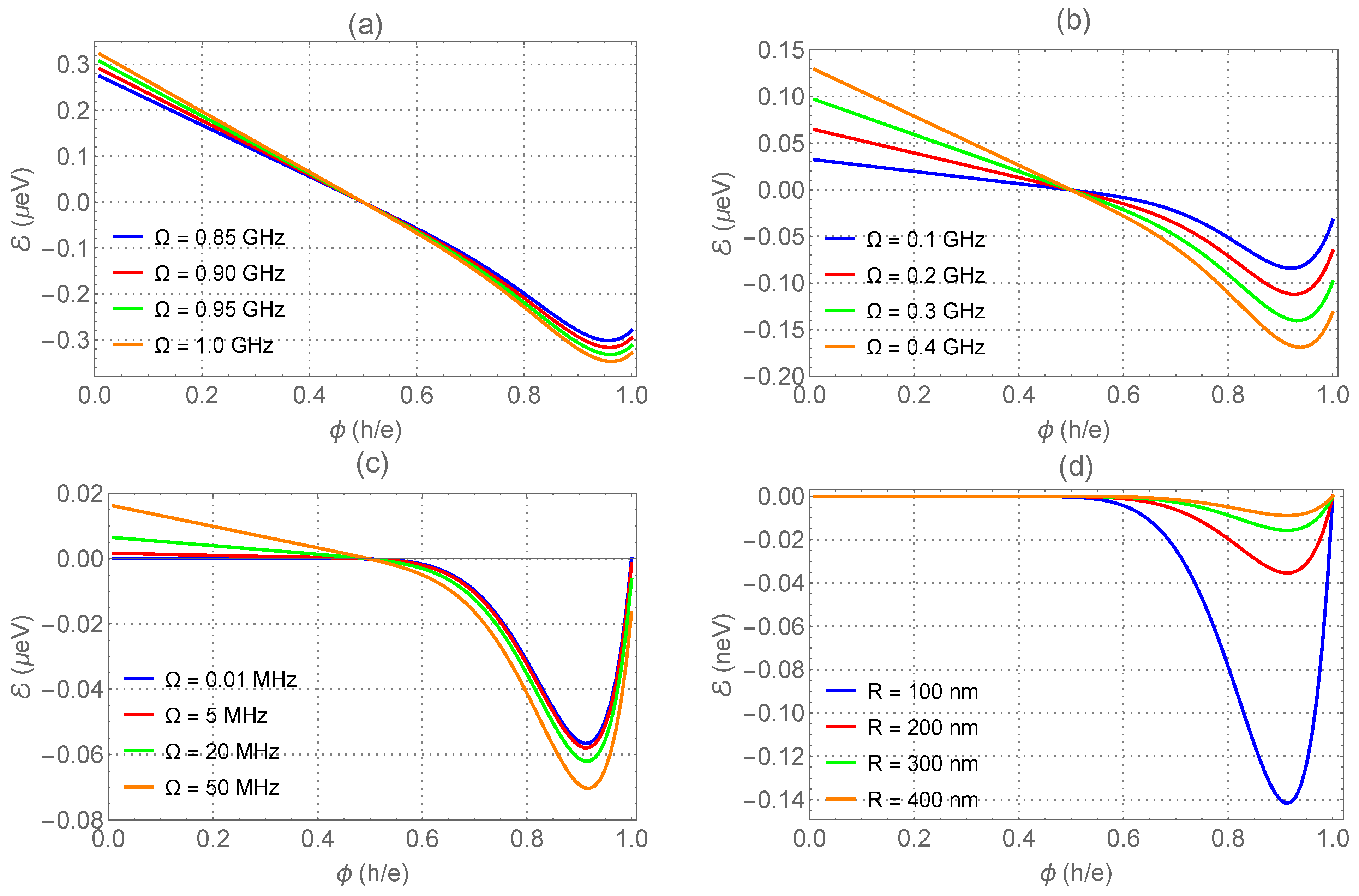
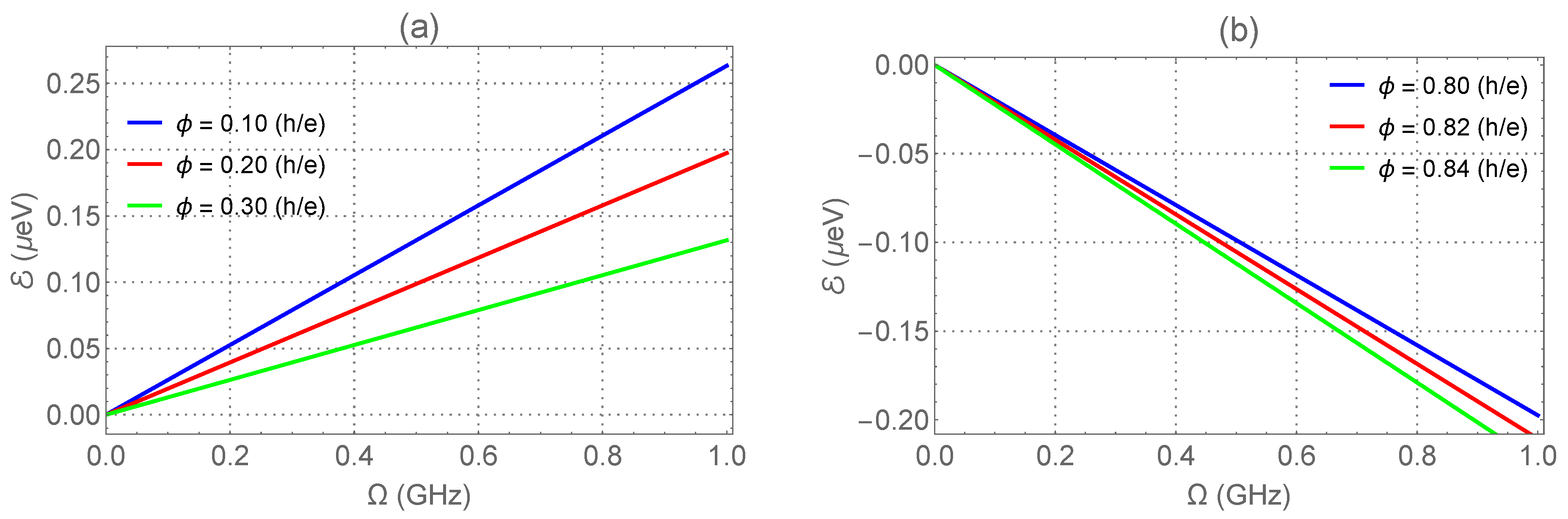
4. Numerical Analysis and Discussion of the Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Value for the deviation in the year 2008. |
| 2 |
References
- Aharonov, Y.; Bohm, D. Significance of Electromagnetic Potentials in the Quantum Theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Ford, L.; Vilenkin, A. A gravitational analogue of the Aharonov-Bohm effect. J. Phys. A Math. Gen. 1981, 14, 2353. [Google Scholar] [CrossRef]
- Nouri-Zonoz, M.; Parvizi, A. Gaussian curvature and global effects: Gravitational Aharonov-Bohm effect revisited. Phys. Rev. D 2013, 88, 023004. [Google Scholar] [CrossRef] [Green Version]
- Bezerra, V.B. Gravitational analogs of the Aharonov–Bohm effect. J. Math. Phys. 1989, 30, 2895–2899. [Google Scholar] [CrossRef]
- Davidowitz, H.; Steinberg, V. On an analog of the Aharonov-Bohm effect in superfluid helium. Europhys. Lett. (EPL) 1997, 38, 297–300. [Google Scholar] [CrossRef]
- Besharat, A.; Miri, M.; Nouri-Zonoz, M. Optical Aharonov–Bohm effect due to toroidal moment inspired by general relativity. J. Phys. Commun. 2019, 3, 115019. [Google Scholar] [CrossRef]
- Li, E.; Eggleton, B.J.; Fang, K.; Fan, S. Photonic Aharonov–Bohm effect in photon–phonon interactions. Nat. Commun. 2014, 5, 3225. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.T.; Yang, C.N. Concept of nonintegrable phase factors and global formulation of gauge fields. Phys. Rev. D 1975, 12, 3845–3857. [Google Scholar] [CrossRef] [Green Version]
- Peshkin, M. Aharonov-Bohm effect in bound states: Theoretical and experimental status. Phys. Rev. A 1981, 23, 360–361. [Google Scholar] [CrossRef]
- Schelter, J.; Recher, P.; Trauzettel, B. The Aharonov–Bohm effect in graphene rings. Solid State Commun. 2012, 152, 1411–1419. [Google Scholar] [CrossRef] [Green Version]
- Recher, P.; Trauzettel, B.; Rycerz, A.; Blanter, Y.M.; Beenakker, C.W.J.; Morpurgo, A.F. Aharonov-Bohm effect and broken valley degeneracy in graphene rings. Phys. Rev. B 2007, 76, 235404. [Google Scholar] [CrossRef] [Green Version]
- Matsunaga, R.; Matsuda, K.; Kanemitsu, Y. Evidence for Dark Excitons in a Single Carbon Nanotube due to the Aharonov-Bohm Effect. Phys. Rev. Lett. 2008, 101, 147404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alden Mead, C. The molecular Aharonov—Bohm effect in bound states. Chem. Phys. 1980, 49, 23–32. [Google Scholar] [CrossRef]
- Azevedo, S.; Moraes, F. Topological Aharonov-Bohm effect around a disclination. Phys. Lett. A 1998, 246, 374–376. [Google Scholar] [CrossRef]
- Ahmed, F. Aharonov-Bohm effect for bound states on spin-0 massive charged particles in a Gödel-type space–time with Coulomb potential. Commun. Theor. Phys. 2020, 72, 075102. [Google Scholar] [CrossRef]
- Bakke, K.; Furtado, C. The analogue of the aharonov–bohm effect for bound states for neutral particles. Mod. Phys. Lett. A 2011, 26, 1331–1341. [Google Scholar] [CrossRef]
- Furtado, C.; Bezerra, V.B.; Moraes, F. Aharonov–bohm effect for bound states in kaluza–klein theory. Mod. Phys. Lett. A 2000, 15, 253–258. [Google Scholar] [CrossRef]
- Leite, E.; Belich, H.; Bakke, K. Aharonov-Bohm effect for bound states on the confinement of a relativistic scalar particle to a coulomb-type potential in Kaluza-Klein theory. Adv. High Energy Phys. 2015, 2015, 925846. [Google Scholar] [CrossRef] [Green Version]
- Osipov, V. Aharonov-Bohm effect in planar systems with disclination vortices. Phys. Lett. A 1992, 164, 327–330. [Google Scholar] [CrossRef]
- Furtado, C.; de Lima Ribeiro, C.; Azevedo, S. Aharonov-Bohm effect in the presence of a density of defects. Phys. Lett. A 2002, 296, 171–175. [Google Scholar] [CrossRef]
- Li, K.; Dulat, S. The Aharonov–Bohm effect in noncommutative quantum mechanics. Eur. Phys. J. C-Part. Fields 2006, 46, 825–828. [Google Scholar] [CrossRef]
- Chaichian, M.; Prešnajder, P.; Sheikh-Jabbari, M.; Tureanu, A. Aharonov–Bohm effect in noncommutative spaces. Phys. Lett. B 2002, 527, 149–154. [Google Scholar] [CrossRef] [Green Version]
- Slobodeniuk, A.O.; Sharapov, S.G.; Loktev, V.M. Aharonov-Bohm effect in relativistic and nonrelativistic two-dimensional electron gases: A comparative study. Phys. Rev. B 2010, 82, 075316. [Google Scholar] [CrossRef] [Green Version]
- Hagen, C.R. Aharonov-Bohm scattering of particles with spin. Phys. Rev. Lett. 1990, 64, 503. [Google Scholar] [CrossRef]
- Hagen, C.R. Spin dependence of the Aharonov-Bohm effect. Int. J. Mod. Phys. A 1991, 6, 3119. [Google Scholar] [CrossRef]
- Hagen, C.R.; Park, D.K. Relativistic Aharonov-Bohm-Coulomb Problem. Ann. Phys. 1996, 251, 45. [Google Scholar] [CrossRef] [Green Version]
- Park, D.K.; Oh, J.G. Self-adjoint extension approach to the spin-1/2 Aharonov-Bohm-Coulomb problem. Phys. Rev. D 1994, 50, 7715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salem, V.; Costa, R.F.; Silva, E.O.; Andrade, F.M. Self-Adjoint Extension Approach for Singular Hamiltonians in (2 + 1) Dimensions. Front. Phys. 2019, 7, 175. [Google Scholar] [CrossRef]
- Shen, J.Q.; He, S.; Zhuang, F. Aharonov-Carmi effect and energy shift of valence electrons in rotating C60 molecules. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2005, 33, 35–38. [Google Scholar] [CrossRef]
- Santos, L.; Barros, C. Scalar bosons under the influence of noninertial effects in the cosmic string spacetime. Eur. Phys. J. C 2017, 77, 186. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Niu, Q. Angular Momentum of Phonons and the Einstein-de Haas Effect. Phys. Rev. Lett. 2014, 112, 085503. [Google Scholar] [CrossRef] [Green Version]
- Ono, M.; Chudo, H.; Harii, K.; Okayasu, S.; Matsuo, M.; Ieda, J.I.; Takahashi, R.; Maekawa, S.; Saitoh, E. Barnett effect in paramagnetic states. Phys. Rev. B 2015, 92, 174424. [Google Scholar] [CrossRef]
- Johnson, B.L. Inertial forces and the Hall effect. Am. J. Phys. 2000, 68, 649–653. [Google Scholar] [CrossRef]
- Dayi, O.F.; Kilinçarslan, E. Nonlinear chiral plasma transport in rotating coordinates. Phys. Rev. D 2017, 96, 043514. [Google Scholar] [CrossRef] [Green Version]
- Hussain, S.; Abdikian, A.; Hasnain, H. Spin density polarization effects in the presence of Coriolis force on ion acoustic waves in quantum plasma. Contrib. Plasma Phys. 2021, 61, e202000189. [Google Scholar] [CrossRef]
- Aharonov, Y.; Carmi, G. Quantum aspects of the equivalence principle. Found. Phys. 1973, 3, 493–498. [Google Scholar] [CrossRef]
- Harris, J.H.; Semon, M.D. A review of the Aharonov-Carmi thought experiment concerning the inertial and electromagnetic vector potentials. Found. Phys. 1980, 10, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Chernodub, M.N. Rotational Diode: Clockwise/Counterclockwise Asymmetry in Conducting and Mechanical Properties of Rotating (semi)Conductors. Symmetry 2021, 13, 1569. [Google Scholar] [CrossRef]
- Danner, A.; Demirel, B.; Kersten, W.; Lemmel, H.; Wagner, R.; Sponar, S.; Hasegawa, Y. Spin-rotation coupling observed in neutron interferometry. NPJ Quantum Inf. 2020, 6, 23. [Google Scholar] [CrossRef]
- Foldy, L.L.; Wouthuysen, S.A. On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit. Phys. Rev. 1950, 78, 29–36. [Google Scholar] [CrossRef]
- Tani, S. Connection between Particle Models and Field Theories, I: The Case Spin 1/2. Prog. Theor. Phys. 1951, 6, 267–285. [Google Scholar] [CrossRef]
- Rizzi, G.; Ruggiero, M.L. (Eds.) Relativity in Rotating Frames; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar] [CrossRef] [Green Version]
- Andrade, F.M.; Silva, E.O.; Pereira, M. Physical regularization for the spin-1/2 Aharonov-Bohm problem in conical space. Phys. Rev. D 2012, 85, 041701(R). [Google Scholar] [CrossRef] [Green Version]
- Andrade, F.M.; Silva, E.O.; Pereira, M. On the spin- 1/2 Aharonov-Bohm problem in conical space: Bound states, scattering and helicity nonconservation. Ann. Phys. 2013, 339, 510–530. [Google Scholar] [CrossRef] [Green Version]
- Casana, R.; Ferreira, M.M.; Passos, E.; dos Santos, F.E.P.; Silva, E.O. New CPT-even and Lorentz-violating nonminimal coupling in the Dirac equation. Phys. Rev. D 2013, 87, 047701. [Google Scholar] [CrossRef] [Green Version]
- de Sousa Gerbert, P. Fermions in an Aharonov-Bohm field and cosmic strings. Phys. Rev. D 1989, 40, 1346. [Google Scholar] [CrossRef]
- De Sousa Gerbert, P.; Jackiw, R. Classical and Quantum Scattering on a Spinning Cone. Commun. Math. Phys. 1989, 124, 229. [Google Scholar] [CrossRef]
- Jackiw, R. Diverse Topics in Theoretical and Mathematical Physics; Advanced Series in Mathematical Physics; World Scientific: Singapore, 1995. [Google Scholar]
- Voropaev, S.; Galtsov, D.; Spasov, D. Bound states for fermions in the gauge Aharonov-Bohm field. Phys. Lett. B 1991, 267, 91–94. [Google Scholar] [CrossRef]
- Bordag, M.; Voropaev, S. Bound states of an electron in the field of the magnetic string. Phys. Lett. B 1994, 333, 238–244. [Google Scholar] [CrossRef]
- Bordag, M.; Voropaev, S. Charged particle with magnetic moment in the Aharonov-Bohm potential. J. Phys. A 1993, 26, 7637. [Google Scholar] [CrossRef]
- Park, D.K. Green’s-function approach to two- and three-dimensional delta-function potentials and application to the spin-1/2 Aharonov-Bohm problem. J. Math. Phys. 1995, 36, 5453. [Google Scholar] [CrossRef]
- Filgueiras, C.; Moraes, F. On the quantum dynamics of a point particle in conical space. Ann. Phys. 2008, 323, 3150–3157. [Google Scholar] [CrossRef] [Green Version]
- Gesztesy, F.; Albeverio, S.; Hoegh-Krohn, R.; Holden, H. Point interactions in two dimensions: Basic properties, approximations and applications to solid state physics. J. Reine Angew. Math. 1987, 380, 87. [Google Scholar] [CrossRef]
- Albeverio, S.; Gesztesy, F.; Hoegh-Krohn, R.; Holden, H. Solvable Models in Quantum Mechanics, 2nd ed.; AMS Chelsea Publishing: Providence, RI, USA, 2004. [Google Scholar]
- Silva, E.O.; Andrade, F.M.; Filgueiras, C.; Belich, H. On Aharonov-Casher bound states. Eur. Phys. J. C 2013, 73, 2402. [Google Scholar] [CrossRef]
- Silva, E.O. On planar quantum dynamics of a magnetic dipole moment in the presence of electric and magnetic fields. Eur. Phys. J. C 2014, 74, 3112. [Google Scholar] [CrossRef] [Green Version]
- Andrade, F.M.; Filgueiras, C.; Silva, E.O. Scattering and Bound States of a Spin-1/2 Neutral Particle in the Cosmic String Spacetime. Adv. High Energy Phys. 2017, 2017, 7. [Google Scholar] [CrossRef]
- Silva, E.O.; Ulhoa, S.C.; Andrade, F.M.; Filgueiras, C.; Amorin, R.G.G. Quantum motion of a point particle in the presence of the Aharonov–Bohm potential in curved space. Ann. Phys. 2015, 362, 739. [Google Scholar] [CrossRef] [Green Version]
- Filgueiras, C.; Silva, E.O.; Oliveira, W.; Moraes, F. The effect of singular potentials on the harmonic oscillator. Ann. Phys. 2010, 325, 2529. [Google Scholar] [CrossRef]
- Kay, B.S.; Studer, U.M. Boundary conditions for quantum mechanics on cones and fields around cosmic strings. Commun. Math. Phys. 1991, 139, 103. [Google Scholar] [CrossRef]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics. II. Fourier Analysis, Self-Adjointness; Academic Press: New York, NY, USA; London, UK, 1975. [Google Scholar]
- Filgueiras, C.; Silva, E.O.; Andrade, F.M. Nonrelativistic quantum dynamics on a cone with and without a constraining potential. J. Math. Phys. 2012, 53, 122106. [Google Scholar] [CrossRef] [Green Version]
- Hagen, C.R. Exact equivalence of spin-1/2 Aharonov-Bohm and Aharonov-Casher effects. Phys. Rev. Lett. 1990, 64, 2347–2349. [Google Scholar] [CrossRef]
- Hagen, C.R. Effects of nongauge potentials on the spin-1/2 Aharonov-Bohm problem. Phys. Rev. D 1993, 48, 5935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Král, P.; Sadeghpour, H.R. Laser spinning of nanotubes: A path to fast-rotating microdevices. Phys. Rev. B 2002, 65, 161401. [Google Scholar] [CrossRef] [Green Version]
- Bubenchikov, A.M.; Bubenchikov, M.A.; Mamontov, D.V.; Lun-Fu, A.V. Md-Simulation of Fullerene Rotations in Molecular Crystal Fullerite. Crystals 2019, 9, 496. [Google Scholar] [CrossRef] [Green Version]

| (h/e) | (neV) | (neV) |
|---|---|---|
| 1.0000 | 0.0000 | 0.0000 |
| 2.0000 | −6.2385 | −3.8990 |
| 2.9999 | −5.7152 | −3.5720 |
| 4.0000 | −1.7292 | −1.0807 |
| 5.0000 | −8.4369 | −5.2731 |
| 5.9999 | −5.2267 | −3.2666 |
| 7.0000 | −1.3833 | −8.6460 |
| 8.0000 | −2.8693 | −1.7933 |
| 8.9999 | −2.3479 | −1.4674 |
| 0.1000 | −1.9991 | −1.2494 |
| 0.1100 | −3.2825 | −2.0516 |
| 0.1200 | −1.5685 | −9.8034 |
| 0.1300 | −2.8999 | −1.8124 |
| 0.1400 | −2.5423 | −1.5889 |
| 0.1499 | −1.2269 | −7.6686 |
| 0.1600 | −3.6457 | −2.2785 |
| 0.1700 | −7.2650 | −4.5406 |
| 0.1799 | −1.0377 | −6.4860 |
| 0.1900 | −1.1199 | −6.9995 |
| 0.2000 | −9.5226 | −5.9516 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lima, D.F.; Cunha, M.M.; Pereira, L.F.C.; Silva, E.O. Bound States for the Spin-1/2 Aharonov-Bohm Problem in a Rotating Frame. Universe 2021, 7, 457. https://doi.org/10.3390/universe7120457
Lima DF, Cunha MM, Pereira LFC, Silva EO. Bound States for the Spin-1/2 Aharonov-Bohm Problem in a Rotating Frame. Universe. 2021; 7(12):457. https://doi.org/10.3390/universe7120457
Chicago/Turabian StyleLima, Daniel F., Márcio M. Cunha, Luís Fernando C. Pereira, and Edilberto O. Silva. 2021. "Bound States for the Spin-1/2 Aharonov-Bohm Problem in a Rotating Frame" Universe 7, no. 12: 457. https://doi.org/10.3390/universe7120457
APA StyleLima, D. F., Cunha, M. M., Pereira, L. F. C., & Silva, E. O. (2021). Bound States for the Spin-1/2 Aharonov-Bohm Problem in a Rotating Frame. Universe, 7(12), 457. https://doi.org/10.3390/universe7120457






