Stellar Chromospheric Variability
Abstract
1. Introduction
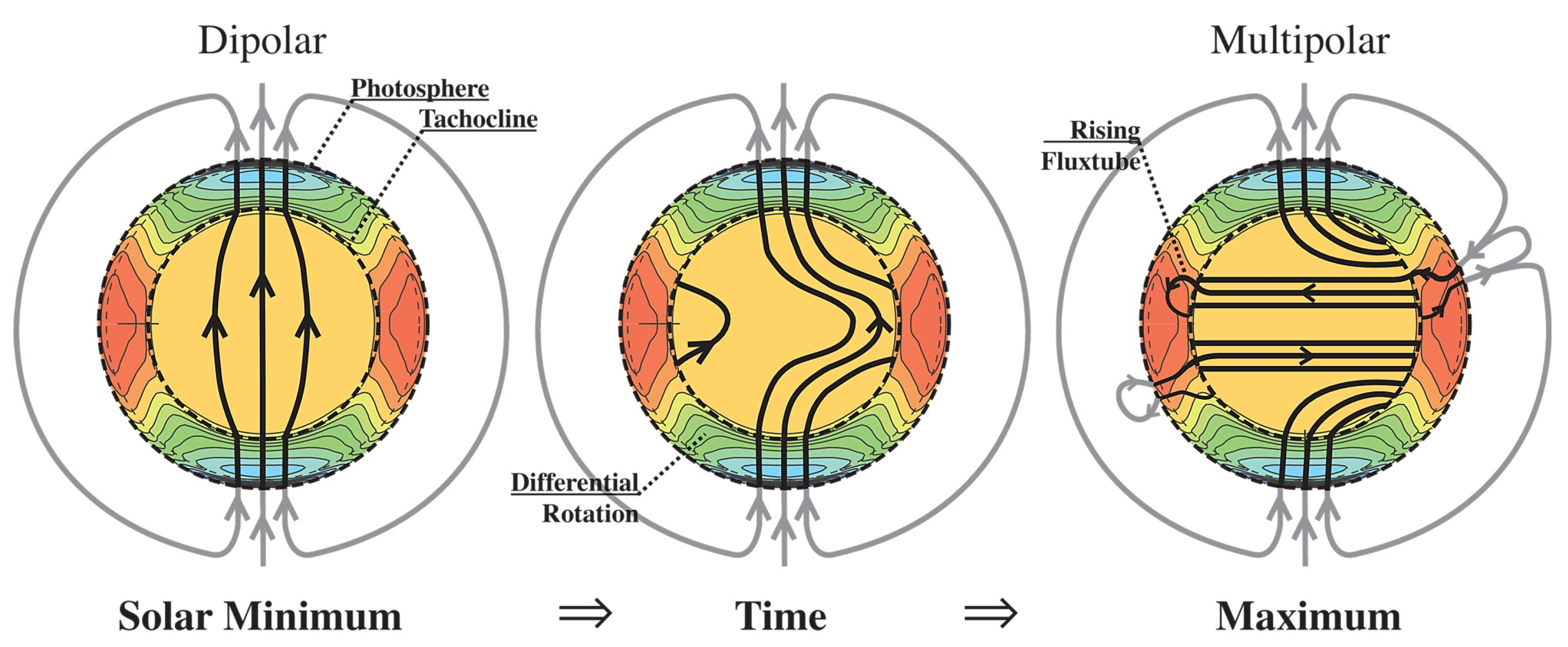
2. Magnetic Activity Cycles and the Solar Dynamo
2.1. The Solar Activity Cycle
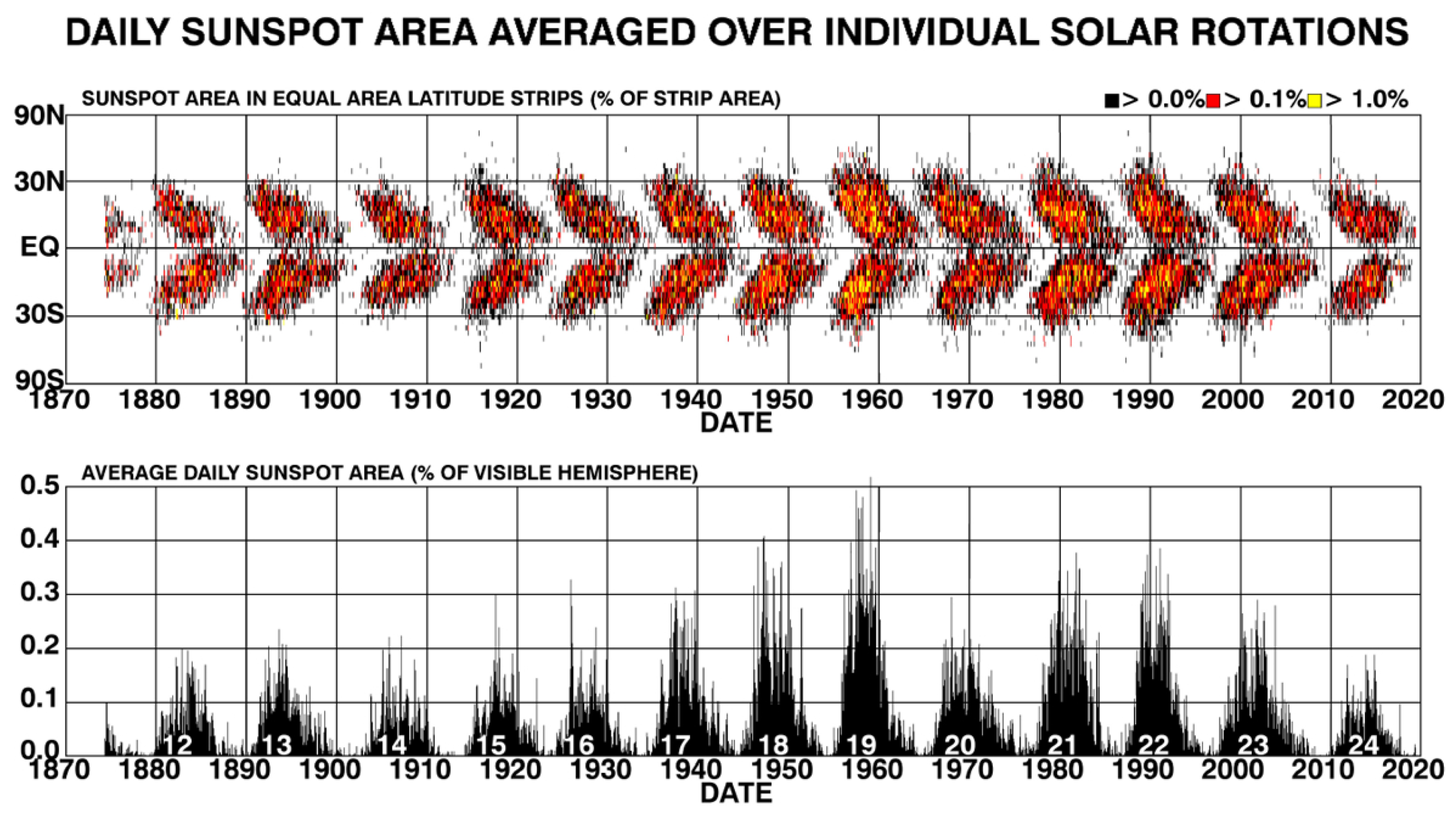
- The solar activity cycle is quasi-periodic. The periods range between 9 and 14 years, with a mean period of 11 years. Additionally, strong fluctuations have been observed in the cycle’s amplitude.
- Sunspots are observed to consist of pairs with opposite magnetic polarities [67]. It was observed that they are generally elongated in the East–West direction, with the leading polarities generally leaning closer to the Equator than the trailing polarities. Additionally, Hale noted that most leading spots have opposite polarities in opposite hemispheres. In addition, a reversal of polar magnetic fields near the time of cycle maximum has also been observed. This reversal is referred to as ‘Hale’s polarity Law’. As a consequence of this law, an underlying magnetic cycle of twice that period (approximately 22 years) is also present.
- Hale et al. [67] also showed that the sunspots observed on the solar surface show a systematic tilt, which increases with latitude, a phenomenon referred to as ‘Joy’s law’.
- The locations of sunspots show an equatorward drift of the active latitude, described by Spörer’s law [68].
- The Sun also exhibits a number of less dominant magnetic cycles [71].
- As we already saw in the Introduction, in addition to these reported observations of cyclic variations and sunspots, there has also been a period between 1645 and 1715 ([72], known as the ‘Maunder Minimum’); featuring an absence in solar activity, with very few sunspots observed.
2.2. The Solar Dynamo
2.2.1. Key Components of Dynamo Theory
- the cyclic polarity reversals with a decadal half-period, equatorward migration of the sunspot-generating deep toroidal field and its inferred strength, poleward migration of the diffuse surface field, the observed /2 phase lag between poloidal and toroidal components, polar field strength, observed antisymmetric equatorial parity and predominantly negative (positive) magnetic helicity in the Northern (Southern) solar hemisphere.
- the amplitude fluctuations, empirical patterns and correlations extracted from the sunspot and proxy records, including the Grand Minima, during which the cycle amplitude—and perhaps the cycle itself—is strongly suppressed over many cycle periods.
- the torsional oscillations in the convective envelope, with proper amplitude and phasing with respect to the magnetic cycle.
2.2.2. Mean-Field Models
2.2.3. Babcock–Leighton Flux Transport Models
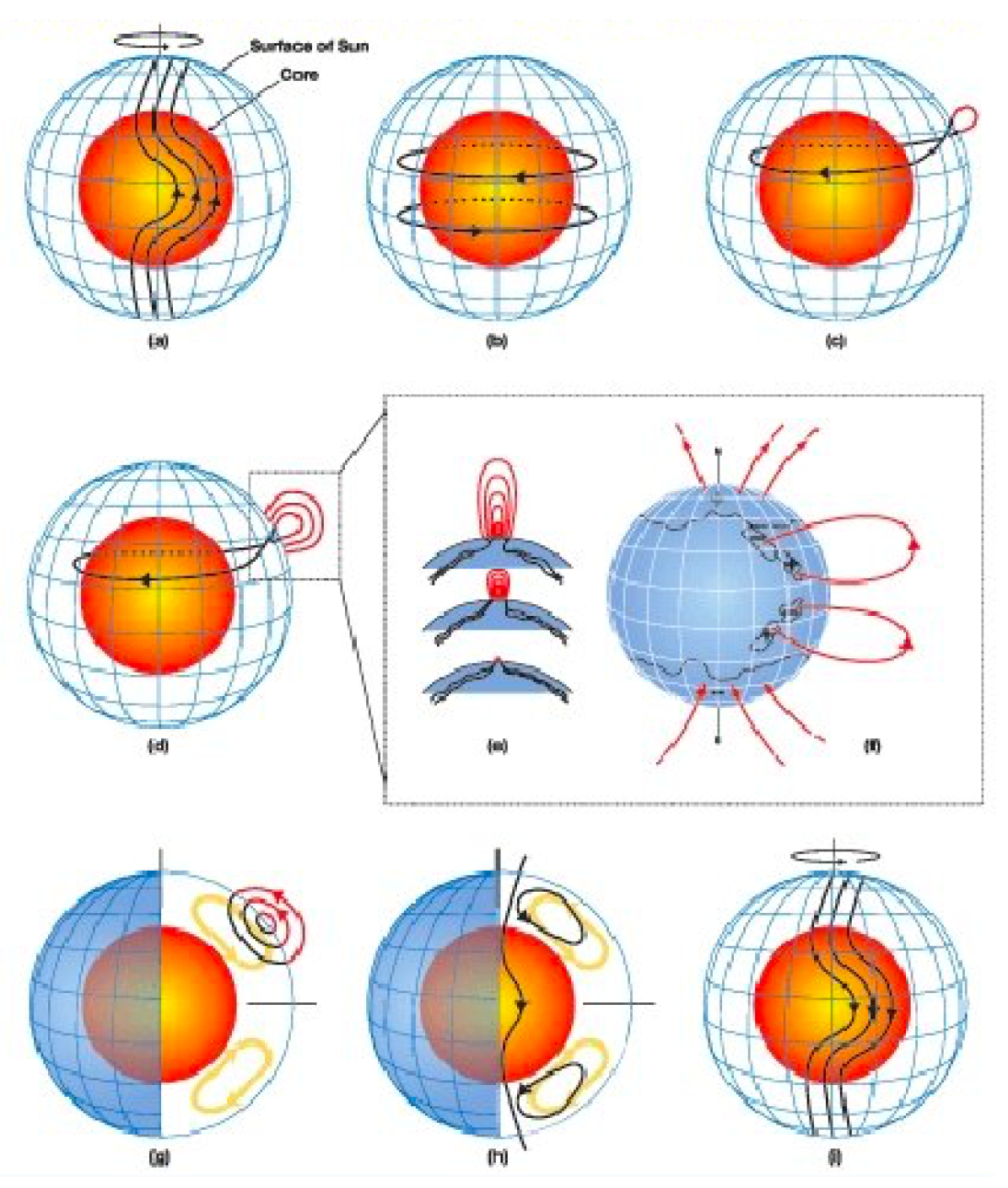
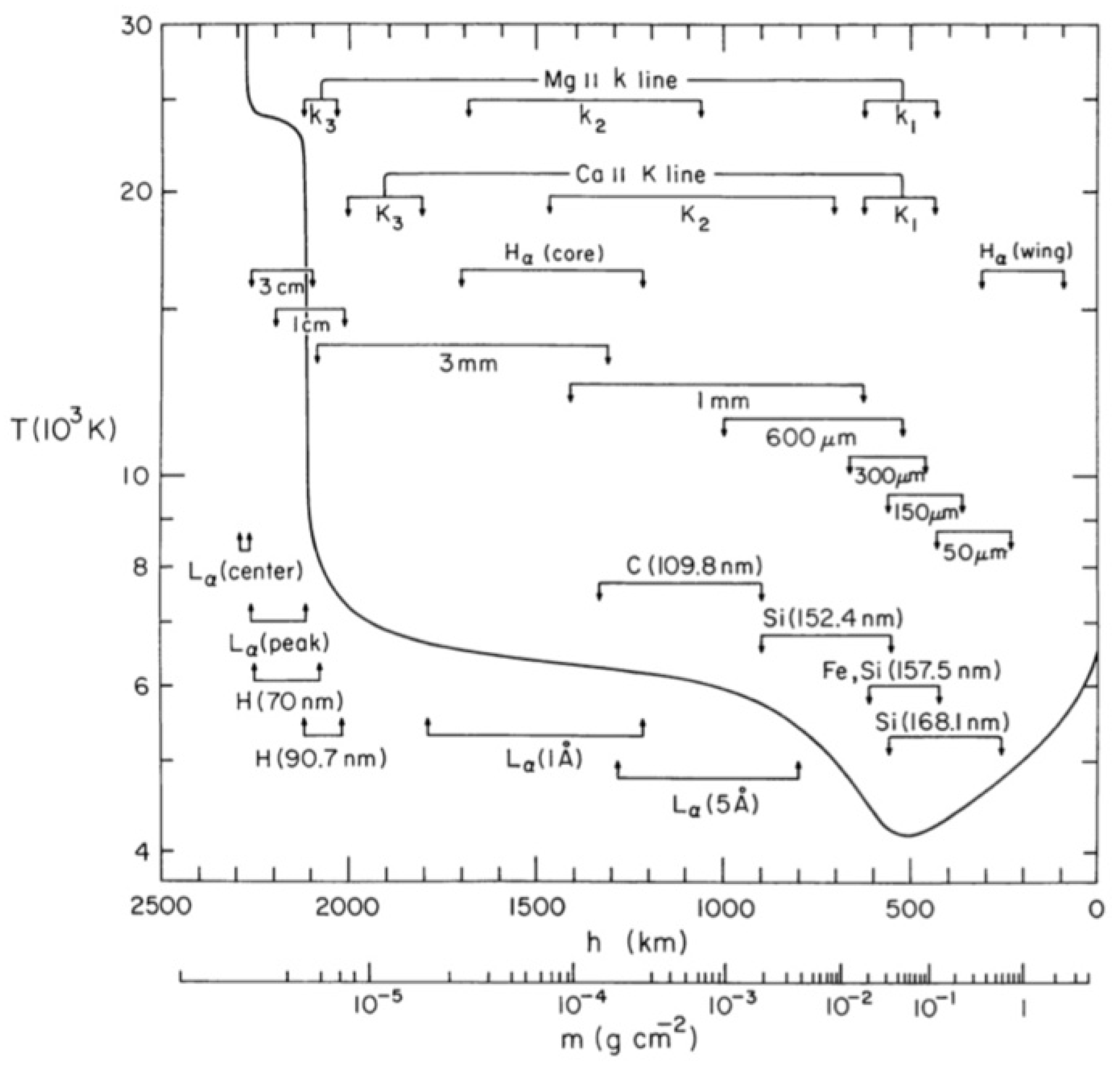
3. Diagnostics
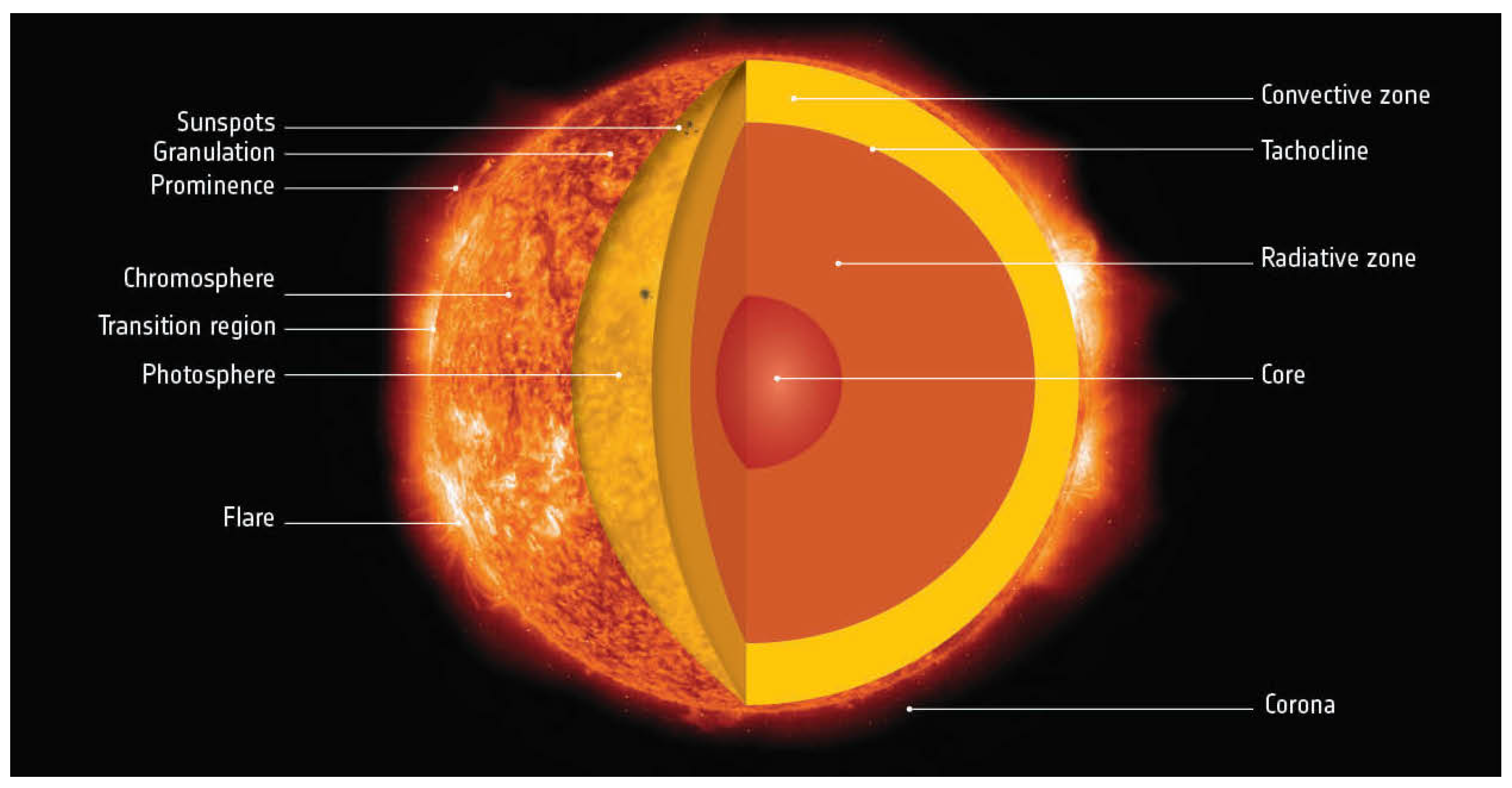
3.1. Spectroscopic Diagnostics
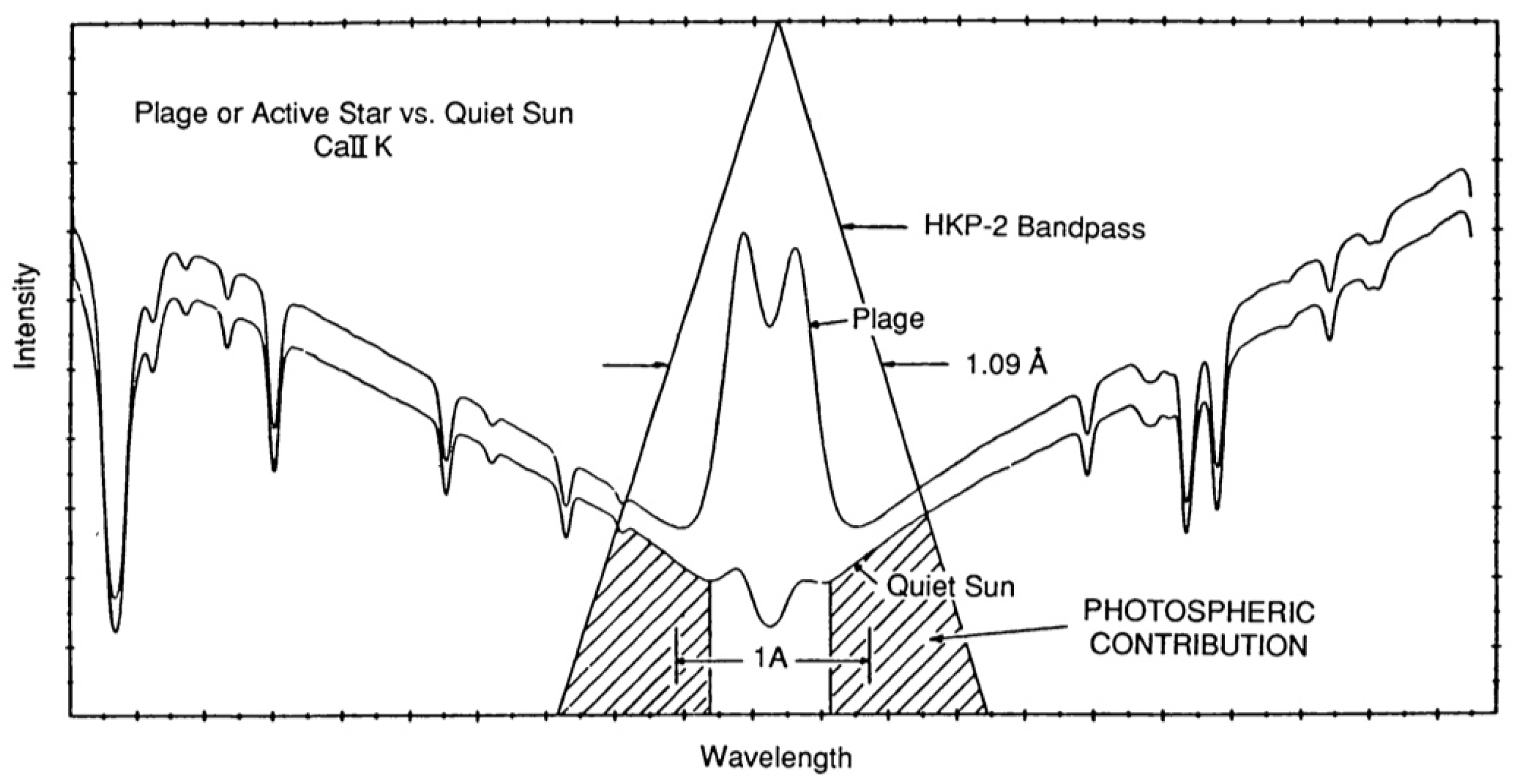
3.2. The Mt Wilson S Index
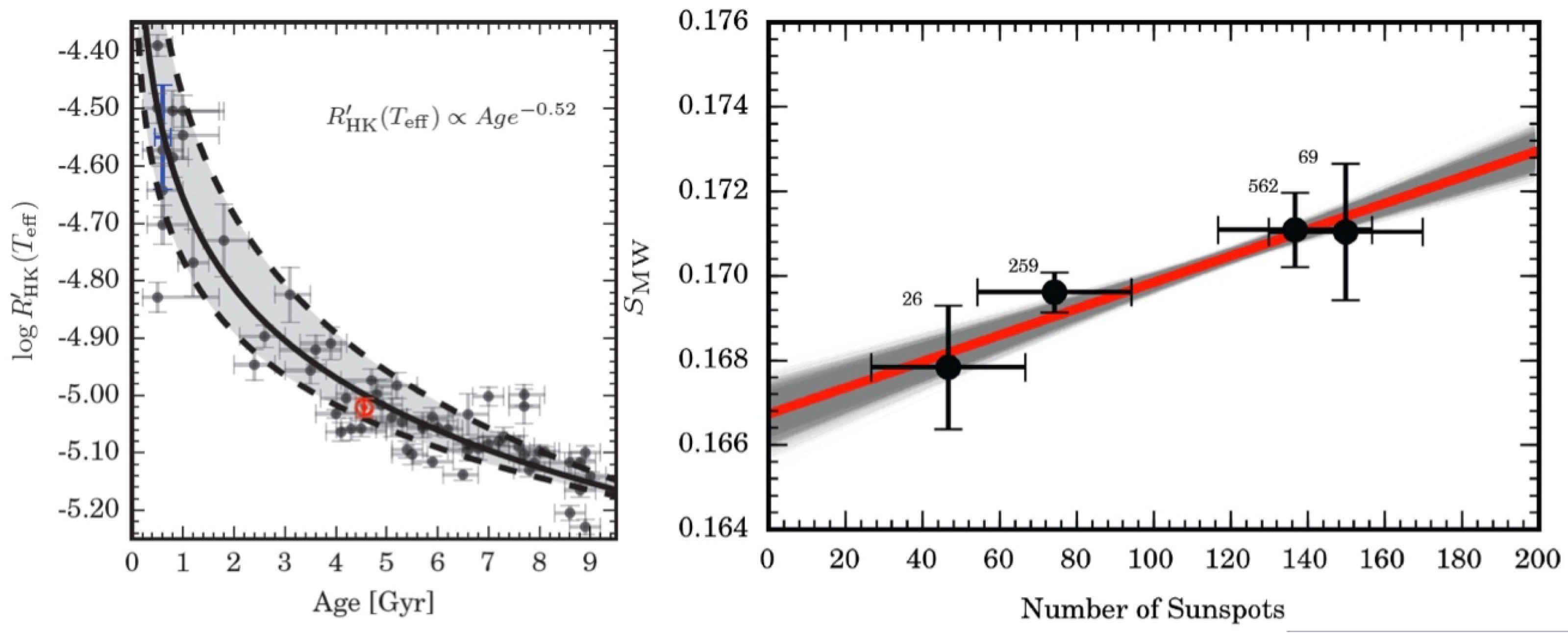
3.3. The Chromospheric Activity–Age Relation
3.4. Correlations with Starspot Number
3.5. The Vaughan–Preston Gap: Dependence on Stellar Rotation
4. Chromospheric Activity across the Hertzsprung–Russell Diagram
4.1. Solar-Type FGK Stars
4.2. Late-Type Giant and Supergiant Stars
4.3. M Dwarfs and L-Type Brown Dwarfs
5. Close Binarity and Stellar Chromospheric Activity
5.1. Rs Canum Venaticorum Systems
- Regular systems, characterised by orbital periods of 1–14 days. The hotter component is of spectral type F or G and luminosity class V (or IV). Strong Ca ii H and K emission is observed outside eclipses;
- Short-period, detached systems with orbital periods day. The hotter component is similar to those of the regular RS CVn systems. One or both components exhibit(s) Ca ii H and K emission;
- Long-period systems with orbital periods days. Either component is of spectral type G–K and luminosity class II–IV. Strong Ca ii H and K emission is observed outside eclipses;
- Flare star systems, where the hotter component is of spectral type dKe (a K-type main-sequence star/dwarf exhibiting emission) or dMe (an M-type red dwarf showing emission) and features strong Ca ii H and K emission;
- V471 -type systems, where the hotter component is a white dwarf and the cooler, G–K-type component again exhibits strong Ca ii H and K emission.
5.2. By Draconis Systems
5.3. W Ursae Majoris Common Envelope Systems
5.4. Algol Binaries
6. Open Questions and Current Trends
- Acoustic frequency spectra instead of monochromatic waves;
- Thermal bifurcation due to CO molecules; and
- Time-dependent ionisation of hydrogen.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://wwwbis.sidc.be/silso/datafiles (accessed on 25 September 2021). |
| 2 | https://www.ztf.caltech.edu (accessed on 25 September 2021). |
| 3 | http://www2.lowell.edu/users/jch/sss/index.php (accessed on 25 September 2021). |
References
- Baliunas, S.L.; Dupree, A.K. Ultraviolet and optical spectrum studies of λ Andromedae: Evidence for atmospheric inhomogeneities. Astrophys. J. 1982, 252, 668–680. [Google Scholar] [CrossRef]
- Dupree, A.K.; Baliunas, S.L.; Guinan, E.F.; Hartmann, L.; Nassiopoulos, G.E.; Sonneborn, G. Periodic Photospheric and Chromospheric Modulation in α Orionis (Betelgeuse). Astrophys. J. Lett. 1987, 317, L85–L89. [Google Scholar] [CrossRef]
- Rutten, R.G.M. Magnetic structure in cool stars. XII. Chromospheric activity and rotation of giants and dwarfs. Astron. Astrophys. 1987, 177, 131–142. [Google Scholar]
- Pasquini, L.; Pallavicini, R. Hα absolute chromospheric fluxes in G and K dwarfs and subgiants. Astron. Astrophys. 1991, 251, 199–209. [Google Scholar]
- Lobel, A.; Dupree, A.K. Spatially Resolved STIS Spectroscopy of α Orionis: Evidence for Nonradial Chromospheric Oscillation from Detailed Modeling. Astrophys. J. 2001, 558, 815–829. [Google Scholar] [CrossRef]
- Dupree, A.K.; Stefanik, R.P. Direct ultraviolet imaging and spectroscopy of Betelgeuse. Eur. Astron. Soc. Publ. Ser. 2013, 60, 77–84. [Google Scholar] [CrossRef][Green Version]
- Oláh, K.; Moór, A.; Kővári, Z.; Granzer, T.; Strassmeier, K.G.; Kriskovics, L.; Vida, K. Magnitude-range brightness variations of overactive K giants. Astron. Astrophys. 2014, 572, A94. [Google Scholar] [CrossRef]
- Ramiaramanantsoa, T.; Moffat, A.F.J.; Harmon, R.; Richardson, N.D.; Howarth, I.D.; Stevens, I.R.; Piaulet, C.; St-Jean, L.; Eversberg, T.; Pigulski, A.; et al. BRITE-Constellation high-precision time-dependent photometry of the early O-type supergiant ζ Puppis unveils the photospheric drivers of its small- and large-scale wind structures. Mon. Not. R. Astron. Soc. 2018, 473, 5532–5569. [Google Scholar] [CrossRef]
- Dupree, A.K.; Lobel, A.; Young, P.R.; Ake, T.B.; Linsky, J.L.; Redfield, S. A Far-Ultraviolet Spectroscopic Survey of Luminous Cool Stars. Astrophys. J. 2005, 622, 629–652. [Google Scholar] [CrossRef]
- Dupree, A.K.; Li, T.Q.; Smith, G.H. Hubble Space Telescope Observations of Chromospheres in Metal-Deficient Field Giants. Astron. J. 2007, 134, 1348–1359. [Google Scholar] [CrossRef][Green Version]
- Spitzer, L. Physics of Fully Ionized Gases, 2nd ed.; Interscience: New York, NY, USA, 1962. [Google Scholar]
- Khomenko, E.; Collados, M.; Díaz, A.; Vitas, N. Fluid description of multi-component solar partially ionized plasma. Phys. Plasmas 2014, 21, 092901. [Google Scholar] [CrossRef]
- Ballester, J.L.; Alexeev, I.; Collados, M.; Downes, T.; Pfaff, R.F.; Gilbert, H.; Khodachenko, M.; Khomenko, E.; Shaikhislamov, I.F.; Soler, R.; et al. Partially Ionized Plasmas in Astrophysics. Space Sci. Rev. 2018, 214, 58. [Google Scholar] [CrossRef]
- Cally, P.S.; Khomenko, E. Fast-to-Alfvén Mode Conversion and Ambipolar Heating in Structured Media. I. Simplified Cold Plasma Model. Astrophys. J. 2019, 885, 58. [Google Scholar] [CrossRef]
- González-Morales, P.A.; Khomenko, E.; Vitas, N.; Collados, M. Joint action of Hall and ambipolar effects in 3D magneto-convection simulations of the quiet Sun. I. Dissipation and generation of waves. Astron. Astrophys. 2020, 642, A220. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Ballester, J.L.; Cally, P.S.; Carlsson, M.; Goossens, M.; Jess, D.B.; Khomenko, E.; Mathioudakis, M.; Murawski, K.; Zaqarashvili, T.V. Chromospheric Heating by Magnetohydrodynamic Waves and Instabilities. J. Geophys. Res. (Space Phys.) 2021, 126, e029097. [Google Scholar] [CrossRef]
- Biermann, L. Zur Deutung der chromosphärischen Turbulenz und des Exzesses der UV-Strahlung der Sonne. Naturwissenschaften 1946, 33, 118–119. [Google Scholar] [CrossRef]
- Parker, E.N. Dynamics of the Interplanetary Gas and Magnetic Fields. Astrophys. J. 1958, 128, 664–676. [Google Scholar] [CrossRef]
- Parker, E.N. Dynamical Theory of the Solar Wind. Space Sci. Rev. 1965, 4, 666–708. [Google Scholar] [CrossRef]
- Solanki, S.K.; Hammer, R. The Solar Atmosphere. Century Space Sci. 2002, I, 1065–1086. [Google Scholar]
- Vernazza, J.E.; Avrett, E.H.; Loeser, R. Structure of the solar chromosphere. III. Models of the EUV brightness components of the quiet Sun. Astrophys. J. Suppl. Ser. 1981, 45, 635–725. [Google Scholar] [CrossRef]
- Karoff, C.; Metcalfe, T.S.; Santos, Â.R.G.; Montet, B.T.; Isaacson, H.; Witzke, V.; Shapiro, A.I.; Mathur, S.; Davies, G.R.; Lund, M.N. The Influence of Metallicity on Stellar Differential Rotation and Magnetic Activity. Astrophys. J. 2018, 852, 46. [Google Scholar] [CrossRef]
- Eddy, J.A. A New Sun: The Solar Results From Skylab; Ise, R., Ed.; NASA SP-402; NASA: Washington, DC, USA, 1979.
- Petit, P.; Dintrans, B.; Solanki, S.K.; Donati, J.-F.; Aurière, M.; Lignières, F.; Morin, J.; Paletou, F.; Ramirez, J.; Catala, C.; et al. Toroidal versus poloidal magnetic fields in Sun-like stars: A rotation threshold. Mon. Not. R. Astron. Soc. 2008, 388, 80–88. [Google Scholar] [CrossRef]
- Parker, E.N. The Generation of Magnetic Fields in Astrophysical Bodies. I. The Dynamo Equations. Astrophys. J. 1970, 162, 665–673. [Google Scholar] [CrossRef]
- Lorenzo-Oliveira, D.; Freitas, F.C.; Meléndez, J.; Bedell, M.; Ramírez, I.; Bean, J.L.; Asplund, M.; Spina, L.; Dreizler, S.; Alves-Brito, A.; et al. The Solar Twin Planet Search. The age–chromospheric activity relation. Astron. Astrophys. 2018, 619, A73. [Google Scholar] [CrossRef]
- Eddy, J.A. Climate and the changing sun. Clim. Chang. 1977, 1, 173–190. [Google Scholar] [CrossRef]
- Sokoloff, D. The Maunder Minimum and the Solar Dynamo. Sol. Phys. 2004, 224, 145–152. [Google Scholar] [CrossRef]
- Miyahara, H.; Sokoloff, D.; Usoskin, I.G. The Solar Cycle at the Maunder Minimum Epoch. Adv. Geosci. 2006, 2, 1–20. [Google Scholar] [CrossRef]
- Cliver, E.W.; Boriakoff, V.; Bounar, K.H. Geomagnetic activity and the solar wind during the Maunder Minimum. Geophys. Res. Lett. 1998, 25, 897–900. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Mursula, K.; Kovaltsov, G.A. Heliospheric modulation of cosmic rays and solar activity during the Maunder minimum. J. Geophys. Res. 2001, 106, 16039–16046. [Google Scholar] [CrossRef]
- Babcock, H.W. The Topology of the Sun’s Magnetic Field and the 22-year Cycle. Astrophys. J. 1961, 133, 572–587. [Google Scholar] [CrossRef]
- Charbonneau, P. Solar Dynamo Theory. Annu. Rev. Astron. Astrophys. 2014, 52, 251–290. [Google Scholar] [CrossRef]
- Skumanich, A. Time Scales for Ca ii Emission Decay, Rotational Braking, and Lithium Depletion. Astrophys. J. 1972, 171, 565–567. [Google Scholar] [CrossRef]
- Soderblom, D.R.; Duncan, D.K.; Johnson, D.R.H. The Chromospheric Emission–Age Relation for Stars of the Lower Main Sequence and Its Implications for the Star Formation Rate. Astrophys. J. 1991, 375, 722–739. [Google Scholar] [CrossRef]
- Rocha-Pinto, H.J.; Maciel, W.J. Metallicity effects on the chromospheric activity–age relation for late-type dwarfs. Mon. Not. R. Astron. Soc. 1998, 298, 332–346. [Google Scholar] [CrossRef]
- Lachaume, R.; Dominik, C.; Lanz, T.; Habing, H.J. Age determinations of main-sequence stars: Combining different methods. Astron. Astrophys. 1999, 348, 897–909. [Google Scholar]
- Pace, G.; Pasquini, L. The age–activity–rotation relationship in solar-type stars. Astron. Astrophys. 2004, 426, 1021–1034. [Google Scholar] [CrossRef]
- Mamajek, E.E.; Hillenbrand, L.A. Improved Age Estimation for Solar-Type Dwarfs Using Activity–Rotation Diagnostics. Astrophys. J. 2008, 687, 1264–1293. [Google Scholar] [CrossRef]
- Pace, G. Chromospheric activity as age indicator. An L-shaped chromospheric-activity versus age diagram. Astron. Astrophys. 2013, 551, L8. [Google Scholar] [CrossRef]
- Lorenzo-Oliveira, D.; Porto de Mello, G.F.; Dutra-Ferreira, L.; Ribas, I. Fine structure of the age–chromospheric activity relation in solar-type stars. I. The Ca ii infrared triplet: Absolute flux calibration. Astron. Astrophys. 2016, 595, A11. [Google Scholar] [CrossRef][Green Version]
- Karoff, C.; Metcalfe, T.S.; Montet, B.T.; Jannsen, N.E.; Santos, A.R.G.; Nielsen, M.B.; Chaplin, W.J. Sounding stellar cycles with Kepler. III. Comparative analysis of chromospheric, photometric, and asteroseismic variability. Mon. Not. R. Astron. Soc. 2019, 485, 5096–5104. [Google Scholar] [CrossRef]
- Denissenkov, P.A.; Pinsonneault, M.; MacGregor, K.B. Magneto-Thermohaline Mixing in Red Giants. Astrophys. J. 2009, 696, 1823–1833. [Google Scholar] [CrossRef]
- Vescovi, D.; Cristallo, S.; Palmerini, S.; Abia, C.; Busso, M. Magnetic-buoyancy-induced mixing in AGB stars: Fluorine nucleosynthesis at different metallicities. Astron. Astrophys. 2021, 652, A100. [Google Scholar] [CrossRef]
- Salabert, D.; García, R.A.; Beck, P.G.; Egeland, R.; Pallé, P.L.; Mathur, S.; Metcalfe, T.S.; do Nascimento, J.-D.; Ceillier, T.; Andersen, M.F.; et al. Photospheric and chromospheric magnetic activity of seismic solar analogs. Observational inputs on the solar–stellar connection from Kepler and Hermes. Astron. Astrophys. 2016, 596, A31. [Google Scholar] [CrossRef]
- Mehrabi, A.; He, H.; Khosroshahi, H. Magnetic Activity Analysis for a Sample of G-type Main Sequence Kepler Targets. Astrophys. J. 2017, 834, 207. [Google Scholar] [CrossRef]
- Karak, B.B.; Kitchatinov, L.L.; Choudhuri, A.R. A Dynamo Model of Magnetic Activity in Solar-like Stars with Different Rotational Velocities. Astrophys. J. 2014, 791, 59. [Google Scholar] [CrossRef]
- Pipin, V.V.; Kosovichev, A.G. Dependence of Stellar Magnetic Activity Cycles on Rotational Period in a Nonlinear Solar-type Dynamo. Astrophys. J. 2016, 823, 133. [Google Scholar] [CrossRef]
- Karoff, C.; Knudsen, M.F.; De Cat, P.; Bonanno, A.; Fogtmann-Schulz, A.; Fu, J.; Frasca, A.; Inceoglu, F.; Olsen, J.; Zhang, Y.; et al. Observational evidence for enhanced magnetic activity of superflare stars. Nat. Commun. 2016, 7, 11058. [Google Scholar] [CrossRef]
- Balona, L.A. Flare stars across the H–R diagram. Mon. Not. R. Astron. Soc. 2015, 447, 2714–2725. [Google Scholar] [CrossRef]
- Roettenbacher, R.M.; Monnier, J.D.; Korhonen, H.; Aarnio, A.N.; Baron, F.; Che, X.; Harmon, R.O.; Kővári, Z.; Kraus, S.; Schaefer, G.H.; et al. No Sun-like dynamo on the active star ζ Andromedae from starspot asymmetry. Nature 2016, 533, 217–220. [Google Scholar] [CrossRef]
- Roettenbacher, R.M.; Monnier, J.D.; Korhonen, H.; Harmon, R.O.; Baron, F.; Hackman, T.; Henry, G.W.; Schaefer, G.H.; Strassmeier, K.; Weber, M.; et al. Contemporaneous Imaging Comparisons of the Spotted Giant σ Geminorum Using Interferometric, Spectroscopic, and Photometric Data. Astrophys. J. 2017, 849, 120. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, H.; Han, X.L.; Jiang, L.; Li, Z.; Zhang, Y.; Hou, Y.; Wang, Y.; Cao, Z. Chromospheric activity of periodic variable stars (including eclipsing binaries) observed in DR2 LAMOST stellar spectral survey. New Astron. 2018, 61, 36–58. [Google Scholar] [CrossRef]
- Kaya, N.Ö.; Dal, H.A. Chromospheric activity behavior of an eclipsing binary system KOI 68AB. Astron. Nachrichten 2019, 340, 539–552. [Google Scholar] [CrossRef]
- Solanki, S.K.; Krivova, N.A.; Haigh, J.D. Solar Irradiance Variability and Climate. Annu. Rev. Astron. Astrophys. 2013, 51, 311–351. [Google Scholar] [CrossRef]
- Ribas, I.; Guinan, E.F.; Güdel, M.; Audard, M. Evolution of the Solar Activity over Time and Effects on Planetary Atmospheres. I. High-Energy Irradiances (1–1700 Å). Astrophys. J. 2005, 622, 680–694. [Google Scholar] [CrossRef]
- Airapetian, V.S.; Usmanov, A.V. Reconstructing the Solar Wind from Its Early History to Current Epoch. Astrophys. J. Lett. 2016, 817, L24. [Google Scholar] [CrossRef]
- do Nascimento, J.-D.; García, R.A.; Mathur, S.; Anthony, F.; Barnes, S.A.; Meibom, S.; da Costa, J.S.; Castro, M.; Salabert, D.; Ceillier, T. Rotation Periods and Ages of Solar Analogs and Solar Twins Revealed by the Kepler Mission. Astrophys. J. Lett. 2014, 790, L23. [Google Scholar] [CrossRef]
- Larmor, J. How could a rotating body such as the Sun become a magnet? Rep. Brit. Assoc. 1919, 87, 159–160. [Google Scholar]
- Cowling, T.G. The magnetic field of sunspots. Mon. Not. R. Astron. Soc. 1933, 94, 39–48. [Google Scholar] [CrossRef]
- Parker, E.N. The Formation of Sunspots from the Solar Toroidal Field. Astrophys. J. 1955, 121, 491. [Google Scholar] [CrossRef]
- Parker, E.N. The generation of magnetic fields in astrophysical bodies. X. Magnetic buoyancy and the solar dynamo. Astrophys. J. 1975, 198, 205–209. [Google Scholar] [CrossRef]
- Fan, Y. Magnetic Fields in the Solar Convection Zone. Living Rev. Sol. Phys. 2009, 6, 4. [Google Scholar] [CrossRef]
- Schwabe, H. Sonnen-Beobachtungen im Jahre 1843. Astron. Nachr 1844, 21, 233–236. [Google Scholar] [CrossRef]
- Hathway, D. The Solar Cycle. Living Rev. Sol. Phys. 2015, 7, 1–91. [Google Scholar] [CrossRef]
- Usoskin, I.G. A history of solar activity over millennia. Living Rev. Sol. Phys. 2017, 14, 3. [Google Scholar] [CrossRef]
- Hale, G.E.; Ellerman, F.; Nicholson, S.B.; Joy, A.H. The magnetic polarity of sun-spots. Astrophys. J. 1919, 49, 153–178. [Google Scholar] [CrossRef]
- Carrington, R.C. Observations of the Spots on the Sun from 9 November 1853, to 24 March 1861, Made at Redhill; Williams and Norgate: London, UK, 1863. [Google Scholar]
- Deng, L.H.; Xiang, Y.Y.; Qu, Z.N.; An, J.M. Systematic Regularity of Hemispheric Sunspot Areas Over the Past 140 Years. Astron. J. 2016, 151, 70. [Google Scholar] [CrossRef]
- Boro Saikia, S.; Marvin, C.J.; Jeffers, S.V.; Reiners, A.; Cameron, R.; Marsden, S.C.; Petit, P.; Warnecke, J.; Yadav, A.P. Chromospheric activity catalogue of 4454 cool stars. Questioning the active branch of stellar activity cycles. Astron. Astrophys. 2018, 616, A108. [Google Scholar] [CrossRef]
- Solanki, S.K.; Inhester, B.; Schüssler, M. The solar magnetic field. Rep. Prog. Phys. 2006, 69, 563–668. [Google Scholar] [CrossRef]
- Eddy, J.A. The Maunder minimum: A reappraisal. Sol. Phys. 1983, 89, 195–207. [Google Scholar] [CrossRef]
- Nandy, D.; Martens, P.C.H.; Obridko, V.; Dash, S.; Georgieva, K. Solar evolution and extrema: Current state of understanding of long-term solar variability and its planetary impacts. Prog. Earth Planet. Sci. 2021, 8, 1–40. [Google Scholar] [CrossRef]
- Charbonneau, P. Dynamo models of the solar cycle. Living Rev. Sol. Phys. 2020, 17, 4. [Google Scholar] [CrossRef]
- Costas, E.A. Structure of the Solar Atmosphere: A Radio Perspective. Front. Astron. Space Sci. 2020, 7, 74. [Google Scholar] [CrossRef]
- Spruit, H.C. Dynamo action by differential rotation in a stably stratified stellar interior. Astron. Astrophys. 2002, 381, 923–932. [Google Scholar] [CrossRef]
- Weiss, N.O. Solar and stellar dynamos. In Lectures on Solar and Planetary Dynamos; Proctor, M.R.E., Gilbert, A.D., Eds.; Cambridge Univ. Press: Cambridge, UK, 1994; pp. 59–95. [Google Scholar]
- Brun, A.S.; Strugarek, A.; Varela, J.; Matt, S.P.; Augustson, K.C.; Emeriau, C.; Long DoCao, O.; Brown, B.; Toomre, J. On differential rotation and overshooting in solar-like stars. Astrophys. J. 2017, 836, 192. [Google Scholar] [CrossRef]
- Böhm-Vitense, E. Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Z. für Astrophys. 1958, 46, 108–143. [Google Scholar]
- Brun, A.S.; Browning, M.K. Magnetism, dynamo action and the solar–stellar connection. Living Rev. Sol. Phys. 2017, 14, 4. [Google Scholar] [CrossRef]
- Chabrier, G.; Gallardo, J.; Baraffe, I. Evolution of low-mass star and brown dwarf eclipsing binaries. Astron. Astrophys. 2007, 472, L17–L20. [Google Scholar] [CrossRef]
- MacDonald, J.; Mullan, D.J. Magnetoconvective models of red dwarfs: Constraints imposed by the lithium abundance. Mon. Not. R. Astron. Soc. 2015, 448, 2019–2029. [Google Scholar] [CrossRef]
- Feiden, G.A.; Chaboyer, B. Magnetic inhibition of convection and the fundamental properties of low-mass stars. II. Fully convective main-sequence stars. Astrophys. J. 2014, 789, 53. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophys. Fluid Dynamics; Springer: New York, NY, USA, 1982. [Google Scholar]
- Zahn, J.P. Circulation and turbulence in rotating stars. Astron. Astrophys. 1992, 256, 115–132. [Google Scholar]
- Tassoul, J.L. Stellar rotation. Cambridge Astrophys. Ser., 36; Cambridge Univ. Press: Cambridge, UK, 2000. [Google Scholar]
- Maeder, A.; Meynet, G. The Evolution of Rotating Stars. Annu. Rev. Astron. Astrophys. 2012, 38, 143–190. [Google Scholar] [CrossRef]
- Hansen, C.J.; Kawaler, S.D. Stellar Interiors. Physical Principles, Structure, and Evolution. Astron. Astrophys. Libr. 1994, 445, 43–144. [Google Scholar] [CrossRef]
- Kippenhahn, R.; Weigert, A. Stellar Structure and Evolution. Astron. Astrophys. Libr. 1990, XVI, 449–472. [Google Scholar]
- Kato, S. Overstable Convection in a Medium Stratified in Mean Molecular Weight. Publ. Astron. Soc. Jpn. 1966, 18, 374–383. [Google Scholar]
- Endal, A.S.; Sofia, S. The evolution of rotating stars. II. Calculations with time-dependent redistribution of angular momentum for 7 and 10 M⊙ stars. Astrophys. J. 1978, 220, 279–290. [Google Scholar] [CrossRef]
- Davidson, P.A. An introduction to magnetohydrodynamics. In Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Kulsrud, R.M. Plasma Physics for Astrophysics; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Jones, C.A. Course 2 Dynamo theory. Les Houches 2008, 88, 45–135. [Google Scholar] [CrossRef]
- Childress, S.; Gilbert, A.D. Stretch, twist, fold: The fast dynamo. Lect. Notes Phys. 1995, 37. [Google Scholar] [CrossRef]
- Mestel, L. Solar Magnetism; Oxford Science Publications: Oxford, UK, 2012. [Google Scholar]
- Nucci, M.C.; Busso, M. Magnetohydrodynamics and Deep Mixing in Evolved Stars. I. Two- and Three-dimensional Analytical Models for the Asymptotic Giant Branch. Astrophys. J. 2014, 787, 141. [Google Scholar] [CrossRef]
- Cameron, R.H.; Duvall, T.L.; Schüssler, M.; Schunker, H. Observing and modeling the poloidal and toroidal fields of the solar dynamo. Astron. Astrophys. 2018, 609, A56. [Google Scholar] [CrossRef]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2005, 417, 1–209. [Google Scholar] [CrossRef]
- Leighton, R.B. Transport of magnetic fields on the Sun. Astrophys. J. 1964, 140, 1547–1562. [Google Scholar] [CrossRef]
- Leighton, R.B. A magneto-kinematic model of the solar cycle. Astrophys. J. 1969, 156, 1–26. [Google Scholar] [CrossRef]
- Cameron, R.; Schüssler, M. The crucial role of surface magnetic fields for the solar dynamo. Science 2015, 347, 1333–1335. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.M.; Sheeley, N.R., Jr. Magnetic flux transport and the Sun’s dipole moment. New twists to the Babcock–Leighton model. Astrophys. J. 1991, 375, 761–770. [Google Scholar] [CrossRef]
- Mackay, D.H.; Yeates, A.R. The Sun’s global photospheric and coronal magnetic fields: Observations and models. Living Rev. Sol. Phys. 2012, 9, 6. [Google Scholar] [CrossRef]
- Charbonneau, P. Dynamo models of the solar cycle. Living Rev. Sol. Phys. 2010, 7, 3. [Google Scholar] [CrossRef]
- Sanchez, S.; Fournier, A.; Pinheiro, K.J.; Aubert, J. A mean-field Babcock–Leighton solar dynamo model with long-term variability. An. Acad. Bras. Cienc. 2014, 86, 11–26. [Google Scholar] [CrossRef]
- Eberhard, G.; Schwarzschild, K. On the reversal of the Calcium lines H and K in stellar spectra. Astrophys. J. 1913, 38, 292–295. [Google Scholar] [CrossRef]
- Weber, M.; Burrows, J.P.; Cebula, R.P. Gome Solar UV/VIS Irradiance Measurements between 1995 and 1997. First Results on Proxy Solar Activity Studies. Sol. Phys. 1998, 177, 63–77. [Google Scholar] [CrossRef]
- Gigolashvili, M.; Kapanadze, N. Behavior of Some Narrow Band of Solar Spectral Irradiance during the Solar Cycles 21. Sun Geosph. 2012, 7, 35–40. [Google Scholar]
- Lyra, W.; Porto de Mello, G.F. Fine structure of the chromospheric activity in Solar-type stars. The Hα line. Astron. Astrophys. 2005, 431, 329–338. [Google Scholar] [CrossRef]
- Montes, D.; López-Santiago, J.; Fernández-Figueroa, M.J.; Gálvez, M.C. Chromospheric activity, lithium and radial velocities of single late-type stars possible members of young moving groups. Astron. Astrophys. 2001, 379, 976–991. [Google Scholar] [CrossRef]
- Zirin, H. Astrophysics of the Sun; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Zhang, L.; Pi, Q.; Han, X.L.; Chang, L.; Wang, D. Chromospheric activity on late-type star DM UMa using high-resolution spectroscopic observations. Mon. Not. R. Astron. Soc. 2016, 459, 854–862. [Google Scholar] [CrossRef][Green Version]
- Göker, Ü.D.; Gigolashvili, M.S.; Kapanadze, N. Solar Spectral Irradiance Variability of Some Chromospheric Emission Lines Through the Solar Activity Cycles 21–23. Serbian Astron. J. 2017, 194, 71–86. [Google Scholar] [CrossRef]
- Libbrecht, T. The Diagnostic Potential of the He i D3 Spectral Line in the Solar Atmosphere. Ph.D. Thesis, Stockholm University, Stockholm, Sweden, 2019. Available online: http://www.diva-portal.org/smash/get/diva2:1295682/FULLTEXT01.pdf (accessed on 25 September 2021).
- Haberreiter, M. Mechanisms for total and spectral solar irradiance variations. Int. Astron. Union Symp. 2010, 264, 231–240. [Google Scholar] [CrossRef]
- Oranje, B.J.; Zwaan, C. Magnetic structure in cool stars. VIII. The Mg ii h and k surface fluxes in relation to the Mt Wilson photometric Ca ii H and K measurements. Astron. Astrophys. 1985, 147, 265–272. [Google Scholar]
- Buccino, A.P.; Mauas, P.J.D. Mg ii h+k emission lines as stellar activity indicators of main sequence F–K stars. Astron. Astrophys. 2008, 483, 903–910. [Google Scholar] [CrossRef]
- Lilensten, J.; Dudok de Wit, T.; Kretzschmar, M.; Amblard, P.-O.; Moussaoul, S.; Aboudarham, J.; Auchère, F. Review on the solar spectral variability in the EUV for space weather purposes. Ann. Geophys. 2008, 26, 269–279. [Google Scholar] [CrossRef][Green Version]
- Linsky, J.L. Stellar Model Chromospheres and Spectroscopic Diagnostics. Annu. Rev. Astron. Astrophys. 2017, 55, 159–211. [Google Scholar] [CrossRef]
- Bopp, B.W. RS CVn stars—Chromospheric phenomena. Int. Astron. Union Colloq. 1983, 71, 363–377. [Google Scholar] [CrossRef]
- Arévalo, M.J.; Lázaro, C. Time-resolved Spectroscopy of RS Canum Venaticorum Short-Period Systems. II. RT Andromedae, WY Cancri, and XY Ursae Majoris. Astron. J. 1999, 118, 1015–1033. [Google Scholar] [CrossRef][Green Version]
- Gu, S.-H.; Tan, H.-S.; Shan, H.-G.; Zhang, F.-H. Chromospheric activity on the RS CVn-type binary UX Arietis. Astron. Astrophys. 2002, 388, 889–898. [Google Scholar] [CrossRef][Green Version]
- Gálvez, M.C.; Montes, D.; Fernández-Figueroa, M.J.; De Castro, E.; Cornide, M. Multiwavelength optical observations of chromospherically active binary systems. V. FF UMa (2RE J0933+624): A system with orbital period variation. Astron. Astrophys. 2007, 472, 587–598. [Google Scholar] [CrossRef]
- Cao, D.-T.; Gu, S.-H. New observations of chromospheric and prominence activity on the RS CVn-type binary SZ Piscium. Astron. Astrophys. 2012, 538, A130. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.-Y.; Pi, Q.-F.; Zhu, Z.-Z. Chromospheric activity in several single late-type stars. Res. Astron. Astrophys. 2015, 15, 252–274. [Google Scholar] [CrossRef][Green Version]
- Mihalas, D. Stellar Atmospheres, 2nd ed.; W. H. Freeman: San Francisco, CA, USA, 1978. [Google Scholar]
- Linsky, J.L.; Worden, S.P.; McClintock, W.; Robertson, R.M. Stellar model chromospheres. X. High-resolution, absolute flux profiles of the Ca ii H and K lines in stars of spectral types F0–M2. Astrophys. J. Suppl. Ser. 1979, 41, 47–74. [Google Scholar] [CrossRef]
- Cauzzi, G.; Reardon, K.P.; Uitenbroek, H.; Cavallini, F.; Falchi, A.; Falciani, R.; Janssen, K.; Rimmele, T.; Vecchio, A.; Wöger, F. The solar chromosphere at high resolution with IBIS. I. New insights from the Ca ii 854.2 nm line. Astron. Astrophys. 2008, 480, 515–526. [Google Scholar] [CrossRef]
- Foing, B.H.; Crivellari, L.; Vladilo, G.; Rebolo, R.; Beckman, J.E. Chromospheres of late-type active and quiescent dwarfs. II. An activity index derived from profiles of the Ca ii λ 8498 Å and λ 8542 Å triplet lines. Astron. Astrophys. Suppl. 1989, 80, 189–200. [Google Scholar]
- Chmielewski, Y. The infrared triplet lines of ionized calcium as a diagnostic tool for F, G, K-type stellar atmospheres. Astron. Astrophys. 2000, 353, 666–690. [Google Scholar]
- Busà, I.; Aznar Cuadrado, R.; Terranegra, L.; Andretta, V.; Gomez, M.T. The Ca ii infrared triplet as a stellar activity diagnostic. II. Test and calibration with high resolution observations. Astron. Astrophys. 2007, 466, 1089–1098. [Google Scholar] [CrossRef]
- Dempsey, R.C.; Bopp, B.W.; Henry, G.W.; Hall, D.S. Observations of the Ca ii Infrared Triplet in Chromospherically Active Single and Binary Stars. Astrophys. J. Suppl. Ser. 1993, 86, 293–306. [Google Scholar] [CrossRef]
- Andretta, V.; Busà, I.; Gomez, M.T.; Terranegra, L. The Ca ii Infrared Triplet as a stellar activity diagnostic. I. Non-LTE photospheric profiles and definition of the RIRT indicator. Astron. Astrophys. 2005, 430, 669–677. [Google Scholar] [CrossRef]
- Terrien, R.C.; Mahadevan, S.; Bender, C.F.; Deshpande, R.; Robertson, P. M Dwarf Luminosity, Radius, and α-enrichment from I-band Spectral Features. Astrophys. J. Lett. 2015, 802, L10. [Google Scholar] [CrossRef]
- Livingston, W.; Holweger, H. Solar luminosity variation. IV. The photospheric lines, 1976–1980. Astrophys. J. 1982, 252, 375–385. [Google Scholar] [CrossRef]
- Fontenla, J.; White, O.R.; Fox, P.A.; Avrett, E.A.; Kurucz, R.L. Calculation of Solar Irradiances. I. Synthesis of the Solar Spectrum. Astrophys. J. 1999, 518, 480–499. [Google Scholar] [CrossRef]
- Biazzo, K.; Frasca, A.; Henry, G.W.; Catalano, S.; Marilli, E. Photospheric temperature measurements in young main sequence stars. Eur. Space Agency Spec. Publ. 2005, 560, 445–448. [Google Scholar]
- Noyes, R.W.; Hartmann, L.W.; Baliunas, S.L.; Duncan, D.K.; Vaughan, A.H. Rotation, convection, and magnetic activity in lower main-sequence stars. Astrophys. J. 1984, 279, 763–777. [Google Scholar] [CrossRef]
- Žerjal, M.; Zwitter, T.; Matijevič, G.; Strassmeier, K.G.; Bienaymé, O.; Bland-Hawthorn, J.; Boeche, C.; Freeman, K.C.; Grebel, E.K.; Kordopatis, G. Chromospherically Active Stars in the RAdial Velocity Experiment (RAVE) Survey. I. The Catalog. Astrophys. J. 2013, 776, 127. [Google Scholar] [CrossRef]
- Schrijver, C.J.; Zwaan, C. Solar and Stellar Magnetic Activity; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Schrijver, C.J.; Dobson, A.K.; Radick, R.R. Nearly simultaneous observations of chromospheric and coronal radiative losses of cool stars. Astron. Astrophys. 1992, 258, 432–448. [Google Scholar]
- Ayres, T.R.; Fleming, T.A.; Simon, T.; Haisch, B.M.; Brown, A.; Lenz, D.; Wamsteker, W.; de Martino, D.; Gonzalez, C.; Bonnell, J.; et al. The RIASS Coronathon: Joint X-ray and Ultraviolet Observations of Normal F–K Stars. Astrophys. J. Suppl. Ser. 1995, 96, 223–259. [Google Scholar] [CrossRef]
- Wilson, O.C. Flux Measurements at the Centers of Stellar H and K Lines. Astrophys. J. 1968, 153, 221–234. [Google Scholar] [CrossRef]
- Duncan, D.K.; Vaughan, A.H.; Wilson, O.C.; Preston, G.W.; Frazer, J.; Lanning, H.; Misch, A.; Mueller, J.; Soyumer, D.; Woodard, L.; et al. Ca ii H and K Measurements Made at Mount Wilson Observatory, 1966–1983. Astrophys. J. Suppl. Ser. 1991, 76, 383–430. [Google Scholar] [CrossRef]
- Baliunas, S.L.; Donahue, R.A.; Soon, W.H.; Horne, J.H.; Frazer, J.; Woodard-Eklund, L.; Bradford, M.; Rao, L.M.; Wilson, O.C.; Zhang, Q.; et al. Chromospheric Variations in Main-Sequence Stars. II. Astrophys. J. 1995, 438, 269–287. [Google Scholar] [CrossRef]
- Wright, J.T. Radial Velocity Jitter in Stars from the California and Carnegie Planet Search at Keck Observatory. Publ. Astron. Soc. Pac. 2005, 117, 657–664. [Google Scholar] [CrossRef]
- Vaughan, A.H.; Preston, G.W.; Wilson, O.C. Flux measurements of Ca ii H and K emission. Publ. Astron. Soc. Pac. 1978, 90, 267–274. [Google Scholar] [CrossRef]
- Isaacson, H.; Fischer, D. Chromospheric Activity and Jitter Measurements for 2630 Stars on the California Planet Search. Astrophys. J. 2010, 725, 875–885. [Google Scholar] [CrossRef]
- Johnson, H.L. Astronomical Measurements in the Infrared. Annu. Rev. Astron. Astrophys. 1966, 4, 193–206. [Google Scholar] [CrossRef]
- Suárez Mascareño, A.; Rebolo, R.; González Hernández, J.I.; Esposito, M. Rotation periods of late-type dwarf stars from time series high-resolution spectroscopy of chromospheric indicators. Mon. Not. R. Astron. Soc. 2015, 452, 2745–2756. [Google Scholar] [CrossRef]
- Suárez Mascareño, A.; Rebolo, R.; González Hernández, J.I. Magnetic cycles and rotation periods of late-type stars from photometric time series. Astron. Astrophys. 2016, 595, A12. [Google Scholar] [CrossRef]
- Hartmann, L.; Soderblom, D.R.; Noyes, R.W.; Burnham, N.; Vaughan, A.H. An analysis of the Vaughan–Preston survey of chromospheric emission. Astrophys. J. 1984, 276, 254–265. [Google Scholar] [CrossRef]
- Rutten, R.G.M. Magnetic structure in cool stars. VII. Absolute surface flux in Ca ii H and K line cores. Astron. Astrophys. 1984, 130, 353–360. [Google Scholar]
- Middelkoop, F. Magnetic structure in cool stars. IV. Rotation and Ca ii H and K emission of main-sequence stars. Astron. Astrophys. 1982, 107, 31–35. [Google Scholar]
- Schrijver, C.J. Magnetic structure in cool stars. XI. Relations between radiative fluxes measuring stellar activity, and evidence for two components in stellar chromospheres. Astron. Astrophys. 1987, 172, 111–123. [Google Scholar]
- Rutten, R.G.M.; Schrijver, C.J.; Lemmens, A.F.P.; Zwaan, C. Magnetic structure in cool stars. XVII. Minimum radiative losses from the outer atmosphere. Astron. Astrophys. 1991, 252, 203–219. [Google Scholar]
- Mittag, M.; Schmitt, J.H.M.M.; Schröder, K.-P. Ca ii H+K fluxes from S-indices of large samples: A reliable and consistent conversion based on PHOENIX model atmospheres. Astron. Astrophys. 2013, 549, A117. [Google Scholar] [CrossRef]
- Pérez Martínez, M.I.; Schröder, K.-P.; Hauschildt, P. The non-active stellar chromosphere: Ca ii basal flux. Mon. Not. R. Astron. Soc. 2014, 445, 270–279. [Google Scholar] [CrossRef]
- Schrijver, C.J.; Dobson, A.K.; Radick, R.R. The Magnetic, Basal, and Radiative Equilibrium Components in Mount Wilson Ca ii H+K Fluxes. Astrophys. J. 1989, 341, 1035–1044. [Google Scholar] [CrossRef]
- Schrijver, C.J. Basal heating in the atmospheres of cool stars. Astron. Astrophys. Rev. 1995, 6, 181–223. [Google Scholar] [CrossRef]
- Livingston, W.; Wallace, L.; White, O.R.; Giampapa, M.S. Sun-as-a-Star Spectrum Variations 1974–2006. Astrophys. J. 2007, 657, 1137–1149. [Google Scholar] [CrossRef]
- Hall, J.C. Stellar Chromospheric Activity. Living Rev. Sol. Phys. 2008, 5, 2. [Google Scholar] [CrossRef]
- Bercik, D.J.; Fisher, G.H.; Johns-Krull, C.M.; Abbett, W.P. Convective Dynamos and the Minimum X-ray Flux in Main-Sequence Stars. Astrophys. J. 2005, 631, 529–539. [Google Scholar] [CrossRef][Green Version]
- Cuntz, M.; Rammacher, W.; Ulmschneider, P.; Musielak, Z.E.; Saar, S.H. Two-Component Theoretical Chromosphere Models for K Dwarfs of Different Magnetic Activity: Exploring the Ca ii Emission–Stellar Rotation Relationship. Astrophys. J. 1999, 522, 1053–1068. [Google Scholar] [CrossRef][Green Version]
- Reiners, A.; Mohanty, S. Radius-dependent Angular Momentum Evolution in Low-mass Stars. I. Astrophys. J. 2012, 746, 43. [Google Scholar] [CrossRef]
- Mohanty, S.; Basri, G. Rotation and Activity in Mid-M to L Field Dwarfs. Astrophys. J. 2003, 583, 451–472. [Google Scholar] [CrossRef]
- Reiners, A.; Basri, G. Chromospheric Activity, Rotation, and Rotational Braking in M and L Dwarfs. Astrophys. J. 2008, 684, 1390–1403. [Google Scholar] [CrossRef]
- Saar, S.H. Maunder Minimum Dwarfs: Defined Out Of Existence? Bull. Am. Astron. Soc. 2006, 37, 12.01. [Google Scholar]
- Jenkins, J.S.; Jones, H.R.A.; Pavlenko, Y.; Pinfield, D.J.; Barnes, J.R.; Lyubchik, Y. Metallicities and activities of southern stars. Astron. Astrophys. 2008, 485, 571–584. [Google Scholar] [CrossRef]
- Saar, S.H.; Testa, P. Stars in magnetic grand minima: Where are they and what are they like? Proc. Int. Astron. Union Symp. 2012, 286, 335–345. [Google Scholar] [CrossRef]
- Barnes, S.A.; Spada, F.; Weingrill, J. Some aspects of cool main sequence star ages derived from stellar rotation (gyrochronology). Astron. Nachrichten 2016, 337, 810–814. [Google Scholar] [CrossRef]
- Curtis, J.L. No ‘Maunder Minimum’ Candidates in M67: Mitigating Interstellar Contamination of Chromospheric Emission Lines. Astron. J. 2017, 153, 275. [Google Scholar] [CrossRef]
- Meibom, S.; Mathieu, R.D. A Robust Measure of Tidal Circularization in Coeval Binary Populations: The Solar-Type Spectroscopic Binary Population in the Open Cluster M35. Astrophys. J. 2005, 620, 970–983. [Google Scholar] [CrossRef]
- Meibom, S.; Mathieu, R.D.; Stassun, K.G. An Observational Study of Tidal Synchronization in Solar-Type Binary Stars in the Open Clusters M35 and M34. Astrophys. J. 2006, 653, 621–635. [Google Scholar] [CrossRef]
- Bertello, L.; Pevtsov, A.; Tlatov, A.; Singh, J. Correlation Between Sunspot Number and Ca ii K Emission Index. Sol. Phys. 2016, 291, 2967–2979. [Google Scholar] [CrossRef]
- Stix, M. The Sun: An Introduction; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Mandal, S.; Chatterjee, S.; Banerjee, D. Association of Plages with Sunspots: A Multi-Wavelength Study Using Kodaikanal Ca ii K and Greenwich Sunspot Area Data. Astrophys. J. 2017, 835, 158. [Google Scholar] [CrossRef]
- Xu, F.; Gu, S.; Ioannidis, P. Starspot evolution, differential rotation, and correlation between chromospheric and photospheric activities on Kepler-411. Mon. Not. R. Astron. Soc. 2021, 501, 1878–1890. [Google Scholar] [CrossRef]
- Rosario, M.J.; Heckert, P.A.; Mekkaden, M.V.; Raveendran, A.V. Spot activity in the RS CVn binary DM Ursae Majoris. Mon. Not. R. Astron. Soc. 2009, 394, 872–881. [Google Scholar] [CrossRef][Green Version]
- Taş, G.; Evren, S. A New Approach to the Long-Term Activity Behavior of DM UMa. Open Astron. 2012, 21, 435–446. [Google Scholar] [CrossRef][Green Version]
- Dziembowski, W.A.; Goode, P.R. Helioseismic Probing of Solar Variability: The Formalism and Simple Assessments. Astrophys. J. 2004, 600, 464–479. [Google Scholar] [CrossRef][Green Version]
- Dziembowski, W.A.; Goode, P.R. Sources of Oscillation Frequency Increase with Rising Solar Activity. Astrophys. J. 2005, 625, 548–555. [Google Scholar] [CrossRef]
- Radick, R.R.; Lockwood, G.W.; Henry, G.W.; Hall, J.C.; Pevtsov, A.A. Patterns of Variation for the Sun and Sun-like Stars. Astrophys. J. 2018, 855, 75. [Google Scholar] [CrossRef]
- López-Santiago, J.; Montes, D.; Fernández-Figueroa, M.J.; Ramsey, L.W. Rotational modulation of the photospheric and chromospheric activity in the young, single K2-dwarf PW And. Astron. Astrophys. 2003, 411, 489–502. [Google Scholar] [CrossRef][Green Version]
- Biazzo, K.; Frasca, A.; Catalano, S.; Marilli, E. Photospheric and chromospheric active regions on three single-lined RS CVn binaries. Astron. Astrophys. 2006, 446, 1129–1138. [Google Scholar] [CrossRef]
- Frasca, A.; Biazzo, K.; Kővári, Z.; Marilli, E.; Çakirli, Ö. Photospheric and chromospheric activity on the young solar-type star HD 171488 (V889 Herculis). Astron. Astrophys. 2010, 518, A48. [Google Scholar] [CrossRef]
- Cao, D.-T.; Gu, S.-H. Chromospheric Activity and Rotational Modulation on the Young, Single K2 Dwarf LQ Hya. Astron. J. 2014, 147, 38. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.; Pi, Q.; Zhu, Z.; Zhang, X.; Li, Z. Chromospheric activity on late-type star LQ Hya. New Astron. 2014, 32, 1–5. [Google Scholar] [CrossRef]
- Morris, B.M.; Curtis, J.L.; Douglas, S.T.; Hawley, S.L.; Agüeros, M.A.; Bobra, M.G.; Agol, E. Are Starspots and Plages Co-located on Active G and K Stars? Astron. J. 2018, 156, 203. [Google Scholar] [CrossRef]
- Morris, B.M.; Hebb, L.; Davenport, J.R.A.; Rohn, G.; Hawley, S.L. The Starspots of HAT-P-11: Evidence for a Solar-like Dynamo. Astrophys. J. 2017, 846, 99. [Google Scholar] [CrossRef]
- Saar, S.H.; Baliunas, S.L. Recent Advances in Stellar Cycle Research. Astron. Soc. Pac. Conf. Ser. 1992, 27, 150–167. [Google Scholar]
- Brandenburg, A.; Saar, S.H.; Turpin, C.R. Time Evolution of the Magnetic Activity Cycle Period. Astrophys. J. Lett. 1998, 498, L51–L54. [Google Scholar] [CrossRef]
- Saar, S.H.; Brandenburg, A. Time Evolution of the Magnetic Activity Cycle Period. II. Results for an Expanded Stellar Sample. Astrophys. J. 1999, 524, 295–310. [Google Scholar] [CrossRef]
- Brandenburg, A.; Mathur, S.; Metcalfe, T.S. Evolution of Co-existing Long and Short Period Stellar Activity Cycles. Astrophys. J. 2017, 845, 79. [Google Scholar] [CrossRef]
- Vaughan, A.H.; Preston, G.W. A survey of chromospheric Ca ii H and K emission in field stars of the solar neighborhood. Publ. Astron. Soc. Pac. 1980, 92, 385–391. [Google Scholar] [CrossRef]
- Henry, T.J.; Soderblom, D.R.; Donahue, R.A.; Baliunas, S.L. A Survey of Ca ii H and K Chromospheric Emission in Southern Solar-Type Stars. Astron. J. 1996, 111, 439–465. [Google Scholar] [CrossRef]
- Durney, B.R.; Mihalas, D.; Robinson, R.D. A preliminary interpretation of stellar chromospheric Ca ii emission variations within the framework of stellar dynamo theory. Publ. Astron. Soc. Pac. 1981, 93, 537–543. [Google Scholar] [CrossRef]
- Böhm-Vitense, E. Chromospheric Activity in G and K Main-Sequence Stars, and What It Tells Us about Stellar Dynamos. Astrophys. J. 2007, 657, 486–493. [Google Scholar] [CrossRef]
- Metcalfe, T.S.; Egeland, R.; van Saders, J. Stellar Evidence That the Solar Dynamo May Be in Transition. Astrophys. J. Lett. 2016, 826, L2. [Google Scholar] [CrossRef]
- Pace, G.; Melendez, J.; Pasquini, L.; Carraro, G.; Danziger, J.; François, P.; Matteucci, F.; Santos, N.C. An investigation of chromospheric activity spanning the Vaughan–Preston gap: Impact on stellar ages. Astron. Astrophys. 2009, 499, L9–L12. [Google Scholar] [CrossRef][Green Version]
- Oláh, K.; Kővári, Z.; Petrovay, K.; Soon, W.; Baliunas, S.; Kolláth, Z.; Vida, K. Magnetic cycles at different ages of stars. Astron. Astrophys. 2016, 590, A133. [Google Scholar] [CrossRef]
- Baliunas, S.L.; Donahue, R.A.; Soon, W.; Henry, G.W. Activity Cycles in Lower Main Sequence and Post Main Sequence Stars: The HK Project. Astron. Soc. Pac. Conf. Ser. 1998, 154, 153–172. [Google Scholar]
- Baliunas, S.L.; Nesme-Ribes, E.; Sokoloff, D.; Soon, W.H. A Dynamo Interpretation of Stellar Activity Cycles. Astrophys. J. 1996, 460, 848–854. [Google Scholar] [CrossRef]
- Oláh, K.; Kolláth, Z.; Granzer, T.; Strassmeier, K.G.; Lanza, A.F.; Järvinen, S.; Korhonen, H.; Baliunas, S.L.; Soon, W.; Messina, S.; et al. Multiple and changing cycles of active stars. II. Results. Astron. Astrophys. 2009, 501, 703–713. [Google Scholar] [CrossRef]
- Gomes da Silva, J.; Santos, N.C.; Bonfils, X.; Delfosse, X.; Forveille, T.; Udry, S.; Dumusque, X.; Lovis, C. Long-term magnetic activity of a sample of M-dwarf stars from the HARPS program. II. Activity and radial velocity. Astron. Astrophys. 2012, 541, A9. [Google Scholar] [CrossRef]
- Savanov, I.S. Activity cycles of M dwarfs. Astron. Rep. 2012, 56, 716–721. [Google Scholar] [CrossRef]
- Reiners, A. The narrowest M-dwarf line profiles and the rotation-activity connection at very slow rotation. Astron. Astrophys. 2007, 467, 259–268. [Google Scholar] [CrossRef]
- Rempel, M. Solar and stellar activity cycles. J. Phys. Conf. Ser. 2008, 118, 012032. [Google Scholar] [CrossRef]
- Jetsu, L.; Pelt, J.; Tuominen, I. Spot and flare activity of FK Comae Berenices: Long-term photometry. Astron. Astrophys. 1993, 278, 449–462. [Google Scholar]
- Berdyugina, S.V.; Tuominen, I. Permanent active longitudes and activity cycles on RS CVn stars. Astron. Astrophys. 1998, 336, L25–L28. [Google Scholar]
- Järvinen, S.P.; Berdyugina, S.V.; Tuominen, I.; Cutispoto, G.; Bos, M. Magnetic activity in the young solar analog AB Dor. Active longitudes and cycles from long-term photometry. Astron. Astrophys. 2005, 432, 657–664. [Google Scholar] [CrossRef]
- Korhonen, H.; Berdyugina, S.V.; Tuominen, I. Study of FK Comae Berenices. IV. Active longitudes and the ‘flip-flop’ phenomenon. Astron. Astrophys. 2002, 390, 179–185. [Google Scholar] [CrossRef]
- Oláh, K.; Korhonen, H.; Kővári, Z.; Forgács-Dajka, E.; Strassmeier, K.G. Study of FK Comae Berenices. VI. Spot motions, phase jumps and a flip-flop from time-series modelling. Astron. Astrophys. 2006, 452, 303–309. [Google Scholar] [CrossRef]
- Hackman, T.; Pelt, J.; Mantere, M.J.; Jetsu, L.; Korhonen, H.; Granzer, T.; Kajatkari, P.; Lehtinen, J.; Strassmeier, K.G. Flip-flops of FK Comae Berenices. Astron. Astrophys. 2013, 553, A40. [Google Scholar] [CrossRef]
- Oláh, K.; Kolláth, Z.; Strassmeier, K.G. Multiperiodic light variations of active stars. Astron. Astrophys. 2000, 356, 643–653. [Google Scholar]
- Messina, S.; Guinan, E.F. Magnetic activity of six young solar analogues. I. Starspot cycles from long-term photometry. Astron. Astrophys. 2002, 393, 225–237. [Google Scholar] [CrossRef]
- McNally, D. Stellar Rotation. Sci. Prog. (1933–) 1965, 53, 601–607. [Google Scholar]
- Schröder, C.; Reiners, A.; Schmitt, J.H.M.M. Ca ii HK emission in rapidly rotating stars. Evidence for an onset of the solar-type dynamo. Astron. Astrophys. 2009, 493, 1099–1107. [Google Scholar] [CrossRef]
- Viviani, M.; Warnecke, J.; Käpylä, M.J.; Käpylä, P.J.; Olspert, N.; Cole-Kodikara, E.M.; Lehtinen, J.J.; Brandenburg, A. Transition from axi- to nonaxisymmetric dynamo modes in spherical convection models of solar-like stars. Astron. Astrophys. 2018, 616, A160. [Google Scholar] [CrossRef]
- Warnecke, J. Dynamo cycles in global convection simulations of solar-like stars. Astron. Astrophys. 2018, 616, A72. [Google Scholar] [CrossRef]
- Marsden, S.C.; Petit, P.; Jeffers, S.V.; Morin, J.; Fares, R.; Reiners, A.; do Nascimento, J.-D.; Aurière, M.; Bouvier, J.; Carter, B.D.; et al. A BCool magnetic snapshot survey of solar-type stars. Mon. Not. R. Astron. Soc. 2014, 444, 3517–3536. [Google Scholar] [CrossRef]
- Mathur, S.; García, R.A.; Morgenthaler, A.; Salabert, D.; Petit, P.; Ballot, J.; Régulo, C.; Catala, C. Constraining magnetic-activity modulations in three solar-like stars observed by CoRoT and NARVAL. Astron. Astrophys. 2013, 550, A32. [Google Scholar] [CrossRef]
- Mathur, S.; García, R.A.; Ballot, J.; Ceillier, T.; Salabert, D.; Metcalfe, T.S.; Régulo, C.; Jiménez, A.; Bloemen, S. Magnetic activity of F stars observed by Kepler. Astron. Astrophys. 2014, 562, A124. [Google Scholar] [CrossRef]
- Ferreira Lopes, C.E.; Leão, I.C.; de Freitas, D.B.; Canto Martins, B.L.; Catelan, M.; De Medeiros, J.R. Stellar cycles from photometric data: CoRoT stars. Astron. Astrophys. 2015, 583, A134. [Google Scholar] [CrossRef][Green Version]
- Régulo, C.; García, R.A.; Ballot, J. Magnetic activity cycles in solar-like stars: The cross-correlation technique of p-mode frequency shifts. Astron. Astrophys. 2016, 589, A103. [Google Scholar] [CrossRef]
- Fletcher, S.T.; Broomhall, A.-M.; Salabert, D.; Basu, S.; Chaplin, W.J.; Elsworth, Y.; Garcia, R.A.; New, R. A Seismic Signature of a Second Dynamo? Astrophys. J. Lett. 2010, 718, L19–L22. [Google Scholar] [CrossRef]
- Broomhall, A.-M.; Chaplin, W.J.; Elsworth, Y.; Simoniello, R. Quasi-biennial variations in helioseismic frequencies: Can the source of the variation be localized? Mon. Not. R. Astron. Soc. 2012, 420, 1405–1414. [Google Scholar] [CrossRef]
- Simoniello, R.; Finsterle, W.; Salabert, D.; Garcìa, R.A.; Turck-Chièze, S.; Jiménez, A.; Roth, M. The quasi-biennial periodicity (QBP) in velocity and intensity helioseismic observations. The seismic QBP over solar cycle 23. Astron. Astrophys. 2012, 539, A135. [Google Scholar] [CrossRef]
- Simoniello, R.; Jain, K.; Tripathy, S.C.; Turck-Chièze, S.; Baldner, C.; Finsterle, W.; Hill, F.; Roth, M. The Quasi-biennial Periodicity as a Window on the Solar Magnetic Dynamo Configuration. Astrophys. J. 2013, 765, 100. [Google Scholar] [CrossRef][Green Version]
- Jeffers, S.V.; Mengel, M.; Moutou, C.; Marsden, S.C.; Barnes, J.R.; Jardine, M.M.; Petit, P.; Schmitt, J.H.M.M.; See, V.; Vidotto, A.A. The relation between stellar magnetic field geometry and chromospheric activity cycles. II. The rapid 120-day magnetic cycle of τ Bootis. Mon. Not. R. Astron. Soc. 2018, 479, 5266–5271. [Google Scholar] [CrossRef]
- Uchida, Y.; Bappu, M.K.V. Chromospheric activity of late-type giants and supergiants: Reappearance of dynamo activity in the interior due to the spin-up of the core in evolution. J. Astrophys. Astron. 1982, 3, 277–296. [Google Scholar] [CrossRef]
- Pasquini, L.; Brocato, E.; Pallavicini, R. Chromospheric activity of evolved late-type stars—Chromospheric activity in evolved stars. Astron. Astrophys. 1990, 234, 277–283. [Google Scholar]
- Haisch, B.M. The Coronal Dividing Line. Cool Stars. Stellar Syst. Sun 1987, 291, 269–282. [Google Scholar] [CrossRef]
- Sanz-Forcada, J.; Micela, G.; Ribas, I.; Pollock, A.M.T.; Eiroa, C.; Velasco, A.; Solano, E.; García-Álvarez, D. Estimation of the XUV radiation onto close planets and their evaporation. Astron. Astrophys. 2011, 532, A6. [Google Scholar] [CrossRef]
- Montez, R.; Ramstedt, S.; Kastner, J.H.; Vlemmings, W.; Sanchez, E. A Catalog of GALEX Ultraviolet Emission from Asymptotic Giant Branch Stars. Astrophys. J. 2017, 841, 33. [Google Scholar] [CrossRef]
- Strassmeier, K.G.; Handler, G.; Paunzen, E.; Rauth, M. Chromospheric activity in G an K giants and their rotation–activity relation. Astron. Astrophys. 1994, 281, 855–863. [Google Scholar]
- Jordan, C. Magnetic activity in late-type stars. Quart. J. R. Astron. Soc. 1995, 36, 81–85. [Google Scholar] [CrossRef][Green Version]
- Luttermoser, D.G. The Atmosphere of Mira Variables: A View with the Hubble Space Telescope. Astrophys. J. 2000, 536, 923–933. [Google Scholar] [CrossRef][Green Version]
- Judge, P.G.; Carpenter, K.G. On Chromospheric Heating Mechanisms of ‘Basal Flux’ Stars. Astrophys. J. 1998, 494, 828–839. [Google Scholar] [CrossRef]
- Pérez Martínez, M.I.; Schröder, K.-P.; Cuntz, M. The basal chromospheric Mg ii h+k flux of evolved stars: Probing the energy dissipation of giant chromospheres. Mon. Not. R. Astron. Soc. 2011, 414, 418–427. [Google Scholar] [CrossRef][Green Version]
- Brosius, J.W.; Mullan, D.J. Models of Transition Regions in Hybrid Stars. Astrophys. J. 1986, 301, 650–663. [Google Scholar] [CrossRef]
- Blackman, E.G.; Frank, A.; Markiel, J.A.; Thomas, J.H.; Van Horn, H.M. Dynamos in asymptotic-giant-branch stars as the origin of magnetic fields shaping planetary nebulae. Nature 2001, 409, 485–487. [Google Scholar] [CrossRef]
- Vlemmings, W.H.T.; van Langevelde, H.J.; Diamond, P.J. The magnetic field around late-type stars revealed by the circumstellar H2O masers. Astron. Astrophys. 2005, 434, 1029–1038. [Google Scholar] [CrossRef]
- Uchida, Y. Magnetic Fields and Currents in the Corona. In Proc. Japan–France Seminar on Solar Physics; Moriyama, S.F., Henoux, J.-C., Eds.; Tokyo Astronomical Observatory: Tokyo, Japan, 1980; p. 83. [Google Scholar]
- Schmidt, S.J.; Hawley, S.L.; West, A.A.; Bochanski, J.J.; Davenport, J.R.A.; Ge, J.; Schneider, D.P. BOSS Ultracool Dwarfs. I. Colors and Magnetic Activity of M and L Dwarfs. Astron. J. 2015, 149, 158. [Google Scholar] [CrossRef]
- Aschwanden, M. The Sun. In Encyclopedia of the Solar System, 3rd ed.; Spohn, T., Breuer, D., Johnson, T.V., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; Chapter 11; pp. 235–259. [Google Scholar] [CrossRef]
- Tsuboi, Y.; Maeda, Y.; Feigelson, E.D.; Garmire, G.P.; Chartas, G.; Mori, K.; Pravdo, S.H. Coronal X-ray Emission from an Intermediate-Age Brown Dwarf. Astrophys. J. Lett. 2003, 587, L51–L54. [Google Scholar] [CrossRef]
- Stelzer, B.; Micela, G.; Flaccomio, E.; Neuhäuser, R.; Jayawardhana, R. X-ray emission of brown dwarfs: Towards constraining the dependence on age, luminosity, and temperature. Astron. Astrophys. 2006, 448, 293–304. [Google Scholar] [CrossRef]
- Schmidt, S.J.; Cruz, K.L.; Bongiorno, B.J.; Liebert, J.; Reid, I.N. Activity and Kinematics of Ultracool Dwarfs, Including an Amazing Flare Observation. Astron. J. 2007, 133, 2258–2273. [Google Scholar] [CrossRef]
- Hallinan, G.; Bourke, S.; Lane, C.; Antonova, A.; Zavala, R.T.; Brisken, W.F.; Boyle, R.P.; Vrba, F.J.; Doyle, J.G.; Golden, A. Periodic Bursts of Coherent Radio Emission from an Ultracool Dwarf. Astrophys. J. Lett. 2007, 663, L25–L28. [Google Scholar] [CrossRef]
- Hallinan, G.; Antonova, A.; Doyle, J.G.; Bourke, S.; Lane, C.; Golden, A. Confirmation of the Electron Cyclotron Maser Instability as the Dominant Source of Radio Emission from Very Low Mass Stars and Brown Dwarfs. Astrophys. J. 2008, 684, 644–653. [Google Scholar] [CrossRef]
- Berger, E.; Basri, G.; Fleming, T.A.; Giampapa, M.S.; Gizis, J.E.; Liebert, J.; Martín, E.; Phan-Bao, N.; Rutledge, R.E. Simultaneous Multi-Wavelength Observations of Magnetic Activity in Ultracool Dwarfs. III. X-ray, Radio, and Hα Activity Trends in M and L dwarfs. Astrophys. J. 2010, 709, 332–341. [Google Scholar] [CrossRef]
- Rodríguez-Barrera, M.I.; Helling, C.; Wood, K. Environmental effects on the ionisation of brown dwarf atmospheres. Astron. Astrophys. 2018, 618, A107. [Google Scholar] [CrossRef]
- Sorahana, S.; Suzuki, T.K.; Yamamura, I. A signature of chromospheric activity in brown dwarfs revealed by 2.5–5.0 μm AKARI spectra. Mon. Not. R. Astron. Soc. 2014, 440, 3675–3684. [Google Scholar] [CrossRef][Green Version]
- Gizis, J.E.; Monet, D.G.; Reid, I.N.; Kirkpatrick, J.D.; Liebert, J.; Williams, R.J. New Neighbors from 2MASS: Activity and Kinematics at the Bottom of the Main Sequence. Astron. J. 2000, 120, 1085–1099. [Google Scholar] [CrossRef]
- Mohanty, S.; Basri, G.; Shu, F.; Allard, F.; Chabrier, G. Activity in Very Cool Stars: Magnetic Dissipation in Late M and L Dwarf Atmospheres. Astrophys. J. 2002, 571, 469–486. [Google Scholar] [CrossRef]
- Sorahana, S.; Suzuki, T.K.; Yamamura, I. A Signature of Chromospheric Activity in Brown Dwarfs: A Recent Result from NIRLT Mission Program. Publ. Korean Astron. Soc. 2017, 32, 131–133. [Google Scholar] [CrossRef][Green Version]
- Cushing, M.C.; Marley, M.S.; Saumon, D.; Kelly, B.C.; Vacca, W.D.; Rayner, J.T.; Freedman, R.S.; Lodders, K.; Roellig, T.L. Atmospheric Parameters of Field L and T Dwarfs. Astrophys. J. 2008, 678, 1372–1395. [Google Scholar] [CrossRef]
- Baraffe, I.; Chabrier, G.; Allard, F.; Hauschildt, P.H. Evolutionary models for low-mass stars and brown dwarfs: Uncertainties and limits at very young ages. Astron. Astrophys. 2002, 382, 563–572. [Google Scholar] [CrossRef]
- Helling, C.; Jardine, M.; Witte, S.; Diver, D.A. Ionization in Atmospheres of Brown Dwarfs and Extrasolar Planets. I. The Role of Electron Avalanche. Astrophys. J. 2011, 727, 4. [Google Scholar] [CrossRef]
- Helling, C.; Jardine, M.; Mokler, F. Ionization in Atmospheres of Brown Dwarfs and Extrasolar Planets. II. Dust-induced Collisional Ionization. Astrophys. J. 2011, 737, 38. [Google Scholar] [CrossRef]
- Helling, C.; Jardine, M.; Stark, C.; Diver, D. Ionization in Atmospheres of Brown Dwarfs and Extrasolar Planets. III. Breakdown Conditions for Mineral Clouds. Astrophys. J. 2013, 767, 136. [Google Scholar] [CrossRef]
- Rimmer, P.B.; Helling, C. Ionization in Atmospheres of Brown Dwarfs and Extrasolar Planets. IV. The Effect of Cosmic Rays. Astrophys. J. 2013, 774, 108. [Google Scholar] [CrossRef]
- Stark, C.R.; Helling, C.; Diver, D.A.; Rimmer, P.B. Ionization in Atmospheres of Brown Dwarfs and Extrasolar Planets. V. Alfvén Ionization. Astrophys. J. 2013, 776, 11. [Google Scholar] [CrossRef]
- Berdyugina, S.V. Starspots: A Key to the Stellar Dynamo. Living Rev. Sol. Phys. 2005, 2, 8. [Google Scholar] [CrossRef]
- Strassmeier, K.G. Doppler imaging of stellar surface structure. XI. The super starspots on the K0 giant HD 12545: Larger than the entire Sun. Astron. Astrophys. 1999, 347, 225–234. [Google Scholar]
- Taş, G.; Evren, S. II Pegasi Reached The Largest Amplitude Up To Now. Inform. Bull. Var. Stars 2000, 4992, 1–2. [Google Scholar]
- Hall, D.S. The RS CVn Binaries and Binaries with Similar properties. Astrophys. Space Sci. Libr. 1976, 60, 287–348. [Google Scholar] [CrossRef]
- Fekel, F.C.; Moffett, T.J.; Henry, G.W. A Survey of Chromospherically Active Stars. Astrophys. J. Suppl. Ser. 1986, 60, 551–576. [Google Scholar] [CrossRef]
- Foing, B.H.; Char, S.; Ayres, T.; Catala, C.; Neff, J.E.; Zhai, D.S.; Catalano, S.; Cutispoto, G.; Jankov, S.; Rodono, M.; et al. Multi-site continuous spectroscopy. II. Spectrophotometry and energy budget of exceptional white-light flares on HR1099 from the MUSICOS 89 campaign. Astron. Astrophys. 1994, 292, 543–568. [Google Scholar]
- Montes, D.; Fernandez-Figueroa, M.J.; de Castro, E.; Sanz-Forcada, J. Multiwavelength optical observations of chromospherically active binary systems. I. Simultaneous Hα, Na i D1, D2, and He i D3 observations. Astron. Astrophys. Suppl. 1997, 125, 263–287. [Google Scholar] [CrossRef][Green Version]
- Güdel, M. Stellar Radio Astronomy: Probing Stellar Atmospheres from Protostars to Giants. Annu. Rev. Astron. Astrophys. 2002, 40, 217–261. [Google Scholar] [CrossRef]
- Güdel, M. X-ray astronomy of stellar coronae. Astron. Astrophys. Rev. 2004, 12, 71–237. [Google Scholar] [CrossRef]
- Montes, D.; Crespo-Chacón, I.; Gálvez, M.C.; Fernández-Figueroa, M.J.; López-Santiago, J.; de Castro, E.; Cornide, M.; Hernán-Obispo, M. Cool Stars: Chromospheric Activity, Rotation, Kinematics and Age. Lect. Notes Essays Astrophys. 2004, 1, 119–132. [Google Scholar]
- Kron, G.E. The Probable Detecting of Surface Spots on AR Lacertae B. Publ. Astron. Soc. Pac. 1947, 59, 261–265. [Google Scholar] [CrossRef]
- Kron, G.E. A Photoelectric Study of the Dwarf M Eclipsing Variable YY Geminorum. Astrophys. J. 1952, 115, 301–319. [Google Scholar] [CrossRef]
- Chugainov, P.F. On the Variability of HD 234677. Inform. Bull. Var. Stars 1966, 122, 1–2. [Google Scholar]
- Chugainov, P.F. On the Cause of Periodic Light Variations of Some Red Dwarf Stars. Inform. Bull. Var. Stars 1971, 520, 1–3. [Google Scholar]
- Vogt, S.S. Light and color variations of the flare stars BY Draconis: A critique of starspot properties. Astrophys. J. 1975, 199, 418–426. [Google Scholar] [CrossRef]
- Alekseev, I.Y. Observations of spotted red dwarf stars at the Crimean Astrophysical Observatory. Bull. Crime. Astrophys. Obs. 1999, 95, 69. [Google Scholar]
- Duerbeck, H.W. Constraints for Cataclysmic Binary Evolution as Derived from Space Distributions. Astrophys. Space Sci. 1984, 99, 363–385. [Google Scholar] [CrossRef]
- Eggen, O.J. Contact binaries. II. Mem. R. Astron. Soc. 1967, 70, 111–164. [Google Scholar]
- Hilditch, R.W.; King, D.J.; McFarlane, T.M. The evolutionary state of contact and near-contact binary stars. Mon. Not. R. Astron. Soc. 1988, 231, 341–352. [Google Scholar] [CrossRef]
- Yıldız, M.; Doğan, T. On the origin of W UMa type contact binaries—A new method for computation of initial masses. Mon. Not. R. Astron. Soc. 2013, 430, 2029–2038. [Google Scholar] [CrossRef]
- Maceroni, C.; Vilhu, O.; van’t Veer, F.; van Hamme, W. Surface imaging of late-type contact binaries. I. AE Phoenicis and YY Eridani. Astron. Astrophys. 1994, 288, 529–537. [Google Scholar]
- Hendry, P.D.; Mochnacki, S.W. Doppler Imaging of VW Cephei: Distribution and Evolution of Starspots on a Contact Binary. Astrophys. J. 2000, 531, 467–493. [Google Scholar] [CrossRef]
- Barnes, J.R.; Lister, T.A.; Hilditch, R.W.; Collier Cameron, A. High-resolution Doppler images of the spotted contact binary AE Phe. Mon. Not. R. Astron. Soc. 2004, 348, 1321–1331. [Google Scholar] [CrossRef]
- Rucinski, S.M.; Vilhu, O.; Whelan, J.A.J. The Lyman alpha emission in W Ursae Majoris. Astron. Astrophys. 1985, 143, 153–159. [Google Scholar]
- Li, L.; Han, Z.; Zhang, F. Structure and evolution of low-mass W Ursae Majoris type systems. II. With angular momentum loss. Mon. Not. R. Astron. Soc. 2004, 355, 1383–1398. [Google Scholar] [CrossRef]
- Stȩpień, K.; Schmitt, J.H.M.M.; Voges, W. ROSAT all-sky survey of W Ursae Majoris stars and the problem of supersaturation. Astron. Astrophys. 2001, 370, 157–169. [Google Scholar] [CrossRef]
- Vilhu, O.; Walter, F.M. Chromospheric–Coronal Activity at Saturated Levels. Astrophys. J. 1987, 321, 958–966. [Google Scholar] [CrossRef]
- Duemmler, R.; Doucet, C.; Formanek, F.; Ilyin, I.; Tuominen, I. The radial velocities and physical parameters of ER Vul. Astron. Astrophys. 2003, 402, 745–754. [Google Scholar] [CrossRef]
- Hall, D.S. The Relation Between Rs-Canum and Algol. Space Sci. Rev. 1989, 50, 219–233. [Google Scholar] [CrossRef]
- Albright, G.E.; Richards, M.T. The Transient Accretion Disk in the Algol-Type Binary U Sagittae. Astrophys. J. 1995, 441, 806–820. [Google Scholar] [CrossRef]
- Richards, M.T.; Albright, G.E.; Bowles, L.M. Doppler Tomography of the Gas Stream in Short-Period Algol Binaries. Astrophys. J. Lett. 1995, 438, L103–L106. [Google Scholar] [CrossRef]
- Richards, M.T.; Jones, R.D.; Swain, M.A. Doppler Tomography and S-Wave Analysis of Circumstellar Gas in β Persei. Astrophys. J. 1996, 459, 249–258. [Google Scholar] [CrossRef]
- Richards, M.T.; Albright, G.E. Evidence of Magnetic Activity in Short-Period Algol Binaries. Astrophys. J. Suppl. Ser. 1993, 88, 199–204. [Google Scholar] [CrossRef]
- White, N.E.; Marshall, F.E. An X-ray survey of nine Algol systems. Astrophys. J. Lett. 1983, 268, L117–L120. [Google Scholar] [CrossRef]
- Stewart, R.T.; Slee, O.B.; White, G.L.; Budding, E.; Coates, D.W.; Thompson, K.; Bunton, J.D. Radio Emission from EA Eclipsing Binaries: Evidence for Kilogauss Surface Fields on Both Early-Type and Late-Type Stars. Astrophys. J. 1989, 342, 463–466. [Google Scholar] [CrossRef]
- Umana, G.; Catalano, S.; Rodonó, M.; Gibson, D.M. Radio Emission from Selected Algol Systems. Space Sci. Rev. 1989, 50, 370. [Google Scholar] [CrossRef]
- Applegate, J.H. A Mechanism for Orbital Period Modulation in Close Binaries. Astrophys. J. 1992, 385, 621–629. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, J.; Oswalt, T.D.; Fang, X.; Zhao, G.; Liang, X.; Ye, X.; Zhong, J. Stellar Chromospheric Activity and Age Relation from Open Clusters in the LAMOST Survey. Astrophys. J. 2019, 887, 84. [Google Scholar] [CrossRef]
- Chen, X.; Wang, S.; Deng, L.; de Grijs, R.; Yang, M.; Tian, H. The Zwicky Transient Facility Catalog of Periodic Variable Stars. Astrophys. J. Suppl. Ser. 2020, 249, 18. [Google Scholar] [CrossRef]
- Egeland, R. Long-Term Variability of the Sun in the Context of Solar-Analog Stars. Ph.D. Thesis, Montana State University, Bozeman, MT, USA, 2017. [Google Scholar]
- Schmitt, J.H.M.M.; Schröder, K.-P.; Rauw, G.; Hempelmann, A.; Mittag, M.; González-Pérez, J.N.; Czesla, S.; Wolter, U.; Jack, D.; Eenens, P.; et al. TIGRE: A new robotic spectroscopy telescope at Guanajuato, Mexico. Astron. Nachrichten 2014, 335, 787–796. [Google Scholar] [CrossRef]
- Hempelmann, A.; Mittag, M.; Gonzalez-Perez, J.N.; Schmitt, J.H.M.M.; Schröder, K.P.; Rauw, G. Measuring rotation periods of solar-like stars using TIGRE. A study of periodic Ca ii H+K S-index variability. Astron. Astrophys. 2016, 586, A14. [Google Scholar] [CrossRef]
- Hall, J.C.; Henry, G.W.; Lockwood, G.W. The Sun-like Activity of the Solar Twin 18 Scorpii. Astron. J. 2007, 133, 2206–2208. [Google Scholar] [CrossRef]
- Stenflo, J.O. Limitations and Opportunities for the Diagnostics of Solar and Stellar Magnetic Fields. Astron. Soc. Pac. Conf. Ser. 2001, 248, 639–650. [Google Scholar]
- Strassmeier, K.G.; Pallavicini, R.; Rice, J.B.; Andersen, M.I.; Zerbi, F.M. The science case of the PEPSI high-resolution echelle spectrograph and polarimeter for the LBT. Astron. Nachrichten 2004, 325, 278–298. [Google Scholar] [CrossRef]

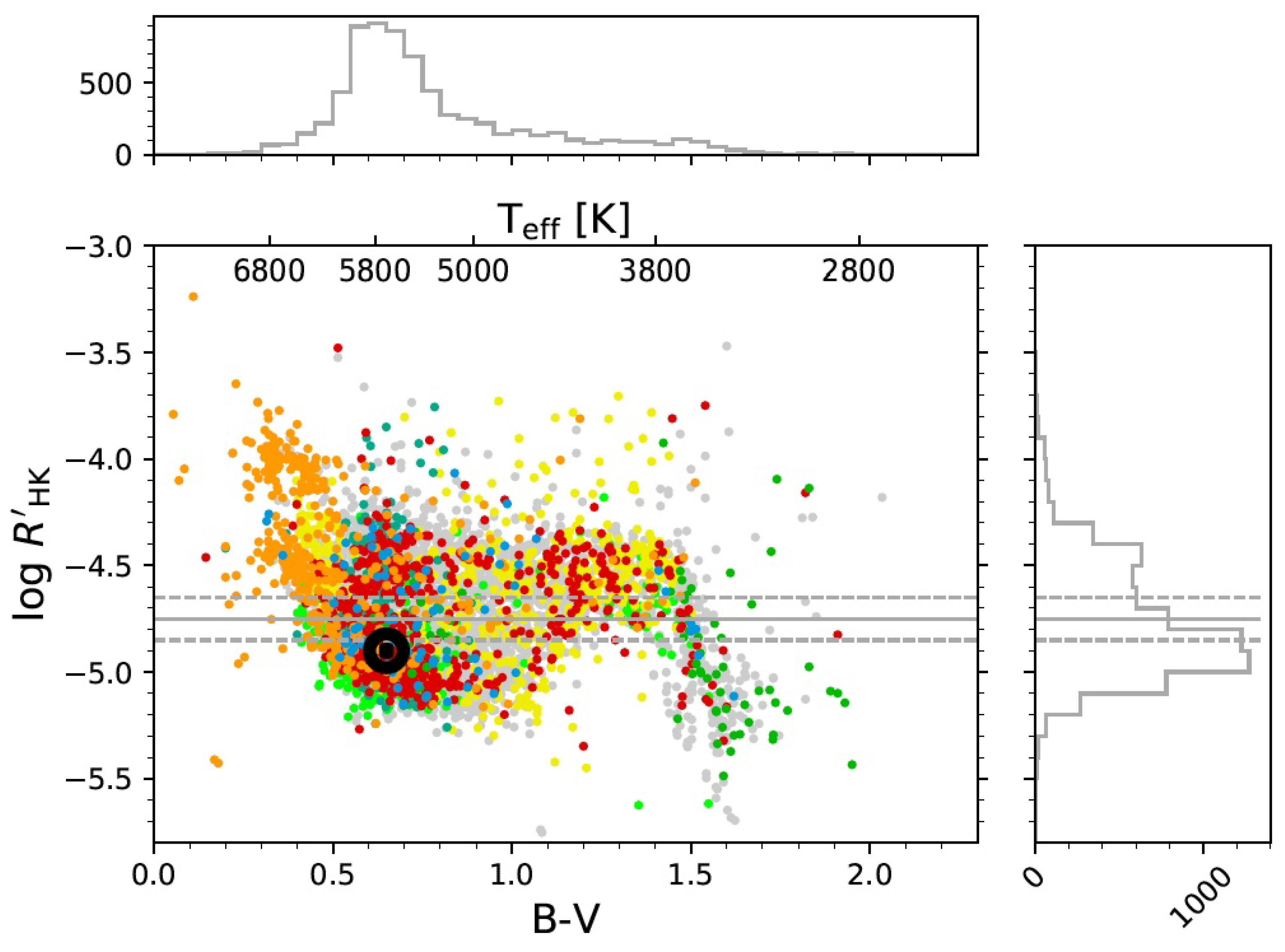
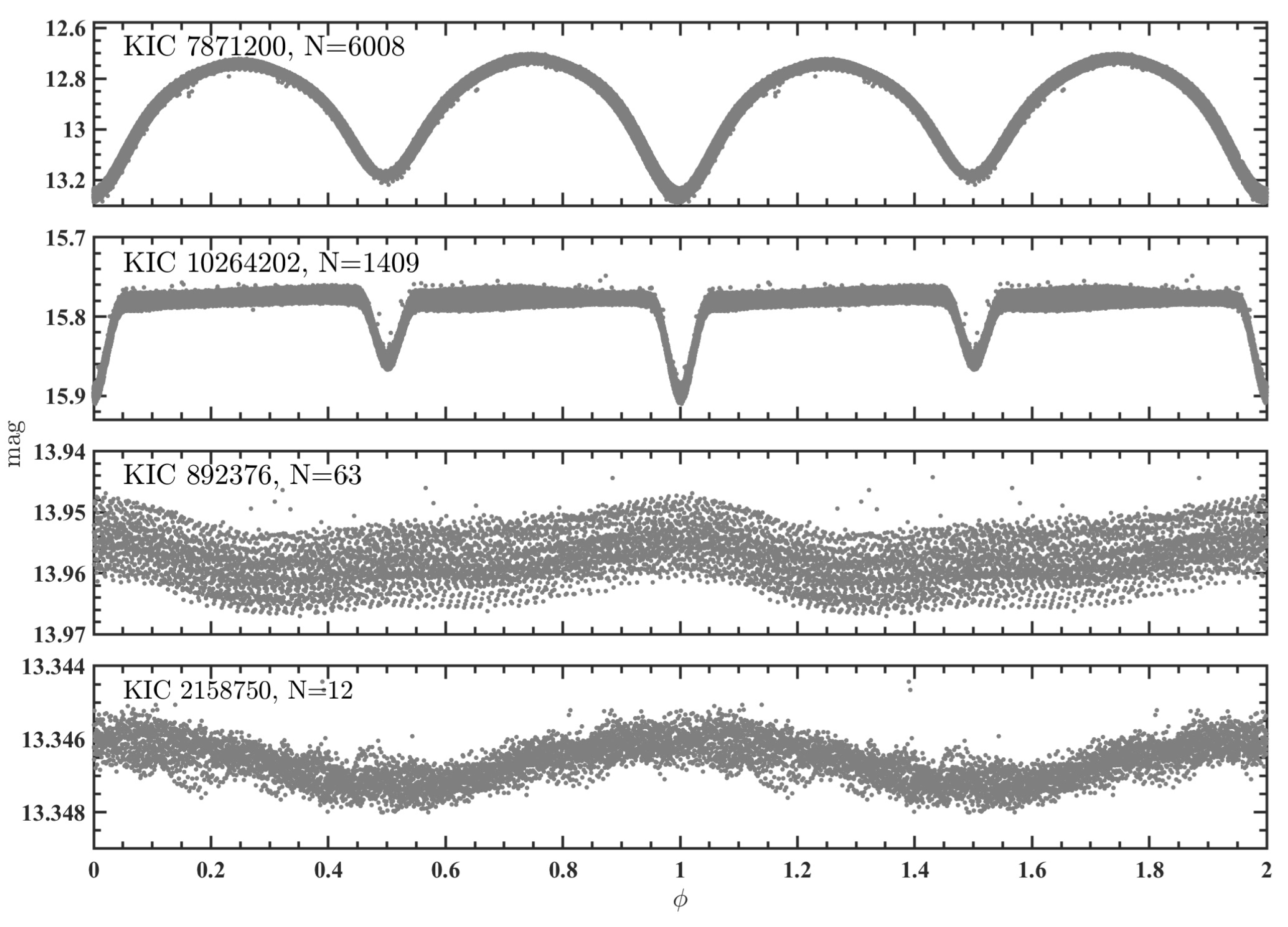
| Type | Components | Variability | Period | Chromospheric |
|---|---|---|---|---|
| (Days) | Diagnostics | |||
| RS CVn | 1: F–K (sub)giant | mag | >a few | Ca ii H,K |
| 2: G–M subgiant/dwarf | H | |||
| BY Dra | 1: K–M red dwarf | mag | 1–5 | Ca ii H,K |
| 2: G–K subgiant/dwarf | ||||
| W UMa (A) | A–F | mag | 0.4–0.8 | Ca ii H,K |
| W UMa (W) | G–K | mag | 0.2–0.4 | Mg ii |
| Algols | 1: B–F main sequence | mag | a few | Ca ii H,K |
| 2: G–K subgiant | H |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Grijs, R.; Kamath, D. Stellar Chromospheric Variability. Universe 2021, 7, 440. https://doi.org/10.3390/universe7110440
de Grijs R, Kamath D. Stellar Chromospheric Variability. Universe. 2021; 7(11):440. https://doi.org/10.3390/universe7110440
Chicago/Turabian Stylede Grijs, Richard, and Devika Kamath. 2021. "Stellar Chromospheric Variability" Universe 7, no. 11: 440. https://doi.org/10.3390/universe7110440
APA Stylede Grijs, R., & Kamath, D. (2021). Stellar Chromospheric Variability. Universe, 7(11), 440. https://doi.org/10.3390/universe7110440






