Automatic Search of Cataclysmic Variables Based on LightGBM in LAMOST-DR7
Abstract
:1. Introduction
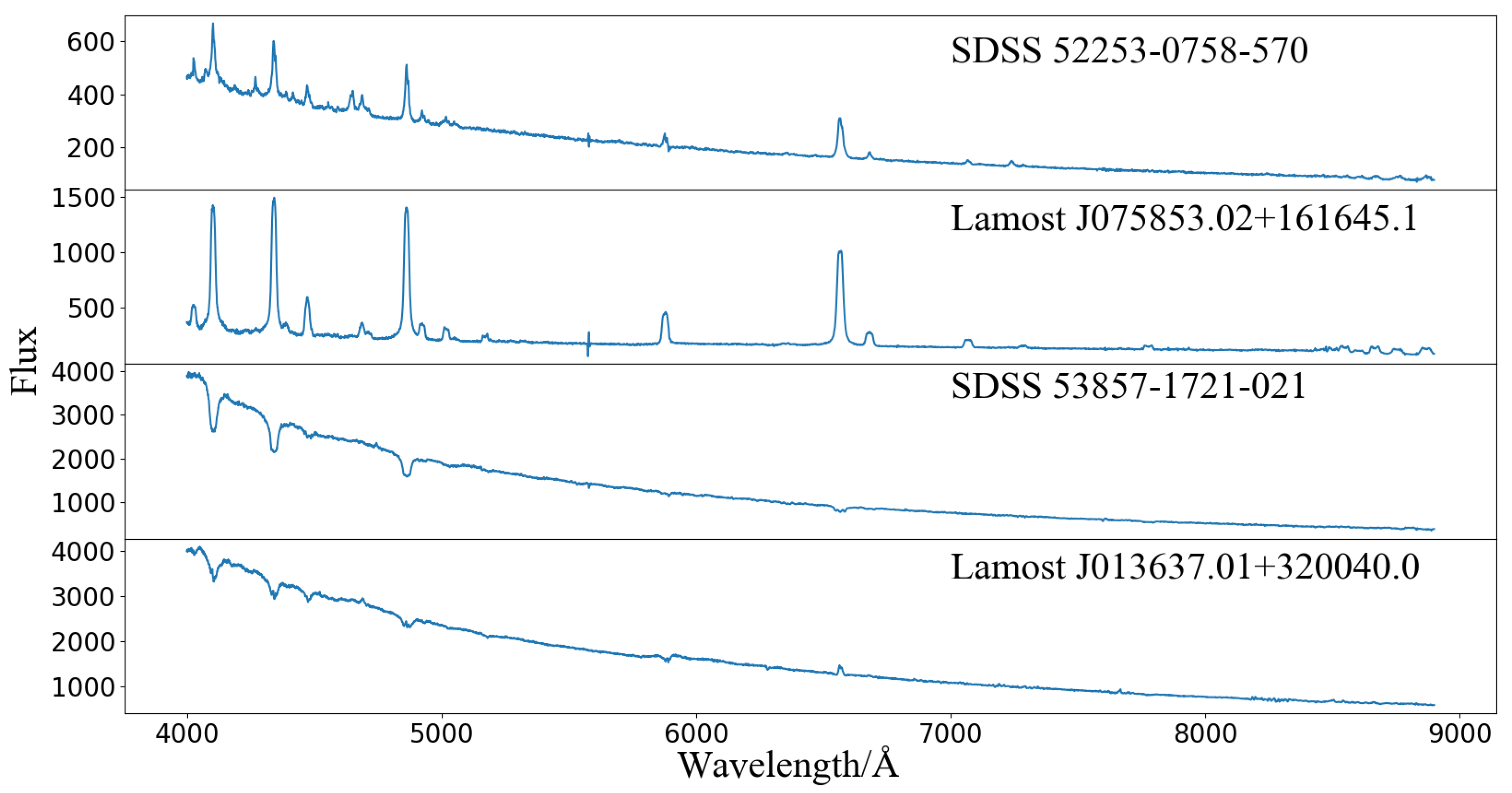
2. Dataset Preparation
3. Method
- (a)
- Histogram algorithm: Compared with a presorted algorithm that consumes more runtime and memory space, LightGBM divides the continuous floating-point values of all features of the sample data into N integer intervals and constructs a histogram containing N bins by counting the number of discrete values falling into n intervals. When the tree model is splitting, LightGBM only traverses N discrete values in the histogram to find the optimal segmentation point, which reduces the memory consumption. The time complexity, which qualitatively describes the runtime of the algorithm, is changed from to , where d is the sample size of the training set, f is the feature size, and N is the number of histograms. For high-dimensional and large-scale spectral data, LightGBM can greatly speed up the calculation;
- (b)
- Leafwise growth [27] algorithm: Traditional decision trees such as XGBoost [37] grow levelwise, in which the leaf nodes in the same layer are split at the same time and then pruned. This splitting mode causes much unnecessary computational consumption. LightGBM uses leafwise growth. The model searches for the node with the maximum gain among all the current nodes every time and then splits and iterates repeatedly until the decision tree is completely generated. Leafwise is more efficient than levelwise, but easily generates too deeply, which leads to overfitting. If the decision tree does not have a max depth limit, the tree will continue to split. Under the same number of splits, the decision tree will more deeply generate with leafwise growth. Excessive splitting of the decision tree will make the model learn the information that is not important for the classification, thus reducing the accuracy of the classifier. The algorithm needs to control the maximum depth of the tree to reduce the risk of overfitting. The two algorithms are shown in Figure 2;
- (c)
- Acceleration of histogram differences: LightGBM accelerates the training process by using the differences of the histograms while constructing them. When splitting, the histogram of the current node is represented by the difference between the histogram of the parent node and the sibling node. This type of acceleration greatly improves the training speed and efficiency [38]. The schematic is shown in Figure 3.
4. Experimental Process and Analysis
4.1. Experimental Metrics
- (i)
- TP means the number of positive samples predicted correctly as CVs;
- (ii)
- FN means the number of positive samples that not predicted as CVs;
- (iii)
- FP means the the number of negative samples predicted incorrectly as CVs;
- (iv)
- TN means the number of negative samples predicted correctly as negative samples.
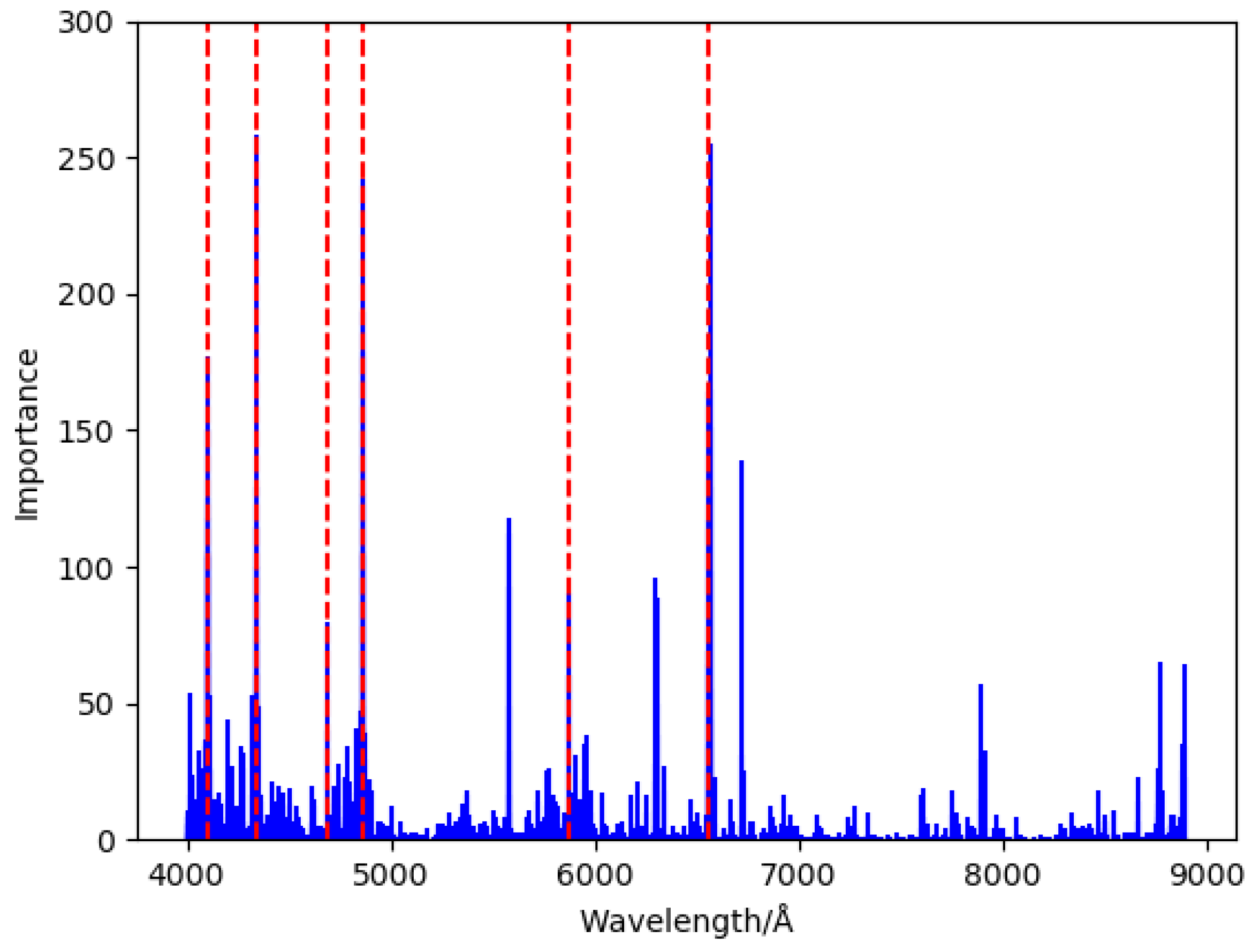
4.2. Process Analysis
- (i)
- The learning rate determines whether and when the objective function converges to the local minimum;
- (ii)
- n_estimators is the number of iterations of the model;
- (iii)
- max_depth limits the maximum depth of the decision tree;
- (iv)
- num_leaves limits the maximum number of leaf nodes of the decision tree.
4.3. Comparison of the Models
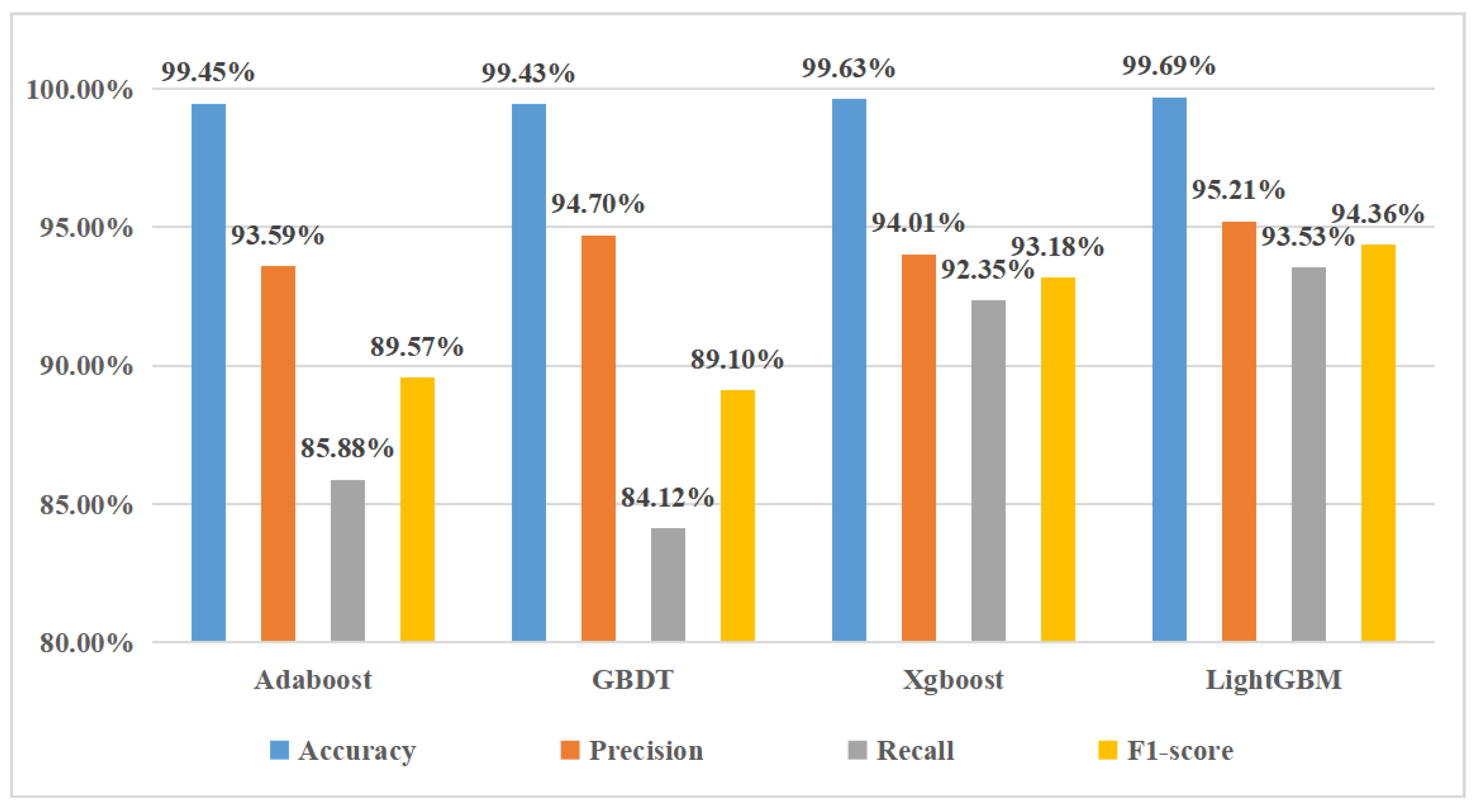
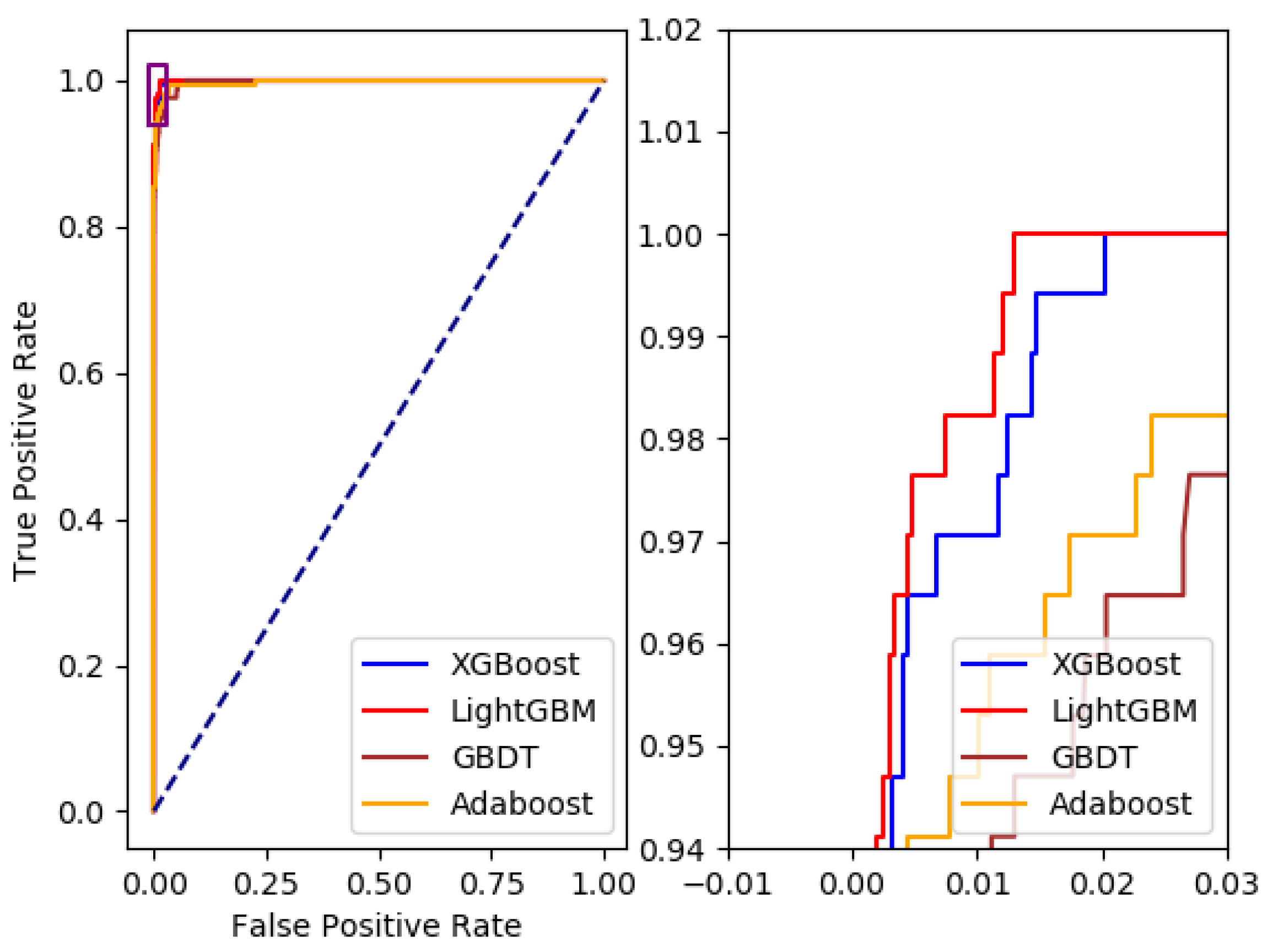
4.4. Experimental Result
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hellier, C. Cataclysmic Variable Stars: How and Why They Vary; Springer: New York, NY, USA, 2001. [Google Scholar]
- Patterson, J. The DQ Herculis stars. Publ. Astron. Soc. Pac. 1994, 106, 209. [Google Scholar] [CrossRef]
- Hack, M.; La Dous, C. Cataclysmic Variables and Related Objects; National Aeronautics and Space Administration, Scientific and Technical: Washington, DC, USA, 1993; Volume 507.
- Sion, E.M. Recent advances on the formation and evolution of white dwarfs. Publ. Astron. Soc. Pac. 1986, 98, 821. [Google Scholar] [CrossRef]
- Warner, B. Cataclysmic Variable Stars, Vol. 28 of Cambridge Astrophysics Series; Cambridge University Press: Cambridge, UK, 1995; Volume 15, p. 20. [Google Scholar]
- Han, X.L.; Zhang, L.Y.; Shi, J.R.; Pi, Q.F.; Lu, H.P.; Zhao, L.B.; Terheide, R.K.; Jiang, L.Y. Cataclysmic variables based on the stellar spectral survey LAMOST DR3. Res. Astron. Astrophys. 2018, 18, 125–146. [Google Scholar] [CrossRef]
- Pan, C.Y.; Dai, Z.B.; Observatories, Y. Investigations on the Observations of Three Types of Periodic Oscillations in Cataclysmic Variables. Acta Astron. Sin. 2019, 60, 35. [Google Scholar]
- Hou, W.; Luo, A.L.; Li, Y.B.; Qin, L. Spectroscopically Identified Cataclysmic Variables from the LAMOST Survey. I. The Sample. Astron. J. 2020, 159, 43. [Google Scholar] [CrossRef]
- Patterson, J. The evolution of cataclysmic and low-mass X-ray binaries. Astrophys. J. Suppl. 1984, 54, 443–493. [Google Scholar] [CrossRef]
- Robinson, E.L. The structure of cataclysmic variables. Annu. Rev. Astron. Astrophys. 1976, 14, 119–142. [Google Scholar] [CrossRef]
- Li, Z.Y. The Observational Properties Of Cataclysmic Variables. Ann. Shanghai Astron. Obs. Chin. Acad. Sci. 1998, 19, 225–229. [Google Scholar]
- Szkody, P.; Anderson, S.F.; Agüeros, M.; Covarrubias, R.; Bentz, M.; Hawley, S.; Margon, B.; Voges, W.; Henden, A.; Knapp, G.R. Cataclysmic variables from the sloan digital sky survey. I. The first results. Astron. J. 2002, 123, 430. [Google Scholar] [CrossRef]
- Szkody, P.; Fraser, O.; Silvestri, N.; Henden, A.; Anderson, S.F.; Frith, J.; Lawton, B.; Owens, E.; Raymond, S.; Schmidt, G. Cataclysmic variables from the sloan digital sky survey. II. The second year. Astron. J. 2003, 126, 1499. [Google Scholar] [CrossRef]
- Szkody, P.; Henden, A.; Fraser, O.; Silvestri, N.; Bochanski, J.; Wolfe, M.A.; Agüeros, M.; Warner, B.; Woudt, P.; Tramposch, J. Cataclysmic Variables from the Sloan Digital Sky Survey. III. The Third Year. Astron. J. 2004, 128, 1882. [Google Scholar] [CrossRef]
- Szkody, P.; Henden, A.; Fraser, O.J.; Silvestri, N.M.; Schmidt, G.D.; Bochanski, J.J.; Wolfe, M.A.; Agüeros, M.; Anderson, S.F.; Mannikko, L. Cataclysmic Variables from Sloan Digital Sky Survey. IV. The Fourth Year (2003). Astron. J. 2005, 129, 2386. [Google Scholar] [CrossRef] [Green Version]
- Szkody, P.; Henden, A.; Agüeros, M.; Anderson, S.F.; Bochanski, J.J.; Knapp, G.R.; Mannikko, L.; Mukadam, A.; Silvestri, N.M.; Schmidt, G.D. Cataclysmic Variables from Sloan Digital Sky Survey. V. The Fifth Year (2004). Astron. J. 2006, 131, 973. [Google Scholar] [CrossRef] [Green Version]
- Szkody, P.; Henden, A.; Mannikko, L.; Mukadam, A.; Schmidt, G.D.; Bochanski, J.J.; Agüeros, M.; Anderson, S.F.; Silvestri, N.M.; Dahab, W.E. Cataclysmic Variables from Sloan Digital Sky Survey. VI. The Sixth Year (2005). Astron. J. 2007, 134, 185. [Google Scholar] [CrossRef] [Green Version]
- Szkody, P.; Anderson, S.F.; Hayden, M.; Kronberg, M.; McGurk, R.; Riecken, T.; Schmidt, G.D.; West, A.A.; Gänsicke, B.T.; Gomez-Moran, A.N. Cataclysmic variables from SDSS. VII. The seventh year (2006). Astron. J. 2009, 137, 4011. [Google Scholar] [CrossRef]
- York, D.G.; Adelman, J.; Anderson, J.E., Jr.; Anderson, S.F.; Annis, J.; Bahcall, N.A.; Bakken, J.A.; Barkhouser, R.; Bastian, S.; Berman, E.; et al. The Sloan Digital Sky Survey: Technical Summary. Astron. J. 2000, 120, 1579. [Google Scholar] [CrossRef]
- Szkody, P.; Anderson, S.F.; Brooks, K.; Gänsicke, B.T.; Kronberg, M.; Riecken, T.; Ross, N.P.; Schmidt, G.D.; Schneider, D.P.; Agüeros, M.A. Cataclysmic variables from the Sloan digital sky survey. VIII. The final year (2007–2008). Astron. J. 2011, 142, 181. [Google Scholar] [CrossRef] [Green Version]
- Djorgovski, S.G.; Drake, A.J.; Mahabal, A.A.; Graham, M.J.; Donalek, C.; Williams, R.; Beshore, E.; Larson, S.M.; Prieto, J.; Catelan, M. The Catalina Real-time Transient Survey. Proc. Int. Astron. Union 2011, 285, 306. [Google Scholar]
- Drake, A.; Gänsicke, B.; Djorgovski, S.; Wils, P.; Mahabal, A.; Graham, M.; Yang, T.C.; Williams, R.; Catelan, M.; Prieto, J.; et al. Cataclysmic variables from the catalina real-time transient survey. Mon. Not. R. Astron. Soc. 2014, 441, 1186–1200. [Google Scholar] [CrossRef] [Green Version]
- Udalski, A. The Optical Gravitational Lensing Experiment. Real Time Data Analysis Systems in the OGLE-III Survey. Acta Astron. 2004, 53, 291–305. [Google Scholar]
- Mróz, P.; Udalski, A.; Poleski, R.; Pietrukowicz, P.; Szymanski, M.; Soszynski, I.; Wyrzykowski, L.; Ulaczyk, K.; Kozlowski, S.; Skowron, J. One thousand new dwarf novae from the OGLE survey. arXiv 2016, arXiv:1601.02617. [Google Scholar]
- Jiang, B.; Luo, A.L.; Zhao, Y.H. Data Mining of Cataclysmic Variables Candidates in Massive Spectra. Spectrosc. Spectr. Anal. 2011, 31, 2278–2282. [Google Scholar]
- Jiang, B.; Luo, A.L.; Zhao, Y.H. Data Mining Approach to Cataclysmic Variables Candidates Based on Random Forest Algorithm. Spectrosc. Spectr. Anal. 2012, 32, 510–513. [Google Scholar]
- Ke, G.L.; Meng, Q.; Finley, T.; Wang, T.F.; Chen, W.; Ma, W.D.; Ye, Q.W.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Zhao, G.; Zhao, Y.H.; Chu, Y.Q.; Jing, Y.P.; Deng, L.C. LAMOST spectral survey—An overview. Res. Astron. Astrophys. 2012, 12, 723. [Google Scholar] [CrossRef] [Green Version]
- Cui, X.Q.; Zhao, Y.H.; Chu, Y.Q.; Li, G.P.; Li, Q.; Zhang, L.P.; Su, H.J.; Yao, Z.Q.; Wang, Y.N.; Xing, X.Z. The large sky area multi-object fiber spectroscopic telescope (LAMOST). Res. Astron. Astrophys. 2012, 12, 1197. [Google Scholar] [CrossRef]
- Luo, A.L.; Zhang, H.T.; Zhao, Y.H.; Zhao, G.; Cui, X.Q.; Li, G.P.; Chu, Y.Q.; Shi, J.R.; Wang, G.; Zhang, J.N. Data release of the LAMOST pilot survey. Res. Astron. Astrophys. 2012, 12, 1243. [Google Scholar] [CrossRef]
- Luo, A.L.; Zhang, H.T.; Zhao, Y.H.; Zhao, G.; Deng, L.C.; Liu, X.W.; Jing, Y.P.; Wang, G.; Zhang, H.T.; Shi, J.R.; et al. The first data release (DR1) of the LAMOST regular survey. Res. Astron. Astrophys. 2015, 15, 1095. [Google Scholar] [CrossRef]
- Chen, S.X.; Sun, W.M.; Kong, X. Difference Analysis of LAMOST Stellar Spectrum and Kurucz Model Based on Grid Clustering. Spectrosc. Spectr. Anal. 2017, 37, 1951–1954. [Google Scholar]
- Pulicherla, P.; Kumar, T.; Abbaraju, N.; Khatri, H. Job Shifting Prediction and Analysis Using Machine Learning. J. Phys. Conf. Ser. 2019, 1228, 012056. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Z.; Yi, Z. An Effective miRNA Classification Method in Breast Cancer Patients. In Proceedings of the 2017 International Conference on Computational Biology and Bioinformatics, Newark, NJ, USA, 18–20 October 2017. [Google Scholar]
- Sun, X.; Liu, M.; Sima, Z. A novel cryptocurrency price trend forecasting model based on LightGBM. Financ. Res. Lett. 2020, 32, 101084. [Google Scholar] [CrossRef]
- Jain, A.; Saini, M.; Kumar, M. Greedy Algorithm. J. Adv. Res. Comput. Sci. Eng. 2015, 2, 11015. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Jing, W.; Yi, Z.-P.; Yue, L.-L.; Dong, H.-F.; Pan, J.-C.; Bu, Y.-D. Spectral Classification of M-Type Stars Based on Ensemble Tree Models. Spectrosc. Spectr. Anal. 2019, 39, 2288–2292. [Google Scholar]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]


| Type | Star | Galaxy | QSO | Unknown |
|---|---|---|---|---|
| Number | 9,531,038 | 193,361 | 64,231 | 819,781 |
| Parameter | Value |
|---|---|
| learning rate | 0.05 |
| n_estimators | 372 |
| max_depth | 8 |
| num_leaves | 40 |
| Accuracy | Precision | Recall | F1-Score | |
|---|---|---|---|---|
| LightGBM | 99.69% | 95.21% | 93.53% | 94.36% |
| Model | AdaBoost | GBDT | XGBoost | LightGBM |
|---|---|---|---|---|
| Time | 341.73 s | 269.25 s | 190.05 s | 75.41 s |
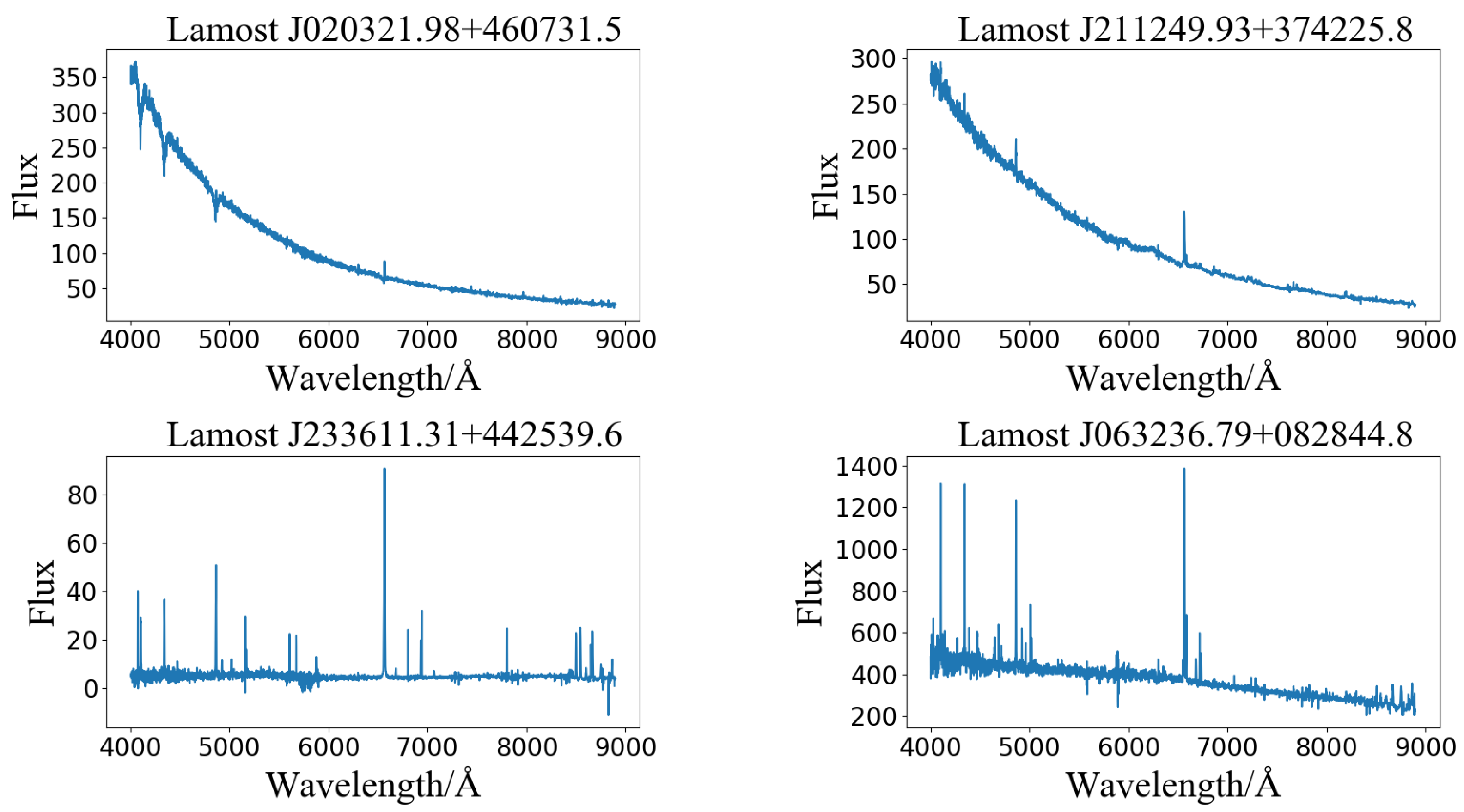
| Designation | Obsid | Obsdate | Ra | Dec |
|---|---|---|---|---|
| J020321.98 + 460731.5 | 631616056 | 17 January 2018 | 30.8415900000 | 46.1254250000 |
| J211249.93 + 374225.8 | 593810181 | 20 October 2017 | 318.2080800000 | 37.7071940000 |
| J233611.31 + 442539.6 | 475914160 | 3 November 2016 | 354.0471500000 | 44.4276800000 |
| J063236.79 + 082844.8 | 605312123 | 17 November 2017 | 98.1533180000 | 8.4791159000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Chen, J.; Jiang, B.; Wang, W. Automatic Search of Cataclysmic Variables Based on LightGBM in LAMOST-DR7. Universe 2021, 7, 438. https://doi.org/10.3390/universe7110438
Hu Z, Chen J, Jiang B, Wang W. Automatic Search of Cataclysmic Variables Based on LightGBM in LAMOST-DR7. Universe. 2021; 7(11):438. https://doi.org/10.3390/universe7110438
Chicago/Turabian StyleHu, Zhiyuan, Jianyu Chen, Bin Jiang, and Wenyu Wang. 2021. "Automatic Search of Cataclysmic Variables Based on LightGBM in LAMOST-DR7" Universe 7, no. 11: 438. https://doi.org/10.3390/universe7110438
APA StyleHu, Z., Chen, J., Jiang, B., & Wang, W. (2021). Automatic Search of Cataclysmic Variables Based on LightGBM in LAMOST-DR7. Universe, 7(11), 438. https://doi.org/10.3390/universe7110438






