Topics in Supersymmetric and Noncommutative Quantum Cosmology

Abstract

In the present article we review the work carried out by us and collaborators on supersymmetric quantum cosmology, noncommutative quantum cosmology and the application of GUPs to quantum cosmology and black holes. The review represents our personal view on these subjects and it is presented in chronological order.

1. Introduction

Quantum gravity is a prospect of a physical theory describing the quantum phenomena associated to the gravitational field. At the present time nobody knows with certainty how this theory will look like. There are several proposals in the literature describing the possible nature of the fundamental degrees of freedom and checking the internal consistency by connecting it to the correct limits as the low energy macroscopic general relativity and quantum mechanical laws. These theories have some features which are quite interesting by themselves, as the modification of the spacetime structure near Planck scale (for an exposition of the different approaches, see for instance, [1,2]). String theory and loop quantum gravity are among the most prominent examples. In the present article we review our advances on another approach to quantum gravity as quantum cosmology. This proposal has its origins in the Arnowitt, Deser and Misner (ADM) canonical formalism of quantum gravity [3]. This is an approach to quantum gravity that possess some of the features of the complete theory and it allows to formulate some models easily workable (for some reviews on this topic, see [4,5].)

The study of the universe must be done in the framework of the theories in force at present, depending on the scale to be described, although there is no question that it must rely on general relativity. Cosmology links together, as a theory of the evolution of the universe, small with large scales, hence a natural, theoretical framework for it is quantum cosmology.

Cosmology describes the general laws of the universe, i.e., its evolution and structure formation. Mostly, these laws can be formulated classically, in accordance with the observational bounds. However, assuming the past convergence of matter into a singularity, it emerges the question, still open, of its quantum origin. On the other side, there is large evidence and it is generally accepted that classical physics can be explained from quantum physics. Accordingly, there have been broad efforts to formulate a quantum theory of gravity.

The observation of the universe has lead to the knowledge that it behaves as a classical system, it is no subject to quantum uncertainties. This fact refers to the observable universe, which begins with the time of the Cosmic Microwave Background (CMB). Before this time, the universe is well described after the hot big bang, and there is controversy on what happened before, although it is largely accepted, that an inflationary epoch should have been present, originated during a homogeneous phase. Before this phase not much is known, but it is believed that if the universe has expanded from a previous era above Planck scale, a full quantum gravity description is required. On the other side, one of the successes of inflation is that it produces a growth of quantum fluctuations to the size and density required by gravitational instability, without generating too strong primordial gravitational waves. These fluctuations can be explained by the quantization of small inhomogeneous perturbations of the metric, in a homogeneous background, hence from a semiclassical quantum gravity. Therefore, it is valid to study homogeneous cosmology as a quantum theory. This quantization corresponds to quantum mechanics, with a time independent Klein-Gordon equation, given by the Wheeler-DeWitt equation [5,6].

Among the candidates for a unified theory of quantum gravity, supergravity has an important place, as an effective or possibly fundamental theory. As supergravity includes necessarily fermions, it requires to be a quantum theory. Thus, the study of quantum supergravity cosmology is meaningful and relevant. As a bonus, in the supersymmetric framework, the Wheeler-DeWitt equation turns into a system of first order equations.

Supersymmetric quantum cosmology has been first formulated in an attempt to give a systematic approach for a square root for the Wheeler-DeWitt equation in [7]. In this work, a homogeneous theory following from $N=1$ supergravity theory was considered. In this way, an invariance principle for a square root of the WDW equation has been proposed, at the energy scale of quantum cosmology. As the fields in the action depend only on time, not all the original constraints follow from the variation, and the missing constraints should be implemented by hand for consistency.

If one would like to consider the presence of quantum effects through the Heisenberg uncertainty principle in gravitational systems, it is possible to argue that there is a minimal length, which is precisely the Planck length $L_P$. If we increase the energy, the length will be start to be increased again. This behavior is typical of noncommutative field theories and noncommutative gravity [8,9]. One of its prominent examples is the description of instantons on noncommutative spaces. It can be appreciated an effective size of the instantons depending on the noncommutative parameter. A novel proposal was carried out by us in the paper [10], where noncommutative deformation was implemented at the level of Wheeler’s superspace or more concretely at the level of minisuperspace.

If the uncertainty relations are modified by generalizing them, then the ultraviolet (UV) behavior will change. This is precisely the aim of Generalized Uncertainty Principles (GUP), which asserts that in the UV the usual Heisenberg relations should be modified. These generalizations are consistent with some results of very high energy scattering in string theory [11,12,13,14,15,16,17,18].

However, the observed large scale homogeneity of the universe, indicates a primary description in a minisuperspace, with finitely many degrees of freedom. Such a theory has the indubitable advantage, that it accepts a quantum description, and has served also as a test ground for approaches of quantum gravity. Moreover, this theory has given new insights in the study of the early universe, and of the other realm where it is thought that quantum gravity should manifest, the interior of black holes. Among these approaches, we have made several proposals that we shortly review here: supersymmetric cosmology, effective noncommutativity in cosmology and black holes.

In this work we shortly present some of these developments with collaborators, and concentrate on our own point of view, and main contributions. The article is organized as follows: in Section 2 we review supersymmetric quantum cosmology starting from the original proposal [7] and we describe very briefly the other proposals to supersymmetric quantum cosmology in the literature. Section 3 is devoted to give an overview of the noncommutative quantum cosmology. We give the original idea [10] and briefly discuss its further evolution. In Section 4 we describe a recent proposal of the application of GUPs to quantum cosmology following Ref. [19]. In Section 5 we review the application of the GUPs to black holes, this is based in Ref. [20].

2. Supersymmetric Quantum Cosmology

The starting point is the Freedman-Nieuwenhuizen-Ferrara action [21]. The fields are the tetrad $e_{\mu }^a$, the spin connection ${\omega }_{\mu }^{ab}$, and the Rarita-Schwinger Majorana $\frac{3}{2}$-spinor field ${\psi }_{\mu }^a$, i.e., it satisfies ${\overline{\psi }}_{\mu }={\psi }_{\mu }^{T}C$, where C is the charge conjugation matrix. The lagrangian is

$$L=\frac{1}{2{\kappa }^2}\left[\sqrt{-g}R\left(\omega \right)-{\epsilon }^{\mu \nu \rho \sigma }{\overline{\psi }}_{\mu }{\gamma }_5{\gamma }_{\nu }{D}_{\rho }{\psi }_{\sigma }\right],$$

(1)

where the bosonic part is the Palatini lagrangian, which depends on the tetrad and the spin connection. The derivative of the Rarita-Schwinger field is covariant with respect to Lorentz transformations. After its elimination by its equations of motion, the spin connection turns into the Ricci rotation coefficients, modified by the supersymmetric torsion term

$${\omega }_{\lambda \mu \nu }=\frac{1}{2}\left(-{\mathrm{\Omega }}_{\lambda \mu \nu }+{\mathrm{\Omega }}_{\mu \nu \lambda }+{\mathrm{\Omega }}_{\nu \lambda \mu }\right),$$

(2)

where ${\mathrm{\Omega }}_{\lambda \mu \nu }=e_{\lambda a}\left({\partial }_{\mu }{e}_{\nu }^a-{\partial }_{\nu }{e}_{\mu }^a-\frac{i}{2}{\overline{\psi }}_{\mu }{\gamma }^a{\psi }_{\nu }\right)$.

Similar to Yang-Mills theories, the components $e_0^a$, ${\omega }_0^{ab}$, and ${\psi }_0^a$ are non-dynamical, and their conjugated momenta $p_a$, $p_{ab}$ and ${\pi }_a$ vanish. The hamiltonian is [22,23]

$$\mathcal{H}=e_0^a{H}_a+{\omega }_0^{ab}{L}_{ab}+{\psi }_0^{\alpha }{S}_{\alpha }+{\lambda }^a{p}_a+{\lambda }^{ab}{p}_{ab}+{\lambda }^{\alpha }{\pi }_{\alpha },$$

(3)

where $H_0$ is the hamiltonian constraint, $H_i,(i=1,2,3)$ the momentum constraints, $L_{ab}$ the Lorentz constraints, and $S_{\alpha }$ the supersymmetry fermionic constraints. All these constraints are first class.

In general the fermionic variables have first order kinetic term, from which follow second class constraints, which require Dirac brackets. Thus, the canonical brackets of ${\psi }_m^{\alpha }$ form a Clifford algebra $(m=1,2,3)$. The equal time bracket constraint algebra closes [22], modulo Lorentz transformations,

$$\{S_{\alpha }\left(\overrightarrow{x}\right),S_{\beta }\left({\overrightarrow{x}}^{\prime }\right)\}=-{\left({\gamma }^{a}C\right)}_{\alpha \beta }{H}_a\left(\overrightarrow{x}\right)\delta (\overrightarrow{x}-{\overrightarrow{x}}^{\prime }).$$

(4)

The canonical quantization of the bosonic variables is implemented by derivatives of the conjugated variables, as for canonical quantum gravity [6]. The fermionic variables can be quantized in a similar way [24]. Another way is, as in the case of the spinning particle, representing the fermionic variables by Dirac matrices, leading to the Dirac equation [25]. The constraints are implemented as operator equations $\mathcal{H}\mathrm{\Psi }=0$, on a wave function $\mathrm{\Psi }$ that will be a functional of the fields of configuration space, called also superspace. Thus, the solutions do not depend on the non-dynamical fields, are scalar by the Lorentz constraints, and depend on 3-metrics through space diffeomorphisms invariant classes, due to the momentum constraints $H_i$, see e.g., [5]. On the other side, these solutions satisfy the supersymmetric constraints $S_{\alpha }\mathrm{\Psi }=0$, then the hamiltonian and momentum constraints will be satisfied, $H_a\mathrm{\Psi }=0$, due to (4).

At the beginning of the nineties, supersymmetric quantum cosmology has attracted the attention of theoretical cosmologists and was developed in several directions, for early developments see [26], and the extensive more recent review [27,28].

As fermionic degrees of freedom of the universe could describe anisotropies, frequently a supergravity description of a homogeneous universes has been done for Bianchi models [7,29], whose metric has the general form, in the ADM formulation, $d{s}^2=[N^2\left(t\right)-N_i\left(t\right)N_i\left(t\right)]d{t}^2-2N_m\left(t\right)dt{\omega }^m-h_{mn}\left(t\right){\omega }^m{\omega }^n$, where $h_{mn}\left(t\right)=e^{2\mathrm{\Omega }\left(t\right)}{\left(e^{2\beta \left(t\right)}\right)}_{mn}$, $\beta \left(t\right)$ is a $3\times 3$ matrix, and the one-forms ${\omega }^m$ are determined by the Bianchi type. With this metric, a tetrad can be given by $e_0^0=N$, $e_0^i=e^{\mathrm{\Omega }}{\left(e^{-\beta }\right)}_{ij}$, $e_m^0=0$, $e_m^i=e^{-\mathrm{\Omega }}{\left(e^{\beta }\right)}_{mi}$, where $i,j,\cdots$ are Lorentz space indices, and $m,n,\cdots$ are world space indices. Usually, the Misner parametrization is taken $\beta =\mathrm{diag}({\beta }_{+}+\sqrt{3}{\beta }_{-},{\beta }_{+}-\sqrt{3}{\beta }_{-},-2{\beta }_{+})$. These choices amount to a gauge fixing, corresponding to space homogeneity and Lorentz invariance of the tetrad. As a consequence, there are no Lorentz constraints, as noted in [7]. However, as usual in gauge theory QFT, in this case, the Lorentz constraints must be taken into account [29]. In [7,29] the Bianchi I model has been studied, ${\omega }^m=d{x}^m$. In [7] a matrix representation has been taken for the fermionic variables, with a spinor wave function, and in [29] a power series in the fermionic variables. In fact, in [30] the Bianchi IX model has been studied, considering the 12 dynamical fermionic degrees of freedom, which require a $64\times 64$ Dirac-matrix representation. In this case, as there is no dependence on space coordinates, the Lorentz constraints act only on the fermionic variables and are algebraic. Their application to the 64-D spinorial wave function is straightforward and, as shown it [30], the wave function reduces to only two non-vanishing components

$${\psi }_{\pm }=C{e}^{\pm e^{-2\mathrm{\Omega }}[2e^{2{\beta }_{+}}\mathrm{Cosh}\left(2\sqrt{3}{\beta }_{-}\right)+e^{-4{\beta }_{-}}]}.$$

(5)

This result confirms the observation in [29], that the Lorentz constraints restrict strongly the solutions of the WDW equation. In [31], a thorough analysis of this model has been done without considering the Lorentz constraints. In [32] this model has been studied under the inclusion of a cosmological constant, with results indicating that there may be no physical quantum states.

In [33], the Bianchi IX model has been considered by the observation that it has the structure of a sigma model in classical mechanics, on a manifold with three degrees of freedom $q=(a,{\beta }_{+},{\beta }_{-})$, i.e., geometrodynamics with a specific metric for Bianchi IX, $G^{ij}=\mathrm{diag}(-1,1,1)$, and whose hamiltonian constraint can be written as

$$H_0=G^{ij}\left(q\right)\left[p_i{p}_j+\frac{\partial \varphi \left(q\right)}{\partial q^i}\frac{\partial \varphi \left(q\right)}{\partial q^j}\right],$$

(6)

where $p_i$ are the conjugate momenta, and $\varphi \left(q\right)=\frac{1}{6}{e}^{2a}\mathrm{T}r{e}^{2\beta }$. As the hamiltonian (6) is quadratic, a global supersymmetric extension can be given straightforwardly, see e.g., [34,35,36], with the supersymmetric charges $Q={\psi }^i(p_i+i\frac{\partial \varphi }{\partial q^i})$ and $\overline{Q}={\overline{\psi }}^i(p_i-i\frac{\partial \varphi }{\partial q^i})$, and $H=\{Q,\overline{Q}\}=H_0+\frac{\hslash }{2}\frac{{\partial }^2\varphi }{\partial q^i\partial q^j}\left[{\overline{\psi }}^i{\psi }^j\right]$. The fermionic variables satisfy $\{{\psi }^i,{\psi }^j\}=\{{\psi }^i,{\psi }^j\}=0$, and $\{{\psi }^i,{\overline{\psi }}^j\}=G^{ij}$. Time reparametrization invariance is restored in [37], by the introduction of the lapse function and its fermionic superpartner in the inverse Legendre transformation. This formulation has been worked out to introduce a cosmological term in [37] and scalar matter in [38].

A superfield formulation has been given in [39,40], by a realization of general time reparametrizations on superspace1 $(t,\theta ,\overline{\theta })$

$$\begin{array}{cc}\hfill \delta t& =\zeta \left(t\right)+\frac{i}{2}[\theta \xi \left(t\right)+\overline{\theta }\overline{\xi }(t\left)\right],\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \delta \theta & =\frac{1}{2}\overline{\xi }\left(t\right)+\frac{1}{2}\theta [\dot{\zeta }\left(t\right)+ib\left(t\right)]+\frac{i}{2}\theta \overline{\theta }\dot{\xi }\left(t\right),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \delta \overline{\theta }& =\frac{1}{2}\xi \left(t\right)+\frac{1}{2}\overline{\theta }[\dot{\zeta }\left(t\right)-ib\left(t\right)]-\frac{i}{2}\theta \overline{\theta }\dot{\overline{\xi }}\left(t\right).\hfill \end{array}$$

(9)

where $(\zeta \left(t\right),\xi \left(t\right),\overline{\xi }\left(t\right))$ are the parameters of superspace transformation, and $b\left(t\right)$ is the parameter of the $U\left(1\right)$ R-symmetry transformation, which acts on the $(\xi ,\overline{\xi })$ space. As this is a one dimensional field theory, there are no Lorentz transformations. The fields are replaced by superfields, but their components must be suitably rescaled to have the correct weight under time reparametrizations. There are superfields for the parameters of time and supersymmetry transformations, as in superspace supergravity, see e.g., [41]. The lapse field is also replaced by a superfield, although there is not an invariant volume element for superspace is not considered. However, this formulation allows to write invariant superfield actions, whose bosonic sector agrees with the corresponding non-supersymmetric action. The constraint algebra contains the hamiltonian and supersymmetric constraints, and it closes properly. An interesting feature is that it includes additionally, as a constraint, the fermion number operator, which ensures equal number of bosonic and fermionic degrees of freedom; the corresponding Lagrange multiplier is the highest component of the lapse superfield.

This formalism has been applied in [42,43] to a FRLW cosmology with a scalar field, where the spontaneous symmetry breaking of supersymmetry has been explored. In these works a canonical quantization has been performed, with matrix representations for the fermionic variables, and the wave function has been computed. It has been shown that a similar mechanism of supersymmetry breaking as in supergravity applies here, as the scalar potential is not positive definite, which written in terms of the auxiliary fields is

$$V\left(\varphi \right)=\frac{1}{2}{F}^2-\frac{3}{{\kappa }^2{a}^2}{B}^2,$$

(10)

where F and B are auxiliary fields, given by their equations of motion $F=2\frac{\partial g\left(\phi \right)}{\partial \phi }$, $B=-{\kappa }^{2}ag\left(\phi \right)$, and $g\left(\phi \right)$ is the superfield potential, i.e., the superpotential in supergravity. Thus, supersymmetry is broken if at an extremum ${\phi }_0$ of the potential, $V\left({\phi }_0\right)=0$, and $F\ne 0$; the superpartner of the lapse, the gravitino, acquires a nonvanishing mass, similar to the Higgs mechanism. The wave function has four components, two of them are not normalizable, and the other two are the ‘conjugated’ states, one of them normalizable, depending on the sign of the superpotential

$$\begin{array}{c}\hfill {\psi }_{\pm }(a,\phi )=C{a}^{\frac{3}{4}}{e}^{\mp 2a^{3}g\left(\phi \right)\pm 3\sqrt{k}{M}_{pl}^2{a}^2}.\end{array}$$

(11)

In order to appreciate phenomenological consequences of the previous model, it has been studied in [44] in a semiclassical setting by the WKB method, with the solutions (11) written as $e^{S_a+S_{\phi }}$ see also [45]. For each one of these solutions follow different classical evolution equations for the scale factor and the scalar field. In these equations there are supersymmetric contributions with the behavior of radiation and stiff matter. A detailed numerical analysis has been made for an exponential superpotential and flat space, where, in particular, inflationary stages can be observed. An interesting relation of a $SU\left(2\right)$ matrix model with supersymmetric quantum cosmology has been uncovered in [46], arising from the quantization of the 11-dimensional supermembrane, which has a zero energy solution of the same form of a wave function known from supersymmetric quantum cosmology [27].

The superspace approach in supergravity has the drawback, that the component fields of superfields in general are not Lorentz spinors (bosonic or fermionic). This problem has a solution in the formalism of the so called “new” $\mathrm{\Theta }$- variables [41,47]. The fermionic power expansion in superfields is redefined as

$$\varphi (x,\theta )=\sum \frac{1}{n!}{\theta }^{{\eta }_1}\cdots {\theta }^{{\eta }_n}{\partial }_{{\eta }_1}\cdots {\partial }_{{\eta }_n}{\varphi (x,\theta )|}_{\theta =0}$$

$$\to \mathrm{\Phi }(x,\mathrm{\Theta })=\sum \frac{1}{n!}{\mathrm{\Theta }}^{{\alpha }_1}\cdots {\mathrm{\Theta }}^{{\alpha }_n}{\mathcal{D}}_{{\alpha }_1}\cdots {\mathcal{D}}_{{\alpha }_n}{\varphi (x,\theta )|}_{\theta =0},$$

(12)

where ${\mathcal{D}}_{\alpha }\varphi (x,\theta )$ are Lorentz covariant fermionic derivatives under local superspace coordinate transformations $(x,\theta )\to (x^{\prime },{\theta }^{\prime })$ and local Lorentz transformations. The supergravity transformations are field dependent local superspace plus Lorentz transformations ${\delta }_{\xi }{\mathrm{\Phi }}_A(x,\theta )=-{\xi }^B{\mathcal{D}}_B{\mathrm{\Phi }}_A(x,\theta )$, where $A=(\mu ,\alpha )$ are multiindices formed by a spacetime index, and a Lorentz $\frac{1}{2}$-spin index. For consistency, this formulation requires a covariant formulation of the Wess-Zumino gauge [47]. In [48] it is shown how to apply this formalism to homogeneous spaces, and how to construct invariant supergravity actions. In this framework, in [49,50], the FRLW model with a scalar field has been worked out, with a wave function similar to (11), differing only by the power of the scalar factor in front of it, due to a different operator ordering. Further, in these works the interpretation of the scalar field as time is considered, with an effective time dependent wave function, which corresponds to the conditional probability for a given value of the scalar field

$$\mathrm{\Psi }(a,t)={\left.\frac{\psi (a,\varphi )}{\sqrt{{\int }_0^{\infty }da{\left|\psi (a,\varphi )\right|}^2}}\right|}_{\varphi =t}.$$

(13)

With this wave function, the mean value of the scalar factor gives a classical evolution [49]

$$a\left(t\right)={\int }_0^{\infty }a{\left|\mathrm{\Psi }(a,t)\right|}^{2}da=\mathrm{\Gamma }\left(4/3\right){\left[\frac{\hslash c}{2\left|W\right(t\left)\right|}\right]}^{1/3}.$$

(14)

As a consistency check, a computation of the uncertainty relation gives $\Delta a\Delta {\pi }_a\approx 0.53\hslash$.

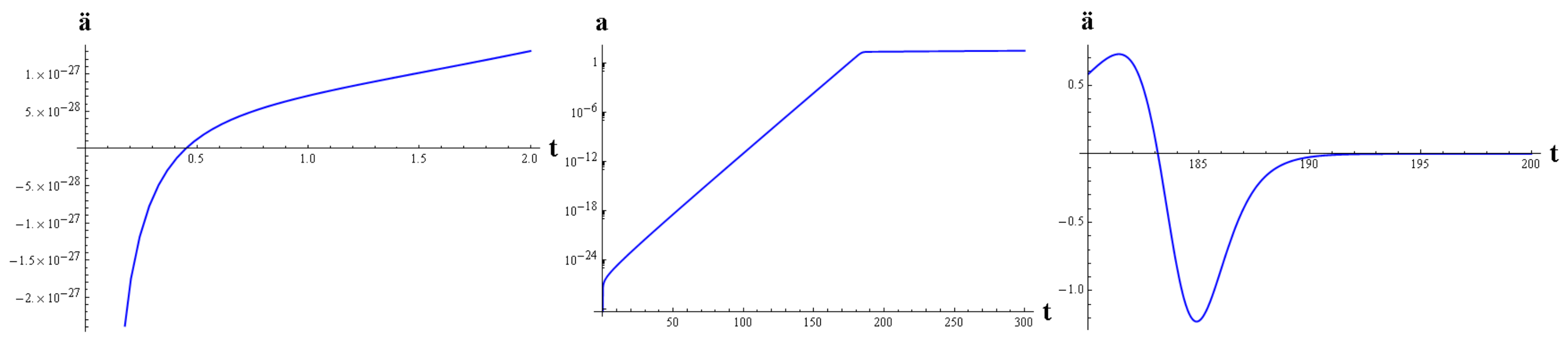
Moreover, with an exponential superpotential an inflationary scenario can be obtained, which lasts enough e-folds [50]. The exit of inflation requires fine tuning of a constant which must be added to the superpotential. To illustrate it, we consider a Gaussian superpotential

$$W\left(t\right)=\frac{c^4{M}_p^3}{{\hslash }^2}{t}^{-2}\left(\frac{1}{\lambda }{e}^{-t}+1\right)$$

(15)

with $\lambda ={10}^{-80}$, and $c=1$, $\hslash =1$, $M_p=1$. With this potential it can be seen that $a\left(0\right)=0$, $\dot{a}\left(0\right)=\infty$, and $\ddot{a}\left(0\right)=-\infty$. The acceleration increases quickly, and becomes positive at $t\approx 0.45$, and stays positive up to $t\approx 183$. 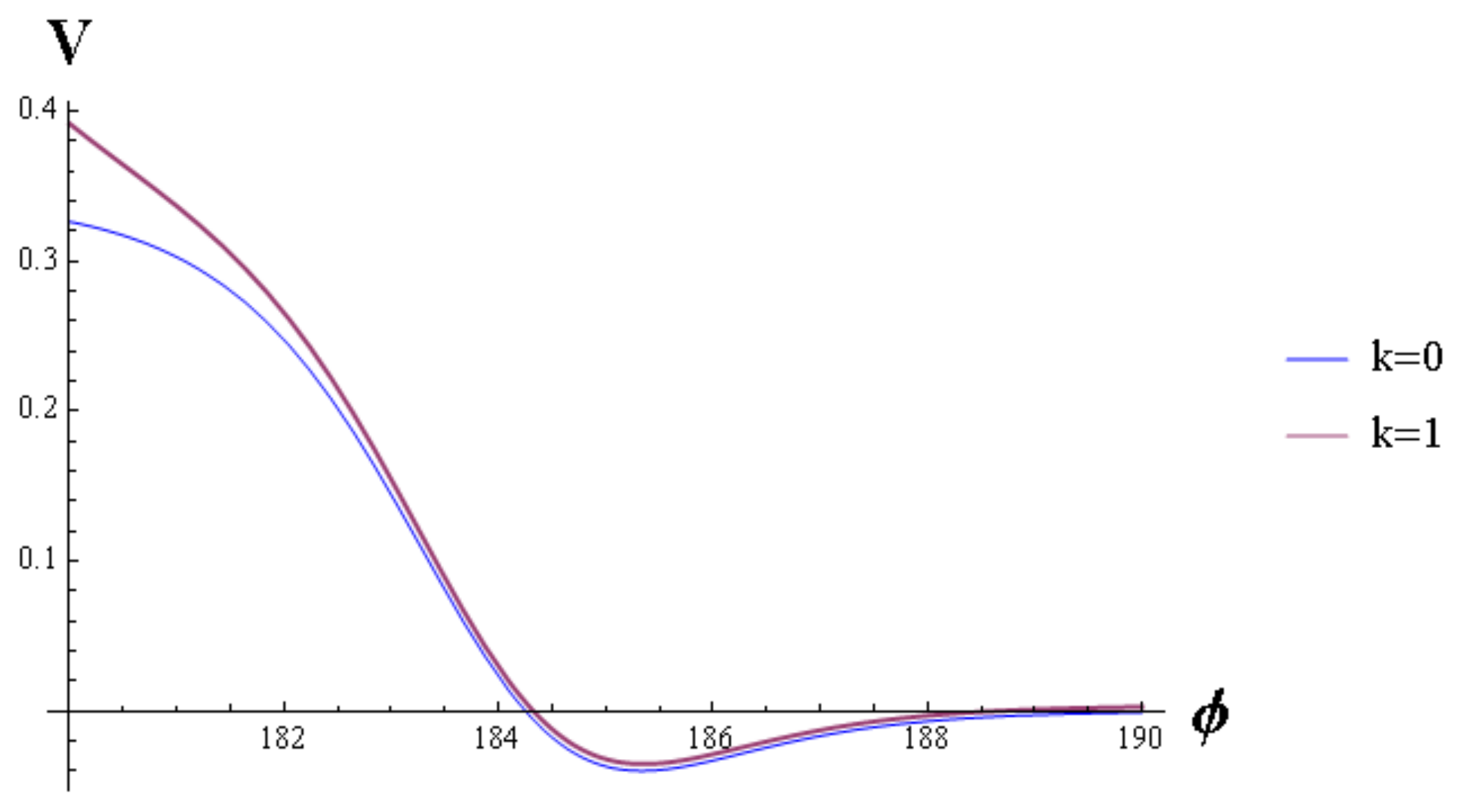In this time interval, there are $log\left(a\right(183)/a(0.45\left)\right)\approx 65$e-folds, see Figure 1 and Figure 2. We show also the potentials corresponding to this behavior in the analog FLRW model with a scalar field $\varphi$, for $k=0,1$, Figure 3.

3. Noncommutative Quantum Cosmology

Noncommutative field theories [8,9], have many remarkable properties as the UV/IR mixing. Some similar features were studied in the case of gravitational theories. There are many articles on the subject, in particular, our group participated with a number of gravity proposals in various versions [51,52,53]. In the context of some noncommutative gravity theories, one natural question was to carry out a canonical quantization analysis following ADM formalism [3]. However the situations turns out quite complicated. Instead of that in Ref. [10], we proposed to carry out the standard ADM formalism to get the WDW equation and at that level, to propose a non-commutative deformation of the WDW equation and look for solutions to this deformed equation.

The first example considered in this context was an anisotropic universe, the Kantowski-Sach model [10]. Further development (without pretending to be exhaustive) on this subject can be found in Refs. [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71]. In Misner’s parametrization the metric is written as

$$d{s}^2=-N^{2}d{t}^2+e^{2\sqrt{3}\beta }d{r}^2+e^{-2\sqrt{3}\beta }{e}^{-2\sqrt{3}\mathrm{\Omega }}(d{\theta }^2+{sin}^2\theta d{\phi }^2)$$

(16)

The quantum model of Kantowski-Sach cosmology is implemented through the quantization of its WDW equation, i.e., the hamiltonian constraint

$$e^{\sqrt{3}\beta +2\sqrt{3}\mathrm{\Omega }}\left[P_{\mathrm{\Omega }}^2-P_{\beta }^2+48e^{-2\sqrt{3}\mathrm{\Omega }}\right]\psi (\mathrm{\Omega },\beta )=0,$$

(17)

where $P_{\mathrm{\Omega }}=-i\frac{\partial }{\partial \mathrm{\Omega }}$ and $P_{\beta }=-i\frac{\partial }{\partial \beta }$. The physical observables in coordinate representation are the position operators $q_j$ and the conjugate momenta $p_k$, where $q_1=\mathrm{\Omega }$, $q_2=\beta$ and $p_1=P_{\mathrm{\Omega }}$, $p_2=P_{\beta }$. These operators satisfy the commutation relations

$$[q_j,p_k]=i{\delta }_{jk},[q_j,q_k]=0,[p_j,p_k]=0.$$

(18)

The noncommutative Wheeler-DeWitt equation is

$$e^{\sqrt{3}\beta +2\sqrt{3}\mathrm{\Omega }}\star \left\{-\frac{{\partial }^2}{\partial {\mathrm{\Omega }}^2}+\frac{{\partial }^2}{\partial {\beta }^2}+48e^{-2\sqrt{3}\mathrm{\Omega }}\right\}\star \psi (\mathrm{\Omega },\beta )=0,$$

(19)

where ⋆ is the Moyal product (for a complete review, see for instance, [72])

$$f(\mathrm{\Omega },\beta )\star g(\mathrm{\Omega },\beta )=f(\mathrm{\Omega },\beta )exp\left\{i\frac{\theta }{2}\left({\overleftarrow{\partial }}_{\mathrm{\Omega }}{\overrightarrow{\partial }}_{\beta }-{\overleftarrow{\partial }}_{\beta }{\overrightarrow{\partial }}_{\mathrm{\Omega }}\right)\right\}g(\mathrm{\Omega },\beta ),$$

(20)

for a constant noncommutativity parameter $\theta$.

Thus the Moyal deformed WDW equation is given by

$$\left\{-\frac{{\partial }^2}{\partial {\mathrm{\Omega }}^2}+\frac{{\partial }^2}{\partial {\beta }^2}+V(\mathrm{\Omega },\beta )\right\} \star \psi (\mathrm{\Omega },\beta )=0,$$

(21)

where $V(\mathrm{\Omega },\beta )=48e^{-2\sqrt{3}\mathrm{\Omega }}$ is the potential. Using the properties of the star product, Equation (20), we have $V(\mathrm{\Omega },\beta )\star \psi (\mathrm{\Omega },\beta )=V(\mathrm{\Omega }-\frac{1}{2}\theta P_{\beta },\beta -\frac{1}{2}\theta P_{\mathrm{\Omega }})\psi (\mathrm{\Omega },\beta )$, and it can be rewritten as

$$\left\{-\frac{{\partial }^2}{\partial {\mathrm{\Omega }}^2}+\frac{{\partial }^2}{\partial {\beta }^2}+48e^{-2\sqrt{3}\mathrm{\Omega }+\sqrt{3}\theta P_{\beta }}\right\}\psi (\mathrm{\Omega },\beta )=0.$$

(22)

A solution to Equation (22) can be found using the solution to the same equation with $\theta =0$, which is the usual WDW equation for the Kantowski-Sachs model in GR. This solution in GR is given by

$${\psi }_{\nu }^{\pm }(\mathrm{\Omega },\beta )=e^{\pm i\sqrt{3}\nu \beta }{K}_{i\nu }\{4exp\left[-\sqrt{3}\mathrm{\Omega }\right]\}.$$

(23)

Now assuming an ansatz for the deformed Equation (22) in the form

$${\psi }_{\nu }^{\pm }(\mathrm{\Omega },\beta )=e^{\pm i\sqrt{3}\nu \beta }\chi \left(\mathrm{\Omega }\right).$$

(24)

Taking into account the translation $e^{\sqrt{3}\theta P_{\beta }}\psi (\mathrm{\Omega },\beta )=\psi (\mathrm{\Omega },\beta -i\sqrt{3}\theta )$, it is possible to find that the function $\chi \left(\mathrm{\Omega }\right)$ satisfies the modified Bessel equation and Equation (22). Thus, it was shown in [10] that Equation (22) has a solution given by

$${\psi }_{\nu }^{\pm }(\mathrm{\Omega },\beta )=e^{\pm i\sqrt{3}\nu \beta }{K}_{i\nu }\left\{4exp\left[-\sqrt{3}\left(\mathrm{\Omega }\mp \frac{\sqrt{3}}{2}\nu \theta \right)\right]\right\}.$$

(25)

Equation (22) represents a noncommutative deformation of the ordinary WDW equation for the Kantowski-Sachs cosmological model. This implies an additional correction to the ordinary WDW equation due to an assumed noncommutative structure of the minisuperspace. This noncommutativity is regarded as an indirect consequence of the noncommutive gravity in spacetime, which seems to be a better approach to study microscopic properties of gravity. In Ref. 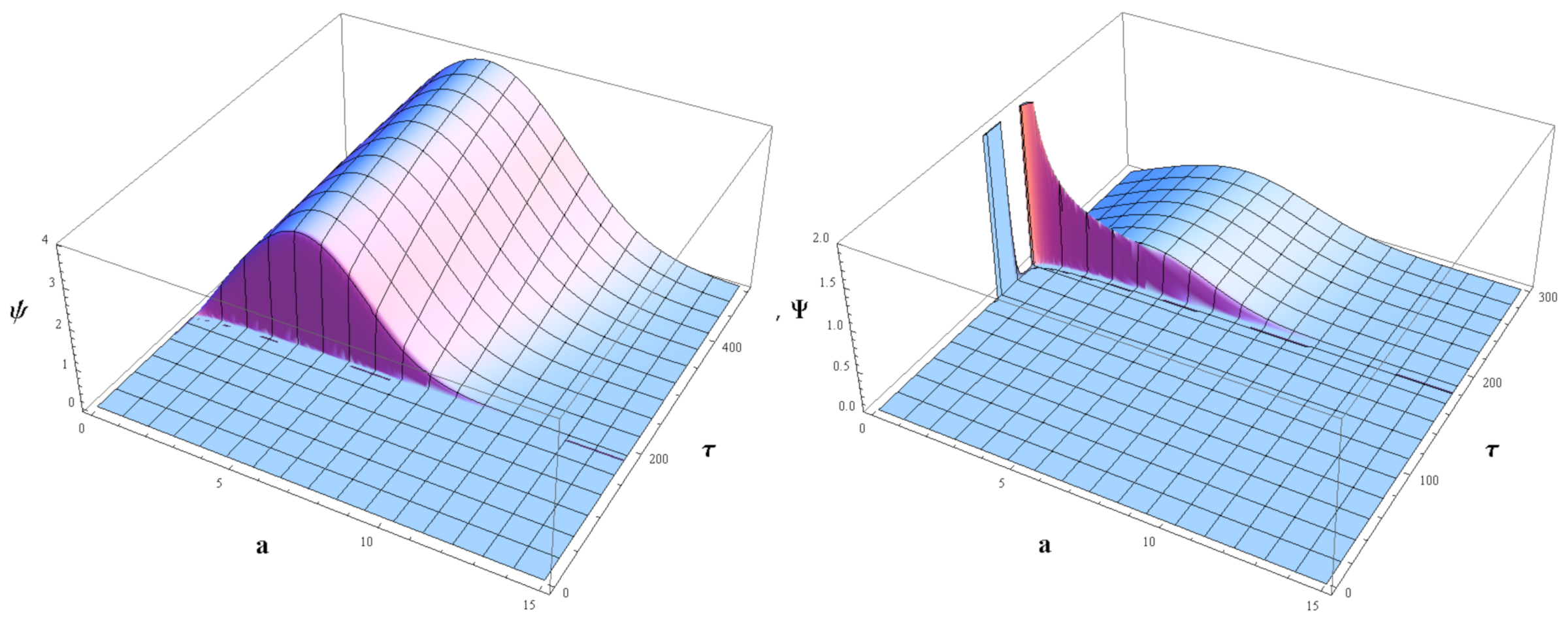[10] it was plotted the probability, constructed from the wave function solution (25), depending on coordinates $\mathrm{\Omega }$ and $\beta$ for various values of $\theta$, including the case of GR with $\theta =0$. In GR the probability obtained from the solution (weighted with a Gaussian wave packet) has just one peak near $\mathrm{\Omega }=0$ and $\beta =0$ which indicates where the universe is more probable to be placed. For nonvanishing theta $\theta \ne 0$ it was found a different behavior than that of GR. In this last case there was a big peak together with other many different smaller peaks, which were interpreted as other (baby) additional universes where the universe may to stay. Thus a bold consequence of the noncommutative minisuperspace is the emergence of many other universes in which the universe can carry out vacuum transitions by tunneling.

4. GUP’s in Quantum Cosmology

In this section we review an application of Generalized Uncertainty Principles (GUP) to quantum cosmology [19,61,62,64,66]. In order to be concrete in [19] it was considered the Kantowski-Sachs model, an homogeneous and anisotropic cosmological model in the minisuperspace. The GUP involves a modification of the Heisenberg uncertainty relation at very high energies (near the Planck scale), a behavior expected for the very early universe. This implies a modification of the Heisenberg algebra of commutators, by terms with powers of the momentum. As it is shown in [19], this implies a deformation of the Wheeler-DeWitt equation. It is worth mentioning that the application of the GUP in this context involves a minimal uncertainty of the quantum dynamical variables in the minisuperspace. This UV modification of the Heisenberg algebra is for the phase space minisuperspace variables, and not properly for spacetime variables. However, very interesting consequences of this hypothesis arise, such as black holes without singularity as we will review in the next section.

The WDW Equation (17) has four quantum dynamical variables: the operators $\mathrm{\Omega }$ and $\beta$, and their conjugate momenta $P_{\mathrm{\Omega }}$ and $P_{\beta }$, which satisfy the commutation relations (18).

Now, if we consider the commutation relation

$$[q_j,p_k]=i{\delta }_{jk}[1+{\gamma }^2{p}_{\ell }{p}_{\ell }],$$

(26)

where $q_1=\mathrm{\Omega }$, $q_2=\beta$, $p_1=P_{\mathrm{\Omega }}$ and $p_2=P_{\beta }$, and $\gamma$ is a parameter with units of the inverse of the momentum.

The procedure involves to perform a suitable change of variables

$$q_j=(1+{\gamma }^2{p}_{\ell }{p}_{\ell })q_j^{\prime },$$

(27)

where $q_j^{\prime }=i\frac{\partial }{\partial p_j}$ such that $[q_j^{\prime },p_k]=i{\delta }_{jk}$. This change does not respect entirely the Heisenberg algebra, but a noncommutative extension since

$$[q_j,q_k]=2i{\gamma }^2(1+{\gamma }^2{p}_{\ell }{p}_{\ell })(p_j{q}_k^{\prime }-p_k{q}_j^{\prime }).$$

(28)

In particular, for the KS model we have that the potential $V(\mathrm{\Omega },\beta )$ will be modified within the deformed algebra. An approximation to order ${\gamma }^2$ for the potential V can be written as

$$V\approx -48e^{-2\sqrt{3}(1-4{\gamma }^2){\mathrm{\Omega }}^{\prime }}{e}^{-2\sqrt{3}{\gamma }^2{\mathrm{\Omega }}^{\prime }(-P_{\mathrm{\Omega }}^2+P_{\beta }^2)}{e}^{12i{\gamma }^2{\mathrm{\Omega }}^{\prime }{P}_{\mathrm{\Omega }}}.$$

(29)

Assume a representation $P_{\mathrm{\Omega }}=-i\frac{\partial }{\partial {\mathrm{\Omega }}^{\prime }}$ and $P_{\beta }=-i\frac{\partial }{\partial {\beta }^{\prime }}$, it is easy to see that

$$e^{12i{\gamma }^2{\mathrm{\Omega }}^{\prime }{P}_{\mathrm{\Omega }}}\psi ({\mathrm{\Omega }}^{\prime },\beta )=\psi (e^{12{\gamma }^2}{\mathrm{\Omega }}^{\prime },\beta ).$$

(30)

Thus under the same ansatz as in the noncommutative case [10]

$$\psi (e^{12{\gamma }^2}{\mathrm{\Omega }}^{\prime },{\beta }^{\prime })=e^{\sqrt{3}\nu {\beta }^{\prime }}\chi \left({\mathrm{\Omega }}^{\prime }\right),$$

(31)

the WDW Equation (17) turns out to be

$$\left(\frac{d^2}{d{\mathrm{\Omega }}^{\prime 2}}+V_{\gamma ,\nu }+{\gamma }^2\tilde{V}\right)\chi \left({\mathrm{\Omega }}^{\prime }\right)=0,$$

(32)

where

$$V_{\gamma ,\nu }=3{\nu }^2+48e^{-2\sqrt{3}(1-4{\gamma }^2){\mathrm{\Omega }}^{\prime }}$$

(33)

and

$$\tilde{V}=-4608\sqrt{3}{\mathrm{\Omega }}^{\prime }{e}^{-4\sqrt{3}(1-4{\gamma }^2){\mathrm{\Omega }}^{\prime }}.$$

(34)

The potential $V_{\gamma ,\nu }$ is the modified potential of the ordinary Kantowski-Sach model. Moreover, $\tilde{V}$ is the first correction due to the modified uncertainty relation (26). The relevant contribution of the later potential is concentrated about the value of ${\mathrm{\Omega }}^{\prime }$ given by ${\mathrm{\Omega }}^{\prime }=\frac{1}{4\sqrt{3}(1-4{\gamma }^2)}$.

It can be observed that the potential $V_{\gamma ,\nu }$ dominates over $\tilde{V}$ for values of $\gamma$ satisfying $\gamma <<\frac{1}{2}\sqrt{\frac{e^{3/2}}{24+e^{3/2}}}\approx 0.198$. For values $\gamma \ge \frac{1}{2}\sqrt{\frac{e^{3/2}}{24+e^{3/2}}}$ the potential $\tilde{V}$ dominates over $V_{\gamma ,\nu }$ and it produces a well. One can see that this well has a local minimum at

$${\mathrm{\Omega }}_{\min }^{\prime }=\frac{\sqrt{3}\left[1-2W(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})\right]}{12(1-4{\gamma }^2)},$$

(35)

where $W\left(z\right)$ is the Lambert function satisfying the equation $z=W{e}^W$. This function has real values for $\gamma >\frac{1}{2}\sqrt{\frac{e^{3/2}}{24+e^{3/2}}}$. In Figure 4 we show how the potential of Equation (32), $V_{\gamma ,\nu }+{\gamma }^2\tilde{V}$, changes under the variation of the Barbero-Immirzi parameter $\gamma$.

Thus, under a variables change $y\equiv {\mathrm{\Omega }}^{\prime }-{\mathrm{\Omega }}_{\min }^{\prime }$, Equation (32) turns out into a quantum mechanical harmonic oscillator equation

$$\left[-\frac{d^2}{d{y}^2}+{\omega }^2{y}^2\right]\chi \left(y\right)=E\chi \left(y\right),$$

(36)

where $\omega$ is the frequency of the oscillator and E is the energy which can be written as

$${\omega }^2=3{(1-4{\gamma }^2)}^3\frac{\left[W(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})+1\right]}{{\gamma }^2{W}^2(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})},$$

(37)

$$E=-\frac{3}{2}\left\{\nu -\frac{1-4{\gamma }^2}{12{\gamma }^{2}W(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})}-\frac{1-4{\gamma }^2}{24{\gamma }^2{W}^2(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})}\right\}.$$

(38)

The requirement that $E>0$ to obtain a bounded state from below implies that

$$\left|\nu \right|<-\frac{\sqrt{(1-4{\gamma }^2)[12W(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})+6]}}{12\gamma W(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})}.$$

(39)

Thus, the condition of the existence for real values of $\nu$ implies that $\gamma \ge \frac{1}{2}\sqrt{\frac{e}{12+e}}$. Then the quantum spectrum of the harmonic oscillator is given by

$$E=\omega \left(n+\frac{1}{2}\right),$$

(40)

where n is a natural number. As a consequence of this fact, the parameter $\nu$ is quantized in the form

$$\nu =\frac{\sqrt{1-4{\gamma }^2}}{2\sqrt{6}}{\left\{\frac{2W(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})+1}{{\gamma }^2{W}^2(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})}+8\sqrt{3}(2n+1)\frac{\sqrt{(1-4{\gamma }^2)\left[W(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})+1\right]}}{\gamma W(-\frac{\sqrt{e}(1-4{\gamma }^2)}{96{\gamma }^2})}\right\}}^{1/2}.$$

(41)

In this derivation it was assumed a quadratic degree of approximation in an expansion of $\gamma$. It is possible to obtain some higher order terms, the subsequent terms in the expansion which turn the harmonic oscillator into an anharmonic oscillator. This systems can be solved in perturbation theory, considering the nonlinear terms as a perturbation. Thus it is possible to find perturbatively the first correction to the energy levels and the corresponding Hilbert space.

5. Deformed Dynamics and the Interior of Black Holes

In this section we comment on other application of GUP to gravitational systems. We review the case of the application of GUP to the study of the dynamics in the interior of a Schwarzschild black hole (SBH). SBH is parametrized by the Schwarzschild coordinates $(t,r,\theta ,\varphi )$. The interior of a SBH is described by a Kantowski-Sach metric (see Equation (16)) defined on a spacetime with topology $\mathbb{R}\times {\mathbf{S}}^2$, which has an infinite volume since the noncompact nature of it. However, for a fiducial finite interval $L_0$ in $\mathbb{R}$, this spacetime has finite volume. We can define local coordinates in the four dimensional spacetime ${\mathbb{R}}^2\times {\mathbf{S}}^2$ to be $(T,x,\theta ,\varphi )$.

The idea of [20] consists to apply GUP to the hamiltonian classical dynamics described by the Ashtekar-Barbero hamiltonian $H_{AB}$, and deform the canonical algebra in terms of the GUP parameter $\gamma$. First, we described the classical hamiltonian dynamics. The dynamical variables $(b,p_b,c,p_c)$ are smooth functions depending only on the variable T or t. After gauge fixing the hamiltonian it reads

$$H_{AB}=-\frac{1}{2G\gamma }\left[(b^2+{\gamma }^2)\frac{p_b}{b}+2c{p}_c\right].$$

(42)

The canonical algebra is given by

$$\{b,p_b\}=G\gamma ,\{c,p_c\}=2G\gamma .$$

(43)

The equations of motion of $H_{AB}$ are

$$\frac{db}{dT}=\{b,H_{AB}\}=-\frac{1}{2}\left(b+\frac{{\gamma }^2}{b}\right),$$

(44)

$$\frac{d{p}_b}{dT}=\{p_b,H_{AB}\}=\frac{p_b}{2}\left(1-\frac{{\gamma }^2}{b^2}\right),$$

(45)

$$\frac{dc}{dT}=\{c,H_{AB}\}=-2c,$$

(46)

$$\frac{d{p}_c}{dT}=\{p_c,H_{AB}\}=2p_c.$$

(47)

In the Schwarzschild time t the solutions take the form

$$b\left(t\right)=\pm \gamma \sqrt{\frac{2GM}{t}-1},$$

(48)

$$p_b\left(t\right)=\ell L_{0}t\sqrt{\frac{2GM}{t}-1},$$

(49)

$$c\left(t\right)=\mp \frac{\gamma GM\ell L_0}{t^2},$$

(50)

$$p_c\left(t\right)=t^2,$$

(51)

where ℓ satisfies the equation $p_b^2\left(t\right)=\ell \left(\frac{2GM}{t}-1\right)L_0^2{t}^2$. Here $p_c$ can be interpreted as the square of the radius of the infalling 2-spheres and consequently is zero at $t=0$. This interpretation results from the fact that the Kretschmann invariant $K=R_{abcd}{R}^{abcd}$ is proportional to $\frac{1}{p_c^3}$.

Now, it is possible to deform the classical algebra (43) with the GUP, and find a modified dynamics. This can be achieved imposing minimal uncertainty in $p_b$ and $p_c$. Thus the modified algebra according to GUP is

$$\{\overline{b},p_b\}=1,\{\overline{c},p_c\}=1$$

(52)

such that

$${\{b,p_b\}}_{\overline{q},p}=1+{\beta }_b{b}^2,{\{c,p_c\}}_{\overline{q},p}=1+{\beta }_c{c}^2,$$

(53)

where ${\beta }_b$ and ${\beta }_c$ are suitable parameters. The modified algebra with a minimal uncertainty in $p_b$ and $p_c$ is

$$[b,p_b]=iG\gamma (1+{\beta }_b{b}^2),[c,p_c]=i2G\gamma (1+{\beta }_c{c}^2).$$

(54)

Equivalently this yields

$$\Delta b\Delta p_b\ge \frac{G\gamma }{2}\left[1+{\beta }_b{(\Delta b)}^2\right],$$

(55)

$$\Delta c\Delta p_c\ge G\gamma \left[1+{\beta }_c{(\Delta c)}^2\right].$$

(56)

The GUP modified equations of motion are

$$\frac{db}{dT}=\{b,H_{AB}\}=-\frac{1}{2}\left(b+\frac{{\gamma }^2}{b}\right)(1+{\beta }_b{b}^2),$$

(57)

$$\frac{d{p}_b}{dT}=\{p_b,H_{AB}\}=\frac{p_b}{2}\left(1-\frac{{\gamma }^2}{b^2}\right)(1+{\beta }_b{b}^2),$$

(58)

$$\frac{dc}{dT}=\{c,H_{AB}\}=-2c(1+{\beta }_c{c}^2),$$

(59)

$$\frac{d{p}_c}{dT}=\{p_c,H_{AB}\}=2p_c(1+{\beta }_c{c}^2).$$

(60)

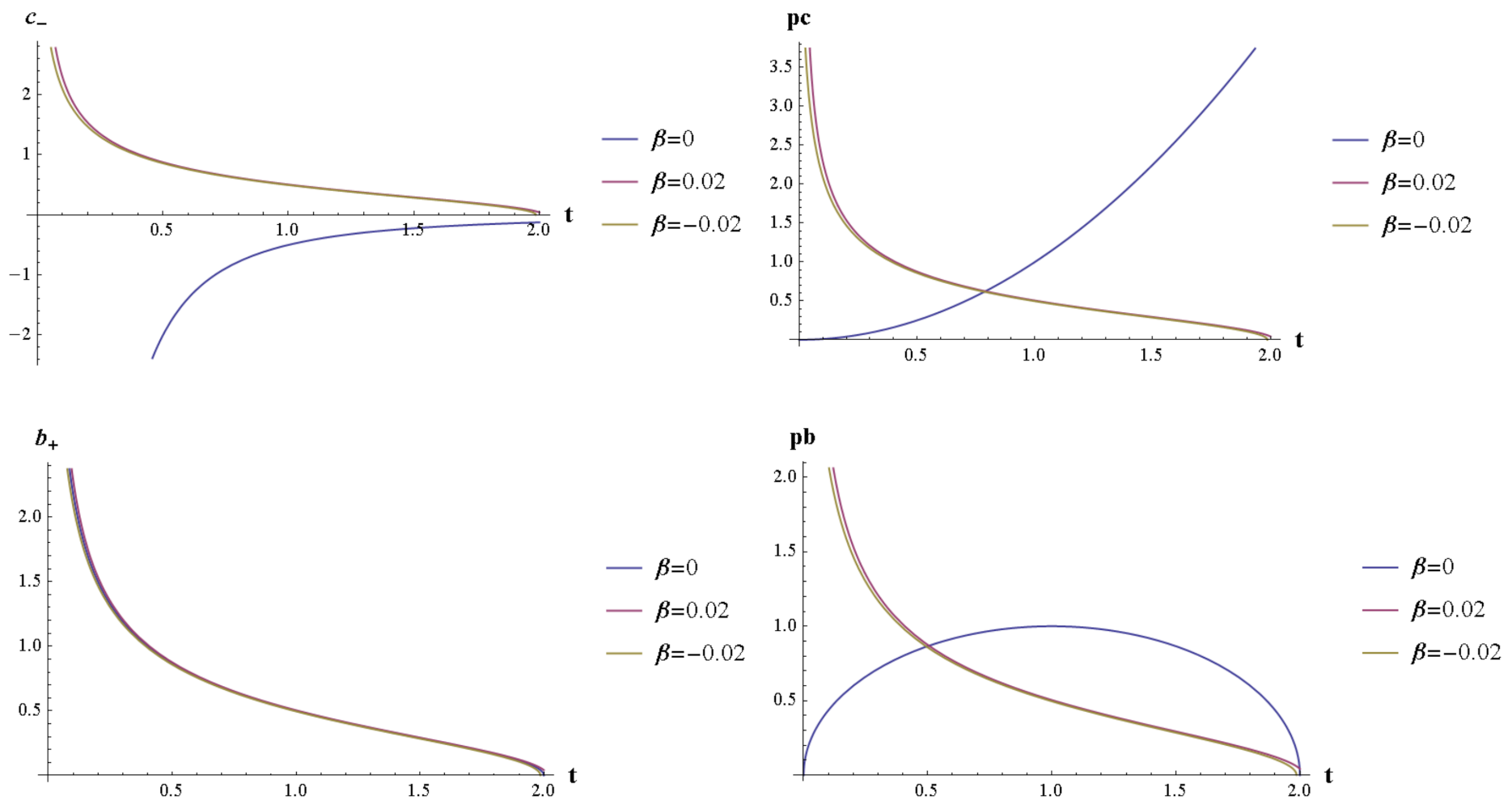
In the Schwarzschild time t the solutions take the form

$$b\left(t\right)=\pm \gamma \frac{\sqrt{2GM{t}^{{\beta }_b{\gamma }^2}-t{\left(2{\gamma }^{2}GM\right)}^{{\beta }_b{\gamma }^2}}}{\sqrt{t{\left(2{\gamma }^{2}GM\right)}^{{\beta }_b{\gamma }^2}-2{\beta }_b{\gamma }^{2}GM{t}^{{\beta }_b{\gamma }^2}}},$$

(61)

$$p_b\left(t\right)=\frac{{\ell }_c}{\sqrt{-{\beta }_c}}{t}^{-{\beta }_b{\gamma }^2}\sqrt{\left[2GM{t}^{{\beta }_b{\gamma }^2}-t{\left(2{\gamma }^{2}GM\right)}^{{\beta }_b{\gamma }^2}\right]\left[t{\left(2{\gamma }^{2}GM\right)}^{{\beta }_b{\gamma }^2}-2{\beta }_b{\gamma }^{2}GM{t}^{{\beta }_b{\gamma }^2}\right]},$$

(62)

$$c\left(t\right)=\mp \frac{{\ell }_c}{\sqrt{-{\beta }_c}}\frac{\gamma GM}{\sqrt{t^4+{\ell }_c^2{\gamma }^2{G}^2{M}^2}},$$

(63)

$$p_c\left(t\right)=\sqrt{t^4+{\ell }_c^2{\gamma }^2{G}^2{M}^2},$$

(64)

where it was introduced the fundamental physical length ${\ell }_c\equiv -{\beta }_c{L}_0$. This can be considered as a prescription to cure the dependence on the fiducial length $L_0$. Moreover, the mentioned interpretation of $p_c\left(t\right)$, as the 2-sphere inside the black hole, leads from the last Equation (64) to the existence of a minimum value for $p_c$ and consequently the resolution of the black hole singularity at $t=0$. See Figure 5.