Penrose Process: Its Variants and Astrophysical Applications
Abstract
:1. Introduction
2. Kerr Black Holes and the Penrose Process
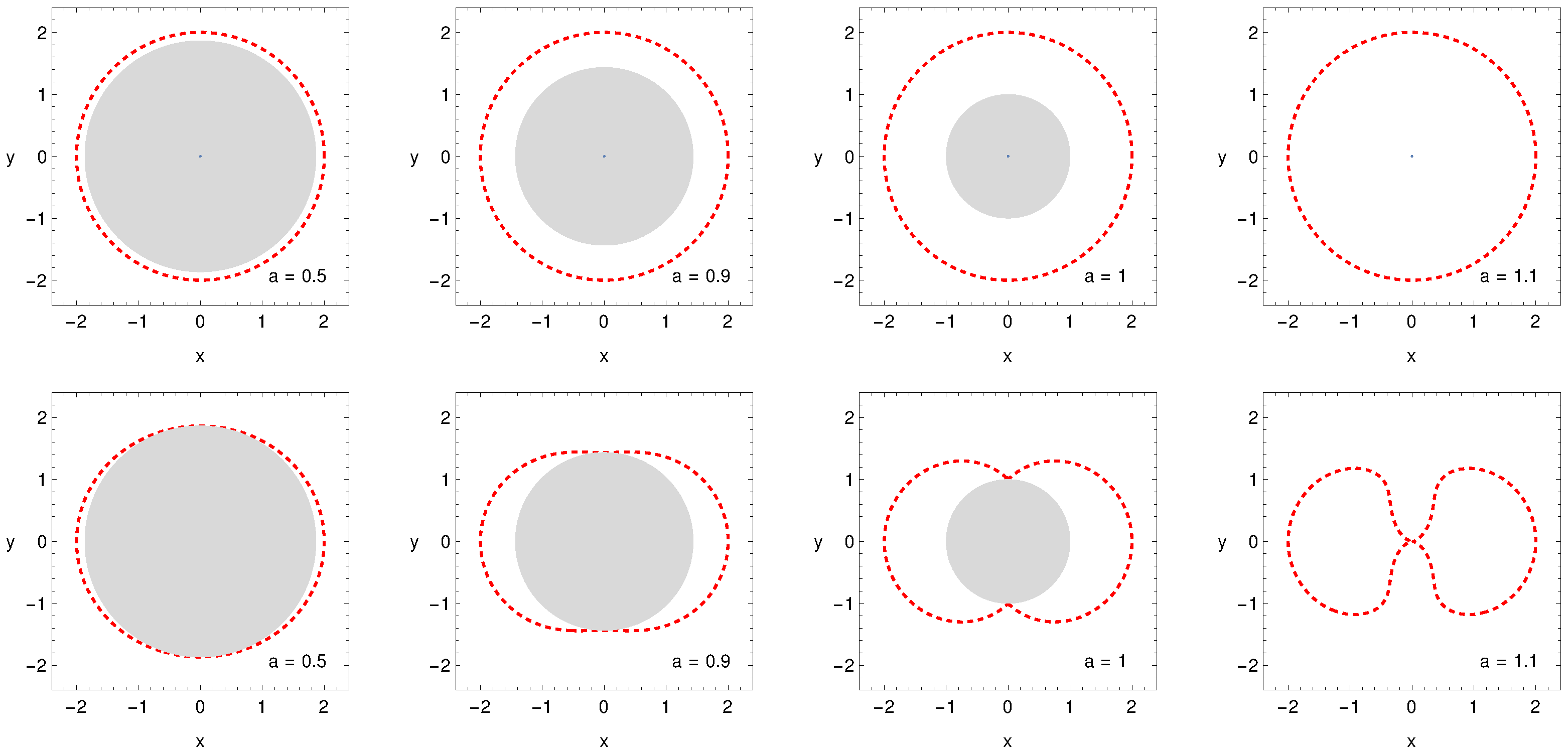
2.1. Kerr Geometry and Ergosphere
2.2. Test Particle Motion and Locally Non-Rotating Frames
2.3. The Penrose Process
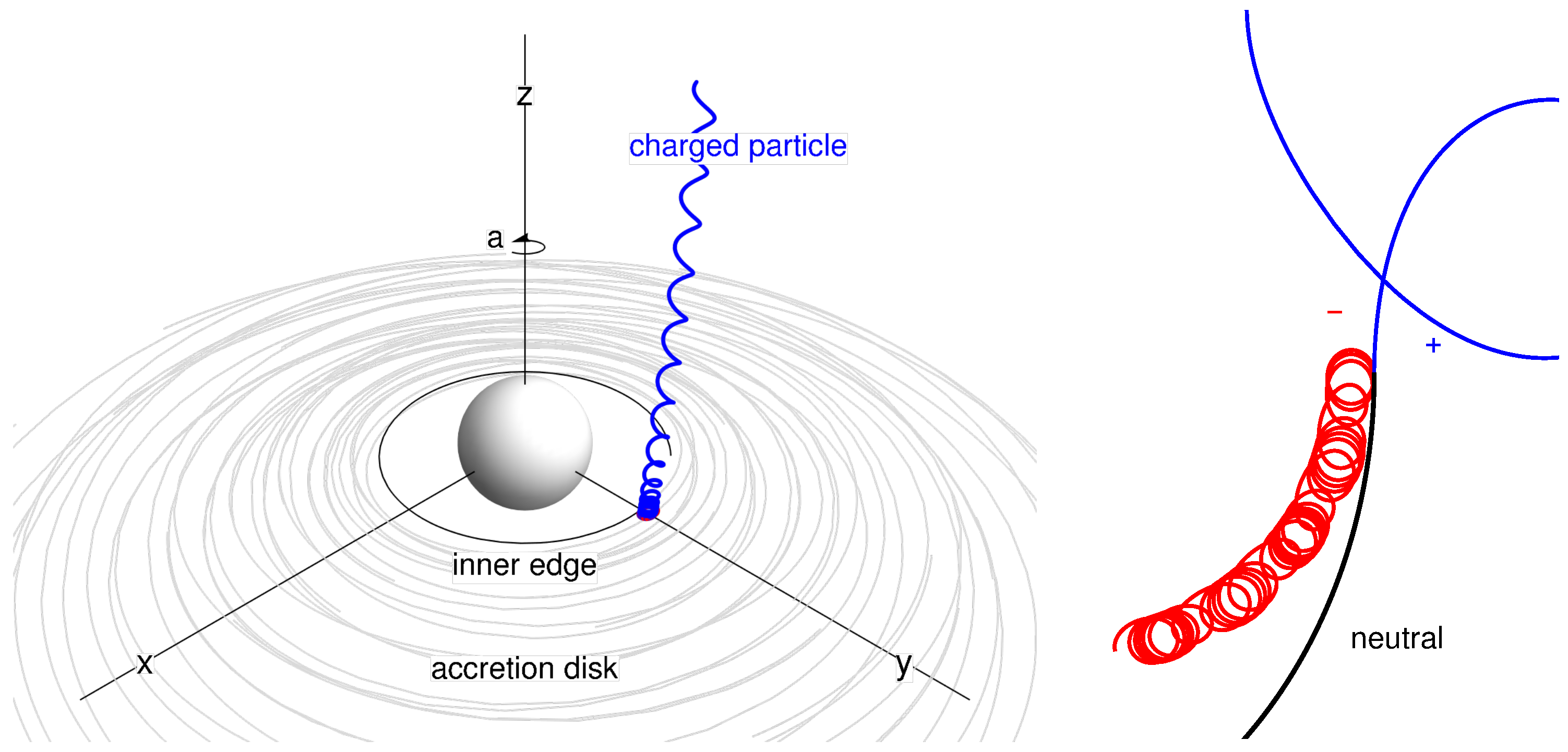
3. Magnetized Kerr Black Holes and Magnetic Penrose Process
3.1. The Role of Magnetic Fields in Black Hole Physics
3.2. Asymptotically Uniform Magnetic Field as Basic Approximation
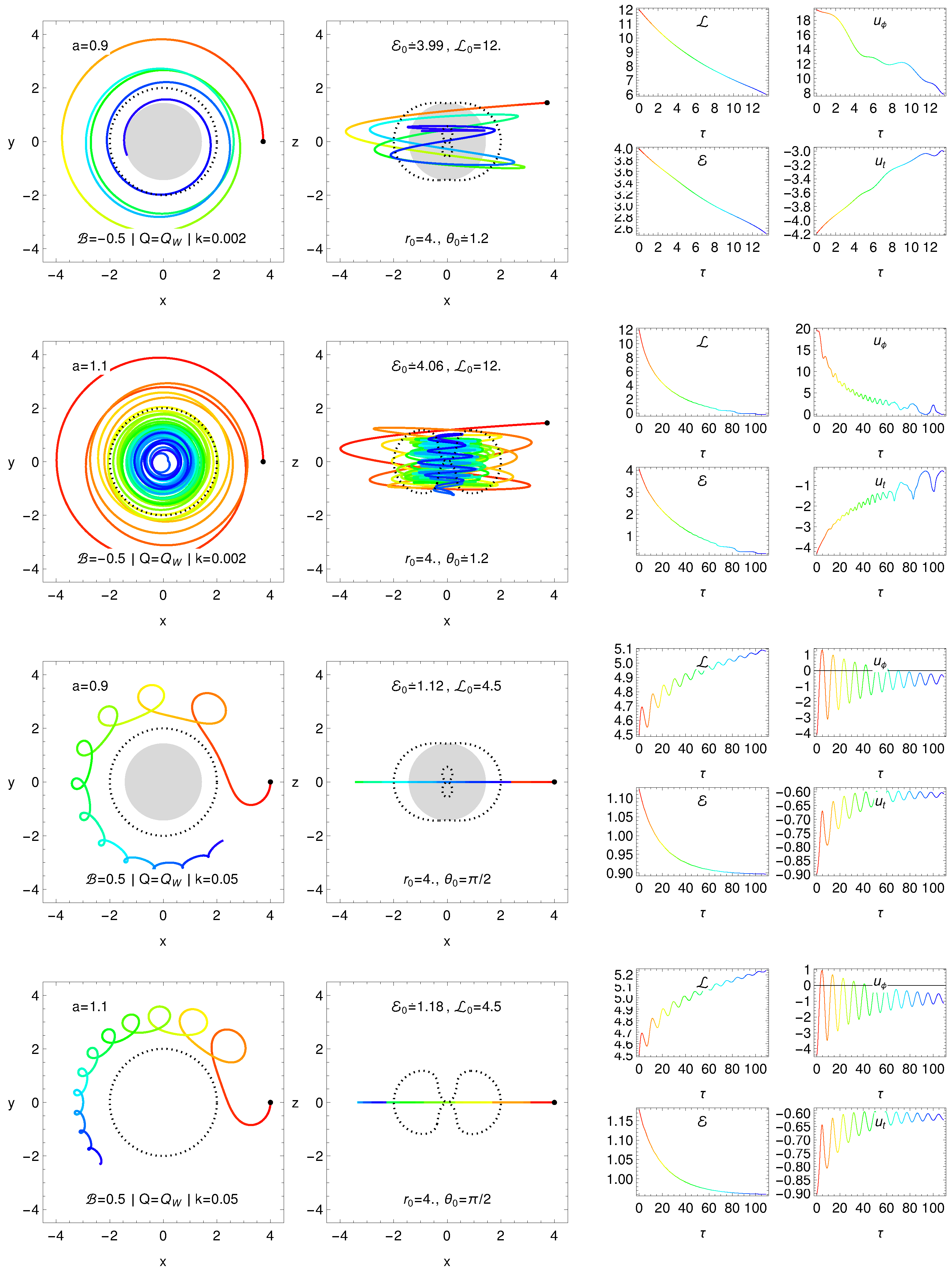
3.3. Motion of Charged Test Particles
3.3.1. Hamiltonian Formalism and Effective Potential of the Motion
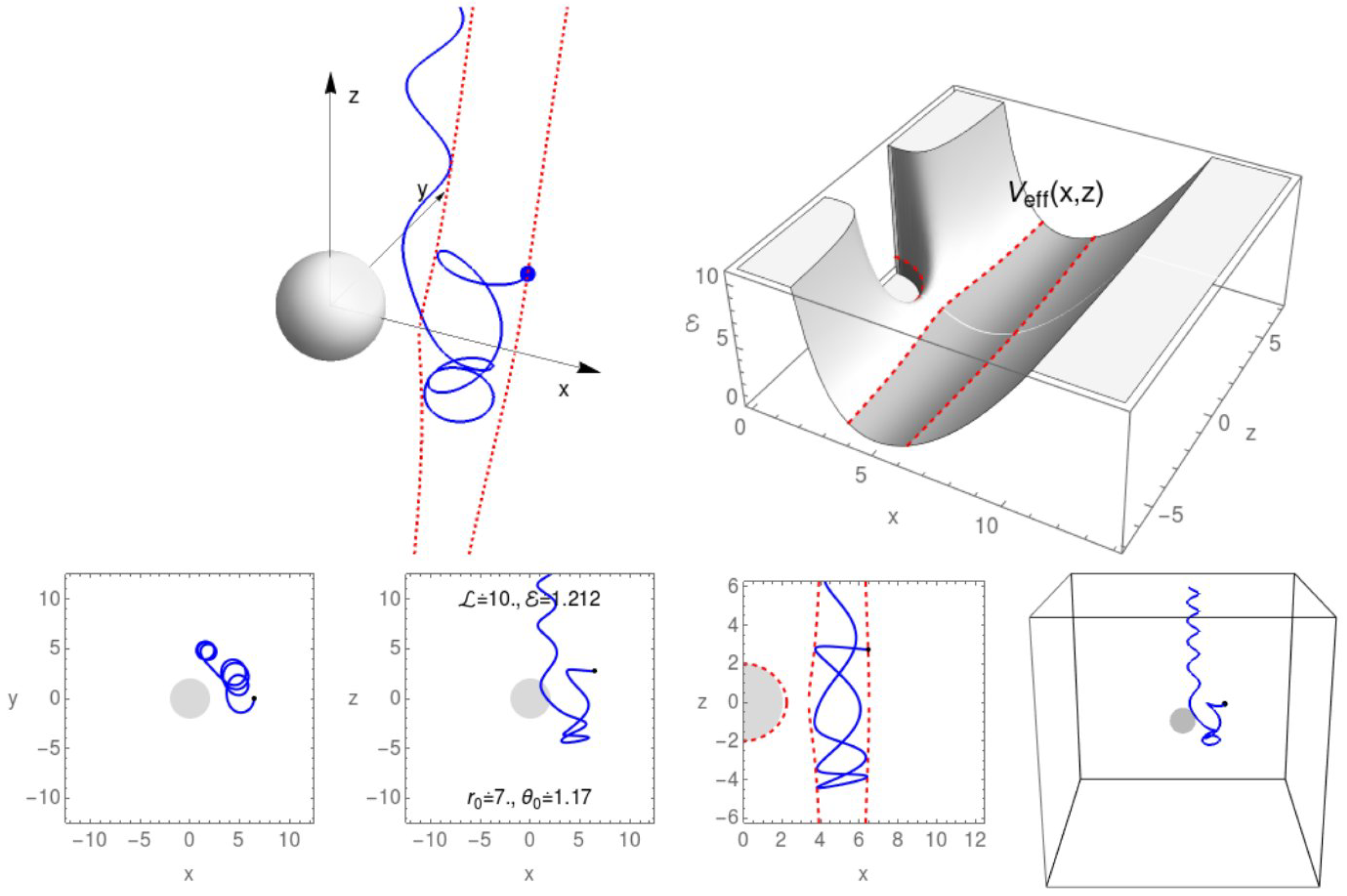
3.3.2. Chaotic Scattering
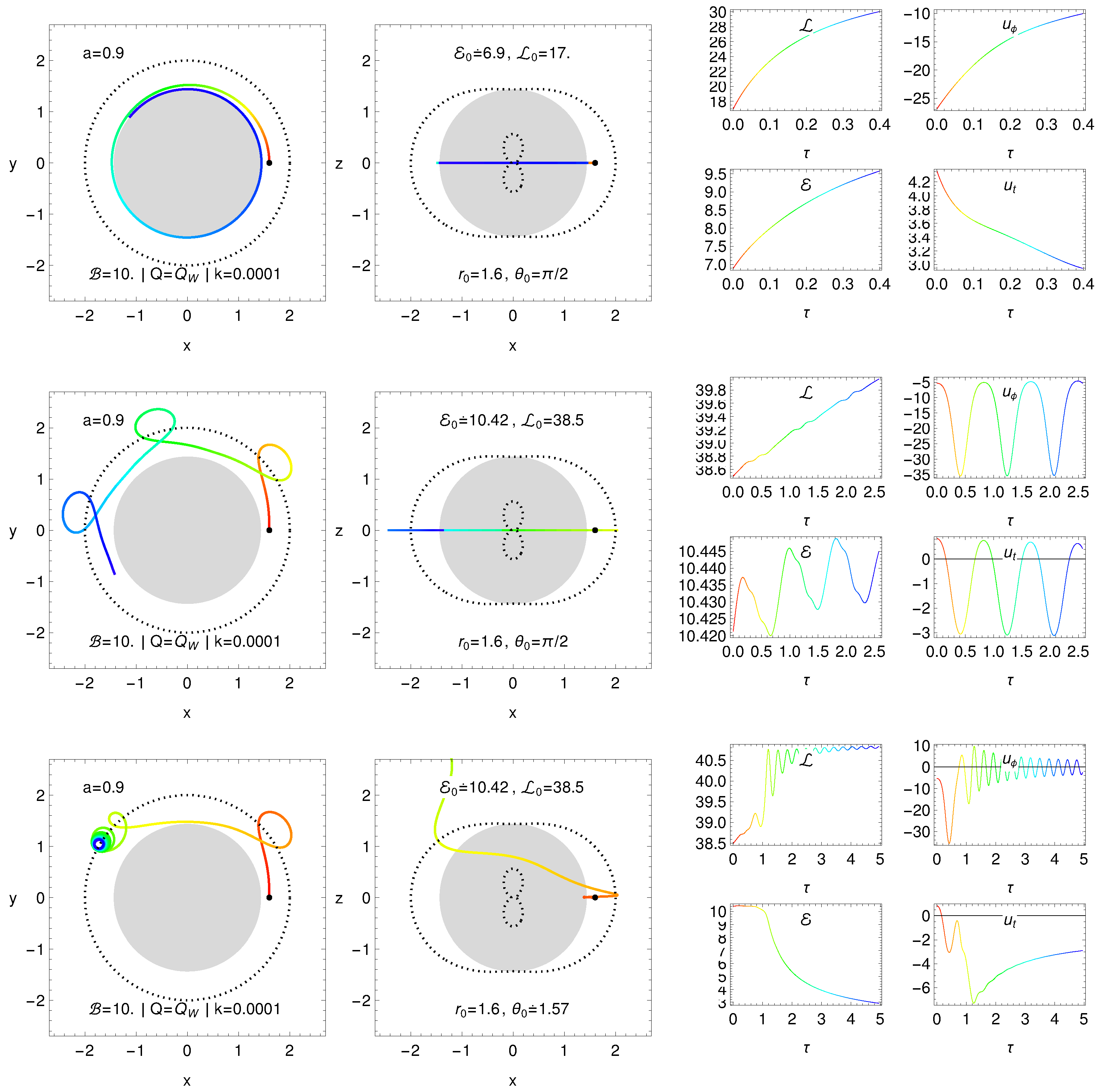
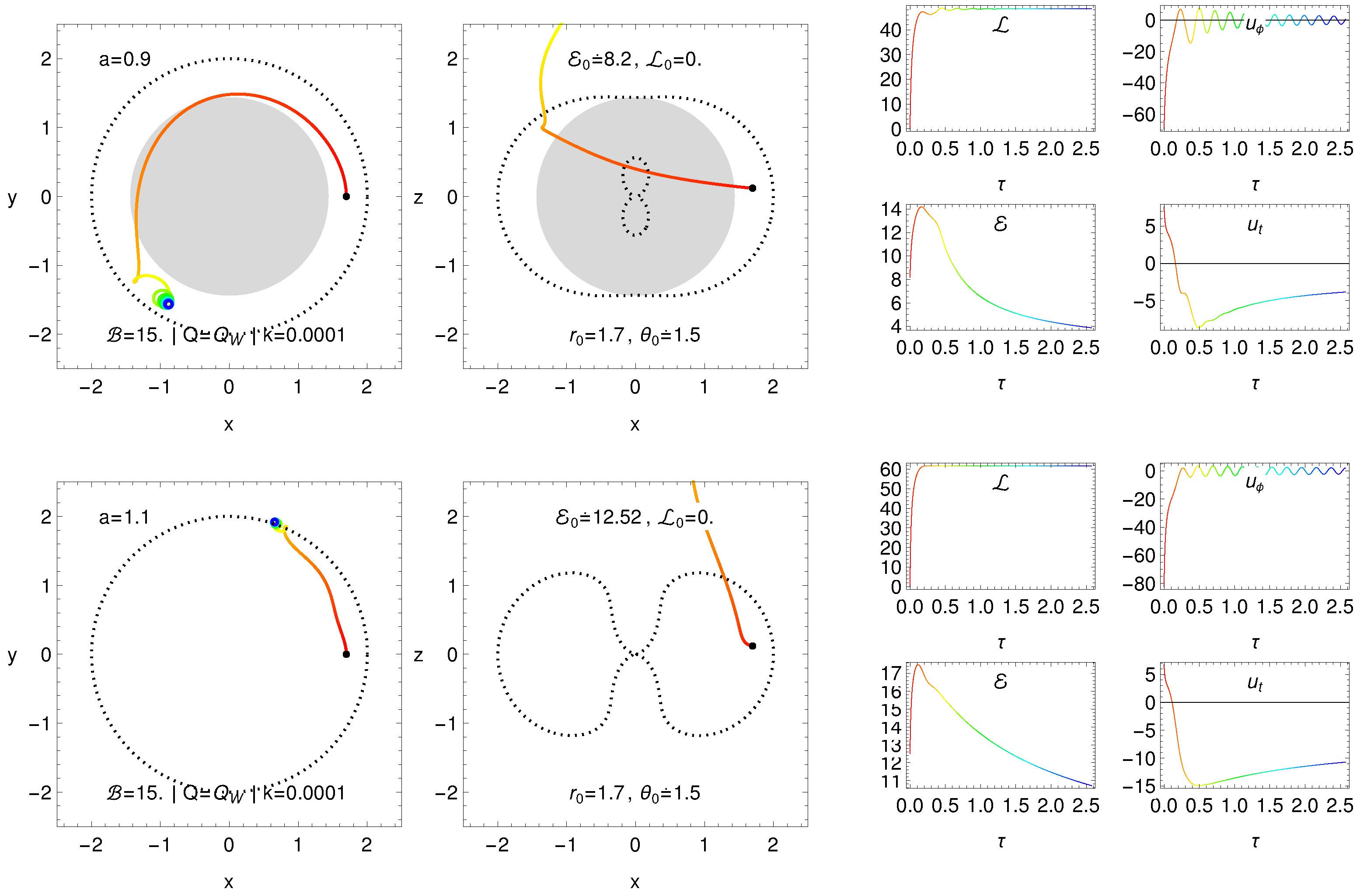
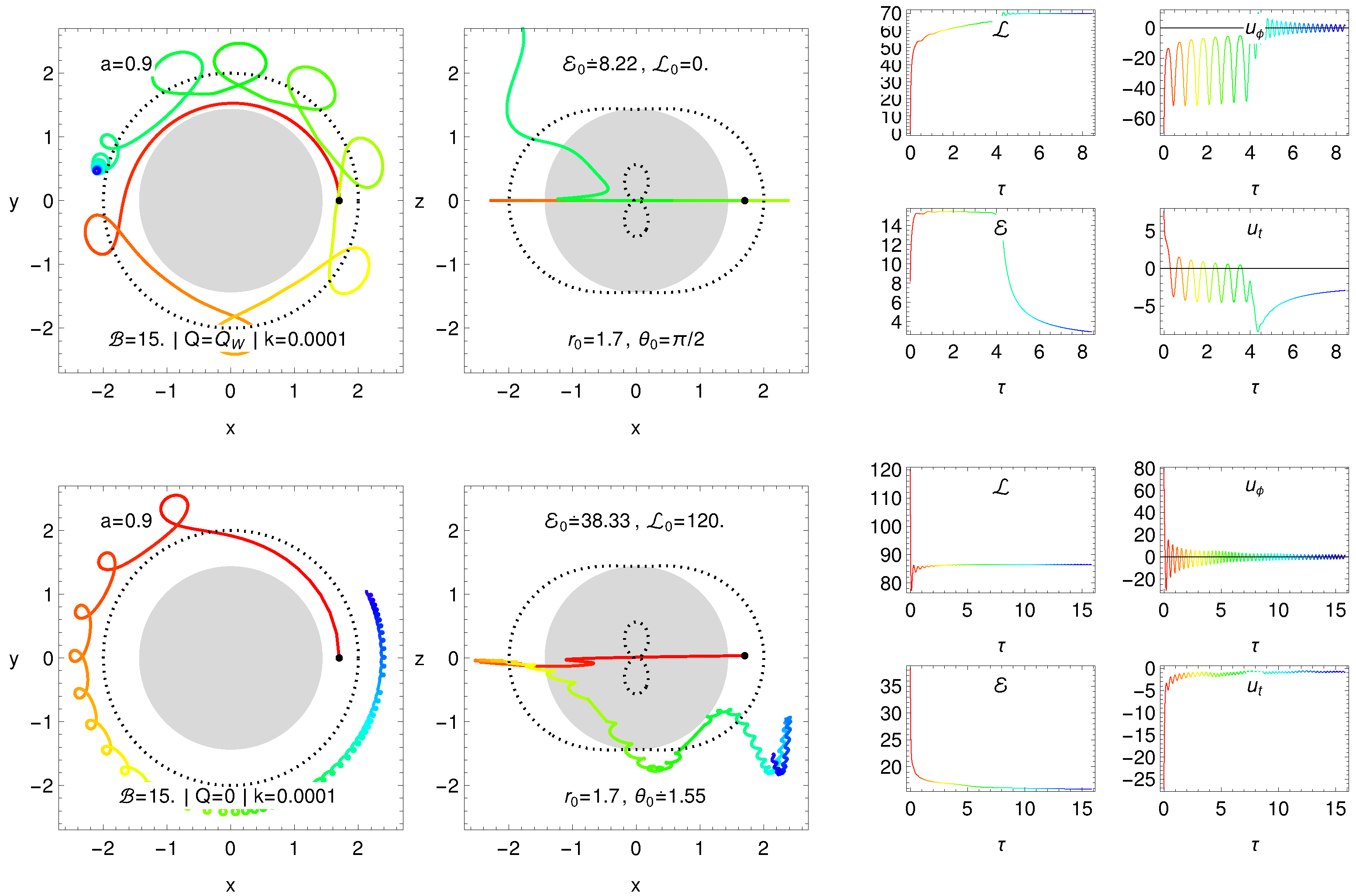
3.4. Magnetic Penrose Process and Creation of Jets
3.4.1. Moderately Efficient Regime of Mpp
3.4.2. Extremely Efficient Regime of Mpp
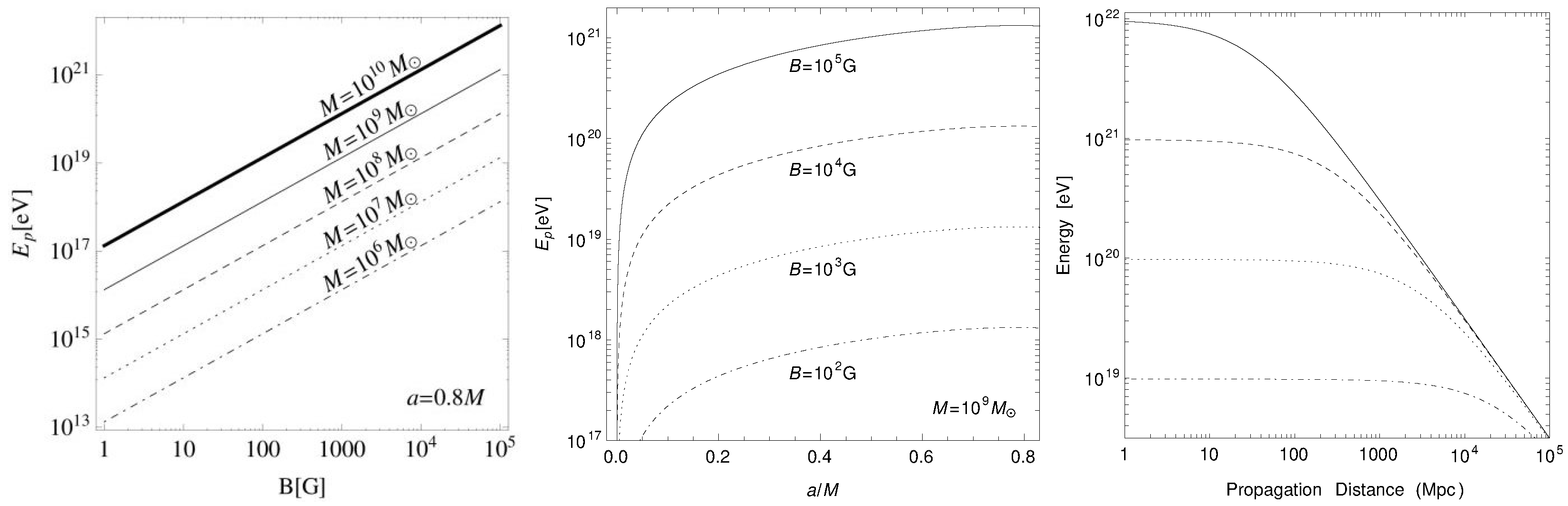
3.4.3. Ultra-High Energy Cosmic Rays as Products of Mpp in the Extreme Regime
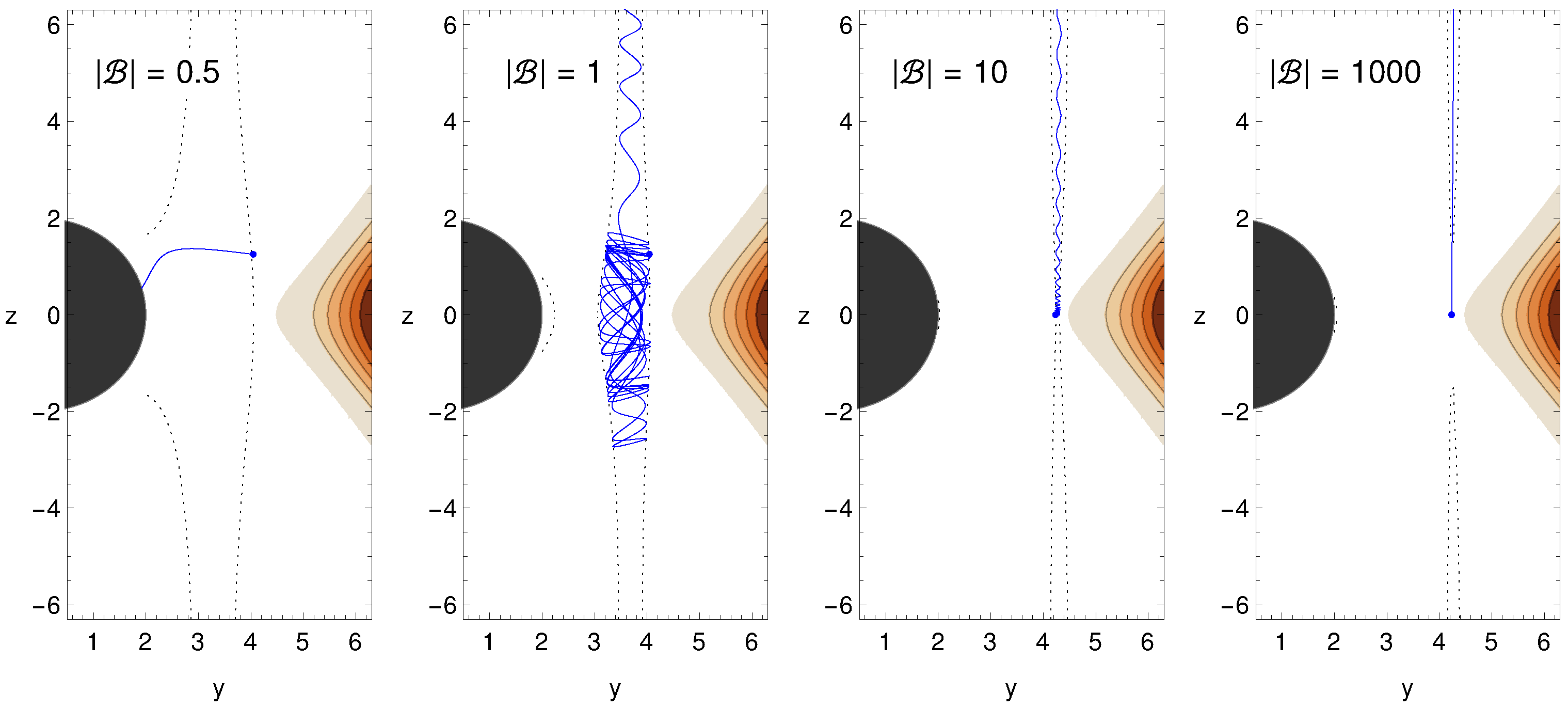
3.4.4. Synchrotron Radiation of Accelerated Charged Particles
4. Electric Penrose Process
4.1. Charged Particles around Weakly Charged Schwarzschild Black Hole
4.2. Energy of Ionized Particles
5. Radiative Penrose Process
5.1. Landau–Lifshitz Equations of Motion under Radiative Force
5.2. Negative Energy Photons inside the Ergosphere and Energy Gain by Radiating Particle
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Penrose, R. Gravitational Collapse: The Role of General Relativity. Nuovo C. Riv. Ser. 1969, 1, 252. [Google Scholar]
- Tchekhovskoy, A. Launching of Active Galactic Nuclei Jets. In Astrophysics and Space Science Library; Contopoulos, I., Gabuzda, D., Kylafis, N., Eds.; Springer International Publishing Switzerland: Cham, Switzerland, 2015; Volume 414, p. 45. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Dadhich, N.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. The distinguishing signature of magnetic Penrose process. Mon. Not. R. Astron. Soc. 2018, 478, L89–L94. [Google Scholar] [CrossRef] [Green Version]
- Tursunov, A.; Dadhich, N. Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process. Universe 2019, 5, 125. [Google Scholar] [CrossRef] [Green Version]
- Stuchlík, Z.; Kološ, M.; Tursunov, A.A. Magnetized Black Holes: Ionized Keplerian Disks and Acceleration of Ultra-High Energy Particles. Proceedings 2019, 17, 13. [Google Scholar] [CrossRef] [Green Version]
- Abramowicz, M.A.; Fragile, P.C. Foundations of Black Hole Accretion Disk Theory. Living Reviews in Relativity 2013, 16, 1. [Google Scholar] [CrossRef] [Green Version]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Kozlowski, M.; Jaroszynski, M.; Abramowicz, M.A. The analytic theory of fluid disks orbiting the Kerr black hole. Astron. Astrophys. 1978, 63, 209–220. [Google Scholar]
- Pugliese, D.; Stuchlík, Z. Ringed Accretion Disks: Equilibrium Configurations. Astrophys. J. Suppl. 2015, 221, 25. [Google Scholar] [CrossRef]
- Pugliese, D.; Stuchlík, Z. Ringed Accretion Disks: Instabilities. Astrophys. J. Suppl. 2016, 223, 27. [Google Scholar] [CrossRef] [Green Version]
- Pugliese, D.; Stuchlík, Z. Ringed Accretion Disks: Evolution of Double Toroidal Configurations. Astrophys. J. Suppl. 2017, 229, 40. [Google Scholar] [CrossRef] [Green Version]
- Stuchlík, Z. Influence of the RELICT Cosmological Constant on Accretion Discs. Mod. Phys. Lett. 2005, 20, 561–575. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef] [Green Version]
- Stuchlik, Z. The Motion of Test Particles in Black-Hole Backgrounds with Non-Zero Cosmological Constant. Bull. Astron. Institutes Czechoslov. 1983, 34, 129. [Google Scholar]
- Stuchlík, Z.; Hledík, S. Some properties of the Schwarzschild-de Sitter and Schwarzschild-anti-de Sitter spacetimes. Phys. Rev. D 1999, 60, 044006. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Hledík, S.; Novotný, J. General relativistic polytropes with a repulsive cosmological constant. Phys. Rev. D 2016, 94, 103513. [Google Scholar] [CrossRef] [Green Version]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- de Felice, F. Repulsive Phenomena and Energy Emission in the Field of a Naked Singularity. Astron. Astrophys. 1974, 34, 15. [Google Scholar]
- Stuchlík, Z. Equatorial circular orbits and the motion of the shell of dust in the field of a rotating naked singularity. Bull. Astron. Institutes Czechoslov. 1980, 31, 129–144. [Google Scholar]
- Stuchlík, Z.; Hledík, S.; Truparová, K. Evolution of Kerr superspinars due to accretion counterrotating thin discs. Class. Quantum Gravity 2011, 28, 155017. [Google Scholar] [CrossRef]
- Gimon, E.G.; Horava, P. Over-Rotating Black Holes, Godel Holography and the Hypertube. arXiv 2004, arXiv:hep-th/hep-th/0405019. [Google Scholar]
- Stuchlík, Z.; Schee, J. Appearance of Keplerian discs orbiting Kerr superspinars. Class. Quantum Gravity 2010, 27, 215017. [Google Scholar] [CrossRef] [Green Version]
- Stuchlík, Z.; Schee, J. Observational phenomena related to primordial Kerr superspinars. Class. Quantum Gravity 2012, 29, 065002. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J. Ultra-high-energy collisions in the superspinning Kerr geometry. Class. Quantum Gravity 2013, 30, 075012. [Google Scholar] [CrossRef]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Possible signature of the magnetic fields related to quasi-periodic oscillations observed in microquasars. Eur. Phys. J. 2017, 77, 860. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. 2016, 76, 32. [Google Scholar] [CrossRef] [Green Version]
- Tursunov, A.; Stuchlík, Z.; Kološ, M.; Dadhich, N.; Ahmedov, B. Supermassive Black Holes as Possible Sources of Ultrahigh-energy Cosmic Rays. Astrophys. J. 2020, 895, 14. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Tursunov, A.; Kološ, M.; Stuchlík, Z.; Galtsov, D.V. Radiation Reaction of Charged Particles Orbiting a Magnetized Schwarzschild Black Hole. Astrophys. J. 2018, 861, 2. [Google Scholar] [CrossRef]
- Tursunov, A.A.; Kološ, M.; Stuchlík, Z. Orbital widening due to radiation reaction around a magnetized black hole. Astron. Nachrichten 2018, 339, 341–346. [Google Scholar] [CrossRef] [Green Version]
- Ruffini, R. On the energetics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 451–546. [Google Scholar]
- Komar, A. Positive-Definite Energy Density and Global Consequences for General Relativity. Phys. Rev. 1963, 129, 1873–1876. [Google Scholar] [CrossRef]
- Carter, B. Black hole equilibrium states. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 57–214. [Google Scholar]
- Christodoulou, D. Reversible and Irreversible Transformations in Black-Hole Physics. Phys. Rev. Lett. 1970, 25, 1596–1597. [Google Scholar] [CrossRef]
- Christodoulou, D.; Ruffini, R. Reversible Transformations of a Charged Black Hole. Phys. Rev. D 1971, 4, 3552–3555. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Ruffini, R.; Wilson, J.R. Relativistic magnetohydrodynamical effects of plasma accreting into a black hole. Phys. Rev. D 1975, 12, 2959–2962. [Google Scholar] [CrossRef]
- Bicak, J.; Stuchlik, Z. The fall of the shell of dust on to a rotating black hole. Mon. Not. R. Astron. Soc. 1976, 175, 381–393. [Google Scholar] [CrossRef]
- Bicak, J.; Stuchlik, Z. On the latitudinal and radial motion in the field of a rotating black hole. Bull. Astron. Institutes Czechoslov. 1976, 27, 129–133. [Google Scholar]
- Bardeen, J.M. Timelike and null geodesics in the Kerr metric. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 215–239. [Google Scholar]
- Dhurandhar, S.V.; Dadhich, N. Energy-extraction processes from a Kerr black hole immersed in a magnetic field. I. Negative-energy states. Phys. Rev. D 1984, 29, 2712–2720. [Google Scholar] [CrossRef]
- Dhurandhar, S.V.; Dadhich, N. Energy-extraction processes from a Kerr black hole immersed in a magnetic field. II. The formalism. Phys. Rev. D 1984, 30, 1625–1631. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A powerful local shear instability in weakly magnetized disks. I—Linear analysis. II—Nonlinear evolution. Astrophys. J. 1991, 376, 214–233. [Google Scholar] [CrossRef]
- Kološ, M.; Stuchlík, Z.; Tursunov, A. Quasi-harmonic oscillatory motion of charged particles around a Schwarzschild black hole immersed in a uniform magnetic field. Class. Quantum Gravity 2015, 32, 165009. [Google Scholar] [CrossRef] [Green Version]
- Tursunov, A.; Stuchlík, Z.; Kološ, M. Circular orbits and related quasi-harmonic oscillatory motion of charged particles around weakly magnetized rotating black holes. Phys. Rev. D 2016, 93, 084012. [Google Scholar] [CrossRef] [Green Version]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Radiative Penrose process: Energy gain by a single radiating charged particle in the ergosphere of rotating black hole. Phys. Rev. D 2021, 103, 024021. [Google Scholar] [CrossRef]
- Kovář, J.; Stuchlík, Z.; Karas, V. Off-equatorial orbits in strong gravitational fields near compact objects. Class. Quantum Gravity 2008, 25, 095011. [Google Scholar] [CrossRef] [Green Version]
- Kovář, J.; Kopáček, O.; Karas, V.; Stuchlík, Z. Off-equatorial orbits in strong gravitational fields near compact objects - II: Halo motion around magnetic compact stars and magnetized black holes. Class. Quantum Gravity 2010, 27, 135006. [Google Scholar] [CrossRef]
- Kovář, J. Spiral motion formation in astrophysics. Eur. Phys. J. Plus 2013, 128, 142. [Google Scholar] [CrossRef]
- Komissarov, S.S. General relativistic magnetohydrodynamic simulations of monopole magnetospheres of black holes. Mon. Not. R. Astron. Soc. 2004, 350, 1431–1436. [Google Scholar] [CrossRef] [Green Version]
- Kovář, J.; Slaný, P.; Stuchlík, Z.; Karas, V.; Cremaschini, C.; Miller, J.C. Role of electric charge in shaping equilibrium configurations of fluid tori encircling black holes. Phys. Rev. D 2011, 84, 084002. [Google Scholar] [CrossRef] [Green Version]
- Kovář, J.; Slaný, P.; Cremaschini, C.; Stuchlík, Z.; Karas, V.; Trova, A. Electrically charged matter in rigid rotation around magnetized black hole. Phys. Rev. D 2014, 90, 044029. [Google Scholar] [CrossRef] [Green Version]
- Kovář, J.; Slaný, P.; Cremaschini, C.; Stuchlík, Z.; Karas, V.; Trova, A. Charged perfect fluid tori in strong central gravitational and dipolar magnetic fields. Phys. Rev. D 2016, 93, 124055. [Google Scholar] [CrossRef]
- Pugliese, D.; Stuchlík, Z. Relating Kerr SMBHs in active galactic nuclei to RADs configurations. Class. Quantum Gravity 2018, 35, 185008. [Google Scholar] [CrossRef] [Green Version]
- Pugliese, D.; Stuchlík, Z. RADs energetics and constraints on emerging tori collisions around super-massive Kerr black holes. Eur. Phys. J. C 2019, 79, 288. [Google Scholar] [CrossRef]
- Pugliese, D.; Stuchlík, Z. Jet collision with accreting tori around SMBHs GRHD and light surface constraints in aggregates of misaligned tori. Publ. Astron. Soc. Jpn. 2021. [Google Scholar] [CrossRef]
- Cremaschini, C.; Kovář, J.; Slaný, P.; Stuchlík, Z.; Karas, V. Kinetic Theory of Equilibrium Axisymmetric Collisionless Plasmas in Off-equatorial Tori around Compact Objects. Astrophys. J. Suppl. 2013, 209, 15. [Google Scholar] [CrossRef] [Green Version]
- Gal’tsov, D.V.; Petukhov, V.I. Black hole in an external magnetic field. Sov. J. Exp. Theor. Phys. 1978, 47, 419. [Google Scholar]
- Bicak, J.; Janis, V. Magnetic fluxes across black holes. Mon. Not. R. Astron. Soc. 1985, 212, 899–915. [Google Scholar] [CrossRef] [Green Version]
- Moradi, R.; Rueda, J.A.; Ruffini, R.; Wang, Y. The newborn black hole in GRB 191014C proves that it is alive. Astron. Astrophys. 2021, 649, A75. [Google Scholar] [CrossRef]
- Zajaček, M.; Tursunov, A.; Eckart, A.; Britzen, S. On the charge of the Galactic centre black hole. Mon. Not. R. Astron. Soc. 2018, 480, 4408–4423. [Google Scholar] [CrossRef]
- Bičák, J.; Ledvinka, T. Electromagnetic fields around black holes and Meissner effect. Nuovo C. Ser. 2000, 115, 739. [Google Scholar]
- Komissarov, S.S. Blandford-Znajek Mechanism versus Penrose Process. J. Korean Phys. Soc. 2009, 54, 2503. [Google Scholar] [CrossRef] [Green Version]
- Punsly, B. Black Hole Gravitohydromagnetics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Frolov, V.P.; Shoom, A.A. Motion of charged particles near a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2010, 82, 084034. [Google Scholar] [CrossRef] [Green Version]
- Petterson, J.A. Magnetic field of a current loop around a Schwarzschild black hole. Phys. Rev. D 1974, 10, 3166–3170. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The mathematical theory of black holes. In Proceedings of the General Relativity and Gravitation Conference, Padua, Italy, 4–9 July 1984; pp. 5–26. [Google Scholar]
- Bičák, J.; Stuchlík, Z.; Balek, V. The motion of charged particles in the field of rotating charged black holes and naked singularities. Bull. Astron. Institutes Czechoslov. 1989, 40, 65–92. [Google Scholar]
- Lasota, J.P.; Gourgoulhon, E.; Abramowicz, M.; Tchekhovskoy, A.; Narayan, R. Extracting black-hole rotational energy: The generalized Penrose process. Phys. Rev. D 2014, 89, 024041. [Google Scholar] [CrossRef] [Green Version]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion disks and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef] [Green Version]
- Greisen, K. End to the Cosmic-Ray Spectrum? Phys. Rev. Lett. 1966, 16, 748–750. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuz’min, V.A. Upper Limit of the Spectrum of Cosmic Rays. Sov. J. Exp. Theor. Phys. Lett. 1966, 4, 78. [Google Scholar]
- Parsa, M.; Eckart, A.; Shahzamanian, B.; Karas, V.; Zajaček, M.; Zensus, J.A.; Straubmeier, C. Investigating the Relativistic Motion of the Stars Near the Supermassive Black Hole in the Galactic Center. Astrophys. J. 2017, 845, 22. [Google Scholar] [CrossRef] [Green Version]
- Eckart, A.; Schödel, R.; Meyer, L.; Trippe, S.; Ott, T.; Genzel, R. Polarimetry of near-infrared flares from Sagittarius A*. Astron. Astrophys. 2006, 455, 1–10. [Google Scholar] [CrossRef]
- Eckart, A.; Hüttemann, A.; Kiefer, C.; Britzen, S.; Zajaček, M.; Lämmerzahl, C.; Stöckler, M.; Valencia-S, M.; Karas, V.; García-Marín, M. The Milky Way’s Supermassive Black Hole: How Good a Case Is It? Found. Phys. 2017, 47, 553–624. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1976. [Google Scholar]
- Poisson, E. The Motion of Point Particles in Curved Spacetime. Living Rev. Relativ. 2004, 7, 6. [Google Scholar] [CrossRef] [Green Version]
- DeWitt, B.S.; Brehme, R.W. Radiation damping in a gravitational field. Ann. Phys. 1960, 9, 220–259. [Google Scholar] [CrossRef]
- Hobbs, J. A vierbein formalism of radiation damping. Ann. Phys. 1968, 47, 141–165. [Google Scholar] [CrossRef]
- Chrzanowski, P.L.; Misner, C.W. Geodesic synchrotron radiation in the Kerr geometry by the method of asymptotically factorized Green’s functions. Phys. Rev. D 1974, 10, 1701–1721. [Google Scholar] [CrossRef]
- Gal’tsov, D.V. Radiation reaction in the Kerr gravitational field. J. Phys. Math. Gen. 1982, 15, 3737–3749. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Ternov, I.M.; Aliev, A.N.; Gal’tsov, D.V. Synchrotron radiation in curved space—time. Sov. Phys. J. 1983, 26, 36–40. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Gal’tsov, D.V.; Petukhov, V.I. Radiation emitted by relativistic particles moving in the vicinity of the Schwarzschild black hole, immersed in an external magnetic field. Phys. Lett. A 1978, 68, 1–2. [Google Scholar] [CrossRef]
- Shoom, A.A. Synchrotron radiation from a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2015, 92, 124066. [Google Scholar] [CrossRef] [Green Version]
- Piotrovich, M.Y.; Silant’ev, N.A.; Gnedin, Y.N.; Natsvlishvili, T.M. Magnetic fields and quasi-periodic oscillations of black hole radiation. Astrophys. Bull. 2011, 66, 320–324. [Google Scholar] [CrossRef]
- Baczko, A.K.; Schulz, R.; Kadler, M.; Ros, E.; Perucho, M.; Krichbaum, T.P.; Böck, M.; Bremer, M.; Grossberger, C.; Lindqvist, M.; et al. A highly magnetized twin-jet base pinpoints a supermassive black hole. Astron. Astrophys. 2016, 593, A47. [Google Scholar] [CrossRef] [Green Version]
- Zajacek, M.; Tursunov, A. The Electric Charge of Black Holes: Is It Really Always Negligible. Obesity 2019, 139, 231–236. [Google Scholar]
- Tursunov, A.; Zajaček, M.; Eckart, A.; Kološ, M.; Britzen, S.; Stuchlík, Z.; Czerny, B.; Karas, V. Effect of Electromagnetic Interaction on Galactic Center Flare Components. Astrophys. J. 2020, 897, 99. [Google Scholar] [CrossRef]
- Weingartner, J.C.; Draine, B.T.; Barr, D.K. Photoelectric Emission from Dust Grains Exposed to Extreme Ultraviolet and X-Ray Radiation. Astrophys. J. 2006, 645, 1188–1197. [Google Scholar] [CrossRef]
- Tursunov, A.; Bakhtinur, J.; Stuchlík, Z.; Kološ, M. Electric Penrose process: High-energy acceleration of ionized particles by non-rotating weakly charged black hole. Phys. Rev. D 2021, 104, 084099. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Charbulák, D.; Schee, J. Light escape cones in local reference frames of Kerr-de Sitter black hole spacetimes and related black hole shadows. Eur. Phys. J. C 2018, 78, 180. [Google Scholar] [CrossRef] [Green Version]
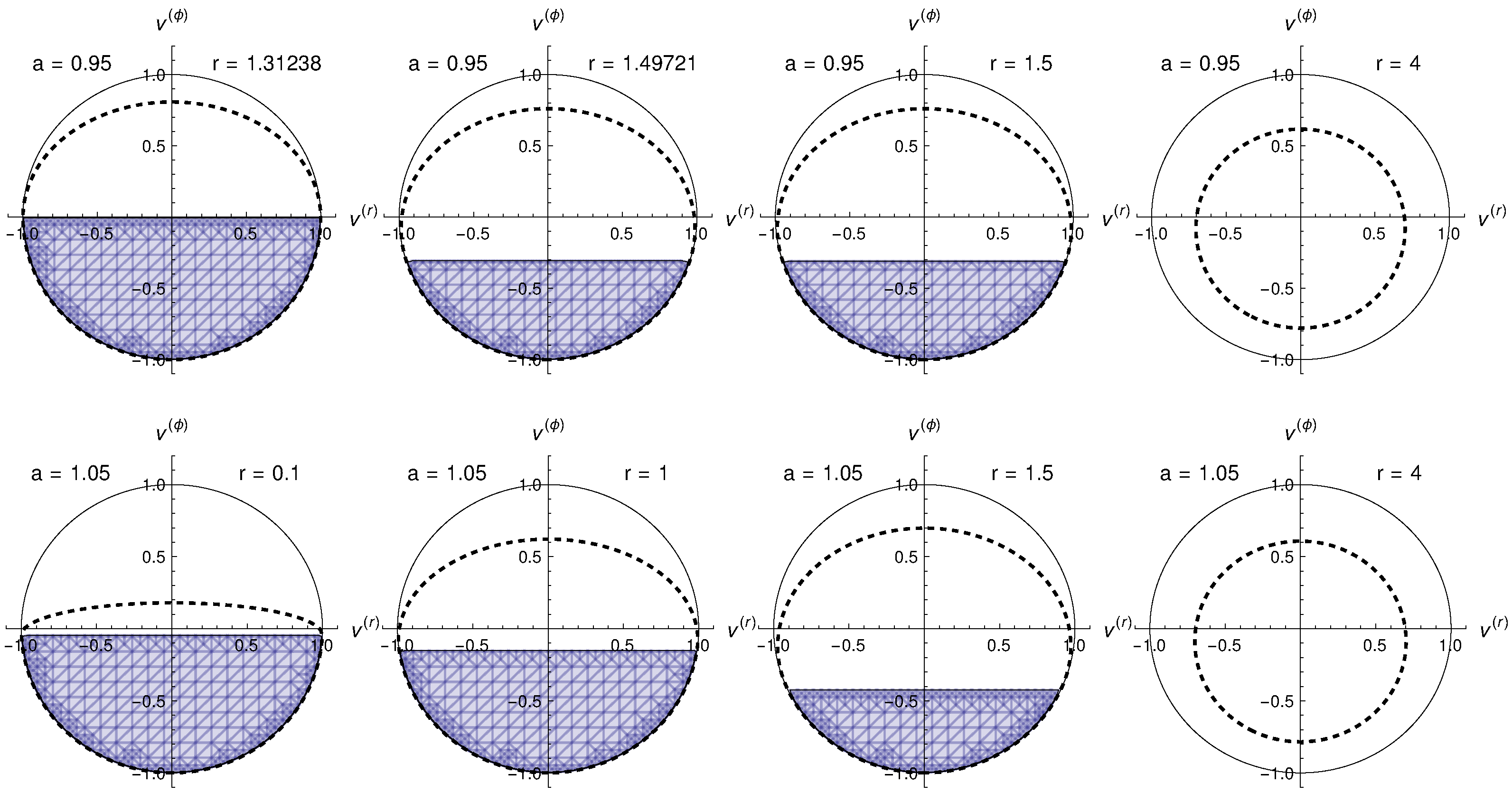
| / | Electron | Proton | Fe+ | Charged Dust |
|---|---|---|---|---|
| B (Gauss) | (s) | (s) |
|---|---|---|
| 1 | ||
| 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stuchlík, Z.; Kološ, M.; Tursunov, A. Penrose Process: Its Variants and Astrophysical Applications. Universe 2021, 7, 416. https://doi.org/10.3390/universe7110416
Stuchlík Z, Kološ M, Tursunov A. Penrose Process: Its Variants and Astrophysical Applications. Universe. 2021; 7(11):416. https://doi.org/10.3390/universe7110416
Chicago/Turabian StyleStuchlík, Zdeněk, Martin Kološ, and Arman Tursunov. 2021. "Penrose Process: Its Variants and Astrophysical Applications" Universe 7, no. 11: 416. https://doi.org/10.3390/universe7110416
APA StyleStuchlík, Z., Kološ, M., & Tursunov, A. (2021). Penrose Process: Its Variants and Astrophysical Applications. Universe, 7(11), 416. https://doi.org/10.3390/universe7110416







