Counterexamples to the Maximum Force Conjecture

Abstract

Dimensional analysis shows that the speed of light and Newton’s constant of gravitation can be combined to define a quantity $F_{*}=c^4/G_N$ with the dimensions of force (equivalently, tension). Then in any physical situation we must have $F_{\mathrm{physical}}=f{F}_{*}$, where the quantity f is some dimensionless function of dimensionless parameters. In many physical situations explicit calculation yields $f=\mathcal{O}\left(1\right)$, and quite often $f\le 1/4$. This has led multiple authors to suggest a (weak or strong) maximum force/maximum tension conjecture. Working within the framework of standard general relativity, we will instead focus on idealized counter-examples to this conjecture, paying particular attention to the extent to which the counter-examples are physically reasonable. The various idealized counter-examples we shall explore strongly suggest that one should not put too much credence into any truly universal maximum force/maximum tension conjecture. Specifically, idealized fluid spheres on the verge of gravitational collapse will generically violate the weak (and strong) maximum force conjectures. If one wishes to retain any truly general notion of “maximum force” then one will have to very carefully specify precisely which forces are to be allowed within the domain of discourse.

1. Introduction

The maximum force/maximum tension conjecture was independently mooted some 20 years ago by Gary Gibbons [1] and Christoph Schiller [2]. At its heart one starts by noting that in (3 + 1) dimensions the quantity

$$\begin{array}{c}\hfill F_{*}=\frac{c^4}{G_N}\approx 1.2\times {10}^{44}\mathrm{N}\end{array}$$

(1)

has the dimensions of force (equivalently, tension). Here c is the speed of light in a vacuum and $G_N$ is Newton’s gravitational constant. Thereby any physical force can always be written in the form

$$F_{\mathrm{physical}}=f{F}_{*},$$

(2)

where the quantity f is some dimensionless function of dimensionless parameters. In very many situations [1,2,3,4] explicit calculations yield $f\le \frac{1}{4}$, though sometimes numbers such as $f\le \frac{1}{2}$ also arise [5]. Specifically, Yen Chin Ong [5] formulated strong and weak versions of the conjecture:

• Strong form: $f\le \frac{1}{4}$.
• Weak form: $f=\mathcal{O}\left(1\right)$.

Note that $F_{*}=E_{\mathrm{Planck}}/L_{\mathrm{Planck}}$ can also be interpreted as the Planck force, though it is not intrinsically quantum as the various factors of ℏ cancel, at least in (3 + 1) dimensions.

Furthermore it is sometimes interesting [6] to note that the Einstein equations

$$G_{ab}=8\pi \frac{G_N}{c^4}{T}_{ab},$$

(3)

can be written in terms of $F_{*}$ as

$$T_{ab}=\frac{F_{*}}{8\pi }{G}_{ab}.$$

(4)

When recast in this manner, maximum force conjectures have tentatively been related to Jacobson’s entropic derivation of the Einstein equations [7].

Considerable work has also gone into attempts at pushing various modifications of the maximum force conjecture beyond the framework of standard general relativity [8,9]. Overall, while there is little doubt that the quantity $F_{*}$ is physically important, we feel that the precise status of the maximum force conjecture is much less certain, and is less than universal.

We shall investigate these conjectures within the context of standard general relativity, focusing on illustrative idealized counter-examples based on simple physical systems, analyzing the internal forces, and checking the extent to which the counter-examples are physically reasonable. Specifically, we shall ignore rotation and (as is entirely usual) consider static spherically symmetric fluid spheres [10,11,12,13,14,15,16,17,18] as a first approximation to a relativistic star. We shall investigate both radial forces (between inner and outer layers) and, by considering the “great disk” spanned by any great circle on the surface of the fluid sphere, will calculate the forces between any two equal hemispheres. We shall also include an analysis of the speed of sound, and the relevant classical energy conditions, specifically the dominant energy condition (DEC), see [19,20,21,22,23,24,25,26,27,28]. We shall see that even the most elementary static spherically symmetric fluid sphere, Schwarzschild’s constant density star, raises significant issues for the maximum force conjecture. Other models, such as the Tolman IV solution and its variants are even worse. Generically, we shall see that any idealized perfect fluid sphere on the verge of gravitational collapse will violate the weak (and strong) maximum force conjectures. Consequently, if one wishes to retain any truly universal notion of “maximum force” then one will at the very least have to very carefully delineate precisely which forces are to be allowed within the domain of discourse.

2. Spherical Symmetry

Consider spherically symmetric spacetime, with the metric given in Schwarzschild curvature coordinates:

$$d{s}^2=g_{tt}d{t}^2+g_{rr}d{t}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2).$$

(5)

We do not yet demand pressure isotropy, and for the time being allow radial and transverse pressures to differ; that is $p_r\ne p_t$.

Pick an arbitrary but fixed spherical surface at some specified value of the radial coordinate r. Define

$$F_r\left(r\right)=\int p_r\left(r\right)dA=4\pi p_r\left(r\right)r^2.$$

(6)

This quantity simultaneously represents the compressive force exerted by outer layers of the system on the core, and the supporting force exerted by the core on the outer layers of the system.

Consider any arbitrary but fixed great circle on the surface of the fluid sphere. This great circle will span a “great disk” dividing the fluid sphere into two equal hemispheres. The force across this great disk will be:

$$F_{hemi}=\int p_t\left(r\right)dA=2\pi {\int }_0^{R_s}\sqrt{g_{rr}}{p}_t\left(r\right)rdr.$$

(7)

This quantity simultaneously represents the force exerted by either of these two hemispheres on the other hemisphere. Here $R_s$ is the location of the surface of the object (potentially taken as infinite). As we are investigating spherically symmetric systems, the specific choice of hemisphere is irrelevant.

3. Perfect Fluid Spheres

3.1. Generalities

The perfect fluid condition excludes pressure anisotropy so that the radial and transverse pressures are set equal: $p\left(r\right)=p_r\left(r\right)=p_t\left(r\right)$. Once this is done, the radial and hemispherical forces simplify

$$F_r\left(r\right)=\int p\left(r\right)dA=4\pi p\left(r\right)r^2;$$

(8)

$$F_{hemi}=\int p\left(r\right)dA=2\pi {\int }_0^{R_s}\sqrt{g_{rr}}p\left(r\right)rdr.$$

(9)

Additionally, we shall impose the conditions that pressure is positive and decreases as one moves outwards with zero pressure defining the surface of the object [10,11,12,13,14,15,16,17,18]. (There is a minor technical change in the presence of a cosmological constant, the surface is then defined by $p\left(R_s\right)=p_{\mathsf{\Lambda }}$). Similarly, density is positive and does not increase as one moves outwards, though density need not be and typically is not zero at the surface [10,11,12,13,14,15,16,17,18].

We note that for the radial force we have by construction

$$F_r\left(0\right)=0;F_r\left(R_s\right)=0;\mathrm{and}\mathrm{for}r\in (0,R_s):F_r\left(r\right)>0.$$

(10)

In particular, in terms of the central pressure $p_0$ we have the particularly simple bound

$$F_r\left(r\right)<4\pi p_0{R}_s^2.$$

(11)

This suggests that in general an (extremely) weak version of the maximum force conjecture might hold for the radial force, at least within the framework outlined above, and as long as the central pressure is finite. Unfortunately without some general relationship between central pressure $p_0$ and radius $R_s$ this bound is less useful than one might hope. For the strong version of the maximum force conjecture no such simple argument holds for $F_r$, and one must perform a case-by-case analysis. For the hemispherical force $F_{hemi}$ there is no similar argument of comparable generality, and one must again perform a case-by-case analysis.

Turning now to the classical energy conditions [19,20,21,22,23,24,25,26,27,28], they add extra restrictions to ensure that various physical properties remain well-behaved. For our perfect fluid solutions, these act as statements relating the pressure p and the density $\rho$ given by the stress–energy tensor $T_{\widehat{\mu }\widehat{\nu }}$. Since (in view of our fundamental assumptions that pressure and density are both positive) the null, weak, and strong energy conditions (NEC, WEC, SEC) are always automatically satisfied, we will only be interested in the dominant energy condition (DEC). In the current context the dominant energy condition only adds the condition $\left|p\right|\le \rho$. However, since in the context of perfect fluid spheres, the pressure is always positive, it is more convenient to simply write this as

$$\frac{p}{\rho }\le 1;\mathrm{that}\mathrm{is}p\le \rho .$$

(12)

The best physical interpretation of the DEC is that it guarantees that any timelike observer with 4-velocity $V^a$ will observe a flux $F^a=T^{ab}{V}_b$ that is non-spacelike (either timelike or null) [25]. However, it should be pointed out that the DEC, being the strongest of the classical energy conditions, is also the easiest to violate—indeed there are several known situations in which the classical DEC is violated by quantum effects [20,21,22,23,24,25,26,27,28].

The DEC is sometimes (somewhat misleadingly) interpreted in terms of the speed of sound not being superluminal: naively $v_s^2=\partial p/\partial \rho \le 1$; whence $p\le \rho -{\rho }_{\mathrm{surface}}<\rho$. However, the implication is only one-way, and in addition the argument depends on extra technical assumptions to the effect that the fluid sphere is well-mixed with a unique barotropic equation of state $p\left(\rho \right)$ holding throughout the interior. To clarify this point, suppose the equation of state is not barotropic, so that $p=p(\rho ,z_i)$, with the $z_i$ being some collection of intensive variables (possibly chemical concentrations, entropy density, or temperature). Then we have

$$\frac{dp}{dr}=\frac{\partial p}{\partial \rho }\frac{d\rho }{dr}+\sum _i\frac{\partial p}{\partial z^i}\frac{d{z}^i}{dr}=v_s^2(\rho ,z^i)\frac{d\rho }{dr}+\sum _i\frac{\partial p}{\partial z^i}\frac{d{z}^i}{dr}.$$

(13)

Then, noting that $d\rho /dr$ is non-positive as one moves outwards, enforcing the speed of sound to not be superluminal implies

$$\frac{dp}{dr}\ge \frac{d\rho }{dr}+\sum _i\frac{\partial p}{\partial z^i}\frac{d{z}^i}{dr}.$$

(14)

Integrating this from the surface inwards we have

$$p\left(r\right)\le \rho \left(r\right)-\rho \left(R_s\right)+\sum _i{\int }_r^{R_s}\frac{\partial p(\rho ,z^i)}{\partial z^i}\frac{d{z}^i}{dr}dr.$$

(15)

Consequently, unless one either makes an explicit barotropic assumption $\partial p/\partial z^i=0$, or otherwise at the very least has some very tight control over the partial derivatives $\partial p/\partial z^i$, one simply cannot use an assumed non-superluminal speed of sound to deduce the DEC. Neither can the DEC be used to derive a non-superluminal speed of sound, at least not without many extra and powerful technical assumptions. We have been rather explicit with this discussion since we have seen considerable confusion on this point. Finally, we note that there is some disagreement as to whether or not the DEC is truly fundamental [21,22,23,24].

3.2. Schwarzschild’s Constant Density Star

We shall now consider a classic example of perfect fluid star, Schwarzschild’s constant density star [29] (often called the Schwarzschild interior solution), which was discovered very shortly after Schwarzschild’s original vacuum solution [30] (often called the Schwarzschild exterior solution).

It is commonly argued that Schwarzschild’s constant density star is “unphysical” on the grounds that it allegedly leads to an infinite speed of sound. However, this is a naive result predicated on the physically unreasonable hypothesis that the star is well-mixed with a barotropic equation of state $p=p\left(\rho \right)$. To be very explicit about this, all realistic stars are physically stratified with non-barotropic equations of state $p=p(\rho ,z_i)$, with the $z_i$ being some collection of intensive variables (possibly chemical concentrations, entropy density, or temperature). We have already seen that

$$\frac{dp}{dr}=\frac{\partial p}{\partial \rho }\frac{d\rho }{dr}+\sum _i\frac{\partial p}{\partial z^i}\frac{d{z}^i}{dr}=v_s^2(\rho ,z^i)\frac{d\rho }{dr}+\sum _i\frac{\partial p}{\partial z^i}\frac{d{z}^i}{dr}.$$

(16)

Thence, for a constant density star, $d\rho /dr=0$, we simply deduce

$$\frac{dp}{dr}=\sum _i\frac{\partial p}{\partial z^i}\frac{d{z}^i}{dr}.$$

(17)

This tells us nothing about the speed of sound, one way or the other—it does tell us that there is a fine-tuning between the pressure p and the intensive variables $z^i$, but that is implied by the definition of being a “constant density star”. We have again been rather explicit with this discussion since we have seen considerable confusion on this point. Schwarzschild’s constant density star is not “unphysical”; it may be “fine-tuned” but it is not a priori “unphysical”.

Specifically, the Schwarzschild interior solution describes the geometry inside a static spherically symmetric perfect fluid constant density star with radius $R_s$ and mass M by the metric:

$$d{s}^2=-\frac{1}{4}{\left(3\sqrt{1-\frac{2M}{R_s}}-\sqrt{1-\frac{2M{r}^2}{R_s^3}}\right)}^{2}d{t}^2+{\left(1-\frac{2M{r}^2}{R_s^3}\right)}^{-1}d{r}^2+r^{2}d{\mathsf{\Omega }}^2.$$

(18)

Here we have adopted geometrodynamic units ($c\to 1$, $G_N\to 1$). Calculating the non-zero orthonormal stress–energy components from the Einstein equations applied to this metric yields:

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{t}}& =& \rho =\frac{3M}{4\pi R_s^3};\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill T_{\widehat{r}\widehat{r}}& =& T_{\widehat{\theta }\widehat{\theta }}=T_{\widehat{\varphi }\widehat{\varphi }}=p=\rho \frac{\sqrt{1-\frac{2M{r}^2}{R_s^3}}-\sqrt{1-\frac{2M}{R_s}}}{3\sqrt{1-\frac{2M}{R_s}}-\sqrt{1-\frac{2M{r}^2}{R_s^3}}}.\hfill \end{array}$$

(20)

This gives us the relation between density and pressure, as well as demonstrating the perfect fluid condition ($p=p_r=p_t$), and also verifying that the density is (inside the star) a position-independent constant. In these geometrodynamic units both density and pressure have units 1/(length)${}^2$, while forces are dimensionless. Note that the pressure does in fact go to zero at $r\to R_s$, so $R_s$ really is the surface of the “star”. Rewriting the relation between pressure and density in terms of the simplified dimensionless quantities $\chi =\frac{2M}{R_s}$ and $y=\frac{r^2}{R_s^2}$ we see

$$\begin{array}{c}\hfill p=\rho \frac{\sqrt{1-\chi y}-\sqrt{1-\chi }}{3\sqrt{1-\chi }-\sqrt{1-\chi y}}.\end{array}$$

(21)

Here, $0\le y\le 1$ and $0\le \chi <\frac{8}{9}$. The first of these ranges is obvious from the definition of y, while the second comes from considering the central pressure at $y=0$:

$$p_0=\rho \frac{1-\sqrt{1-\chi }}{3\sqrt{1-\chi }-1}.$$

(22)

Demanding that the central pressure be finite requires $\chi <\frac{8}{9}$. (This is actually a rather more general result of general relativistic stellar dynamics, not restricted to constant density; see various discussions of the Buchdahl–Bondi bound [31,32]).

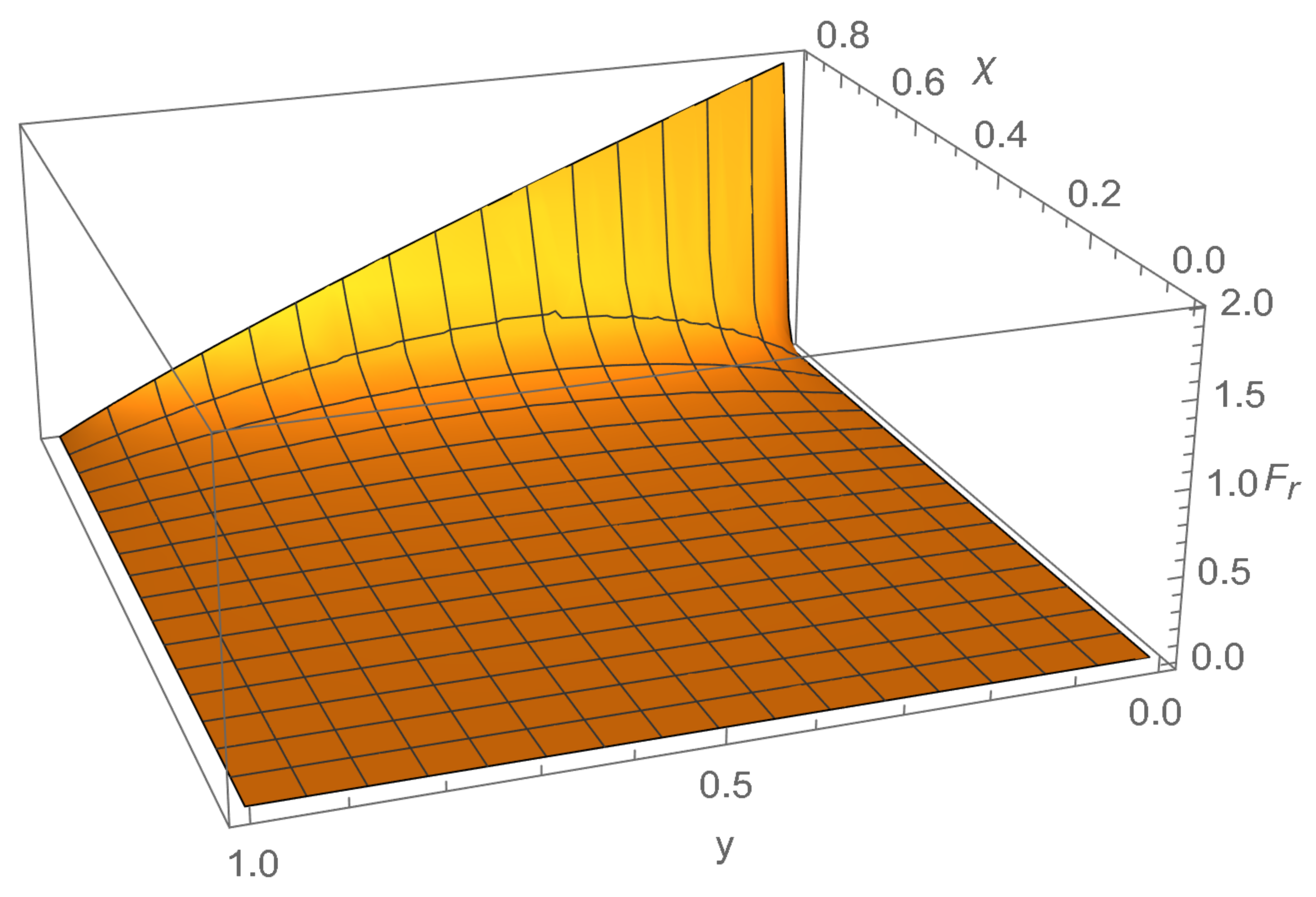
3.2.1. Radial Force

The radial force $F_r$ as defined by Equation (8) can be combined with the pressure–density relation given by Equation (21), giving:

$$F_r=4\pi p{r}^2=4\pi \rho R_s^{2}y\frac{\sqrt{1-\chi y}-\sqrt{1-\chi }}{3\sqrt{1-\chi }-\sqrt{1-\chi y}}=\frac{3}{2}\chi y\frac{\sqrt{1-\chi y}-\sqrt{1-\chi }}{3\sqrt{1-\chi }-\sqrt{1-\chi y}}.$$

(23)

As advertised in both the abstract and introduction, this quantity is indeed a dimensionless function of dimensionless variables. Furthermore, this quantity is defined on the bounded range $0\le y\le 1$, $0\le \chi <\frac{8}{9}$. To find if $F_r$ itself is bounded we analyze the multi-variable derivative for critical points.

For ${\partial }_{\chi }{F}_r$ we find:

$${\partial }_{\chi }{F}_r=-\frac{3y}{2}\left(\frac{\{4-\chi (3+y)\}\sqrt{1-\chi }\sqrt{1-\chi y}-\{4-\chi (3+5y-4\chi y)\}}{\sqrt{1-\chi }\sqrt{1-\chi y}{(3\sqrt{1-\chi }-\sqrt{1-\chi y})}^2}\right).$$

(24)

For ${\partial }_y{F}_r$ we find:

$${\partial }_y{F}_r=-\frac{3\chi }{2}\left(\frac{\{4-\chi (3+y)\}\sqrt{1-\chi y}-\{4-5\chi y\}\sqrt{1-\chi }}{\sqrt{1-\chi y}{(3\sqrt{1-\chi }-\sqrt{1-\chi y})}^2}\right).$$

(25)

In particular we see that

$$\chi {\partial }_{\chi }{F}_r-y{\partial }_y{F}_r=\frac{3{\chi }^{2}y}{2}\left(\frac{\sqrt{1-\chi y}}{\sqrt{1-\chi }{(3\sqrt{1-\chi }-\sqrt{1-\chi y})}^2}\right).$$

(26)

To have a critical point, ${\partial }_{\chi }{F}_r={\partial }_y{F}_r=0$, we certainly require $\chi y=0$. Therefore, either $\chi =0$ or $y=0$. However, for $y=0$, and $\chi \in (0,\frac{8}{9})$ we have

$${\partial }_y{F}_r⟶\frac{3\chi (3\chi +4\sqrt{1-\chi }-4)}{2{(3\sqrt{1-\chi }-1)}^2}>0.$$

(27)

In contrast, for $\chi =0$, and $y\in (0,1)$, we have ${\partial }_{\chi }{F}_r\to 0$. Therefore the only critical points lie on one of the boundary segments:

$${\partial }_{\chi }{F}_r={\partial }_y{F}_r=0\iff \chi =0.$$

(28)

Therefore to find the maxima of $F_r(\chi ,r)$ we must inspect all four of the boundary segments of the viable region. Along three of the boundary segments we can see that the three lines corresponding to $\chi =0$, $y=0$, and $y=1$ all give $F_r(\chi ,r)=0$, leaving only $\chi \to \frac{8}{9}$ to be investigated.

We note

$$\underset{\chi \to \frac{8}{9}}{lim}{F}_r(\chi ,y)=\frac{4y}{3}\frac{(\sqrt{9-8y}-1)}{3-\sqrt{9-8y}}.$$

(29)

Inserting this into the partial derivative ${\partial }_y{F}_r$ reveals:

$$\underset{\chi \to \frac{8}{9}}{lim}{\partial }_y{F}_r=-\frac{4}{3}\left(1+\frac{1}{\sqrt{9-8y}}\right).$$

(30)

This is a strictly negative function in the range $0\le y\le 1$.

Thus the maximum of $F_r(\chi ,y)$ can be found by taking the limit ${lim}_{y\to 0}$ giving:

$${\left(F_r\right)}_{\max }=\underset{y\to 0}{lim}\underset{\chi \to \frac{8}{9}}{lim}{F}_r=2.$$

(31)

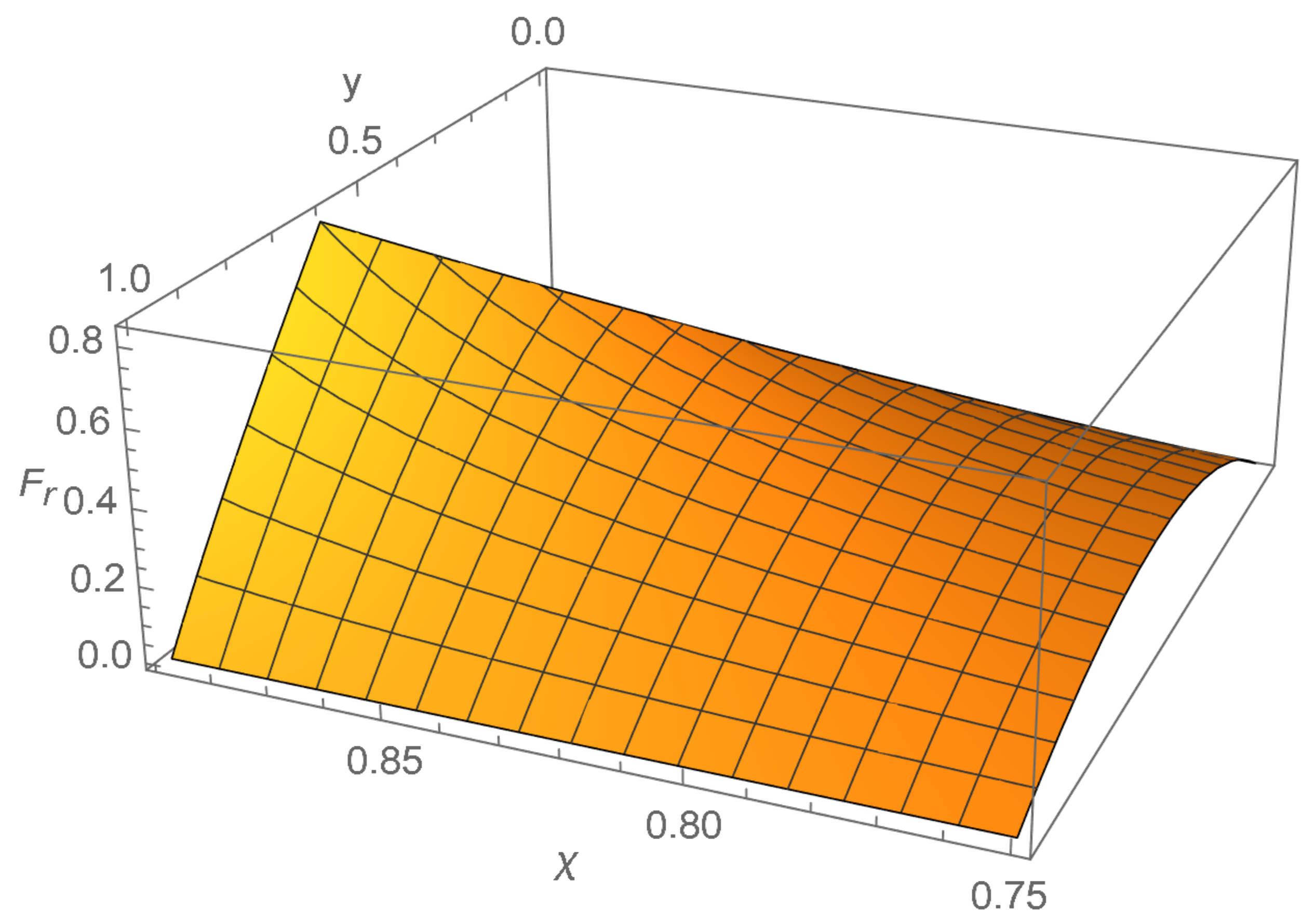
This is therefore bounded, with the radial force approaching its maximum at the centre of a fluid star that is on the verge of collapse. This force violates the strong maximum force conjecture, though it satisfies the weak maximum force conjecture. This limit can easily be seen graphically in Figure 1.

3.2.2. Hemspherical Force

Using Equation (9) and the metric defined in Equation (18), with the relabelling of the previous subsection in terms of $\chi$ and y gives:

$$\begin{array}{c}\hfill F_{hemi}\left(\chi \right)=\frac{3}{8}\chi {{\displaystyle \int }}_0^1\frac{1}{\sqrt{1-\chi y}}\left(\frac{\sqrt{1-\chi y}-\sqrt{1-\chi }}{3\sqrt{1-\chi }-\sqrt{1-\chi y}}\right)dy.\end{array}$$

(32)

The integral evaluates to:

$$\begin{array}{ccc}\hfill F_{hemi}\left(\chi \right)& =& \frac{3}{4}{\left.\left[\sqrt{1-\chi y}+2\sqrt{1-\chi }ln(3\sqrt{1-\chi }-\sqrt{1-\chi y})\right]\right|}_{y=0}^{y=1}.\hfill \end{array}$$

(33)

Ultimately

$$\begin{array}{ccc}\hfill F_{hemi}\left(\chi \right)& =& \frac{3}{4}\left[\sqrt{1-\chi }\left\{1+ln(4-4\chi )-2ln(3\sqrt{1-\chi }-1)\right\}-1\right].\hfill \end{array}$$

(34)

However, due to the presence of the $-ln(3\sqrt{1-\chi }-1)$ term in this equation, it can be seen that as $\chi \to \frac{8}{9}$, $F_{hemi}\left(\chi \right)\to +\infty$. Indeed

$$F_{hemi}\left(\chi \right)=\frac{ln(\frac{8}{9}-\chi )}{2}+\mathcal{O}\left(1\right),$$

(35)

implying that the hemispherical force in this space-time will grow without bound as the star approaches the critical size (just prior to gravitational collapse), in violation of both the strong and weak maximum force conjectures.

Therefore, while the interior Schwarzschild solution has provided a nice example of a bounded radial force, $F_r(y,\chi )$, it also clearly provides an explicit counter-example, where the hemispherical force $F_{hemi}\left(\chi \right)$ between two hemispheres of the fluid star grows without bound.

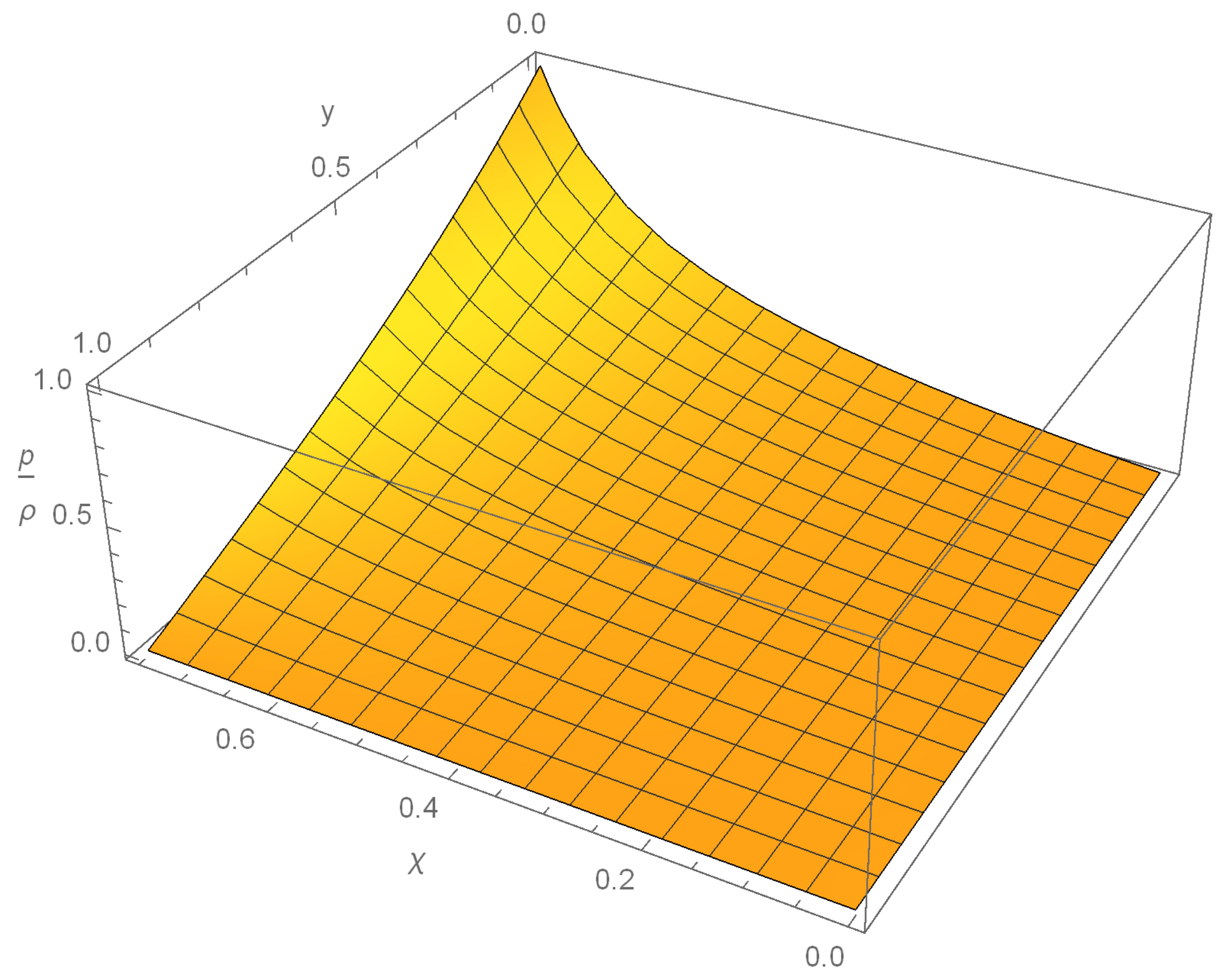
3.2.3. DEC

Imposing the DEC (Equation (12)) within the fluid sphere we would require:

$$\frac{p}{\rho }=\frac{\sqrt{1-\chi y}-\sqrt{1-\chi }}{3\sqrt{1-\chi }-\sqrt{1-\chi y}}\le 1$$

(36)

That is

$$\sqrt{1-\chi y}\le 4\sqrt{1-\chi },$$

(37)

whence

$$1-\chi y\le 16(1-\chi ).$$

(38)

Applying the boundary conditions of $0\le \chi \le \frac{8}{9}$, $0\le y\le 1$, we have a solution range:

$$\left(0\le \chi \le \frac{3}{4},0\le y\le 1\right)\bigcup \left(\frac{3}{4}<\chi \le \frac{8}{9},4-\frac{3}{\chi }\le y\le 1\right).$$

(39)

See Figure 2 and Figure 3.

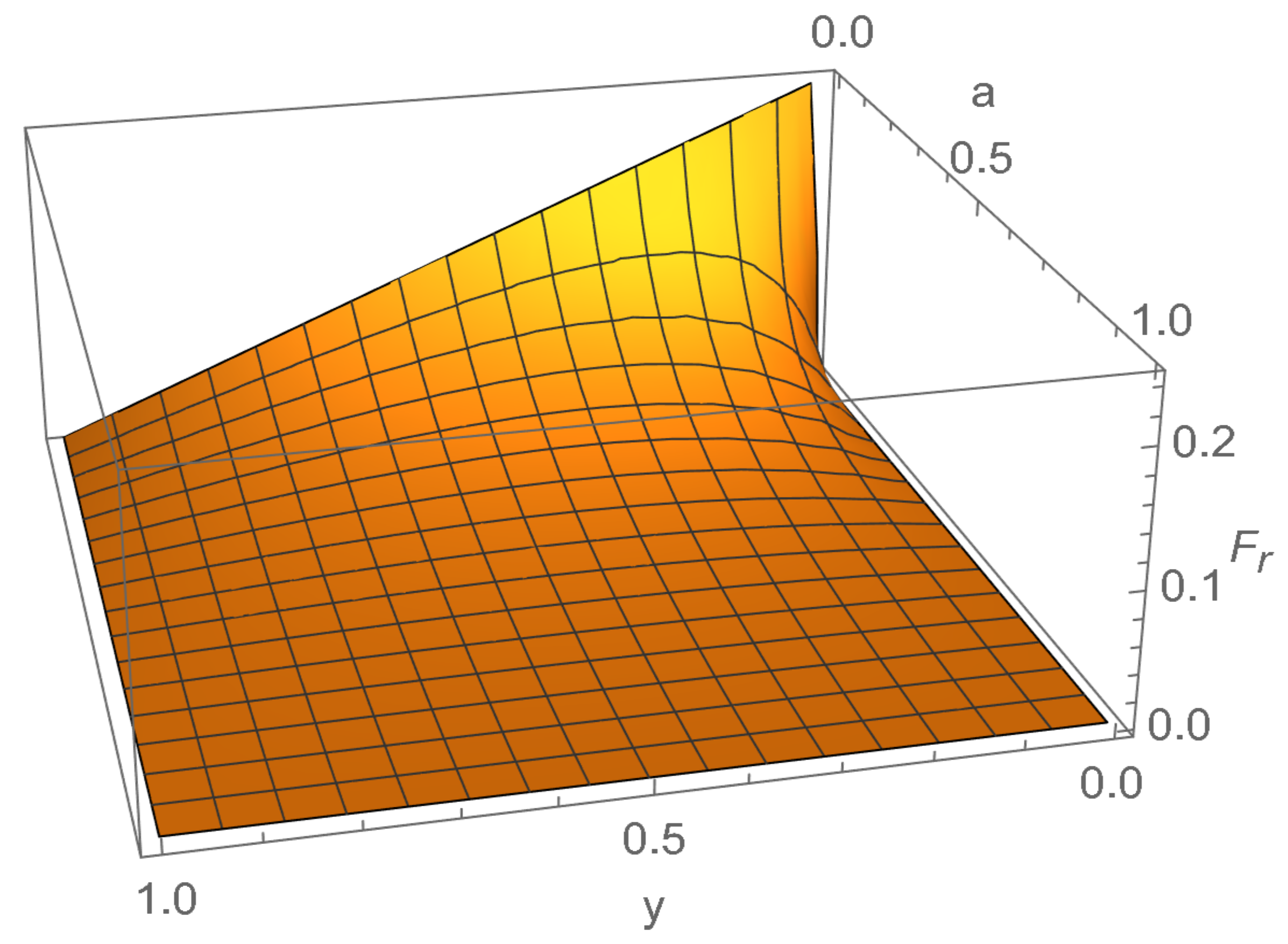
Within the first region $0\le \chi \le \frac{3}{4},0\le y\le 1$, the radial force is maximized at:

$$\chi =\frac{3}{4},y=\frac{1}{6}(5-\sqrt{5})\approx 0.46;\to F_r=\frac{3}{16}(\sqrt{5}-1)\approx 0.23<\frac{1}{4}.$$

(40)

Under these conditions the strong maximum force conjecture is satisfied. This can be seen visually in Figure 4.

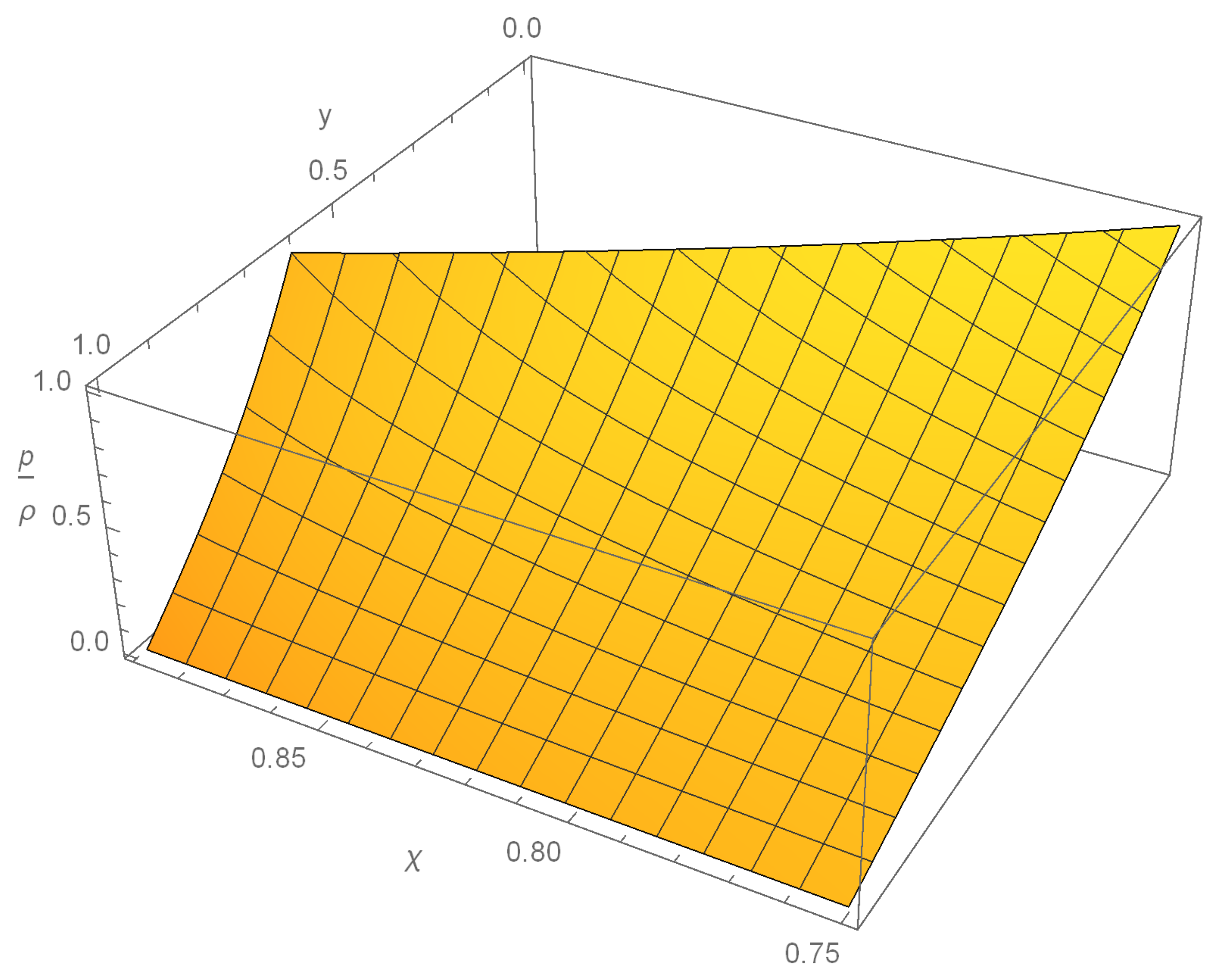
Within the second region $\frac{3}{4}<\chi \le \frac{8}{9},3-\frac{4}{\chi }\le y\le 1$, the radial force is maximized at:

$$\chi =\frac{8}{9},y=\frac{5}{8};\to F_r=\frac{5}{6}>\frac{1}{4}.$$

(41)

Under these conditions the strong maximum force conjecture is violated, though the weak maximum force conjecture is satisfied. This can be seen visually in Figure 5.

Turning to the hemispherical force, we see that the integrand used to define the integral for $F_{hemi}\left(\chi \right)$ satisfies the DEC only within the range $0\le \chi \le \frac{3}{4}$. Using the result for $F_{hemi}\left(\chi \right)$ given above, Equation (34), we have:

$${\left(F_{hemi}\right)}_{\max ,\mathrm{DEC}}=F_{hemi}(\chi =3/4)=\frac{3}{8}(2ln2-1)\approx 0.1448603854<\frac{1}{4}.$$

(42)

This now satisfies the strong maximum force conjecture.

3.2.4. Summary (Schwarzschild Interior)

Only if we enforce the DEC can we then make Schwarzschild’s constant density star satisfy the weak and strong maximum force conjectures. Without adding the DEC Schwarzschild’s constant density star will violate both the weak and strong maximum force conjectures. Since it is not entirely clear that the DEC represents fundamental physics [21,22,23,24], it is perhaps a little sobering to see that one of the very simplest idealized stellar models already raises issues for the maximum force conjecture. We shall soon see that the situation is even worse for the Tolman IV model (and its variants).

3.3. Tolman IV Solution

The Tolman IV solution is another perfect fluid star space-time; however, it does not have the convenient (albeit fine-tuned) property of constant density like the interior Schwarzschild solution. The metric can be written in the traditional form [10]:

$$d{s}^2=-\left(1+\frac{r^2}{A^2}\right)d{t}^2+\frac{1+\frac{2r^2}{A^2}}{\left(1-\frac{r^2}{R^2}\right)\left(1+\frac{r^2}{A^2}\right)}d{r}^2+r^{2}d{\mathsf{\Omega }}^2.$$

(43)

Here A and R represent some arbitrary scale factors with units of length. This metric yields the orthonormal stress–energy tensor:

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{t}}& =& \rho =\frac{1}{8\pi }\frac{6r^4+(7A^2+2R^2)r^2+3A^2(A^2+R^2)}{R^2{(A^2+2r^2)}^2};\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill T_{\widehat{r}\widehat{r}}& =& T_{\widehat{\theta }\widehat{\theta }}=T_{\widehat{\varphi }\widehat{\varphi }}=p=\frac{1}{8\pi }\frac{R^2-A^2-3r^2}{R^2(A^2+2r^2)}.\hfill \end{array}$$

(45)

This demonstrates the non-constancy of the energy-density $\rho$, as well as the perfect fluid conditions. Physically, the surface of a fluid star is defined as the zero pressure point, which is now at:

$$R_s=\sqrt{\frac{R^2-A^2}{3}}.$$

(46)

Likewise, we can find the surface density ($\rho$ at $R_0$):

$${\rho }_s=\frac{3}{4\pi }\frac{2A^2+R^2}{R^2(A^2+2R^2)}.$$

(47)

The central pressure and central density are

$$p_0=\frac{1}{8\pi }\frac{R^2-A^2}{R^2{A}^2};{\rho }_0=\frac{1}{8\pi }\frac{3(R^2+A^2)}{R^2{A}^2}.$$

(48)

Moving forwards, we will likewise calculate the radial and hemispherical forces in this space-time.

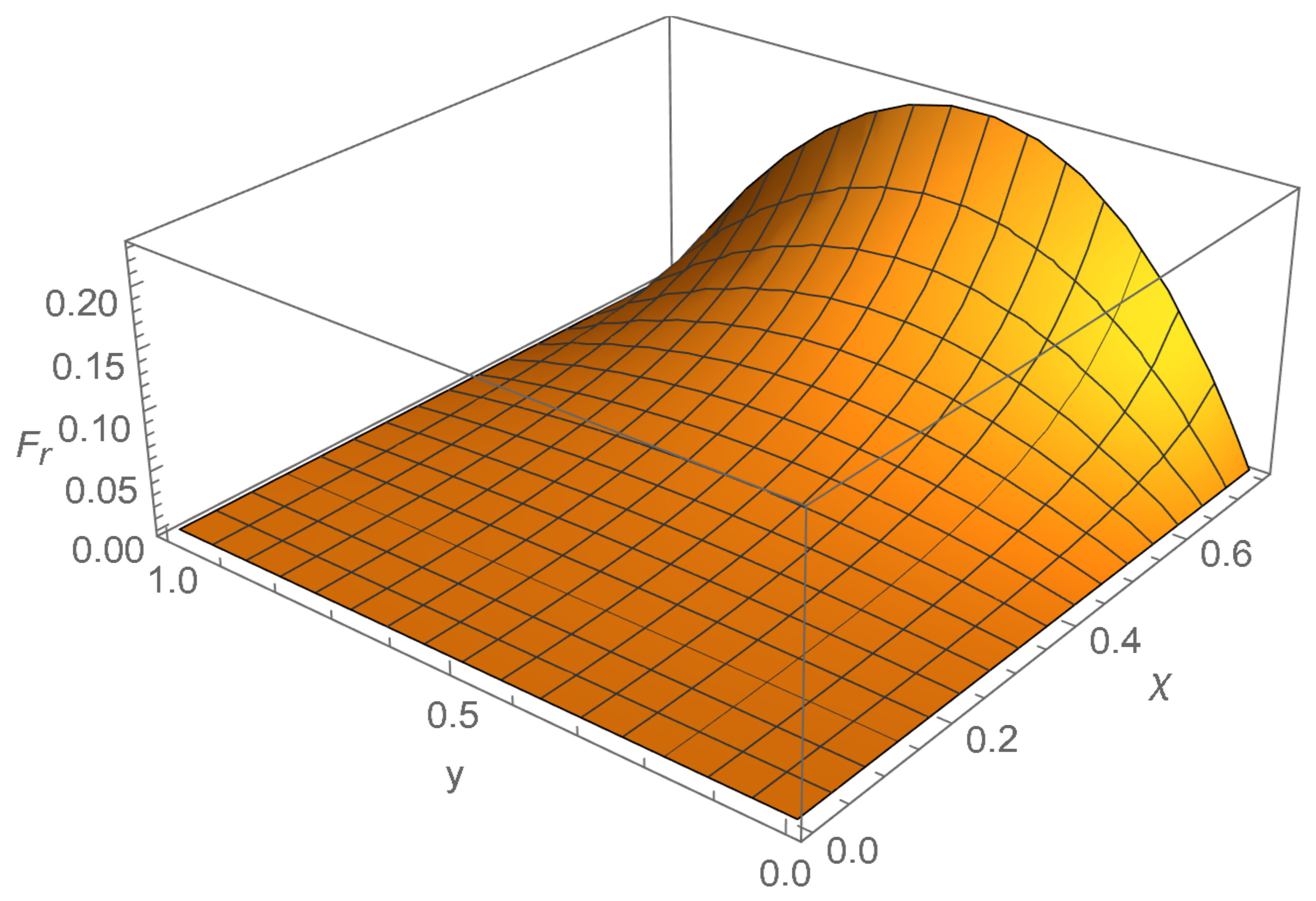
3.3.1. Radial Force

Using the previously defined radial force Equation (6), we can write the radial force for the Tolman IV space-time as:

$$F_r(r,R,A)=4\pi p_r{r}^2=\frac{r^2}{2R^2}\left(\frac{R^2-A^2-3r^2}{A^2+2r^2}\right).$$

(49)

Defining $y=r^2/R_s^2$ and $a=A^2/R^2$ we have $y\in (0,1)$ and $a\in (0,1)$. The radial force then simplifies to

$$F_r(a,y)=\frac{{(1-a)}^{2}y(1-y)}{6a+4(1-a)y}.$$

(50)

Note this is, as expected, a dimensionless function of dimensionless variables.

The multivariable derivatives are:

$${\partial }_a{F}_r(a,y)=\frac{y(1-y)(1-a)(2ay-3a-2y-3)}{2{(2ay-3a-2y)}^2}.$$

(51)

$${\partial }_y{F}_r(a,y)=\frac{{(1-a)}^2(2a{y}^2-6ay-2y^2-3a)}{2{(2ay-3a-2y)}^2}.$$

(52)

For both derivatives to vanish (within the physical region), we require $a=1$. However $a=1$ actually minimizes the function with $F_r(a,y)=0$. Therefore, we need to look at the boundaries of the physical region. Both $y=0$ and $y=1$ also minimize the function with $F_r(a,y)=0$. We thus consider $a=0$:

$$F_r(0,y)=\frac{1}{4}(1-y),$$

(53)

where then it is clear that the function is maximized at $a=0$, $y\to 0$, which corresponds to ${\left(F_r\right)}_{\max }=\frac{1}{4}$. This can be seen visually in Figure 6. Thus $F_r(a,y)$ for the Tolman IV solution is compatible with the strong maximum force conjecture, but as for the Schwarzschild constant density star, we shall soon see that the hemispherical force does not behave as nicely.

3.3.2. Hemispherical Force

Using Equation (9) for this space-time, and combining it with the radial surface result of Equation (46), we obtain:

$$F_{hemi}=2\pi {\int }_0^{R_s}\sqrt{g_{rr}}p\left(r\right)rdr=\frac{1}{4}{{\displaystyle \int }}_0^{\sqrt{\frac{R^2-A^2}{3}}}\sqrt{\frac{1+\frac{2r^2}{A^2}}{\left(1-\frac{r^2}{R^2}\right)\left(1+\frac{r^2}{A^2}\right)}}\frac{R^2-A^2-3r^2}{R^2(A^2+2r^2)}rdr.$$

(54)

As an integral this converges; however, the resultant function is intractable. Instead, we will opt for a simpler approach by finding a simple bound. Since the radial coordinate is physically bound by $0\le r\le R_s=\sqrt{\frac{R^2-A^2}{3}}<R$, we find that in that range:

$$\begin{array}{c}\hfill g_{rr}=\frac{1}{1-\frac{r^2}{R^2}}\frac{1+\frac{2r^2}{A^2}}{1+\frac{r^2}{A^2}}\ge \frac{1+\frac{2r^2}{A^2}}{1+\frac{r^2}{A^2}}\ge 1.\end{array}$$

(55)

This is actually a much more general result; for any perfect fluid sphere we have

$$g_{rr}=\frac{1}{1-2m\left(r\right)/r},$$

(56)

where $m\left(r\right)$ is the Misner–Sharp quasi-local mass.

So as long as $m\left(r\right)$ is positive, which is guaranteed by positivity of the density $\rho \left(r\right)$, we have $g_{rr}>1$, and so in all generality we have

$$F_{hemi}>2\pi {\int }_0^{R_s}p\left(r\right)rdr.$$

(57)

For the specific case of Tolman IV we can write

$$\begin{array}{ccc}\hfill F_{hemi}& >& \frac{1}{4}{{\displaystyle \int }}_0^{\sqrt{\frac{R^2-A^2}{3}}}\frac{R^2-A^2-3r^2}{R^2(A^2+2r^2)}rdr.\hfill \end{array}$$

(58)

Now make the substitutions $y=r^2/R_s^2$ and $a=A^2/R^2$. We find

$$F_{hemi}>\pi r_s^2{\int }_0^{1}pdy=\frac{1}{8}{\int }_0^1\frac{{\left(1-a\right)}^2\left(1-y\right)}{2\left(1-a\right)y+3a}dy.$$

(59)

This integral yields

$$F_{hemi}>{\left.\left\{\frac{(a+2)ln\left[\right(2y-3)a-2y]}{32}-\frac{(1-a)y}{16}\right\}\right|}_0^1.$$

(60)

Thence

$$F_{hemi}>\frac{(a+2)[ln(2+a)-ln(3a\left)\right]}{32}-\frac{(1-a)}{16}.$$

(61)

Under the limit $a\to 0$ we find that the term $-log\left(3a\right)\to +\infty$. Therefore, the inequality (61) diverges to infinity, demonstrating that the hemispherical force in the Tolman-IV space-time can be made to violate the weak maximum force conjecture.

Thus, as in the case of the interior Schwarzschild solution, we have shown that the radial force is bounded (and in this case obeys both the weak and strong maximum force conjectures). However, the hemispherical force can be made to diverge to infinity and act as a counter-example to both weak and strong conjectures.

3.3.3. DEC

To see if the DEC is satisfied over the range of integration for the hemispherical force, we inquire as to whether or not

$$\frac{p}{\rho }=\frac{(A^2+2r^2)(R^2-A^2-3r^2)}{3A^4+7A^2{r}^2+6r^4+(3A^2+2r^2)R^2}\le 1?$$

(62)

It is straightforward to check that this inequality will always hold in the physical region. Using the definitions $a=A^2/R^2$ and $z=r^2/R^2$, so that $a\in (0,1)$, and $z\in (0,\frac{1-a}{3})$, we can write this as

$$\frac{p}{\rho }-1=-\frac{2(2a^2+6az+a+6z^2)}{(7a+2)z+3a(a+1)+6z^2}<0,$$

(63)

which is manifestly negative. Therefore, adding the DEC does not affect or change our conclusions. Indeed, we have already seen that the hemispherical force diverges in the limit of $a\to 0$ implying $A\to 0$. Applying this limit to the ratio $p/\rho$ gives:

$$\underset{A\to 0}{lim}\frac{p}{\rho }=1-\frac{6r^2}{3r^2+R^2}=1-\frac{6y}{1+3y}\le 1.$$

(64)

Again, this is always true within any physical region, so we verify that adding the DEC does not change our conclusions.

3.3.4. Summary (Tolman IV)

For the Tolman IV solution, while the radial force is bounded (and obeys both the weak and strong maximum force conjectures), the hemispherical force can be made to diverge to infinity in certain parts of parameter space ($A\to 0$) and acts as a counter-example to both weak and strong maximum force conjectures. For the Tolman IV solution, adding the DEC does not save the situation; the violation of both weak and strong maximum force conjectures is robust.

3.4. Buchdahl–Land Spacetime: $\rho ={\rho }_s+p$

The Buchdahl–Land spacetime [33] is a special case of the Tolman IV spacetime, corresponding to the limit $A\to 0$ (equivalently $a\to 0$). It is sufficiently simple that it is worth some discussion in its own right. The Tolman IV metric (with a re-scaled time coordinate $t\to At$) can be written:

$$d{s}^2=-(A^2+r^2)d{t}^2+\frac{1+\frac{2r^2}{A^2}}{\left(1-\frac{r^2}{R^2}\right)\left(1+\frac{r^2}{A^2}\right)}d{r}^2+r^{2}d{\mathsf{\Omega }}^2.$$

(65)

Under the limit $A\to 0$, this becomes [33]:

$$d{s}^2=-r^{2}d{t}^2+\frac{2R^2}{R^2-r^2}d{r}^2+r^{2}d{\mathsf{\Omega }}^2.$$

(66)

Then the orthonormal stress–energy components are:

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{t}}& =& \rho =\frac{1}{16\pi }\left(\frac{1}{r^2}+\frac{3}{R^2}\right);\hfill \\ \hfill T_{\widehat{r}\widehat{r}}& =& T_{\widehat{\theta }\widehat{\theta }}=T_{\widehat{\varphi }\widehat{\varphi }}=p=\frac{1}{16\pi }\left(\frac{1}{r^2}-\frac{3}{R^2}\right).\hfill \end{array}$$

(67)

The surface is located at

$$R_s=\frac{R}{\sqrt{3}};\mathrm{with}{\rho }_s=\frac{3}{8\pi R^2}=\frac{1}{8\pi R_s^2}.$$

(68)

At the centre the pressure and density both diverge—more on this point later.

We recast the metric as

$$d{s}^2=-r^{2}d{t}^2+\frac{2}{1-\frac{1}{3}\frac{r^2}{R_s^2}}d{r}^2+r^{2}d{\mathsf{\Omega }}^2.$$

(69)

This is simply a relabeling of Equation (66). The orthonormal stress–energy tensor is now relabeled as:

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{t}}& =& \rho =\frac{1}{16\pi }\left(\frac{1}{r^2}+\frac{1}{R_s^2}\right);\hfill \\ \hfill T_{\widehat{r}\widehat{r}}& =& T_{\widehat{\theta }\widehat{\theta }}=T_{\widehat{\varphi }\widehat{\varphi }}=p=\frac{1}{16\pi }\left(\frac{1}{r^2}-\frac{1}{R_s^2}\right).\hfill \end{array}$$

(70)

Note that

$$p=\rho -{\rho }_s;\mathrm{that}\mathrm{is}\rho ={\rho }_s+p.$$

(71)

That is, the Buchdahl–Land spacetime represents a “stiff fluid”. This perfect fluid solution has a naked singularity at $r=0$ and a well behaved surface at finite radius. The singularity at $r=0$ is not really a problem as one can always excise a small core region near $r=0$ to regularize the model.

3.4.1. Radial Force

Due to the simplicity of the pressure, the radial force can be easily calculated as:

$$F_r=\frac{1}{4}\left(1-\frac{r^2}{R_s^2}\right).$$

(72)

The radial force is trivially bounded with a maximum of $\frac{1}{4}$ at the center of the star. This obeys the strong (and so also the weak) maximum force conjecture.

3.4.2. Hemispherical Force

The hemispherical force is:

$$\begin{array}{ccc}\hfill F_{hemi}& =& 2\pi {{\displaystyle \int }}_0^{R_s}\sqrt{\frac{2}{1-\frac{1}{3}\frac{r^2}{R_s^2}}}\frac{1}{16\pi }\left(\frac{1}{r^2}-\frac{1}{R_s^2}\right)rdr.\hfill \end{array}$$

(73)

This is now simple enough to handle analytically. Using the dimensionless variable $y=r^2/R_s^2$, with range $y\in (0,1)$, we see:

$$\begin{array}{ccc}\hfill F_{hemi}& =& \frac{1}{16}{{\displaystyle \int }}_0^1\sqrt{\frac{2}{1-\frac{1}{3}y}}\left(1-y\right)\frac{dy}{y}.\hfill \end{array}$$

(74)

This is manifestly dimensionless, and manifestly diverges to $+\infty$. If we excise a small region $r<r_{\mathrm{core}}$ (corresponding to $y<y_{\mathrm{core}}$) to regularize the model, replacing $r<r_{\mathrm{core}}$ with some well-behaved fluid ball, then we have the explicit logarithmic divergence

$$F_{hemi}=-\frac{1}{16}ln{y}_{\mathrm{core}}+\mathcal{O}\left(1\right).$$

(75)

This violates the weak (and so also the strong) maximum force conjecture.

3.4.3. DEC

The DEC for this space-time is given by:

$$\begin{array}{c}\hfill \frac{p}{\rho }=\frac{\rho -{\rho }_s}{\rho }=1-\frac{{\rho }_s}{\rho }\le 1.\end{array}$$

(76)

which is always true for positive values of r, ${\rho }_s$.

3.4.4. Summary (Buchdahl–Land)

Thus we see that the Buchdahl–Land spacetime provides yet another counter-example to the weak maximum force conjecture, a counter-example that again obeys the classical energy conditions.

3.5. Scaling Solution

The scaling solution is

$$d{s}^2=-r^{\frac{4w}{1+w}}d{t}^2+\left(\frac{w^2+6w+1}{{(1+w)}^2}\right)d{r}^2+r^{2}d{\mathsf{\Omega }}^2.$$

(77)

This produces the following stress–energy tensor:

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{t}}& =& \rho =\frac{w}{2\pi (w^2+6w+1)r^2};\hfill \\ \hfill T_{\widehat{r}\widehat{r}}& =& T_{\widehat{\theta }\widehat{\theta }}=T_{\widehat{\varphi }\widehat{\varphi }}=p=\frac{w^2}{2\pi (w^2+6w+1)r^2}.\hfill \end{array}$$

(78)

This perfect fluid solution has a naked singularity at $r=0$ and does not have a finite surface—it requires $r\to \infty$ for the pressure to vanish. Nevertheless, apart from a small region near $r=0$ and small fringe region near the surface $r=R_s$, this is a good approximation to the bulk geometry of a star that is on the verge of collapse [34,35]. To regularize the model we excise two small regions, a core region at $r\in (0,r_{\mathrm{core}})$ and an outer shell at $r\in (r_{\mathrm{fringe}},R_s)$, replacing them by segments of well-behaved fluid spheres. Note that for $r\in (r_{\mathrm{core}},r_{\mathrm{fringe}})$ we have $p/\rho =w$ (and since $\rho >0$ we must have $w>0$), so the DEC implies $w\in (0,1]$.

3.5.1. Radial Force

Using Equation (6), we find that the radial force is very simply given by:

$$F_r=\frac{2w^2}{w^2+6w+1}.$$

(79)

This is independent of r and attains a maximum value of $\frac{1}{4}$ when $w=1$, giving a bounded force obeying the strong maximum force conjecture.

3.5.2. Hemispherical Force

Now, using Equation (9), the hemispherical force can be calculated as:

$$F_{hemi}={{\displaystyle \int }}_{r_{\mathrm{core}}}^{r_{\mathrm{fringe}}}\sqrt{\frac{w^2+6w+1}{{(1+w)}^2}}\left(\frac{w^2}{(w^2+6w+1)r}\right)dr+\mathcal{O}\left(1\right).$$

(80)

That is

$$F_{hemi}=\frac{w^2}{(1+w)\sqrt{w^2+6w+1}}ln(r_{\mathrm{fringe}}/r_{\mathrm{core}})+\mathcal{O}\left(1\right),$$

(81)

which trivially diverges logarithmically as either $r_{\mathrm{core}}\to 0$ or $r_{\mathrm{fringe}}\to \infty$, providing a counter-example to the weak maximum force conjecture.

3.5.3. Summary (Scaling Spacetime Geometry)

For the scaling spacetime geometry we again have an explicit model where the radial force $F_r$ is well-behaved, but the hemispherical force $F_{hemi}$ provides an explicit counter-example to weak maximum force conjecture. This counter-example is compatible with the DEC.

3.6. TOV Equation

Let us now see how far we can push this sort of argument using only the TOV equation for the pressure profile in perfect fluid spheres—we will (as far as possible) try to avoid making specific assumptions on the metric components and stress-energy. The TOV equation is

$$\frac{dp\left(r\right)}{dr}=-\frac{\{\rho \left(r\right)+p\left(r\right)\}\{m\left(r\right)+4\pi p\left(r\right)r^3\}}{r^2\{1-2m\left(r\right)/r\}}.$$

(82)

3.6.1. Radial Force

From the definition of radial force $F_r=4\pi p{r}^2$, we see that at the maximum of $F_r$ we must have

$${\left.(2pr+r^2{p}^{\prime })\right|}_{r_{\max }}=0.$$

(83)

Thence, at the maximum

$${\left(F_r\right)}_{\max }={\left(4\pi p{r}^2\right)}_{\max }=-2\pi {\left.\left(r^3{p}^{\prime }\right)\right|}_{r_{\max }}.$$

(84)

In particular, now using the TOV at the location $r_{\max }$ of the maximum of $F_r$:

$${\left(F_r\right)}_{\max }=2\pi {\left.\left[\frac{(\rho +p)r(m+4\pi p{r}^3)}{(1-2m/r)}\right]\right|}_{r_{\max }}.$$

(85)

Let us define the two parameters

$$\chi ={\left[\frac{2m\left(r\right)}{r}\right]}_{r_{\max }}=\frac{2m\left(r_{\max }\right)}{r_{\max }},\mathrm{and}w={\left[\frac{p\left(r\right)}{\rho \left(r\right)}\right]}_{r_{\max }}=\frac{p\left(r_{\max }\right)}{\rho \left(r_{\max }\right)}.$$

(86)

Then

$${\left(F_r\right)}_{\max }=\frac{1}{2}{\left.\left(\frac{4\pi p(1+\frac{1}{w})r^2(\chi /2+4\pi p{r}^2)}{1-\chi }\right)\right|}_{r_{\max }}.$$

(87)

Simplifying, we see:

$${\left(F_r\right)}_{\max }=\frac{1}{2}\frac{{\left(F_r\right)}_{\max }[1+1/w][{\left(F_r\right)}_{\max }+\chi /2]}{1-\chi }$$

(88)

Discarding the unphysical solution ${\left(F_r\right)}_{\max }=0$, we find

$${\left(F_r\right)}_{\max }=\frac{4w-\chi -5w\chi }{2(1+w)}=\frac{2w}{1+w}-\chi \frac{1+5w}{1+w}.$$

(89)

The physical region corresponds to $0\le \chi <1$, while $w>0$. Furthermore we have ${\left(F_r\right)}_{\max }>0$, whence $4w-\chi -5w\chi >0$, implying $\chi <4w/(1+5w)<4/5$. That is, at the location $r_{\max }$ of the maximum of $F_r$ we have

$${\left[\frac{2m\left(r\right)}{r}\right]}_{r_{\max }}=\frac{2m\left(r_{\max }\right)}{r_{\max }}<\frac{4}{5}.$$

(90)

This is not the Buchdahl–Bondi bound, it is instead a bound on the compactness of the fluid sphere at the internal location $r_{\max }$ where $F_r$ is maximized.

Observe that ${\left(F_r\right)}_{\max }$ is maximized when $\chi =0$ and $w=\infty$, when ${\left(F_r\right)}_{\max }\to 2$. This violates the strong maximum force conjecture but not the weak maximum force conjecture. If we impose the DEC then $w\le 1$, and ${\left(F_r\right)}_{\max }$ is maximized when $\chi =0$ and $w=1$, when ${\left(F_r\right)}_{\max }\to 1$. This still violates the strong maximum force conjecture but not the weak maximum force conjecture. Consequently the weak conjecture for $F_r$ generically holds for any perfect fluid sphere satisfying the TOV.

3.6.2. Hemispherical Force

As we have by now come to expect, dealing with the hemispherical force will be considerably trickier. In view of the non-negativity of the Misner–Sharp quasi-local mass we have:

$$F_{hemi}=2\pi {\int }_0^{R_s}\sqrt{g_{rr}}prdr=2\pi {\int }_0^{R_s}\frac{1}{\sqrt{1-2m\left(r\right)/r}}prdr>2\pi {\int }_0^{R_s}prdr.$$

(91)

To make the integral ${\int }_0^{R_s}prdr$ converge it is sufficient to demand $p\left(r\right)=o(1/r^2)$. However, for stars on the verge of gravitational collapse it is known that $p\left(r\right)\sim K/r^2$; see for instance [34,35]. More specifically, there is some core region $r\in (0,r_{\mathrm{core}})$ designed to keep the central pressure finite but arbitrarily large, a large scaling region $r\in (r_{\mathrm{core}},r_{\mathrm{fringe}})$ where $p\sim K/r^2$, and an outer fringe $r\in (r_{\mathrm{fringe}},R_s)$ where one has $p\left(r\right)\to p\left(R_s\right)=0$. Then we have the identity

$${\int }_0^{R_s}prdr={\int }_0^{r_{\mathrm{core}}}prdr+{\int }_{r_{\mathrm{core}}}^{r_{\mathrm{fringe}}}prdr+{\int }_{r_{\mathrm{fringe}}}^{R_s}prdr.$$

(92)

However, under the assumed conditions this implies

$${\int }_0^{R_s}prdr=\mathcal{O}\left(1\right)+\left[{\int }_{r_{\mathrm{core}}}^{r_{\mathrm{fringe}}}\frac{K}{r}dr+\mathcal{O}\left(1\right)\right]+\mathcal{O}\left(1\right).$$

(93)

Thence

$${\int }_0^{R_s}prdr=Kln\left(r_{\mathrm{fringe}}/r_{\mathrm{core}}\right)+\mathcal{O}\left(1\right).$$

(94)

Finally

$$F_{hemi}>2\pi Kln\left(r_{\mathrm{fringe}}/r_{\mathrm{core}}\right)+\mathcal{O}\left(1\right).$$

(95)

This can be made arbitrarily large for a star on the verge of gravitational collapse, so the weak and strong maximum force conjectures are both violated.

Note that technical aspects of the argument are very similar to what we saw for the exact scaling solution to the Einstein equations, but the physical context is now much more general.

3.6.3. Summary (TOV)

We see that the weak maximum force conjecture generically holds for the radial force $F_r$ when considering perfect fluid spheres satisfying the TOV. In contrast we see that the weak maximum force conjecture fails for the hemispherical force $F_{hemi}$ when considering perfect fluid spheres satisfying the TOV that are close to gravitational collapse.

4. Discussion

With the notion of a natural unit of force $F_{*}=F_{\mathrm{Planck}}=c^4/G_N$ in hand, one can similarly define a natural unit of power [36]1, [37,38,39]

$$P_{*}=P_{\mathrm{Planck}}=\frac{c^5}{G_N}=1\mathrm{Dyson}\approx 3.6\times {10}^{52}\mathrm{W},$$

(96)

a natural unit of mass-loss-rate

$${\left(\dot{m}\right)}_{*}={\left(\dot{m}\right)}_{\mathrm{Planck}}=\frac{c^3}{G_N}\approx 4.0\times {10}^{35}\mathrm{kg}/\mathrm{s},$$

(97)

and even a natural unit of mass-per-unit-length

$${\left(m^{\prime }\right)}_{*}={\left(m^{\prime }\right)}_{\mathrm{Planck}}=\frac{c^2}{G_N}\approx 1.36\times {10}^{27}\mathrm{kg}/\mathrm{m}.$$

(98)

Despite being Planck units, all these concepts are purely classical (the various factors of ℏ cancel, at least in (3 + 1) dimensions).

Indeed, consider the classical Stoney units, which pre-date Planck units by some 20 years [40,41,42], and use $G_N$, c, and Coulomb’s constant $\frac{e^2}{4\pi {ϵ}_0}$, instead of $G_N$, c, and Planck’s constant ℏ. Then we have $F_{*}=F_{\mathrm{Planck}}=F_{\mathrm{Stoney}}$. Similarly we have $P_{*}=P_{\mathrm{Planck}}=P_{\mathrm{Stoney}}$, ${\left(\dot{m}\right)}_{*}={\left(\dot{m}\right)}_{\mathrm{Planck}}={\left(\dot{m}\right)}_{\mathrm{Stoney}}$, and ${\left(m^{\prime }\right)}_{*}={\left(m^{\prime }\right)}_{\mathrm{Planck}}={\left(m^{\prime }\right)}_{\mathrm{Stoney}}$. Based ultimately on dimensional analysis, any one of these quantities might be used to advocate for a maximality conjecture: maximum luminosity [36,37,38,39], maximum mass-loss-rate, or maximum mass-per-unit-length. Among these conjectures, the maximum luminosity conjecture is often misattributed to Freeman Dyson. In reply to an enquiry by Christoph Schiller, Freeman Dyson replied on 14 February 2011:

“It is not true that I proposed the formula $c^5/G$ as a luminosity limit for anything. I make no such claim. Perhaps this notion arose from a paper that I wrote in 1962 with the title, “Gravitational Machines”, published as Chapter 12 in the book, “Interstellar Communication” edited by Alastair Cameron, [New York, Benjamin, 1963]. Equation (11) in that paper is the well-known formula $128V^{10}/5G{c}^5$ for the power in gravitational waves emitted by a binary star with two equal masses moving in a circular orbit with velocity V. As V approaches its upper limit c, this gravitational power approaches the upper limit $128c^5/5G$. The remarkable thing about this upper limit is that it is independent of the masses of the stars. It may be of some relevance to the theory of gamma-ray bursts”.

See footnote 5 in reference [37]. The specific counter-examples to the maximum force conjecture that we have discussed above suggest that it might also be worth looking for specific counter-examples to these other conjectures [38].

5. Conclusions

Through the analysis of radial and hemispherical forces within idealized perfect fluid spheres in general relativity, we have produced a number of idealized counter-examples to both the strong and weak forms of the maximum force conjecture. These idealized counter-examples highlight significant issues with the current phrasing and understanding of this conjecture, as merely specifying (without qualifying conditions) that forces are bounded within the framework of general relativity is manifestly a falsehood. As such, should one wish some version of the maximum force conjecture to be considered viable as a potential physical principle, it must be very clearly specified as to what types of forces they pertain to.