Weak Deflection Angle and Shadow by Tidal Charged Black Hole
Abstract
:1. Introduction
2. Optical Metric of TCBH
3. Deflection Angle of TCBH
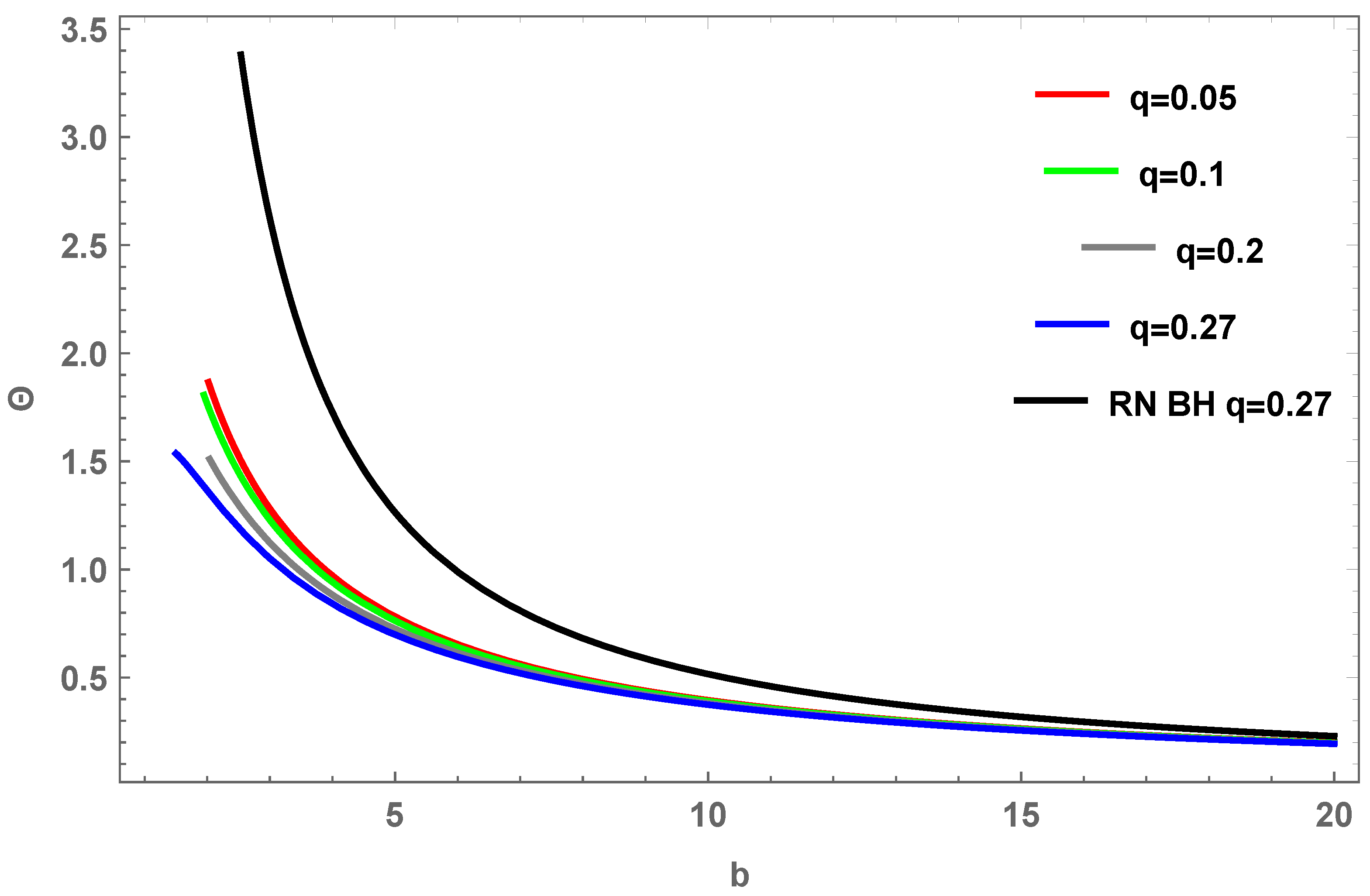
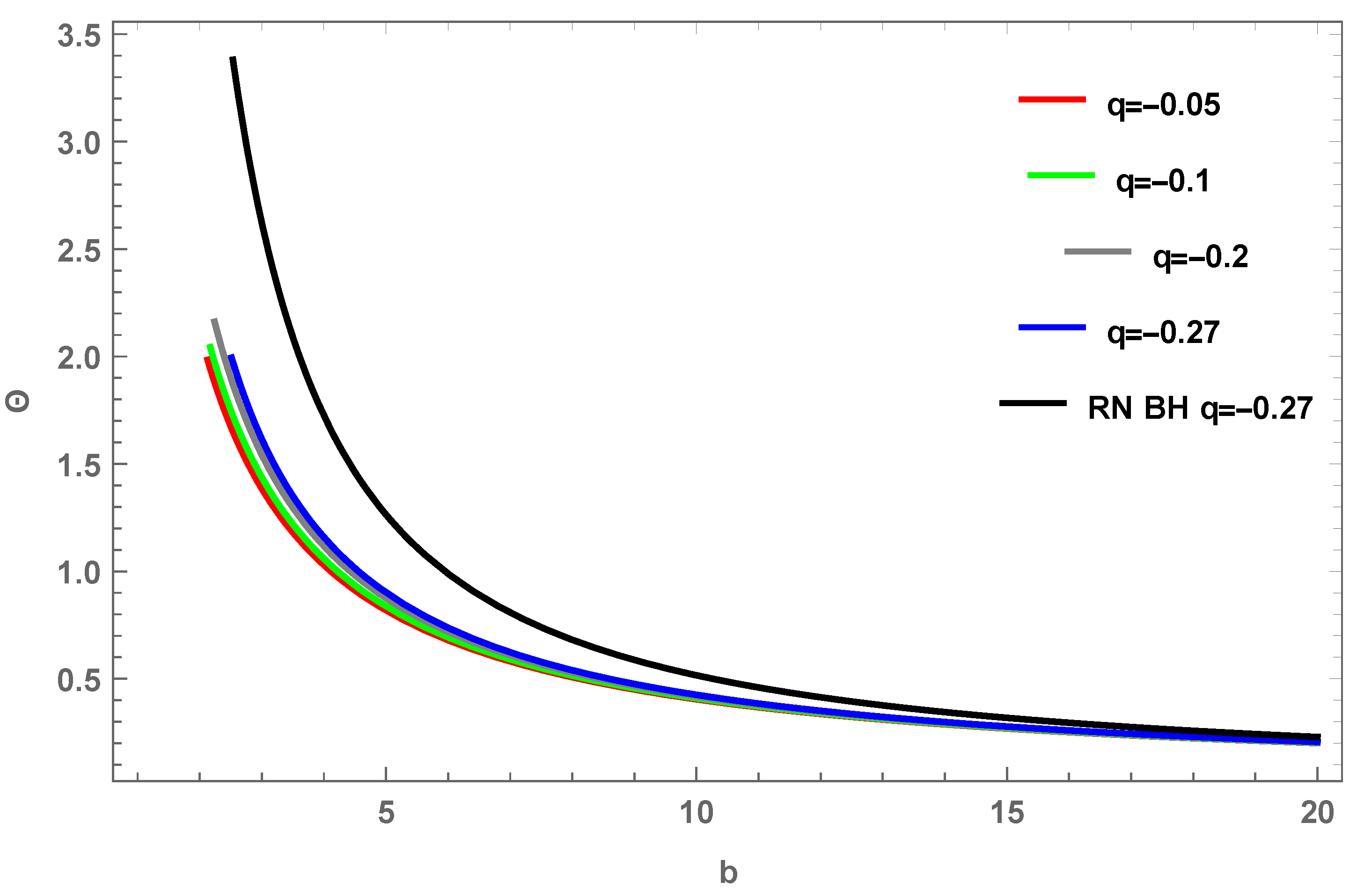
4. Graphical Analysis for Non-Plasma Medium
5. Effect of Plasma on Gravitational Lensing
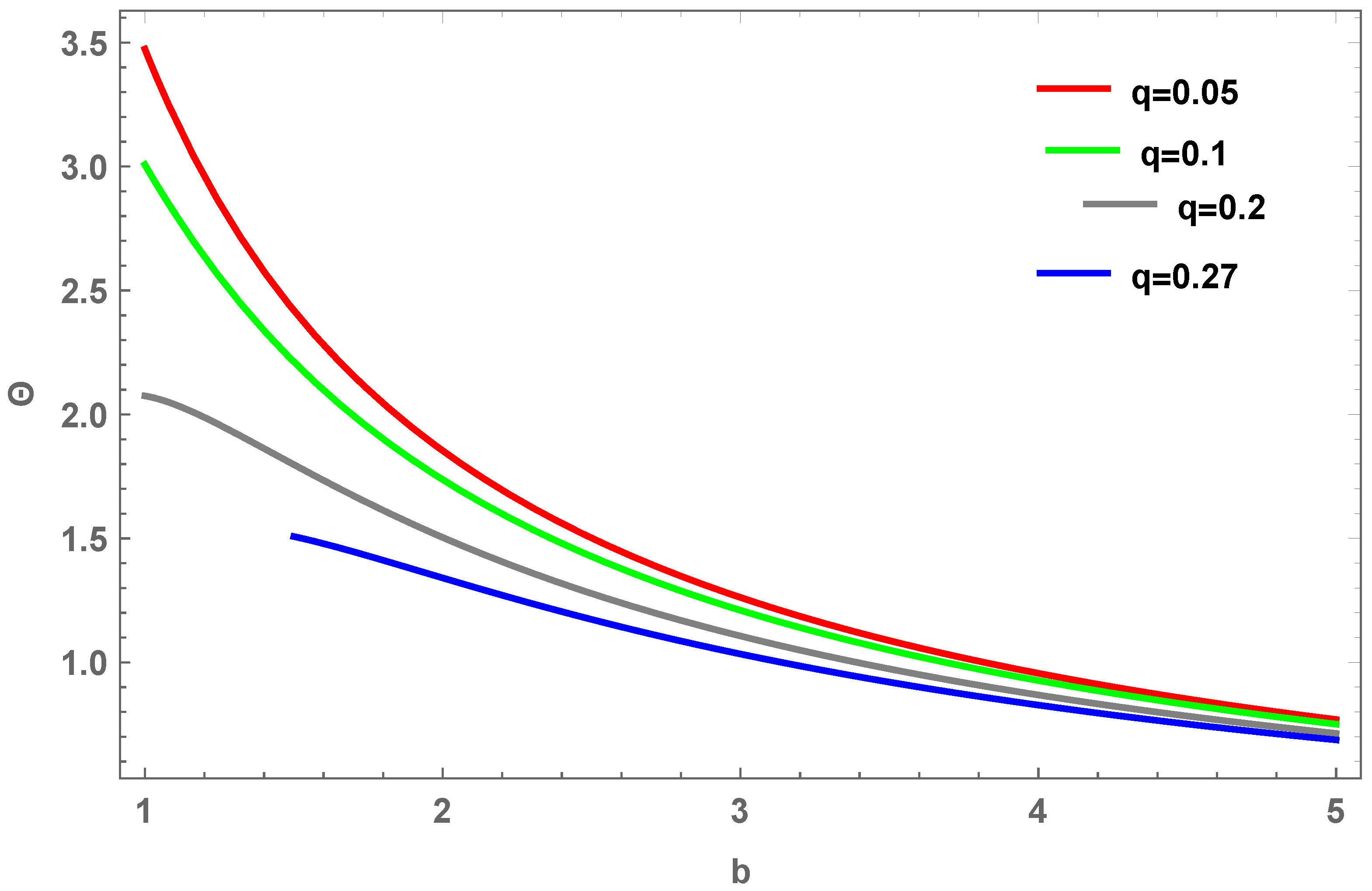
6. Graphical Analysis for Plasma Medium
7. Null Geodesic in a TCBH
8. Shadow of TCBH
9. Effect of Plasma on Shadow of TCBH
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Einstein, A. Lens-Like Action of a Star by the Deviation of Light in the Gravitational Field. Science 1936, 84, 506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Akiyama, K.; Antxon, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar]
- Mathur, S.D. The information paradox: A pedagogical introduction. Class. Quant. Grav. 2009, 26, 224001. [Google Scholar] [CrossRef] [Green Version]
- Bartelmann, M. Gravitational lensing. Class. Quant. Grav. 2010, 27, 233001. [Google Scholar] [CrossRef] [Green Version]
- Keeton, C.R.; Kochanek, C.S.; Falco, E.E. The Optical Properties of Gravitational Lens Galaxies as a Probe of Galaxy Structure and Evolution. Astrophys. J. 1998, 509, 561. [Google Scholar] [CrossRef] [Green Version]
- Bhadra, A. Gravitational lensing by a charged black hole of string theory. Phys. Rev. D 2003, 67, 103009. [Google Scholar] [CrossRef] [Green Version]
- Whisker, R. Strong gravitational lensing by braneworld black holes. Phys. Rev. D 2005, 71, 064004. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.B.; Jing, J.L. Strong field gravitational lensing in the deformed Hořava-Lifshitz black hole. Phys. Rev. D 2009, 80, 024036. [Google Scholar] [CrossRef] [Green Version]
- Nandi, K.K.; Zhang, Y.Z.; Zakharov, A.V. Gravitational lensing by wormholes. Phys. Rev. D 2006, 74, 024020. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, A.F. Constraints on a charge in the Reissner-Nordström metric for the black hole at the Galactic Center. Phys. Rev. D 2014, 90, 062007. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, A.F. Constraints on tidal charge of the supermassive black hole at the Galactic Center with trajectories of bright stars. Eur. Phys. J. C 2018, 78, 689. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, A.F. Constraints on a tidal charge of the supermassive black hole in M87* with the EHT observations in April 2017. arXiv 2021, arXiv:2108.01533. [Google Scholar]
- Neves, J.C.S. Constraining the tidal charge of brane black holes using their shadows. Eur. Phys. J. C 2020, 80, 717. [Google Scholar] [CrossRef]
- Eiroa, E.F.; Romero, G.E.; Torres, D.F. Reissner-Nordström black hole lensing. Phys. Rev. D 2002, 66, 024010. [Google Scholar] [CrossRef] [Green Version]
- Mao, S.; Paczynski, B. Gravitational Microlensing by Double Stars and Planetary Systems. Astrophys. J. 1991, 374, L37. [Google Scholar] [CrossRef]
- Bozza, V. Gravitational lensing in the strong field limit. Phys. Rev. D 2002, 66, 103001. [Google Scholar] [CrossRef] [Green Version]
- Hoekstra, H.; Yee, H.K.C.; Gladders, M.D. Properties of Galaxy Dark Matter Halos from Weak Lensing. Astrophys. J. 2004, 606, 67. [Google Scholar] [CrossRef] [Green Version]
- Virbhadra, K.S.; Ellis, G.F.R. Gravitational lensing by naked singularities. Phys. Rev. D 2002, 65, 103004. [Google Scholar] [CrossRef]
- Övgün, A. Black hole with confining electric potential in scalar-tensor description of regularized 4-dimensional Einstein-Gauss-Bonnet gravity. Phys. Lett. B 2021, 820, 136517. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef] [Green Version]
- Kasikci, O.; Deliduman, C. Gravitational lensing in Weyl gravity. Phys. Rev. D 2019, 100, 024019. [Google Scholar] [CrossRef] [Green Version]
- Gallo, E.; Moreschi, O.M. Gravitational lens optical scalars in terms of energy-momentum distributions. Phys. Rev. D 2011, 83, 083007. [Google Scholar] [CrossRef] [Green Version]
- Crisnejo, G.; Gallo, E. Expressions for optical scalars and deflection angle at second order in terms of curvature scalars. Phys. Rev. D 2018, 97, 084010. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Iftikhar, S. Strong gravitational lensing in non-commutative wormholes. Astrophys. Space Sci. 2015, 357, 85. [Google Scholar] [CrossRef]
- Gibbons, G.W. No glory in cosmic string theory. Phys. Lett. B 1993, 308, 237. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Edery, A.; Paranjape, M.B. Classical tests for Weyl gravity: Deflection of light and time delay. Phys. Rev. D 1998, 58, 024011. [Google Scholar] [CrossRef] [Green Version]
- Bodenner, J.; Will, C. Deflection of light to second order: A tool for illustrating principles of general relativity. Am. J. Phys. 2003, 71, 770. [Google Scholar] [CrossRef] [Green Version]
- Nakajima, K.; Asada, H. Deflection angle of light in an Ellis wormhole geometry. Phys. Rev. D 2012, 85, 107501. [Google Scholar] [CrossRef] [Green Version]
- Cao, W.G.; Xie, Y. Weak deflection gravitational lensing for photons coupled to Weyl tensor in a Schwarzschild black hole. Eur. Phys. J. C 2018, 78, 191. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Y.; Shen, Y.F.; Xie, Y. Inflation with R2 term in the Palatini formulation. J. Cosmol. Astropart. Phys. 2019, 2019, 022. [Google Scholar] [CrossRef] [Green Version]
- Gibbons, G.W.; Werner, M.C. Applications of the Gauss–Bonnet theorem to gravitational lensing. Class. Quantum Gravity 2008, 25, 235009. [Google Scholar] [CrossRef]
- Werner, M.C. Gravitational lensing in the Kerr-Randers optical geometry. Gen. Rel. Grav. 2012, 44, 3047–3057. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Sakalli, I.; Övgün, A. Effect of Lorentz symmetry breaking on the deflection of light in a cosmic string spacetime. Phys. Rev. D 2017, 96, 024040. [Google Scholar]
- Li, Z.; Övgün, A. Finite-Distance Gravitational Deflection of Massive Particles by the Kerr-like Black Hole in the Bumblebee Gravity Model. Phys. Rev. D 2020, 101, 024040. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Övgün, A. Gravitational lensing by rotating wormholes. Phys. Rev. D 2018, 97, 024042. [Google Scholar] [CrossRef] [Green Version]
- Kumaran, Y.; Övgün, A. Weak deflection angle of extended uncertainty principle black holes. Chin. Phys. C 2020, 44, 025101. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Övgün, A.; Saavedra, J.; Vasquez, Y.; Gonzalez, P.A. Deflection of light by rotating regular black holes using the Gauss-Bonnet theorem. Phys. Rev. D 2018, 97, 124024. [Google Scholar] [CrossRef] [Green Version]
- Sakalli, I.; Ovgun, A. Hawking radiation and deflection of light from Rindler modified Schwarzschild black hole. Europhys. Lett. 2017, 118, 60006. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Övgün, A. Light Deflection by a Quantum Improved Kerr Black Hole Pierced by a Cosmic String. Int. J. Geom. Meth. Mod. Phys. 2019, 16, 1950116. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Övgün, A. Effect of the cosmological constant on the deflection angle by a rotating cosmic string. Phys. Rev. D 2018, 97, 064030. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; He, G.; Zhou, T. Gravitational deflection of relativistic massive particles by wormholes. Phys. Rev. D 2020, 101, 044001. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A.; Gyulchev, G.; Jusufi, K. Weak Gravitational lensing by phantom black holes and phantom wormholes using the Gauss–Bonnet theorem. Ann. Phys. 2019, 406, 152. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhou, T. Equivalence of Gibbons-Werner method to geodesics method in the study of gravitational lensing. Phys. Rev. D 2020, 101, 044043. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Övgün, A.; Banerjee, A.; Sakalli, I. Gravitational lensing by wormholes supported by electromagnetic, scalar, and quantum effects. Eur. Phys. J. Plus 2019, 134, 428. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Jia, J. The finite-distance gravitational deflection of massive particles in stationary spacetime: A Jacobi metric approach. Eur. Phys. J. C 2020, 80, 157. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Werner, M.C.; Banerjee, A.; Övgün, A. Light deflection by a rotating global monopole spacetime. Phys. Rev. D 2017, 95, 104012. [Google Scholar] [CrossRef] [Green Version]
- Takizawa, K.; Ono, T.; Asada, H. Gravitational deflection angle of light: Definition by an observer and its application to an asymptotically nonflat spacetime. Phys. Rev. D 2020, 101, 104032. [Google Scholar] [CrossRef]
- Ono, T.; Ishihara, A.; Asada, H. Deflection angle of light for an observer and source at finite distance from a rotating global monopole. Phys. Rev. D 2019, 99, 124030. [Google Scholar] [CrossRef] [Green Version]
- Ono, T.; Ishihara, A.; Asada, H. Deflection angle of light for an observer and source at finite distance from a rotating wormhole. Phys. Rev. D 2018, 98, 044047. [Google Scholar] [CrossRef] [Green Version]
- Ono, T.; Asada, H. The effects of finite distance on the gravitational deflection angle of light. Universe 2019, 5, 218. [Google Scholar] [CrossRef] [Green Version]
- Pantig, R.C.; Rodulfo, E.T. Weak lensing of a dirty black hole. Chin. J. Phys. 2020, 66, 691–702. [Google Scholar] [CrossRef]
- Övgün, A.; Jusufi, K.; Sakalli, I. Gravitational lensing under the effect of Weyl and bumblebee gravities: Applications of Gauss–Bonnet theorem. Ann. Phys. 2018, 399, 193. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A.; Jusufi, K.; Sakalli, I. Exact traversable wormhole solution in bumblebee gravity. Phys. Rev. D 2019, 99, 024042. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A.; Sakalli, I.; Saavedra, J. Shadow cast and Deflection angle of Kerr-Newman-Kasuya spacetime. JCAP 2018, 1810, 041. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A. Deflection Angle of photons through dark matter by black holes and wormholes using Gauss–Bonnet theorem. Universe 2019, 5, 115. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A. Light deflection by Damour-Solodukhin wormholes and Gauss-Bonnet theorem. Phys. Rev. D 2018, 98, 044033. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A.; Sakalli, I.; Saavedra, J. Weak gravitational lensing by Kerr-MOG black hole and Gauss–Bonnet theorem. Annals Phys. 2019, 411, 167978. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A. Weak field deflection angle by regular black holes with cosmic strings using the Gauss-Bonnet theorem. Phys. Rev. D 2019, 99, 104075. [Google Scholar] [CrossRef] [Green Version]
- Javed, W.; Babar, R.; Övgün, A. Effect of the Brane-Dicke coupling parameter on weak gravitational lensing by wormholes and naked singularities. Phys. Rev. D 2019, 99, 084012. [Google Scholar] [CrossRef] [Green Version]
- Javed, W.; Babar, R.; Övgün, A. Effect of the dilaton field and plasma medium on deflection angle by black holes in Einstein-Maxwell-dilaton-axion theory. Phys. Rev. D 2019, 100, 104032. [Google Scholar] [CrossRef] [Green Version]
- Javed, W.; Abbas, J.; Övgün, A. Effect of the hair on deflection angle by asymptotically flat black holes in Einstein-Maxwell-dilaton theory. Phys. Rev. D 2019, 100, 044052. [Google Scholar] [CrossRef] [Green Version]
- Javed, W.; Abbas, J.; Övgün, A. Deflection angle of photon from magnetized black hole and effect of nonlinear electrodynamics. Eur. Phys. J. C 2019, 79, 694. [Google Scholar] [CrossRef] [Green Version]
- Javed, W.; Khadim, M.B.; Övgün, A.; Abbas, J. Weak gravitational lensing by stringy black holes. Eur. Phys. J. Plus 2020, 135, 314. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, A.; Suzuki, Y.; Ono, T.; Kitamura, T.; Asada, H. Gravitational bending angle of light for finite distance and the Gauss-Bonnet theorem. Phys. Rev. D 2016, 94, 084015. [Google Scholar] [CrossRef] [Green Version]
- Ono, T.; Ishihara, A.; Asada, H. Gravitomagnetic bending angle of light with finite-distance corrections in stationary axisymmetric spacetimes. Phys. Rev. D 2017, 96, 104037. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, A.; Suzuki, Y.; Ono, T.; Asada, H. Finite-distance corrections to the gravitational bending angle of light in the strong deflection limit. Phys. Rev. D 2017, 95, 044017. [Google Scholar] [CrossRef] [Green Version]
- Crisnejo, G.; Gallo, E. Weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss-Bonnet theorem. A unified treatment. Phys. Rev. D 2018, 97, 124016. [Google Scholar] [CrossRef] [Green Version]
- Bisnovatyi-Kogan, G.S.; Tsupko, O.Y. Gravitational radiospectrometer. Gravit. Cosmol. 2009, 15, 20. [Google Scholar] [CrossRef]
- Okyay, M.; Övgün, A. Nonlinear electrodynamics effects on the black hole shadow, deflection angle, quasinormal modes and greybody factors. arXiv 2021, arXiv:2108.07766. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Tsupko, O.Y. Gravitational lensing in a non-uniform plasma. Mon. Not. R. Astron. Soc. 2010, 404, 1790. [Google Scholar] [CrossRef] [Green Version]
- Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Gravitational lensing in plasma: Relativistic images at homogeneous plasma. Phys. Rev. D 2013, 87, 124009. [Google Scholar] [CrossRef] [Green Version]
- Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Influence of plasma on relativistic images of gravitational lensing. Nonlin. Phenom. Complex Syst. 2014, 17, 455. [Google Scholar]
- Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Gravitational lensing in the presence of plasmas and strong gravitational fields. Gravit. Cosmol. 2014, 20, 220. [Google Scholar] [CrossRef]
- Perlick, V.; Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Influence of a plasma on the shadow of a spherically symmetric black hole. Phys. Rev. D 2015, 92, 104031. [Google Scholar] [CrossRef] [Green Version]
- Bisnovatyi-Kogan, G.S.; Tsupko, O.Y. Gravitational lensing in plasmic medium. Plasma Phys. Rep. 2015, 41, 562. [Google Scholar] [CrossRef] [Green Version]
- Pantig, R.C.; Rodulfo, E.T. Rotating dirty black hole and its shadow. Chin. J. Phys. 2020, 68, 236–257. [Google Scholar] [CrossRef]
- Perlick, V.; Tsupko, O.Y. Light propagation in a plasma on Kerr spacetime: Separation of the Hamilton-Jacobi equation and calculation of the shadow. Phys. Rev. D 2017, 95, 104003. [Google Scholar] [CrossRef] [Green Version]
- Bisnovatyi-Kogan, G.; Tsupko, O. Gravitational lensing in presence of Plasma: Strong lens systems, black hole lensing and shadow. Universe 2017, 3, 57. [Google Scholar] [CrossRef] [Green Version]
- Morozova, V.S.; Ahmedov, B.J.; Tursunov, A.A. Gravitational lensing by a rotating massive object in a plasma. Astrophys. Space Sci. 2013, 346, 513. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.; Juraev, B.; Ahmedov, B.; Stuchlik, Z. Shadow of rotating wormhole in plasma environment. Astrophys. Space Sci. 2016, 361, 226. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Toshmatov, B.; Stuchlik, Z.; Ahmedov, B. Shadow of the rotating black hole with quintessential energy in the presence of plasma. Int. J. Mod. Phys. Conf. Ser. 2017, 26, 1750051. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Toshmatov, B.; Schee, J.; Stuchlik, Z.; Ahmedov, B. Gravitational lensing by regular black holes surrounded by plasma. Int. J. Mod. Phys. D 2017, 26, 1741011. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B.; Dadhich, N.; Atamurotov, F. Optical properties of a braneworld black hole: Gravitational lensing and retrolensing. Phys. Rev. D 2017, 96, 084017. [Google Scholar] [CrossRef]
- Turimov, B.; Ahmedov, B.; Abdujabbarov, A.; Bambi, C. Gravitational lensing by a magnetized compact object in the presence of plasma. Int. J. Mod. Phys. D 2019, 28, 2040013. [Google Scholar] [CrossRef] [Green Version]
- Rogers, A. Frequency-dependent effects of gravitational lensing within plasma. Mon. Not. R. Astron. Soc. 2015, 451, 17. [Google Scholar] [CrossRef]
- Rogers, A. Escape and trapping of low-frequency gravitationally lensed rays by compact objects within plasma. Mon. Not. R. Astron. Soc. 2017, 465, 2151. [Google Scholar] [CrossRef] [Green Version]
- Rogers, A. Gravitational lensing of rays through the levitating atmospheres of compact objects. Universe 2017, 3, 3. [Google Scholar] [CrossRef] [Green Version]
- Er, X.; Rogers, A. Two families of astrophysical diverging lens models. Mon. Not. R. Astron. Soc. 2018, 475, 867. [Google Scholar] [CrossRef] [Green Version]
- Kocherlakota, P.; Rezzolla, L.; Falcke, H.; Fromm, C.M.; Kramer, M.; Mizuno, Y.; Nathanail, A.; Olivares, H.; Younsi, Z.; Akiyama, K.; et al. Constraints on black-hole charges with the 2017 EHT observations of M87*. Phys. Rev. D 2021, 103, 104047. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Pappas, T.; Zhidenko, A. Einstein-scalar-Gauss-Bonnet black holes: Analytical approximation for the metric and applications to calculations of shadows. Phys. Rev. D 2020, 101, 044054. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.A. Shadow of a black hole surrounded by dark matter. Phys. Lett. B 2019, 795, 1. [Google Scholar] [CrossRef]
- Lu, X.; Xie, Y. Weak and strong deflection gravitational lensing by a renormalization group improved Schwarzschild black hole. Eur. Phys. J. C 2019, 79, 1016. [Google Scholar] [CrossRef] [Green Version]
- Allahyari, A.; Khodadi, M.; Vagnozzi, S.; Mota, D.F. Magnetically charged black holes from non-linear electrodynamics and the Event Horizon Telescope. JCAP 2002, 2020, 003. [Google Scholar] [CrossRef] [Green Version]
- Narayan, R.; Johnson, M.D.; Gammie, C.F. The Shadow of a Spherically Accreting Black Hole. Astrophys. J. 2019, 885, L33. [Google Scholar] [CrossRef] [Green Version]
- Ding, C.; Liu, C.; Casana, R.; Cavalcante, A. Exact Kerr-like solution and its shadow in a gravity model with spontaneous Lorentz symmetry breaking. Eur. Phys. J. C 2020, 80, 178. [Google Scholar] [CrossRef] [Green Version]
- Shaikh, R.; Joshi, P.S. Can we distinguish black holes from naked singularities by the images of their accretion disks? JCAP 2019, 1910, 064. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, I.; Chakraborty, S.; SenGupta, S. Silhouette of M87*: A New Window to Peek into the World of Hidden Dimensions. Phys. Rev. D 2020, 101, 041301. [Google Scholar] [CrossRef] [Green Version]
- Carter, B. Global structure of the Kerr family of gravitational fields. Phys. Rev. 1968, 174, 1559. [Google Scholar] [CrossRef] [Green Version]
- Bardeen, J. Black holes. In Proceeding of the Les Houches Summer School, Session 215239; Cécile DeWitt and Bryce DeWitt; Gordon and Breach: New York, NY, USA, 1973. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Dadhich, N.; Maartens, R.; Papadopoulos, P.; Rezania, V. Black holes on the brane. Phys. Lett. B 2000, 487, 1. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, P. Circular Geodesics in Tidal Charged Black Hole. Int. J. Geom. Meth. Mod. Phys. 2017, 15, 1850011. [Google Scholar] [CrossRef] [Green Version]
- Keeton, C.R. and Petters, A.O. Formalism for testing theories of gravity using lensing by compact objects: Static, spherically symmetric case. Phys. Rev. D 2005, 72, 104006. [Google Scholar] [CrossRef] [Green Version]
- Synge, J.L. The Escape of Photons from Gravitationally Intense Stars. Mon. Not. R. Astron. Soc. 1966, 131, 463. [Google Scholar] [CrossRef]
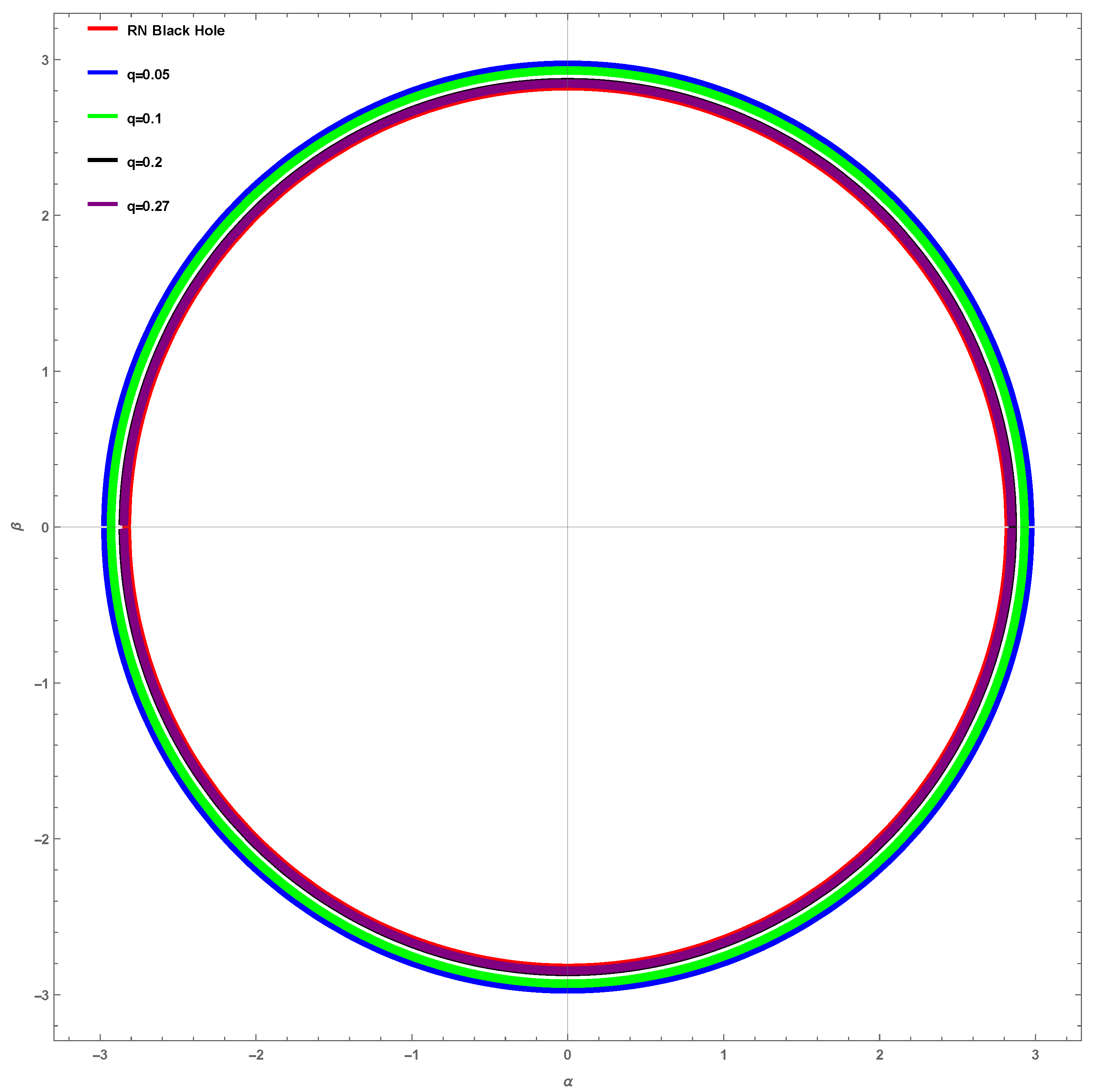
| q | ||
|---|---|---|
| 0.05 | 2.86015 | 2.96572 |
| 0.1 | 2.70416 | 2.92949 |
| 0.2 | 2.30623 | 2.8537 |
| 0.27 | 1.8 | 2.84605 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javed, W.; Hamza, A.; Övgün, A. Weak Deflection Angle and Shadow by Tidal Charged Black Hole. Universe 2021, 7, 385. https://doi.org/10.3390/universe7100385
Javed W, Hamza A, Övgün A. Weak Deflection Angle and Shadow by Tidal Charged Black Hole. Universe. 2021; 7(10):385. https://doi.org/10.3390/universe7100385
Chicago/Turabian StyleJaved, Wajiha, Ali Hamza, and Ali Övgün. 2021. "Weak Deflection Angle and Shadow by Tidal Charged Black Hole" Universe 7, no. 10: 385. https://doi.org/10.3390/universe7100385
APA StyleJaved, W., Hamza, A., & Övgün, A. (2021). Weak Deflection Angle and Shadow by Tidal Charged Black Hole. Universe, 7(10), 385. https://doi.org/10.3390/universe7100385







