An SU(2) Gauge Principle for the Cosmic Microwave Background: Perspectives on the Dark Sector of the Cosmological Model
Abstract
1. Introduction
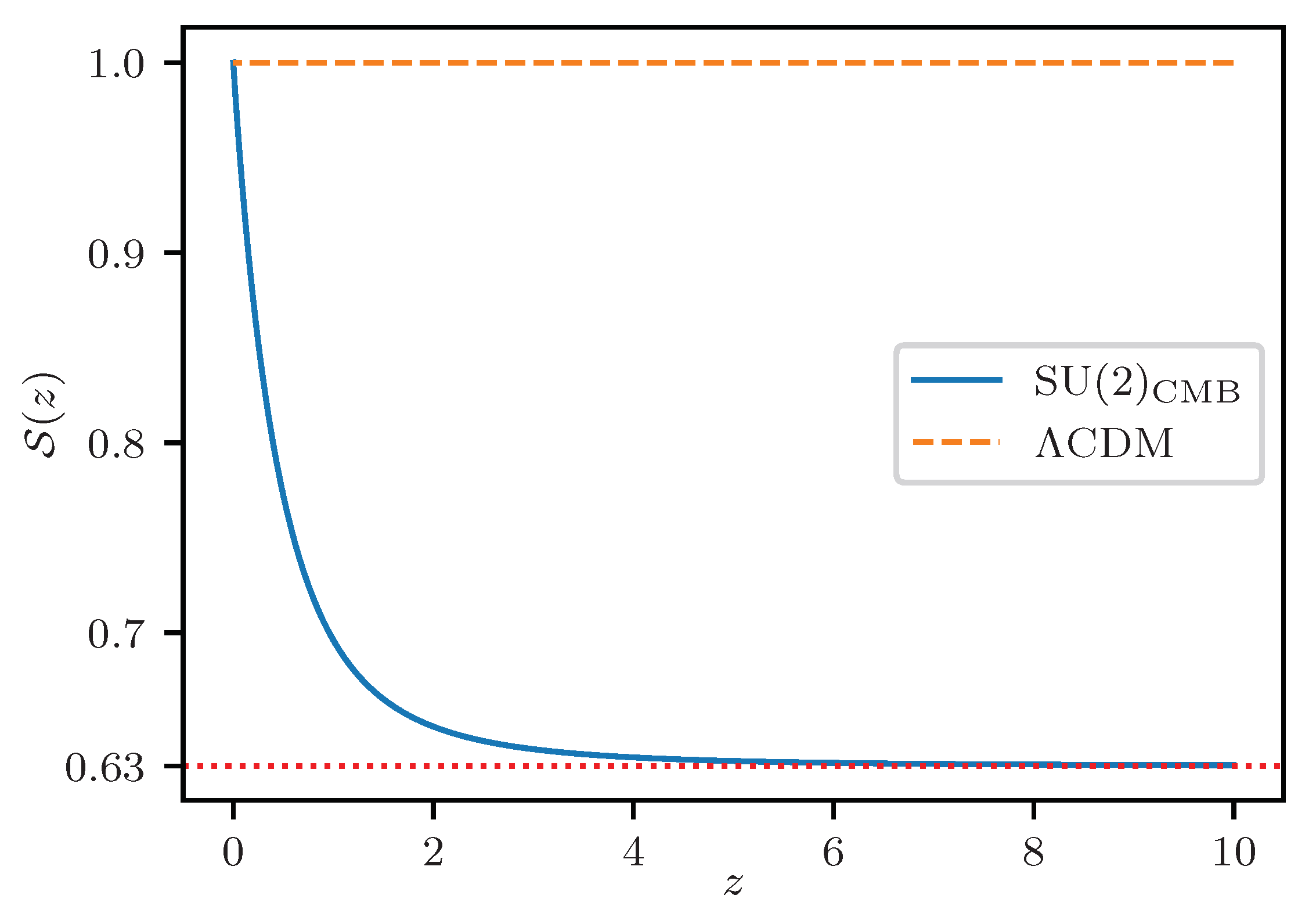
2. SU(2) vs. Conventional CMB Photon Gas in CDM
3. SU(2) Fit of Cosmological Parameters to Planck Data
4. Axionic Dark Sector and Galactic Dark-Matter Densities
5. Conclusions
Funding
Conflicts of Interest
References
- Eisenstein, D.J.; Weinberg, D.H.; Agol, E.; Aihara, H.; Prieto, C.A.; Anderson, S.F.; Arns, J.A.; Aubourg, É.; Bailey, S.; Balbinot, E.; et al. SDSS-III Massive Spectroscopic Surveys of the Distant Universe, the Milky Way, and Extra-Solar Planetary Systems. Astron. J. 2011, 142, 24. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; et al. [Dark Energy Survey Collaboration] Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Month. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Ivezić, Ž.; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. Astrophys. J. 2019, 873, 111. [Google Scholar] [CrossRef]
- Vargas-Magaña, M.; Brooks, D.D.; Levi, M.M.; Tarle, G.G. Unravelling the Universe with DESI. arXiv 2019, arXiv:1901.01581. [Google Scholar]
- Mather, J.C.; Cheng, E.S.; Cottingham, D.A.; Eplee, R.E., Jr.; Fixsen, D.J.; Hewagama, T.; Isaacman, R.B.; Jensen, K.A.; Meyer, S.S.; Noerdlinger, P.D.; et al. Measurement of the cosmic microwave background spectrum by the COBE FIRAS instrument. Astrophys. J. 1994, 420, 439. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basaket, S.; et al. Planck 2018 results. VI Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurement of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1998, 517, 565. [Google Scholar] [CrossRef]
- Dhawan, S.; Brout, D.; Scolnik, D.; Goobar, A.; Riess, A.G.; Miranda, V. Cosmological model insensitivity of local H0 from the Cepheid distance ladder. arXiv 2020, arXiv:2001.09260. [Google Scholar]
- Marra, V.; Amendola, L.; Sawicki, I.; Valkenburg, W. Cosmic Variance and the Measurement of the Local Hubble Parameter. Phys. Rev. Lett. 2013, 110, 241305. [Google Scholar] [CrossRef] [PubMed]
- Oddersov, I.; Hannestad, S.; Haugbølle, T. On the local variation of the Hubble constant. J. Cosmol. Astropart. Phys. 2014, 10, 028. [Google Scholar] [CrossRef]
- Oddersov, I.; Hannestad, S.; Brandbyge, J. The variance of the locally measured Hubble parameter explained with different estimators. J. Cosmol. Astropart. Phys. 2017, 03, 022. [Google Scholar] [CrossRef]
- Wu, H.-Y.; Huterer, D. Sample variance in the local measurement of the Hubble constant. Month. Not. R. Astron. Soc. 2017, 471, 4946. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- De Jaeger, T.; Stahl, B.E.; Zheng, W.; Filippenko, A.V.; Riess, A.G.; Galbany, L. A measurment of the Hubble constant from Type II supernovae. Month. Not. R. Astron. Soc. 2020, 496, 3402. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Anderson, J.; Mackenty, J.W.; Bowers, J.B.; Clubb, K.I.; Filippenko, A.V.; Jones, D.O.; et al. New Parallaxes of Galacic Cepheids from Spatially Scanning the Hubble Space Telescope: Implications for the Hubble Constant. Astrophys. J. 2018, 855, 136. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Jang, I.S.; Lee, M.G. The Tip of the Red Giant Branch Distances to Type Ia Supernova Host Galaxies. IV. Color Dependence and Zero-Point Calibration. Astrophys. J. 2017, 835, 28. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.-S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astrophys. J. 2019, 882, 34. [Google Scholar] [CrossRef]
- Huang, C.D.; Riess, A.G.; Hoffmann, S.L.; Klein, C.; Bloom, J.; Yuan, W.; Macri, L.M.; Jones, D.O.; Whitelock, P.A.; Casertano, S.; et al. A Near-infrared Period-Luminosity Relation for Miras in NGC 4258, an Anchor for a New Distance Ladder. Astrophys. J. 2018, 857, 67. [Google Scholar] [CrossRef]
- Ma, C.-P.; Bertschinger, E. Cosmological Perturbation Theory in the Synchronous and Conformal Newtonian Gauges. Astrophys. J. 1995, 455, 7. [Google Scholar] [CrossRef]
- Raghunathan, S.; Patil, S.; Baxter, E.; Benson, B.A.; Bleem, L.E.; Crawford, T.M.; Holder, G.P.; McClintock, T.; Reichardt, C.L.; Varga, T.N.; et al. Detection of CMB-Cluster Lensing using Polarization Data from SPTpol. Phys. Rev. Lett. 2019, 123, 181301. [Google Scholar] [CrossRef] [PubMed]
- Birrer, S.; Amara, A.; Refregier, A. The mass-sheet degeneracy and time-delay cosmography analysis of the strong lens RXJ1131-1231. J. Cosmol. Astropart. Phys. 2016, 8, 20. [Google Scholar] [CrossRef]
- Bonvin, V.; Courbin, F.; Suyu, S.H.; Marshall, P.J.; Rusu, C.E.; Sluse, D.; Tewes, M.; Wong, K.C.; Collett, T.; Fassnacht, C.D.; et al. HoLiCOW—V. New COSOMGRAIL time delays of HE 0435-1223: H0 to 3.8 per cent precision from strong lensing in a flat ΛCDM model. Month. Not. R. Astron. Soc. 2017, 465, 4914. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.-F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. HoLiCOW-XIII. A 2.4% measurement of H0 from lensed quasars: 5.3 σ tension between early and late-Universe probes. Month. Not. R. Astron. Soc. 2020. [Google Scholar] [CrossRef]
- Schutz, B.F. Determining he Hubble constant from gravitational wave observations. Nature 1986, 323, 310. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Fishbach, M.; Holz, D.E. A two percent Hubble constant measurement from standard sirens within five years. Nature 2018, 562, 545. [Google Scholar] [CrossRef]
- Handley, W.; Lemos, P. Quantifying tensions in cosmological parameters: Interpreting the DES evidence ratio. Phys. Rev. D 2019, 100, 043504-1. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Copi, C.J.; Huterer, D.; Starkman, G.D. CMB anomalies after Planck. Class. Quantum. Grav. 2016, 33, 184001. [Google Scholar] [CrossRef]
- Hofmann, R. Low-frequency line temperatures of the CMB (Cosmic Microwave Background). Annalen Phys. 2009, 18, 634. [Google Scholar] [CrossRef]
- Fixsen, D.J.; Kogut, A.; Levin, S.; Limon, M.; Lubin, P.; Mirel, P.; Seiffert, M.; Singal, J.; Wollack, E.; Villela, T.; et al. ARCADE 2 measurement of the absolute sky brightness at 3–90 GHz. Astrophys. J. 2011, 734, 5. [Google Scholar] [CrossRef]
- Hahn, S.; Hofmann, R.; Kramer, D. SU(2)CMB and the cosmological model: Angular power spectra. Mon. Not. R. Astron. Soc. 2019, 482, 4290. [Google Scholar] [CrossRef]
- Becker, R.H.; Fan, X.; White, R.L.; Strauss, M.A.; Narayanan, V.K.; Lupton, R.H.; Gunn, J.E.; Annis, J.; Bahcall, N.A.; Brinkmann, J.; et al. Evidence for Reionization at z∼6: Detection of a Gunn-Peterson Trough in a z=6.28 Quasar. Astrophys. J. 2001, 122, 2850. [Google Scholar]
- Ludescher, J.; Hofmann, R. Thermal photon dispersion law and modified black-body spectra. Annalen Phys. 2009, 18, 271. [Google Scholar] [CrossRef]
- Hofmann, R. The fate of statistical isotropy. Nat. Phys. 2013, 9, 686. [Google Scholar] [CrossRef]
- Harrington, B.J.; Shepard, H.K. Periodic Euclidean solutions and the finite-temperature Yang–Mills gas. Phys. Rev. D 1978, 17, 2122. [Google Scholar] [CrossRef]
- Herbst, U.; Hofmann, R. Emergent Inert Adjoint Scalar Field in SU(2) Yang–Mills Thermodynamics due to Coarse-Grained Topological Fluctuations. ISRN High Energy Phys. 2012, 2012, 373121. [Google Scholar] [CrossRef]
- Grandou, T.; Hofmann, R. Thermal ground state and nonthermal probes. Adv. Math. Phys. 2015, 2015, 197197. [Google Scholar] [CrossRef]
- Hofmann, R. The Thermodynamics of Quantum Yang–Mills Theory: Theory and Application, 2nd ed.; World Scientific: Singapore, 2016. [Google Scholar]
- Schwarz, M.; Hofmann, R.; Giacosa, F. Radiative corrections to the pressure and the one-loop polarization tensor of massless modes in SU(2) Yang–Mills thermodynamics. Int. J. Mod. Phys. A 2007, 22, 1213. [Google Scholar] [CrossRef]
- Falquez, C.; Hofmann, R.; Baumbach, T. Modification of black-body radiance at low temperatures and frequencies. Ann. Phys. 2010, 522, 904. [Google Scholar] [CrossRef]
- Diakonov, D.; Gromov, N.; Petrov, V.; Slizovskiy, S. Quantum weights of dyons and of instantons with nontrivial holonomy. Phys. Rev. D 2004, 70, 036003. [Google Scholar] [CrossRef]
- Szopa, M.; Hofmann, R. A Model for CMB anisotropies on large angular scales. J. Cosmol. Astropart. Phys. 2008, 3, 001. [Google Scholar] [CrossRef]
- Ludescher, J.; Hofmann, R. CMB dipole revisited. arXiv 2009, arXiv:0902.3898. [Google Scholar]
- Hahn, S.; Hofmann, R. Exact determination of asymptotic CMB temperature-redshift relation. Mod. Phys. Lett. A 2018, 33, 1850029. [Google Scholar] [CrossRef]
- Adler, S.L. Axial-Vector Vertex in Spinor Electrodynamics. Phys. Rev. 1969, 177, 2426. [Google Scholar] [CrossRef]
- Adler, S.L.; Bardeen, W.A. Absence of Higer-Order Corrections in the Anomalous Axial-Vector Divergence Equation. Phys. Rev. 1969, 182, 1517. [Google Scholar] [CrossRef]
- Bell, J.S.; Jackiw, R. A PCAC Puzzle: π0→γγ in the σ model. Nuovo Cim. A 1969, 60, 47. [Google Scholar] [CrossRef]
- Fujikawa, K. Path-Integral Measure for Gauge-Invariant Fermion Theories. Phys. Rev. Lett. 1979, 42, 1195. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. Constraints imposed by CP conservation in the presence of pseudoparticles. Phys. Rev. D 1977, 16, 1791. [Google Scholar] [CrossRef]
- Blas, D.; Lesgourges, J.; Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS). Part II: Approximation schemes. J. Cosmol. Astropart. Phys. 2011, 07, 034. [Google Scholar] [CrossRef]
- Hofmann, R. Relic photon temperature versus redshift and the cosmic neutrino background. Annalen Phys. 2015, 527, 254. [Google Scholar] [CrossRef]
- Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; Battaner, E.; et al. Planck 2015 results. XI. CMB power spectra, likelyhoods, and robustness of parameters. Astron. Astrophys. 2016, 594, A11. [Google Scholar]
- Cooke, R.J.; Pettini, M.; Nollett, K.M.; Jorgenson, R. The primordial deuterium abundance of the most metal-poor damped Lyα system. Astrophys. J. 2016, 830, 148. [Google Scholar] [CrossRef]
- Nicastro, F.; Kaastra, J.; Krongold, Y.; Borgani, S.; Branchini, E.; Cen, R.; Dadina, M.; Danforth, C.W.; Elvis, M.; Fiore, F.; et al. Observations of the missing baryons in the warm hot intergalactic medium. Nature 2018, 558, 406. [Google Scholar] [CrossRef]
- Johnson, S.D.; Mulchaey, J.S.; Chen, H.-W.; Wijers, N.A.; Connor, T.; Muzahid, S.; Schaye, J.; Cen, R.; Carlsten, S.G.; Charlton, J.; et al. The Physical Origins of the Identified and Still Missing Components of the Warm–Hot Intergalactic Medium: Insights from Deep Surveys in the Field of Blazar 1ES1553+113. Astrophys. J. Lett. 2019, 884, L31. [Google Scholar] [CrossRef]
- Macquart, J.-P.; Prochaska, J.X.; McQuinn, M.; Bannister, K.W.; Bhandari, S.; Day, C.K.; Deller, A.T.; Ekers, R.D.; James, C.W.; Marnoch, L.; et al. A census of baryons in the Universe from localized fast radio bursts. Nature 2020, 581, 391. [Google Scholar] [CrossRef]
- Frieman, J.A.; Hill, C.T.; Stebbins, A.; Waga, I. Cosmology with Ultralight Pseudo Nambu-Goldstone Bosons. Phys. Rev. Lett. 1995, 75, 2077. [Google Scholar] [CrossRef]
- Giacosa, F.; Hofmann, R. A Planck-scale axion and SU(2) Yang–Mills dynamics: Present acceleration and the fate of the photon. Eur. Phys. J. C 2007, 50, 635. [Google Scholar] [CrossRef]
- Weber, M.; de Boer, W. Determination of the local dark matter density in our Galaxy. Astron. Astrophys. 2010, 509, A25. [Google Scholar] [CrossRef]
- Sin, S.-J. Late-time phase transition and the galactic halo as a Bose liquid. Phys. Rev. D 1994, 50, 3650. [Google Scholar] [CrossRef]
- Hofmann, R. The isolated electron: De Broglie’s “hidden” thermodynamics, SU(2) Quantum Yang–Mills theory, and a strongly perturbed BPS monopole. Entropy 2017, 19, 575. [Google Scholar] [CrossRef]
- Grandou, T.; Hofmann, R. On emergent particles and stable neutral plasma balls in SU(2) Yang–Mills thermodynamics. arXiv 2020, arXiv:2007.08460. [Google Scholar]
| 1 | Lump sizes could well match those of galactic dark-matter halos, see Section 4. |
| 2 | That the deep Rayleigh–Jeans regime is indeed subject to classical wave propagation is assured by the fact that wavelengths that are greater than the spatial scale , separating a(n) (anti)caloron center from its periphery where its (anti)selfdual gauge field is that of a dipole [40]. The expression for s contains the modulus of the emergent, adjoint Higgs field (eV the Yang–Mills scale of SU(2)), associated with densely packed (anti)caloron centers, and, explicitely, temperature T. |

| Parameter | CDM | |
|---|---|---|
| − | ||
| − | ||
| − | ||
| − | ||
| km sMpc | ||
| Age/Gyr | ||
| 10,640 | 10,495 | |
| 9207 | 9210 | |
| 1.156 | 1.140 | |
| 10,552.6 | 9951.47 | |
| 9547 | 9550 | |
| 1.105 | 1.042 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmann, R. An SU(2) Gauge Principle for the Cosmic Microwave Background: Perspectives on the Dark Sector of the Cosmological Model. Universe 2020, 6, 135. https://doi.org/10.3390/universe6090135
Hofmann R. An SU(2) Gauge Principle for the Cosmic Microwave Background: Perspectives on the Dark Sector of the Cosmological Model. Universe. 2020; 6(9):135. https://doi.org/10.3390/universe6090135
Chicago/Turabian StyleHofmann, Ralf. 2020. "An SU(2) Gauge Principle for the Cosmic Microwave Background: Perspectives on the Dark Sector of the Cosmological Model" Universe 6, no. 9: 135. https://doi.org/10.3390/universe6090135
APA StyleHofmann, R. (2020). An SU(2) Gauge Principle for the Cosmic Microwave Background: Perspectives on the Dark Sector of the Cosmological Model. Universe, 6(9), 135. https://doi.org/10.3390/universe6090135




