Abstract
We review some aspects of our longstanding research concerning the analogous Hawking effect in dispersive dielectric media. We introduce nonlinear contributions in the polarization field in the relativistically covariant version of the Hopfield model and then, in order to provide a simplified description aimed at avoiding some subtleties in the quantization of the original model, we discuss the so-called -model. We show that the nonlinearity allows for introducing in a self-consistent way the otherwise phenomenological dependence of the susceptibility and of the resonance frequency on the spacetime variables, and this is a consequence of the linearization of the model around solitonic solutions representing propagating perturbations of the refractive index, to be then associated with the Hawking effect.
1. Introduction
Since its theoretical discovery, the Hawking effect [1] has represented a very important topic for theoretical physics. First of all, it provided a semantic link to the so far only syntactic analogy between the laws of thermodynamics and the laws of black hole mechanics. Further on, it gave a formidable impulse to the studies of quantum field theory in curved spacetime. Notwithstanding, an evident drawback emerged: any hope of experimental verification for the Hawking effect received a strong hindrance by the too low temperature which could be associated with astrophysical black holes, as, e.g., in the case of a Sun-mass black hole the predicted temperature for a distant observer would amount to a few tenth of nanoKelvins, and, as such, its measurement would be deeply hindered e.g., by the 2.7 K of the cosmic background radiation. Further possible contributions emerging by primordial black holes were hardly viable. Still, in 1981, W.G. Unruh [2] realized his deep intuition about the possibility to reproduce the essentials of Hawking radiation in condensed matter systems. Instead of a real event horizon, a sufficient condition for obtaining pair-production of particles with a thermal spectrum consists of creating a kinematical horizon: in a fluid flowing in a waterfall, it would be the line where the flow velocity v reaches the sound velocity c in the fluid itself, and overcomes it beyond that line. As a consequence, there is a physical hindrance for the sound waves to move upstream beyond the aforementioned horizon. As is evident, there is not an absolute hindrance for all possible particles, but only for phonons. Still, for quantum effects, there is a radiation flux which is analogous to the Hawking radiation, composed of phonons which are emitted with a thermal spectrum with a temperature which is proportional to the gradient at the horizon of the velocity field. There is a huge literature on this subject in the so-called non-dispersive case, where Unruh proved that the sound field perturbations can be described in terms of a Klein–Gordon equation on a curved spacetime background displaying a horizon in the above-mentioned sense. We limit ourselves to quote a review [3]. A decade later, the picture of the original study was enriched by taking into account dispersive effects [4,5]. The main point is that condensed matter physics, on one hand, contributes for the presence of so-called dispersive effects, consisting of an enlarged spectrum of modes with respect to the standard picture for the Hawking effect, and, on the other hand, it deeply modifies the nature of the effect itself, presenting e.g., at least a (partial) resolution of the so-called transplanckian problem. In any case, at least in the limit of weak dispersive effects, the analogous Hawking temperature maintains the same geometrical behavior as in the nondispersive case. See also [6] for a partial review and detailed references.
We do not delve into a discussion of the experiments involving various settings. We limit ourselves to point out also that this research field is going to become a further very relevant chapter in studies for quantum field theory in condensed matter systems, nowadays more focused on topological effects.
In this brief review, we summarize some aspects of our longstanding studies aimed at providing an analytical deduction of thermality of the analogue Hawking emission in dielectric media. Among the methods proposed for the measurement of Hawking radiation in analogous systems, a very interesting one is represented by analogous black holes in dielectric media. The original idea [7] is to generate a moving perturbation through an intense laser pulse propagating in the dielectric medium. The Kerr effect [8,9] occurring in dispersive nonlinear materials is involved in the generation of the perturbation.
In particular, the Hawking effect in nonlinear dielectric media affected by the Kerr effect is associated with the aforementioned dielectric perturbation propagating in the dielectric medium. This moving dielectric perturbation amounts to a traveling perturbation of the refractive index, to which the possibility to generate analogous Hawking radiation is strictly related under suitable conditions allowing the existence of a black hole/white hole horizon (or both) [7,10,11,12,13,14,15,16,17,18,19]. A very sketchy idea of how this happens is discussed in [12], Section 4 therein, and we sum up the basic steps. The nonlinear contribution in the Maxwell equation is represented by a polarization field proportional to the third power of the electric field. An expansion in terms of a strong field plus a weak perturbation can be suitably reinterpreted as a linear equation for the perturbation where the original susceptibility is replaced by a non-constant susceptibility including a Kerr-type correction. The aforementioned linear equation, in the eikonal approximation, is associated with a metric (see also Appendix A).
Our reference model will be the covariant Hopfield model discussed in [20,21,22], which represents our basic tool for analyzing the conceptual issues characterizing the physics at hand. Nevertheless, we will also discuss a simplified model introduced in [16], which is still covariant, that maintains the main physical characteristics and, in particular, provides the same dispersion relation, but has a great advantage to not be involved in a constrained quantization procedure. See also [23]. The -model involves only two scalar fields, and , replacing the (four-potential of the) electromagnetic and the polarization field respectively. Still, its physical content is nontrivial, and can allow for a number of very interesting physical situations, which can also be experimentally tested. It is important to mention that the full Hopfield model can also be solved exactly in the same physical situations, with the difference that it is much more difficult to be handled.
The main focus is on a self-consistent introduction of a dielectric field perturbation, which is propagating in the lab frame, and is such that the analogous Hawking effect can take place. Further steps towards an analytical deduction of the thermality for dielectric black holes in the simplified model are then sketched.
2. The Covariant Generalization of the Hopfield Model
One of the simplest ways in order to describe the interaction between the electomagnetic field with matter is the Hopfield model. In such model, the dielectric material is extremely simplified, since one is interested in the properties of the electromagnetic field and wants to minimize the description of the medium: it is described by a continuum (or lattice) of dipoles having characteristic frequency , linearly interacting with the electromagnetic field through a coupling constant g. In other words, the dielectric material is described just in terms of a field representing the polarization of the material, which is coupled to the in the usual way with the electric field so that the system is described by the Lagrangian
where and are the scalar potential and the vector potential, respectively, related to the electric and magnetic fields by
Therefore, the interaction terms in the second line are nothing but
the usual linear interaction between the electric field and an electric dipole, but with a coupling constant g. We have written them in a symmetrized form, ready for the quantization. The reason for leaving g unfixed is that it can be helpfully used to simulate parametrically some perturbations originated by nonlinear effects. For example, we are interested in describing a perturbation in the refractive index generated by a fourth order nonlinearity, the so called Kerr effect, moving with constant velocity in the medium. In [16,20], a generic uniformly traveling perturbation can be described by assuming , , and . This allows for discussing the phenomenon we are interested in, in a way independent from how it is generated (is it the Kerr effect or not). A first-principle introduction of the Kerr effect, like e.g., the one obtained by introducing a fourth power of requires modifications of the Lagrangian, as discussed in [19] and partially summarized below.
The reason why we need to introduce such a traveling perturbation in the refractive index is to simulate black holes in the dielectric. The idea is quite simple and intuitively as follows. For simplicity, let us think about fiber optics, with a symmetry axis in the direction x, along which a bell shaped (always in the direction x) intense pulse is moving along the direction x with constant speed. We can forget the transverse direction to catch the idea. If the fiber optics is made of Kerr material, the intense pulse will generate a proportional modification of the refractive index, , where is a constant and the pulse intensity. Suppose now that a photon is sent toward the pulse, chasing it. It will move with velocity , where c is the speed of light in vacuum and n the refractive index of the material. Let us assume that the pulse is moving with a velocity . Then, the photon will reach it approaching it from the back. At this point, the refractive index seen by the photon increases as , so it slows down to . If the maximum of the bell shaped is such that , it is clear that there will be a point before this maximum where so the photon and the pulse have the same velocity. The photon cannot cross that point, which is then a barrier for it to enter the pulse. This point behaves exactly as a white hole horizon. By symmetry, in front of the pulse, there will be an analogous point satisfying the same condition . This is a point from which a photon cannot escape forward, so it represents a black hole horizon. A further point is that, in describing the motion of photons in the limit of geometric optics, using a frame where the pulse is at rest (so it is an inertial frame moving with speed v), one gets that the trajectories of the photons are just geodetics in a spacetime metric which has event horizons at the positions described above, and this makes the intuitive analogy, just described, working also at a quantitative level. See the appendix for more details. However, such an oversimplified description does not include the nontrivial dispersion relation that makes an important difference between Hawking emission by analogue horizons in dielectrics and the one in astrophysical black holes. Thus, we need a more fundamental description of such a system, as the Hopfield moves, but we also need to make it relativistically covariant1 since we need to move easily from the lab frame to the one comoving with the pulse.
Thus, we have to bring the Hopfield model in a covariant form. For what concerns the pure electromagnetic part, this is of course immediate, but we need to tackle the problem of finding a covariant form for the polarization part of the Hopfield Lagrangian, which is not such a trivial task. To this aim, we first notice that, if we want to interpret as the spatial components of a spacetime vector , then, in a rest frame for the dielectric, we must have . This is equivalent to say
where is the four-velocity of the dielectric in the rest frame. This allows us to define the polarization field in a covariant frame, simply assuming that it is a four-vector valued field satisfying the (covariant) constraint . We remark that is the 4-velocity of the bulk dielectric medium that is the velocity of the dielectric sample, not to be confused with the velocity of the dielectric perturbation. Finally, remembering that the dipole couples with the electric field in the rest frame, which is as seen by an arbitrary inertial observer, we can finally rewrite the above Lagrangian density in the covariant form2
This is the relativistic Hopfield model with a single polarization field with resonance frequency , as presented in [20]. Here, we have also added the auxiliary scalar field B, to keep under control the gauge invariance, as usual. This model can be quantized exactly, either in the canonical or in the path integral formulation. In both cases, the quantization is ensured by the invertibility of the wave operator, which is granted once the gauge is fixed (this explaining the insertion of the field B), together with a prescription cutting out the zero modes (on-shell modes) of the wave operator. The latter are the classical solutions of the equations of motion, which indeed exist if suitable dispersion relations are satisfied. A careful analysis of these has been done in [22]. We limit ourselves to report here that when the parameters , , and g are constant, then the physical modes are subjected to the dispersion relation in the lab frame
This is nice since it reproduces the Sellmeier dispersion relation with a single resonance, usually adopted in phenomenological description of transparent dielectrics. More realistic Sellmeier dispersion relations, with more than one characteristic resonance, can be obtained by including more polarization fields, one for each resonance. To keep the exposition as simple as possible, we will keep just one polarization field.
We want to stress again the price we paid in order to get a covariant version of the Hopfield model. Covariance of the Lagrangian forced us to introduce a zeroth component of the polarization field, which now appears to be a four-vector. This component is absent in the rest frame and appears to have no physical meaning. In a general frame, this is equivalent to impose the constraint (5), so that in general the new component is not an independent one, but is a function of the spatial components. It is worth mentioning that this condition is the correct one for our harmonic oscillator field P coupled to the electromagnetic field, regardless of its specific nature of polarization field.
Finally, we want to keep into account the nonlinear Kerr effect by adding a nonlinear self interaction in the polarization field (Kerr nonlinearity) [19]:
A fourth order term in nonlinear optical media is not novel, see e.g., [24], where a fourth order term in the displacement field can be introduced in the case of an optical fiber. Even if we refer to our fourth order term as associated with Kerr nonlinearity, our approach does not represent the standard way to approach the Kerr effect (see also [25,26]). Still, we shall show that our toy-model with a fourth order term in the polarization field eventually can be related to the Kerr effect. This brings an important simplification of the equations of motion that allows us to get explicit exact solutions of the nonlinear equations of motion.
We have introduced the totally symmetric rank-four tensor . The contraction of any of its indexes with produces a vanishing result. We can assume homogeneity and isotropy of the tensor, and then it is constant and invariant under the action of the little group (the subset of the Lorentz group) leaving invariant. is a compact group isomorphic to . Then, the space of rank four tensors invariant under is a three-dimensional vector space of the form
where
Indeed, any index must transform in the or . The tensor belongs in the representation , which decomposes as
which shows that the space of invariant tensors is three-dimensional. (9) easily follows from the fact that (10) is indeed invariant and orthogonal to .
Since is totally symmetric, invariance under permutations requires . Hence, taking into account the constraint , we get
where .
The equations of motion then take the form
which have to be considered together with the defining constraint .
2.1. Linearized Quantum Theory
In order to understand the Hawking effect in the dielectric medium, it is not necessary to quantize the whole nonlinear model. For this reason, we focus our attention on the equations of motion for the fluctuations on a given background solution of the Hopfield–Kerr equations of motion, by means of a linearization of the Lagrangian [19]. Let us define the quantum fluctuations of the fields w.r.t. a background solution , of the whole nonlinear system, to be , and , so that
The Lagrangian density appearing in (8), as a consequence of the linearization above, can be re-written as
We also define such that
and consider background solutions which, for the polarization field, take the form
The linearization is undertaken by dropping out the last two terms in :
As to polarizations for , one is parallel and two are perpendicular to . We have
This allows us to infer that passing from the linear Hopfield Lagrangian to the Hopfield–Kerr linearized Lagrangian amounts to the following modification:
with fixed, and where we have defined which depends on the polarization:
We note that is positive, independently from the specific solution.
As in [19], by introducing a modified space-dependent3 susceptibility and resonant frequency, we obtain:
Now, we are interested in understanding how the refractive index changes due to the propagating perturbation. For the transverse modes, the dispersion relation in the lab frame, where (see Figure 1) is, with respect to the homogeneous case (7)
which can be obtained in the WKB approximation as in [19], or simply by considering the shift rules (24) and (25). In the homogeneous case, the phase and group velocity in the lab frame are [19]
where we have defined .
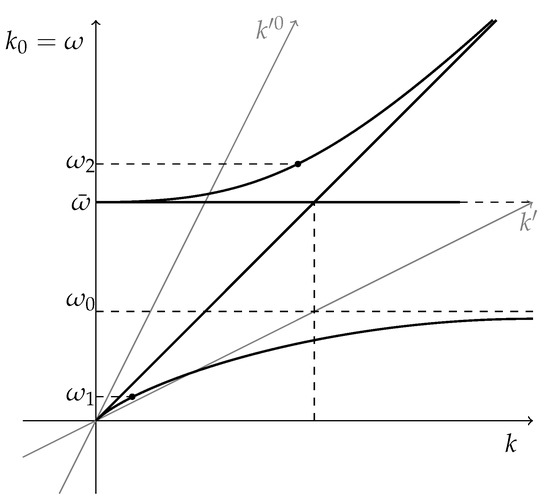
Figure 1.
This picture is the same as in [19]. The thick black lines represent the dispersion relations as seen in the lab frame, shown for positive frequencies and wave-numbers. The grey lines represent the axes of a frame boosted with velocity . There are two positive branches for the transverse dispersion relation (curved thick lines): and . From the expression of the group velocity we see that for any given value of , there are always two corresponding positive values and , one for each positive branch. These points determine the superluminal and subluminal regions, w.r.t. the given group velocity.
As a consequence, the phase refractive index is
Taking into account the shift rules (24) and (25), we thus get that in the presence of a background solution the new index becomes
From here, we see that is negative for both and , i.e., the perturbation induces a decrease in the phase refractive index on both branches (see the following discussion).
For the group velocity, with , an analogous result holds [19]. This means that the relativistic linearized Hopfield–Kerr model realizes a negative Kerr effect4 on both branches of the transverse spectrum, for both the phase refractive index and the group refractive index. This is not an unphysical result, since there exist materials, called metamaterials, realizing this kind of nonlinearity. In addition, from the point of view of understanding the Hawking effect, it is irrelevant since the result is just of reversing the order of black and white horizons.
One might correct the aforementioned behaviour by assuming , which would restore the expected positive Kerr effect. However, of course, this could represent a serious problem because the energy for would be unbounded from below. Nevertheless, as discussed in [19], also a sixth order perturbation with the positive sign could be added in order to obtain again an energy bounded from below. Indeed, this would be sufficient in order to restore the presence of a finite lower bound for the energy, and then for ensuring the presence of a ground state. Of course, one should also provide that the further sixth order term can actually be neglected, at least as far as the Kerr effect in itself is concerned. In this sense, this is substantially the same idea as for the classical anharmonic model for centrosymmetric media, where the potential energy associated with the restoring force acting on an electron involves a negative quartic term, which would be responsible for an energy unbounded from below. In that case, one assumes that the electronic displacement is small in such a way that higher order terms (which are implicitly assumed) are safely negligible [25]. It is then legitimate to consider our ansatz for a quartic polarization term as the lowest order correction to the polarization field.
As a final note of this subsection, we stress that we called this phenomenon a Kerr effect, even if for small the variation of the refractive index is proportional to rather than to the intensity I of the electromagnetic signal. Still, for the solitonic solution we are going to discuss in Equation (46), we find that and then we can call it ‘Kerr effect’ in a proper way, as then one finds . Cf (44) below.
2.2. Exact Solitonic Solutions
The next step is to look for explicit solutions of the whole nonlinear system of the equations of motion, in order to fix the background solution. As we said above, our solution is expected to move with constant velocity with respect to the lab system, with a polarization transversal to the velocity of the solution itself. In addition, the profile of the dielectric perturbation is expected to evolve very slowly (adiabatically) with respect to the Hawking process. Therefore, it is convenient to work in the comoving frame, where such a kind of solution is static. In this frame, we do the ansatz
where is a constant vector and is as in Equation (18). We also set , so that , and set , so that the equations of motion take the form
Before looking for a solution, a remark is in order. In the ansatz for , we used for the same symbol we proposed for the polarization field in the rest frame. The reason is that the conditions (18) imply that is invariant under boosts in the direction.
The second equation above, as described in [19], suggests that the electromagnetic potential should also be proportional to , so that we put . The condition then implies , which simplifies the first equation so that we have
A compatible choice for is , so that, from the first equation (setting the integration constant to zero), one gets
Then, it is easy to obtain for the second equation
which can be written in the form
with K an integration constant.
In order to keep the solutions as simple as possible, we set . Moreover, we assume
Therefore, we get
whose integration provides us the solution
This is one of the key-results we obtained in [19]: the Hopfield–Kerr model admits an exact solitonic solution, which, in the comoving frame and for the polarization field, becomes
where is as defined in Equation (18).
Now, a few remarks are in order: first, we have imposed the condition (39). This does not mean that, if not imposed, then exact solutions do not exist, but just that we would get a periodic solution with the substitution in (42). It would also be a singular solution since sec is. This would not be what we were looking for. In addition, we have set two integration constants to zero. In principle, it would be possible to solve the equations exactly for any values of such integration constants, after reducing the above system to a Weierstrass equation. However, using general properties of the Weierstrass function, it is not difficult to prove that all solutions found this way are periodic with just an exceptional degenerating (from the point of view of Weierstrass functions) case, which is exactly the one we have determined in an elementary way.
Second, we notice that the form for the gauge four-potential immediately implies that the electric field vanishes in the comoving frame, independently from the exact form of h, since both and (in the comoving frame z is just a spatial coordinate). Therefore, our exact solutions (included the periodic ones) are purely magnetic in the comoving frame. It is not clear if there is a deep physical reason below or not, since, in any case, we made a number of ansätze to simplify the equations. We can only notice that it seems that a crucial ingredient has been the requirement of staticity. This requires a vanishing Poynting vector field and may be the origin of the vanishing of the electric field. A more general solution would probably require a longitudinal component for the 4-potential (but not for the polarization field of course).
As for the magnetic field, in the comoving frame, one obtains another key-result of [19]:
As outlined at the end of the previous subsection, this confirms that our interpretation of the refractive index modification induced by this solitonic solution as a Kerr effect is indeed correct. Indeed, the pulse intensity is
where we included a 0 subscript to recall that we are considering a background solution.
Let us further investigate the condition (39). We start by noting that, for standard transparent materials, the Sellmeier coefficient is typically smaller than 1. This means that the solitonic solution displayed in (42) is acceptable only as long as is large enough. If we define to be the velocity of the comoving frame, i.e., , we obtain
as a condition for the existence of the solitonic solution, which is not obvious. We limit ourselves to note that, as the phase refractive index in the lab frame, in the present setting and, as the refractive index for is , this condition implies that the perturbation must be superluminal, i.e., it must exceed the velocity of light in the medium (in the limit of negligible optical dispersion). Of course, this feature of our analytic solution does not necessarily imply that any dielectric perturbation must implement this condition, as we can only assert that this feature occurs for our particular solution of the nonlinear equations we discussed above. One must point out that standard solitonic solutions for the nonlinear Schrödinger equation in nonlinear optics are not involved with this kind of limitation (see, e.g., [26]). Still, we think that our result is robust, as is confirmed also by the simplified model discussed in the following section.
In concluding this review of our results [19], we wish to consider positive velocities parallel to e.g., the x-axis, with the aim of mimicking experimental settings, in particular, we choose , where v is the absolute value of the chosen frame’s velocity. As a consequence, the background solution depends on the spatial variable x, and we obtain for it the form
where we have defined
corresponds to the amplitude of the soliton and is inversely proportional to the width of the solitonic envelope. In the limit , the solitonic solution can be seen to flatten on the real line and fade away.
In the following section, we take into account a simplified model which allows us to avoid many subtleties associated with the full Hopfield model with nonlinear contributions in the polarization we have just summarized above. Again, with particular reference to the problem of solitonic background solutions, we discuss a model which preserves many relevant physical properties of the Hopfield model but without subtleties mainly associated with gauge invariance.
3. The -Model
The electromagnetic Lagrangian for the full Hopfield model is quite involved. It is not much manageable for testing quantum effects, so, in order to gain insights into the real situation and carry out analytical calculations as far as possible, we now introduce a simplified model where the electromagnetic field and the polarization field are simulated by a pair of scalar fields, , and , respectively. Obviously, we are interested in constructing a model in such a way to maintain exactly the same dispersion relation and to simulate the same coupling as in the full case. Our model is related to the two-dimensional reduction of the Hopfield model adopted in [15]. We introduce also a fourth-order contribution for the polarization field, aimed at simulating the Kerr effect also in this simplified version of the actual electromagnetic model. For completeness, we also restore c in our equations.
Let us introduce
where plays the role of the dielectric susceptibility, is the usual four-velocity vector of the dielectric, is the proper frequency of the medium, and g is the coupling constant between the fields. The latter constant is henceforth put equal to one, as its original motivation (see [16]) can be relaxed without problems in a more advanced discussion (cf. also [27]). Instead of working with a phenomenological model where we can leave room for a spacetime dependence of the microscopic parameters , the nonlinear contribution in the polarization field allows for obtaining such a dependence as a consequence of a linearization of the field equations around a soliton-like static solution aimed to represent the effects of a strong laser impulse in the dielectric medium: a dielectric perturbation which corresponds to a static solution of the full nonlinear equations in the comoving frame, and a perturbation travelling with constant velocity in the lab frame (where the dielectric medium is at rest). We are also allowed to extending the model in such a way to also include polarization fields , each one with its own resonance frequency , susceptibility .
Omitting spacetime arguments, the equations of motion are
We look for static solutions (in the comoving frame, with ):
From the first equation, we select the solution
which, substituted into the second equation above, provides us with the following nonlinear equation:
If we multiply by each term of this equation, we easily obtain
As a consequence, by choosing a further integration constant as equal to zero, we get the following equation:
with
The condition to be implemented, in order to get real solutions, is to put . By taking into account that the refractive index n is related to the susceptibility by the well-known formula (limit of negligible dispersion), it is easy to infer that amounts to
i.e., a solution of the given equation exists only if it represents a soliton which moves in the lab at a velocity greater than the light velocity in the medium. Notice that this is even more stringent than the vectorial model, since now subluminal solutions are not allowed at all. Notice that now the staticity is essentially the only requirement we made, so we may infer that this is the reason for the condition, even for the original Hopfield model. In addition, we have to mention that, even if subluminal solutions are allowed for the vectorial case, the energy of such solutions is infinite.
The solution is
where we have put without loss of generality the maximum of the solution at . We can also obtain
We linearize around a solitonic solution of the exact equations of motion inherited from the above action. As a consequence, we obtain the linearized equations of motion
We observe that, as in the original Hopfield model discussed in the previous section, this amounts to the following shifts in and in with respect to the linear case :
in such a way that remains invariant: .
3.1. Current Conservation and Inner Product
In order to quantize the theory, it is necessary to introduce a scalar product on the space of classical solutions. This can be obtained in different ways, for example by complexification of the Poisson structure. As described in [16], a practical way is to use Noether’s theorem in order to determine the conserved current associated with invariance of the redefinition of the phases of the fields (after complexification of the fields). One easily finds
which is conserved along the equation of motion: . This provides the conserved charge
which is what we need in order to define a conserved scalar product. In particular, we obtain
which will obviously play a particularly important role in the definition of the quantum states for the model at hand.
3.2. Quantization of the Fields
In this subsection and in the following one, we adopt the following convention for frequencies and wave vectors: will be relative to the lab frame, will be associated with the comoving frame (moving with the dielectric perturbation). The conserved scalar product induces the norm of the states as follows:
This is not positive definite, but in quantum field theory, particle states correspond to positive norm states, whereas negative norm states correspond to antiparticles. This can be exemplified in the homogeneous case, i.e., in absence of the perturbation. For plane wave solutions, one finds that
so that ; we stress that this corresponds to what happens in the electromagnetic case. In particular, particles in the lab frame are defined by the condition . Correspondingly, in the comoving frame, the particle states are defined by the condition . These conditions represent a good indication for particle and antiparticle states also for the full problem, as asymptotically, under suitable conditions, the situation is homogeneous.
This discussion corroborates the common use of the asymptotic dispersion relation in order to identify particle and antiparticle states. We will refer to these as (DR)-asymptotic in the following; Figure 2 is an example. When working at low frequencies, we can then use the so called Cauchy approximation that means
where is , B is a constant, and the Kerr effect induces the right-moving perturbation . In the comoving frame, one obtains a space-dependent refractive index . Analytical solutions of the equations of motion reveal that there is a turning point which corresponds to the condition
and we can shift such a turning point at without loss of generality. Such a turning point behaves as a horizon, with a black hole region occurring where . One may also note that the above turning point equation coincides with the horizon condition one may deduce in the nondispersive case (see, e.g., the Appendix for more details). We also introduce the notion of ingoing and outgoing states, where ‘outgoing’ is relative to states going to infinity, whereas ‘ingoing’ is used for states traveling towards the horizon . There are six propagating states, and we are going to discuss their nature, focusing in particular on the ones directly involved in the Hawking process. For simplicity, we consider the Cauchy approximation, and the comoving frame, where the two branches of the dispersion relation are given by
corresponds to the monotone branch, whereas is the branch involved in the Hawking effect. The (DR)-asymptotic displays in the external region three states on the same branch defined by Equation (75), all having the same in the comoving frame: the positive group velocity particle state (outgoing), which we call H state, the negative group velocity particle state (ingoing), which we call the P state, and a negative group velocity antiparticle state N (ingoing).
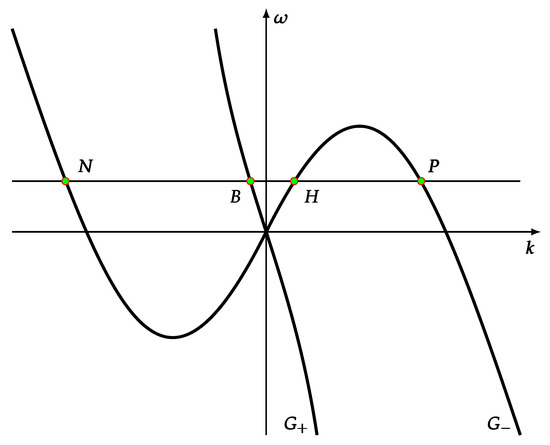
Figure 2.
Asymptotic dispersion relation in the external region for the Cauchy case in the comoving frame. The monotone branch is , the non-monotone one is . The line at const is also drawn, and relevant states introduced in the text are explicitly indicated.
In the black hole case, are early time scattering states, and H is the emergent one (the Hawking state [18,19]). There are two further states living in the internal region (black hole), one is the Hawking partner , and the other is a mode D, both outgoing. The states have negative norm.
The quantization of the fields, with respect to the full electromagnetic case, presents the important simplification deriving by the absence of constraints, which makes the whole treatment much easier and standard. In particular, in the static comoving frame, we have (see e.g., [16])
where is a normalization factor, indicates that we are considering “on shell” solutions, and U and V are positive norm solutions and negative norm solutions of the field equations, respectively. As in the standard S-matrix approach, initial states, if one considers as -modes, the ones moving towards the turning point (horizon) and as -modes the ones moving towards infinity (i.e., ), one may write
with
and
where the labels refer to the above-mentioned states inside and outside the black hole region, and where by means of we indicate solutions of the equations of motion (for the , fields introduced above). See [27] for more details of the calculations.
The on shell quantization described above, in a two-dimensional model, can give rise both to an -representation, where only the integration in is left, or also to a k-representation, where the dispersion relation is used to leave only the integral in .
3.3. Amplitudes and Thermality
In order to compute amplitudes for pair-creation, let us expand in plane waves both the H state and the states involved in the scattering process. As e.g., in [18], in terms of creation-annihilation operators, one may write
where the various amplitudes are obtained as follows: the ratio giving the particle-creation rate is
where represents the conserved current (68), while the indexes N, H indicate the N-particle states and the H-particle states, respectively, and
can also be introduced. Current conservation (unitarity) leads to
In particular, of utmost relevance is the ratio
as thermality corresponds just to finding
where
is the inverse of the expected Hawking temperature. It can be shown that it coincides with the temperature which can be associated with the black hole metric in the nondispersive case. See the Appendix herein. Such a result can be reached through different schemes of approximation [16,18,19], still sharing this same temperature, and we refer in particular to [27] for details. For completeness, we still sketch how analytical calculations are developed. The model-calculation was provided by Corley in [28]. See also [29,30]. There are fundamentally two steps:
- A WKB analysis is produced, which holds in the asymptotic region and also in part of the so called linear region, except for a neighborhood of the horizon . WKB wave functions are obtained [28].
- A near horizon approximation is developed [28]. Saddle point techniques and contour integrals around branch cut(s) are common tools in this calculation.
Matching of the states obtained in the near horizon approximation and asymptotic states in the asymptotic DR is then considered. This allows for obtaining the S-matrix for the complete scattering process. Again, thermality can be identified by studying the number of negative norm states identified in the process, as discussed above.
3.4. More on the Linearized Equation
In place of showing explicitly the usual calculation leading to the thermal regime, here we propose another possible strategy to tackle the linearized system (64) and (65). After taking the Fourier transform, they become
where
and
Here, is the four-velocity, with
From this system, we obtain the integral equation
Notice that it is independent from the coupling . This proves the non perturbative nature of the background solitonic solution. It is also worth noticing that the linear convolution operator M defined by
is a strictly positive bounded, injective, selfadjoint operator over , being the Lebesgue measure. It has a continuum spectrum , where the norm of the operator is
The boundedness of the operator , to be compared with the unboundedness of the unperturbed part of Equation (94), suggests that one can try to solve (94) in a recursive way: let us introduce a parameter , to be put equal to 1 at the end of the calculation, and let us consider as an contribution, to be compared with the contribution of the unperturbed part, and let us also put
The above method is essentially the Adomian Decomposition Method for integral equations [31]. In order to simplify a little bit the expressions, we now proceed assuming just one dimension. The solution of Equation (98) is the unperturbed usual one:
and then for the first order correction we get
which is to be computed. If we set
we can rewrite it as
This expression requires a prescription since it has poles on the zeros of the first denominator. The right -prescription preserving causality has been explored in [23] and gives rise to the correct solution
The integral can be done explicitly, noticing that the zeros of the argument of the delta distribution are the solutions of the equation
which could be solved by means of Cardano’s formula. However, the explicit solution is quite cumbersome, we limit ourselves to commenting that the number of real zeros is just one for large enough, but it may become three for small values of . The Fourier anti transform of gives the first approximation to the solution of the linearized equations around the soliton. It defines the vacuum state on such a background and could be used to compute the Bogoliubov coefficients relating it to the vacuum in the absence of the soliton. It could be interesting to be able to do it analytically in some approximation, since it could provide a description of particle production in a region far from the limit of weak dispersion. We shall consider a full analysis in future works. For further aspects concerning solitonic solutions in a Sellmeier dielectric, see also [32].
4. Conclusions
We reviewed and discussed nonlinear contributions in the polarization field in the relativistically covariant version of the Hopfield model and its simplified version represented by the -model. Instead of starting from a model where there is a phenomenological dependence of the susceptibility and of the resonance frequency on the spacetime variables, we have obtained such a dependence by means of the introduction of nonlinear contributions in the polarization field. The aforementioned dependence naturally arises after a linearization around solitonic solutions is performed. The aim of this analysis was twofold: on the one hand, a less phenomenological modelization of the dielectric perturbation traveling in a dielectric medium because of the Kerr effect was obtained. On the other hand, explicit solitonic solutions were provided. The presented framework is associated with the analogue Hawking effect in dielectric media, the bases of which were sketched. Possible developments of our present discussion are represented on a more extensive analysis of our Equation (94) of Section 3.4, which is providing a new possible way of understanding the analogue Hawking spectrum far from the weak dispersion region, together with a better comprehension of the quantization around solitonic solutions. Furthermore, a modeling of the fiber optic case would be also of great interest, again also in relation with the Hawking effect and its experimental verification [33]. In this respect, it would be interesting to further improve the modeling of the Kerr effect, for example, by starting from a microscopic model. In addition, a more deep analysis in the multiresonance case of dielectric media should be in order. A further observation is that the highly nonlinear dispersion relation combined with the unitarity condition (the Kramers–Kronig relations) is expected to provide a non-trivial contribution to the absorption. All these topics need to be fully investigated in order to provide a detailed control of an experimental setup.
Author Contributions
The authors have contributed equally to the present review. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We acknowledge in particular the participation of Francesco Dalla Piazza and Michele Doronzo to a number of works this review is based on.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Black Hole Metric for the Nondispersive Case
We describe herein the metric associated with a dielectric perturbation traveling in a dielectric medium, which can be related also to the solitonic solutions described above. We refer to the simplest case, and refer to [6,10,12,34] for more discussions and details. In order to avoid unnecessary technical complications and keep all the analysis as simple as possible, it is convenient to replace the electric field with a scalar field , which, then, must satisfy the wave equation
where are inertial coordinates in the laboratory frame. We are thinking the refractive index to be obtained by means of an intense laser pulse in a nonlinear dielectric medium via Kerr effect. The dielectric perturbation does not depend on the transverse coordinates, so that it is infinitely extended in the transverse dimensions. In an actual experiment, one could restrict to a finite geometry, for example by considering a dielectric in fibre optics, but this would not change the substance of the Hawking effect, thus the approximation is well justified and facilitates the comparison with the geometrical description of the effect, beyond simplifying all calculations, including the quantum field theoretical treatment. We assume
where is positive, representing the smallness of the Kerr index, and denotes the normalized intensity of the pulse, a smooth rapidly decaying function a single maximum at , of height 1. A scheme of the dielectric perturbation is shown in Figure A1.
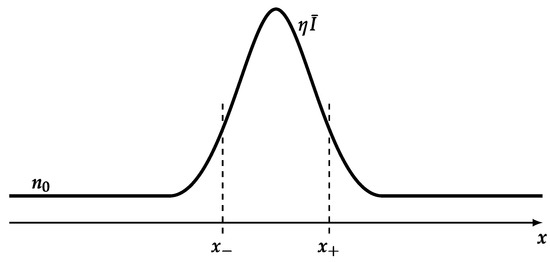
Figure A1.
Example of the dielectric perturbation geometry. and indicate the black hole and white hole horizon positions, respectively.
The relation with spacetime geometry arises by observing that Equation (A1) can be obtained from the Klein–Gordon equation for a scalar field in the metric background
assuming the eikonal approximation. By means of the boost,
where
is the usual relativistic gamma factor, we get the metric in the comoving frame
This form of the metric is manifestly stationary. We however know that in this case the Frobenius theorem is satisfied, hence it exists a coordinate transformation that brings the metric in an explicit static form. Indeed, consider the change of time coordinate
where
The metric becomes
which is manifestly static (w.r.t. the time ), where
This form of the metric is immediately comparable with the Schwarzschild one. If we look at the -part, we see that the more relevant different represented by the factor in front of the temporal component of the metric. The horizons are determined by the condition :
or, equivalently,
When
there will be two horizons: a black hole horizon in , described by the (hyper)plane of equation , located on the rising edge of the dielectric perturbation (i.e., ) and a white hole horizon in , described by the (hyper)plane of equation , on the falling edge (i.e., ).
As we have a static metric with an horizon, we can, as usual, predict that the dielectric black hole horizon will emit particles with a temperature proportional to the “surface gravity” at the black hole horizon:
which gives
One can deduce formula (A18) in several ways. Then, the temperature is given by the now familiar formula
where we restore ħ, c and .
References
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Unruh, W.G. Experimental black hole evaporation. Phys. Rev. Lett. 1981, 46, 1351. [Google Scholar] [CrossRef]
- Barcelo, C.; Liberati, S.; Visser, M. Analogue gravity. Living Rev. Relativ. 2005, 8, 12. [Google Scholar] [CrossRef] [PubMed]
- Unruh, W.G. Sonic analog of black holes and the effects of high frequencies on black hole evaporation. Phys. Rev. D 1995, 51, 2827. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, T. On the origin of the outgoing black hole modes. Phys. Rev. D 1996, 53, 7082. [Google Scholar] [CrossRef]
- Belgiorno, F.D.; Cacciatori, S.L.; Faccio, D. Hawking Radiation: From Astrophysical Black Holes to Analogous Systems in Lab; World Scientific Publishing Company: Singapore, Singapore, 2018; ISBN 9789814508537. [Google Scholar]
- Philbin, T.G.; Kuklewicz, C.; Robertson, S.; Hill, S.; König, F.; Leonhardt, U. Fiber-optical analog of the event horizon. Science 2008, 319, 1367–1370. [Google Scholar] [CrossRef]
- Kerr, J. A new relation between electricity and light: Dielectrified media Birefringent. Philos. Mag. Ser. 1875, 50, 337–348. [Google Scholar] [CrossRef]
- Kerr, J. A new relation between electricity and light: Dielectrified media birefringent (second paper). Philos. Mag. Ser. 1875, 50, 446–458. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Ortenzi, G.; Rizzi, L.; Gorini, V.; Faccio, D. Dielectric black holes induced by a refractive index perturbation and the Hawking effect. Phys. Rev. 2011, 83, 024015. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Clerici, M.; Gorini, V.; Ortenzi, G.; Rizzi, L.; Rubino, E.; Sala, V.G.; Faccio, D. Hawking radiation from ultrashort laser pulse filaments. Phys. Rev. Lett. 2010, 105, 203901. [Google Scholar] [CrossRef]
- Rubino, E.; Belgiorno, F.; Cacciatori, S.L.; Clerici, M.; Gorini, V.; Ortenzi, G.; Rizzi, L.; Sala, V.G.; Kolesik, M.; Faccio, D. Experimental evidence of analogue Hawking radiation from ultrashort laser pulse filaments. New J. Phys. 2011, 13, 085005. [Google Scholar] [CrossRef]
- Petev, M.; Westerberg, N.; Moss, D.; Rubino, R.; Rimoldi, C.; Cacciatori, S.L.; Belgiorno, F.; Faccio, D. Blackbody emission from light interacting with an effective moving dispersive medium. Phys. Rev. Lett. 2013, 111, 043902. [Google Scholar] [CrossRef] [PubMed]
- Finazzi, S.; Carusotto, I. Quantum vacuum emission in a nonlinear optical medium illuminated by a strong laser pulse. Phys. Rev. 2013, 87, 023803. [Google Scholar] [CrossRef]
- Finazzi, S.; Carusotto, I. Spontaneous quantum emission from analog white holes in a nonlinear optical medium. Phys. Rev. 2014, 89, 053807. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Dalla Piazza, F. Hawking effect in dielectric media and the Hopfield model. Phys. Rev. 2015, 91, 124063. [Google Scholar] [CrossRef]
- Jacquet, M.; König, F. Quantum vacuum emission from a refractive-index Front. Phys. Rev. A 2015, 92, 023851. [Google Scholar] [CrossRef]
- Linder, M.F.; Schützhold, R.; Unruh, W.G. Derivation of Hawking radiation in dispersive dielectric media. Phys. Rev. 2016, 93, 104010. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Dalla Piazza, F.; Doronzo, M. Hopfield–Kerr model and analogue black hole radiation in dielectrics. Phys. Rev. D 2017, 96, 096024. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Dalla Piazza, F. The Hopfield model revisited: Covariance and Quantization. Phys. Scr. 2016, 91, 015001. [Google Scholar] [CrossRef][Green Version]
- Belgiorno, F.; Cacciatori, S.L.; Dalla Piazza, F. Perturbative photon production in a dispersive medium. Eur. Phys. J. 2014, 68, 134. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Dalla Piazza, F.; Doronzo, M. Exact quantisation of the relativistic Hopfield model. Ann. Phys. 2016, 374, 338–365. [Google Scholar] [CrossRef][Green Version]
- Belgiorno, F.; Cacciatori, S.L.; Dalla Piazza, F.; Doronzo, M. Φ-Ψ model for electrodynamics in dielectric media: Exact quantisation in the Heisenberg representation. Eur. Phys. J. 2016, 76, 308. [Google Scholar] [CrossRef]
- Drummond, P.D.; Hillery, M. The Quantum Theory of Nonlinear Optics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Boyd, R. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2011; Volume 47. [Google Scholar]
- Belgiorno, F.; Cacciatori, S.L.; Viganò, A. Analogue Hawking Effect: A Master Equation. arXiv 2020, arXiv:2003.04236. [Google Scholar]
- Corley, S. Computing the spectrum of black hole radiation in the presence of high frequency dispersion: An analytical approach. Phys. Rev. D 1998, 57, 6280. [Google Scholar] [CrossRef]
- Unruh, W.G.; Schützhold, R. Universality of the Hawking effect. Phys. Rev. D 2005, 71, 024028. [Google Scholar] [CrossRef]
- Coutant, A.; Parentani, R.; Finazzi, S. Black hole radiation with short distance dispersion, an analytical S-matrix approach. Phys. Rev. D 2012, 85, 024021. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A First, Course in Integral Equations; World Scientific: Singapore, Singapore, 2015. [Google Scholar]
- Belgiorno, F.; Cacciatori, S.L.; Viganò, A. Spectral boundary conditions and solitonic solutions in a classical Sellmeier dielectric. Eur. Phys. J. C 2017, 77, 404. [Google Scholar] [CrossRef]
- Drori, J.; Rosenberg, Y.; Bermudez, D.; Silberberg, Y.; Leonhardt, U. Observation of Stimulated Hawking Radiation in an Optical Analogue. Phys. Rev. Lett. 2019, 122, 010404. [Google Scholar] [CrossRef]
- Cacciatori, S.L.; Belgiorno, F.; Gorini, V.; Ortenzi, G.; Rizzi, L.; Sala, V.G.; Faccio, D. Space-time geometries and light trapping in travelling refractive index perturbations. New J. Phys. 2010, 12, 095021. [Google Scholar] [CrossRef]
| 1. | Notice that we cannot expect for the model to be relativistically invariant, since Poincaré invariance is broken by the field , which selects a preferential class of frames: the ones where the dielectric is at rest. |
| 2. | For the Minkowski metric the standard signature used for quantum field theory is chosen. |
| 3. | Henceforth, as in [19], we will use the accent to denote a spacetime dependence on the given parameter. |
| 4. | By negative Kerr effect, we indicate a decrease in the refractive index of the medium in response to the passage of an electromagnetic pulse. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).