Statistical Analysis of Field-Aligned Alfvénic Turbulence and Intermittency in Fast Solar Wind
Abstract
1. Introduction
2. Data Selection Criteria for Magnetic Fluctuation
- Magnetic field and velocity must be aligned within at all scales in the turbulent inertial range for the whole interval, i.e., both local and global mean magnetic field must be aligned with the bulk velocity;
- The total duration cannot be less than 1 hour, with maximal percentage of missing data ≤20%;
- The whole interval must be enclosed within a fast SW stream ( km s);
- It must have low magnetic compressibility (), measured in the inertial range at scale of 20 min, where is defined as the ratio between the variance of the magnetic field intensity fluctuations and the total variance of the fluctuations, [23];
- The total pressure (with n, T, and B are, respectively, the proton number density, the temperature, and magnetic field intensity) must satisfy the condition nPa, in order to avoid discontinuities or shocks [24].
3. Empirical Mode Decomposition and Arbitrary Order Hilbert Spectra
4. Statistical Analysis of HSA Slopes and Scaling Exponents for Alfvénic Turbulence
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bruno, R.; Carbone, V. The Solar Wind as a Turbulence Laboratory. Living Rev. Sol. Phys. 2013, 10, 2. [Google Scholar] [CrossRef]
- Horbury, T.; Wicks, R.; Chen, C. Anisotropy in Space Plasma Turbulence: Solar Wind Observations. Space. Sci. Rev. 2012, 172, 325. [Google Scholar] [CrossRef]
- Shebalin, J.V.; Matthaeus, W.H.; Montgomery, D. Anisotropy in MHD turbulence due to a mean magnetic field. J. Plasma Phys. 1983, 29, 525–547. [Google Scholar] [CrossRef]
- Goldreich, P.; Sridhar, S. Toward a theory of interstellar turbulence. II. Strong Alfvénic turbulence. Astrophys. J. 1995, 438, 763–775. [Google Scholar] [CrossRef]
- Boldyrev, S. Spectrum of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2006, 96, 115002. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Mallet, A.; Yousef, T.A.; Schekochihin, A.A.; Horbury, T.S. Anisotropy of Alfvénic turbulence in the solar wind and numerical simulations. Mon. Not. R. Astron. Soc. 2011, 415, 3219–3226. [Google Scholar] [CrossRef]
- Iroshnikov, P.S. Turbulence of a Conducting Fluid in a Strong Magnetic Field. Sov. Astron. 1964, 7, 566. [Google Scholar]
- Kraichnan, R.H. Inertial-Range Spectrum of Hydromagnetic Turbulence. Phys. Fluids 1965, 8, 1385–1387. [Google Scholar] [CrossRef]
- Montgomery, D.; Turner, L. Anisotropic magnetohydrodynamic turbulence in a strong external magnetic field. Phys. Fluids 1981, 24, 825–831. [Google Scholar] [CrossRef]
- Goldreich, P.; Sridhar, S. Toward a Theory of Interstellar Turbulence. I. Weak Alfvenic Turbulence Astrophys. J. 1994, 432, 612–621. [Google Scholar]
- Horbury, T.S.; Forman, M.; Oughton, S. Anisotropic Scaling of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2008, 101, 175005. [Google Scholar] [CrossRef] [PubMed]
- Podesta, J.J. Dependence of Solar-Wind Power Spectra on the Direction of the Local Mean Magnetic Field. Astrophys. J. 2009, 698, 986–999. [Google Scholar] [CrossRef]
- Wicks, R.T.; Horbury, T.S.; Chen, C.H.K.; Schekochihin, A.A. Power and spectral index anisotropy of the entire inertial range of turbulence in the fast solar wind. Mon. Not. R. Astron. Soc. Lett. 2010, 407, L31–L35. [Google Scholar] [CrossRef]
- Forman, M.A.; Wicks, R.T.; Horbury, T.S. Detailed FIT of “Critical Balance” Theory to Solar Wind Turbulence Measurements. Astrophys. J. 2011, 733, 76. [Google Scholar] [CrossRef]
- Roberts, O.W.; Narita, Y.; Escoubet, C.P. Direct Measurement of Anisotropic and Asymmetric Wave Vector Spectrum in Ion-scale Solar Wind Turbulence. Astrophys. J. 2017, 851, L11. [Google Scholar] [CrossRef]
- Li, G.; Miao, B.; Hu, Q.; Qin, G. Effect of Current Sheets on the Solar Wind Magnetic Field Power Spectrum from the Ulysses Observation: From Kraichnan to Kolmogorov Scaling. Phys. Rev. Lett. 2011, 106, 125001. [Google Scholar] [CrossRef]
- Wang, X.; Tu, C.; He, J.; Marsch, E.; Wang, L. The Influence of Intermittency on the Spectral Anisotropy of Solar Wind Turbulence. Astrophys. J. 2014, 783, L9. [Google Scholar] [CrossRef]
- Telloni, D.; Carbone, F.; Bruno, R.; Sorriso-Valvo, L.; Zank, G.P.; Adhikari, L.; Hunana, P. No Evidence for Critical Balance in Field-aligned Alfvénic Solar Wind Turbulence. Astrophys. J. 2019, 887, 160. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Goldstein, M.L.; Roberts, D.A. Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind. J. Geophys. Res. Space Phys. 1990, 95, 20673–20683. [Google Scholar] [CrossRef]
- Zank, G.P.; Matthaeus, W.H. Waves and turbulence in the solar wind. J. Geophys. Res. Space Phys. 1992, 97, 17189–17194. [Google Scholar] [CrossRef]
- Dasso, S.; Milano, L.J.; Matthaeus, W.H.; Smith, C.W. Anisotropy in Fast and Slow Solar Wind Fluctuations. Astrophys. J. 2005, 635, L181–L184. [Google Scholar] [CrossRef]
- Zank, G.P.; Adhikari, L.; Hunana, P.; Shiota, D.; Bruno, R.; Telloni, D. Theory and Transport of Nearly Incompressible Magnetohydrodynamic Turbulence. Astrophys. J. 2017, 835, 147. [Google Scholar] [CrossRef]
- Bavassano, B.; Dobrowolny, M.; Fanfoni, G.; Mariani, F.; Ness, N.F. Statistical properties of MHD fluctuations associated with high-speed streams from Helios-2 observations. Sol. Phys. 1982, 78, 373–384. [Google Scholar] [CrossRef]
- Telloni, D.; Antonucci, E.; Bemporad, A.; Bianchi, T.; Bruno, R.; Fineschi, S.; Magli, E.; Nicolini, G.; Susino, R. Detection of Coronal Mass Ejections at L1 and Forecast of Their Geoeffectiveness. Astrophys. J. 2019, 885, 120. [Google Scholar] [CrossRef]
- Ogilvie, K.; Chornay, D.; Fritzenreiter, R.; Hunsaker, F.; Keller, J.; Lobell, J.; Miller, G.; Scudder, J.D.; Sittler, E.C.; Torbert, R.B.; et al. The WIND magnetic field investigation. Space Sci. Rev. 1995, 71, 55. [Google Scholar] [CrossRef]
- Lepping, R.P.; Acũna, M.H.; Burlaga, L.F.; Farrell, W.M.; Slavin, J.A.; Schatten, K.H.; Mariani, F.; Ness, N.F.; Neubauer, F.M.; Whang, Y.C.; et al. The WIND magnetic field investigation. Space Sci. Rev. 1995, 71, 207–229. [Google Scholar] [CrossRef]
- Treumann, R.A.; Baumjohann, W.; Narita, Y. On the applicability of Taylor’s hypothesis in streaming magnetohydrodynamic turbulence. Earth Planets Space 2019, 71, 41. [Google Scholar] [CrossRef]
- Mitchell, D.G.; Roelof, E.C.; Sanderson, T.R.; Reinhard, R.; Wenzel, K.-P. ISEE/IMP observations of simultaneous upstream ion events. J. Geophys. Res. Space Phys. 1983, 88, 5635–5644. [Google Scholar] [CrossRef]
- Haggerty, D.K.; Roelof, E.C.; Smith, C.W.; Ness, N.F.; Tokar, R.L.; Skoug, R.M. Interplanetary magnetic field connection to the L1 Lagrangian orbit during upstream energetic ion events. J. Geophys. Res. Space Phys. 2000, 105, 25123–25131. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. In Proceedings of the IEEE-Eurasip Workshop on Nonlinear Signal and Image Processing NSIP-03, Grado, Italy, 8–11 June 2003. [Google Scholar]
- Jánosi, I.M.; Müller, R. Empirical mode decomposition and correlation properties of long daily ozone records. Phys. Rev. E 2005, 71, 056126. [Google Scholar] [CrossRef]
- Carbone, F.; Landis, M.S.; Gencarelli, C.N.; Naccarato, A.; Sprovieri, F.; De Simone, F.; Hedgecock, I.M.; Pirrone, N. Sea surface temperature variation linked to elemental mercury concentrations measured on Mauna Loa. Geophys. Res. Lett. 2016, 43, 7751–7757. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Prentice Hall PTR Englewood Cliffs: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Huang, Y.X.; Schmitt, F.G.; Lu, Z.M.; Liu, Y.L. An amplitude-frequency study of turbulent scaling intermittency using Empirical Mode Decomposition and Hilbert Spectral Analysis. EPL Europhys. Lett. 2008, 84, 40010. [Google Scholar] [CrossRef]
- Huang, Y.X.; Schmitt, F.G.; Lu, Z.M.; Fougairolles, P.; Gagne, Y.; Liu, Y.L. Second-order structure function in fully developed turbulence. Phys. Rev. E 2010, 82, 026319. [Google Scholar] [CrossRef] [PubMed]
- Carbone, F.; Gencarelli, C.N.; Hedgecock, I.M. Lagrangian statistics of mesoscale turbulence in a natural environment: The Agulhas return current. Phys. Rev. E 2016, 94, 063101. [Google Scholar] [CrossRef] [PubMed]
- Carbone, F.; Alberti, T.; Sorriso-Valvo, L.; Telloni, D.; Sprovieri, F.; Pirrone, N. Scale-Dependent Turbulent Dynamics and Phase-Space Behavior of the Stable Atmospheric Boundary Layer. Atmosphere 2020, 11, 428. [Google Scholar] [CrossRef]
- Carbone, F.; Yoshida, H.; Suzuki, S.; Fujii, A.; Strangi, G.; Versace, C.; Ozaki, M. Clustering of elastic energy due to electrohydrodynamics instabilities in nematic liquid crystals. EPL Europhys. Lett. 2010, 89, 46004. [Google Scholar] [CrossRef]
- Sorriso-Valvo, L.; Carbone, F.; Leonardis, E.; Chen, C.H.; Šafránková, J.; Němeček, Z. Multifractal analysis of high resolution solar wind proton density measurements. Adv. Space Res. 2017, 59, 1642–1651. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. A Math. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Flandrin, P.; Goncalves, P. Empirical mode decomposition as data-driven wavelet-like expansions. Int. J. Wavelets Multiresolution Inf. Process. 2004, 1, 477–496. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, S.S.P. (Eds.) The Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2005. [Google Scholar]
- Carbone, F.; Sorriso-Valvo, L.; Alberti, T.; Lepreti, F.; Chen, C.H.K.; Němeček, Z.; Šafránková, J. Arbitrary-order Hilbert Spectral Analysis and Intermittency in Solar Wind Density Fluctuations. Astrophys. J. 2018, 859, 27. [Google Scholar] [CrossRef]
- Carbone, F.; Telloni, D.; Bruno, A.G.; Hedgecock, I.M.; De Simone, F.; Sprovieri, F.; Sorriso-Valvo, L.; Pirrone, N. Scaling Properties of Atmospheric Wind Speed in Mesoscale Range. Atmosphere 2019, 10, 611. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. CR Acad. Sci. URSS 1941, 30, 301–305. [Google Scholar]
- Frisch, U. (Ed.) Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge UK, 1995. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R. A New View of Nonlinear Water Waves: The Hilbert Spectrum1. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Huang, N.E.; Chen, X.; Lo, M.T.; Wu, Z. On Hilbert Spectral Representation: A True Time-Frequency Representation for Nonlinear and Nonstationary Data. Adv. Adapt. Data Anal. 2011, 3, 63–93. [Google Scholar] [CrossRef]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics: Mechanics of Turbulence; Dover: New York, NY, USA, 2007. [Google Scholar]
- Bradley, E.; Robert, J.T. An Introduction to the Bootstrap (Chapman & Hall CRC Monographs on Statistics & Applied Probability), 1st ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 1994. [Google Scholar]
- Boos, D.; Stefanski, L. Efron’s bootstrap. Significance 2010, 7, 186–188. [Google Scholar] [CrossRef]
- Mudelsee, M. Climate Time Series Analysis: Classical Statistical and Bootstrap Methods, 2nd ed.; Atmospheric and Oceanographic Sciences Library 51, Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Efron, B.; Rogosa, D.; Tibshirani, R. Resampling Methods of Estimation. In International Encyclopedia of the Social & Behavioral Sciences, 2nd ed.; Wright, J.D., Ed.; Elsevier: Oxford, UK, 2015; pp. 492–495. [Google Scholar] [CrossRef]
- Wu, C.F.J. Jackknife, Bootstrap and Other Resampling Methods in Regression Analysis. Ann. Statist. 1986, 14, 1261–1295. [Google Scholar] [CrossRef]
- Rao, J.N.K.; Wu, C.F.J. Resampling Inference with Complex Survey Data. J. Am. Stat. Assoc. 1988, 83, 231–241. [Google Scholar] [CrossRef]
- Dale, L.G.; William, L.; Ron, T. Does PLS Have Advantages for Small Sample Size or Non-Normal Data? MIS Q. 2012, 36, 981–1001. [Google Scholar]
- Wilcox, R.R. Fundamentals of Modern Statistical Methods: Substantially Improving Power and Accuracy, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Wang, X.; Tu, C.; He, J.; Marsch, E.; Wang, L.; Salem, C. The Spectral Features of Low-Amplitude Magnetic Fluctuations in the Solar Wind and Their Comparison with Moderate-Amplitude Fluctuations. Astrophys. J. 2015, 810, L21. [Google Scholar] [CrossRef]
- Wu, H.; Tu, C.; Wang, X.; He, J.; Yang, L.; Wang, L. Isotropic Scaling Features Measured Locally in the Solar Wind Turbulence with Stationary Background Field. Astrophys. J. 2020, 892, 138. [Google Scholar] [CrossRef]
- Benzi, R.; Ciliberto, S.; Tripiccione, R.; Baudet, C.; Massaioli, F.; Succi, S. Extended self-similarity in turbulent flows. Phys. Rev. E 1993, 48, R29–R32. [Google Scholar] [CrossRef] [PubMed]
- Arneodo, A.; Baudet, C.; Belin, F.; Benzi, R.; Castaing, B.; Chabaud, B.; Chavarria, R.; Ciliberto, S.; Camussi, R.; Chillà, F.; et al. Structure functions in turbulence, in various flow configurations, at Reynolds number between 30 and 5000, using extended self-similarity. EPL Europhys. Lett. 1996, 34, 411–416. [Google Scholar] [CrossRef]
- Paret, J.; Tabeling, P. Intermittency in the two-dimensional inverse cascade of energy: Experimental observations. Phys. Fluids 1998, 10, 3126. [Google Scholar] [CrossRef]
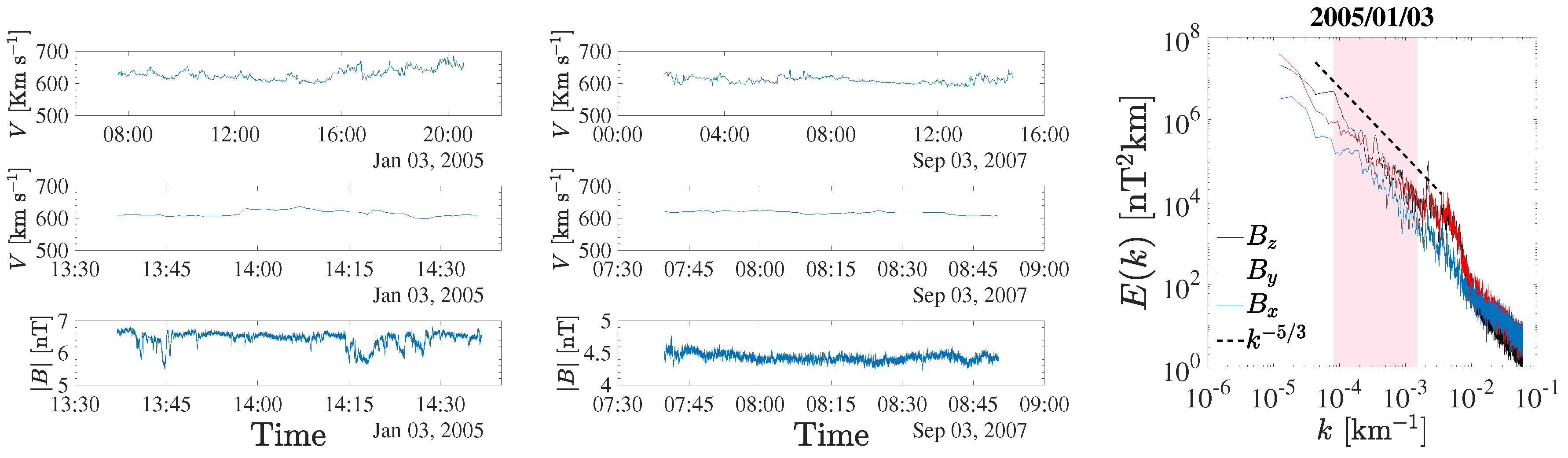
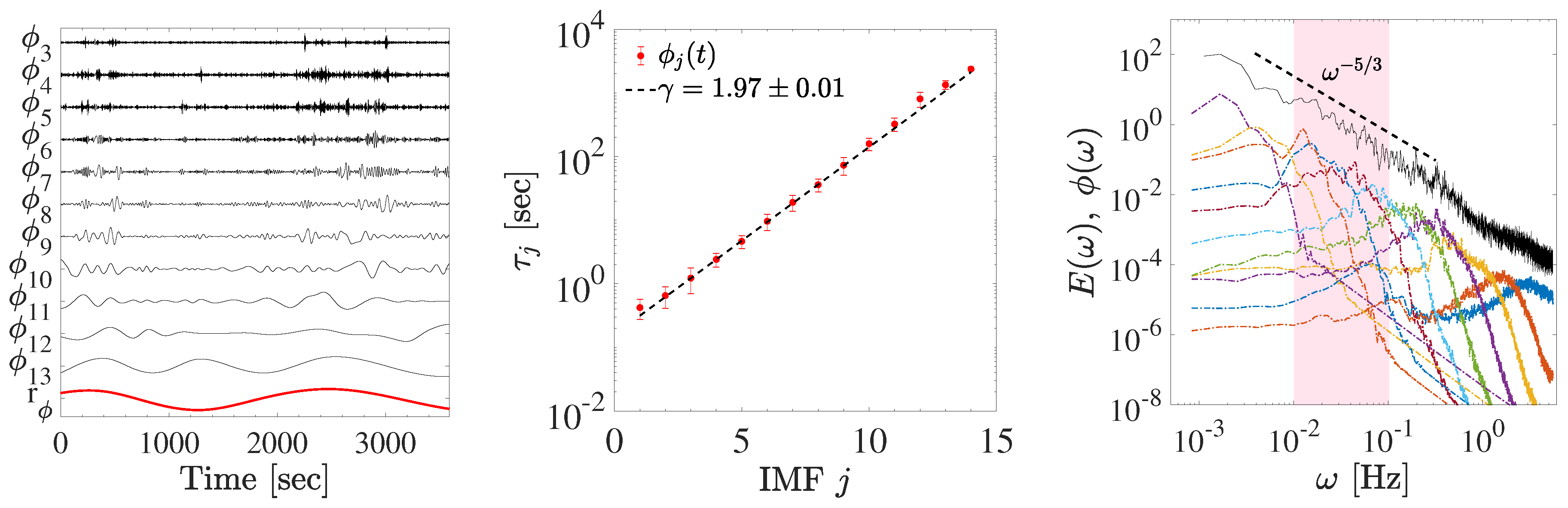
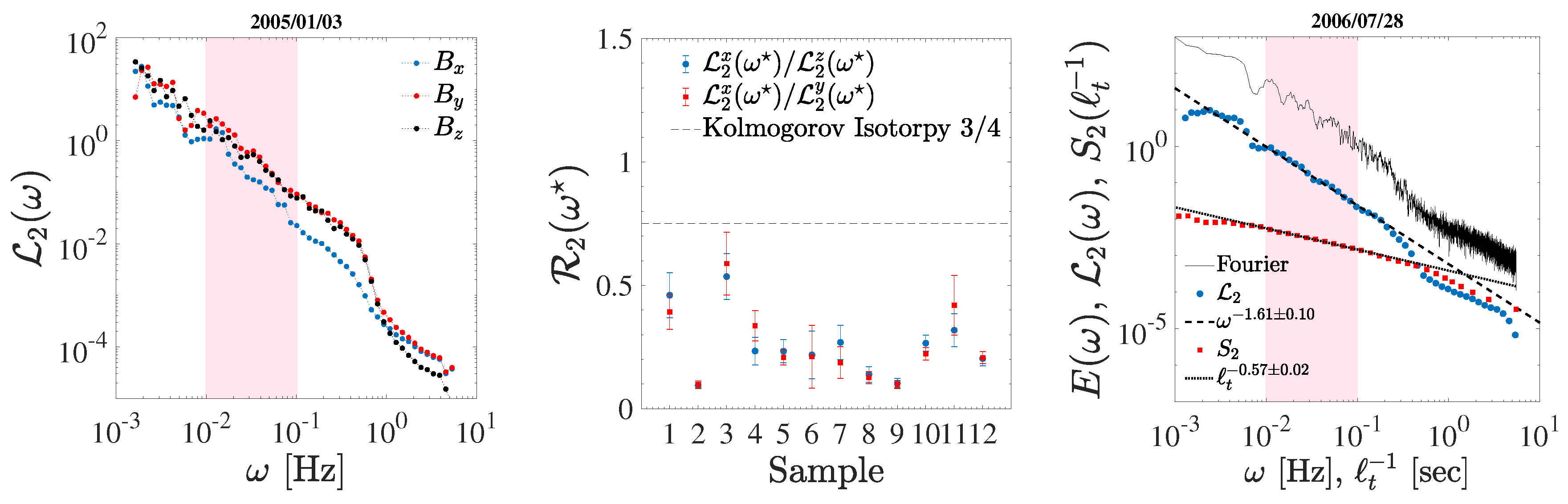
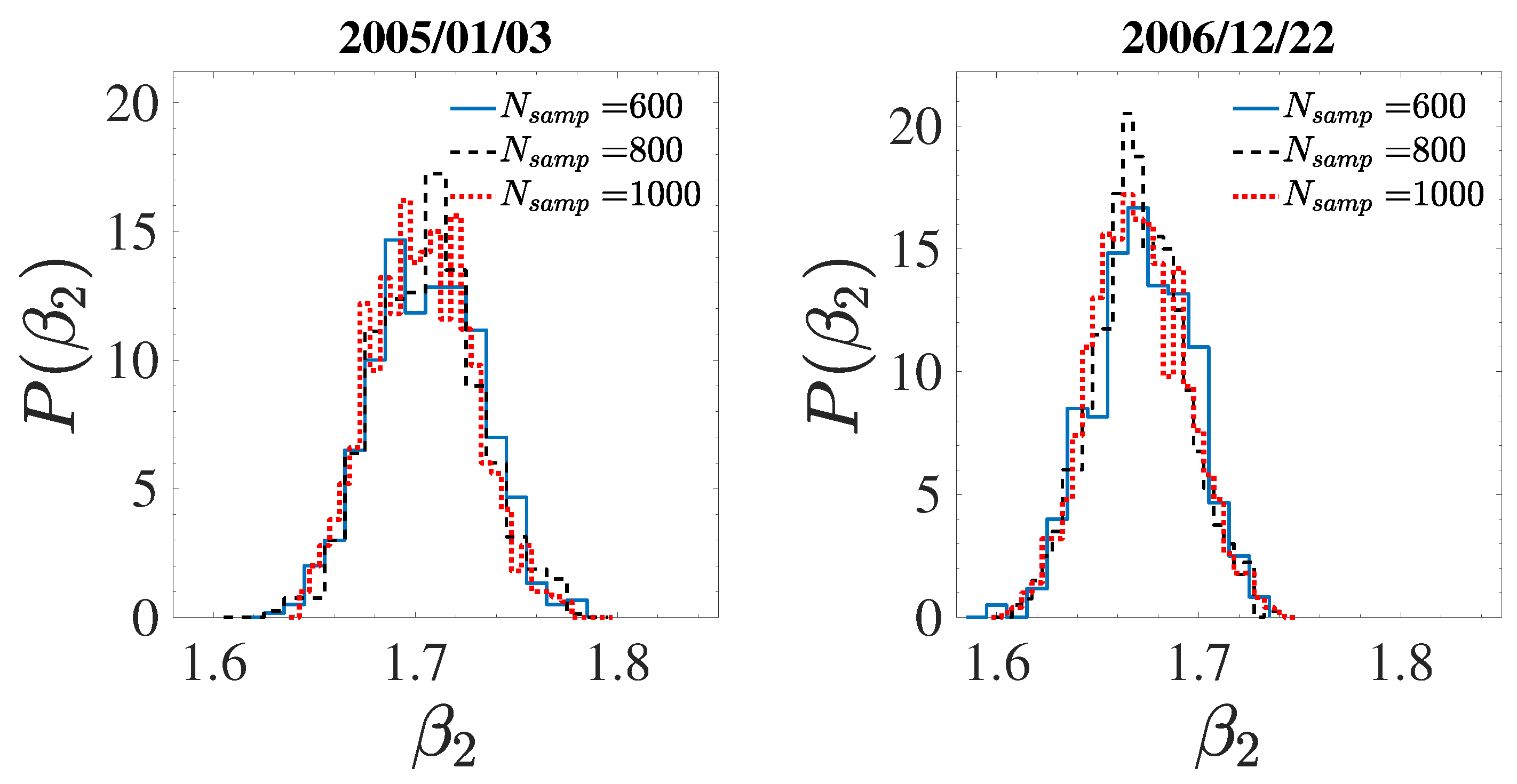
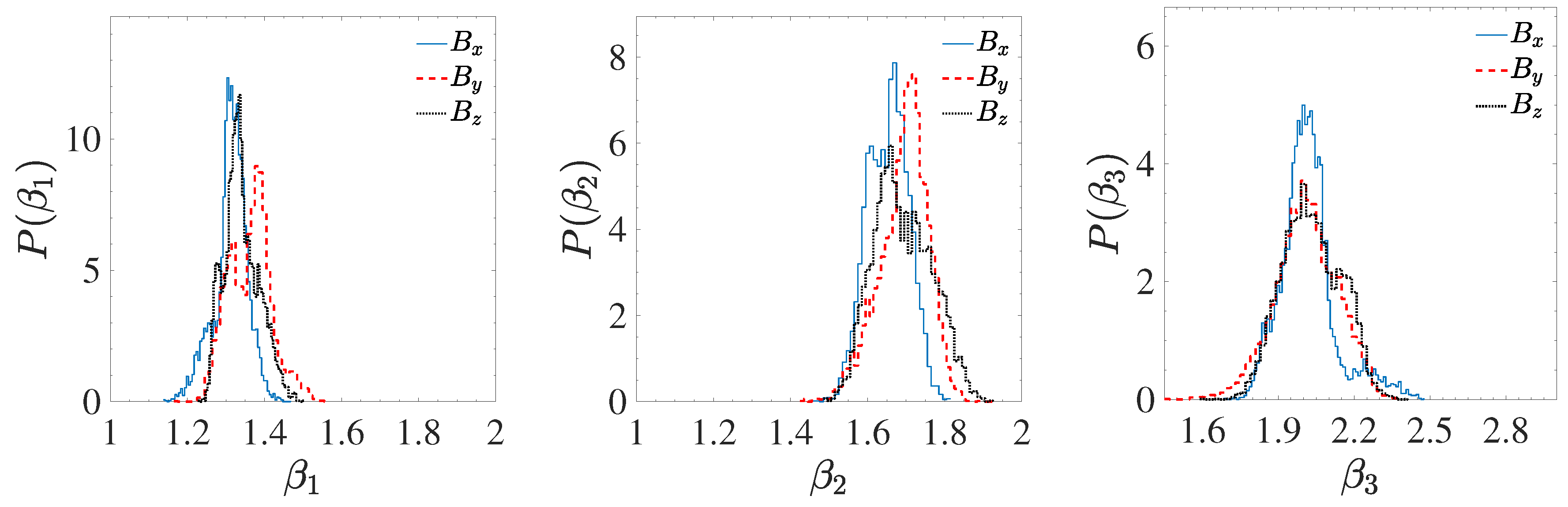
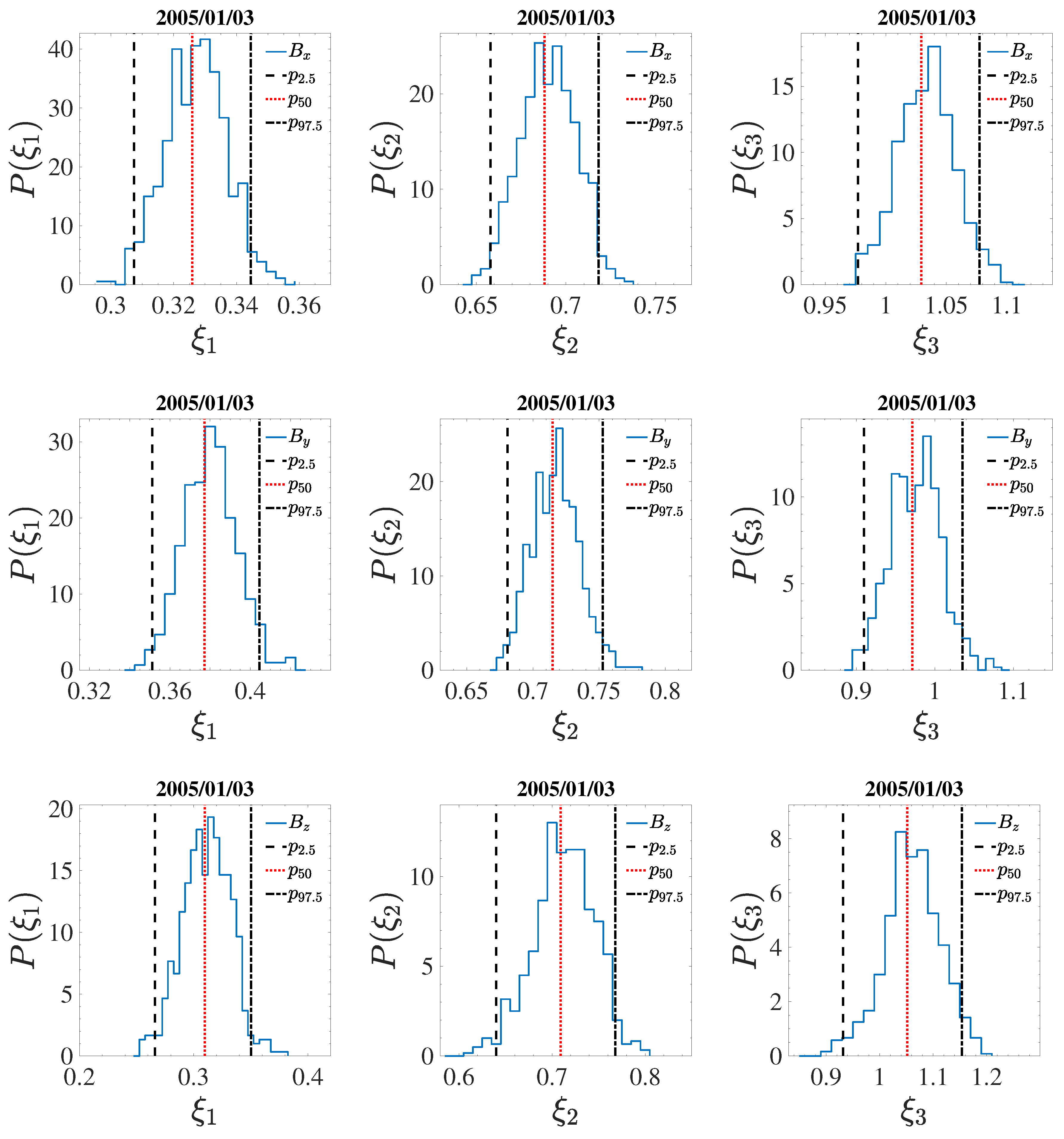
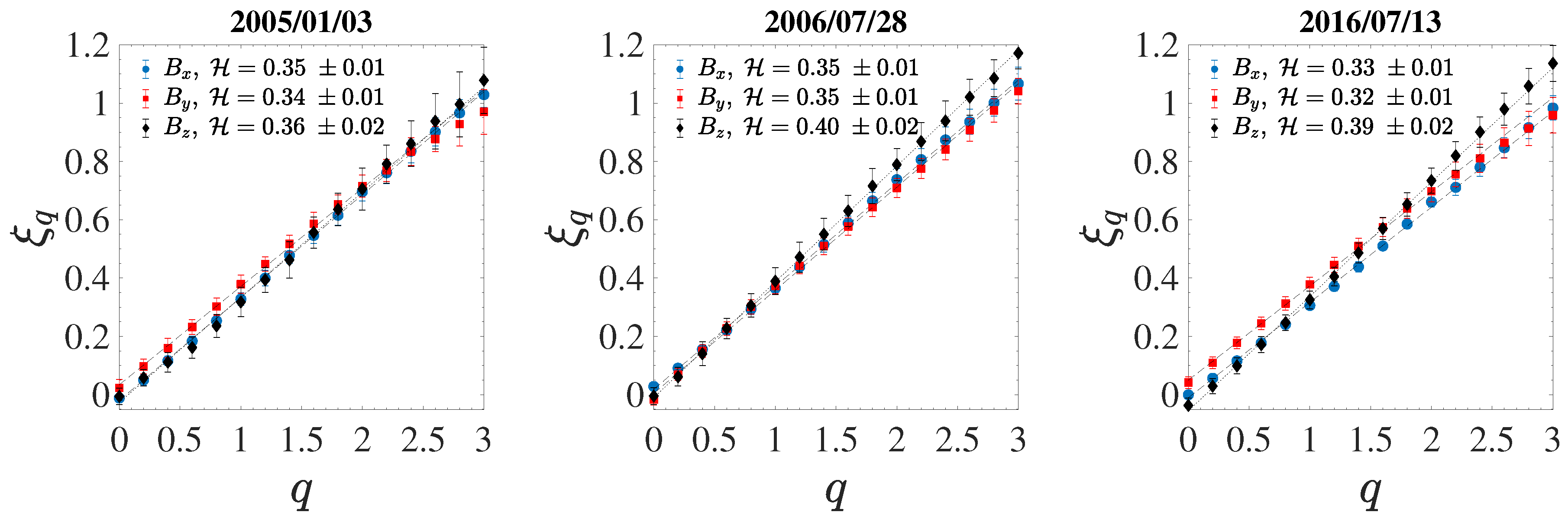
| Date | Start Time | End Time | [km s] | [nPa] | [%] | [deg] |
|---|---|---|---|---|---|---|
| 2005/01/03 | 13:36:56 | 14:36:43 | 631.7 | 0.026 | 22 | 10.07 |
| 2005/05/09 | 10:06:10 | 11:16:43 | 639.2 | 0.033 | 8 | 7.13 |
| 2006/06/18 | 14:02:36 | 15:13:07 | 579.6 | 0.014 | 23 | 13.20 |
| 2006/07/28 | 21:13:08 | 22:28:15 | 564.0 | 0.007 | 19 | 9.60 |
| 2006/12/23 | 23:33:56 | 00:33:43 | 640.9 | 0.017 | 7 | 9.75 |
| 2007/09/03 | 07:39:48 | 08:50:19 | 592.8 | 0.014 | 10 | 10.64 |
| 2007/10/27 | 00:24:16 | 01:51:39 | 576.9 | 0.028 | 16 | 9.63 |
| 2011/04/13 | 01:31:56 | 02:31:43 | 554.9 | 0.020 | 10 | 10.04 |
| 2014/06/09 | 01:06:48 | 02:55:39 | 588.8 | 0.016 | 18 | 10.41 |
| 2015/03/22 | 14:00:40 | 15:28:03 | 647.0 | 0.044 | 13 | 9.99 |
| 2016/07/13 | 01:14:48 | 02:17:39 | 575.4 | 0.021 | 21 | 9.67 |
| 2016/07/13 | 05:17:04 | 07:25:51 | 574.7 | 0.018 | 15 | 9.10 |
| Component | Order q | Percentile p | ||
|---|---|---|---|---|
| 1 | 1.21 | 1.31 | 1.39 | |
| 2 | 1.55 | 1.65 | 1.75 | |
| 3 | 1.83 | 2.01 | 2.31 | |
| 1 | 1.26 | 1.36 | 1.47 | |
| 2 | 1.55 | 1.70 | 1.80 | |
| 3 | 1.75 | 2.00 | 2.24 | |
| 1 | 1.26 | 1.33 | 1.44 | |
| 2 | 1.56 | 1.68 | 1.83 | |
| 3 | 1.81 | 2.02 | 2.24 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carbone, F.; Telloni, D.; Sorriso-Valvo, L.; Zank, G.; Zhao, L.; Adhikari, L.; Bruno, R. Statistical Analysis of Field-Aligned Alfvénic Turbulence and Intermittency in Fast Solar Wind. Universe 2020, 6, 116. https://doi.org/10.3390/universe6080116
Carbone F, Telloni D, Sorriso-Valvo L, Zank G, Zhao L, Adhikari L, Bruno R. Statistical Analysis of Field-Aligned Alfvénic Turbulence and Intermittency in Fast Solar Wind. Universe. 2020; 6(8):116. https://doi.org/10.3390/universe6080116
Chicago/Turabian StyleCarbone, Francesco, Daniele Telloni, Luca Sorriso-Valvo, Gary Zank, Lingling Zhao, Laxman Adhikari, and Roberto Bruno. 2020. "Statistical Analysis of Field-Aligned Alfvénic Turbulence and Intermittency in Fast Solar Wind" Universe 6, no. 8: 116. https://doi.org/10.3390/universe6080116
APA StyleCarbone, F., Telloni, D., Sorriso-Valvo, L., Zank, G., Zhao, L., Adhikari, L., & Bruno, R. (2020). Statistical Analysis of Field-Aligned Alfvénic Turbulence and Intermittency in Fast Solar Wind. Universe, 6(8), 116. https://doi.org/10.3390/universe6080116







