Approximate Analytical Periodic Solutions to the Restricted Three-Body Problem with Perturbation, Oblateness, Radiation and Varying Mass
Abstract
1. Introduction
2. Equations of Motion
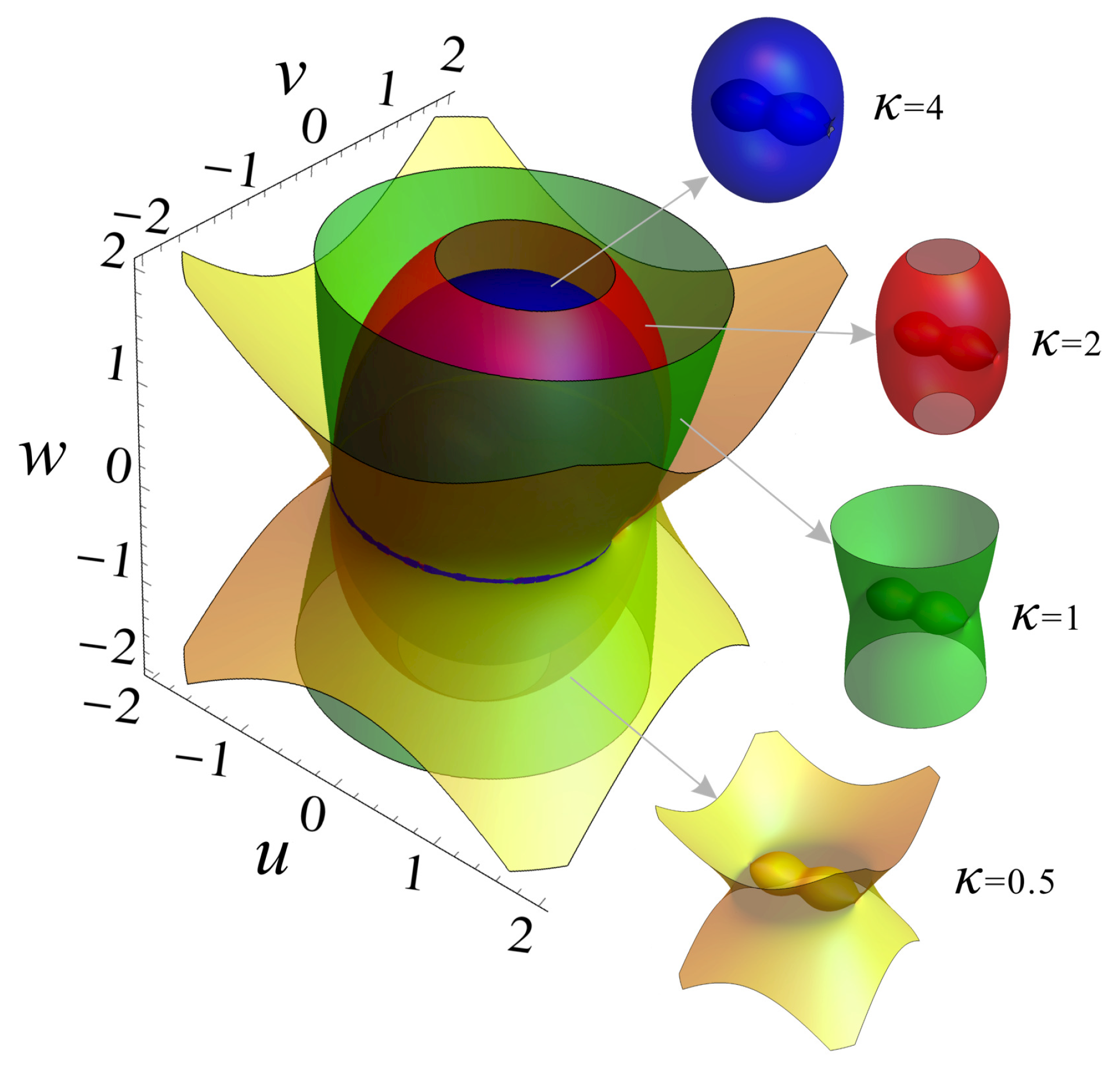
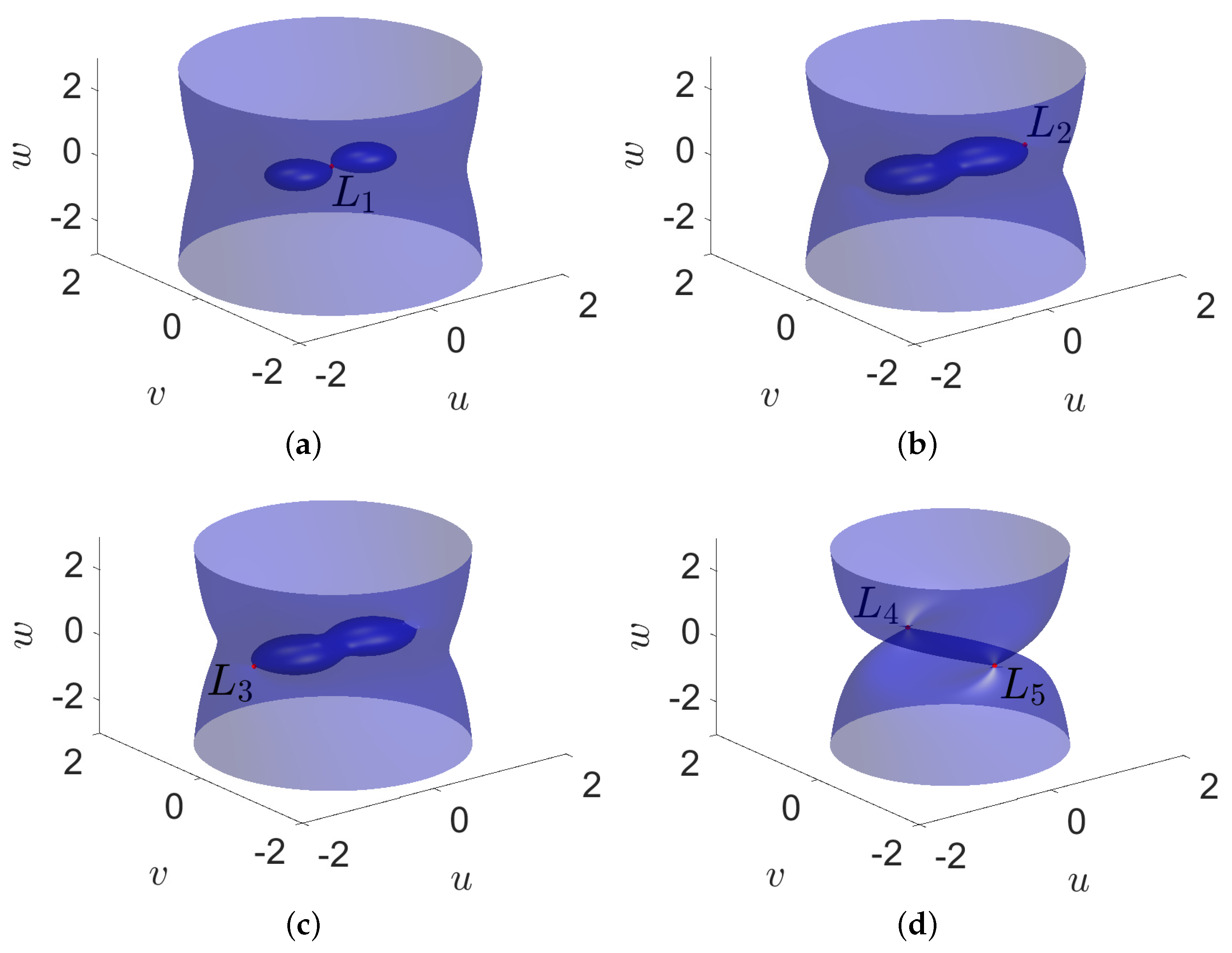
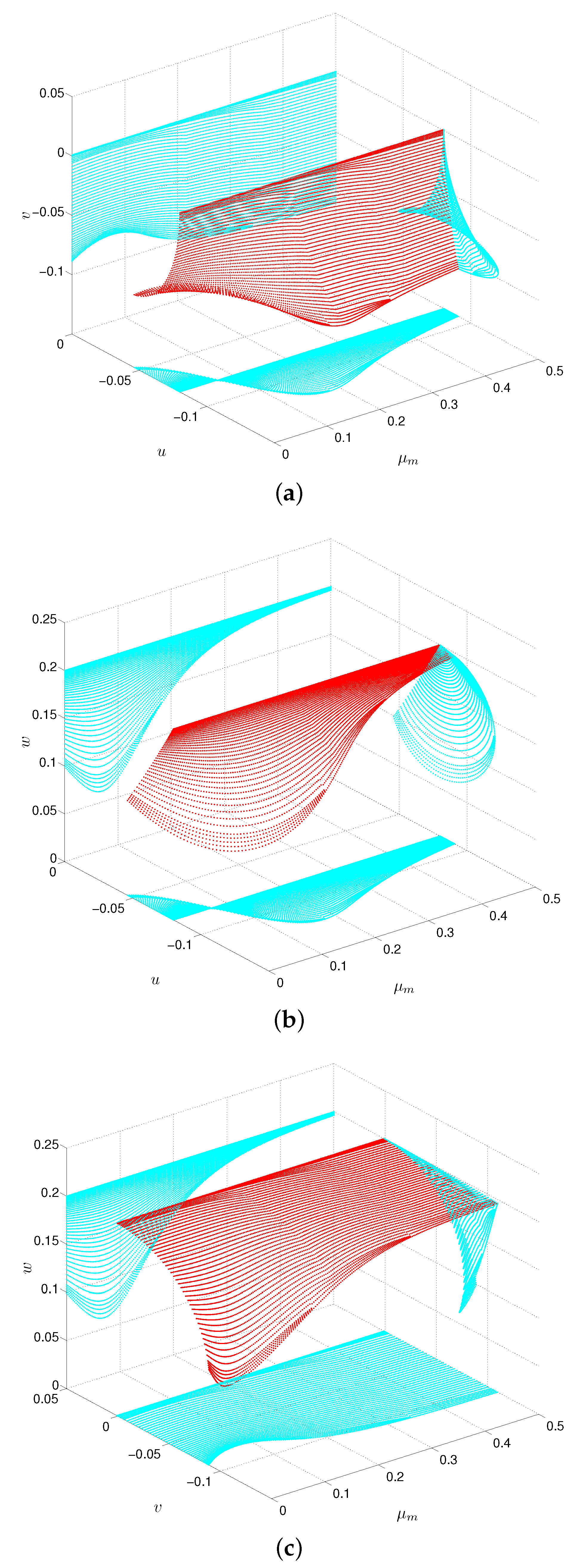
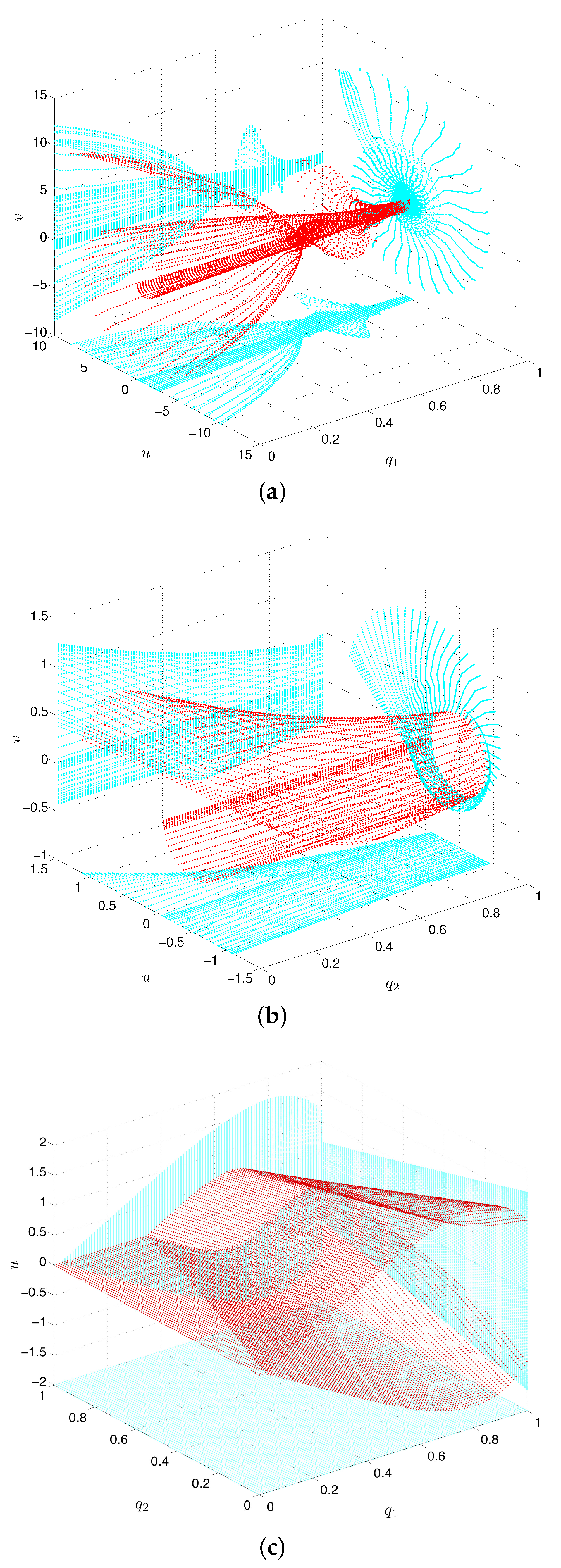
3. Zero Velocity Surfaces and Curves
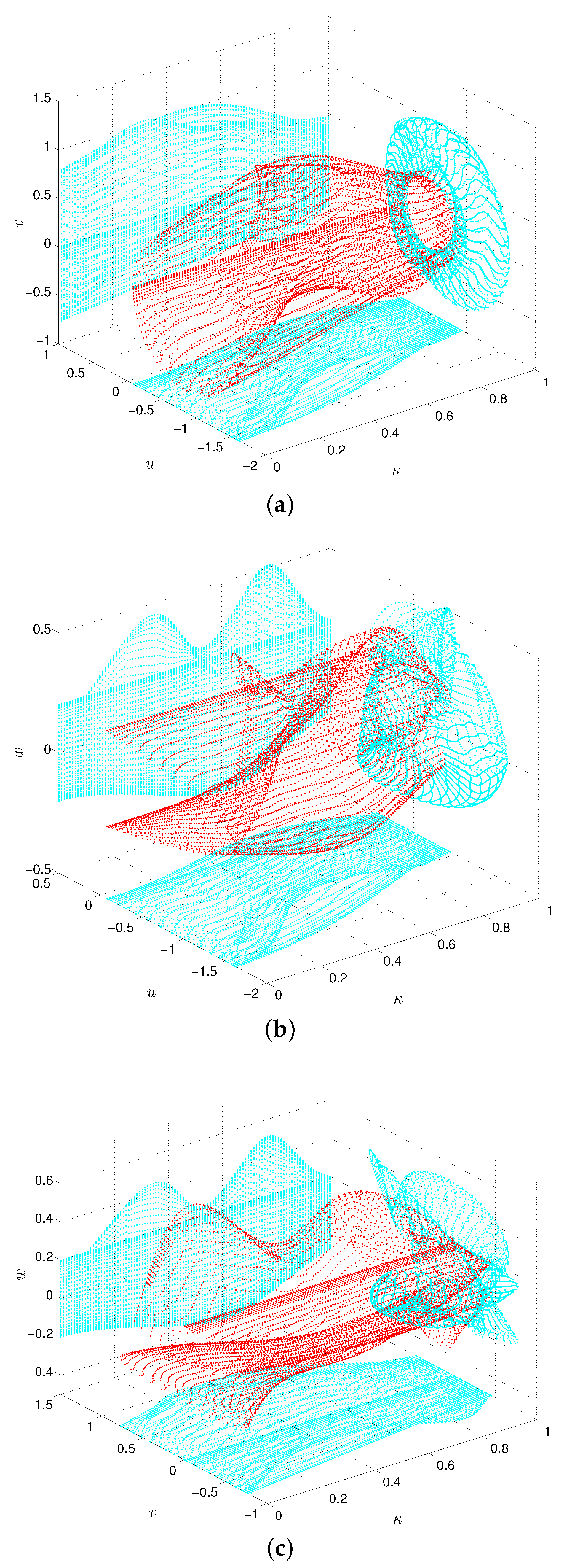
4. Bifurcation Analysis
5. Periodic Solutions near the Collinear Libration Points
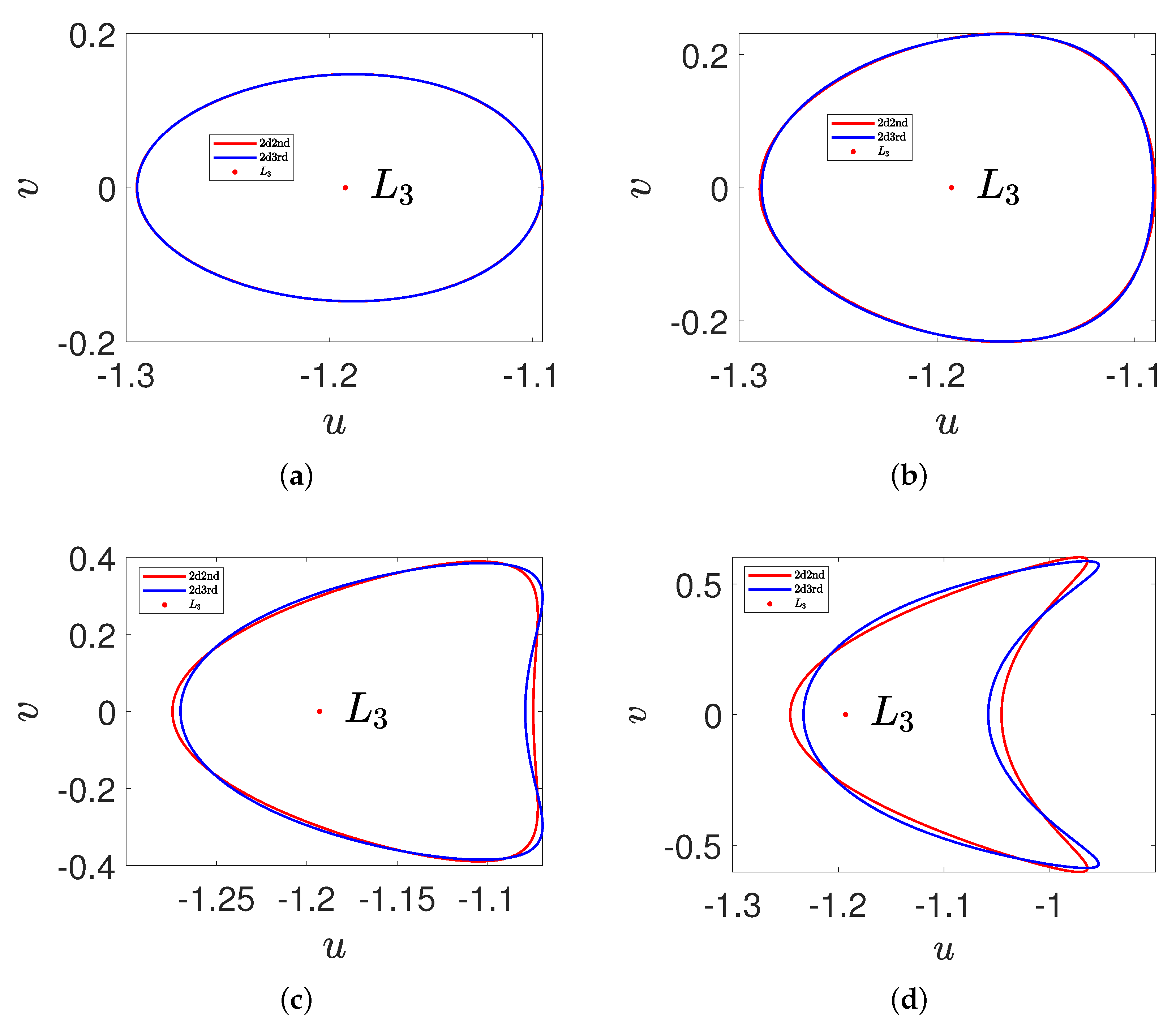
5.1. Expansion of Two-Dimensional Dynamic Equations
Two-Dimensional Periodic Solutions
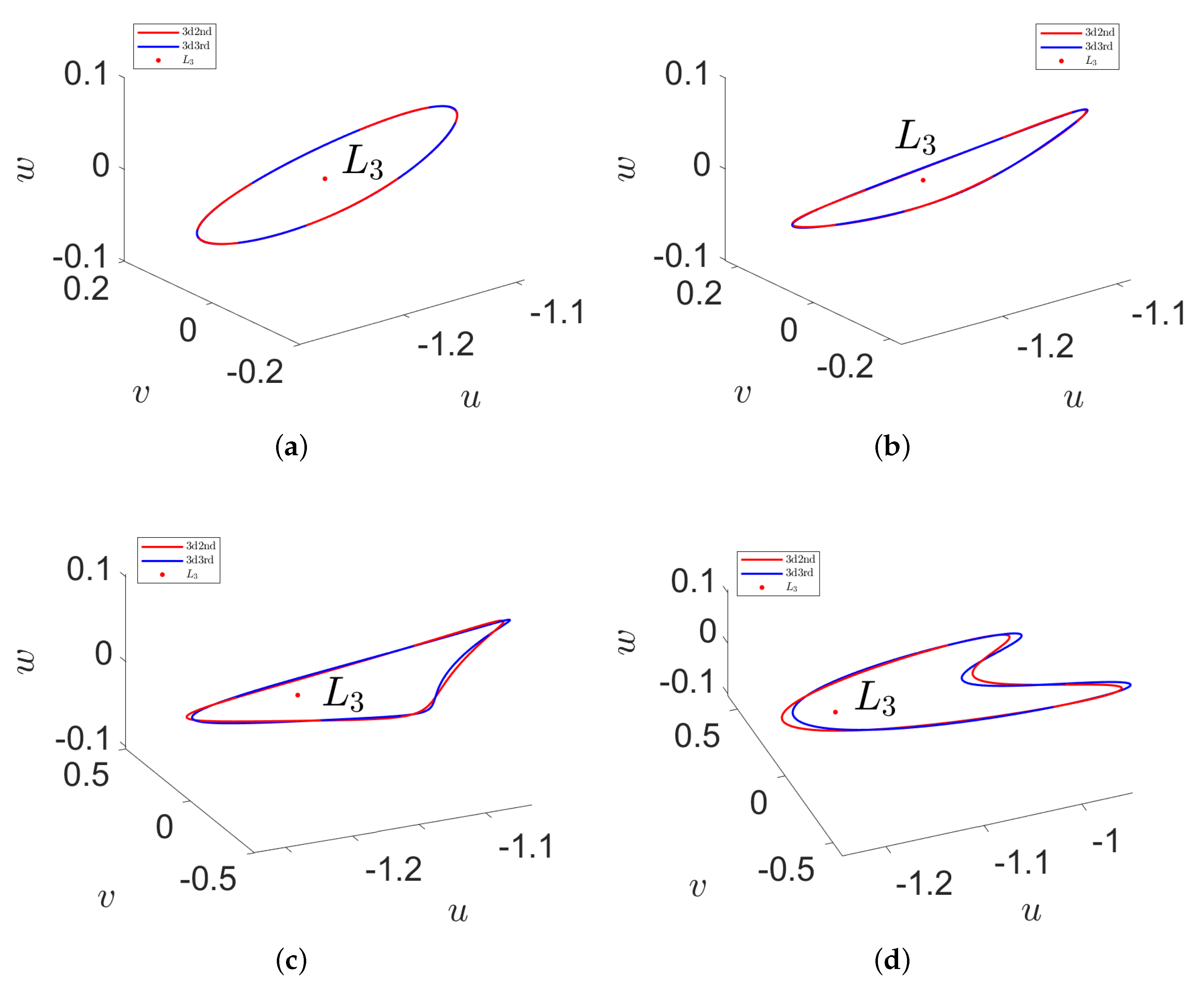
5.2. Expansion of Three-Dimensional Dynamic Equations
Three-Dimensional Periodic Solutions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Marchal, C. The Three-Body Problem; Elsevier Science: New York, NY, USA, 1990. [Google Scholar]
- Ioka, K.; Chiba, T.; Tanaka, T.; Nakamura, T. Black hole binary formation in the expanding universe: Three body problem approximation. Phys. Rev. D 1998, 58, 063003. [Google Scholar] [CrossRef]
- Nakamura, T.; Sasaki, M.; Tanaka, T.; Thorne, K.S. Gravitational waves from coalescing black hole MACHO binaries. Astrophys. J. Lett. 1997, 487, L139. [Google Scholar] [CrossRef]
- Zhou, T.Y.; Cao, W.G.; Xie, Y. Collinear solution to the three-body problem under a scalar-tensor gravity. Phys. Rev. D 2016, 93, 064065. [Google Scholar] [CrossRef]
- Lindner, J.F.; Roseberry, M.I.; Shai, D.E.; Harmon, N.J.; Olaksen, K.D. Precession and chaos in the classical two-body problem in a spherical universe. Int. J. Bifurc. Chaos 2008, 18, 455–464. [Google Scholar] [CrossRef]
- Gao, F.B.; Wang, R.F. Bifurcation analysis and periodic solutions of the HD 191408 system with triaxial and radiative perturbations. Universe 2020, 6, 35. [Google Scholar] [CrossRef]
- Beletsky, V.V. Generalized restricted circular three-body problem as a model for dynamics of binary asteroids. Cosm. Res. 2007, 45, 408–416. [Google Scholar] [CrossRef]
- Hou, X.Y.; Xin, X.S.; Feng, J.L. Forced motions around triangular libration points by solar radiation pressure in a binary asteroid system. Astrodynamics 2020, 4, 17–30. [Google Scholar] [CrossRef]
- Braaten, E.; Kang, D.; Laha, R. Production of dark-matter bound states in the early universe by three-body recombination. J. High Energy Phys. 2018, 2018, 84. [Google Scholar] [CrossRef]
- Trani, A.A.; Fujii, M.S.; Spera, M. The Keplerian three-body encounter. I. Insights on the origin of the S-stars and the G-objects in the galactic center. Astrophys. J. 2019, 875, 42. [Google Scholar] [CrossRef]
- Muzzio, J.C.; Wachlin, F.C.; Carpintero, D.D. Regular and chaotic motion in a restricted three-body problem of astrophysical interest. Int. Astron. Union Colloq. 2000, 174, 281–285. [Google Scholar] [CrossRef]
- Logoteta, D.; Bombaci, I. Constraints on microscopic and phenomenological equations of state of dense matter from GW170817. Universe 2019, 5, 204. [Google Scholar] [CrossRef]
- Fahn, M.J.; Giesel, K.; Kobler, M. Dynamical properties of the Mukhanov-Sasaki Hamiltonian in the context of adiabatic vacua and the Lewis-Riesenfeld invariant. Universe 2019, 5, 170. [Google Scholar] [CrossRef]
- Gao, F.B.; Zhang, W. A study on periodic solutions for the circular restricted three-body problem. Astron. J. 2014, 148, 116. [Google Scholar] [CrossRef]
- Alshaery, A.A.; Abouelmagd, E.I. Analysis of the spatial quantized three-body problem. Results Phys. 2020, 17, 103067. [Google Scholar] [CrossRef]
- Zotos, E.E.; Chen, W.; Abouelmagd, E.I.; Han, H.T. Basins of convergence of equilibrium points in the restricted three-body problem with modified gravitational potential. Chaos Solitons Fractals 2020, 134, 109704. [Google Scholar] [CrossRef]
- Alzahrani, F.; Abouelmagd, E.I.; Guirao, J.L.G.; Hobiny, A. On the libration collinear points in the restricted three-body problem. Open Phys. 2017, 15, 58–67. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Guirao, J.L.G.; Llibre, J. Periodic orbits for the perturbed planar circular restricted 3-body problem. Discret. Contin. Dyn. Syst.-Ser. B 2019, 24, 1007–1020. [Google Scholar] [CrossRef]
- Selim, H.H.; Guirao, J.L.G.; Abouelmagd, E.I. Libration points in the restricted three-body problem: Euler angles, existence and stability. Discret. Contin. Dyn. Syst.-Ser. B 2019, 12, 703–710. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Mostafa, A.; Guirao, J.L.G. A first order automated lie transform. Int. J. Bifurc. Chaos 2015, 25, 1540026. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Asiri, H.M.; Sharaf, M.A. The effect of oblateness in the perturbed restricted three-body problem. Meccanica 2013, 48, 2479–2490. [Google Scholar] [CrossRef]
- Pathak, N.; Thomas, V.O.; Abouelmagd, E.I. The perturbed photogravitational restricted three-body problem: Analysis of resonant periodic orbits. Discret. Contin. Dyn. Syst.-Ser. B 2019, 12, 849–875. [Google Scholar] [CrossRef]
- Niederman, L.; Pousse, A.; Robutel, P. On the co-orbital motion in the three-body problem: Existence of quasi-periodic horseshoe-shaped orbits. Commun. Math. Phys. 2020, 377, 551–612. [Google Scholar] [CrossRef]
- Koon, W.S.; Lo, M.W.; Marsden, J.E.; Ross, S.D. Dynamical Systems, the Three-Body Problem and Space Mission Design; Marsden Books: Wellington, New Zealand, 2011; ISBN 978-0-615-24095-4. [Google Scholar]
- Qian, Y.J.; Yang, X.D.; Yang, L.Y.; Zhang, W. Approximate analytical methodology for the restricted three-body and four-body models based on polynomial series. Int. J. Aerosp. Eng. 2016, 2016, 9747289. [Google Scholar] [CrossRef]
- Pathak, N.; Abouelmagd, E.I.; Thomas, V.O. On higher order resonant periodic orbits in the photo-gravitational planar restricted three-body problem with oblateness. J. Astronaut. Sci. 2019, 66, 475–505. [Google Scholar] [CrossRef]
- Hénon, M. Generating Families in the Restricted Three-Body Problem; Springer: New York, NY, USA, 1997. [Google Scholar]
- Chenciner, A.; Montgomery, R. A remarkable periodic solution of the three-body problem in the case of equal masses. Ann. Math. 2000, 152, 881–901. [Google Scholar] [CrossRef]
- Šuvakov, M.; Dmitrašinović, V. Three classes of Newtonian three-body planar periodic solutions. Phys. Rev. Lett. 2013, 110, 114301. [Google Scholar] [CrossRef]
- Janković, M.R.; Dmitrašinović, V.; Šuvakov, M. A guide to hunting periodic three-body orbits with non-vanishing angular momentum. Comput. Phys. Commun. 2020, 250, 107052. [Google Scholar] [CrossRef]
- Li, X.M.; Liao, S.J. More than six hundred new families of Newtonian periodic planar collisionless three-body orbits. Sci. China Phys. Mech. Astron. 2017, 60, 129511. [Google Scholar] [CrossRef]
- Kalantonis, V.S. Numerical investigation for periodic solutions in the Hill three-body problem. Universe 2020, 6, 72. [Google Scholar] [CrossRef]
- Singh, J. Photogravitational restricted three-body problem with variable mass. Indian Indian J. Pure Appl. Math. 2003, 34, 335–341. [Google Scholar]
- Singh, J.; Leke, O. Stability of the photogravitational restricted three-body problem with variable masses. Astrophys. Space Sci. 2010, 326, 305–314. [Google Scholar] [CrossRef]
- Singh, J.; Leke, O. Equilibrium points and stability in the restricted three-body problem with oblateness and variable masses. Astrophys. Space Sci. 2012, 340, 27–41. [Google Scholar] [CrossRef]
- Singh, J.; Leke, O. Effect of oblateness, perturbations, radiation and varying masses on the stability of equilibrium points in the restricted three-body problem. Astrophys. Space Sci. 2013, 344, 51–61. [Google Scholar] [CrossRef]
- Singh, J.; Haruna, S. Equilibrium points and stability under effect of radiation and perturbing forces in the restricted problem of three oblate bodies. Astrophys. Space Sci. 2014, 349, 107–116. [Google Scholar] [CrossRef]
- Singh, J.; Perdiou, A.E.; Gyegwe, J.M.; Kalantonis, V.S. Periodic orbits around the collinear equilibrium points for binary Sirius, Procyon, Luhman 16, α-Centuari and Luyten 726-8 systems: The spatial case. J. Phys. Commun. 2017, 1, 025008. [Google Scholar] [CrossRef]
- Singh, J.; Perdiou, A.E.; Gyegwe, J.M.; Perdios, E.A. Periodic solutions around the collinear equilibrium points in the perturbed restricted three-body problem with triaxial and radiating primaries for binary HD 191408, Kruger 60 and HD 155876 systems. Appl. Math. Comput. 2018, 325, 358–374. [Google Scholar] [CrossRef]
- Abdulraheem, A.R.; Singh, J. Combined effects of perturbations, radiation and oblateness on the periodic solutions in the restricted three-body problem. Astrophys. Space Sci. 2008, 317, 9–13. [Google Scholar] [CrossRef]
- Abdulraheem, A.R.; Singh, J. Combined effects of perturbations, radiation, and oblateness on the stability of equilibrium points in the restricted three-body problem. Astron. J. 2006, 131, 1880. [Google Scholar] [CrossRef]
- Singh, J.; Ishwar, B. Effect of perturbations on the location of equilibrium points in the restricted problem of three bodies with variable mass. Celestial Mech. 1984, 32, 297–305. [Google Scholar] [CrossRef]
- Bhatnagar, K.B.; Chawla, J.M. A study of the Lagrangian points in the photogravitational restricted three-body problem. Indian J. Pure Appl. Math. 1979, 10, 1443–1451. [Google Scholar]
- Szebehely, V. Stability of the points of equilibrium in the restricted problem. Astron. J. 1967, 72, 7–9. [Google Scholar] [CrossRef]
- Subba Rao, P.V.; Sharma, R.K. Perturbations of the critical mass in the restricted three-body problem. Astrophys. Space Sci. 1976, 42, L17–L18. [Google Scholar]
- Sharma, R.K. Perturbations of Lagrangian points in the restricted three-body problem. Indian J. Pure Appl. Math. 1975, 6, 1099–1102. [Google Scholar]
- Sharma, R.K.; Subba Rao, P.V. Stationary solutions and their characteristic exponents in the restricted three-body problem when the more massive primary is an oblate spheroid. Celestial Mech. 1976, 13, 137–149. [Google Scholar] [CrossRef]
- Abdullah, A.A.; Alhussain, Z.A.; Kellil, R. Locations and stability of the libration points in the CR3BP with perturbations. J. Math. Anal. 2017, 8, 131–144. [Google Scholar]
- Abouelmagd, E.I.; Alzahrani, F.; Hobiny, A.; Guirao, J.L.G.; Alhothuali, M. Periodic solutions around the collinear libration points. J. Nonlinear Sci. Appl. 2016, 9, 1716–1727. [Google Scholar] [CrossRef]
- Bekov, A.A. Particular solutions in the restricted collinear three body problem with variable masses. Soviet Astron. 1991, 35, 103–106. [Google Scholar]
- Zotos, E.E. How does the oblateness coefficient influence the nature of solutions in the restricted three-body problem? Astrophys. Space Sci. 2015, 358, 33. [Google Scholar] [CrossRef]
- Bhatnagar, K.B.; Hallan, P.P. Effect of perturbations in Coriolis and centrifugal forces on the stability of libration points in the restricted problem. Celestial Mech. 1978, 18, 105–112. [Google Scholar] [CrossRef]
- Subbarao, P.V.; Sharma, R.K. A note on the stability of the triangular points of equilibrium in the restricted three-body problem. Astron. Astrophys. 1975, 43, 381–383. [Google Scholar]
- Gyldén, H. Die bahnbewegungen in einem systeme von zwei Körpern in dem falle, dass die massen veränderungen unterworfen sind. Astron. Nachr. 1884, 109, 1–6. [Google Scholar] [CrossRef]
- Bekov, A.A. Periodic solutions of the Gylden-Meshcherskii problem. Astron. Rep. 1993, 37, 651–654. [Google Scholar]
- Bekov, A.A.; Momynov, S.B. Parametric solutions of the Gylden-Meshchersky problem. Int. J. Non-Linear Mech. 2019, 116, 195–199. [Google Scholar] [CrossRef]
- Meshcherskii, I.V. Works on the Mechanics of Bodies of Variable Mass; GITTL: Moscow, Russia, 1952; p. 205. (In Russian) [Google Scholar]
- Kalantonis, V.S.; Perdios, E.A.; Perdiou, A.E.; Vrahatis, M.N. Computing with certainty individual members of families of periodic orbits of a given period. Celestial Mech. Dyn. Astron. 2001, 80, 81–96. [Google Scholar] [CrossRef]
- Hu, H.Y. Applied Nonlinear Dynamics; China Aeronautical Industry Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
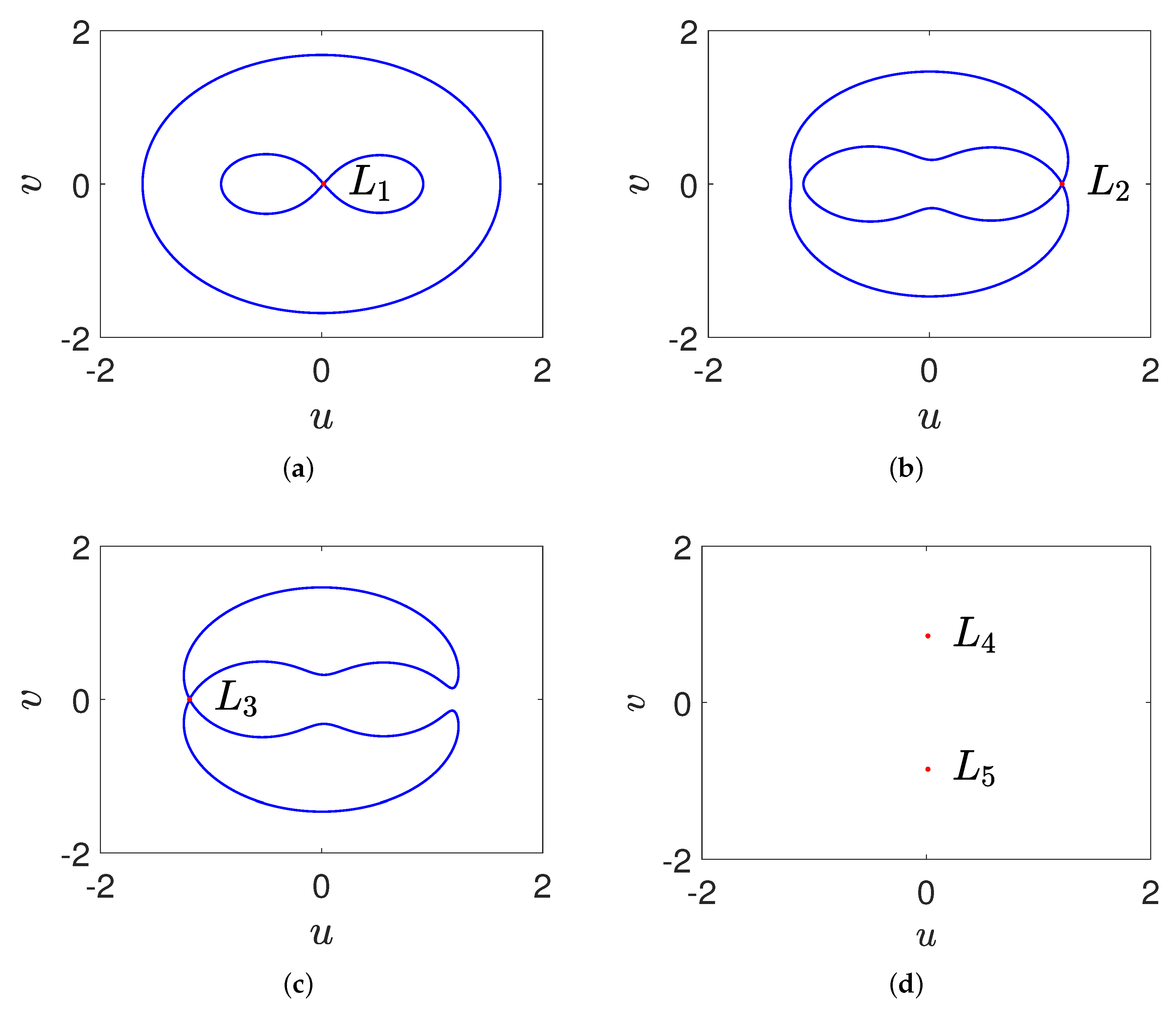


| Parameters | |||||||
| Values | 0.48785 | 0.9988 | 0.9985 | 0.024 | 0.02 | 1.001 | 1.002 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, F.; Wang, Y. Approximate Analytical Periodic Solutions to the Restricted Three-Body Problem with Perturbation, Oblateness, Radiation and Varying Mass. Universe 2020, 6, 110. https://doi.org/10.3390/universe6080110
Gao F, Wang Y. Approximate Analytical Periodic Solutions to the Restricted Three-Body Problem with Perturbation, Oblateness, Radiation and Varying Mass. Universe. 2020; 6(8):110. https://doi.org/10.3390/universe6080110
Chicago/Turabian StyleGao, Fabao, and Yongqing Wang. 2020. "Approximate Analytical Periodic Solutions to the Restricted Three-Body Problem with Perturbation, Oblateness, Radiation and Varying Mass" Universe 6, no. 8: 110. https://doi.org/10.3390/universe6080110
APA StyleGao, F., & Wang, Y. (2020). Approximate Analytical Periodic Solutions to the Restricted Three-Body Problem with Perturbation, Oblateness, Radiation and Varying Mass. Universe, 6(8), 110. https://doi.org/10.3390/universe6080110





